Graph-Bert: Only Attention is Needed for Learning Graph Representations

In the sequel of this paper, we will use the lower case letters (e.g., $x$) to represent scalars, lower case bold letters (e.g., $\mathbf{x}$) to denote column vectors, bold-face upper case letters (e.g., $\mathbf{X}$) to denote matrices, and upper case calligraphic letters (e.g., $\mathcal{X}$) to denote sets or high-order tensors. Given a matrix $\mathbf{X}$, we denote $\mathbf{X}(i,:)$ and $\mathbf{X}(:,j)$ as its $i_{th}$ row and $j_{th}$ column, respectively. The ($i_{th}$, $j_{th}$) entry of matrix $\mathbf{X}$ can be denoted as either $\mathbf{X}(i,j)$. We use $\mathbf{X}^{\top}$ and $\mathbf{x}^{\top}$ to represent the transpose of matrix $\mathbf{X}$ and vector $\mathbf{x}$. For vector $\mathbf{x}$, we represent its $L_{p}$-norm as $\left\|\mathbf{x}\right\|_{p}=(\sum_{i}|\mathbf{x}(i)|^{p})^{\frac{1}{p}}$. The Frobenius-norm of matrix $\mathbf{X}$ is represented as $\left\|\mathbf{X}\right\|_{F}=(\sum_{i,j}|\mathbf{X}(i,j)|^{2})^{\frac{1}{2}}$. The element-wise product of vectors $\mathbf{x}$ and $\mathbf{y}$ of the same dimension is represented as $\mathbf{x}\otimes\mathbf{y}$, whose concatenation is represented as $\mathbf{x}\sqcup\mathbf{y}$.

Prior to talking about the subgraph batching method, we would like to present the problem settings first. Formally, we can represent the input graph data as $G=(\mathcal{V},\mathcal{E},w,x,y)$, where $\mathcal{V}$ and $\mathcal{E}$ denote the sets of nodes and links in graph $G$, respectively. Mapping $w:\mathcal{E}\to\mathbbm{R}$ projects links to their weight; whereas mappings $x:\mathcal{V}\to\mathcal{X}$ and $y:\mathcal{V}\to\mathcal{Y}$ can project the nodes to their raw features and labels. The graph size can be represented by the number of involved nodes, i.e., $|\mathcal{V}|$. The above term defines a general graph concept. If the studied $G$ is unweighted, we will have $w(v_{i},v_{j})=1,\forall(v_{i},v_{j})\in\mathcal{E}$; whereas $\forall(v_{i},v_{j})\in\mathcal{V}\times\mathcal{V}\setminus\mathcal{E}$, we have $w(v_{i},v_{j})=0$. Notations $\mathcal{X}$ and $\mathcal{Y}$ denote feature space and label space, respectively. In this paper, we can simply represent $\mathcal{X}=\mathbbm{R}^{d_{x}}$ and $\mathcal{Y}=\mathbbm{R}^{d_{y}}$. For node $v_{i}$, we can also simplify its raw feature and label vector representations as $\mathbf{x}_{i}=x(v_{i})\in\mathbbm{R}^{d_{x}}$ and $\mathbf{y}_{i}=y(v_{i})\in\mathbbm{R}^{d_{y}}$. The Graph-Bert model pre-training doesn’t require any label supervision information actually, but partial of the labels will be used for the fine-tuning application task on node classification to be introduced later.

Instead of working on the complete graph $G$, Graph-Bert will be trained with linkless subgraph batches sampled from the input graph instead. It will effectively enable the learning of Graph-Bert to parallelize (even though we will not study parallel computing of Graph-Bert in this paper) on extremely large-sized graphs that the existing graph neural networks cannot handle. Different approaches can be adopted here to sample the subgraphs from the input graph as studied inZhang et al. (2018). However, to control the randomness involved in the sampling process, in this paper, we introduce the top-k intimacy sampling approach instead. Such a sampling algorithm works based on the graph intimacy matrix $\mathbf{S}\in\mathbbm{R}^{|\mathcal{V}|\times|\mathcal{V}|}$, where entry $\mathbf{S}(i,j)$ measures the intimacy score between nodes $v_{i}$ and $v_{j}$.

There exist different metrics to measure the intimacy scores among the nodes within the graph, e.g., Jaccard’s coefficienty Jaccard (1901), Adamic/Adar Adamic and Adar (2003), Katz Katz (1953). In this paper, we define matrix $\mathbf{S}$ based on the pagerank algorithm, which can be denoted as

$$\mathbf{S}=\alpha\cdot\left(\mathbf{I}-(1-\alpha)\cdot\bar{\mathbf{A}}\right)^{-1},$$

(1)

where factor $\alpha\in[0,1]$ (which is usually set as $0.15$). Term $\bar{\mathbf{A}}=\mathbf{A}\mathbf{D}^{-1}$ denotes the colum-normalized adjacency matrix. In its representation, $\mathbf{A}$ is the adjacency matrix of the input graph, and $\mathbf{D}$ is its corresponding diagonal matrix with $\mathbf{D}(i,i)=\sum_{j}\mathbf{A}(i,j)$ on its diagonal.

Formally, for any target node $v_{i}\in\mathcal{V}$ in the input graph, based on the intimacy matrix $\mathbf{S}$, we can define its learning context as follows:

We may need to add a remark: for all the nodes in $v_{i}$’ learning context $\Gamma(v_{i})$, they can cover both local neighbors of $v_{i}$ as well as the nodes which are far away. In this paper, we define the threshold $\theta_{i}$ as the $k_{th}$ entry of $\mbox{sorted}(\mathbf{S}(i,:))$ (with $v_{i}$ being excluded), i.e., $\Gamma(v_{i})$ covers the top-k intimate nodes of $v_{i}$ in graph $G$. Based on the node context concept, we can also represent the set of sampled graph batches for all the nodes as set $\mathcal{G}=\{g_{1},g_{2},\cdots,g_{|\mathcal{V}|}\}$, and $g_{i}$ denotes the subgraph sampled for $v_{i}$ (as the target node). Formally, $g_{i}$ can be represented as $g_{i}=(\mathcal{V}_{i},\emptyset)$, where the node set $\mathcal{V}_{i}=\{v_{i}\}\cup\Gamma(v_{i})$ covers both $v_{i}$ and its context nodes and the link set is null. For large-sized input graphs, set $\mathcal{G}$ can further be decomposed into several mini-batches, i.e., $\mathcal{B}\subseteq\mathcal{G}$, which will be fed to train the Graph-Bert model.

Different from image and text data, where the pixels and words/chars have their inherent orders, nodes in graphs are orderless. The Graph-Bert model to be learned in this paper doesn’t require any node orders of the input sampled subgraph actually. Meanwhile, to simplify the presentations, we still propose to serialize the input subgraph nodes into certain ordered list instead. Formally, for all the nodes $\mathcal{V}_{i}$ in the sampled linkless subgraph $g_{i}\in\mathcal{B}$, we can denote them as a node list $[v_{i},v_{i,1},\cdots,v_{i,k}]$, where $v_{i,j}$ will be placed ahead of $v_{i,m}$ if $\mathbf{S}(i,j)>\mathbf{S}(i,m),\forall v_{i,j},v_{i,m}\in\mathcal{V}_{i}$. For the remaining of this subsection, we will follow the identical node orders as indicated above by default to define their input vector embeddings.

The input vector embeddings to be fed to the graph-transformer model actually cover four parts: (1) raw feature vector embedding, (2) Weisfeiler-Lehman absolute role embedding, (3) intimacy based relative positional embedding, and (4) hop based relative distance embedding, respectively.

Based on the computed embedding vectors defined above, we will be able to aggregate them together to define the initial input vectors for nodes, e.g., $v_{j}$, in the subgraph $g_{i}$ as follows:

$$\mathbf{h}_{j}^{(0)}=\mbox{Aggregate}({\mathbf{e}}_{j}^{(x)},{\mathbf{e}}_{j}^{(r)},{\mathbf{e}}_{j}^{(p)},{\mathbf{e}}_{j}^{(d)}).$$

(6)

In this paper, we simply define the aggregation function as the vector summation. Furthermore, the initial input vectors for all the nodes in $g_{i}$ can organized into a matrix $\mathbf{H}^{(0)}=[\mathbf{h}_{i}^{(0)},\mathbf{h}_{i,1}^{(0)},\cdots,\mathbf{h}_{i,k}^{(0)}]^{\top}\in\mathbbm{R}^{(k+1)\times d_{h}}$. The graph-transformer based encoder to be introduced below will update the nodes’ representations iteratively with multiple layers ($D$ layers), and the output by the $l_{th}$ layer can be denoted as

	$\displaystyle\mathbf{H}^{(l)}$	$\displaystyle=\mbox{G-Transformer}\left(\mathbf{H}^{(l-1)}\right)$		(7)
		$\displaystyle=\mbox{softmax}\left(\frac{\mathbf{Q}\mathbf{K}^{\top}}{\sqrt{d_{h}}}\right)\mathbf{V}+\mbox{G-Res}\left(\mathbf{H}^{(l-1)},\mathbf{X}_{i}\right),$

where

$$\begin{cases}\mathbf{Q}&=\mathbf{H}^{(l-1)}\mathbf{W}_{Q}^{(l)},\\ \mathbf{K}&=\mathbf{H}^{(l-1)}\mathbf{W}_{K}^{(l)},\\ \mathbf{V}&=\mathbf{H}^{(l-1)}\mathbf{W}_{V}^{(l)}.\\ \end{cases}\vspace{-2pt}$$

(8)

In the above equations, $\mathbf{W}_{Q}^{(l)},\mathbf{W}_{K}^{(l)},\mathbf{W}_{K}^{(l)}\in\mathbbm{R}^{d_{h}\times d_{h}}$ denote the involved variables. To simplify the presentations in the paper, we assume nodes’ hidden vectors in different layers have the same length. Notation $\mbox{G-Res}\left(\mathbf{H}^{(l-1)},\mathbf{X}_{i}\right)$ represents the graph residual term introduced in Zhang and Meng (2019), and $\mathbf{X}_{i}\in\mathbbm{R}^{(k+1)\times d_{x}}$ is the raw features of all nodes in the subgraph $g_{i}$. Also different from conventional residual learning, we will add the residual terms computed for the target node $v_{i}$ to the hidden state vectors of all the nodes in the subgraph at each layer. Based on the graph-transformer function defined above, we can represent the representation learning process of Graph-Bert as follows:

$$\begin{cases}\vspace{5pt}\mathbf{H}^{(0)}&=[\mathbf{h}_{i}^{(0)},\mathbf{h}_{i,1}^{(0)},\cdots,\mathbf{h}_{i,k}^{(0)}]^{\top},\\ \vspace{5pt}\mathbf{H}^{(l)}&=\mbox{G-Transformer}\left(\mathbf{H}^{(l-1)}\right),\forall l\in\{1,2,\cdots,D\},\\ \mathbf{z}_{i}&=\mbox{Fusion}\left(\mathbf{H}^{(D)}\right).\end{cases}$$

(9)

Different from the application of conventional transformer model on NLP problems, which aims at learning the representations of all the input tokens. In this paper, we aim to apply the graph-transformer to get the representations of the target node only. In the above equation, function $\mbox{Fusion}\left(\cdot\right)$ will average the representations of all the nodes in input list, which defines the final state of the target $v_{i}$, i.e., $\mathbf{z}_{i}\in\mathbbm{R}^{d_{h}\times 1}$. Both vector $\mathbf{z}_{i}$ and matrix $\mathbf{H}^{(D)}$ will be outputted to the following functional component attached to Graph-Bert. Depending on the application tasks, the functional component and learning objective (i.e., the loss function) will be different. We will show more detailed information in the following section on Graph-Bert pre-training and fine-tuning.

The node raw attribute reconstruction task focuses on capturing the node attribute information in the learned representations, whereas the graph structure recovery task focuses more on the graph connection information instead.

In applying the learned Graph-Bert into new learning tasks, the learned graph representations can be either fed into the new tasks directly or with necessary adjustment, i.e., fine-tuning. In this part, we can take the node classification and graph clustering tasks as the examples, where graph clustering can use the learned representations directly but fine-tuning will be necessary for the node classification task.

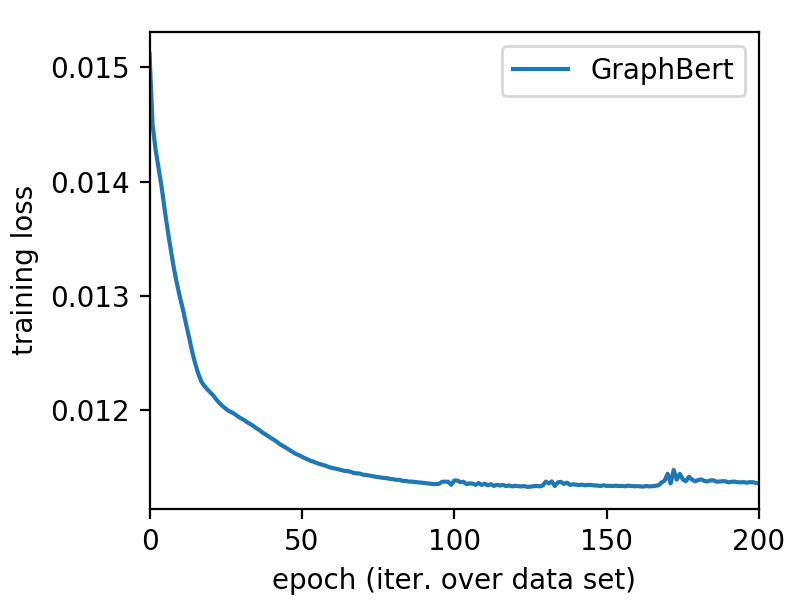
The graph benchmark datasets used in the experiments include Cora, Citeseer and Pubmed Yang et al. (2016), which are used in most of the recent state-of-the-art graph neural network research works Kipf and Welling (2016); Veličković et al. (2018); Zhang and Meng (2019). Based on the input graph data, we will first pre-compute the node intimacy scores, based on which subgraph batches will be sampled subject to the subgraph size $k\in\{1,2,\cdots,10,15,20,\cdots,50\}$. In addition, we will also pre-compute the node pairwise hop distance and WL node codes. By minimizing the node raw feature reconstruction loss and graph structure recovery loss, Graph-Bert can be effectively pre-trained, whose learned variables will be transferred to the follow-up node classification and graph clustering tasks with/without fine-tuning. In the experiments, we first pre-train Graph-Bert based on the node attribute reconstruction task with 200 epochs, then load and pre-train the same Graph-Bert model again based on the graph structure recovery task with another 200 epochs. In Figure 2, we show the learning performance of Graph-Bert on node attribute reconstruction and graph recovery, which converges very fast on both of these tasks.

Graph-Bert is a powerful mode and it can be applied to address various graph learning tasks in the standalone mode. To show the effectiveness of Graph-Bert, we will first provide the experimental results of Graph-Bert on the node classification task without pre-training here, whereas the pre-trained Graph-Bert based node classification results will be provided in Section 5.4 in more detail. Here, we will follow the identical train/validation/test set partitions used in the existing graph neural network papers Yang et al. (2016) for fair comparisons.

In Table 5, we show the learning results of Graph-Bert on graph clustering without any pre-training on the three datasets. Formally, the clustering component used in Graph-Bert is KMeans, which takes the nodes’ raw feature vectors as the input. The results are evaluated with several different metrics shown above.

The results reported in the previous subsections are all based on the Graph-Bert without pre-training actually. Here, we will provide the experimental results on Graph-Bert with pre-training to show their differences. According to the experiments, given enough training epochs, models with/without pre-training can both converge to very good learning results. Therefore, to highlight the differences, we will only use $\frac{1}{5}$ of the normal training epochs here for fine-tuning Graph-Bert, and the results are provided in Table 6. We also show the performance of Graph-Bert without pre-training here for comparison.

According to the scores, for most of the datasets, pre-training do give Graph-Bert a good initial state, which helps the model achieve better performance with only a very small number of fine-tuning epochs. On Cora and Citeseer, pre-training helps both the node classification and graph clustering tasks. Meanwhile, for Pubmed, pre-training helps node classification but degrades the results on graph clustering. Also pre-training with both node classification and graph recovery help the model to capture more information from the graph data, which also lead to higher scores than the models with single pre-training tasks.