Graph-based Model for Beam Management
in Mmwave Vehicular Networks
Abstract
Mmwave bands are being widely touted as a very promising option for future 5G networks, especially in enabling such networks to meet highly demanding rate requirements. Accordingly, the usage of these bands is also receiving an increasing interest in the context of 5G vehicular networks, where it is expected that connected cars will soon need to transmit and receive large amounts of data. Mmwave communications, however, require the link to be established using narrow directed beams, to overcome harsh propagation conditions. The advanced antenna systems enabling this also allow for a complex beam design at the base station, where multiple beams of different widths can be set up. In this work, we focus on beam management in an urban vehicular network, using a graph-based approach to model the system characteristics and the existing constraints. In particular, unlike previous work, we formulate the beam design problem as a maximum-weight matching problem on a bipartite graph with conflicts, and then we solve it using an efficient heuristic algorithm. Our results show that our approach easily outperforms advanced methods based on clustering algorithms.
I Introduction
Due to the sheer amount of bandwidth available in millimeter-wave (mmwave) bands, they are becoming an increasingly attractive choice for various types of wireless networks. They are already included in the standardization efforts for 5G [1, 2], and, as such, they are set to become an essential resource for 5G-enabled vehicular networks. Indeed, the increasing need for on-board high-definition maps, their real-time updates, as well as the data generated by the vehicles themselves, make conncted cars prime consumers and producers of network traffic, which can be catered to only by a substantial amount of bandwidth, readily available in mmwaves.
However, due to the high operating frequency, these bands are known to experience harsh propagation conditions, and are highly susceptible to blockages, which has rendered them unusable until very recently [3]. Advances in large smart antenna systems, composed of many antenna elements, can overcome these problems by establishing communication links over narrow beams with high beamforming gains. In addition, these advanced systems can support several simultaneous beams of varying witdth [4].
The fact that the communications are conducted over highly directed beams introduces both challenges and opportunities. Narrow beams, when efficiently used, can ensure a high degree of isolation from interference due to other ongoing communications, but they also significantly curb coverage and range of the mmwave base stations (gNBs). This means that beam management aspects in future networks will be no small feat. For this reason, it is not expected that mmwave service will be deployed in a stand-alone fashion, but rather in tandem with networks operating in sub-6 GHz frequencies, to alleviate shortcomings, especially during initial access and link establishment [5].
A signifcant body of work has addressed this issue, either in the context of initial access and link establishment, or beam alignment/configuration and user association. In [6] the authors present a framework that combines matching theory and swarm intelligence to dynamically and efficiently perform user association and beam alignment in a vehicle-to-vehicle communication network. Methods aided by location information have been proposed in [7], as have methods which use information from road-side and vehicle sensors [8, 9]. In our own previous work [10], a method leveraging traffic regulating signals was proposed to alleviate the need for real-time beam realignment. An optimal mutli-user, non-interactive beam alignment approach is proposed in [11], which however focuses on a single-cell network.
In this work we take a novel graph-based approach to the beam management problem. In particular, we address it by casting the joint beam design and user association task as a conflict-aware matching problem in a weighted bipartite graph, with the goal of ensuring broad coverage while maximizing the network data rate. Few works in the literature have applied graph theory in general, to address beam management in mmwaves [12, 13]. In both [12, 13], the authors propse a graph-based approach to reduce the inter-cell interference, whereby each mmwave cell/link is modelled as a vertex and the edges between them respresent the mutual inferference caused. The goal is to find a subgraph that minimizes the number of beam collisions.
To summarize, in this work we make the following main contributions:
-
•
we formulate the beam design problem, i.e., the joint selection of the number, width and direction of beams, as an optimization problem, aiming at maximizing the rate of the covered users, while respecting all practical constraints;
-
•
we develop a graph-based model of the mmwave system, which captures the most essential features. The optimization problem is thus turned into a problem of bipartite weighted matching with conflicts, which can be solved in linear time using heuristic algorithms. In particular, the introduction of conflicts within the graph model enables us to accomodate the practical constraints of mmwave communications;
-
•
we evaluate our approach leveraging a large-scale trace, including the real-world urban topology and realistic vehicular mobility of Luxembourg City, Luxembourg, and compare it against a state-of-the-art cluster-based beam design approach. Our results show that the proposed scheme is able to provide better performance, in particular thanks to its ability to accomodate practical constraints into the solution mechanism.
Unlike previous work, which mainly addressed a single parameter at a time, our approach jointly selects, for each gNB, three beam-design parameters: the number of simultaneous beams, their width, and their direction. Note that, while weighted bipartite matching without conflicts is a fairly well-studied problem, the same problem with conflicts has been much less explored and applied.
The remainder of the paper is organized as follows. After detailing the system model and our vehicular network in Sec. II, we formulate the optimization problem and introduce our graph-based approach in Sec. III. In Sec. IV, through extensive simulations using real-world vehicular traces, we present the performance evaluation. Finally, Sec. V concludes the paper.
II The mmwave vehicular network
We consider a realistic vehicular network in an urban setting, based on real-world publicly available data for the city of Luxembourg [14]. This data contains sufficient information about the topology of the city, the road layout (e.g., regulated intersections), as well as the mobility traces of around 14,000 vehicles traveling within the city center, accumulated over a 12-hour window. Based on this data, we construct a scenario as depicted in Fig. 1, in which a set of gNBs, denoted by , are colocated with traffic lights to serve a set of vehicles, i.e., the mmwave users, denoted by .
gNBs and users are equipped with uniform planar array (UPA) antennas, composed of a grid of and antenna elements, respectively, spaced by . Array antennas at the gNB can support up to beams simultaneously, limited by the number of available RF chains, while vehicles can use only one beam at a time. For the mmwave communication between gNBs and users to be successful, the beams need to be fully aligned at both the transmitting and receiving end, or in the case of no line of sight (nLoS), directed in such a manner that the angle of arrival of the incoming waves coincides with the direction of the receiving beam. Moreover, the directivity and gain of a beam are inversely proportional to the width of the beam, i.e., the narrower the beam, the higher the gain. The number and width of the beams determine the range and coverage of the gNB, while the direction of the beam ensures alignment with the receiving beam, and isolation from interfering signals. It is clear therefore that the number, width, and directions of the beams are critical aspects that need to be addressed in a mmwave vehicular network.
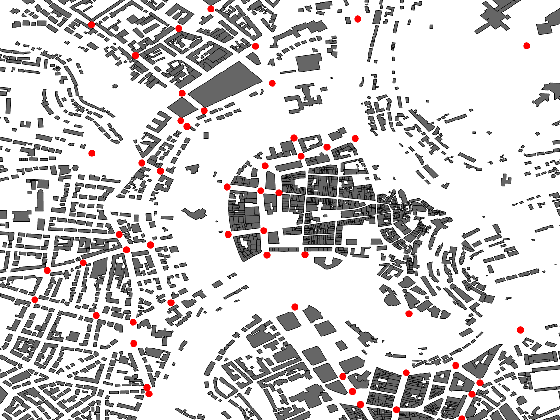
In this paper, we focus on downlink communications, although the work can easily be extended to the uplink direction as well. Furthermore, multiple vehicles can be multiplexed within the same beam, using multiple access techniques. Coordinated multi point transmission (CoMP) is also supported, i.e., we assume that a vehicle can receive data through its single beam from several gNBs. Finally, to make the model more tractable, we divide the network area under consideration into equal-sized square zones. We denote the set of zones by and make them sufficiently small so that their size is negligigle with respect to the footprint of any beam. It follows that we can consider that all vehicles within a specific zone expericence the same propagation and LoS conditions with respect to the surrounding gNBs.
III Beam matching and user association
We now focus on the main aspects of the mmwave vehicular network we address and present our approach to overcome the existing hurdles. In particular, Sec. III-A formally formulates the optimization problem for the user-gNB association, stating its objective and constraints. Then Sec. III-B introduces our graph-based model with constraints and a heuristic algorithm that effectively solves the problem in linear time.
III-A The optimization problem
Given the set of gNBs , , the number of supported beams at each gNB, and the set of zones , our aim is to jointly address the two following questions while maximizing the overall achieved network rate: i) what beam design should each gNB employ, i.e., how many beams, of what width, and direction; and ii) which zones should be associated to which gNB and scheduled on which beam.
To this end, we formulate an optimization problem that needs to be solved periodically at every time step . Given the solution, this is provided to the set of gNBs, which update their beams design accordingly. Since the problem formulation holds at every time step, to simplify the notation, in the following we drop the time index .
Let us first define a set of beams available at every gNB. Each beam is defined by a direction and half-power beamwidth . If we consider a finite set of possible directions and a finite set of possible beamwidths , then the set of beams, , at the gNB would contain potential beams.
Let be the binary variable indicating whether beam at gNB is employed or not, and let be the binary variable indicating that zone is associated with gNB on beam . To assess whether a beam at gNB can cover a zone , we proceed as follows. First, for each zone , we derive geometrically the LoS direction from a gNB , i.e., the angle of departure, denoted as 111All directions are defined in reference to a global coordinate system.. We then denote with the set of all tuples covering zone , i.e., all tuples for which and which fulfil the condition222Recall that a zone size is negligible with respect to any beam footprint. .
The optimization problem is then defined as follows:
| (1) |
where is the achieveable rate at zone from gNB on beam , given the set of indicator variables and .
The achieveable rate at zone is given by the following expression:
| (2) |
where is the system bandwidth, while the second term within the logarithmic function is the signal-to-interference-and-noise (SINR) ratio. In the numerator, represents the channel gain between gNB and the vehicles in zone on beam , while is the power allocated to beam by . At the denominator, represents the white noise power, while represents the interference experienced by the vehicle in the zone from all other active tuples in to which is not associated with. For any vehicle in zone , can be expressed as:
| (3) |
The channel gains, which account for propagation losses and the beamforming gains, are derived according to [15].
Next, we define the constraints characterizing the system under study. First, we limit the number of simultaneous beams that can be used by the gNB:
| (4) |
gNBs must also adhere to a power budget and ensure that power is not allocated to unused beams, , namely:
| (5) |
| (6) |
Finally, we must ensure that beams do not overlap with each other, i.e., for every two beams at , for which , the following condition must hold:
| (7) |
We then impose constraints on the receiving end of the communication. First, we ensure that no zone is associated with a tuple that cannot cover that zone:
| (8) |
and that no zone is scheduled on an inactive beam:
| (9) |
In addition, for CoMP-like communications, in which several gNBs coordinate to transmit the same data to a certain zone, we impose that:
| (10) |
where is the maximum number of gNBs that can partake in the coordinated tranmission. Clearly, when no CoMP is enabled, .
The problem contanis nonlinear equations, e.g., (2), and contains integer variables, namely, and ; it therefore falls into the category of nonlinear integer programming [16]. Such problems are more complex than mixed-integer linear programming (MILP) problems, which are themselves known to be NP-hard [17]. While there are algorithms that do solve MILP problems to the optimum, solution strategies for non-linear integer problems only find local optima in the general case.
III-B A graph-based approach
To overcome the complexity of the above problem, we proceed as follows. First, we develop a graph-based model of the system that captures all the essential aspects of the mmwave vehicular networks. Second, we leverage such a model to devise an effective, linear-complexity heuristic.
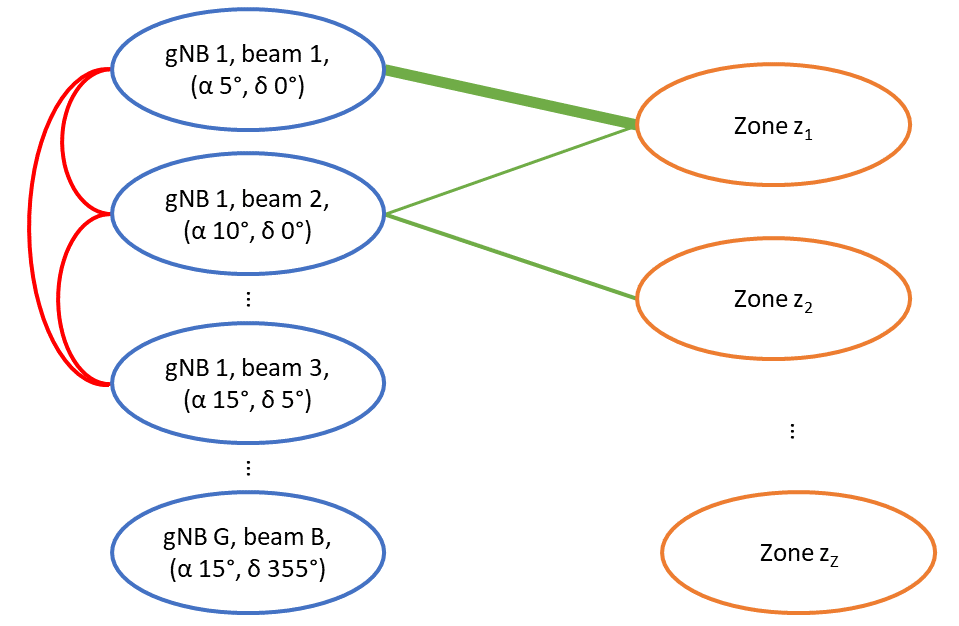
As already mentioned, an effective beam design requires to jointly set (i) the number of beams of each gNB, (ii) their width, and (iii) their direction, while respecting the system constraints. Making these decisions sequentially, e.g., first deciding the width of beams and then their directions, is possible but likely to result in suboptimal solutions. On the other hand, making them jointly requires recognizing and accounting for the conflicts between decisions, i.e., the fact that several options are mutually exclusive and taking one renders the others invalid. To this end, we first cast the task of beam design and user association into a problem of bipartite weighted matching with conflicts. Specifically, we build a bipartite graph similar to the one in Fig. 2, where:
-
•
left-hand side vertices represent tuples;
-
•
right-hand side vertices represent zones;
-
•
edges between left- and right-hand side vertices represent the fact that a certain beam covers a certain zone, i.e., that ;
-
•
the edge weights correspond to the achievable rate between left-hand vertex and right-hand vertex ;
-
•
conflict edges, drawn between left-hand side vertices, denote combinations that are mutually exclusive.
With reference to the example in Fig. 2, we can observe that conflict edges are drawn between vertices corresponding to the same gNB, with incompatible beam choices, e.g., combinations of decisions that would result in beams of the same gNB overlapping. To make the matching problem tractable, the weights of the edges, i.e., the achievable rates, are calculated by taking into account only the noise-limited rate, which is a fair assumption considering that mmwave networks have in general very limited interference. The selection of an edge between the left-hand and right-hand vertices corresponds to setting both binary variables .
Although the problem of weighted bipartite matching with conflicts is NP-hard [18], some heuristic algorithms are available in the literature, which we can be used for an efficient and effective solution of the beam design problem. Specifically, we leverage the algorithm presented in [18, Sec. 4.3], which operates in linear time, at the cost of a linear competitive ratio.
IV Numerical results
The performance of our approach is evaluated through numerical simulations of an urban vehicular network constructed through the publicly available traces for the city of Luxembourg as described in Sec. II.
We limit our scenario to a 4 km2 area of the city, covering most of its centre, in which 51 gNBs are distributed as depcited in Fig. 1. The system parameters are as follows. The central frequency is set at GHz [19], while the bandwidth is set at MHz as foreseen in 5G networks [1]. All gNBs are equipped with UPA, with antenna elements spaced by , that can transmit up to beams simultaneously. The transmit power is limited to dBm for any gNB. The vehicles are equipped with UPA, and can receive on a single beam at a time, which is always directed towards the associated gNB. The composite effect of channel and beamforming gains are modeled in accordance with [15], as well as LoS and outage probability which are tailored to the Luxembourg scenario. Furthermore, we consider three supported beamwidths , while beam directions can be any integer number between and .
We compare the performance of the proposed approach against a clustering-based technique, using the low-complexity but efficient DBSCAN algorithm [20] to generate the number and directions of the beams. This is used as a benchmark approach. It should be noted that DBSCAN cannot determine the width of the beams, therefore, we try all possible values and take the one resulting in the best performance. Both algorithms are executed periodically every 1 s, and the total simulation duration is 20 s. The underlying allocation of resources is performed using the Proportional-Fair scheduling algorithm. In the following plots, CAWBM denotes the proposed conflict-aware weighted bi-partite matching approach.
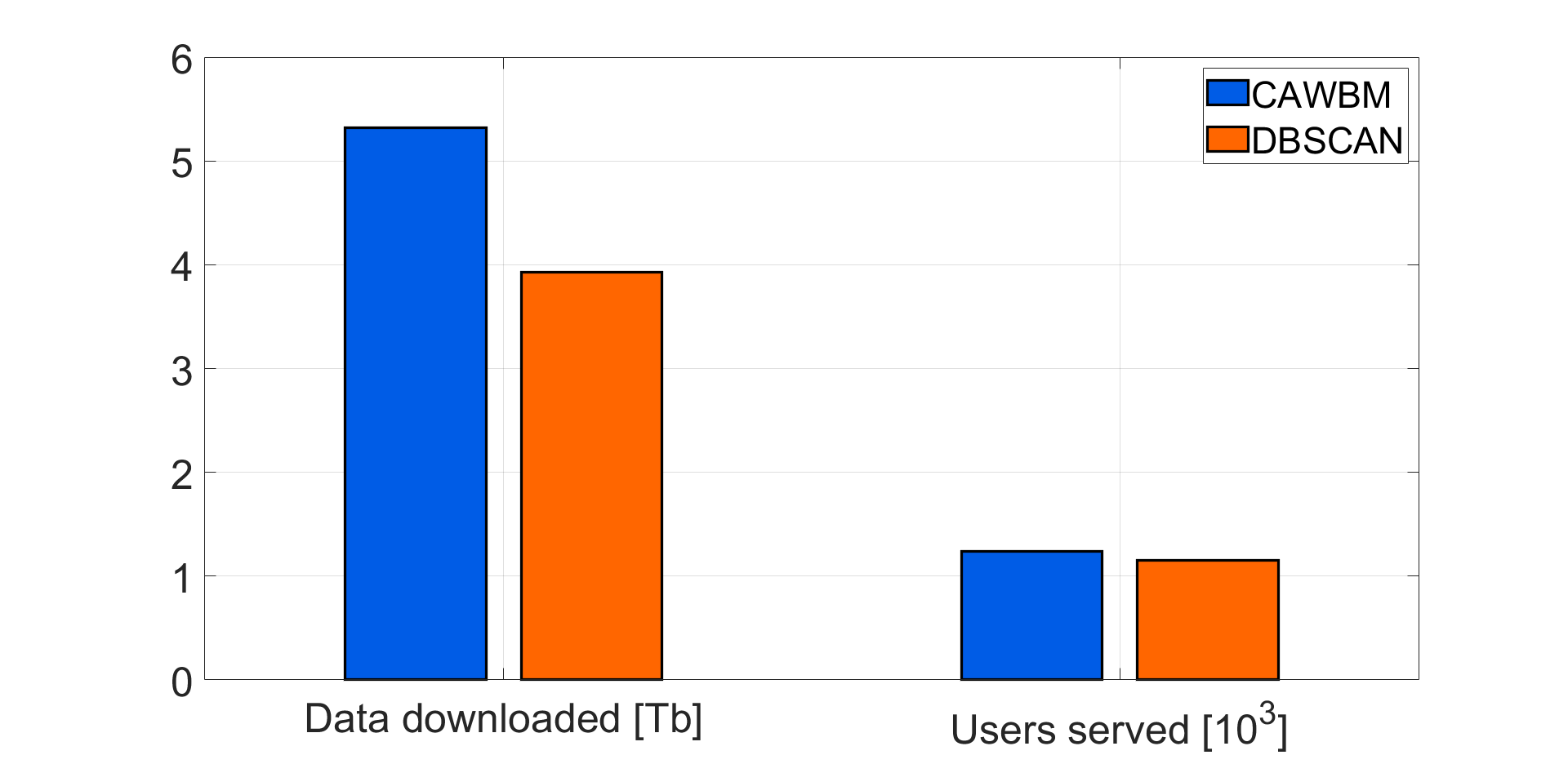
We first look at the perfomance of both approaches in absolute terms, by evaluating the total number of users served over the 20-s period and the amount of data downloaded, as shown in Fig. Fig. 3. CAWBM can serve around 35%, roughly 1.4 Tb, more data than DBSCAN, and around 7% more users. In particular, CAWBM serves 92% of all vehicles in the network, while DBSCAN serves around 85% of them.
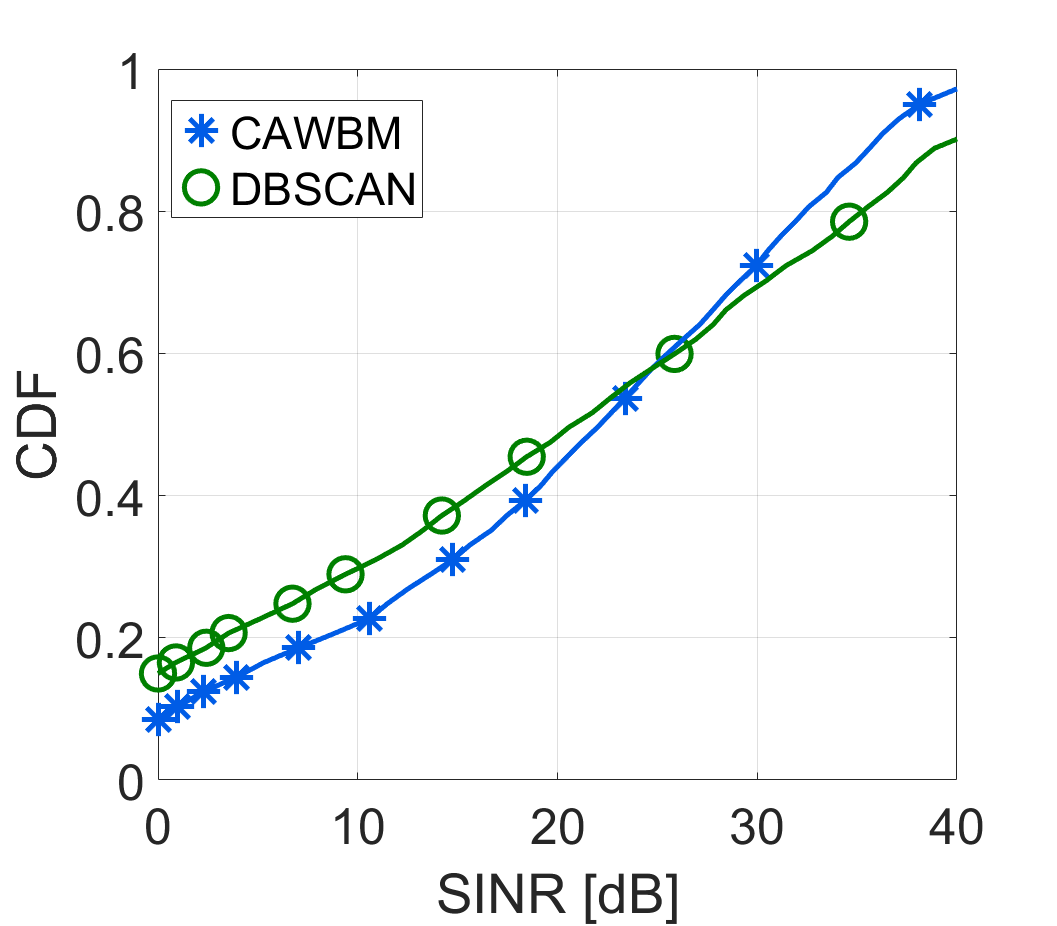
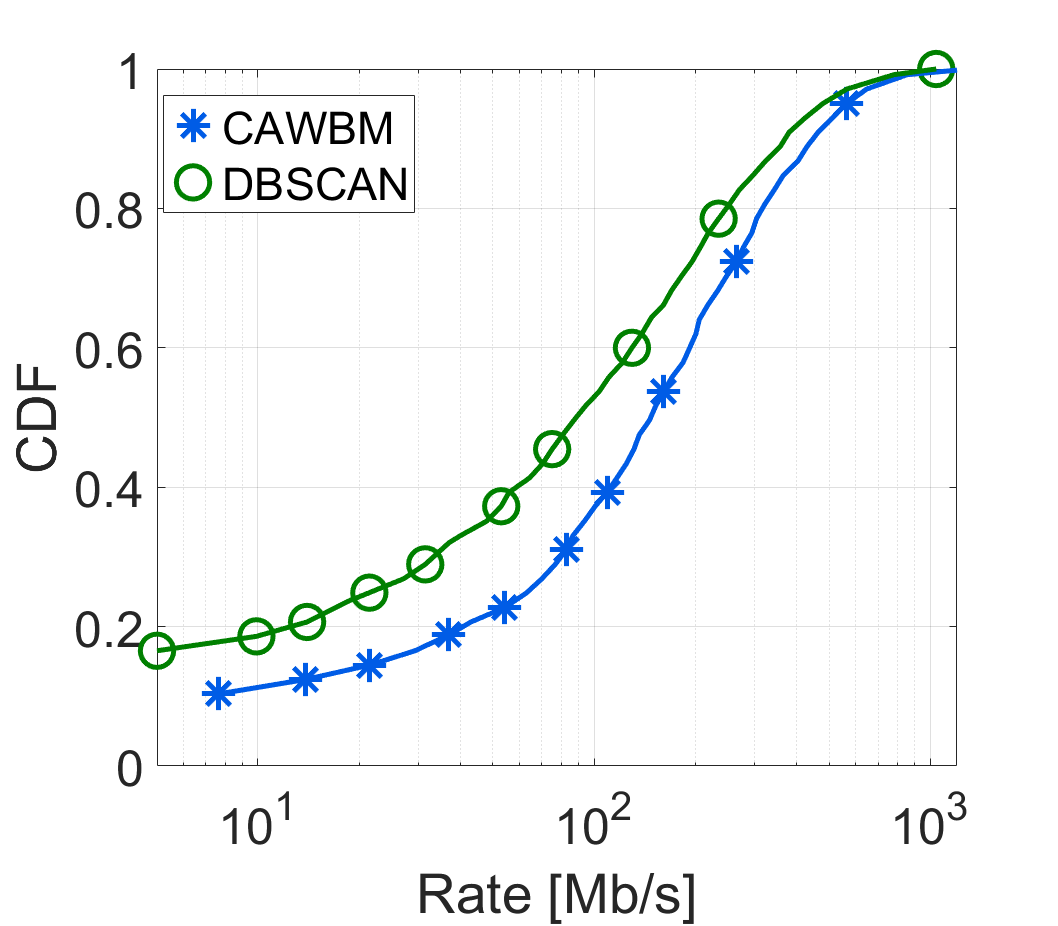
Next, we look at the cummulative distribution function (CDF) of the experienced average SINR and data rates achieved by the vehicles. During the simulations, the SINR was calculated taking into account both the noise and interference, and then mapped into the data rate by using the 4-bit channel quality indicator (CQI) table in [2]. It is interesting to note that while DBSCAN can ensure slightly better SINR values for the top 40% of the users, as seen in Fig. 4(left), this behavior is not reflected in the achieved rates by the vehicles, shown in Fig. 4(right).
This can be explained by the fact that the CAWBM approach serves both more vehicles per beam (as shown in Fig. 5(left)) and for a longer period of time (Fig. 5(right)).
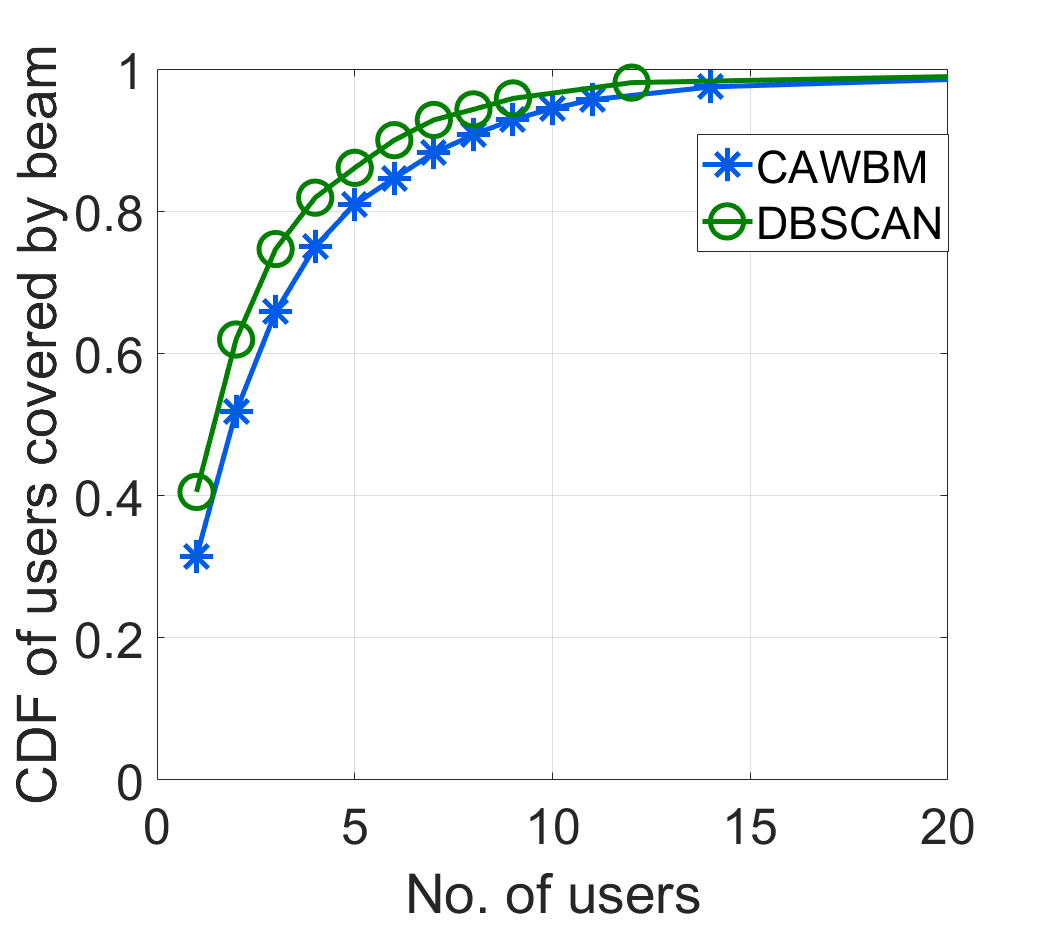
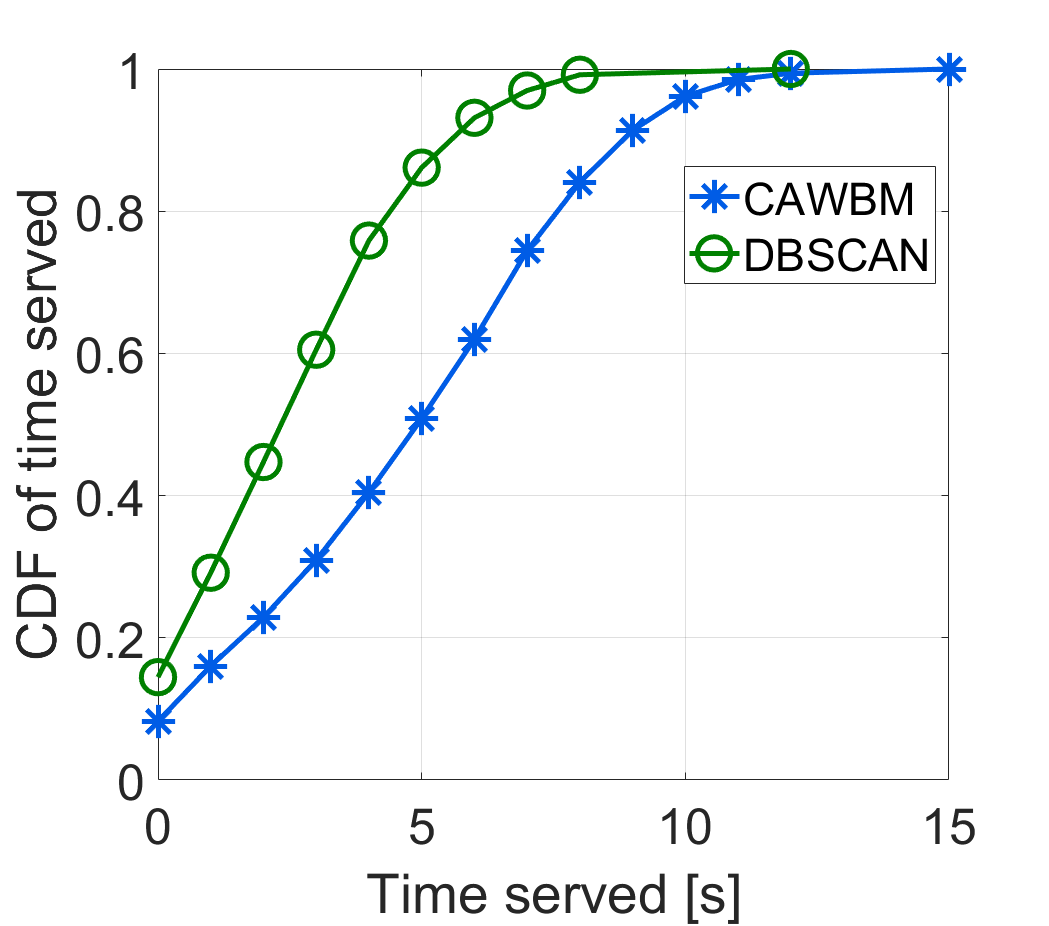
The improvement in performance brought by CAWBM when compared to DBSCAN can be attributed to the fact that the former takes into account the rates of all potential vehicles within the small area of the zone. DBSCAN, on the other hand, acts only on the information regarding the vehicle relative LoS direction towards the gNBs. In addition, CAWBM is likely to favor beams that cover zones that are both more frequented and well positioned to experience higher levels of SINR. This is the reason why over 50% of the vehicles are served more than 5 s with CAWBM, while, under DBSCAN, the corresponding percentage of vehicles is just 15%.
V Conclusions and future work
While mmwave communications have emerged as a promising candidate technology for future vehicular networks, the performance of mmwave networks heavily depends upon beam management aspects. The need for adequate alignment of beams between gNBs and vehicles is critical, and, as such, efficient beam design becomes paramount. We adressed both beam design aspects and user association though a graph-based approach. Once we modeled our system as a weighted bipartite graph, we were able to cast the problem at hand as a conflict-aware matching problem, which can be efficiently solved in linear time, through heuristic algorithms. Our performance evaluation, based on real-world topology and mobility information, has provided relevant insights. Thanks to the conflict-aware approach, the solution we proposed significantly outperforms our benchmark scheme leveraging a clustering algorithm.
Future work will focus on further improving the mmWave graph model, and further investigating the interaction between gNBs during the beam design phase.
Acknowledgement
This work has been performed in the framework of the European Union’s Horizon 2020 project 5G-CARMEN co-funded by the EU under grant agreement No. 825012, and has also been partially supported by the Academy of Arts and Sciences of Kosovo.
References
- [1] M. Giordani, M. Polese, A. Roy, D. Castor, and M. Zorzi, “A tutorial on beam management for 3gpp nr at mmwave frequencies,” IEEE Comm. Mag., 2016.
- [2] 3GPP, “Evolved Universal Terrestrial Radio Access (E-UTRA) – Physical layer procedures – Release 15,” 3rd Generation Partnership Project (3GPP), Tech. Rep. 36.213, 2018.
- [3] T. S. Rappaport, G. R. MacCartney, M. K. Samimi, and S. Sun, “Wideband millimeter-wave propagation measurements and channel models for future wireless communication system design,” IEEE Trans. on Comm., 2015.
- [4] M. N. Kulkarni, A. Ghosh, and J. G. Andrews, “A comparison of mimo techniques in downlink millimeter wave cellular networks with hybrid beamforming,” IEEE Trans.on Comm., 2016.
- [5] M. Polese, M. Giordani, M. Mezzavilla, S. Rangan, and M. Zorzi, “Improved handover through dual connectivity in 5g mmwave mobile networks,” IEEE JSAC, 2017.
- [6] C. Perfecto, J. Del Ser, and M. Bennis, “Millimeter-wave v2v communications: Distributed association and beam alignment,” IEEE JSAC, 2017.
- [7] I. Orikumhi, J. Kang, C. Park, J. Yang, and S. Kim, “Location-aware coordinated beam alignment in mmwave communication,” in IEEE Allerton, 2018.
- [8] I. Filippini, V. Sciancalepore, F. Devoti, and A. Capone, “Fast Cell Discovery in mm-wave 5G Networks with Context Information,” IEEE Trans. on Mobile Computing, 2017.
- [9] A. Ali, N. Gonzalez-Prelcic, R. W. Heath Jr., and A. Ghosh, “Leveraging sensing at the infrastructure for mmwave communication,” arXiv, 2019.
- [10] Z. Limani Fazliu, F. Malandrino, and C. F. Chiasserini, “mmWave in vehicular networks: Leveraging traffic signals for beam design,” in IEEE WoWMoM Workshop on Communication, Computing, and Networking in Cyber Physical Systems (CCNCPS), 2019.
- [11] A. Khaliliy, S. Shahsavariz, M. A. A. Khojastepour, and E. Erkip, “On Optimal Multi-user Beam Alignment in Millimeter Wave Wireless Systems,” arXiv preprint arXiv:2001.06595, 2020.
- [12] H. Shokri-Ghadikolaei, L. Gkatzikis, and C. Fischione, “Graph theory based beam scheduling for inter-cell interference avoidance in mmwave cellular networks,” 2015.
- [13] Z. Sha, Z. Wang, S. Chen, and L. Hanzo, “Graph theory based beam scheduling for inter-cell interference avoidance in mmwave cellular networks,” IEEE Transactions on Vehicular Technology, 2020.
- [14] L. Codeca, R. Frank, S. Faye, and T. Engel, “Luxembourg sumo traffic (LuST) scenario: Traffic demand evaluation,” IEEE Intelligent Transportation Systems Magazine, 2017.
- [15] M. Rebato, J. Park, P. Popovski, E. De Carvalho, and M. Zorzi, “Stochastic geometric coverage analysis in mmwave cellular networks with realistic channel and antenna radiation models,” IEEE Trans. on Comm., 2019.
- [16] R. Hemmecke, M. Köppe, J. Lee, and R. Weismantel, “Nonlinear integer programming,” in 50 Years of Integer Programming 1958-2008. Springer, 2010, pp. 561–618.
- [17] S. Boyd and L. Vandenberghe, Convex optimization. Cambridge university press, 2004.
- [18] C. Chen, L. Zheng, V. Srinivasan, A. Thomo, K. Wu, and A. Sukow, “Conflict-aware weighted bipartite b-matching and its application to e-commerce,” IEEE Transactions on Knowledge and Data Engineering, 2016.
- [19] B. Antonescu, M. T. Moayyed, and S. Basagni, “mmwave channel propagation modeling for v2x communication systems,” in IEEE PIMRC, Oct 2017.
- [20] D. Birant and A. Kut, “St-dbscan: An algorithm for clustering spatial–temporal data,” Data & Knowledge Engineering, vol. 60, no. 1, pp. 208–221, 2007.