Gradient Descent Temporal Difference-difference Learning

In related approaches to ours, some previous studies have attempted to improve Gradient-TD algorithms by adding regularization terms to the objective function. These approaches have used have used $l_{1}$ regularization on weights to learn sparse representations of value functions [Liu:12], or $l_{2}$ regularization on weights [Ghiassian:20]. Our work is different from these approaches in two ways. First, whereas these previous studies investigated a variant of TD learning with gradient corrections, we take the GTD2 algorithm as our starting point. Second, unlike these previous approaches, our approach modifies the error objective function by using a distance constraint rather than a penalty on weights. The distance constraint works by restricting the search to some region around the evaluation obtained in the most recent time step. With this modification, our method provides a learning rule that contains second-order differences in successive parameter updates.

Our approach is similar to trust region policy optimization [Schulman:15] or relative entropy policy search [Peters:10], which penalize large changes being learned in policy learning. In these methods, constrained optimization is used to update the policy by considering the constraint on some measure between the new policy and the old policy. Here, however, our aim is to find the optimal value function, and the regularization term uses the previous value function estimate to avoid drastic changes in the updating process.

Our approach bears similarity to the natural gradient approach widely used in reinforcement learning [Amari:98, Bh:09, Degris:12, DT:14, Thomas:16], which also features a constrained optimization form. However, Gradient-DD is distinct from the natural gradient. The essential difference is that, unlike the natural gradient, Gradient-DD is a trust region method, which defines the trust region according to the difference between the current value and the value obtained from the previous step. From the computational cost viewpoint, unlike natural TD [DT:14], which needs to update an estimate of the metric tensor, the computational cost of Gradient-DD is essentially the same as that of GTD2.

In this section, we formalize the problem of learning the value function for a given policy under the Markov decision process (MDP) framework. In this framework, the agent interacts with the environment over a sequence of discrete time steps, $t=1,2,\ldots$. At each time step the agent observes a state $s_{t}\in\mathcal{S}$ and selects an action $a_{t}\in\mathcal{A}$. In response, the environment emits a reward $r_{t}\in\mathbb{R}$ and transitions the agent to its next state $s_{t+1}\in\mathcal{S}$. The state and action sets are finite. State transitions are stochastic and dependent on the immediately preceding state and action. Rewards are stochastic and dependent on the preceding state and action, as well as on the next state. The process generating the agent’s actions is termed the behavior policy. In off-policy learning, this behavior policy is in general different from the target policy $\pi:\mathcal{S}\rightarrow\mathcal{A}$. The objective is to learn an approximation to the state-value function under the target policy in a particular environment:

where $\gamma\in[0,1)$ is the discount rate.

In problems for which the state space is large, it is practical to approximate the value function. In this paper we consider linear function approximation, where states are mapped to feature vectors with fewer components than the number of states. Specifically, for each state $s\in\mathcal{S}$ there is a corresponding feature vector $\mathbf{x}(s)\in\mathbb{R}^{p}$, with $p\leq|\mathcal{S}|$, such that the approximate value function is given by

The goal is then to learn the parameters $\mathbf{w}$ such that $V_{\mathbf{w}}(s)\approx V(s)$.

A major breakthrough for the study of the convergence properties of MDP systems came with the introduction of the GTD and GTD2 learning algorithms [SSM09, SMP09]. We begin by briefly recapitulating the GTD algorithms, which we will then extend in the following sections. To begin, we introduce the Bellman operator $\mathbf{B}$ such that the true value function $\mathbf{V}\in\mathbb{R}^{|\mathcal{S}|}$ satisfies the Bellman equation:

where $\mathbf{R}$ is the reward vector with components $\text{E}(r_{n}|s_{n}=s)$, and $\mathbf{P}$ is a matrix of the state transition probabilities under the behavior policy. In temporal difference methods, an appropriate objective function should minimize the difference between the approximate value function and the solution to the Bellman equation.

Having defined the Bellman operator, we next introduce the projection operator $\mathbf{\Pi}$, which takes any value function $\mathbf{V}$ and projects it to the nearest value function within the space of approximate value functions of the form Eqn. (2). Letting $\mathbf{X}$ be the matrix whose rows are $\mathbf{x}(s)$, the approximate value function can be expressed as $\mathbf{V}_{\mathbf{w}}=\mathbf{X}\mathbf{w}$. The projection operator is then given by

where the matrix $\mathbf{D}$ is diagonal, with each diagonal element $d_{s}$ corresponding to the probability of visiting state $s$.

The natural measure of how closely the approximation $\mathbf{V}_{\mathbf{w}}$ satisfies the Bellman equation is the mean-squared Bellman error:

where the norm is weighted by $\mathbf{D}$, such that $\|\mathbf{V}\|^{2}_{\mathbf{D}}=\mathbf{V}^{\top}\mathbf{D}\mathbf{V}$. However, because the Bellman operator follows the underlying state dynamics of the Markov chain, irrespective of the structure of the linear function approximator, $\mathbf{B}\mathbf{V}_{\mathbf{w}}$ will typically not be representable as $\mathbf{V}_{\mathbf{w}}$ for any $\mathbf{w}$. An alternative objective function, therefore, is the mean squared projected Bellman error (MSPBE), which we define as

Following [SMP09], our objective is to minimize this error measure. As usual in stochastic gradient descent, the weights at each time step are then updated by $\Delta\mathbf{w}=-\alpha\nabla J(\mathbf{w})$, where $\alpha>0$, and

For notational simplicity, we have denoted the feature vector associated with $s_{n}$ as $\mathbf{x}_{n}=\mathbf{x}({s_{n}})$. We have also introduced the temporal difference error $\delta_{n}=r_{n}+(\gamma\mathbf{x}_{n+1}-\mathbf{x}_{n})^{\top}\mathbf{w}_{n}$. Let $\boldsymbol{\eta}_{n}$ denote the estimate of $[\text{E}(\mathbf{x}_{n}\mathbf{x}_{n}^{\top})]^{-1}\text{E}(\delta_{n}\mathbf{x}_{n})$ at the time step $n$. Because the factors in Eqn. (5) can be directly sampled, the resulting updates in each step are

These updates define the GTD2 learning algorithm, which we will build upon in the following section.

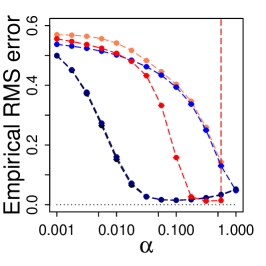
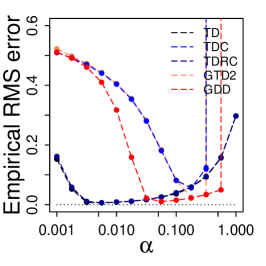
As a first test of Gradient-DD learning, we conducted a simple random walk task [Sutton:2018]. The random walk task has a linear arrangement of $m$ states plus an absorbing terminal state at each end. Thus there are $m+2$ sequential states, $S_{0},S_{1},\cdots,S_{m},S_{m+1}$, where $m=$ 10, 20, or 40. Every walk begins in the center state. At each step, the walk moves to a neighboring state, either to the right or to the left with equal probability. If either edge state ($S_{0}$ or $S_{m+1}$) is entered, the walk terminates. A walk’s outcome is defined to be $r=0$ at $S_{0}$ and $r=1$ at $S_{m+1}$. Our aim is to learn the value of each state $V(s)$, where the true values are $(1,\cdots,m)/(m+1)$. In all cases the approximate value function is initialized to the intermediate value $V_{0}(s)=0.5$. We first consider tabular representation of the value function. We also consider linear approximation representation and obtain the similar results, which are reported in Fig. 10 of the appendix. We consider that the learning rate $\alpha_{n}$ is tapered according to the schedule $\alpha_{n}=\alpha(10^{3}+1)/(10^{3}+n)$. We tune $\alpha\in\{10^{-12/4},10^{-11/4},\cdots,10^{-1/4},1\}$. We also consider the constant step sizes and obtain the similar results, which are reported in Fig. 9 of the appendix. For GTD2 and TDC, we set $\beta_{n}=\zeta\alpha_{n}$ with $\zeta\in\{1/64,1/16,1/4,1,4\}$.

We first compare the methods by plotting the empirical RMS error from averaging the final 100 steps as a function of step size $\alpha$ in Fig. 2, where 20,000 episodes are used. We also plot the average error of all episodes during training and report these results in Fig. 5 of the Appendix. From these figures, we can make several observations. (1) Gradient-DD clearly performs better than the GTD2 and TDC methods. This advantage is consistent in various settings, and gets bigger as the state space becomes large. (2) Gradient-DD performs similarly to TDRC and conventional TD learning, with a similar dependence on $\alpha$, although Gradient-DD exhibits greater sensitivity to the value of $\alpha$ in the log domain than these other algorithms. In summary, Gradient-DD exhibits clear advantages over the GTD2 algorithm, and its performance is also as good as TDRC and conventional TD learning.

Next we look closely at the performance during training in Fig. 2. For each method, we tuned $\alpha\in\{10^{-12/4},\cdots,10^{-1/4},1\}$ by minimizing the average error of the last 100 episodes. We also compare the performance when $\alpha$ is tuned by minimizing the average error of the last 100 episodes and report in Fig. 5 of the appendix. From these results, we draw several observations. (1) For all conditions tested, Gradient-DD converges much more rapidly than GTD2 and TDC. The results also indicate that Gradient-DD even converges as fast as TDRC and conventional TD learning. (2) The advantage of Gradient-DD learning over GTD2 grows as the state space increases in size. (3) Gradient-DD has consistent and good performance under both the constant step size setting and under the tapered step size setting. In summary, the Gradient-DD learning curves in this task show improvements over other gradient-based methods and performance that matches conventional TD learning.

Like TDRC, the updates of Gradient-DD only have a single shared step size $\alpha_{n}$, i.e., $\beta_{n}=\alpha_{n}$, rather than two independent step sizes $\alpha_{n}$ and $\beta_{n}$ as in the GTD2 and TDC algorithms. A possible concern is that the performance gains in our second-order algorithm could just as easily be obtained with existing methods by adopting this two-timescale approach, where the value function weights are updated with a smaller step size than the second set of weights. Hence, in addition to investigating the effects of the learning rate, size of the state space, and magnitude of the regularization parameter, we also investigate the effect of using distinct values for the two learning rates, $\alpha_{n}$ and $\beta_{n}$, although we set $\beta_{n}=\zeta\alpha_{n}$ with $\zeta=1$. To do this, we set $\beta_{n}=\zeta\alpha_{n}$ for GDD, with $\zeta\in\{1/64,1/16,1/4,1,4\}$, and report the results in Fig. 7 of the appendix. The results show that comparably good performance of Gradient-DD is obtained under these various $\zeta$, providing evidence that the second-order difference term in our approach provides an improvement beyond what can be obtained with previous gradient-based methods using the two time scale approach.

We next investigate Gradient-DD learning on the Boyan-chain problem, which is a standard task for testing linear value-function approximation [Boyan02]. In this task we allow for $4p-3$ states, each of which is represented by a $p$-dimensional feature vector, with $p=20,50,$ or $100$. The $p$-dimensional representation for every fourth state from the start is $[1,0,\cdots,0]$ for state $s_{1}$, $[0,1,0,\cdots,0]$ for $s_{5}$, $\cdots$, and $[0,0,\cdots,0,1]$ for the terminal state $s_{4p-3}$. The representations for the remaining states are obtained by linearly interpolating between these. The optimal coefficients of the feature vector are $(-4(p-1),-4(p-2),\cdots,0)/5$. In each state, except for the last one before the end, there are two possible actions: move forward one step or move forward two steps, where each action occurs with probability 0.5. Both actions lead to reward -0.3. The last state before the end just has one action of moving forward to the terminal with reward -0.2. We tune $\alpha\in\{10^{-2},10^{-1.5},10^{-1},10^{-3/4},10^{-1/2},10^{-1/4},10^{-1/8},1,10^{1/8},10^{1/4}\}$ for each method by minimizing the average error of the final 100 episodes. The step size is tapered according to the schedule $\alpha_{n}=\alpha(2\times 10^{3}+1)/(2\times 10^{3}+n)$. For GTD2 and TDC, we set $\beta_{n}=\zeta\alpha_{n}$ with $\zeta\in\{1/64,1/16,1/4,1,4\}$. In this task, we set $\gamma=1$.

We report the performance as a function of $\alpha$ and the performance over episodes in Fig. 3, where we tune $\alpha$ by the performance based on the average error of the last 100 episodes. We also compare the performance based on the average error of all episodes during training and report the results in Fig. 11 of the appendix. These figures lead to conclusions similar to those already drawn in the random walk task. (1) Gradient-DD has much faster convergence than GTD2 and TDC, and generally converges to better values. (2) Gradient-DD is competitive with TDRC and conventional TD learning despite being somewhat slower at the beginning episodes. (3) The improvement over GTD2 or TDC grows as the state space becomes larger. (4) Comparing the performance with constant step size versus that with tapered step size, the Gradient-DD method performs better with tapered step size than it does with constant step size.

We also verify the performance of Gradient-DD on Baird’s off-policy counterexample [Baird:95, Sutton:2018], illustrated schematically in Fig. 4, for which TD learning famously diverges. We show results from Baird’s counterexample with $N=7,20$ states. The reward is always zero, and the agent learns a linear value approximation with $N+1$ weights $w_{1},\cdots,w_{N+1}$: the estimated value of the $j$-th state is $2w_{j}+w_{N+1}$ for $j\leq N-1$ and that of the $N$-th state is $w_{N}+2w_{N+1}$. In the task, the importance sampling ratio for the dashed action is $(N-1)/N$, while the ratio for the solid action is $N$. Thus, comparing different state sizes illustrates the impact of importance sampling ratios in these algorithms. The initial weight values are $(1,\cdots,1,10,1)^{\top}$. Constant $\alpha$ is used in this task. We set $\gamma=0.99$. For TDC and GTD2, thus we tune $\zeta\in\{4^{-2},4^{-1},1,4^{2},4^{3}\}$. Meanwhile we tune $\alpha$ for TDC in a wider region. For Gradient-DD, we tune $\kappa\in\{4^{-1},1,4\}$. We tune $\alpha$ separately for each algorithm by minimizing the average error from the final 100 episodes.

Fig. 4 demonstrates that Gradient-DD works better on this counterexample than GTD2, TDC, and TDRC. It is worthwhile to observe that when the state size is 20, TDRC become unstable, meaning serious unbalance of importance sampling ratios may cause TDRC unstable. We also note that, because the linear approximation leaves a residual error in the value estimation due to the projection error, the RMS errors of GTD2, TDC, and TDRC in this task do not go to zero. In contrast to other algorithms, the errors from our Gradient-DD converge to zero.