GRaCE: Balancing Multiple Criteria to Achieve
Stable, Collision-Free, and Functional Grasps
Abstract
This paper addresses the multi-faceted problem of robot grasping, where multiple criteria may conflict and differ in importance. We introduce a probabilistic framework, Grasp Ranking and Criteria Evaluation (GRaCE), which employs hierarchical rule-based logic and a rank-preserving utility function for grasps based on various criteria such as stability, kinematic constraints, and goal-oriented functionalities. GRaCE’s probabilistic nature means the framework handles uncertainty in a principled manner, i.e., the method is able to leverage the probability that a given criteria is satisfied. Additionally, we propose GRaCE-OPT, a hybrid optimization strategy that combines gradient-based and gradient-free methods to effectively navigate the complex, non-convex utility function. Experimental results in both simulated and real-world scenarios show that GRaCE requires fewer samples to achieve comparable or superior performance relative to existing methods. The modular architecture of GRaCE allows for easy customization and adaptation to specific application needs.
I Introduction
Grasping an object is typically influenced by the intended goal, which directly impacts the choice of grasp. For instance, we naturally grasp scissors by the handle for cutting, but by the blade when passing them safely to someone else. However, the goal isn’t the sole or primary factor in determining a grasp; if the blade is obstructed or inaccessible, as illustrated in Fig. 1, we would opt to grasp the scissors by the handle, even if the intention was to hand it over. This scenario highlights that (i) multiple criteria influence the selection of a grasp and (ii) there exists a hierarchy of priorities among these criteria. The necessity for the grasp to be stable, accessible, and to avoid collisions with surrounding objects (like a mug) takes precedence over the functional goal of the grasp.
In this work, we are motivated by the problem of generating grasps that satisfy multiple criteria of differing importance. We apply hierarchical rule-based logic to robot grasping [1] and introduce a grasp utility function that is rank-preserving [2], i.e., it assigns larger utility values to grasps that satisfy higher ranked constraints. For example, robots are bound by their kinematic and dynamic constraints, which limits whether a proposed grasp can be performed, and environmental constraints (e.g., grasps should not collide with other objects). A stable grasp that satisfies these constraints should have larger utility than one that sacrifices these criteria for a functionally appropriate (but non-executable) grasp.
We take a probabilistic approach and optimize the expected utility of a grasp, where the probability of a grasp satisfying a specific criteria is given by a classifier. Additional classifiers (whether data-driven or hand-crafted) can be added (or removed) depending on the precise requirements of the application. This modular approach — which we call Gasp Ranking and Criteria Evaluation (GRaCE) — enables a robot to trade-off multiple conflicting criteria in complex contexts where not all desired objectives can be satisfied. GRaCE’s probabilistic nature incorporates uncertainty in a principled manner. This is crucial in real-world robotic scenarios, which often involve partial observability and noise. By utilizing the likelihood of a grasp meeting various criteria, GRaCE moves beyond binary satisfaction assessments and reduces the risk of misclassification inherent in the true/false assignments used in prior work (e.g., [3]).
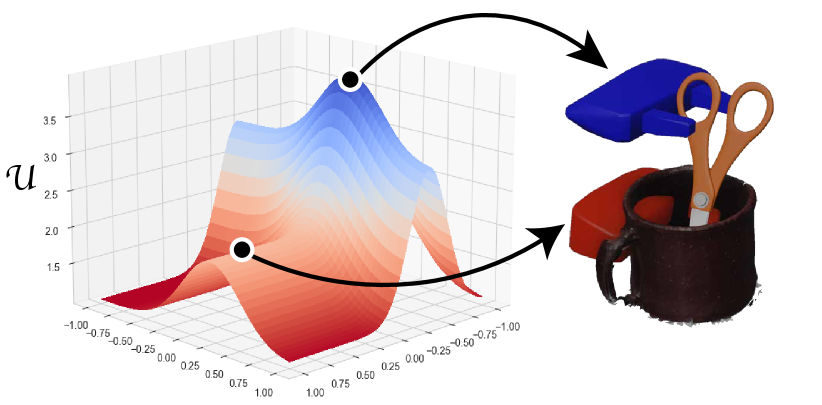
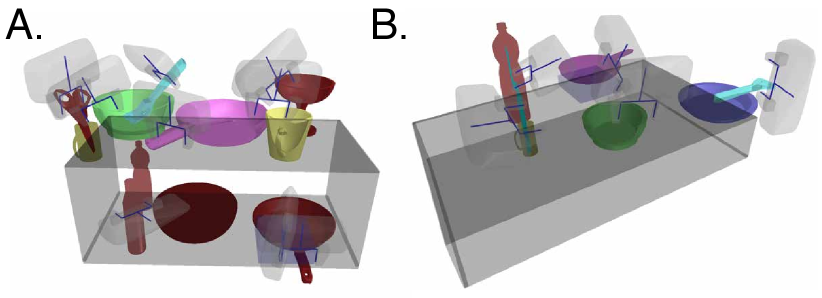
Although the utility function enables scoring of grasps, it is a complicated non-convex function to optimize, especially when the classifiers are themselves complex (e.g., a deep neural network). Inspired by progress in gradient-free methods (e.g., [4]), we propose GRaCE-OPT — a hybrid optimization method that combines gradient-based and gradient-free optimization. Specifically, GRaCE-OPT applies gradient-free optimization, an Evolutionary Strategy (ES) [5], to conduct a more “diverse” exploration over the landscape and prevent the optimization process from getting stuck at local optima. However, on its own, this gradient-free method can be slow to converge. As such, we use gradient-based optimization on a surrogate function, the lower-bound of the utility, to improve convergence speed. Experiments in complex environments show that GRaCE-OPT requires significantly fewer samples and less time to achieve comparable (or better) performance to a filtering method used in prior works [6, 7]. Our evaluations involved two simulated grasping scenarios — shelf and diner (Fig. 2) — in IsaacGym [8] and two real-world scenarios; these test scenarios are designed to be challenging (cluttered with small optimal grasping regions) and where the probability of satisfying multiple criteria may be traded-off.
To summarize, this paper contributes GRaCE which comprises a utility function that assigns higher values following user-specified hierarchical rules and an optimization method that uses both gradient-free and gradient-based optimization of the expected utility. Code and implementation details can be found online at https://github.com/clear-nus/GRaCE.
II Background and Related Work
GRaCE is a probabilistic framework for optimizing 6-DoF grasps. It builds upon related work on 6-DoF grasp candidate generation and prior work on the optimization of multiple criteria specified via rule/constraint hierarchies. We briefly review these topics in this section.
6-DoF Grasp Filtering and Refinement. Generating appropriate 6-DoF grasping remains an active area of research. One common approach is to first sample a set of grasp, either through data-driven methods [9, 10], heuristics [6] or a combination of both [7], then filter the grasps using evaluators to select the most promising candidates for execution. This sample-and-filter approach is common and can be very effective in practice [6]. However, it can be time-consuming in complex environments even with state-of-the-art samplers, especially the optimal grasp regions are small.
An alternative approach to optimize grasps directly. Early work on multi-fingered end-effector grasping [11] demonstrated that a scoring function for grasp quality (a pre-trained classifier) can be used to optimize grasps toward high quality regions. More recent work have applied optimization together with sample-and-filter methods, e.g., GraspNet [9] optimizes/refines grasp samples using the quality evaluator. These methods focus on a single quality criterion, where else our work addresses the problem of trading-off multiple conflicting criteria.
GRaCE can also be seen as a contrasting approach to “end-to-end” data-driven 6-DoF grasping [12, 13] where the sampler is trained to generate grasps that satisfy multiple criteria. However, these methods require retraining when a new criterion is added/removed, which is computationally expensive. GRaCE enables the inclusion and removal of grasp criterion “on-the-fly”, which we believe is more practical for many real-world applications. This aspect is similar to very recent work [10] that refines grasps using gradient flows, but GRaCE enables the ranking of multiple criteria and we propose a hybrid optimization technique.
Task/Functional Grasping. Ensuring the functionality of a grasp is one of the most challenging aspects of grasp synthesis. Functional grasps depend on the semantic knowledge of the object and the target task. For instance, in a handover task involving scissors, the robot should grasp the blade so the human can take the handle. These grasps are referred to in the literature as functional [14], task-oriented [15], or semantic grasps [16, 17].
Current methods for achieving task functional grasping are largely based on a sample-and-filter methodology with two-stage filtering. To elaborate, grasps are first sampled and non-stable ones are filtered out. Then, the remaining grasps are filtered based on appropriate affordances by segmenting objects [18, 19, 20]. Deep learning methods are often used provide a grasp score given a grasp and a specific target task [15]. Very recent methods employ Multimodal Large Language Models (LLMs) to reason about functional grasps [17, 21, 22, 23]. However, robustness of these models remains a challenge and research on LLMs for task-oriented grasps is ongoing.
The modularity of the GRaCE framework allows the use of many existing differentiable methods for assessing grasp functionality. In our work, we use TaskGrasp [15] as a criterion evaluator due to code availability and its good performance on various objects.
Hierarchical Optimization of Multiple Criteria. A key component of our framework is a utility function, which leverages a rule hierarchy. Rule hierarchies have a long history in optimization, with early works dating back to 1967 [24]. More recent methods encode rule hierarchies using temporal logic [25, 2]. Unlike these methods, our framework is differentiable and we do not have to rely on external SAT solvers for optimization. Our work is closely related to very recent research on planning with a rank-preserving reward function for autonomous vehicles [3]. Our grasp utility function has a similar structure to their proposed reward function, but our approach is probabilistic to handle uncertainty and we optimize the expected rank of the grasp via a hybrid optimization method.
III Ranking Grasps via Utility Functions
In this section, we present our approach for trading-off criteria for grasp generation. A grasp is typically defined as a set of contact points with an object which restricts movement when external forces are applied [26]. For simplicity, we will refer to end-effector poses as grasps (or grasp candidates) and denote them as , even if they do not satisfy the definition above (e.g., the pose does not make contact with the object). We first discuss how grasp criteria can be ranked, followed by our a utility function, and, finally, formulate an optimization based grasp generation method.
| Priority | Rule | Probability |
|---|---|---|
| 1 | ||
Criteria, Priority, and Rules. We define a grasp criterion as a predicate where is the criterion’s priority (with descending importance) for a grasp and is an index of criterion, . is a number of criteria with the same priority . A rule is defined as a conjunction of criteria .
Let be the probability that criterion is satisfied under observed context . For notational simplicity, we will drop the explicit dependence of , and on and . We assume that criteria are conditionally independent given the grasp and context. As such, the probability that a rule is satisfied is given by . Table I shows a list of priorities, rules, and their associated probabilities.
Rule Hierarchy and Rank of a Grasp. A rule hierarchy is defined as a sequence of rules . The rule hierarchy induces a total order on the grasps, enabling us to rank grasps. A grasp that satisfies all the rules has the highest rank, i.e., rank 1. A grasp that satisfies all the rules except the lowest priority rule has rank 2. This continues on, with grasps satisfying none of the rules having the lowest rank. Formally, we define a rank of a grasp as:
Definition 1
Let to be rule hierarchy with rules. Let be a function that evaluates rule to be 1 if the rule is satisfied, 0 otherwise. Then the rank of the grasp is defined as:
| Satisfied Rules | Probability | |
|---|---|---|
Table II summarizes grasp ranks for the rule hierarchy and our utility is defined as the negative expected rank,
| (1) |
This simplified form can be obtained by observing that is a Bernoulli variable with probability ,
| (by definition) | ||||
Problem Statement. We seek to find a grasp that maximizes the utility function:
| (2) |
The key challenge is that Eq. (2) is a non-convex function of the grasps that can trap standard gradient-based methods. Moreover, the multiplication of probabilities leads to numerical instabilities with vanishing gradients when used with deep neural classifiers [27, 28]. In the next section, we describe how to optimize this function using GRaCE-OPT.
IV Hybrid Optimization of Grasps
In this section, we introduce GRaCE-OPT, a hybrid optimization technique that leverages both gradient-free and gradient-based methods to optimize Equation (2). As an initial step, we considered optimizing a lower-bound of Eq. 2 using Jensen’s inequality:
where is a constant independent of . Empirically, we find to be easier to optimize and numerically stable, but inspection of its form shows that it is no longer rank preserving since the utilities are factored out.
As such, we only use this gradient-based optimization as an inner-loop within a gradient-free ES setup [5], shown in Algorithm 1 below. We assume that we have access to a grasp sampler from which we can sample initial grasps from (line 1). In practice, can be any grasp candidate sampler, e.g., GraspNet-VAE [9] or a heuristic sampler such as GPD [6]. We then optimize these grasps over outer gradient-free iterations (lines 2-10). In detail: new batches of grasps are sampled using a multivariate Gaussian distribution with mean and covariance matrix . The covariance is manually selected in our experiments but can also be adaptive [29]. Lines 4 to 6 optimizes the lower bound . Line 8 and 9 assesses grasps using and selects the top grasps. In preliminary experiments and ablations (Sec. VIII), we found GRaCE-OPT to be superior to using either gradient-based or gradient-free methods alone.
V Criteria for successful 6-DoF grasps
In this section, we describe different grasp criteria used in our experiments. We assume a setup where a human user is asking the robot to perform a task, e.g., to “handover the scissors”. The robot has access to the natural language utterance from the human as well as observations of the environment (a point cloud).
As previously mentioned, we assume a probabilistic setup where the probability of criteria satisfaction is given by a classifier . We used four different classifiers that capture different quality aspects of a grasp: stability, executability, collision-free, and functional. We discuss these classifiers at a high-level and leave implementation details to the online code repository (made public if accepted).
Stability Classifier (S). We use the stability evaluator in [10]. The classifier takes as inputs a grasp pose and a point cloud of the object, and outputs a prediction of grasp stability.
Execution Classifier (E). Our execution classifier captures two important aspects of robot poses: reachability map [30] and kinematic singularity [31].

We calculate the manipulability score for a given grasp:
| (3) |
where is the Jacobian matrix and is the Inverse Kinematics (IK) solution. Then, we define the predicted grasp pose, , using the IK solution:
Finally, we combine this two quantities to yield,
| (4) |
where is the logistic sigmoid, and are scaling coefficients, is a lowest manipulability threshold that allows safe grasp execution, is a distance function between predicted grasp pose from the IK solution and current pose calculated in SE(3) [32] and is a IK tolerance.
Collision Detection Classifier (C). The backbone of our Collision Detection Classifier is the 3-D Signed Distance Function (SDF) [33]. For simplicity, we use the original version of SDF that is designed for convex objects. Let represent a point cloud represented with respect to the world frame with points and be a point within . The SDF for the box is defined as
| (5) |
where is the half-extent of the box in Cartesian coordinates. We decompose the gripper into three boxes , and as shown in Fig. 3.The SDF is differentiable and we use it to create our collision detection classifier:
| (6) |
where is a user-defined threshold and is a scale coefficient.
Intention Classifier (N). Our intention classifier outputs the probability that the grasp location coincides with their intent. We first extract the user’s intent (e.g., “Handover”) from their utterance (e.g., “Hand over the knife”) using JointBERT [34]. Our JointBERT model is trained on a curated dataset of programmatically generated queries and evaluated on sentences surveyed from test users. To evaluate if the grasp matches the intention, we use TaskGrasp [15] as it can identify affordance-rich and affordance-poor regions of objects. TaskGrasp evaluates grasps with respect to the point cloud and task, and outputs . As TaskGrasp inherently assumes that all grasps are stable before inference, we lower the score to zero if the grasp is more than 3cm away from the nearest point in the point cloud; we find that this modification helps to reduce false positives.
Summary and Ranking. The above classifiers are all differentiable and gradients can be obtained using modern auto-differention libraries such as PyTorch [35]. In our experiments, we rank the criteria as follows: the S-classifier has rank 1, the E-classifier and C-classifier have rank 2, and the N-classifier has rank 3.
VI Simulation Experiment
The goal of our experiments is to establish if using the GRaCE framework (i) yields suitable grasps in a complex environment, and (ii) trade-off multiple criteria. Moreover, GRaCE-OPT is more computationally expensive compared to a simple sample-and-filter approach (principally due to gradient computation). Is this added cost justified? Moreover, are the multiple criteria necessary for finding successful grasps and if so, can they be traded-off effectively? Our experiments are aimed at answering these questions. To simplify exposition, we will refer to the process of using GRaCE-OPT to optimize the expected utility in (2) as GRaCE.
VI-A Simulated Environments
We used IsaacGym from NVIDIA [8], which is a state-of-the-art simulator capable of simulating robot movement and object grasping. We engineered two simulation environments, namely a Shelf module and a Diner module:
-
•
Shelf consists of a two-layered shelf with common everyday items placed on both layers. The Shelf module is designed to be cluttered and complex. Hence, the optimal grasping region for each object is confined to a small area, reducing the effectiveness of sampling-based methods.
-
•
Diner consists of items that may be present in a typical dining setup, such as bowls, forks, a pan, and a spatula.
The graspable objects in these environments are from the ShapeNet dataset, and the shelves and tables were created using Blender. We packaged the Shelf and Diner modules as a set of OBJ files that can be loaded into any simulator capable of importing OBJ meshes.
VI-B Experiment Process
Perception. We first record point cloud data through IsaacGym’s simulated depth and segmentation cameras from multiple views, and segment out the target object from the environment.
Grasp Sampling and Optimization. GraspNet VAE [9] is then used to sample grasps and optimized with GRaCE. The resulting output is a list of grasp poses, along with their utility scores.
Hyperparameters. The scaling coefficients for the E and C classifiers are set at to approximate the behavior of a differentiable Heaviside function. A minimum manipulability threshold is established at , below which the robot’s operational capability is compromised. The collision threshold is defined as , aligning with the planner’s tolerance level. The learning rate for GRaCE-OPT is determined through trial and error, set at for translational adjustments and for rotational adjustments.
Grasp Planning, Execution, and Evaluation. The optimized grasps are passed to Moveit! [36] to generate trajectory plan. To minimize collision, instead of planning to the grasp pose, we plan the trajectory to a pre-grasp configuration 5cm linearly behind the actual grasp pose. The robot performs the grasping by moving the end-effector towards the object and closing its grippers. To execute the plan, we use a configuration-space controller to closely mimic and execute the planned trajectories. As IsaacGym is deterministic across sessions, only one execution attempt of each trajectory was performed. A grasp was termed as successful if the target object is held by the gripper fingers after the trajectory was executed. Note that this measure of success excludes the intention criteria (which is subjective and handled separately).
Baseline Methods. We compared the following methods:
-
•
GRaCE as described with all four classifers.
-
•
GRaCE with only the S-classifier. This ablation uses a single criteria (stability) and is similar to the refinement used in GraspNet [9] and its variants. This baseline serves to represent grasping methods where only a single criteria is applied.
-
•
Ablations of GRaCE by removing criteria, e.g., SE denotes that only the stability and execution classifier were used. These ablations enable us to see if excluding important criteria leads to more failures.
-
•
Sample-and-Filter, termed as “Filter”, initially samples candidate grasps and subsequently filters them according to a predefined threshold of the grasp utility function. When used with the GraspNet VAE (as in our experiments), this baseline represents a modern deep-generative approach to grasping that allows for multiple criteria.

VI-C Results
In this section, we summarize our main findings. In general, we find GRaCE to be superior to filtering on both the Shelf and Diner scenarios. Moreover, it is able to prioritize important criteria to find higher utility grasps.
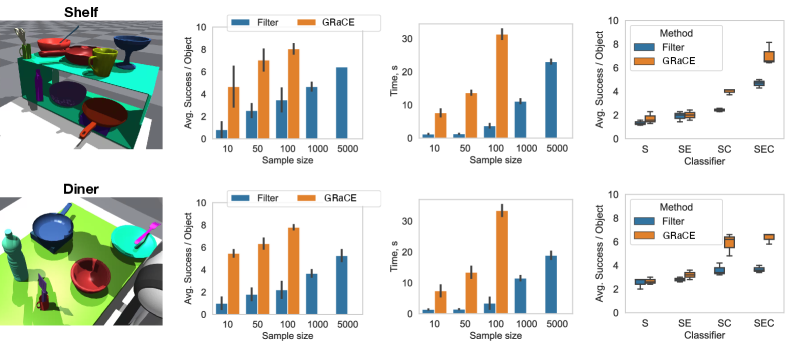
Is optimization really necessary? Does GRaCE outperform Sample-and-Filter? We evaluated GRaCE (SEC) against sample-and-filter with different sample sizes (10, 50, 100). Fig. 4 shows the average number of successes per object for the top-10 grasps across the different objects in the Shelf and Diner environments (seven and five objects, respectively). Note that the intention criterion was excluded as compliance with user intent involves subjective evaluation.
In Fig. 4, we observe that GRaCE outperforms Filter across the same sampling sizes (10, 50, 100). We further ran Filter with larger sample sizes (1000 and 5000), which enabled it to achieve attain similar performance to GRaCE. At 5000 samples, Filter performs similarly to GRaCE using 50 samples. However, this also resulted in it requiring almost 2x longer compute times. In short, although GRaCE is more expensive per sample, it is able to achieve better grasps with fewer samples.
Can GRaCE optimize multiple criteria to find successful grasps? The results of our GRaCE ablations are shown in Fig. 4. We observe that the using all three classifiers (SEC) resulted in the best performance. The marked increase in performance from SE to SC may be attributed to the cluttered nature of Shelf and Diner, where many candidate grasp poses can collide with other objects. Qualitatively, the successful grasps for the pan (shown in blue in Fig. 6) are biased towards collision-free areas when other objects are on the shelf objects.
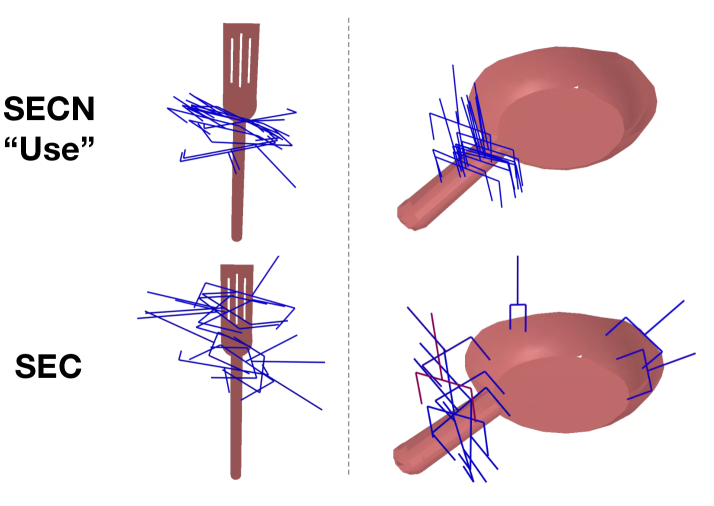


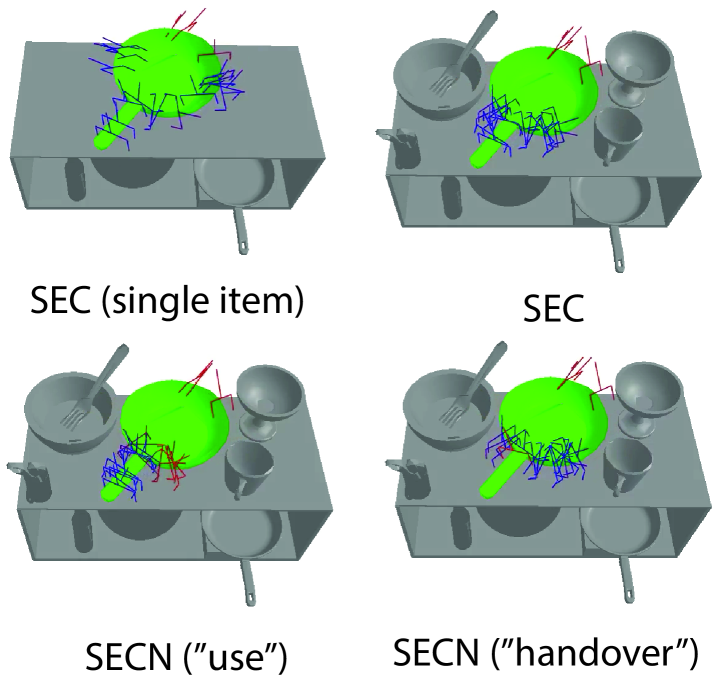
Does GRaCE with the intention classifier generate successful functional grasps? More precisely, we sought to evaluate if (i) GRaCE would generate grasps in regions matching the user intent if the higher-ranked criteria can be satisfied, and (ii) prioritize the higher-ranked criteria, even if the resulting grasp has violates the the functional criteria. To that end, we selected four objects (shown in Fig. 5) and paired with pan and spatula with the “Use” intention, and the scissors and fork with the “handover” intention.
Fig. 7 shows the grasps generated with and without the intention criteria. To elaborate, the spatula can be separated into two regions: handle, which is ideal to grasp for “use”, and the head, which should not be grasped for this purpose. Notably, both of these regions satisfy the stability, executable, and collision-free criteria. We see that GRaCE using only SEC generated grasps in both regions, while GRaCE with SECN produced grasps only at the handle. Similar grasps can be observed for the pan. Turning our attention to the “handover” intent, the scissors and fork are in placements that limit access to regions that have coincide with the “handover” intention. In this case, we observe GRaCE (with SECN) to forgoes these regions and instead produces grasps that satisfy the other, more highly ranked, criteria (examples in Fig. 8). In Fig. 6, the “use” and “handover” intentions bias grasps toward the handle and body of the pan, respectively.
VII Real-world Experiments
Thus far, we have discussed GRaCE in simulation settings, but does GRaCE’s performance carry over to the real world? We conducted real-world tests comparing GRaCE against the filter baseline, similar to the simulation setup.
Experimental Setup. We use a Franka Emika Panda with a RGB-D camera (Intel RealSense L515 [37]) attached to the last link of the robot. The general execution pipeline for the real-world experiments are similar to the simulations except for perception. We use Detectron2 [38] to segment out the mask for our object of the interest. Then, we apply this mask to the corresponding depth map, and calculate the point clouds using the camera’s intrinsic and extrinsic matrices. We also use built-in filter functions of Open3D library [39] to remove outliers for pointcloud. During our experiments, we find that this method of processing the pointcloud resulted in more robust points compared to data driven methods such as Unseen Object Clustering [40] and Squeezesegv3 [41].
Scenarios. We tested our setup to grasp objects in two different scenarios:
-
•
Box, where the robot was tasked to generate grasps for 10 different items in a clutter. Here, there is no intention criteria and the goal was to execute a stable grasp and lift the object.
-
•
Bowl, where the robot attempted to grasp one of three different items (a wooden spoon, a knife, or a screwdriver) with the intent to handover the object. A grasp was successful if the robot managed to lift the object out of the bowl and hand it over to the experimenter.
Both these settings are challenging due to (i) noisy perception and (ii) the feasible grasp region for each object was generally small due to the clutter. In each experiment, we conducted 10 trials for each object to be grasped and recorded the number of grasp successes; in total, our experiment involved 260 real-world grasps. We set GRaCE to use 50 samples, while Filter used 1000 samples. Both methods have comparable timings; GRaCE took an average of seconds to obtain a grasp, while Filter took seconds. Note that these timings are for un-optimized Python implementations and future work can look into reducing this computation time.

| Method | Box | Bowl |
|---|---|---|
| GRaCE | 65% (0.10) | 57% (0.06) |
| Filter | 31% (0.12) | 33% (0.06) |
Does GRaCE find successful multi-criteria grasps in real-world scenarios? Our results, summarized in Table III, show that GRaCE outperforms Filter in both domains by a significant margin. In both cases, GRaCE achieves approximately double the success rate of Filter. Fig. 9 depicts various successful 6-DoF grasps in the real-world experiment for the box and bowl scenarios. Qualitatively, we found GRaCE to more reliably return a feasible grasp; in contrast, Filter failed to return any suitable grasp in 26 out of the 130 trials (20%). Other failures in both cases were commonly due to perception errors and robot trajectories executed near singular configurations, leading to grasp offsets, collisions, and robot errors (see Table IV). Overall, our findings affirm that GRaCE sustains its performance in real-world conditions.
| Box | Bowl | |||
|---|---|---|---|---|
| Filter | GRaCE | Filter | GRaCE | |
| RE | 16% (0.03) | 31% (0.03) | 12% (0.06) | 20% (0.014) |
| GF | 58% (0.12) | 69% (0.08) | 50% (0.1) | 30% (0.07) |
| NG | 26% (0.12) | 0% (0.00) | 38% (0.06) | 50% (0.07) |
VIII Further Ablation Experiments
In this section, we report on additional ablation experiments designed to evaluate changes in priorities affect outcomes, and the effect of GRaCE-OPT’s hyperparameters (specifically, the number of steps and lower-bound update steps ). In the following experiments, we re-ran our simulation experiment in the Shelf environment with the Stability (S), Execution (E), and Collision (C) criteria.
Does changing criteria priorities alter the resultant grasps? In this ablation, we changed the priorities of the Execution and the Collision criteria. Table V shows the average scores of the grasps for each of the different criteria. Compared to the initial sampled grasps, GRaCE improves scores differently depending on the specified priorities. For example, when C was prioritized over E (SCE), the average score for the collision criteria was 0.89. This fell to 0.63 when the E classifier had a higher priority (SEC). The score for the Stability criteria remained relatively unchanged since its priority wasn’t altered.
| S | E | C | |
|---|---|---|---|
| Initial | 0.26 | 0.57 | 0.30 |
| S>C=E | 0.70 | 0.63 | 0.83 |
| S>C>E | 0.69 | 0.56 | 0.89 |
| S>E>C | 0.72 | 0.76 | 0.63 |
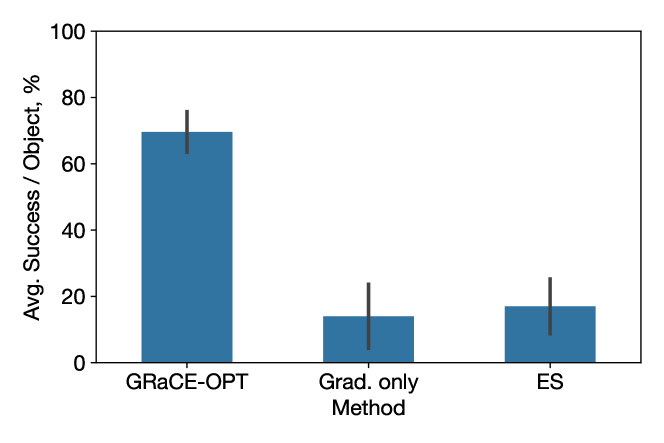
Is combining gradient-based and gradient-free optimization beneficial? GRaCE-OPT uses a hybrid optimization scheme that blends derivative-free search with gradient-based local search. Fig. 11 shows GRaCE-OPT significantly outperforms using either solely gradient-based expected utility maximization (50 samples) or gradient-free optimization via ES (1000 samples). In the Shelf environment, GRaCE-OPT achieves more than double the average success rate compared to the competing methods.
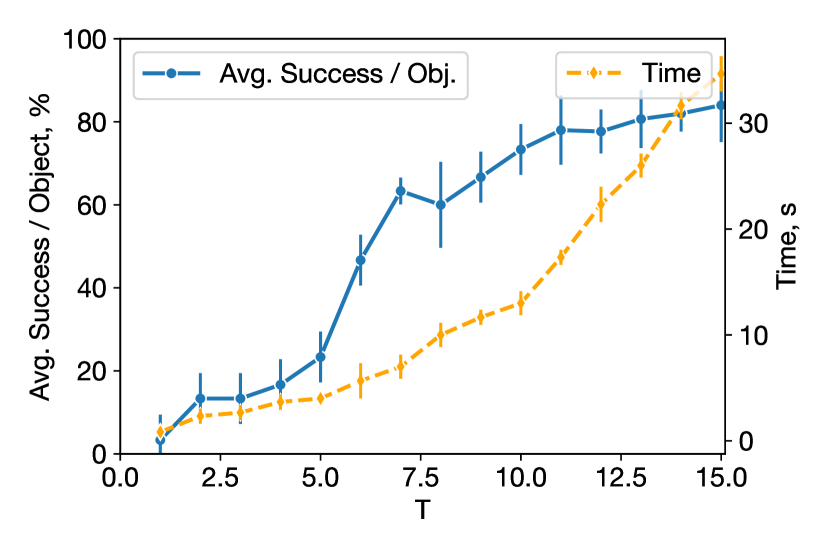
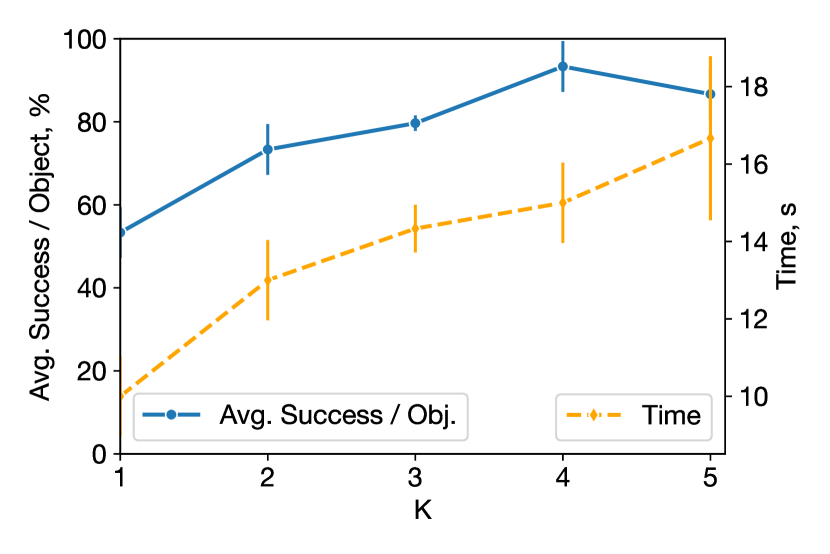
What is the effect of changing the number of update steps and in GRaCE-OPT? In our experiments, we chose and based on our computational budget. Higher values of and lead to longer optimization times and improved grasp outcomes as shown in Fig. 12.
IX Conclusions and Future Work
In this study, we introduced GRaCE, a probabilistic hierarchical rank-based modular framework designed for optimizing robotic grasps based on multiple, often conflicting, criteria. We formulated these criteria as a utility function based on the expected ranks of grasp; this takes into account the uncertainty inherent in many real-world grasping scenarios. In addition, we presented GRaCE-OPT as a hybrid optimization technique to optimize grasps using both gradient-based and gradient-free methods. Our experimental evaluations show GRACE’s efficacy in generating high-quality grasps in complex, cluttered environments both in simulation and real-world experiments.
Limitations and Future Work. The proposed work faces two primary limitations. Firstly, the reliance of GRaCE-OPT on gradient calculations leads to increased computational costs with the addition of more criteria to the framework. A direct approach would be to improve the efficiency of the gradient computations, e.g., via approximations. Alternatively, one could explore exclusively gradient-free methods. Secondly, while GRaCE has been tested with key criteria like reachability, singularity, and collision, the aspect of plannability remains unexplored. A lack of a feasible plan could render the final grasp unexecutable. A potential solution for future work involves integrating a planner-based classifier into the framework. Additionally, GRaCE could be expanded to include more criteria, such as tactile feedback (e.g., [42, 43]) for grasping of soft or deformable objects. We believe GRaCE’s flexibility and modularity opens up promising avenues for future research.
Acknowledgements
This research is supported by the National Research Foundation Singapore and DSO National Laboratories under the AI Singapore Programme (AISG Award No: AISG2-RP-2020-016).
References
- [1] M. Wilson and A. Borning, “Hierarchical constraint logic programming,” The Journal of Logic Programming, vol. 16, no. 3-4, pp. 277–318, 1993.
- [2] J. Tuumova, L. I. R. Castro, S. Karaman, E. Frazzoli, and D. Rus, “Minimum-violation ltl planning with conflicting specifications,” in 2013 American Control Conference. IEEE, 2013, pp. 200–205.
- [3] S. Veer, K. Leung, R. Cosner, Y. Chen, and M. Pavone, “Receding horizon planning with rule hierarchies for autonomous vehicles,” arXiv preprint arXiv:2212.03323, 2022.
- [4] A. Pourchot and O. Sigaud, “Cem-rl: Combining evolutionary and gradient-based methods for policy search,” arXiv preprint arXiv:1810.01222, 2018.
- [5] H.-G. Beyer and H.-P. Schwefel, “Evolution strategies–a comprehensive introduction,” Natural computing, vol. 1, pp. 3–52, 2002.
- [6] A. Ten Pas, M. Gualtieri, K. Saenko, and R. Platt, “Grasp pose detection in point clouds,” The International Journal of Robotics Research, vol. 36, no. 13-14, pp. 1455–1473, 2017.
- [7] H. Liang, X. Ma, S. Li, M. Görner, S. Tang, B. Fang, F. Sun, and J. Zhang, “Pointnetgpd: Detecting grasp configurations from point sets,” in 2019 International Conference on Robotics and Automation (ICRA). IEEE, 2019, pp. 3629–3635.
- [8] V. Makoviychuk, L. Wawrzyniak, Y. Guo, M. Lu, K. Storey, M. Macklin, D. Hoeller, N. Rudin, A. Allshire, A. Handa, and G. State, “Isaac gym: High performance gpu-based physics simulation for robot learning,” 2021.
- [9] A. Mousavian, C. Eppner, and D. Fox, “6-dof graspnet: Variational grasp generation for object manipulation,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019, pp. 2901–2910.
- [10] T. Taunyazov, H. Zhang, J. P. Eala, N. Zhao, and H. Soh, “Refining 6-dof grasps with context-specific classifiers,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, 2023.
- [11] Y. Zhou and K. Hauser, “6dof grasp planning by optimizing a deep learning scoring function,” in Robotics: Science and systems (RSS) workshop on revisiting contact-turning a problem into a solution, vol. 2, 2017, p. 6.
- [12] M. Sundermeyer, A. Mousavian, R. Triebel, and D. Fox, “Contact-graspnet: Efficient 6-dof grasp generation in cluttered scenes,” in 2021 IEEE International Conference on Robotics and Automation (ICRA), 2021.
- [13] H.-S. Fang, C. Wang, M. Gou, and C. Lu, “Graspnet-1billion: A large-scale benchmark for general object grasping,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2020, pp. 11 444–11 453.
- [14] Y. Zhang, J. Hang, T. Zhu, X. Lin, R. Wu, W. Peng, D. Tian, and Y. Sun, “Functionalgrasp: Learning functional grasp for robots via semantic hand-object representation,” IEEE Robotics and Automation Letters, 2023.
- [15] A. Murali, W. Liu, K. Marino, S. Chernova, and A. Gupta, “Same object, different grasps: Data and semantic knowledge for task-oriented grasping,” in Conference on Robot Learning, 2020.
- [16] H. Dang and P. K. Allen, “Semantic grasping: planning task-specific stable robotic grasps,” Autonomous Robots, vol. 37, pp. 301–316, 2014.
- [17] K. Li, J. Wang, L. Yang, C. Lu, and B. Dai, “Semgrasp: Semantic grasp generation via language aligned discretization,” arXiv preprint arXiv:2404.03590, 2024.
- [18] A. Nguyen, D. Kanoulas, D. G. Caldwell, and N. G. Tsagarakis, “Detecting object affordances with convolutional neural networks,” in 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2016, pp. 2765–2770.
- [19] Y. Li, L. Schomaker, and S. H. Kasaei, “Learning to grasp 3d objects using deep residual u-nets,” in 2020 29th IEEE International Conference on Robot and Human Interactive Communication (RO-MAN). IEEE, 2020, pp. 781–787.
- [20] P. Mandikal and K. Grauman, “Learning dexterous grasping with object-centric visual affordances,” in 2021 IEEE international conference on robotics and automation (ICRA). IEEE, 2021, pp. 6169–6176.
- [21] X. Chang and Y. Sun, “Text2grasp: Grasp synthesis by text prompts of object grasping parts,” arXiv preprint arXiv:2404.15189, 2024.
- [22] R. Mirjalili, M. Krawez, S. Silenzi, Y. Blei, and W. Burgard, “Lan-grasp: Using large language models for semantic object grasping,” arXiv preprint arXiv:2310.05239, 2023.
- [23] C. Tang, D. Huang, L. Meng, W. Liu, and H. Zhang, “Task-oriented grasp prediction with visual-language inputs,” in 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2023, pp. 4881–4888.
- [24] F. Waltz, “An engineering approach: hierarchical optimization criteria,” IEEE Transactions on Automatic Control, vol. 12, no. 2, pp. 179–180, 1967.
- [25] R. Dimitrova, M. Ghasemi, and U. Topcu, “Maximum realizability for linear temporal logic specifications,” in Automated Technology for Verification and Analysis: 16th International Symposium, ATVA 2018, Los Angeles, CA, USA, October 7-10, 2018, Proceedings 16. Springer, 2018, pp. 458–475.
- [26] A. Bicchi and V. Kumar, “Robotic grasping and contact: A review,” in Proceedings 2000 ICRA. Millennium conference. IEEE international conference on robotics and automation. Symposia proceedings (Cat. No. 00CH37065), vol. 1. IEEE, 2000, pp. 348–353.
- [27] S. Hochreiter, “The vanishing gradient problem during learning recurrent neural nets and problem solutions,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, vol. 6, no. 02, pp. 107–116, 1998.
- [28] B. Hanin, “Which neural net architectures give rise to exploding and vanishing gradients?” Advances in neural information processing systems, vol. 31, 2018.
- [29] C. Igel, N. Hansen, and S. Roth, “Covariance matrix adaptation for multi-objective optimization,” Evolutionary computation, vol. 15, no. 1, pp. 1–28, 2007.
- [30] A. Makhal and A. K. Goins, “Reuleaux: Robot base placement by reachability analysis,” in 2018 Second IEEE International Conference on Robotic Computing (IRC). IEEE, 2018, pp. 137–142.
- [31] M. Rubagotti, T. Taunyazov, B. Omarali, and A. Shintemirov, “Semi-autonomous robot teleoperation with obstacle avoidance via model predictive control,” IEEE Robotics and Automation Letters, vol. 4, no. 3, pp. 2746–2753, 2019.
- [32] C. Belta and V. Kumar, “Euclidean metrics for motion generation on se (3),” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, vol. 216, no. 1, pp. 47–60, 2002.
- [33] T. Chan and W. Zhu, “Level set based shape prior segmentation,” in 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), vol. 2. IEEE, 2005, pp. 1164–1170.
- [34] Q. Chen, Z. Zhuo, and W. Wang, “Bert for joint intent classification and slot filling,” 2019. [Online]. Available: https://arxiv.org/abs/1902.10909
- [35] S. Imambi, K. B. Prakash, and G. Kanagachidambaresan, “Pytorch,” Programming with TensorFlow: Solution for Edge Computing Applications, pp. 87–104, 2021.
- [36] S. Chitta, I. Sucan, and S. Cousins, “Moveit! [ros topics],” IEEE Robotics & Automation Magazine, vol. 19, no. 1, pp. 18–19, 2012.
- [37] F. Lourenço and H. Araujo, “Intel realsense sr305, d415 and l515: Experimental evaluation and comparison of depth estimation.” in VISIGRAPP (4: VISAPP), 2021, pp. 362–369.
- [38] Y. Wu, A. Kirillov, F. Massa, W.-Y. Lo, and R. Girshick, “Detectron2,” https://github.com/facebookresearch/detectron2, 2019.
- [39] Q.-Y. Zhou, J. Park, and V. Koltun, “Open3d: A modern library for 3d data processing,” arXiv preprint arXiv:1801.09847, 2018.
- [40] Y. Xiang, C. Xie, A. Mousavian, and D. Fox, “Learning rgb-d feature embeddings for unseen object instance segmentation,” in Conference on Robot Learning (CoRL), 2020.
- [41] C. Xu, B. Wu, Z. Wang, W. Zhan, P. Vajda, K. Keutzer, and M. Tomizuka, “Squeezesegv3: Spatially-adaptive convolution for efficient point-cloud segmentation,” in Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part XXVIII 16. Springer, 2020, pp. 1–19.
- [42] T. Taunyazoz, W. Sng, H. H. See, B. Lim, J. K. andAbdul Fatir Ansari, B. Tee, and H. Soh, “Event-driven visual-tactile sensing and learning for robots,” in Proceedings of Robotics: Science and Systems, July 2020.
- [43] T. Taunyazov, L. S. Song, E. Lim, H. H. See, D. Lee, B. C. K. Tee, and H. Soh, “Extended tactile perception: Vibration sensing through tools and grasped objects,” in IEEE International Conference on Intelligent Robots and Systems (IROS), 2021.