GNN-SKAN: Harnessing the Power of SwallowKAN to Advance Molecular Representation Learning with GNNs

Ruifeng Li^1,2, Mingqian Li², Wei Liu³, Hongyang Chen^2*

Abstract

Effective molecular representation learning is crucial for advancing molecular property prediction and drug design. Mainstream molecular representation learning approaches are based on Graph Neural Networks (GNNs). However, these approaches struggle with three significant challenges: insufficient annotations, molecular diversity, and architectural limitations such as over-squashing, which leads to the loss of critical structural details. To address these challenges, we introduce a new class of GNNs that integrates the Kolmogorov-Arnold Networks (KANs), known for their robust data-fitting capabilities and high accuracy in small-scale AI + Science tasks. By incorporating KANs into GNNs, our model enhances the representation of molecular structures. We further advance this approach with a variant called SwallowKAN (SKAN), which employs adaptive Radial Basis Functions (RBFs) as the core of the non-linear neurons. This innovation improves both computational efficiency and adaptability to diverse molecular structures. Building on the strengths of SKAN, we propose a new class of GNNs, GNN-SKAN, and its augmented variant, GNN-SKAN+, which incorporates a SKAN-based classifier to further boost performance. To our knowledge, this is the first work to integrate KANs into GNN architectures tailored for molecular representation learning. Experiments across 6 classification datasets, 6 regression datasets, and 4 few-shot learning datasets demonstrate that our approach achieves new state-of-the-art performance in terms of accuracy and computational cost. The code is available at https://github.com/Lirain21/GNN-SKAN.git.

Refer to caption — Figure 1: The visualization of our models’ performance compared to the SOTAs on the HIV dataset. The circle size represents per-epoch computational cost. Purple circles represent self-supervised methods, green and yellow circles represent supervised methods, and blue circles represent our proposed methods (GNN-SKAN, GNN-SKAN+).

1 Introduction

Precisely predicting the physicochemical properties of molecules (Livingstone 2000; Li et al. 2022), drug activities (Datta and Grant 2004; Sadybekov and Katritch 2023), and material characteristics (Pilania 2021; Jablonka et al. 2024) is essential for advancing drug discovery and material science. The success of these predictions significantly hinges on the quality of molecular representation learning, which transforms molecular structures into high-dimensional representations (Fang et al. 2022; Yang et al. 2019). However, there are two significant challenges in this field: 1) a lack of adequate labeled data due to low screening success rates (Wieder et al. 2020); 2) wide variations in molecular structures, compositions, and properties, which reflect molecular diversity (Guo et al. 2022).

In molecular representation learning, mainstream GNN-based methods (Yi et al. 2022; Fang et al. 2022; Yu and Gao 2022; Chen et al. 2024; Pei et al. 2024) model the topological structure of molecules by representing atoms as nodes and bonds as edges. Most approaches commonly employ the message-passing (MP) mechanism (Gilmer et al. 2020), known as MP-GNNs, to aggregate and update representations across molecular graphs. Notable efforts include Graph Convolutional Network (GCN) (Kipf and Welling 2017), Graph Attention Network (GAT) (Veličković et al. 2018), and Graph Isomorphism Network (GIN) (Xu et al. 2018). Remarkably, interactions among distant atoms or functional groups within a molecule are crucial for molecular representation learning (Xiong et al. 2019). However, GNN-based approaches often encounter the challenge of over-squashing, where information is overly compressed when passed between long-distance atoms (Di Giovanni et al. 2023). This compression may lead to the loss of crucial structural details, impairing the accuracy of molecular representations.

Liu et al. recently introduce the Kolmogorov-Arnold Network (KAN), which has been widely acknowledged for its high accuracy in small-scale AI + Science tasks. Unlike Multi-Layer Perceptrons (MLPs) (Cybenko 1989), which use fixed activation functions on nodes (“neurons”), KAN employs learnable activation functions on edges (“weights”). This unique design greatly enhances KAN’s performance, achieving 100 times greater accuracy than a four-layer MLP when solving partial differential equations (PDEs) with a two-layer structure (Liu et al. 2024). Additionally, KAN excels in various tasks, including image recognition (Azam and Akhtar 2024; Wang et al. 2024), image generation (Li et al. 2024), and time series prediction tasks (Vaca-Rubio et al. 2024; Xu, Chen, and Wang 2024). Despite its success, KAN has not yet become the standard on public molecular representation benchmarks.

In this paper, we observe that KAN’s robust data-fitting ability and high accuracy in small-scale AI + Science tasks make it ideal for addressing the challenges of insufficient labeled data in molecular representation learning. Additionally, KAN’s ability to effectively capture important molecular structure details helps to mitigate the limitations of GNN-based architectures, such as over-squashing. Several studies (Kiamari, Kiamari, and Krishnamachari 2024; Bresson et al. 2024; Zhang and Zhang 2024) have integrated KAN into graph-based tasks, highlighting its potential. However, these efforts often overlook the efficiency challenges of KAN. Moreover, there has been limited effort to adapt KAN specifically for molecular representation learning. Consequently, integrating KAN into standard GNNs for molecular representation learning remains an open problem.

To bridge this gap, we introduce a new class of GNNs, GNN-SKAN, and its augmented variant, GNN-SKAN+, tailored for molecular representation learning. Our key innovation lies in adapting KAN to molecular graphs by developing a variant that preserves KAN’s high accuracy in small-scale tasks while improving efficiency and flexibility in handling diverse molecular structures. Herein, we propose SwallowKAN (SKAN), which replaces B-splines with adaptive RBFs to achieve these goals. By combining the strengths of SKAN and GNNs, we have developed a robust and versatile approach to molecular representation learning. Specifically, we design a hybrid architecture that integrates GNN and SKAN, using a KAN-enhanced message-passing mechanism. To ensure versatility, SKAN is used as the update function to boost the expressiveness of the message-passing process. Additionally, we introduce GNN-SKAN+ which employs SKAN as the classifier to further reinforce model performance. Notably, our approach holds three key benefits: 1) Superior Performance: GNN-SKAN and GNN-SKAN+ demonstrate superior prediction ability, robust generalization to unseen molecular scaffolds, and versatile transferability across different GNN architectures. 2) Efficiency: Our models achieve comparable or superior results to the SOTA self-supervised methods, while requiring less computational time and fewer parameters (Figure 1. 3) Few-shot Learning Ability: GNN-SKAN shows great potential in few-shot learning scenarios, achieving an average improvement of 6.01% across few-shot benchmarks.

The main contributions of this work are summarized as follows:

•

To the best of our knowledge, we are the first to integrate KAN’s exceptional approximation capabilities with GNNs’ strengths in handling molecular graphs. This integration has led us to propose a new class of GNNs, termed GNN-SKAN, and its augmented variant, GNN-SKAN+, for molecular representation learning.
•

We propose SwallowKAN (SKAN), which introduces learnable RBFs as base function. This modification not only effectively addresses the slow speed of the original KAN but also significantly enhances the model’s adaptability to diverse data distributions.
•

We conduct a theoretical analysis of the parameter counts and computational complexity of KAN and SKAN. Our comparative analysis shows that SKAN exhibits a higher computational efficiency.
•

Our method achieves high accuracy and robust generalization on molecular property prediction tasks, surpassing or matching the SOTA models with lower time and memory requirements (Figure 1). It also excels in few-shot scenarios, with an average improvement of 6.01% across 4 few-shot learning benchmarks (Section 4).

2 Related Work

Molecular Representation Learning.

Existing molecular representation learning approaches can be broadly classified into three categories: 1) GNN-based approaches: Methods like MolCLR (Wang et al. 2022) and KANO (Fang et al. 2023) leverage contrastive learning framework, while MGSSL (Zhang et al. 2021) and GraphMAE (Hou et al. 2022) employ generative pre-training strategies. Although these methods effectively learn molecular representations, they face the challenge of over-squashing (Black et al. 2023). 2) Transformer-based approaches: Models such as MolBERT (Fabian et al. 2020), ChemBERTa (Chithrananda, Grand, and Ramsundar 2020), ChemBERTa-2 (Ahmad et al. 2022), SELFormer (Yüksel et al. 2023), and MolGen (Fang et al. 2024) enhance molecular representation learning with the self-attention mechanism, but they suffer from the quadratic complexity (Vaswani et al. 2017). 3) Combination of both (Graph Transformers): These models, including Graphormer (Ying et al. 2021), GPS (Rampášek et al. 2022), Grover (Rong et al. 2020), and Uni-Mol (Zhou et al. 2023), which combine message-passing neural networks with Transformer to enhance expressive power. However, they also suffer from high computational complexity (Keles, Wijewardena, and Hegde 2023). Unlike previous methods, we uniquely integrate GNNs with SKAN, a proposed KAN variant, to overcome the challenges present in existing molecular representation learning approaches.

Kolmogorov-Arnold Networks (KANs).

KAN is well-regarded for its ability to approximate complex functions using learnable activation functions on edges (Liu et al. 2024). Recent work has extended KAN to the graph-structured domain. For instance, GKAN (Kiamari, Kiamari, and Krishnamachari 2024; De Carlo, Mastropietro, and Anagnostopoulos 2024), KAGNNs (Bresson et al. 2024), and GraphKAN (Zhang and Zhang 2024) integrate KAN into GNNs to enhance performance. However, these approaches do not address KAN’s efficiency issues. For example, GKAN incurs computational costs approximately 100 times higher than the standard GNNs on the Cora dataset (De Carlo, Mastropietro, and Anagnostopoulos 2024), significantly hindering the broader adoption of KAN in graph-based applications. To improve the efficiency of KAN, several approaches have been proposed to replace B-splines with simpler base functions (Ta 2024). Notably, FastKAN (Li 2024) addresses this issue by replacing B-splines with RBFs (Wu et al. 2012), and GP-KAN (Chen 2024) employs Gaussian Processes (GPs) (Seeger 2004) as an alternative, particularly for image classification tasks. Unlike these approaches, we introduce SKAN, a new KAN variant that incorporates adaptable RBFs specifically designed for efficient molecular representation learning. The differences between KAN, FastKAN and our SKAN are shown in Figure 2.

3 The proposed approach: GNN-SKAN

3.1 Overview

The framework of GNN-SKAN is illustrated in Figure 3. This section focuses on the details of the implementation of our method. These details are crucial for ensuring the speed and reliability of the network.

Notation.

Let $G=(\mathcal{V},\mathcal{E})$ be a molecular graph, where $\mathcal{V}$ represents the set of nodes and $\mathcal{E}$ represents the set of edges. The number of nodes is $N=|\mathcal{V}|$ . Let $\mathbf{H}=\{\mathbf{h}_{v}^{(0)}|v\in\mathcal{V}\}$ denote the initial features of nodes, and $\mathbf{E}=\{\mathbf{b}_{uv}|(u,v)\in\mathcal{E}\}$ denote the edge features. Let $\mathbf{z}$ represent the graph-level representation, $\hat{y}$ represent the graph-level prediction, and $y$ represent the molecular property label (i.e., the ground-truth label). For the RBF, $c_{w}$ and $bw_{w}$ are the learnable center and bandwidth, respectively.

3.2 Preliminary

Kolmogorov-Arnold Representation Theorem (KART).

KART (Arnold 2009; Kolmogorov 1957; Braun and Griebel 2009) states that any multivariate continuous function defined on a bounded domain can be expressed as a finite composition of continuous single-variable functions and addition operations. Formally, for a smooth function $f:[0,1]^{n}\rightarrow\mathbb{R}$ with $n$ variables $\mathbf{x}=x_{1},x_{2},\ldots,x_{n}$ , the theorem guarantees the existence of the following representation:

f\left(x_{1},\ldots,x_{n}\right)=\sum_{q=1}^{2n+1}\Phi_{q}\left(\sum_{p=1}^{n}\varphi_{q,p}\left(x_{p}\right)\right)\text{, }

(1)

where $\Phi_{q}:\mathbb{R}\rightarrow\mathbb{R}$ and $\varphi_{q,p}:[0,1]\rightarrow\mathbb{R}$ .

The Design of KAN.

Unlike the simple 2-layer KAN described by Eq. 1, which follows a $[n,2n+1,1]$ structure, KAN can be generalized to arbitrary widths and depths. Specifically, KAN consists of $L$ layers and generates outputs based on the input vector $\mathbf{x}\in\mathbb{R}^{n}$ :

\operatorname{KAN}(\mathbf{x})=\left(\Phi_{L-1}\circ\Phi_{L-2}\circ\cdots\circ\Phi_{1}\circ\Phi_{0}\right)\mathbf{x}\text{, }

(2)

where $\Phi_{l}$ represents the function matrix of the $l^{th}$ layer. Each layer of KAN, defined by the function matrix $\Phi_{l}$ , is formed as follows:

\mathbf{x}_{l+1}=\underbrace{\left(\begin{array}[]{cccc}\phi_{l,1,1}(\cdot)&\phi_{l,1,2}(\cdot)&\cdots&\phi_{l,1,n_{l}}(\cdot)\\ \phi_{l,2,1}(\cdot)&\phi_{l,2,2}(\cdot)&\cdots&\phi_{l,2,n_{l}}(\cdot)\\ \vdots&\vdots&&\vdots\\ \phi_{l,n_{l+1},1}(\cdot)&\phi_{l,n_{l+1},2}(\cdot)&\cdots&\phi_{l,n_{l+1},n_{l}}(\cdot)\end{array}\right)}_{\bm{\Phi}_{l}}\mathbf{x}_{l}\text{, }

(3)

where $\phi_{l,j,i}$ denotes the activation function connecting neuron $i$ in layer $l$ to neuron $j$ in layer $l+1$ . The network utilizes $n_{l}\times n_{l+1}$ such activation functions between each layer.

KAN enhances its learning capability by utilizing residual activation functions $\phi(x)$ that integrate a basis function and a spline function:

\phi(x)=w_{b}b(x)+w_{s}\operatorname{Spline}(x)\text{, }

(4)

where $b(x)$ is the $silu(x)$ function, and $\operatorname{Spline}(x)$ is a linear combination of B-splines (Unser, Aldroubi, and Eden 1993). The parameters $w_{b}$ and $w_{s}$ are learnable.

3.3 Architecture

Molecular representation learning with MP-GNNs generally involves three key steps: Aggregation, Update, and Readout. In this work, we generalize KAN to molecular graphs for molecular representation learning. To address KAN’s limitations in computational efficiency and adaptability, we introduce SwallowKAN (SKAN), a variant of KAN that employs learnable RBFs as activation functions. SKAN adjusts its parameters adaptively based on the data distribution, enabling effective modeling of molecules with diverse scaffolds. Building on the strengths of SKAN, we propose a new class of GNNs, GNN-SKAN, and its advanced version, GNN-SKAN+, which use a KAN-enhanced message-passing mechanism to improve molecular representation learning. Specifically, SKAN is employed as the update function, allowing seamless integration into any MP-GNN. For GNN-SKAN+, SKAN also serves as the classifier to further enhance performance. The complete algorithm of our approach is shown in Algorithm 1.

Step 1: Aggregation.

In a molecular graph $G=(\mathcal{V},\mathcal{E})$ , let $\mathbf{h}^{(0)}\in\mathbb{R}^{n}$ represent the initial node features and $\mathbf{b}\in\mathbb{R}^{n}$ represent the initial edge features. At the $d^{th}$ layer, GNN utilizes an aggregation function to combine information from the neighboring nodes of $v$ , forming a new message representation $\mathbf{m}_{v}^{(d)}\in\mathbb{R}^{n}$ :

	$\displaystyle\mathbf{m}_{v}^{(d)}=$	$\displaystyle\operatorname{AGGREGATE}^{(d)}\left(\left\{\left(\mathbf{h}_{v}^{(d-1)},\mathbf{h}_{u}^{(d-1)},\mathbf{b}_{vu}\right)\right.\right.$
		$\displaystyle\left.\left.\mid u\in\mathcal{N}(v)\right\}\right)$		(5)

where $u\in\mathcal{N}(v)$ denotes the set of neighboring nodes of node $v$ .

Step 2: Update.

After computing the aggregated message $\mathbf{m}_{v}^{(d)}$ for node $v$ , the message is used to update the representation of node $v$ at layer $d$ :

\mathbf{h}_{v}^{(d)}=\operatorname{UPDATE}^{(d)}\left(\mathbf{h}_{v}^{(d-1)},\mathbf{m}_{v}^{(d)}\right)\text{.}

(6)

To efficiently adapt to various data distributions, we design an augmented KAN, SwallowKAN (SKAN), with learnable RBFs to replace the original update function. The data center $c_{w}$ and the bandwidth $bw_{w}$ efficiently adapt to the data distribution. The update function can be rewritten as follows:

\mathbf{h}_{v}^{(d)}=\operatorname{SKAN}^{(d)}\left(\left(1+\epsilon^{(d)}\right)\cdot\mathbf{h}_{v}^{(d-1)}+\mathbf{m}_{v}^{(d)}\right)\text{,}

(7)

where $\epsilon^{(d)}$ is a parameter. Specifically, let $\mathbf{x}=\left(1+\epsilon^{(d)}\right)\cdot\mathbf{h}_{v}^{(d-1)}+\mathbf{m}_{v}^{(d)}$ . The residual activation function of SKAN at the $d^{th}$ layer is defined as:

\phi\left(x\right)=w_{b}b\left(x\right)+w_{r}\exp\left(-\frac{1}{2}\left(\frac{x-c_{w}}{bw_{w}}\right)^{2}\right)\text{.}

(8)

SKAN’s adaptive parameter adjustment allows it to effectively handle the varied nature of molecular structures, leading to a more robust and adaptable model with improved generalization across diverse molecular datasets.

Step 3: Readout.

After performing Steps 1 and 2 for $D$ iterations, we use the MEAN function as the readout mechanism to obtain the molecular representation. The readout operation is defined as:

\mathbf{g}=\operatorname{READOUT}\left(\left\{\mathbf{h}_{v}^{(D)}\mid v\in\mathcal{V}\right\}\right)\text{,}

(9)

where $\mathbf{g}\in\mathbb{R}^{n}$ represents molecular representation.

Step 4: Prediction.

Next, we leverage an MLP to obtain the final prediction $\hat{y}$ :

\hat{y}=\operatorname{MLP}\left(\mathbf{g}\right)\in\mathbb{R}^{n_{t}}\text{,}

(10)

where $n_{t}$ denotes the number of tasks in the molecular property classification or regression datasets. For the advanced version, GNN-SKAN+, we utilize a 2-layer SKAN as the classifier:

\hat{y}=\operatorname{SKAN}\left(\mathbf{g}\right)\in\mathbb{R}^{n_{t}}\text{.}

(11)

Algorithm 1 GNN-SKAN and GNN-SKAN+ for Molecular representation Learning

1: Input: Molecular graph

G=(\mathcal{V},\mathcal{E})

with initial node features

\mathbf{H}=\{\mathbf{h}_{v}^{(0)}|v\in\mathcal{V}\}

and edge features

\mathbf{E}=\{\mathbf{b}_{uv}|(u,v)\in\mathcal{E}\}

, number of layers

D

2: Output: Molecular property prediction

\hat{y}

3: Initialize node representations:

\mathbf{h}_{v}^{(0)}

for all

v\in V

4: for each iteration

d=1

D

5: for each node

v\in V

6: Aggregate messages from neighbors by Eq. 3.3

7: end for

8: for each node

v\in V

9: Update node representation by Eq. 7

10: end for

11: end for

12: Perform readout for molecular representation by Eq. 9

13: Predict molecular property by Eq. 10 (for GNN-SKAN) or Eq. 11 (for GNN-SKAN+)

14: return

\hat{y}

3.4 The efficiency of SKAN

For a SKAN network, we denote $L$ as the number of layers in the network, $N$ as the number of nodes in each layer, and $M$ as the number of RBFs.

Model	BBBP $\uparrow$	Tox21 $\uparrow$	ToxCast $\uparrow$	SIDER $\uparrow$	HIV $\uparrow$	BACE $\uparrow$
GCN	0.622 $\pm$ 0.037	0.738 $\pm$ 0.003	0.624 $\pm$ 0.006	0.611 $\pm$ 0.012	0.748 $\pm$ 0.007	0.696 $\pm$ 0.048
GCN-GKAN	-	0.742 $\pm$ 0.005	-	-	-	0.732 $\pm$ 0.013
GCN-SKAN	0.652 $\pm$ 0.009	0.737 $\pm$ 0.003	0.632 $\pm$ 0.006	0.603 $\pm$ 0.002	0.757 $\pm$ 0.021	0.754 $\pm$ 0.023
GCN-SKAN+	0.676 $\pm$ 0.014	0.747 $\pm$ 0.005	0.643 $\pm$ 0.004	0.614 $\pm$ 0.005	0.786 $\pm$ 0.015	0.747 $\pm$ 0.009
GAT	0.640 $\pm$ 0.032	0.732 $\pm$ 0.003	0.635 $\pm$ 0.012	0.578 $\pm$ 0.017	0.751 $\pm$ 0.010	0.653 $\pm$ 0.016
GAT-GKAN	-	0.725 $\pm$ 0.008	-	-	-	0.712 $\pm$ 0.014
GAT-SKAN	0.649 $\pm$ 0.007	0.723 $\pm$ 0.005	0.633 $\pm$ 0.003	0.603 $\pm$ 0.004	0.746 $\pm$ 0.016	0.755 $\pm$ 0.028
GAT-SKAN+	0.688 $\pm$ 0.015	0.748 $\pm$ 0.004	0.640 $\pm$ 0.004	0.620 $\pm$ 0.002	0.784 $\pm$ 0.004	0.731 $\pm$ 0.060
GINE	0.644 $\pm$ 0.018	0.733 $\pm$ 0.009	0.612 $\pm$ 0.009	0.596 $\pm$ 0.003	0.744 $\pm$ 0.014	0.612 $\pm$ 0.056
GINE-GKAN	-	0.734 $\pm$ 0.011	-	-	-	0.706 $\pm$ 0.018
GINE-SKAN	0.652 $\pm$ 0.012	0.738 $\pm$ 0.008	0.627 $\pm$ 0.005	0.586 $\pm$ 0.004	0.764 $\pm$ 0.008	0.768 $\pm$ 0.011
GINE-SKAN+	0.688 $\pm$ 0.016	0.750 $\pm$ 0.002	0.630 $\pm$ 0.005	0.613 $\pm$ 0.004	0.785 $\pm$ 0.009	0.762 $\pm$ 0.027

Table 1: Comparison with the base MP-GNNs on six molecular classification benchmarks. The best results are in bold. The mean and standard deviation of ROC-AUC over five independent test runs are reported. ‘-’ indicates out of memory.

Parameter Counts.

In the original KAN, the total number of parameters is $O(LN^{2}(G+k))$ , where $G$ represents the number of grid points and $k$ (typically $k=3$ ) is the order of each spline. Since $k$ is much smaller than $G$ (Liu et al. 2024) and its impact on the total number of parameters is usually negligible, $O(N^{2}L(G+k))$ simplifies to $O(N^{2}LG)$ . In comparison, SKAN has a total of $O(LN^{2}M)$ parameters, where $M\leq 8$ , which is smaller than $G$ . Thus, SKAN requires fewer parameters than the original KAN.

Computational Complexity.

The computational complexity of the original KAN is $O((LN^{2})k)$ , where $k$ is the order of the spline. In contrast, SKAN’s computational complexity is $O(LN^{2})$ because each RBF has a complexity of $O(1)$ .

Overall, SKAN demonstrates clear advantages over the original KAN in terms of parameter efficiency and computational complexity, leading to greater scalability. Notably, with its efficiency and high accuracy, our GNN-SKAN and GNN-SKAN+ models, despite having two layers, outperform the 5-layer base GNNs and show comparable or superior performance to self-supervised SOTA methods while achieving higher efficiency.

4 Experiments

Molecular Benchmark Datasets.

We evaluate our GNN-SKAN and GNN-SKAN+ across a wide range of public molecular property prediction benchmarks. The evaluation includes three types: 1) Molecular Classification Datasets: BBBP, Tox21, ToxCast, SIDER, HIV, and BACE; 2) Molecular Regression Datasets: Lipo, FreeSolv, Esol, QM7, QM8, and QM9; and 3) Few-shot Learning Datasets: Tox21, SIDER, MUV, and ToxCast from PAR (Wang et al. 2021a).

Experimental Setup.

Following the experimental protocols established by Hu* et al. (2020) and Hou et al. (2022), we use ROC-AUC as the evaluation metric for classification tasks and mean absolute error (MAE) for regression tasks. The results are reported as the mean and standard deviation across five independent test runs. Our model employs a 2-layer GNN-SKAN as the encoder with 256 hidden units, paired with an MLP as the classifier. All base models use a 5-layer architecture. Additionally, we introduce GNN-SKAN+ with a 2-layer SKAN classifier. The learning rate ranges from 0.01 to 0.001 and the number of adaptive RBFs ranges from 3 to 8. All experiments are conducted on a single NVIDIA RTX A6000 GPU.

4.1 Classification Tasks

Model	Lipo $\downarrow$	FreeSolv $\downarrow$	Esol $\downarrow$	QM7 $\downarrow$	QM8 $\downarrow$	QM9 $\downarrow$
GCN	0.809 $\pm$ 0.053	2.891 $\pm$ 0.249	1.241 $\pm$ 0.086	79.393 $\pm$ 2.789	0.025 $\pm$ 0.001	0.311 $\pm$ 0.008
GCN-SKAN	0.921 $\pm$ 0.064	1.888 $\pm$ 0.043	1.261 $\pm$ 0.049	79.443 $\pm$ 0.649	0.023 $\pm$ 0.000	0.266 $\pm$ 0.004
GCN-SKAN+	0.771 $\pm$ 0.015	1.893 $\pm$ 0.052	1.410 $\pm$ 0.074	77.512 $\pm$ 0.987	0.023 $\pm$ 0.000	0.260 $\pm$ 0.007
GAT	0.800 $\pm$ 0.025	2.360 $\pm$ 0.501	1.345 $\pm$ 0.095	112.989 $\pm$ 4.884	0.025 $\pm$ 0.001	0.380 $\pm$ 0.008
GAT-SKAN	0.824 $\pm$ 0.015	1.935 $\pm$ 0.123	1.348 $\pm$ 0.089	105.494 $\pm$ 4.758	0.026 $\pm$ 0.001	0.374 $\pm$ 0.007
GAT-SKAN+	0.777 $\pm$ 0.020	2.077 $\pm$ 0.174	1.347 $\pm$ 0.079	100.664 $\pm$ 3.939	0.024 $\pm$ 0.000	0.371 $\pm$ 0.010
GINE	1.158 $\pm$ 0.227	2.086 $\pm$ 0.092	1.275 $\pm$ 0.077	94.559 $\pm$ 23.708	0.034 $\pm$ 0.013	0.347 $\pm$ 0.013
GINE-SKAN	0.934 $\pm$ 0.121	1.722 $\pm$ 0.125	1.098 $\pm$ 0.018	78.200 $\pm$ 1.536	0.022 $\pm$ 0.000	0.250 $\pm$ 0.004
GINE-SKAN+	0.782 $\pm$ 0.002	1.715 $\pm$ 0.130	1.175 $\pm$ 0.022	77.315 $\pm$ 2.114	0.024 $\pm$ 0.001	0.254 $\pm$ 0.002

Table 2: Comparison with standard GNNs on six molecular regression benchmarks. The best results are indicated in bold. The mean and standard deviation of the test mean absolute error on five independent runs are reported.

Model	#Param.	Tox21 (10-shot)	SIDER (10-shot)	MUV (10-shot)	ToxCast (10-shot)
TPN	2,076.73K	0.795 $\pm$ 0.002	0.675 $\pm$ 0.003	0.783 $\pm$ 0.007	0.708 $\pm$ 0.006
TPN-SKAN	982.51K	0.834 $\pm$ 0.002	0.799 $\pm$ 0.004	0.835 $\pm$ 0.005	0.755 $\pm$ 0.001
MAML	1,814.94K	0.762 $\pm$ 0.001	0.707 $\pm$ 0.001	0.814 $\pm$ 0.002	0.699 $\pm$ 0.017
MAML-SKAN	736.55K	0.809 $\pm$ 0.002	0.828 $\pm$ 0.001	0.784 $\pm$ 0.002	0.703 $\pm$ 0.015
ProtoNet	1,814.36K	0.634 $\pm$ 0.001	0.592 $\pm$ 0.001	0.719 $\pm$ 0.001	0.637 $\pm$ 0.015
ProtoNet-SKAN	732.63K	0.705 $\pm$ 0.002	0.589 $\pm$ 0.001	0.705 $\pm$ 0.002	0.639 $\pm$ 0.012
PAR	2,377.91K	0.804 $\pm$ 0.002	0.680 $\pm$ 0.001	0.780 $\pm$ 0.001	0.698 $\pm$ 0.004
PAR-SKAN	1,124.70K	0.830 $\pm$ 0.003	0.829 $\pm$ 0.001	0.831 $\pm$ 0.001	0.751 $\pm$ 0.002

Table 3: Comparison of common few-shot learning methods on four few-shot molecular property prediction benchmarks. The best results are in bold. Mean and standard deviation of test ROC-AUC across five independent runs.

Comparison with Base MP-GNNs.

Table 1 summarizes the performance of three base MP-GNNs—GCN (Kipf and Welling 2017), GAT (Veličković et al. 2018), and GINE (Hu* et al. 2020)—with their augmented versions, including GKAN (Kiamari, Kiamari, and Krishnamachari 2024), SKAN, and SKAN+, across six classification benchmarks. Given the architectural similarities among GKAN, GraphKAN (Zhang and Zhang 2024), and KAGNNs (Bresson et al. 2024), we extend the recently proposed GKAN as a baseline to other MP-GNNs. In Table 1, our augmented models, GNN-SKAN and GNN-SKAN+, consistently outperform the base MP-GNNs and GNN-GKAN across most benchmarks. Notably, GCN-SKAN improves by 4.82% over GCN, and GCN-SKAN+ improves by 8.68% over GCN on the BBBP dataset. Using scaffold splitting (Mayr et al. 2018; Yang et al. 2019) to evaluate generalization, the augmented models show solid performance on new scaffolds. For instance, GINE-SKAN outperforms GINE by 25.49% on the BACE dataset, demonstrating robust generalization. These results indicate that the augmented models effectively capture structural information of molecules and adapt to diverse molecular scaffolds. Additionally, our augmented models demonstrate outstanding performance across different base MP-GNNs, highlighting their transferability and versatility.

Comparison with SOTAs.

Figure 1 compares the best results of our augmented models from Table 1 with the SOTAs on the HIV dataset. The baselines are divided into two categories: 1) Supervised methods: GCN (Kipf and Welling 2017), GAT (Veličković et al. 2018), GINE (Hu* et al. 2020), and CMPNN (Song et al. 2020); 2) Self-supervised methods: MolCLR (Wang et al. 2022), MGSSL (Zhang et al. 2021), and GraphMAE (Hou et al. 2022). Additional comparisons with Graph Transformer methods are provided in Appendix B. In Figure 1, our models, GNN-SKAN and GNN-SKAN+, consistently outperform or match the SOTA methods. They also demonstrate a significantly reduction in the number of parameters—approximately 563K and 565K, respectively— compared to the models like GraphMAE ( $\sim$ 1363K) and MGSSL ( $\sim$ 1858K), while maintaining comparable performance. Moreover, GNN-SKAN and GNN-SKAN+ show a faster training speeds per epoch. In contrast, models with more parameters, such as GraphMAE and MolCLR, require significantly longer training times. This indicates that our models can complete training more quickly, improving efficiency for practical applications.

4.2 Regression Tasks

Table 2 presents a comparison between the base MP-GNNs and their augmented counterparts, GNN-SKAN and GNN-SKAN+, across six regression benchmarks in physical chemistry and quantum mechanics. The augmented models consistently outperform their base counterparts across most datasets, highlighting the effectiveness of SKAN. Remarkable advancements are observed in the Lipo and FreeSolv datasets. Specifically, GCN-SKAN+ and GINE-SKAN+ improve by 4.70% and 32.47% on the Lipo dataset and by 34.52% and 17.78% on the FreeSolv dataset. In summary, these findings underscore the potential of GNN-SKAN and GNN-SKAN+ to enhance the accuracy and reliability of GNNs in molecular regression tasks.

4.3 Few-shot Learning Tasks

Table 3 demonstrates the effectiveness of SKAN in addressing the few-shot learning problem. We select four common few-shot baselines: TPN (Liu et al. 2018), MAML (Finn, Abbeel, and Levine 2017), ProtoNet (Snell, Swersky, and Zemel 2017), and PAR (Wang et al. 2021b). All experiments are conducted in a 2-way 10-shot setting. We do not include 1-shot experiments, as they are less meaningful in drug discovery. In Table 3, the augmented models consistently outperform their base counterparts across most datasets, with average improvements of 9.14% for TPN-SKAN, 5.04% for MAML-SKAN, 2.26% for ProtoNet-SKAN, and 7.59% for PAR-SKAN. These augmentations with the SKAN architecture result in higher ROC-AUC values, improving the accuracy and reliability of few-shot molecular property prediction methods.

4.4 Visualization

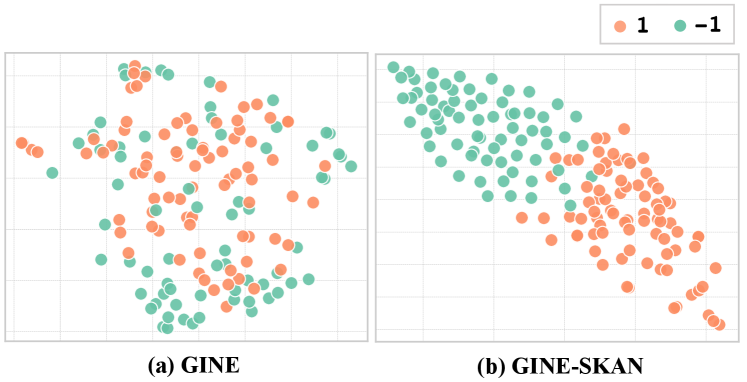
Figure 4 shows the t-SNE visualization of molecular representations learned by GINE and GINE-SKAN on the BACE dataset. In the left plot, GINE appears to struggle with over-squashing, potentially losing key molecular structural details and resulting in overly similar representations. In contrast, the right plot, which displays the results from GINE-SKAN+, shows a clearer separation between the green dots (negative samples) and orange dots (positive samples). This improvement suggests that SKAN enhances the model’s ability to capture and differentiate molecular structures, effectively alleviating the over-squashing issues common in standard GNNs.

Additionally, the examples in Figure 5 illustrate that GCN-SKAN exhibits higher confidence in its predictions for both TPPO and Baicalein on the HIV dataset. This further indicates that SKAN improves the model’s generalization ability across diverse molecular structures, thereby improving overall predictive performance.

4.5 Ablation Study

We conduct ablation studies to evaluate the design choices for each component of the architecture. First, we examine the effectiveness of SKAN and its integration within GNNs.

The Effectiveness of SKAN.

Figure 6 (a) compares the performance of GINE and its KAN variants across three datasets. GINE-SKAN shows notably superior performance over GINE and other variants (GINE-KAN and GINE-FastKAN). The adaptive bandwidths and centers in SKAN enhance its ability to adapt to data distribution, thereby improving flexibility. Figure 6 (b) presents the computational efficiency analysis. While GINE-KAN incurs significantly higher computation time per epoch compared to the base model (GINE), our model exhibits lower computation time.

Agg.

with

SKAN

Update

with

SKAN

Classifier

with

SKAN

Result

ROC-AUC

✗

0.744

\pm

0.014

✓

✗

0.746

\pm

0.014

✗

✓

✗

0.764

\pm

0.010^a

✗

✓

0.762

\pm

0.008

✓

✗

0.767

\pm

0.009

✓

✗

✓

0.761

\pm

0.015

✗

✓

0.785

\pm

0.009

✓

0.782

\pm

0.011^b

a

GINE-SKAN.
b

GINE-SKAN+.

Table 4: Ablation study of SKAN in Aggregation and Update functions and classifier with GINE on the HIV dataset. The highlights are the first, second, and third best results.

SKAN Integration in GNNs.

Table 4 compares the performance of GINE with SKAN integrated into different components (Aggregation and Update, and Classifier) on the HIV dataset. The results are presented as the mean and standard deviation of the test ROC-AUC across five runs. The results indicate that integrating SKAN into the update function (GINE-SKAN) is more effective than integrating it into the aggregation function (GINE-SKAN (Agg.)). This advantage is likely due to the update function’s role in executing nonlinear feature transformations at each GNN layer. Additionally, using SKAN as the classifier, our model (GINE-SKAN+) achieves state-of-the-art performance.

5 Conclusion

This work introduces GNN-SKAN and GNN-SKAN+, a new class of GNNs that integrate traditional GNN architectures with KAN. The core of our approach is SwallowKAN (SKAN), a novel KAN variant specifically designed to address the challenges of molecular diversity and enhance computational efficiency. We evaluate our models on widely used molecular benchmark datasets, including six classification, six regression, and four few-shot learning datasets. The results show that our approach significantly enhances molecular representation learning. In future work, we plan to explore the integration of Graph Transformer architectures with KAN to address the high computational complexity inherent in these models. This would potentially further enhance molecular representation learning tasks.

\nobibliography

References

Ahmad et al. (2022) Ahmad, W.; Simon, E.; Chithrananda, S.; Grand, G.; and Ramsundar, B. 2022. Chemberta-2: Towards chemical foundation models.
Arnold (2009) Arnold, V. I. 2009. On the representation of functions of several variables as a superposition of functions of a smaller number of variables. Collected works: Representations of functions, celestial mechanics and KAM theory, 1957–1965, 25–46.
Azam and Akhtar (2024) Azam, B.; and Akhtar, N. 2024. Suitability of KANs for Computer Vision: A preliminary investigation.
Black et al. (2023) Black, M.; Wan, Z.; Nayyeri, A.; and Wang, Y. 2023. Understanding oversquashing in gnns through the lens of effective resistance. In International Conference on Machine Learning, 2528–2547. PMLR.
Braun and Griebel (2009) Braun, J.; and Griebel, M. 2009. On a constructive proof of Kolmogorov’s superposition theorem. Constructive approximation, 30: 653–675.
Bresson et al. (2024) Bresson, R.; Nikolentzos, G.; Panagopoulos, G.; Chatzianastasis, M.; Pang, J.; and Vazirgiannis, M. 2024. Kagnns: Kolmogorov-arnold networks meet graph learning.
Chen (2024) Chen, A. S. 2024. Gaussian Process Kolmogorov-Arnold Networks.
Chen et al. (2024) Chen, D.; Zhu, Y.; Zhang, J.; Du, Y.; Li, Z.; Liu, Q.; Wu, S.; and Wang, L. 2024. Uncovering neural scaling laws in molecular representation learning. Advances in Neural Information Processing Systems, 36.
Chithrananda, Grand, and Ramsundar (2020) Chithrananda, S.; Grand, G.; and Ramsundar, B. 2020. ChemBERTa: large-scale self-supervised pretraining for molecular property prediction.
Cybenko (1989) Cybenko, G. 1989. Approximation by superpositions of a sigmoidal function. Mathematics of control, signals and systems, 2(4): 303–314.
Datta and Grant (2004) Datta, S.; and Grant, D. J. 2004. Crystal structures of drugs: advances in determination, prediction and engineering. Nature Reviews Drug Discovery, 3(1): 42–57.
De Carlo, Mastropietro, and Anagnostopoulos (2024) De Carlo, G.; Mastropietro, A.; and Anagnostopoulos, A. 2024. Kolmogorov-arnold graph neural networks.
Di Giovanni et al. (2023) Di Giovanni, F.; Giusti, L.; Barbero, F.; Luise, G.; Lio, P.; and Bronstein, M. M. 2023. On over-squashing in message passing neural networks: The impact of width, depth, and topology. In International Conference on Machine Learning, 7865–7885. PMLR.
Fabian et al. (2020) Fabian, B.; Edlich, T.; Gaspar, H.; Segler, M.; Meyers, J.; Fiscato, M.; and Ahmed, M. 2020. Molecular representation learning with language models and domain-relevant auxiliary tasks.
Fang et al. (2022) Fang, X.; Liu, L.; Lei, J.; He, D.; Zhang, S.; Zhou, J.; Wang, F.; Wu, H.; and Wang, H. 2022. Geometry-enhanced molecular representation learning for property prediction. Nature Machine Intelligence, 4(2): 127–134.
Fang et al. (2024) Fang, Y.; Zhang, N.; Chen, Z.; Guo, L.; Fan, X.; and Chen, H. 2024. Domain-Agnostic Molecular Generation with Chemical Feedback. In The Twelfth International Conference on Learning Representations.
Fang et al. (2023) Fang, Y.; Zhang, Q.; Zhang, N.; Chen, Z.; Zhuang, X.; Shao, X.; Fan, X.; and Chen, H. 2023. Knowledge graph-enhanced molecular contrastive learning with functional prompt. Nature Machine Intelligence, 5(5): 542–553.
Finn, Abbeel, and Levine (2017) Finn, C.; Abbeel, P.; and Levine, S. 2017. Model-agnostic meta-learning for fast adaptation of deep networks. In International conference on machine learning, 1126–1135. PMLR.
Gilmer et al. (2020) Gilmer, J.; Schoenholz, S. S.; Riley, P. F.; Vinyals, O.; and Dahl, G. E. 2020. Message passing neural networks. Machine learning meets quantum physics, 199–214.
Guo et al. (2022) Guo, M.; Shou, W.; Makatura, L.; Erps, T.; Foshey, M.; and Matusik, W. 2022. Polygrammar: grammar for digital polymer representation and generation. Advanced Science, 9(23): 2101864.
Hou et al. (2022) Hou, Z.; Liu, X.; Cen, Y.; Dong, Y.; Yang, H.; Wang, C.; and Tang, J. 2022. Graphmae: Self-supervised masked graph autoencoders. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 594–604.
Hu* et al. (2020) Hu*, W.; Liu*, B.; Gomes, J.; Zitnik, M.; Liang, P.; Pande, V.; and Leskovec, J. 2020. Strategies for Pre-training Graph Neural Networks. In International Conference on Learning Representations.
Jablonka et al. (2024) Jablonka, K. M.; Schwaller, P.; Ortega-Guerrero, A.; and Smit, B. 2024. Leveraging large language models for predictive chemistry. Nature Machine Intelligence, 6(2): 161–169.
Keles, Wijewardena, and Hegde (2023) Keles, F. D.; Wijewardena, P. M.; and Hegde, C. 2023. On the computational complexity of self-attention. In International Conference on Algorithmic Learning Theory, 597–619. PMLR.
Kiamari, Kiamari, and Krishnamachari (2024) Kiamari, M.; Kiamari, M.; and Krishnamachari, B. 2024. GKAN: Graph Kolmogorov-Arnold Networks.
Kipf and Welling (2017) Kipf, T. N.; and Welling, M. 2017. Semi-Supervised Classification with Graph Convolutional Networks. In International Conference on Learning Representations.
Kolmogorov (1957) Kolmogorov, A. N. 1957. On the representation of continuous functions of several variables as superpositions of continuous functions of one variable and addition. In Reports of the Academy of Sciences, volume 114, 953–956. Russian Academy of Sciences.
Li et al. (2024) Li, C.; Liu, X.; Li, W.; Wang, C.; Liu, H.; and Yuan, Y. 2024. U-KAN Makes Strong Backbone for Medical Image Segmentation and Generation.
Li (2024) Li, Z. 2024. Kolmogorov-arnold networks are radial basis function networks.
Li et al. (2022) Li, Z.; Jiang, M.; Wang, S.; and Zhang, S. 2022. Deep learning methods for molecular representation and property prediction. Drug Discovery Today, 27(12): 103373.
Liu et al. (2018) Liu, Y.; Lee, J.; Park, M.; Kim, S.; Yang, E.; Hwang, S. J.; and Yang, Y. 2018. Learning to propagate labels: Transductive propagation network for few-shot learning. arXiv preprint arXiv:1805.10002.
Liu et al. (2024) Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T. Y.; and Tegmark, M. 2024. Kan: Kolmogorov-arnold networks. arXiv preprint arXiv:2404.19756.
Livingstone (2000) Livingstone, D. J. 2000. The characterization of chemical structures using molecular properties. A survey. Journal of chemical information and computer sciences, 40(2): 195–209.
Mayr et al. (2018) Mayr, A.; Klambauer, G.; Unterthiner, T.; Steijaert, M.; Wegner, J. K.; Ceulemans, H.; Clevert, D.-A.; and Hochreiter, S. 2018. Large-scale comparison of machine learning methods for drug target prediction on ChEMBL. Chemical science, 9(24): 5441–5451.
Pei et al. (2024) Pei, H.; Chen, T.; Chen, A.; Deng, H.; Tao, J.; Wang, P.; and Guan, X. 2024. Hago-net: Hierarchical geometric massage passing for molecular representation learning. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 38, 14572–14580.
Pilania (2021) Pilania, G. 2021. Machine learning in materials science: From explainable predictions to autonomous design. Computational Materials Science, 193: 110360.
Rampášek et al. (2022) Rampášek, L.; Galkin, M.; Dwivedi, V. P.; Luu, A. T.; Wolf, G.; and Beaini, D. 2022. Recipe for a general, powerful, scalable graph transformer. Advances in Neural Information Processing Systems, 35: 14501–14515.
Rong et al. (2020) Rong, Y.; Bian, Y.; Xu, T.; Xie, W.; Wei, Y.; Huang, W.; and Huang, J. 2020. Self-supervised graph transformer on large-scale molecular data. Advances in neural information processing systems, 33: 12559–12571.
Sadybekov and Katritch (2023) Sadybekov, A. V.; and Katritch, V. 2023. Computational approaches streamlining drug discovery. Nature, 616(7958): 673–685.
Seeger (2004) Seeger, M. 2004. Gaussian processes for machine learning. International journal of neural systems, 14(02): 69–106.
Snell, Swersky, and Zemel (2017) Snell, J.; Swersky, K.; and Zemel, R. 2017. Prototypical networks for few-shot learning. Advances in neural information processing systems, 30.
Song et al. (2020) Song, Y.; Zheng, S.; Niu, Z.; Fu, Z.-H.; Lu, Y.; and Yang, Y. 2020. Communicative Representation Learning on Attributed Molecular Graphs. In IJCAI, volume 2020, 2831–2838.
Ta (2024) Ta, H.-T. 2024. BSRBF-KAN: A combination of B-splines and Radial Basic Functions in Kolmogorov-Arnold Networks.
Unser, Aldroubi, and Eden (1993) Unser, M.; Aldroubi, A.; and Eden, M. 1993. B-spline signal processing. I. Theory. IEEE transactions on signal processing, 41(2): 821–833.
Vaca-Rubio et al. (2024) Vaca-Rubio, C. J.; Blanco, L.; Pereira, R.; and Caus, M. 2024. Kolmogorov-arnold networks (kans) for time series analysis.
Vaswani et al. (2017) Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A. N.; Kaiser, Ł.; and Polosukhin, I. 2017. Attention is all you need. Advances in neural information processing systems, 30.
Veličković et al. (2018) Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; and Bengio, Y. 2018. Graph Attention Networks. In International Conference on Learning Representations.
Wang et al. (2021a) Wang, Y.; ABUDUWEILI, A.; quanming yao; and Dou, D. 2021a. Property-Aware Relation Networks for Few-Shot Molecular Property Prediction. In Beygelzimer, A.; Dauphin, Y.; Liang, P.; and Vaughan, J. W., eds., Advances in Neural Information Processing Systems.
Wang et al. (2021b) Wang, Y.; Abuduweili, A.; Yao, Q.; and Dou, D. 2021b. Property-aware relation networks for few-shot molecular property prediction. Advances in Neural Information Processing Systems, 34: 17441–17454.
Wang et al. (2022) Wang, Y.; Wang, J.; Cao, Z.; and Barati Farimani, A. 2022. Molecular contrastive learning of representations via graph neural networks. Nature Machine Intelligence, 4(3): 279–287.
Wang et al. (2024) Wang, Y.; Yu, X.; Gao, Y.; Sha, J.; Wang, J.; Gao, L.; Zhang, Y.; and Rong, X. 2024. SpectralKAN: Kolmogorov-Arnold Network for Hyperspectral Images Change Detection.
Wieder et al. (2020) Wieder, O.; Kohlbacher, S.; Kuenemann, M.; Garon, A.; Ducrot, P.; Seidel, T.; and Langer, T. 2020. A compact review of molecular property prediction with graph neural networks. Drug Discovery Today: Technologies, 37: 1–12.
Wu et al. (2012) Wu, Y.; Wang, H.; Zhang, B.; and Du, K.-L. 2012. Using radial basis function networks for function approximation and classification. International Scholarly Research Notices, 2012(1): 324194.
Xiong et al. (2019) Xiong, Z.; Wang, D.; Liu, X.; Zhong, F.; Wan, X.; Li, X.; Li, Z.; Luo, X.; Chen, K.; Jiang, H.; et al. 2019. Pushing the boundaries of molecular representation for drug discovery with the graph attention mechanism. Journal of medicinal chemistry, 63(16): 8749–8760.
Xu, Chen, and Wang (2024) Xu, K.; Chen, L.; and Wang, S. 2024. Kolmogorov-Arnold Networks for Time Series: Bridging Predictive Power and Interpretability.
Xu et al. (2018) Xu, K.; Hu, W.; Leskovec, J.; and Jegelka, S. 2018. How Powerful are Graph Neural Networks? In International Conference on Learning Representations.
Yang et al. (2019) Yang, K.; Swanson, K.; Jin, W.; Coley, C.; Eiden, P.; Gao, H.; Guzman-Perez, A.; Hopper, T.; Kelley, B.; Mathea, M.; et al. 2019. Analyzing learned molecular representations for property prediction.
Yi et al. (2022) Yi, H.-C.; You, Z.-H.; Huang, D.-S.; and Kwoh, C. K. 2022. Graph representation learning in bioinformatics: trends, methods and applications. Briefings in Bioinformatics, 23(1): bbab340.
Ying et al. (2021) Ying, C.; Cai, T.; Luo, S.; Zheng, S.; Ke, G.; He, D.; Shen, Y.; and Liu, T.-Y. 2021. Do transformers really perform badly for graph representation? Advances in neural information processing systems, 34: 28877–28888.
Yu and Gao (2022) Yu, Z.; and Gao, H. 2022. Molecular representation learning via heterogeneous motif graph neural networks. In International Conference on Machine Learning, 25581–25594. PMLR.
Yüksel et al. (2023) Yüksel, A.; Ulusoy, E.; Ünlü, A.; and Doğan, T. 2023. SELFormer: molecular representation learning via SELFIES language models. Machine Learning: Science and Technology, 4(2): 025035.
Zhang and Zhang (2024) Zhang, F.; and Zhang, X. 2024. GraphKAN: Enhancing Feature Extraction with Graph Kolmogorov Arnold Networks.
Zhang et al. (2021) Zhang, Z.; Liu, Q.; Wang, H.; Lu, C.; and Lee, C.-K. 2021. Motif-based graph self-supervised learning for molecular property prediction. Advances in Neural Information Processing Systems, 34: 15870–15882.
Zhou et al. (2023) Zhou, G.; Gao, Z.; Ding, Q.; Zheng, H.; Xu, H.; Wei, Z.; Zhang, L.; and Ke, G. 2023. Uni-Mol: A Universal 3D Molecular Representation Learning Framework. In The Eleventh International Conference on Learning Representations.