Global Bifurcation of Non-Radial Solutions for Symmetric Sub-linear Elliptic Systems on the Planar Unit Disc
Abstract.
In this paper, we prove a global bifurcation result for the existence of non-radial branches of solutions to the paramterized family of -symmetric equations , on the unit disc with , where is an orthogonal -representation, is a sub-linear -equivariant continuous function, differentiable with respect to at zero and satisfying the conditions for all and .
Mathematics Subject Classification: Primary: 37G40, 35B06; Secondary: 47H11, 35J57, 35J91, 35B32, 47J15
Key Words and Phrases: global bifurcation, non-linear Laplace equation, symmetric bifurcation, bifurcation invariant, non-radial solutions, equivariant Brouwer degree.
1. Introduction
We draw our motivation from natural phenomena that are modeled by parameterized systems of autonomous Partial Differential Equations (PDEs), where the possible states of each phenomenon are represented by solutions of the associated system of equations at corresponding parameter values. These solutions can be categorized as trivial or non-trivial. Trivial solutions are so-named because they persist for all parameter values and their existence is straightforward to determine. In contrast, non-trivial solutions may only exist for a particular range of parameter values and often exhibit exotic properties that enhance our understanding of the model. The classical bifurcation problem is concerned with the existence and global behaviour of branches of non-trivial solutions emerging from their trivial counterparts. Phenomena which admit the symmetries of a certain group (represented by the -equivariance of the associated equations) may be studied as equivariant bifurcation problems, with additional consideration placed on the symmetric properties of these branches (cf. [1, 3, 9, 11, 19, 21, 22, 23, 24, 25]). The application of topological methods to the study of differential equations, as with most tools in the arsenal of the nonlinear analyst, traces back to M. Poincare [13]. More recently, the Local/Equivariant Brouwer Degrees and their infinite dimensional generalizations – the Local/Equivariant Leray-Schauder Degrees – have proven prodigiously effective in obtaining existence results for solutions to a wide class of nonlinear differential equations. Somewhat remarkably, these degree theories are also instrumental in solving classical and equivariant bifurcation problems. The first use of the Leray-Schauder degree for the detection of (local) bifurcation in a parameterized system of nonlinear differential equations is attributed to the seminal work of M.A. Krasnosel’skii, in which sufficient conditions for the existence of a branch of non-trivial solutions are established (cf. [17]). Only a decade later, P. Rabinowitz (cf. [20]) proposed his famous Rabinowitz alternative, which provides sufficient conditions for the unboundedness of a branch of non-trivial solutions. In this paper, we employ equivariant analogues of Krasnosel’skii and Rabinowitz type results to solve an equivariant bifurcation problem. Specifically, our objective is to study the equivariant bifurcation problem for a symmetric system of parameterized nonlinear Laplace equations subject to Dirichlet boundary conditions. The bifurcation and global behaviour of solutions for such systems has been extensively studied, due to their significance in applied mathematics and physics. In the case that the nonlinearity arises as the gradient of some potential function, the bifurcation problem can be studied as a parameterized variational problem and appropriate topological methods such as Morse theory, index theory, and the equivariant gradient degree (cf. [14]) can be administered (cf. [6, 7, 8, 10, 12, 11, 21, 22, 23, 24, 25, 26]). However, these approaches are not applicable for systems which lack variational structure. The degree theoretic methods used in this paper impose no variational requirements on the equations and, as such, are broadly applicable to a wider class of problems. Consider the following parameterized family of symmetric Laplace equations:
| (1) |
where is the unit planar disc, is an orthogonal representation of a finite group and is a continuous, odd, radially symmetric and -equivariant family of functions of sub-linear growth, which are differentiable with respect to at the origin in . In particular, we assume that satisfies the following conditions:
-
()
for all , and ;
-
()
for all , and ;
-
()
for all , and ;
-
()
there exist continuous functions , and a number such that for each one has
-
()
there exist continuous functions and a number such that for each the following inequality holds
Conditions () () and () imply the -symmetry of system (1) in the sense that is -invariant with respect to the -action given by , and -equivariant with respect to the action given by . On the other hand, conditions () and () guarantee differentiability at the origin and sublinearity, respectively.
Remark 1.1.
Since the zero function is a solution to (1) for all values , all trivial solutions to the system are of the form . Non-trivial solutions to (1), on the other hand, fall into two categories, namely:
-
(i)
radial solutions, which depend only on the magnitude of any disc element (although less obvious than the trivial solution, radial solutions can often be identified using classical methods, eg. by reducing (1) to a second order ODE);
-
(ii)
and non-radial solutions, which exhibit dependency on the angular variable.
Our objective is to identify branches of non-radial solutions to (1), describe their possible symmetric properties, and characterize their global behavior.
The methods used in this paper are inspired by [2], where an existence result was obtained for a similar sublinear elliptic system using equivariant degree theory. For a more thorough exposition of these topics, we direct readers to the recent monograph [4] or, alternatively, the older text [5]. The equivariant degree is intimately connected with the classical Brouwer degree. Although its application is relatively simple, technical difficulties arise when dealing with algebraic computations related to unfamiliar group structures. Many of these issues can be resolved with usage of the G.A.P. system, and the G.A.P. package EquiDeg (created by Haopin Wu), which is available online at https://github.com/psistwu/equideg (cf. [28]). In the remainder of this paper, we employ tools from the equivariant degree theory to determine under what conditions branches of non-trivial solutions may bifurcate from a trivial solution, under what conditions these branches consist only of non-radial solutions and under what conditions these branches are unbounded. Subsequent sections are organized as follows: In Section 2 the problem (1) is reformulated in an appropriate functional setting. In Section 3 we recall the abstract equivariant bifurcation results, including the equivariant analogues of the classical Krasnosel’skii and Rabinowitz theorems. In Section 4, we apply the equivariant degree theory methods to establish local and global bifurcation results for (1). Finally, in Section 5 we present a motivating example of vibrating membranes where our main results, Theorem 4.1 and 4.3, are applied to demonstrate the existence of unbounded branches of non-radial solutions admitting all possible maximal orbit types. For convenience, the Appendices include an explanation of notations used, a summary of the spectral properties of the Laplace operator on the unit disc, and a brief introduction to the Brouwer equivariant degree theory. Acknowledgment: We are deeply grateful to our advisor, Professor Krawcewicz, whose invaluable guidance and unwavering support made this work possible. We would also like to acknowledge Professor Garcia-Azpetia for insightful discussions regarding the estimation of the behaviour of our system near a bifurcation point.
2. Functional Space Reformulation and a priori Bounds
Consider the Sobolev space equipped with the usual norm
where , , and . It is well known that the Laplacian operator given by
| (2) |
is a linear isomorphism. Let be the scalar from condition (). If one chooses (for example, it is enough to take (cf. assumption ()), then there is the standard Sobolev embedding
| (3) |
and also its associated Nemytski operator
| (4) |
Proof.
It suffices to demonstrate that for any and one has . Combining () with the Hölder inequality, one has:
| (5) |
where the result follows from . Notice that the equation
| (6) |
is equivalent to system (1) in the sense that is a solution to (1) for some if and only if satisfies (6). In turn, the invertibility of together with Lemma (2.1) imply that the map given by
| (7) |
is well-defined. Hence, system (1) is also equivalent to the equation
| (8) |
In what follows, we will call (8) the operator equation associated with (1).
Lemma 2.2.
3. Abstract Local and Global Equivariant Bifurcation
In this section we present a concise exposition, following [4] and [5], of an equivariant Brouwer degree method to study symmetric bifurcation problems. Given a compact Lie group , an isometric Banach -representation and a completely continuous -equivariant field , we use the Leray-Schauder Equivariant -Degree to describe local and global properties of the solution set to the equation,
| (11) |
To simplify our exposition and for compatibility with the system of interest (8), we make the following two assumptions.
-
()
The set of trivial solutions to (11) is given by
-
()
There exists a continuous family of linear operators such that, for every , the derivative exists and
Solutions to (11) which do not belong to are called nontrivial. Let denote the set of all non-trivial solutions, i.e.
Clearly, the set of non-trivial solutions is -invariant.
3.1. The Local Bifurcation Invariant and Krasnosel’skii’s Theorem
Formulation of a Krasnosel’skii type local bifurcation result for equation (11) necessitates the introduction of additional notations and terminology (for more details, the reader is referred to [1, 4]). Our first definition clarifies what is meant by a bifurcation of the equation (11).
Definition 3.1.
A trivial solution is said to be a bifurcation point for the equation (11) if every open neighborhood of the point has non-trivial intersection with .
It is well-known that a necessary condition for any trivial solution to be a bifurcation point for the equation (11) is that the linear operator is not an isomorphism. This leads to the following definition.
Definition 3.2.
A trivial solution is said to be a regular point for the equation (11) if is an isomorphism and a critical point otherwise. Moreover, a critical point is said to be isolated if there exists a deleted -neighborhood such that for all , the point is regular.
The set of all critical points for equation (11), denoted , is called the critical set, i.e.
| (12) |
The next definition concerns our interest in the continuation of non-trivial solution emerging from a bifurcation point .
Definition 3.3.
A trivial solution is said to be a branching point for the equation (11) if there exists a non-trivial continuum with and the maximal connected set containing the branching point we call a branch of nontrivial solutions bifurcating from the point .
Whereas the classical Krasnosiel’skii bifurcation result is only concerned with the existence of a branch of nontrivial solutions for the equation (11) bifurcating from a given critical point , the equivariant Krasnosiel’skii bifurcation result, which we employ in this paper, is also concerned with the symmetric properties of such a branch.
Definition 3.4.
Given a subgroup , denote by the corresponding -fixed point space of non-trivial solutions. A branch of solutions is said to have symmetries at least if .
Let be an isolated critical point with a deleted -neighborhood
on which is an isomorphism and choose with . Since are non-singular, there exists a number sufficiently small such that, adopting the notations , , one has
and are -admissibly -homotopic to . Moreover, since acts isometrically on , the ball is clearly -invariant. It follows, from the homotopy property of the -equivariant Leray-Schauder degree (cf. Appendix C), that are admissible -pairs in and also that , where is the open unit ball in . We call the Burnside Ring element
| (13) |
the local bifurcation invariant at . The reader is referred to [4] or [5] for proof that the invariant (13) does not depend on the choice of or radius , and also for the proof of the following local bifurcation result, which is a consequence of the equivariant version of a classical result of K. Kuratowski (cf. [18], Thm. 3, p. 170).
Theorem 3.1.
(M.A. Krasnosel’skii-Type Local Bifurcation) Let be a completely continuous -equivariant field satisfying the assumptions () and () and with an isolated critical point . If , then
-
(i)
there exists a branch of nontrivial solutions to system (11) with branching point ;
-
(ii)
moreover, if is an orbit type with
then there exists a branch of non-trivial solutions bifurcating from with symmetries at least .
3.2. Global Bifurcation and the Rabinowitz Alternative
In order to employ the Leray-Schauder -equivariant degree to describe the global properties of a branch of non-trivial solutions bifurcating from an isolated critical point of the equation (11), we need to make an additional assumption.
-
()
The critical set (given by (12)) is discrete.
Notice that the local bifurcation invariant at any critical point is well-defined under assumption (). Moreover, if is an open bounded -invariant set, then its intersection with the critical set is finite. These observations will be important for the statement of the following global bifurcation result, the proof of which can be found in [4], [5].
Theorem 3.2.
(The Rabinowitz Alternative) Suppose that is a completely continuous -equivariant field satisfying conditions ()–() and let be an open bounded -invariant set with . If is a branch of nontrivial solutions to (11) bifurcating from the critical point , then one has the following alternative:
-
either ;
-
or there exists a finite set
satisfying the following relation
Remark 3.1.
Suppose that Theorem 3.1 is used to demonstrate the existence of a branch of nontrivial solutions to (11) bifurcating from a critical point and that certain conditions are met such that, for any open bounded -invariant neighborhood with , the alternative is impossible. Then, according to Theorem 3.2, the branch must be unbounded.
4. Local and Global Bifurcation of Non-radial Solutions in (1)
Returning to the functional reformulation of our original problem described in Section 2, consider the product group and notice that the Sobolev space is a natural Banach -representation with respect to the isometric -action given by
| (14) | ||||
where is the complex conjugation of and is the standard complex multiplication.
Remark 4.1.
Before approaching the question of bifurcation in the equation (1), we must derive a workable formula for the computation of the degree , where is the open unit ball in and is any parameter value for which is an isomorphism. Assuming that a complete list of the irreducible -representations is made available we denote by the corresponding list of irreducible -representations, where the superscript is meant to indicate that each irreducible -representation has been equipped with the antipodal -action in the standard way (cf. [4], [5]). As a -representation, is also a natural -representation with the -isotypic decomposition
where each -isotypic component component is modeled on the irreducible -representation in the sense that is equivalent to the direct sum of some number of copies of , i.e.
The exact number of irreducible -representations ‘contained’ in the -isotypic component is called the -isotypic multiplicity of and is calculated according to the ratio,
To simplify our computations, we introduce an additional condition on the linearization of (1):
-
()
For each there exists a continuous map with
On the other hand, for every we denote by the irreducible -representation equipped with the -action
and by the irreducible -representation with the trivial -action. In pursuit of a -isotypic decomposition of , let us consider the spectrum of the Laplacian operator (2), understood in this context as an unbounded operator in . Namely, one has
where denotes the -th positive zero of the -th Bessel function of the first kind . Corresponding to each eigenvalue , there is an associated eigenspace which can be expressed, using standard polar coordinates , as follows
Clearly, one has
for each such that admits the -isotypic decomposition
where the closure is taken in . In particular, adopting the notations
| (16) |
and
one has
Hence, admits the -isotypic
To be clear, each -isotypic component is modeled on the irreducible -representation .
Lemma 4.1.
Proof.
Indeed, since is -equivariant, one has
such that
where one easily obtains (see for example [2, 4])
The product property of the Leray-Schauder -equivariant degree (cf. Appendix C) permits us to express , at any regular point of equation (8), in terms of a Burnside ring product of the Leray-Schauder -equivariant degrees of the various restrictions of the -equivariant linear isomorphism to the -subrepresentations on their respective open unit balls as follows
| (17) |
Notice that one has for almost all indices , and , so that the product (17) is well-defined. Indeed, each Leray-Schauder -equivariant degree is fully specified by the -isotypic multiplicities together with the real spectra of according to formula,
| (18) |
where is the basic degree (cf. Appendix C) associated with the irreducible -representation and is the unit element of the Burnside Ring. In addition, since each basic degree is involutive in the Burnside ring (cf. Appendix C), one has
| (19) |
Putting together (18) and (19), we introduce some notations to keep track of the indices
which contribute non-trivially to the Burnside Ring product (17). To begin, the negative spectrum of is accounted for with the index set
| (20) |
As is well known (see, for example, [27], p. 486), one has
from which it follows that the set (20) is finite. Combining (20) with formulas (17) and (18), one obtains
Computation of (17) can be further reduced by accounting for the even -isotypic multiplicities , whose corresponding basic degrees contribute trivially to the Burnside Product (17). We put,
| (21) |
which, together with (19), yields
| (22) |
4.1. Computation of the Local Bifurcation Invariant
Under the assumptions ()–(), conditions () and () are satisfied for the operator equation (8) (cf. Remarks 1.1, 4.1). Therefore, the existence of a branch of non-trivial solutions to (1) bifurcating from an isolated critical point is reduced, by Theorem 3.1, to computation of the local bifurcation invariant . Adopting the notations from Section 3, choose with , where is chosen such that, for all , the solution is a regular point and put . Then, the local bifurcation invariant at the isolated critical point is given by
| (23) |
where is the open unit ball in . Notice that, since are regular points of (8), computation of the local bifurcation invariant amounts to computation of the Leray-Schuader -equivariant degree of the -equivariant linear isomorphism
Lemma 4.2.
In order to formulate the main local equivariant bifurcation result, we must first consider some additional properties of the basic degree. For a more thorough exposition of these topics we refer the reader to [4], [5]. Take and define the -folding map as the Lie group homomorphism,
Each induces a corresponding Burnside ring homomorphism defined the generators by,
| (25) |
Notice that, for and , there is the following relation between basic degrees
| (26) |
Remark 4.2.
An orbit type which is maximal in is also maximal in . Therefore, any with an isotropy such that is maximal in must be radially symmetric. In order to detect branches of solutions to (7) corresponding to maps which are both non-trivial and non-radial, we must restrict our focus to orbit types which are maximal in for some positive . Indeed, to demonstrate the existence of a branch of non-radial solutions bifurcating from some isolated critical point , it is sufficient to show that for some there is an orbit type with . In such a case, one can additionally conclude that for some there exists a branch non-radial solutions to (7) with symmetries at least bifurcating from .
With motivation from Remark 4.2, we denote by , the set of all maximal orbit types in and by the set of orbit types . Since each is also an orbit type in for at least one , one has
Notice that for any and (in particular, one has ). Hence, any orbit type can be recovered from an orbit type in by the relation .
Remark 4.3.
Take and . For any basic degree and orbit type , the recurrence formula for the Leray-Schauder -equivariant degree (cf. Appendix C) implies
where is such that for all and where the coefficient is determined by the rule
equivalently
where
It follows that non-triviality of the coefficient associated with an orbit type in the basic degree is characterized by the parity of in the following way
The following result concerns the fate of orbit types belonging to in the Burnside Ring product of basic degrees such as (22). In particular, we find that for and , the coefficient of is -nilpotent with respect to the Burnside Ring product in the case that both and are odd.
Lemma 4.3.
Take and . For , one has
equivalently
Proof.
Consider the Burnside Ring product of the relevant basic degrees
where is such that for all , and put , i.e.
Now, if and are both even, then one has and the result follows. On the other hand, if and are both odd, then one has such that
where in either of the cases, and or and , one has . If instead one supposes that and are of different parities, then one has the two corresponding cases, and or and , both of which imply . Naturally, the Lemma (4.3) can be generalized to an orbit type and the Burnside Ring product of the basic degrees with odd for an even number of .
Corollary 4.1.
Take and . For , one has
equivalently
Remarks 4.2 and 4.3 permit us to
further refine our index set (21) as follows.
Let be an isolated critical point with a deleted regular neighborhood on which is an isomorphism. For a given , we put
| (27) |
| (28) |
and
| (29) |
Remark 4.4.
Take , and . If , then . On the other hand, if , then . The converse of each statement is not, in general, true.
In order to keep track of the numbers for which the parities of disagree, we put
| (30) |
and also
| (31) |
Remark 4.5.
Notice that is well defined and that the numbers are of the same parity for any isolated critical point and orbit type .
We are finally in a position to formulate our main local bifurcation result.
Theorem 4.1.
If is an isolated critical point with a deleted regular neighborhood on which the linear operator is an isomorphism and if there is an orbit type such that and for all , where , then one has
Proof.
For convenience, take . Adopting the notation
| (32) |
the local bifurcation invariant (cf. 3.1) becomes
If one also puts
and, for each defines
| (33) |
then the product of basic degrees (32) becomes
since is a partition of the index set (21). It follows, from Lemma (4.3) and its Corollary (4.1), that each of (33) is of the form
where are such that for all and where the coefficients are determined by the rule
equivalently
Since are of the same parity for all , one has
where is such that for all . Therefore, the local bifurcation invariant can be expressed in terms of the quantities (33) as follows
where is such that for all . To complete the proof of Theorem 4.1, we will need the following Lemma.
Lemma 4.4.
Take . Using the notation (33), one has
Proof.
Indeed, consider the relevant Burnside Ring product
| (34) |
where is such that for all . Now, if is even, then and the result follows. Supposing instead that , then (4.1) becomes
where is such that for all and is given by the recursive formula (cf. Appendix C) as follows
Now, if , then and the result follows. In the case that , one has such that and the result follows from the fact that . Completion of the proof of Theorem 4.1 The result follows from Lemma 4.4 together with the observation that
Corollary 4.2.
4.2. Resolution of the Rabinowitz Alternative
Without an appropriate fixed point reduction of the bifurcation problem (8), we are unable to guarantee that a branch of non-trivial solutions to (1) bifurcating from a given isolated critical point whose existence has been established using a Krasnosel’skii type result (e.g. by Theorem 4.1) is not comprised of radial solutions. With this in mind, consider the subgroup and denote by the restriction
| (35) |
of the operator (7) to the -fixed point space . Clearly, any solution to the equation
| (36) |
is also solution to (8). Notice also that any radial solution to (36) belongs to the set of trivial solutions (cf. Condition ())
Therefore, any branch of of non-trivial solutions to the bifurcation problem (36) consists solely of non-radial solutions. In this -fixed point setting, we must adapt each of the notions introduced in Section 3.2 used to describe the Rabinowitz alternative for the equation (8) to the bifurcation map (35). To begin, notice that the -fixed point space is an isometric Hilbert representation of the group with the -isotypic decomposition
We denote by the set of -fixed non-trivial solutions to (8), i.e.
and by the restriction of the operator to , i.e. for each
| (37) |
As before, the critical set of (36), now denoted , is the set of trivial solutions for which is not an isomorphism
Next, we describe the spectrum of (37) in terms of the spectra (cf. Lemma 4.1) as follows
Assume that for a given , the operator is an isomorphism. If we refine the index set (21) to include only those indices relevant to the -fixed point setting with the notation
then the -equivariant degree can be computed as follows
where, to distinguish between -basic degrees and -basic degrees, we have introduced the notation
At this point, Lemma 4.2 can be reformulated for the map as follows:
Lemma 4.5.
Likewise, Theorem 3.2 becomes:
Theorem 4.2.
(Rabinowitz’ Alternative) Under the assumptions ()–(), let be an open bounded -invariant set with . If is a branch of nontrivial solutions to (36) bifurcating from an isolated critical critical point , then one has the following alternative:
-
either ;
-
or there exists a finite set
satisfying the following relation
To further simplify our exposition, we replace assumption () with:
-
()
For each there exists a continuous and bounded map with
Take and . Under assumption (), there is some finite for which implies . Clearly, the quantity
| (39) |
and the set
| (40) |
are well-defined. The elements of can always be indexed in such a way that, if , then . We are now in a position to formulate our main global bifurcation result.
Theorem 4.3.
If there is an orbit type for which , then the system (1) admits an unbounded branch of non-radial solutions with symmetries at least , where . Moreover, one has the following alternative: there exists such that, either
-
(a)
for all with one has , or
-
(b)
for all with one has .
Remark 4.6.
Conditions (a) and (b) in Theorem 4.3 guarantee that the branch of non-radial solutions extends indefinitely either into the direction of increasing or into the decreasing .
Proof.
Notice that, for any critical point , the numbers have the same parity (cf. Remark 4.5). Without loss of generality, assume that and consider any other critical point with . We will show that and are also of the same parity. Indeed, suppose for contradiction that and have different parities. Then there is a folding such that the sets , disagree for some odd numbers of indices (equivalently, the numbers , have different parity). Consequently, there must be an intermediate critical point with and . However, this is in contradiction with the assumption of maximality for . It follows that the quantity is constant for all critical points . On the other hand, let be any two consecutive critical points. From the definition of (40), the numbers must be non-zero. With an argument similar to that the one used above, it can be shown that the numbers and have the same parity, such that
It follows then, from Theorem 4.1, that and also, for any critical point , that . Therefore, if , there exists an unbounded branch of non-radial solutions bifurcating from each critical point in with symmetries at least . Moreover, by Lemma 2.2, the branch cannot extend to infinity with respect to the magnitude of vectors belonging to (for any particular ), the only option is that the branch extends to infinity with respect to .
5. Motivating Example: Vibrating Membranes with Symmetric Coupling
Equations involving the Laplacian operator are sometimes used to describe time-invariant wave or diffusion processes, also called steady-state phenomena. As a preliminary model for steady-state phenomena, consider the Helmholtz equation
| (41) |
defined on the planar unit disc . Solutions of (41) are called normal modes and take the form
where each can be calculated as the -th root of the -th Bessel function of the first kind . The classical Helmholtz equation, as is well-known, has limited applicability to real-world problems, which are often inherently nonlinear. For example, in order to study vibrations of a membrane, it is standard to perturb the system (41) with a nonlinearity as follows
| (42) |
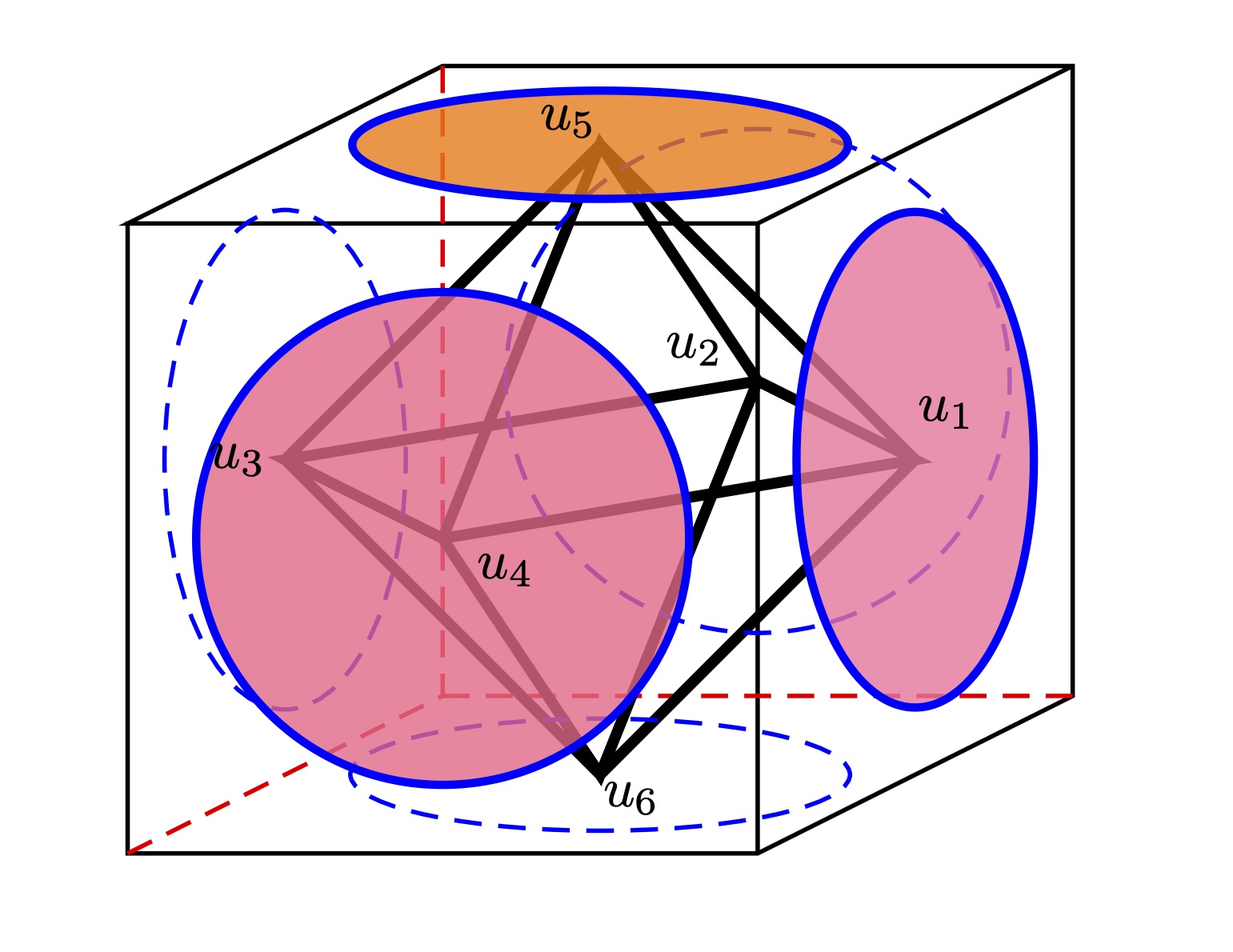
Of course, the single membrane model (42) is still too simplistic to model many physically integrated systems. A more realistic problem might instead involve a configuration of some number of coupled oscillating membranes. Consider, for example, a collection of six membranes arranged on corresponding faces of a cube, each coupled to its adjacent neighbors and modeled by a system of identical non-linear Helmholtz equations
| (43) |
where and is the vector-valued function
| (44) |
For compatibility with the results derived in previous sections, we assume that (44) satisfies the following conditions:
-
()
For all , , and
-
()
For all , , and
-
()
For all , , ,
Here, is used to denote the chiral symmetry group of the cube, whose action on is described by the set of orientation preserving permutations of the corresponding membranes. If we identify with according to the rule
then the faces of the cube (see Figure 1) are naturally permuted as follows
| (45) |
In this way, is an orthogonal -representation with respect to the action (45). The table of characters for
| con. classes | |||||
|---|---|---|---|---|---|
reveals the relation
which can be used to obtain the following -isotypic decomposition of
Under the assumptions ()-(), the function clearly satisfies conditions ()-(). Let us also assume that satisfies the conditions () and () with the matrix given by
| (46) |
where is the identity matrix, is the weighted adjacency matrix
| (47) |
defined for some fixed satisfying the conditions
-
()
, , ,
and where is the sigmoid function
| (48) |
Remark 5.1.
The sigmoid function introduces a nonlinear dependence of the coupling in (43) on the bifurcation parameter . Moreover, the asymptotic behaviour of (48) can be understood as the imposition of coupling strength saturation limits, which might reflect physical constraints such as, for example, bounded ranges for certain material densities.
With the linearization (46), system (43) clearly satisfies the condition (). Indeed, it can be shown that admits three eigenvalues with eigenspaces corresponding to the -isotypic components as follows
| (49) | |||||
Notice also that, if are such that , then the critical set associated with (44) is discrete. Together with the strict monotonicity of the eigenvalues (49) and the distinctness of the numbers , it follows that each critical point of (43) can be specified by a unique triple with the notation
| (50) |
We are now in a position to apply the local equivariant bifurcation results derived in this paper, namely Theorem 4.1 and Corollary 4.2, to the example system (43).
Proposition 5.1.
Proof.
Let be a critical point of (43) with a deleted regular neighborhood on which is an isomorphism and choose any orbit type of maximal kind with . The unique identification of with (cf. (50)) together with the strict monotonicity of the eigenvalues (49) imply the set difference . Therefore, the numbers agree for all and are consecutive in the case of and the result follows from Corollary (4.2). In order to demonstrate how Theorem 4.3, the main global equivariant bifurcation result of this paper, can be applied to a system of the form (43), we introduce the following simplifying assumption:
-
()
there exists an isotypic index , an odd number and a pair of numbers with and such that the Bessel root lies:
-
(i)
within the codomain of if and ;
-
(ii)
outside the codomain of if either, and or , or if for any .
-
(i)
Condition () guarantees that an odd number of critical points will obtain for every orbit type of maximal kind with .
Proposition 5.2.
Proof.
Choose with and notice that, since and for every , one has and the result follows from Theorem 4.3. So that Propositions 5.1 and 5.2 can be verified empirically, let us specify a particular bifurcation problem associated with system (43) by choosing the following values for the constants
| (51) |
For convenience, we include graphs of the three eigenvalues (49) with the assignments (51) in Figure 3 and the numbers for and in Table 2.
| m=0 | 5.783 | 30.471 | 74.887 | 139.04 | 222.932 | 326.563 | 449.934 | 593.043 | 755.891 |
|---|---|---|---|---|---|---|---|---|---|
| m=1 | 14.682 | 49.218 | 103.499 | 177.521 | 271.282 | 384.782 | 518.021 | 671 | 843.718 |
| m=2 | 26.374 | 70.85 | 135.021 | 218.92 | 322.555 | 445.928 | 589.038 | 751.888 | 934.476 |
| m=3 | 40.706 | 95.278 | 169.395 | 263.201 | 376.625 | 509.98 | 662.968 | 835.693 | 1028.15 |
| m=4 | 57.583 | 122.428 | 206.57 | 310.322 | 433.761 | 576.913 | 739.79 | 922.398 | 1124.74 |
| m=5 | 76.939 | 152.241 | 246.495 | 360.245 | 493.631 | 646.702 | 819.483 | 1011.99 | 1224.21 |
| m=6 | 98.726 | 184.67 | 289.13 | 412.934 | 556.303 | 719.321 | 902.024 | 1104.44 | 1326.56 |
| m=7 | 122.908 | 219.67 | 334.436 | 468.356 | 621.751 | 794.743 | 987.392 | 1199.73 | 1431.77 |
| m=8 | 149.453 | 257.21 | 382.38 | 526.481 | 689.946 | 872.946 | 1075.56 | 1297.84 | 1539.81 |
| m=9 | 178.337 | 297.26 | 432.933 | 587.281 | 760.863 | 953.907 | 1166.52 | 1398.77 | 1650.68 |
| m=10 | 209.54 | 339.793 | 486.07 | 650.732 | 834.48 | 1037.6 | 1260.24 | 1502.48 | 1764.35 |
Notice that the critical set for (43) consists of exactly five critical points that can be distinguished, using the notation (50), as follows
| (52) |
In order to employ the results presented in previous sections to our bifurcation problem, we must first identify the maximal orbit types in . The following G.A.P code can be used to generate a complete list of the sets and the corresponding Basic Degrees for .
For any and , the output of the above program can be used to describe the set of maximal orbit types the basic degrees (cf. (25) and (26)), using amalgamated notation (cf. Appendix A), as follows:
We can deduce, from the coefficients of the Basic Degrees (cf. Remark 4.3), that the fixed point space has odd dimension for any and . Since the critical set (52) is manageably small, we also can manually compute the cardinalities (28) for each of the critical points to obtain the quantities
and
Therefore, from Theorem 4.1, it follows that every critical point is a branching point for branches of non-trivial solutions to the problem (43) with symmetries at least in the case of and with symmetries at least in the case of for each orbit type of maximal kind . The following G.A.P code can be used to computationally verify the non-triviality of the local bifurcation invariant (specifically, the non-triviality of the relevant coefficients) at each of the critical points in terms of the basic degrees
and the unit Burnside Ring element according to the rule derived in Lemma (4.2)
The output of the above program can be expressed using amalgamated notation as follows:
Next, we can determine the global behaviour of some of the branches predicted using Theorem (4.1) by establishing the parity of the set (40). Notice that, for every and , the quantity is obtained for exactly one critical point , i.e.
Therefore, any branch of non-trivial solutions with symmetries at least bifurcating from , for every and , consists only of non-radial solutions and is unbounded. Of course, since the critical set (52) is finite, one needs only sum the relevant local bifurcation invariants to arrive at the same conclusion directly from the Rabinowitz alternative (cf. Theorems 4.2 and 4.3).
In closing, let’s consider a closer interpretation of the above results. Take the maximal orbit type and let be a branch of non-radial solutions with symmetries at least emerging from the first critical point . Notice that the kernel of at any critical point is given by the corresponding irreducible -representation (cf. (16)), i.e.
such that any vector with must be of the form
where are the eigenvectors
Computing the generators of the orbit type ,
and examining their action (cf. (14), (45)) on , we observe the radial invariances
which are satisfied trivially for all elements of , the conjugate invariance
which is only satisfied when , and also the permutation invariances
which, for , is satisfied if and only if . Moreover, since one has , the celebrated theorem of Crandall-Rabinowitz (cf. [29]) guarantees that the branch is tangent to the solution at the point . Therefore, can reasonably be used to estimate the behaviour of the branch for parameter values near .

Appendix A Amalgamated Notation of Subgroups
The convention of amalgamated notation is a shorthand for the specification of subgroups and their conjugacy classes in a product group . In order to introduce this convention, we recall a well-known consequence of Goursat’s Lemma (cf. [15]). Namely that, for any closed subgroup in , there are two subgroups , , a group and a pair of epimorphisms , such that
| (53) |
Using amalgamated notation, the subgroup (53) is identified, up to its conjugacy class in , by the quintuple , where and , as follows
In particular, one can always choose the group such that , in which case the conjugacy class of (53) is identified with the quadruple as follows
| (54) |
This compact amalgamated decomposition (54) is the form with which subgroup conjugacy classes are identified in this paper. In addition to the notation defined above, the following list provides some ancillary shorthand used in this paper for the identification of subgroups in
Appendix B Spectral Properties of Operator
In this section, we leverage the spectral properties of the Laplace operator to describe the spectrum of
To begin, consider the following eigenvalue problem defined on the planar unit disc with Dirichlet boundary conditions
In polar coordinates, the Laplacian takes the form
Assuming that can be separated , the eigenvalue problem becomes
Rearranging terms, we obtain
| (55) |
Since the left and right-hand sides of equation (55) depend on different variables, there must exist a constant such that
| (56) | |||
| (57) |
To ensure that is single-valued and continuous on , we impose the periodicity condition . Then, the angular part (57) becomes the ordinary differential equation
which has eigenvalues for with corresponding eigenfunctions and . Notice that, as a consequence of solving for , we have determined the values of constant :
Then, equation (56) becomes
| (58) |
Introducing the change of variables and and substituting into (58), we obtain the classical Bessel equation
The bounded at zero solution is given by , where stands for the -th Bessel function of the first kind. It follows that solutions to (56) are constant multiples of (notice that is finite at zero). Consequently, satisfies the Dirichlet condition if , i.e. . In this way, we obtain that the spectrum of the Laplace operator is given by
Moreover, corresponding to each eigenvalue , there is the eigenfunction
where , and also the eigenspace
In this way, we have determined the spectrum of our operator
Appendix C Equivariant Brouwer Degree Background
We encourage readers interested in exploring the statements made in this section with greater detail to refer to the texts [4], [5]. Equivariant notation. Let be a compact Lie Group. For any subgroup , denote by its conjugacy class, by by its normalizer by its Weyl group in . The set of all subgroup conjugacy classes in , denoted , has a natural partial order defined as follows
In particular, we put and, for any , we denote by the number of subgroups with and . For a -space and , denote by the isotropy group of and call the orbit type of . Put and . For a subgroup , the subspace is called the -fixed-point subspace of . If is another -space, then a continuous map is said to be -equivariant if for each and . [5]. The Burnside Ring and Axioms of Equivariant Brouwer Degree. The free -module becomes the Burnside ring when equipped with a natural multiplicative operation, called the Burnside ring product and defined for any pair of generators as follows
| (59) |
where the coefficients are given by the recurrence formula
| (60) |
Let be an orthogonal -representation with an open bounded -invariant set . A -equivariant map is said to be -admissible if for all , in which case the pair is called an admissible -pair in . We denote by the set of all admissible -pairs in and by the set of all admissible -pairs defined by taking a union over all orthogonal -representations, i.e.
The following statement is the standard axiomatic definition of the -equivariant Brouwer degree:
Theorem C.1.
There exists a unique map , that assigns to every admissible -pair the Burnside Ring element
| (61) |
satisfying the following properties:
-
(Existence) If for some in (61), then there exists such that and .
-
(Additivity) For any two disjoint open -invariant subsets and with , one has
-
(Homotopy) For any -admissible -homotopy, , one has
-
(Normalization) For any open bounded neighborhood of the origin in an orthogonal -representation with the identity operator , one has
The following are additional properties of the map which can be derived from the four axiomatic properties defined above:
-
(Multiplicativity) For any ,
where the multiplication ‘’ is taken in the Burnside ring .
-
(Recurrence Formula) For an admissible -pair , the -degree (61) can be computed using the following Recurrence Formula:
(62) where stands for the number of elements in the set and is the Brouwer degree of the map on the set .
Computation of Brouwer equivariant degree. For an orthogonal -representation with the open unit ball , denote by the set of its irreducible -subrepresentations. In particular, define the basic degree associated with as follows
Now, consider a -equivariant linear isomorphism and assume that has a -isotypic decomposition
where each isotypic component is equivalent to copies of the irreducible -representation . From the Multiplicativity property of the -equivariant Brouwer Degree, one has
where and denotes the real negative spectrum of .
Notice that the basic degrees can be effectively computed from (62):
where
The following fact is well-known (see for example [3]).
Lemma C.1.
For any irreducible -representation , the basic degree is an involutive element of the Burnside Ring, i.e.
References
- [1] Z. Balanov, J. Burnett, W. Krawcewicz, H. Xiao, Global Bifurcation of Periodic Solutions in Reversible Second Order Delay System, Journal of Bifurcation and Chaos, Vol. 31, No. 12, 2150180 (2021), https://doi.org/10.1142/S0218127421501807.
- [2] Z. Balanov, E. Hooton, W. Krawcewicz, D. Rachinskii, Patterns of non-radial solutions to coupled semilinear elliptic systems on a disc, Nonlinear Analysis, (2021) 202, https://www.sciencedirect.com/science/article/pii/S0362546X2030273X, 1–15.
- [3] Z. Balanov, W. Krawcewicz, S. Rybicki and H. Steinlein. A short treatise on the equivariant degree theory and its applications, J.Fixed Point Theory App. 8:1–74, 2010.
- [4] Z. Balanov, W. Krawcewicz, D. Rachinskii, J. Yu and H-P. Wu, Degree Theory and Symmetric Equations assisted by GAP System.
- [5] Z. Balanov, W. Krawcewicz and H. Steinlein. Applied Equivariant Degree. AIMS Series on Differential Equations & Dynamical Systems, Vol.1, 2006.
- [6] T. Bartsch, Topological Methods for Variational Problems with Symmetries, Lecture Notes in Math., 1560, Springer-Verlag, Berlin, 1993.
- [7] T. Bartsch, N. Dancer and Z-Q. Wang, A Liouville theorem, a-priori bounds, and bifurcating branches of positive solutions for a nonlinear elliptic system, Calc. Var. (2010) 37: 345–361
- [8] T. Bartsch and D. G. de Figueiredo, Infinitely many solutions of nonlinear elliptic systems, Topics in Nonlinear Analysis in Progress in Nonlinear Differential Equations and Their Applications book series, PNLDE, volume 35 (1999), pp 51–67.
- [9] J. Bracho, M. Clapp and W. Marzantowicz, Symmetry breaking solutions of nonlinear elliptic system, Top. Meth. in Nonlinear Analysis, 26 (2005), 189–201.
- [10] K.-C. Chang, Infinite Dimensional Morse Theory and Multiple Solution Problems, Birkhäuser, Boston-Basel-Berlin, 1993.
- [11] P. Chossat, R. Lauterbach and I. Melbourne, Steady-state bifurcation with -symmetry, Arch. Ration. Mech. Anal. 113 (1990), 313–376.
- [12] Ph. Clément, D.G. de Figueiredo and E.A. Mitidieri, A priori estimates for positive solutions of semilinear elliptic systems via Hardy-Sobolev inequalities. Pitman Res. Notes in Math. 1996, pp. 73–91.
- [13] H. Poincare, Analysis Situs. Journal de l’École Polytechnique. 1895.
- [14] K. Geba and S. Rybicki, Some remarks on the Euler ring . J. Fixed Point Theory Appl. 3 (2008), no. 1, 143–158.
- [15] E. Goursat, Sur les substitutions orthogonales et les divisions régulières de l’espace, Annales scientifiques de l’École Normale Supérieure, 6 (1889), pp. 9–102.
- [16] M. A. Krasnoselskii, Topological methods in the theory of nonlinear integral equations, Pergamon Press, New York, 1964.
- [17] M. A. Krasnoselskii, Some problems of nonlinear analysis, American Mathematical Society Translations, Series 2 10 (2) (1958) 345-409.
- [18] K. Kuratwoski, Topology, Vol. II, Academic Press, New York-London; PWN - Polish Scientific Publishers, Warsaw, 1968.
- [19] Z. Lou, T. Weth and Z. Zhang, Symmetry breaking via Morse index for equations and systems of Hénon–Schrödinger type, Z. Angew. Math. Phys. (2019) 70: 35
- [20] P.H. Rabinowitz, Some global results for nonlinear eigenvalue problems, J. Funct. Anal. 7 (1971), 487–513.
- [21] S. Rybicki, A degree for -equivariant orthogonal maps and its applications to bifurcation theory, Nonlinear Anal. 23 (1994), 83–102.
- [22] S. Rybicki, Global bifurcations of solutions of Emden-Fowler type equation on an annulus in , , J. Differential Equations 183 (2002), 208–223.
- [23] S. Rybicki, Global bifurcations of solutions of elliptic differential equations, J. Math. Anal. Appl. 217 (1998), 115–128.
- [24] S. Rybicki, A degree for -equivariant orthogonal maps and its applications to bifurcation theory. Nonlinear Anal. 23 (1994), 83–102.
- [25] S. Rybicki, Bifurcations of solutions of -symmetric nonlinear problems with variational structure. In: Handbook of Topological Fixed Point Theory (eds. R. Brown, M. Furi, L. Górniewicz and B. Jiang), Springer, 2005, 339–372.
- [26] X. Wang and A. Qian, Existence and multiplicity of periodic solutions and subharmonic solutions for a class of elliptic equations, J. Nonlinear Sci. App. 10 (2017), 6229-6245.
- [27] G. N. Watson, A Treatise on the Theory of Bessel Functions, The University Press, Cambridge, 1944.
- [28] H-P. Wu, A package EquiDeg. for GAP programming. https://github.com/psistwu/GAP-equideg.
- [29] M. G. Crandall and P. H. Rabinowitz, Bifurcation from simple eigenvalues, J. Functional Analysis, 8(1971), 321–340.https://www.sciencedirect.com/science/article/pii/0022123671900152.