Giant orbital polarization of Ni2+ in square planar environment
Abstract
Understanding the electronic behavior of Ni2+ in a square planar environment of oxygen is the key to unravel the origin of the recently discovered superconductivity in the hole doped nickelate Nd0.8Sr0.2NiO2. To identify the major similarities/dissimilarities between nickelate and cuprate superconductivity, the study of the electronic structure of Ni2+ and Cu2+ in an identical square planar environment is essential. In order to address these questions, we investigate the electronic structure of Sr2CuO3 and Ni doped Sr2CuO3 single crystals containing (Cu/Ni)O4 square planar units. Our polarization dependent X-ray absorption spectroscopy experiments for Ni in Sr2Cu0.9Ni0.1O3 have revealed very large orbital polarization, which is a characteristic feature of high cuprate. This arises due to the low spin =0 configuration with two holes in Ni 3 orbitals - in contrast to the expected high spin =1 state from Hund’s first rule. The presence of such =0 Ni2+ in hole doped nickelate would be analogous to the Zhang Rice singlet. However, the Mott Hubbard insulating nature of the NiO4 unit would point towards a different electronic phase space of nickelates, compared to high cuprates.
INTRODUCTION
Ever since the discovery, understanding the mechanism of high temperature superconductivity in cuprates remains an open problem in condensed matter physics Bednorz:1986p189 . Over the years, the importance of several factors, such as the antiferromagnetic, insulating phase of the parent compound, large orbital polarization, strong hybridization between Cu and O states, and Zhang Rice (ZR) physics have been recognized to play a role in the hole doped superconducting phase Lee:2006p17 ; Fradkin:2015p457 ; Keimer:2015p179 . After the prediction of achieving cuprate like Fermi surface in a three-dimensional compound LaNiO3 through orbital engineering Anisimov:1999p7901 ; Chaloupka:2008p016404 ; Hansmann:2009p016401 , various types of artificial structures of NiO3 family have been extensively investigated Middey:2016p305 ; Freeland:2011p57004 ; Benckiser:2011p189 ; Wu:2013p125124 . However, the observed orbital polarization in an octahedral crystal field is low (maximum 25%) and superconductivity remains elusive there, prompting to search for other Ni based compounds with lower dimensional structure Poltavets:2010p206403 ; Cheng:2012p236403 ; Zhang:2017p864 .
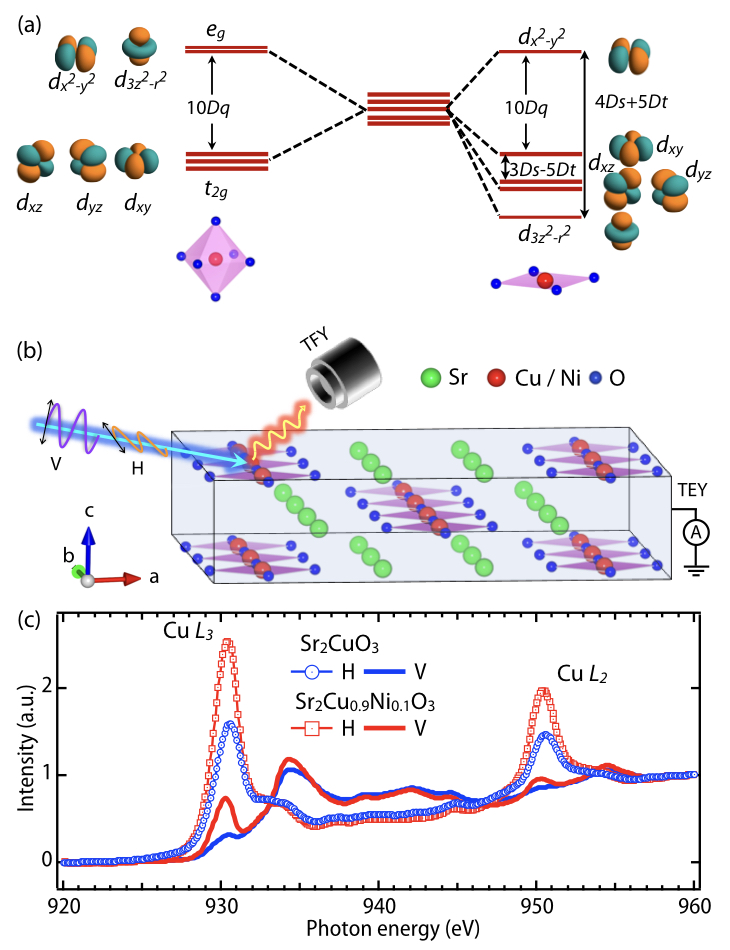
The recent finding of superconductivity in Sr doped NdNiO2 having Ni in a square planar oxygen environment is a monumental development Li:2019p624 , and strongly implies that the local structure ( vs. in Fig. 1(a)) plays a crucial role. This discovery has also led to a large number of works within a short span of time to understand the origin and nature of the superconducting phase Hepting:2020p381 ; li2020superconducting ; zeng:2020phase ; Botana:2020p011024 ; Lechermann:2020p081110 ; Jiang:2019p201106 ; karp:2020 ; Hu:2019p032046 ; adhikary2020orbital ; Mi:2020p207004 ; Hu:2019p032046 ; Zhang2020p023112 ; Zhang:2020p013214 ; Lang:2020doped ; karp:2020many ; Krishna:2020arxiv . While the parent members of the superconducting nickelate and cuprate family are isoelectronic (), several key differences have been noted: unlike the antiferromagnetic insulating phase of the cuprate, NdNiO2 is weakly conducting and nonmagnetic Li:2019p624 . Ni states are found to be strongly hybridized with Nd 5 states Hepting:2020p381 and the superconducting of infinite layer nickelates is much smaller compared to the analogous hole doped CaCuO2 li2020superconducting ; zeng:2020phase ; Azuma:1992p775 . There is also an ongoing strong debate about the location of doped holes (O vs. Ni ) and the nature of Ni spins states (singlet vs. triplet), which would be intimately connected with the orbital configuration and Hund’s coupling Lang:2020doped ; karp:2020many ; Mi:2020p207004 ; Hu:2019p032046 ; Zhang2020p023112 ; Zhang:2020p013214 ; goodge2020doping . However, the actual scenario is unknown due to the very limited amount of experimental literature available. This prompts us to probe other compounds containing both Cu and Ni in four fold coordinated environment of oxygen.
Sr2CuO3 (SCO) contains square planar CuO4 polyhedral units, which form linear chains along the axis, as shown in Fig. 1(b) Motoyama:1996p3212 . This quasi one dimensional system undergoes antiferromagnetic ordering around 5 K Kojima:1997p1787 , and exhibits several intriguing phenomena, including spin-charge separation Neudert:1998p657 , spin-orbital separation Schlappa:2012p82 , and spin Seebeck effect Hirobe:2017p30 . Hole doping in SCO by incorporating excess oxygen further results in superconductivity Hiroi:1993p315 . In addition, one can replace a small fraction of Cu of SCO with Ni without modifying structure Karmakar:2015p224401 , providing us a unique platform to compare the electronic structure of Cu and Ni with a square planar environment.
The electronic properties of transition metal (TM) oxides are described very often within the scheme of well-known Zaanen-Sawatzky-Allen (ZSA) phase diagram Zaanen:1985p418 ; Nimkar:1993p7355 , which considers on-site Coulomb repulsion at TM site (), TM-to-O charge transfer energy () and the electronic hopping interaction strength (). Cu in SCO has an extremely small value of Maiti:1998p1572 , implying that the ground state of Cu2+ in SCO consists of a linear combination of and dominant configurations ( denotes a hole in O 2 state) - contrary to the pure state expected from an ionic picture walters:2009p867 .
In this work, we have investigated the electronic and magnetic structure of Sr2CuO3 (SCO) and Sr2Cu0.9Ni0.1O3 (SCNO) single crystals by magnetic measurement, synchrotron based X-ray linear dichroism (XLD) measurements, density functional theory (DFT) and cluster calculations. We observed extremely large orbital polarization of Ni in Sr2Cu0.9Ni0.1O3 single crystal, which arises due to the low spin =0 configuration with completely unoccupied 3 orbitals of Ni2+. Ni doping of SCO also enhances the contribution of the configuration in the ground state of Cu2+. Our comprehensive study has also affirmed Mott Hubbard insulating nature of the NiO4 unit and larger charge transfer energy compared to high cuprate.
RESULTS
Single crystals of SCO and SCNO, grown by the traveling solvent floating zone technique karmakar:2015p4843 have been investigated in this study. We first discuss the results of polarization dependent XAS (X-ray absorption spectroscopy) experiment on Cu edges, which is known to be a very powerful technique to probe orbital symmetry of cuprates Nucker:1995p8529 ; Knupfer:1997pR7291 ; Neudert:2000p10752 ; Chakhalian:2007p1114 . In Fig. 1(c), we compare linear polarization dependent XAS of Cu and edges for SCO and SCNO. XAS (Iab) of SCO recorded with in-plane (H) polarized light consists of sharp peaks around 930.5 eV and 950.5 eV, which are associated with the transition from the spin-orbit split Cu and Cu core levels, respectively, and the final state configuration is 23 (2 denotes a core hole in Cu 2 states). The much lower intensity of these peaks in XAS (Ic) with the out-of-plane (V) polarization signifies that the upper Hubbard band (UHB) is predominately contributed by Cu orbitals, which is expected for a electronic configuration in symmetry. The features around 934 eV and 954.5 eV, which are much stronger for the out-of-plane polarization, are related to the transitions into Cu 3 derived states, which become partially unoccupied due to the hybridization with Cu 4 states Neudert:2000p10752 . Upon Ni doping, the intensity of the white line increases significantly for both polarizations though the line shape remains unchanged (Fig. 1(c)). The origin of the increase of the configuration upon Ni doping will be discussed later in this paper.
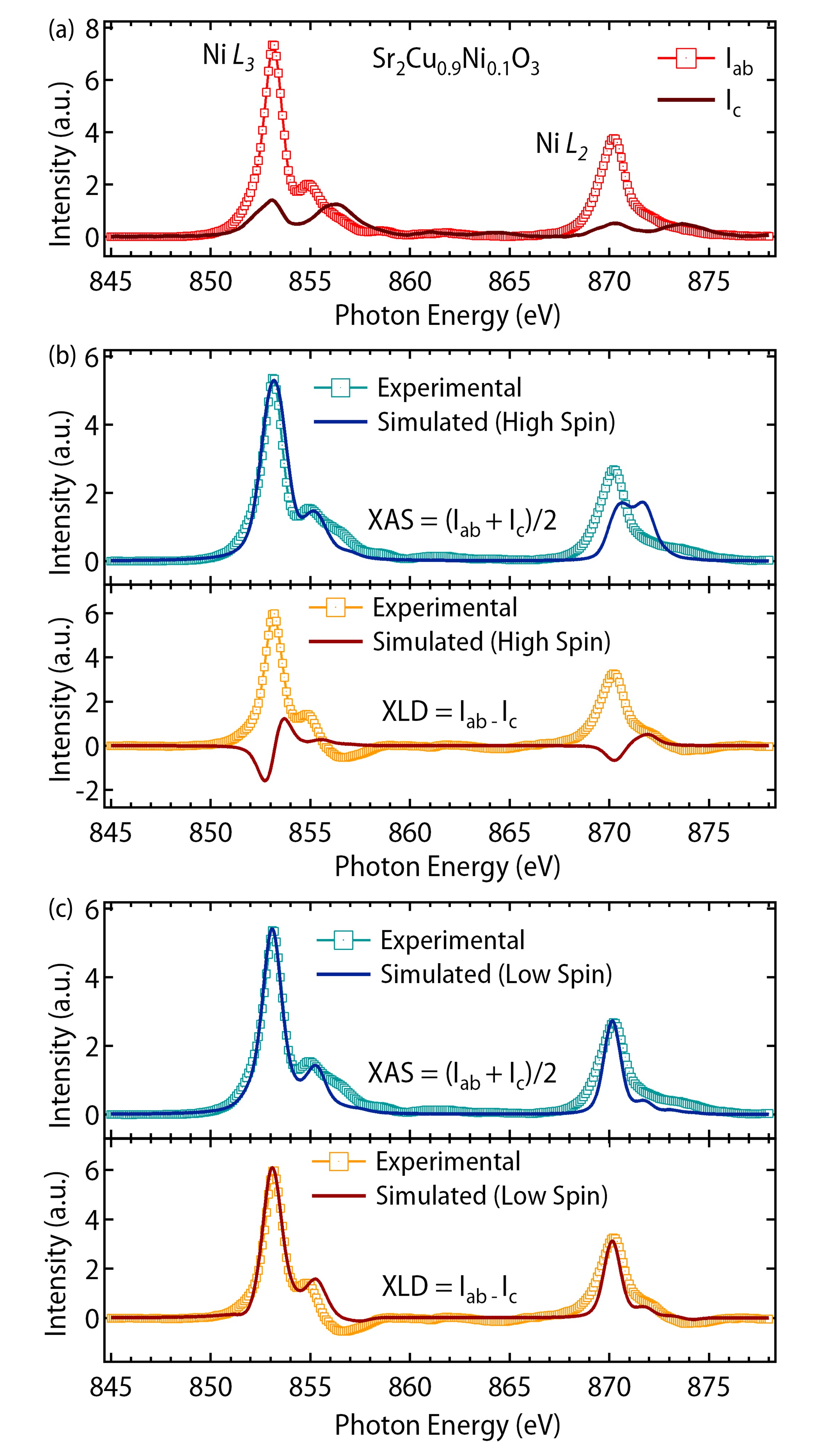
Next, we have performed similar polarization dependent XAS experiments at Ni L3,2 edges of SCNO at 300 K. As shown in Fig. 2(a), the two intense peaks around 853 eV & 870 eV in the spectra (Iab) recorded with the in-plane polarization, correspond to the transitions from Ni and Ni core levels respectively. The spectrum (Ic) recorded with the out-plane polarization shows significantly low intensity indicating that the holes predominantly occupy the bands. The peaks around 856 eV and 874 eV, show higher intensity in Ic than Iab . Similar to the case of Cu, these features are related to the hybridization of Ni 3 and Ni 4 states. Since the experimental realization of large orbital polarization (OP) in Ni based oxides, with important implications for superconductivity, has been a topic of paramount interest Disa:2015p026801 ; Wu:2013p125124 ; Zhang:2017p864 ; Liao_2019 , we have further evaluated OP of Ni in the present case. According to the sum rule of linear polarization, the ratio of holes in and Wu:2013p125124 is defined as
| (1) |
with =. By this definition, =1 corresponds to equal hole population in and orbitals and = 0 signifies 100% character of holes. We have obtained 0.23 (also see Supplementary Materials) in the present case. This implies 81% of the holes occupy Ni 3 orbital, which is the highest among the existing literature of Ni based complex oxides (see Table 1).
| System | % of holes in Ni | Reference | ||
|---|---|---|---|---|
| SrCuO2/LaNiO3 | 0.7 | 59% | Liao_2019, | |
| LaTiO3/LaNiO3/LaAlO3 | 0.55 | 65% | Disa:2015p026801, | |
| La4Ni3O8 | 0.4-0.5 | 67-71% | Zhang:2017p864, | |
| Sr2Cu0.9Ni0.1O3 | 0.23 | 81% | present work |
The orbital polarization () is defined in the literature in terms of the electronic occupation as Wu:2013p125124
| (2) |
where = 2 - and =2 - are the number of electrons in and orbitals, respectively. It is important to note that the value of (= + ) can not be determined unambiguously for many compounds due to the presence of charge transfer from O 2 to Ni 3 orbitals Wu:2013p125124 ; Peil:2014p045128 . In the present case, =2 as the ground state wavefunction is almost entirely contributed by the configuration (discussed in the later part of the paper). We have obtained 63% for the SCNO, which is also larger compared to all existing literatures on Ni based complex oxides Middey:2016p305 ; Disa:2015p026801 ; Wu:2013p125124 ; Middey:2016p056801 ; Zhang:2017p864 ; Liao_2019 .
In order to understand the origin of this unprecedentedly large orbital polarization, we have calculated XAS [(Iab + Ic)/2] and XLD [Iab-Ic] of Ni edges considering a NiO4 cluster with symmetry and Ni2+ ionic configuration using CTM4XAS Stavitski:2010p687 and Quanty retegan_crispy programs that incorporate ligand field multiplet theory. First, we have simulated the XAS and XLD spectra (Fig. 2(b)) for the high spin = 1 configuration Utz_2017 ; van_der_Laan_1988 with = 7 eV and = 9 eV (all other parameters, used for the simulations have been listed in Ref. calc, ). Clearly, neither the simulated XAS nor the XLD matches with the corresponding experimental spectra. In particular, the experimentally observed -edge XAS shows only one peak around 870 eV whereas the simulated spectra shows two peaks. The shape of the simulated XLD is completely different and the amount of anisotropy is significantly lower compared to the experimental data. We have also simulated XAS and XLD with the same values of and but with low spin configuration ( = 0) by adjusting crystal field parameters calc , which ensures the following expected crystal field splitting for a square planar environment Moretti_Sala_2011 . The excellent matching (Fig. 2(c)) between the experimentally observed and simulated spectra with low spin configuration establishes Ni2+ is in =0 state in the square planar environment. The ground state of Ni2+ is strongly dominated by the configuration ( 0.97 + 0.03 ). Simulated spectra with also do not match with experimental observation (see Supplementary Materials), implying electronically NiO4 belongs to the Mott Hubbard insulating region of ZSA phase diagram Zaanen:1985p418 - strikingly similar to the recent experimental reports of the hole doped NdNiO2 Hepting:2020p381 ; goodge2020doping . Due to the large , Ni is less hybridized with O , compared to the Cu -O hybridization. Thus, the replacement of a fraction of Cu by Ni pushes holes from O towards Cu around the dopant Ni. This enhances the relative contribution of configuration (also confirmed by magnetic measurement, discussed later in the paper), resulting in the observed strong increase in the white line intensity in Cu XAS upon Ni doping (Fig. 1(c)).
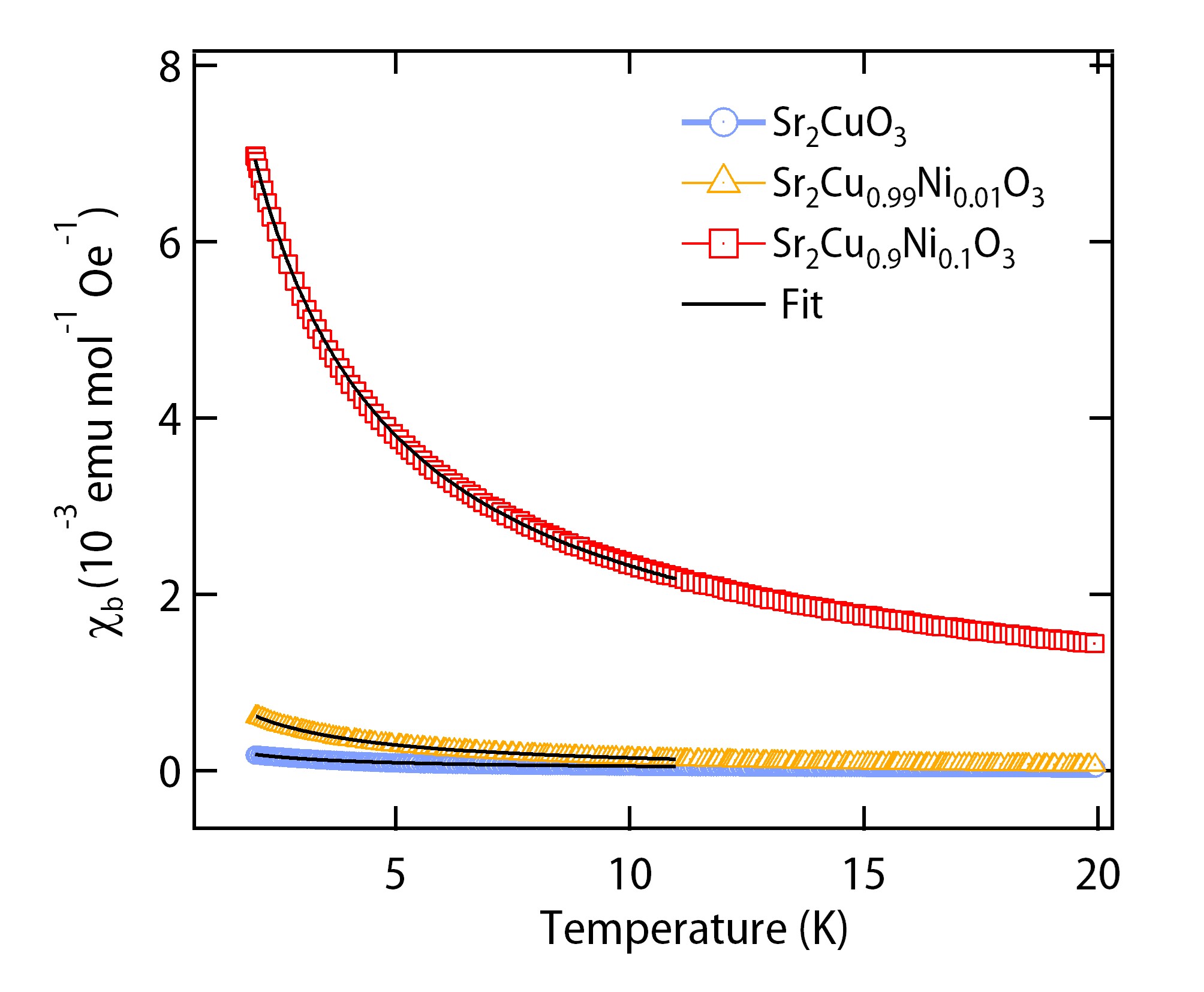
The increase of the component of Cu due to the presence of nonmagnetic Ni2+ is also evident in bulk magnetic measurements. The low-temperature magnetic susceptibility () plots of pristine, 1%, and 10% Ni doped SCO samples are shown in Fig. 3. As expected, for the pristine sample is very small due to the antiferromagnetic coupling between the neighboring Cu spins. Upon doping with Ni at the Cu-site, the -O-Cu-O-Cu-O- chain breaks into finite length segments due to an effective spin 0 on the Ni ion. The number of segments thus produced being + 1 for large , where is the concentration of Ni in the sample. Assuming a statistically random distribution of Ni ions over the chain length, it is reasonable to consider that one-half of the chain segments will have an odd number of Cu spins, and even for the remaining. Since Cu-spins are antiferromagnetically paired, the net moment on the even-length segments tends to 0 at sufficiently low-temperatures Ami:1995p5994 . In contrast, the odd-length segments remain with an uncompensated Cu spin, which results in an enhancement in the magnetic response of Ni doped samples, as seen in our measurement (Fig. 3). A very weak Curie-tail in the pristine sample can be attributed to the presence of intrinsic defects. We fitted the low-temperature susceptibility of our samples using the Curie-Weiss (CW) law: =+ where is the temperature independent contribution arising due to Van Vleck paramagnetism and core diamagnetism, is the Curie-constant, and is the Weiss temperature. The best fit parameters for the three samples are tabulated in Table 2.
| Doping | (emu | (emu | |||
|---|---|---|---|---|---|
| () | mol-1Oe-1) | mol-1Oe-1 K) | (K) | (/f.u.) | (/1/2 Ni) |
| 0 | -5 10-5 | 0.0005(4) | -0.6 | 0.06 | - |
| 0.01 | -3 10-5 | 0.0018(2) | -1(1) | 0.12 | 1.74 |
| 0.1 | 5 10-4 | 0.018(2) | -2(1) | 0.38 | 1.70 |
It is reassuring to note that the value of increases by a factor of 10 on increasing the Ni concentration from = 0.01 to 0.1. for SCNOis positive and about an order of magnitude higher than for SCO. Such an enhancement is likely due to the Van Vleck paramagnetism associated with unoccupied orbital of Ni2+ ion in the low-spin state van1932book . From , the (=) for the two Ni doped samples ( = 0.01 and 0.1) turned out to be 0.12 and 0.38 per formula unit respectively. The average effective moment on the odd-length segments (=) turns out to be 1.74 and 1.70 , respectively for the two samples. These values are close to an effective moment of 1.73 expected for a = 1/2 () system, confirming our conclusion of Cu XAS measurement.
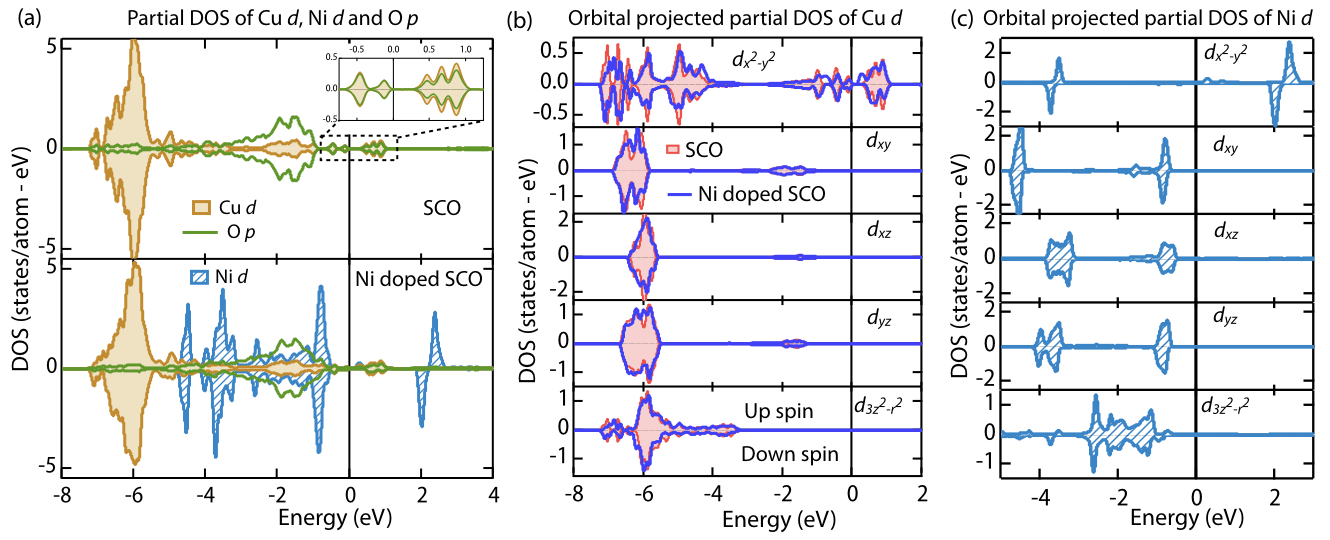
To obtain a microscopic understanding of our experimental observations, we have carried out first-principles density functional theory (DFT) calculations for Sr2CuO3 and Sr2Cu0.875Ni0.125O3 [see Methods for details of the calculations]. The calculated orbital projected density of states (DOS) are shown in Fig. 4. In contrast with the transition metal oxides with positive , the bonding states of SCO are primarily contributed by Cu orbitals due to negative Ushakov:2011p445601 . The Cu , , and bonding states are spread around 6 eV below the Fermi level (Fig. 4(b)). The valence band and conduction band edge of undoped SCO comes predominantly from O states (inset of upper panel of Fig. 4(a)), as expected for the covalent insulating nature of SCO Maiti:1998p1572 . The antibonding states are partially unoccupied and show a pronounced contribution to the upper Hubbard band, in line with our XAS results. We find that the magnetic moment on Cu is close to 0.19 . The slight overestimation of this moment, compared to the experimentally observed moment ( 0.06) Kojima:1997p1787 is likely to be related to the presence of the quantum fluctuation effects in SCO, which are not accounted for in a mean field approach like DFT.. The much smaller moment, compared to the expected moment of 1.73 for a pure (=1/2) configuration, again signifies that the ground state of Cu2+ in SCO is predominantly configuration with small admixture with . In Ni doped SCO, there is a small increase in Cu magnetic moments, which range from 0.19 to 0.25 and a net moment of 0.13 per formulae unit. This also supports our observation about the increase of white line intensity of Cu XAS (Fig. 1(c)) and magnetic measurement i.e. the enhancement of configuration of Cu upon Ni doping. For Ni doped SCO, the contribution arising from different Ni orbitals is shown in Fig. 4(c) (also see lower panel of Fig. 4(a)). We find that the antibonding states of Ni orbital are completely unoccupied, while all other Ni 3 states are completely filled. This low spin =0 configuration of Ni with holes in the orbital is in excellent agreement with our experimental observations.
DISCUSSION
To summarize, our element sensitive X-ray absorption spectroscopy experiments with linear polarized light on Sr2Cu0.9Ni0.1O3 have found that 81% holes of Ni2+ sites occupy the orbital, which is the highest among all Ni containing oxides reported so far. Ni doping in Sr2CuO3 also results in hole transfer from O to Cu orbitals. Cluster calculations have not only confirmed the Mott Hubbard insulating nature of NiO4 units but also revealed that the observed giant orbital polarization arises due to low spin (=0) configuration of Ni2+. This nonmagnetic state of Ni2+ has been further corroborated by theory.
Finally, we also note that our investigated system has several parallels with the recently discovered superconducting nickelates. Our system comprises of NiO4 units forming one dimensional chains, while the superconducting nickelates have a two dimensional NiO2 plane. It is expected that the increase in the dimensionality of the system would further enhance Maiti:1999p12457 , and therefore our conclusions about the Mott-Hubbard nature and the low spin configuration of Ni2+ should also hold for nickelate superconductors. The larger charge transfer energy might be responsible for the observed lower in hole doped nickelates Zhang:2020p013214 ; Lechermann:2020p081110 ; Jiang:2019p201106 .
MATERIALS AND METHODS
Single crystals of SCO and SCNO were grown under O2 atmosphere using the traveling solvent floating zone technique as reported elsewhere karmakar:2015p4843 . All the experiments reported here are carried out on as grown crystals. The magnetic susceptibility was measured using a Physical Property Measurement System, Quantum Design, USA. X-ray absorption spectra (XAS) with vertically (V) and horizontally (H) polarized X-ray were recorded at room temperature in 4-ID-C beamline of Advanced Photon Source, Argonne National Laboratory, USA.
All theoretical calculations have been performed within the framework of density functional theory as implemented in the Quantum Espresso package Giannozzi:2009p395502 . The wave functions are expanded in a plane wave basis set with kinetic and charge density cut offs set to 45 Ry and 450 Ry respectively. The exchange-correlation interactions are taken into account by the Perdew-Burke-Ernzeroff form of generalized gradient approximation Perdew:1996p3865 . The ion-electron interactions are described by ultrasoft pseudopotentials Vanderbilt:1990p7892 . The on-site Coulomb interaction is modeled using LDA+ approach in the linear-response method of Cococcioni and de Gironcoli Cococcioni:2005p3 , with = 5 eV and 9 eV on Ni and Cu, respectively.
References
- (1) J. G. Bednorz, K. A. Muller, Possible high superconductivity in the Ba-La-Cu-O system. Zeitschrift fur Physik B Condensed Matter 64, 189–193 (1986).
- (2) P. A. Lee, N. Nagaosa, X.-G. Wen, Doping a mott insulator: Physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
- (3) E. Fradkin, S. A. Kivelson, J. M. Tranquada, Colloquium: Theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015).
- (4) B. Keimer, S. A. Kivelson, M. R. Norman, S. Uchida, J. Zaanen, From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
- (5) V. I. Anisimov, D. Bukhvalov, T. M. Rice, Electronic structure of possible nickelate analogs to the cuprates. Phys. Rev. B 59, 7901–7906 (1999).
- (6) J. c. v. Chaloupka, G. Khaliullin, Orbital order and possible superconductivity in LaNiO3/LaMO3 superlattices. Phys. Rev. Lett. 100, 016404 (2008).
- (7) P. Hansmann, X. Yang, A. Toschi, G. Khaliullin, O. K. Andersen, K. Held, Turning a nickelate fermi surface into a cupratelike one through heterostructuring. Phys. Rev. Lett. 103, 016401 (2009).
- (8) S. Middey, J. Chakhalian, P. Mahadevan, J. W. Freeland, A. J. Millis, D. D. Sarma, Physics of ultrathin films and heterostructures of rare-earth nickelates. Annual Review of Materials Research 46, 305–334 (2016).
- (9) J. W. Freeland, J. Liu, M. Kareev, B. Gray, J. W. Kim, P. J. Ryan, R. Pentcheva, J. Chakhalian, Orbital control in strained ultra-thin LaNiO3/LaAlO3 superlattices. Europhysics Letters 96, 57004 (2011).
- (10) E. Benckiser, M. W. Haverkort, S. Br ck, E. Goering, S. Macke, A. Frañó, X. Yang, O. K. Andersen, G. Cristiani, H.-U. Habermeier, A. V. Boris, I. Zegkinoglou, P. Wochner, H.-J. Kim, V. Hinkov, B. Keimer, Orbital reflectometry of oxide heterostructures. Nature Materials 10, 189–193 (2011).
- (11) M. Wu, E. Benckiser, M. W. Haverkort, A. Frano, Y. Lu, U. Nwankwo, S. Brück, P. Audehm, E. Goering, S. Macke, V. Hinkov, P. Wochner, G. Christiani, S. Heinze, G. Logvenov, H.-U. Habermeier, B. Keimer, Strain and composition dependence of orbital polarization in nickel oxide superlattices. Phys. Rev. B 88, 125124 (2013).
- (12) V. V. Poltavets, K. A. Lokshin, A. H. Nevidomskyy, M. Croft, T. A. Tyson, J. Hadermann, G. Van Tendeloo, T. Egami, G. Kotliar, N. ApRoberts-Warren, A. P. Dioguardi, N. J. Curro, M. Greenblatt, Bulk magnetic order in a two-dimensional Ni1+/Ni2+ () nickelate, isoelectronic with superconducting cuprates. Phys. Rev. Lett. 104, 206403 (2010).
- (13) J.-G. Cheng, J.-S. Zhou, J. B. Goodenough, H. D. Zhou, K. Matsubayashi, Y. Uwatoko, P. P. Kong, C. Q. Jin, W. G. Yang, G. Y. Shen, Pressure effect on the structural transition and suppression of the high-spin state in the triple-layer - La4Ni3O8. Phys. Rev. Lett. 108, 236403 (2012).
- (14) J. Zhang, A. S. Botana, J. W. Freeland, D. Phelan, H. Zheng, V. Pardo, M. R. Norman, J. F. Mitchell, Large orbital polarization in a metallic square-planar nickelate. Nature Physics 13, 864–869 (2017).
- (15) D. Li, K. Lee, B. Y. Wang, M. Osada, S. Crossley, H. R. Lee, Y. Cui, Y. Hikita, H. Y. Hwang, Superconductivity in an infinite-layer nickelate. Nature 572, 624–627 (2019).
- (16) M. Hepting, D. Li, C. Jia, H. Lu, E. Paris, Y. Tseng, X. Feng, M. Osada, E. Been, Y. Hikita, et al., Electronic structure of the parent compound of superconducting infinite-layer nickelates. Nature materials 19, 381–385 (2020).
- (17) D. Li, B. Y. Wang, K. Lee, S. P. Harvey, M. Osada, B. H. Goodge, L. F. Kourkoutis, H. Y. Hwang, Superconducting dome in infinite layer films. Phys. Rev. Lett. 125, 027001 (2020).
- (18) S. Zeng, C. S. Tang, X. Yin, C. Li, Z. Huang, J. Hu, W. Liu, G. J. Omar, H. Jani, Z. S. Lim, et al., Phase diagram and superconducting dome of infinite-layer nd1-xsrxnio2 thin films. arXiv preprint arXiv:2004.11281 (2020).
- (19) A. S. Botana, M. R. Norman, Similarities and differences between and and implications for superconductivity. Phys. Rev. X 10, 011024 (2020).
- (20) F. Lechermann, Late transition metal oxides with infinite-layer structure: Nickelates versus cuprates. Phys. Rev. B 101, 081110 (2020).
- (21) P. Jiang, L. Si, Z. Liao, Z. Zhong, Electronic structure of rare-earth infinite-layer . Phys. Rev. B 100, 201106 (2019).
- (22) J. Karp, A. S. Botana, M. R. Norman, H. Park, M. Zingl, A. Millis, Many-body electronic structure of ndnio and cacuo . arXiv preprint arXiv:2001.06441 (2020).
- (23) L.-H. Hu, C. Wu, Two-band model for magnetism and superconductivity in nickelates. Phys. Rev. Research 1, 032046 (2019).
- (24) P. Adhikary, S. Bandyopadhyay, T. Das, I. Dasgupta, T. Saha-Dasgupta, Orbital selective superconductivity in a two-band model of infinite-layer nickelates. arXiv preprint arXiv:2005.01243 (2020).
- (25) M. Jiang, M. Berciu, G. A. Sawatzky, Critical nature of the ni spin state in doped . Phys. Rev. Lett. 124, 207004 (2020).
- (26) Y.-H. Zhang, A. Vishwanath, Type-ii model in superconducting nickelate . Phys. Rev. Research 2, 023112 (2020).
- (27) H. Zhang, L. Jin, S. Wang, B. Xi, X. Shi, F. Ye, J.-W. Mei, Effective hamiltonian for nickelate oxides . Phys. Rev. Research 2, 013214 (2020).
- (28) Z.-J. Lang, R. Jiang, W. Ku, Where do the doped hole carriers reside in the new superconducting nickelates? arXiv preprint arXiv:2005.00022 (2020).
- (29) J. Karp, A. S. Botana, M. R. Norman, H. Park, M. Zingl, A. Millis, Many-body electronic structure of ndnio and cacuo . arXiv preprint arXiv:2001.06441 (2020).
- (30) J. Krishna, H. LaBollita, A. O. Fumega, V. Pardo, A. S. Botana, Effects of sr-doping on the electronic and spin-state properties of infinite-layer nickelates. arXiv preprint arXiv:2008.02237 (2020).
- (31) M. Azuma, Z. Hiroi, M. Takano, Y. Bando, Y. Takeda, Superconductivity at 110 k in the infinite-layer compound (sr1-xcax)1-ycuo2. Nature 356, 775–776 (1992).
- (32) B. H. Goodge, D. Li, M. Osada, B. Y. Wang, K. Lee, G. A. Sawatzky, H. Y. Hwang, L. F. Kourkoutis, Doping evolution of the mott-hubbard landscape in infinite-layer nickelates. arXiv preprint arXiv:2005.02847 (2020).
- (33) N. Motoyama, H. Eisaki, S. Uchida, Magnetic susceptibility of ideal spin 1 2 heisenberg antiferromagnetic chain systems, and . Phys. Rev. Lett. 76, 3212–3215 (1996).
- (34) K. M. Kojima, Y. Fudamoto, M. Larkin, G. M. Luke, J. Merrin, B. Nachumi, Y. J. Uemura, N. Motoyama, H. Eisaki, S. Uchida, K. Yamada, Y. Endoh, S. Hosoya, B. J. Sternlieb, G. Shirane, Reduction of ordered moment and néel temperature of quasi-one-dimensional antiferromagnets and . Phys. Rev. Lett. 78, 1787–1790 (1997).
- (35) R. Neudert, M. Knupfer, M. S. Golden, J. Fink, W. Stephan, K. Penc, N. Motoyama, H. Eisaki, S. Uchida, Manifestation of spin-charge separation in the dynamic dielectric response of one-dimensional . Phys. Rev. Lett. 81, 657–660 (1998).
- (36) J. Schlappa, K. Wohlfeld, K. Zhou, M. Mourigal, M. Haverkort, V. Strocov, L. Hozoi, C. Monney, S. Nishimoto, S. Singh, et al., Spin–orbital separation in the quasi-one-dimensional mott insulator sr 2 cuo 3. Nature 485, 82–85 (2012).
- (37) D. Hirobe, M. Sato, T. Kawamata, Y. Shiomi, K.-i. Uchida, R. Iguchi, Y. Koike, S. Maekawa, E. Saitoh, One-dimensional spinon spin currents. Nature Physics 13, 30–34 (2017).
- (38) .-Z. Hiroi, M. Takano, M. Azuma, Y. Takeda, A new family of copper oxide superconductors srn+ 1cuno2n+ 1+ stabilized at high pressure. Nature 364, 315–317 (1993).
- (39) K. Karmakar, S. Singh, Finite-size effects in the quasi-one-dimensional quantum magnets and . Phys. Rev. B 91, 224401 (2015).
- (40) J. Zaanen, G. A. Sawatzky, J. W. Allen, Band gaps and electronic structure of transition-metal compounds. Phys. Rev. Lett. 55, 418–421 (1985).
- (41) S. Nimkar, D. D. Sarma, H. R. Krishnamurthy, S. Ramasesha, Mean-field results of the multiple-band extended hubbard model for the square-planar CuO2 lattice. Phys. Rev. B 48, 7355–7363 (1993).
- (42) K. Maiti, D. D. Sarma, T. Mizokawa, A. Fujimori, Electronic structure of one-dimensional cuprates. Phys. Rev. B 57, 1572–1578 (1998).
- (43) A. C. Walters, T. G. Perring, J.-S. Caux, A. T. Savici, G. D. Gu, C.-C. Lee, W. Ku, I. A. Zaliznyak, Effect of covalent bonding on magnetism and the missing neutron intensity in copper oxide compounds. Nature Physics 5, 867–872 (2009).
- (44) K. Karmakar, R. Bag, S. Singh, Crystal growth of spin chain compound sr2cuo3 doped with quantum defects: Zn, co, ni, and mn. Crystal Growth & Design 15, 4843–4853 (2015).
- (45) N. Nücker, E. Pellegrin, P. Schweiss, J. Fink, S. L. Molodtsov, C. T. Simmons, G. Kaindl, W. Frentrup, A. Erb, G. Müller-Vogt, Site-specific and doping-dependent electronic structure of probed by o 1s and cu 2p x-ray-absorption spectroscopy. Phys. Rev. B 51, 8529–8542 (1995).
- (46) M. Knupfer, R. Neudert, M. Kielwein, S. Haffner, M. S. Golden, J. Fink, C. Kim, Z.-X. Shen, M. Merz, N. Nücker, S. Schuppler, N. Motoyama, H. Eisaki, S. Uchida, Z. Hu, M. Domke, G. Kaindl, Site-specific unoccupied electronic structure of one-dimensional . Phys. Rev. B 55, R7291–R7294 (1997).
- (47) R. Neudert, S.-L. Drechsler, J. Málek, H. Rosner, M. Kielwein, Z. Hu, M. Knupfer, M. S. Golden, J. Fink, N. Nücker, M. Merz, S. Schuppler, N. Motoyama, H. Eisaki, S. Uchida, M. Domke, G. Kaindl, Four-band extended hubbard hamiltonian for the one-dimensional cuprate distribution of oxygen holes and its relation to strong intersite coulomb interaction. Phys. Rev. B 62, 10752–10765 (2000).
- (48) J. Chakhalian, J. W. Freeland, H.-U. Habermeier, G. Cristiani, G. Khaliullin, M. van Veenendaal, B. Keimer, Orbital reconstruction and covalent bonding at an oxide interface. Science 318, 1114-1117 (2007).
- (49) M. M. Sala, V. Bisogni, C. Aruta, G. Balestrino, H. Berger, N. B. Brookes, G. M. de Luca, D. D. Castro, M. Grioni, M. Guarise, P. G. Medaglia, F. M. Granozio, M. Minola, P. Perna, M. Radovic, M. Salluzzo, T. Schmitt, K. J. Zhou, L. Braicovich, G. Ghiringhelli, Energy and symmetry of dd excitations in undoped layered cuprates measured by CuL3resonant inelastic x-ray scattering. New Journal of Physics 13, 043026 (2011).
- (50) A. V. Ushakov, S. V. Streltsov, D. I. Khomskii, Crystal field splitting in correlated systems with negative charge-transfer gap. Journal of Physics: Condensed Matter 23, 445601 (2011).
- (51) A. S. Disa, D. P. Kumah, A. Malashevich, H. Chen, D. A. Arena, E. D. Specht, S. Ismail-Beigi, F. J. Walker, C. H. Ahn, Orbital engineering in symmetry-breaking polar heterostructures. Phys. Rev. Lett. 114, 026801 (2015).
- (52) Z. Liao, E. Skoropata, J. W. Freeland, E.-J. Guo, R. Desautels, X. Gao, C. Sohn, A. Rastogi, T. Z. Ward, T. Zou, T. Charlton, M. R. Fitzsimmons, H. N. Lee, Large orbital polarization in nickelate-cuprate heterostructures by dimensional control of oxygen coordination. Nature Communications 10 (2019).
- (53) O. E. Peil, M. Ferrero, A. Georges, Orbital polarization in strained LaNiO3: Structural distortions and correlation effects. Phys. Rev. B 90, 045128 (2014).
- (54) S. Middey, D. Meyers, D. Doennig, M. Kareev, X. Liu, Y. Cao, Z. Yang, J. Shi, L. Gu, P. J. Ryan, R. Pentcheva, J. W. Freeland, J. Chakhalian, Mott electrons in an artificial graphenelike crystal of rare-earth nickelate. Phys. Rev. Lett. 116, 056801 (2016).
- (55) E. Stavitski, F. M. De Groot, The ctm4xas program for eels and xas spectral shape analysis of transition metal l edges. Micron 41, 687–694 (2010).
- (56) M. Retegan, Crispy: v0.7.3 (2019).
- (57) Y. Utz, F. Hammerath, R. Kraus, T. Ritschel, J. Geck, L. Hozoi, J. van den Brink, A. Mohan, C. Hess, K. Karmakar, S. Singh, D. Bounoua, R. Saint-Martin, L. Pinsard-Gaudart, A. Revcolevschi, B. B chner, H.-J. Grafe, Effect of different in-chain impurities on the magnetic properties of the spin chain compound SrCuO2 probed by NMR. Physical Review B 96 (2017).
- (58) G. van der Laan, B. T. Thole, G. A. Sawatzky, M. Verdaguer, Multiplet structure in the ,3 x-ray-absorption spectra: A fingerprint for high- and low-spin compounds. Phys. Rev. B 37, 6587–6589 (1988).
- (59) = 9 eV, = 7 eV, = 9 eV were used in Cluster calculations. The hopping parameters, related to , , and / orbitals, were chosen to be 2.0, 2.0, 1.0, 1.0 eV, respectively. For the high spin ( = 1) configuration, the crystal field parameters for symmetry were chosen as = 0.235 eV, = 0.1 eV, = 0.05 eV. Whereas, = 0.235 eV, = 0.5eV, = 0.3 eV were used for the low spin ( = 0) configuration.
- (60) D. C. Johnston, R. K. Kremer, M. Troyer, X. Wang, A. Klümper, S. L. Bud’ko, A. F. Panchula, P. C. Canfield, Thermodynamics of spin antiferromagnetic uniform and alternating-exchange heisenberg chains. Phys. Rev. B 61, 9558–9606 (2000).
- (61) S. Fujimoto, S. Eggert, Boundary susceptibility in the spin- chain: Curie-like behavior without magnetic impurities. Phys. Rev. Lett. 92, 037206 (2004).
- (62) J. Sirker, N. Laflorencie, S. Fujimoto, S. Eggert, I. Affleck, Chain breaks and the susceptibility of and other doped quasi-one-dimensional antiferromagnets. Phys. Rev. Lett. 98, 137205 (2007).
- (63) T. Ami, M. K. Crawford, R. L. Harlow, Z. R. Wang, D. C. Johnston, Q. Huang, R. W. Erwin, Magnetic susceptibility and low-temperature structure of the linear chain cuprate . Phys. Rev. B 51, 5994–6001 (1995).
- (64) J. H. Van Vleck, The theory of electric and magnetic susceptibilities (Clarendon Press, 1932).
- (65) K. Maiti, P. Mahadevan, D. D. Sarma, Evolution of electronic structure with dimensionality in divalent nickelates. Phys. Rev. B 59, 12457–12470 (1999).
- (66) P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari, R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. Journal of Physics: Condensed Matter 21, 395502 (2009).
- (67) J. P. Perdew, K. Burke, M. Ernzerhof, Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
- (68) D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Physical Review B 41, 7892–7895 (1990).
- (69) M. Cococcioni, S. de Gironcoli, Linear response approach to the calculation of the effective interaction parameters in the method. Phys. Rev. B 71, 035105 (2005).
Acknowledgement
SM thanks Tanmoy Das and H. R. Krishnamurthy for discussions. SM acknowledges financial support from a SERB Early Career Research Award (ECR/2018/001512) and MHRD STARS 156/2019 project for research funding. SM also thanks the Department of Science and Technology, India (No. SR/NM/Z-07/2015) for the financial support to conduct the synchrotron experiment at the Advanced Photon Source and Jawaharlal Nehru Centre for Advanced Scientific Research (JNCASR) for managing the project. This research used resources of the Advanced Photon Source, a U.S. Department of Energy Office of Science User Facility operated by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. AN acknowledges support from the start-up grant (SG/MHRD-19-0001) of the Indian Institute of Science.