Giant electro-optic and elasto-optic effects in ferroelectric NbOI₂

The linear electro-optic (EO) effect (or Pockels effect) is defined as the variation of the refractive index of a material affected by an external electrical field DiDomenico1969 ; Wemple1969 ; Weber2002 . It has the potential to be used for power-efficient and high-speed optical devices Turner1966 ; Lines1997 ; Wemple1972 ; Saleh1991 ; Yariv2007 ; Boyd2008 ; Bass2009 , such as EO modulators Xu2005 , bistable switches Lorente2017 , and optical resonators Guarino2007 . However, there are very few materials possessing large linear EO effect, which limits its application. The standard material of LiNbO₃ is currently the best choice for optical modulators in the telecommunications industry because of its large linear EO coefficient ($\sim$ 30 pm/V) Weber2002 ; Turner1966 . Finding other materials with even larger EO coefficient is therefore of high importance for practical applications but also for scientific interest by revealing the microscopic reason behind such hypothetical enhancement.

Recently, first-principles calculations predicted very large ferroelectric and piezoelectric effects in the NbOX₂ systems Jia2019 ; Ye2021 ; Wu2022 . These layered niobium oxide dihalides NbOX₂ (X=Cl, Br, I) systems were also discovered to exhibit large second-harmonic generation (SHG) likely due to the interplay between anisotropic polarization and excitonic resonance Fang2021 ; Abdelwahab2022 ; Fu2023 ; Ye2023 ; Guo2023 ; Wang2024 ; Yan2024 ; Chen2024 . Note that the SHG intensity of NbOX₂ family is proportional to the ferroelectric spontaneous polarization, which is highly promising for exploring large second-order optical nonlinearities. However, to the best of our knowledge, electro-optic effects, but also elasto-optic conversion that relates a change of strain with a variation in the refractive index, remain unknown in these materials.

The aim of this Letter is to investigate the linear electro-optic effect and elasto-optic effects in stress-free ferroelectric NbOI₂ bulk and monolayer, as well as the effect of epitaxial strain on such coupling properties in these systems. As we will see, both NbOI₂ bulk and monolayer possess really large EO and elasto-optic coefficients for stress-free conditions, with these responses becoming even giant for some epitaxial strains. The reason behind such enhancement of these non-linear effects is further revealed.

Here, we choose the ground state structures of ferroelectric NbOI₂ bulk and monolayer, which have the $C2$ space group ($2$ point group) and $Pmm2$ space group ($mm2$ point group), respectively. First-principles calculations are performed on the ferroelectric bulk and monolayer structures based on the density functional theory (DFT) with the generalized gradient approximation of the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional form, using the ABINIT package Gonze2002 with the norm-conserving pseudopotentials Hamann2013 ; Setten2018 . We use a $\Gamma$-centered 12$\times$6$\times$1 $k$-point mesh to sample the Brillouin zone of bulk and monolayer NbOI₂ and a plane-wave cutoff of 50 hartrees. For the ferroelectric monolayer NbOI₂, a vacuum space of more than 20 Å is used to avoid the periodic image interactions. Furthermore, the effects of epitaxial biaxial strain on the structural properties of bulk and monolayer NbOI₂ are calculated as well. The considered strains are ranging between $-$3% and $+$3%. For each considered strain, the in-plane lattice vectors are kept fixed, while the out-of-plane lattice vector is allowed to relax for bulk NbOI₂ but kept fixed for the supercell modeling the monolayer and vacuum. The atomic positions are fully relaxed for both the bulk and monolayer NbOI₂ until all the force values acting on the atoms are less than 1$\times$10^-6 hartree/bohr. In order to mimic the van der Waals (vdW) interactions in NbOI₂ bulk, the DFT-D3 method with Becke-Johnson damping Grimme2011 was included in the calculations. The strain-induced structures are then used to calculate the EO tensor but within the local density approximation (LDA) because such calculation is only implemented within LDA. This method can be rather accurate, since it predicts linear and nonlinear EO coefficients for ferroelectric oxides Veithen2004 ; Veithen2005 ; Jiang2020 that agree rather well with experimental results Weber2002 ; Chen2014 . Technically, the linear EO tensor ${r}_{ijk}$ is expressed as:

where $(\varepsilon^{-1})_{ij}$ is the inverse of the electronic dielectric tensor and ${\cal E}_{k}$ is the applied electric field in the Cartesian direction $k$.

The clamped (strain-free) EO tensor can be written as Veithen2004 ; Veithen2005 :

where $r_{ijk}^{\mathrm{el}}$ is the bare electronic contribution, $r_{ijk}^{\mathrm{ion}}$ represents the ionic contribution, $n_{i}$ and $n_{j}$ are the principal refractive indices, $\chi_{ijk}^{(2)}$ is the nonlinear optical dielectric susceptibility, $\Omega_{0}$ is the unit cell volume, $\alpha_{ij}^{m}$ denotes the Raman susceptibility of mode $m$, $p_{k}^{m}$ is the polarity, and $\omega_{m}$ is the phonon mode frequency. Note that the clamped EO tensor and phonon frequencies are directly obtained from density functional perturbation theory (DFPT) calculations Veithen2005 .

The unclamped (stress-free that adds a piezoelectric contribution) EO coefficients can be expressed as

where $p_{ij\alpha\beta}$ is the elasto-optic coefficients and $d_{k\alpha\beta}$ represent the piezoelectric strain coefficients. Note that Eqs. (2) and (3) can be used to calculate the linear clamped and unclamped EO tensor from first-principles Charles2019 ; Jiang2019 ; Paoletta2021 ; Prosandeev2024 . Measurements with time response method (TRM) Abarkan2014 and modulation depth method (MDM) Abarkan2017 can be used to determine the clamped and unclamped EO coefficients.

Moreover, the elasto-optic tensor $p_{ij\alpha\beta}$ is given by the expression Zgonik1994

where $n$ is the refractive index (which is simply equal to the square root of the electronic dielectric tensor) and $x_{\alpha\beta}$ denotes the strain tensor.

We first check the structural parameters of NbOI₂ bulk and monolayer. The lattice parameters of bulk NbOI₂ are found to be $a$ $=$ 3.89 Å, $b$ $=$ 7.51 Å, $c$ $=$ 15.15 Å and $\alpha$ $=$ 105.4^∘, which are in good agreement with the experimental values of $a$ $=$ 3.92 Å, $b$ $=$ 7.52 Å, $c$ $=$ 15.18 Å, and $\alpha$ $=$ 105.5^∘ Rijnsdorp1978 . For ferroelectric NbOI₂ monolayer, the relaxed lattice constants are $a$ $=$ 3.94 Å, $b$ $=$ 7.58 Å, which are precisely those found in Refs. Ye2021 ; Ye2023 .

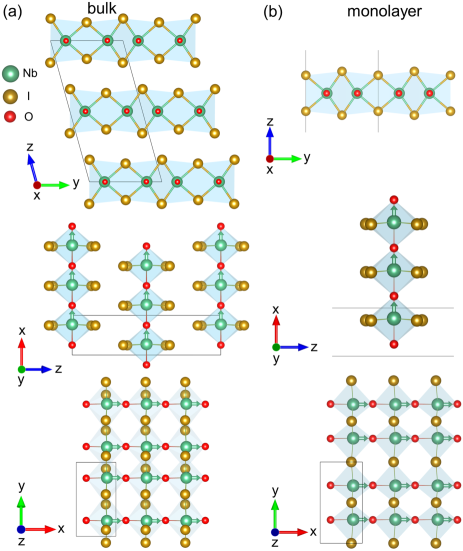
Figure 1 displays the crystal structures of the NbOI₂ bulk and monolayer, respectively. A spontaneous polarization occurs along the $x$-axis direction for both ferroelectric NbOI₂ bulk and monolayer. The EO tensor of NbOI₂ bulk ($2$ point group) has eight independent elements in the Voigt notation Nye1985 : ${r}_{11}$, ${r}_{21}$, ${r}_{31}$, ${r}_{41}$, ${r}_{52}$, ${r}_{53}$, ${r}_{62}$ and ${r}_{63}$, while the EO tensor of the NbOI₂ monolayer ($mm2$ point group) has five independent elements: ${r}_{11}$, ${r}_{21}$, ${r}_{31}$, ${r}_{53}$ and ${r}_{62}$. For the NbOI₂ monolayer, it is important to recall that the calculated EO tensor predicted by the DFT simulations on the supercell has to be rescaled as Jiang2022 ; Jiang2024 :

where $r_{11}^{\textrm{2$\mathrm{D}$}}$, $r_{21}^{\textrm{2$\mathrm{D}$}}$, $r_{31}^{\textrm{2$\mathrm{D}$}}$, $r_{53}^{\textrm{2$\mathrm{D}$}}$ and $r_{62}^{\textrm{2$\mathrm{D}$}}$ are the rescaled 2D EO coefficients; $r_{11}^{\textrm{SC}}$, $r_{21}^{\textrm{SC}}$, $r_{31}^{\textrm{SC}}$, $r_{53}^{\textrm{SC}}$ and $r_{62}^{\textrm{SC}}$ are the EO tensor of the supercell; $\varepsilon_{\textrm{11}}^{\textrm{SC}}$, $\varepsilon_{\textrm{22}}^{\textrm{SC}}$ and $\varepsilon_{\textrm{33}}^{\textrm{SC}}$ are the diagonal elements of the dielectric tensor in the supercell; $\varepsilon_{\textrm{11}}^{\textrm{2D}}$, $\varepsilon_{\textrm{22}}^{\textrm{2D}}$ and $\varepsilon_{\textrm{33}}^{\textrm{2D}}$ are the renormalized 2D dielectric constants; $c$ is the lattice constant of the supercell in monolayer NbOI₂ while $t$ is the effective thickness of the 2D material. The choice of $t$ is based on the van der Waals bond length Jiang2024 ; Laturia2018 . Practically, $t$ is taken to be equal to 7.3 Å here for the NbOI₂ monolayer, which is consistent with the experimental report of Ref. Abdelwahab2022 . The rescaling of the dielectric constants is given by Laturia2018 : $\varepsilon_{\textrm{11}}^{\textrm{2$\mathrm{D}$}}=1+\frac{c}{t}\left(\varepsilon_{\textrm{11}}^{\textrm{SC}}-1\right)$, $\varepsilon_{\textrm{22}}^{\textrm{2$\mathrm{D}$}}=1+\frac{c}{t}\left(\varepsilon_{\textrm{22}}^{\textrm{SC}}-1\right)$, and $\varepsilon_{\textrm{33}}^{\textrm{2$\mathrm{D}$}}=\left[1+\frac{c}{t}\left(\left(\varepsilon_{\textrm{33}}^{\textrm{SC}}\right)^{-1}-1\right)\right]^{-1}$. Note also that the elasto-optic tensor of the monolayer needs to be rescaled in the same way as the EO tensor in 2D systems Jiang2024 while the piezoelectric strain coefficients do not need to because they are independent of the thickness of the vacuum layers Wu2022 .

Table 1 shows the clamped electro-optic tensor in ferroelectric NbOI₂ bulk and monolayer. Regarding NbOI₂ bulk, the predicted clamped EO coefficients are: $r_{11}^{\textrm{$\mathrm{\eta}$}}$ $=$ 58.63 pm/V, $r_{21}^{\textrm{$\mathrm{\eta}$}}$ $=$ 16.17 pm/V, $r_{31}^{\textrm{$\mathrm{\eta}$}}$ $=$ 7.69 pm/V, $r_{41}^{\textrm{$\mathrm{\eta}$}}$ $=$ 0.11 pm/V, $r_{52}^{\textrm{$\mathrm{\eta}$}}$ $=$ $-$0.18 pm/V, $r_{53}^{\textrm{$\mathrm{\eta}$}}$ $=$ 0.004 pm/V, $r_{62}^{\textrm{$\mathrm{\eta}$}}$ $=$ 1.24 pm/V, and $r_{63}^{\textrm{$\mathrm{\eta}$}}$ $=$ $-$0.09 pm/V. The largest clamped EO coefficient in NbOI₂ bulk is therefore about twice larger than the currently most used EO material LiNbO₃ which has a $r_{33}^{\textrm{$\mathrm{\eta}$}}$ $=$ 30.8 pm/V Weber2002 ; Veithen2004 . For NbOI₂ monolayer, the clamped EO coefficients of $r_{11}^{\textrm{$\eta$,2$\mathrm{D}$}}$ $=$ 35.49 pm/V, $r_{21}^{\textrm{$\eta$,2$\mathrm{D}$}}$ $=$ 8.27 pm/V, and $r_{31}^{\textrm{$\eta$,2$\mathrm{D}$}}$ $=$ 3.98 pm/V, are smaller in magnitude than those of bulk. In contrast, the clamped EO coefficients $r_{53}^{\textrm{$\mathrm{\eta,2\mathrm{D}}$}}$ and $r_{62}^{\textrm{$\mathrm{\eta,2\mathrm{D}}$}}$ of monolayer are larger in magnitude than those of the bulk case but both have small values. Note that the predicted EO coefficients $r_{11}^{\textrm{$\eta$,2$\mathrm{D}$}}$ in NbOI₂ monolayer is also larger than the experimental results in LiNbO₃ Weber2002 ; Turner1966 and 2D ferroelectric CuInP₂S₆ (with an effective linear EO coefficient to be 20.28 pm/V) Liu2024 , which emphasizes the high potential of NbOI₂ systems for the design of efficient electro-optic devices.

Table 2 displays some selected unclamped EO coefficients and elasto-optic coefficients of NbOI₂ bulk and monolayer, respectively. For NbOI₂ bulk, the largest unclamped EO coefficient of $r_{11}^{\sigma}$ $=$ 289.76 pm/V, which is about five times larger in magnitude than the clamped one. On the other hand, the values of $r_{21}^{\sigma}$ $=$ 7.05 pm/V and $r_{31}^{\sigma}$ $=$ $-$12.66 pm/V are smaller than the clamped one because of the negative piezoelectric contribution. The unclamped EO coefficient of $r_{11}^{\sigma}$ $=$ 133.63 pm/V is also large in NbOI₂ monolayer, that is about four times stronger than that of the clamped one. The remaining two unclamped EO coefficients in the monolayer case, $r_{21}^{\sigma}$ $=$ 4.96 pm/V and $r_{31}^{\sigma}$ $=$ 3.48 pm/V, are smaller in magnitude than their clamped values due to the negative piezoelectric contribution too.

Let us also indicate that Equation (4) can be used to obtain accurate elasto-optic coefficients from first-principles calculations. For instance, a first-principles scheme predicted a value of $p_{31}$ $=$ 0.17 for bulk LiNbO₃ Chen2015 , which agrees remarkably well with the experimental value of 0.18 Weber2002 . The presently computed elasto-optic coefficients in NbOI₂ bulk are $p_{11}$ $=$ 1.65, $p_{21}$ $=$ 0.61, and $p_{31}$ $=$ 0.39, respectively. The predicted value of $p_{11}$ is therefore very large, namely about 4 times larger in magnitude than that measured in tetragonal BaTiO₃ with $p_{11}$ $=$ 0.425 Weber2002 . The magnitude of the predicted $p_{31}$ is more than two times larger in magnitude than that measured in bulk LiNbO₃ Weber2002 . The rescaled elasto-optic coefficients in NbOI₂ monolayer are also large, with $p_{11}$ $=$ 1.58, $p_{21}$ $=$ 0.46, and $p_{31}$ $=$ 0.39, respectively, which further calls for the use of NbOI₂ in technologies taking advantage of elasto-optic conversions.

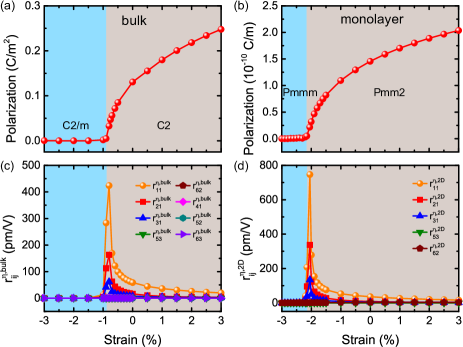
Let us now investigate the effect of strains on some properties in these promising materials. Figure 2 shows the polarization and clamped EO coefficients as a function of biaxial epitaxial strain in NbOI₂ bulk and monolayer, respectively. As mentioned above, a spontaneous polarization $P_{x}$ is along the $x$ direction under stress-free conditions in both NbOI₂ bulk and monolayer. It is computed from the Berry phase method King-Smith1993 ; Resta1994 . Note that the calculated spontaneous polarization in NbOI₂ monolayer is equal to 145.4 pC/m under stress-free conditions, which is in excellent agreement with previous theoretical values of 142.5 pC/m Ye2021 and 143 pC/m Wu2022 . The behaviors of the polarization and EO coefficients allow the determination of two strain regions for both bulk and monolayer. For strains ranging between $+$3% and $-$0.8% in NbOI₂ bulk [Fig. 2(a)], the polarization gradually decreases from 0.25 to 0.03 C/m², with the phase retaining its $C2$ space group. In contrast, the phase for strains between $-$0.9% and $-$3% has the paraelectric $C2/m$ space group, with therefore no polarization and no finite EO coefficients. For NbOI₂ monolayer, the polarization associated with the ferroelectric phase (that has a $Pmm2$ space group) in the range of $+$3% to $-$2.05% decreases from 2.0 $\times$ 10^-10 to 0.2 $\times$ 10^-10 C/m [see Fig. 2(b)]. The polarization and EO coefficients are null for strains between $-$2.1% to $-$3%, since the resulting phase adopts the paraelectric $Pmmm$ space group.

Let us now pay closer attention to the EO response as a function of strain in NbOI₂ bulk and monolayer, as shown in Figs. 2(c) and 2(d). At the boundary between ferroelectric and paraelectric phases in NbOI₂ bulk, large values of the clamped EO coefficients $r_{11}^{\textrm{$\mathrm{\eta,bulk}$}}$ and $r_{21}^{\textrm{$\mathrm{\eta,bulk}$}}$ are predicted (more than 100 pm/V) due to the strain-driven occurrence of a phase transition from $C2$-to-$C2/m$. For the clamped EO coefficients in NbOI₂ monolayer, $r_{11}^{\textrm{$\mathrm{\eta,2D}$}}$ and $r_{21}^{\textrm{$\mathrm{\eta,2D}$}}$ also show very large values near the boundary between $Pmm2$ and $Pmmm$ phases. Strikingly, such large EO coefficients near this critical strain in both bulk and monolayer are larger than the experimental values in LiNbO₃ Weber2002 ; Turner1966 by one order of magnitude—strongly suggesting to employ strained NbOI₂ materials for unprecedented electro-optic devices performance.

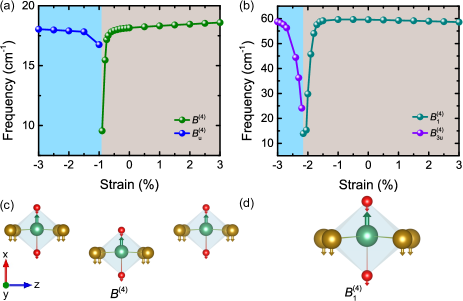
Four lowest phonon modes, expressed as $B_{u}^{(4)}$, $B^{(4)}$, $B_{3u}^{(4)}$, and $B_{1}^{(4)}$ [see Figs. 3(a) and 3(b)] are important in NbOI₂ bulk and monolayer. As a matter of fact, for NbOI₂ bulk, Fig. 3(a) reveals that the $B^{(4)}$ phonon mode becomes very soft around the strain $\sim$ $-$0.8%, which corresponds to the boundary between $C2$ (ferroelectric) and $C2/m$ (paraelectric) phases. Having some frequencies approaching zero is a guarantee to have large EO response, as indicated by the second term of Eq. (2). Indeed, we numerically found that the main contribution of phonon modes for the largest $r_{11}^{\textrm{$\mathrm{\eta,bulk}$}}$ EO coefficient mostly arises from the polar mode $B^{(4)}$. Figure 3(c) displays the atomic displacement of such mode at $-$0.8% strain, with the Nb ions displacing along the [100] direction while O and I ions move along the opposite [$\bar{1}$00] direction in NbOI₂ bulk.

For NbOI₂ monolayer, the continuous evolution from the ferroelectric $Pmm2$ phase to the paraelectric $Pmmm$ state is driven by a softening of the $B_{1}^{(4)}$ and $B_{3u}^{(4)}$ modes. At the phase boundary of $-$2.05% strain, the largest $r_{11}^{\textrm{$\mathrm{\eta,2D}$}}$ coefficient now mostly stems from the polar mode we denote as $B_{1}^{(4)}$, which shows a similar atomic character of eigenvector [see Fig. 3(d)] as the mode $B^{(4)}$ of bulk case. One can thus safely conclude that, in both strained NbOI₂ bulk and monolayer, the large linear EO coefficients mainly originate from a strain-induced softening of the lowest polar mode and a resulting ferroelectric-to-paraelectric phase transition.

In summary, we investigated linear electro-optic and elasto-optic effects in NbOI₂ bulk and monolayer from first-principles calculations. We predict large clamped and unclamped EO and elasto-optic coefficients in both stress-free bulk and monolayer. We also revealed the effect of epitaxial strain on the EO response of NbOI₂ bulk and monolayer. In particular, in both systems, a strain-induced ferroelectric-to-paraelectric phase transition is discovered, being driven by a softening of some lowest phonon modes and which results in very large linear EO responses. The phase transitions and large EO responses are accompanied by change in the atomic bond length and electronic band gap (see the Supplemental Material (SM) SM ). The SM SM further demonstrates that other NbOX₂ materials, namely NbOBr₂ and NbOCl₂, can also hold these spectacular effects. We compare the electro-optic and elasto-optic coefficients in NbOI₂ bulk and monolayer with other ferroelectric materials SM and find that NbOI₂ has the best performance. Note that the phonon dispersions and stability are also discussed in the SM SM . We thus hope that the present study will encourage the experimental investigation of electro-optic and elasto-optic effects in bulk and 2D ferroelectric niobium oxide dihalides.