$g$-mode of neutron stars in pseudo-Newtonian gravity

Case A effective potential is defined by replacing the Newtonian gravitational potential in a spherically symmetric Newtonian hydrodynamic simulation by [3, 10]

where $r$ is the radial coordinate, $\rho$ is the rest-mass density, $P$ is the pressure, $\varrho$ is the specific internal energy, and the total energy density is given by $\epsilon=\rho+\rho\varrho$. The function $m_{\text{TOV}}$ is defined by

with

From Eq. (1) and Eq. (2), we have

We use the Case A and Case A+lapse schemes and the other four schemes to study the $g$-mode originating from the composition gradient and density discontinuity of NS cores in the framework of pseudo-Newtonian gravity. All background and perturbation equations for each scheme are given in the next three subsections and summarized in Table 1.

We consider the following three sets of equilibrium configurations.

1. (I)

   For the Newtonian (N) and Newtonian+lapse function (N+lapse) schemes, the hydrostatic equilibrium equations are

   	$\displaystyle\frac{{\rm d}m}{{\rm d}r}$	$\displaystyle=4\pi r^{2}\rho\,,$		(6)
   	$\displaystyle\frac{{\rm d}P}{{\rm d}r}$	$\displaystyle=-\frac{\rho m}{r^{2}}\,,$		(7)
   	$\displaystyle\frac{{\rm d}\Phi}{{\rm d}r}$	$\displaystyle=-\frac{1}{\rho}\frac{{\rm d}P}{{\rm d}r}\,.$		(8)

   where $\rho$ is the rest-mass density, and $\Phi$ is the Newtonian gravitational potential.

2. (II)

   Instead, if we consider spherical and static stars in GR, we have the Tolman-Oppenheimer-Volkoff (TOV) equations

   	$\displaystyle\frac{{\rm d}m}{{\rm d}r}$	$\displaystyle=4\pi r^{2}\epsilon\,,$		(9)
   	$\displaystyle\frac{{\rm d}P}{{\rm d}r}$	$\displaystyle=-\frac{(\epsilon+P)(m+4\pi r^{3}P)}{r(r-2m)}\,,$		(10)
   	$\displaystyle\frac{{\rm d}\Phi}{{\rm d}r}$	$\displaystyle=-\frac{1}{\epsilon+P}\frac{{\rm d}P}{{\rm d}r}\,.$		(11)

3. (III)

   Lastly, for the Case A and Case A+lapse schemes, the background equations are obtained by replacing the Newtonian gravitational potential by the Case A potential [3, 10], and we have

   	$\displaystyle\frac{{\rm d}m}{{\rm d}r}$	$\displaystyle=4\pi r^{2}\epsilon\Gamma\,,$		(12)
   	$\displaystyle\frac{{\rm d}P}{{\rm d}r}$	$\displaystyle=-\frac{4\pi}{r^{2}}\left(\frac{m}{4\pi}+r^{3}P\right)\frac{1}{\Gamma^{2}}(\epsilon+P)\,,$		(13)
   	$\displaystyle\frac{{\rm d}\Phi}{{\rm d}r}$	$\displaystyle=-\frac{1}{\rho}\frac{\mathrm{d}P}{\mathrm{d}r}\,.$		(14)

We use the modified Newtonian hydrodynamic equations in Zha et al. [9] and Tang and Lin [10], where a lapse function $\alpha$ is added to mimic the time-dilation effect. The modified hydrodynamic equations are:

where $\vec{v}$ is the fluid velocity and the lapse function is defined by

The readers can infer Tang and Lin [10] for a detailed variational derivation of the linearized fluid equations. We will use the same lapse function in our calculations.

As well known that NSs always have real frequency $f$-mode and $p$-mode regimes. However, $g$-mode may have a real, imaginary, and zero frequency, which correspond to convective stability, instability, and marginal stability. We consider the local dynamics of NS cores, focusing on the buoyancy experienced by fluid elements and the associated $g$-mode. The frequencies of $g$-modes are closely related to the Brunt-Väisälä frequency $N$, defined via

where $g_{N}$ is the positive Newtonian gravitational acceleration, $c_{\mathrm{s}}$ is the adiabatic sound speed,

Here the subscript “s” means “adiabatic”, which in this case implies constant composition. The quantity $c_{\mathrm{e}}$ is given by

where the subscript “e” stands for “equilibrium”. If $c_{\mathrm{s}}^{2}=c_{\mathrm{e}}^{2}$, the star exhibits no convective phenomena (zero-buoyancy case). In this work, we consider only the $g$-mode of NS cores, so we set $c_{\mathrm{s}}^{2}=c_{\mathrm{e}}^{2}$ for the crustal region. Again, $c_{\mathrm{s}}^{2}>c_{\mathrm{e}}^{2}$ ($c_{\mathrm{s}}^{2}<c_{\mathrm{e}}^{2}$) denotes convective stability (instability). Combining Eqs. (18–20), we can write the Brunt-Väisälä frequency as

where $A$ is

which is called the Schwarzschild discriminant. If the star model obeys a simple polytropic EOS, $P=K\rho^{\gamma}$, then $\gamma=\rm d\ln P/\rm d\ln\rho$ is defined for the unperturbed background configuration. Hence, the Schwarzschild discriminant becomes

Clearly, if the adiabatic index $\Gamma_{1}>\gamma$, the star is related to the convective stability, in the case of $c_{\mathrm{s}}^{2}>c_{\mathrm{e}}^{2}$. In Sec. III.1, we will calculate the frequencies of $g$-modes for the composition gradient, which is related to the discussion here.

In this section, we study non-radial oscillations of NSs in pseudo-Newtonian gravity. Tang and Lin [10] calculated the quadrupole ($\ell=2$) $f$ and $p$ modes. The perturbation of scalars is expanded in spherical harmonics and the Lagrangian displacement is expanded in vector spherical harmonics [13, 10]. When considering an eigenmode, we have

where $Y_{\ell m}$ is the standard spherical harmonic function, and $\hat{r}$ is the radial unit vector. Then one can obtain the following system of equations for the fluid perturbations (see Tang and Lin [10], for a detailed variational derivation),

To solve these equations, we require the boundary conditions at the center and surface of the NS. At the center, the regularity conditions of the variables yield the following relations [44, 10]

where $B_{0}$ and $C_{0}$ are constants. At the surface of the star, the perturbed pressure must vanish, which provides

The $\delta\tilde{\Phi}$ and ${{\rm d}\delta\tilde{\Phi}}/{{\rm d}r}$ are continuous, so we obtain

Note that in the N, Case A, and TOV schemes, the lapse function equals to 1 ($\alpha=1$).

To test our numerical code, we have redone calculations with the same polytropic EOS as that in the Appendix A of Marek et al. [3], where the polytropic index $\gamma$ and the adiabatic index $\Gamma_{1}>\gamma$ are constant throughout the stellar interior. Detailed numerical results are shown in Table 2. It is noted that our numerical results for the polytropic model with $\Gamma_{1}=\gamma$ agree with Table 3 of Tang and Lin [10]. In Table 2, we compare the frequencies of $p$, $f$, and $g$ modes computed with $\Gamma_{1}>\gamma$ and $\Gamma_{1}=\gamma$ [44, 10]. The frequencies of $p$ and $f$ modes increase with the increase of the adiabatic index $\Gamma_{1}$. In particular, the $g$-mode frequencies also increase with increase of the adiabatic index $\Gamma_{1}$, which indicates a larger buoyancy.

Taking the matter composition into account, and assuming that the model accounts for the presence of neutrons, protons, and electrons, we have a two-parameter EOS, $P=P(n,x)$, which is a function of the baryon number density $n$ and the proton fraction $x=n_{\mathrm{p}}/n$. Specifically, we use shorthand notations: “$\mathrm{n}$” for neutrons, “$\mathrm{p}$” for protons, and “$\mathrm{e}$” for electrons. The energy per baryon of the nuclear matter can be written as [45, 46, 47, 31]

where

is the Fermi kinetic energy of the nucleons, and $m_{n}$ is the nucleon mass. $V_{0}$ mainly specifies the bulk compressibility of the matter, and $V_{2}$ is related to the symmetry energy of nuclear matter [48].

To compare the results of $g$-modes in Newtonian gravity [31], we adopt the same $V_{0}$ and $V_{2}$ for different EOS models, based on the microscopic calculations in Wiringa et al. [47]. Detailed numerical results of $V_{0}$ and $V_{2}$ have been tabulated in Table IV of Wiringa et al. [47]. The approximate formulae of $V_{0}$ and $V_{2}$ are presented in Sec. 4.3 of Lai [31].

In this work, we consider the model “AU” (the EOS based on nuclear potential AV14+UVII in Wiringa et al. [47]) and the model “UU” (the EOS based on nuclear potential UV14+UVII in Wiringa et al. [47]), respectively. For the model AU, $V_{0}$ and $V_{2}$ (in the unit of MeV) are fitted as [31]

where $n$ is the baryon number density in $\rm fm^{-3}$. For the model UU, we have

These fitting formulae are valid for $0.07\,{\rm fm}^{-3}\leq n\leq 1\,\rm fm^{-3}$. For densities $0.001\,{\rm fm}^{-3}<n<0.07\,\rm fm^{-3}$, we employ the EOS of Baym et al. [49], while for $n\leq 0.001\,\rm fm^{-3}$, we employ the EOS of Baym et al. [50].

Once we have this relation, we can work out the mass-energy density, pressure, and adiabatic sound speed. The equilibrium configuration must satisfy the beta equilibrium,

and the charge neutrality

where $\mu_{i}$ are the chemical potentials of the three species of particles. The equilibrium proton fraction $x(n)=x_{\mathrm{e}}(n)$ can be obtained by solving Eqs. (4.12–4.14) of Lai [31]. Hence, the mass-energy density and pressure are determined as

where

is the energy per baryon of relativistic electrons. Here, and in the following, primes denote baryon number density $n$ derivatives (for example, $V_{0}^{\prime}={\rm d}V_{0}/{{\rm d}n}$). The adiabatic sound speed $c_{\mathrm{s}}^{2}$ is

The difference between $c_{\mathrm{s}}^{2}$ and $c_{\mathrm{e}}^{2}$ is given by

From the beta equilibrium [i.e. Eq. (45)], we obtain

Finally, the difference between $c_{\mathrm{s}}^{2}$ and $c_{\mathrm{e}}^{2}$ can be represented as

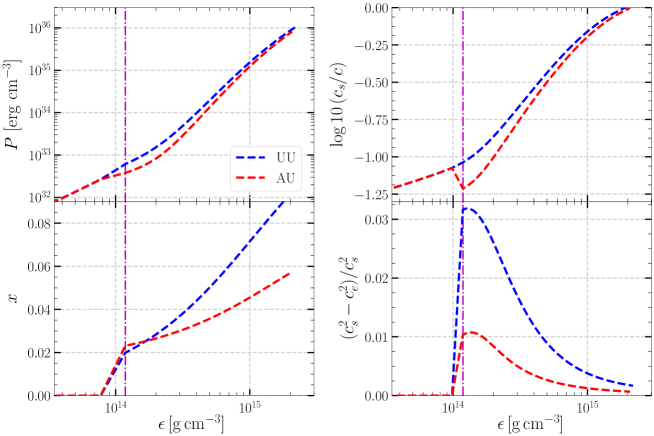
In the upper left panel of Fig. 1, we show the EOS models AU and UU, which include below neutron-drip region [49] and the lower-density crustal region [50]. In the bottom left panel of Fig. 1, we show the relation between the proton fraction $x=n_{\mathrm{p}}/n$ and the mass-energy density $\epsilon$. One notices that the value of $x$ of model UU is larger than that of model AU. In the right panels of Fig. 1, we show the relation between the adiabatic sound speed $c_{\mathrm{s}}$ and the fractional difference between $c_{\mathrm{s}}^{2}$ and $c_{\mathrm{e}}^{2}$, as functions of the mass-energy density. Note that, in our work, we consider only $g$-mode of the NS core, so we set $c_{\mathrm{s}}^{2}=c_{\mathrm{e}}^{2}$ in the lower-density region. As mentioned in Sec. 4 of Lai [31] that $c_{\mathrm{s}}^{2}=c_{\mathrm{e}}^{2}$ in the crustal region indicates effectively suppressing the crustal $g$-mode while concentrating on the core $g$-mode.

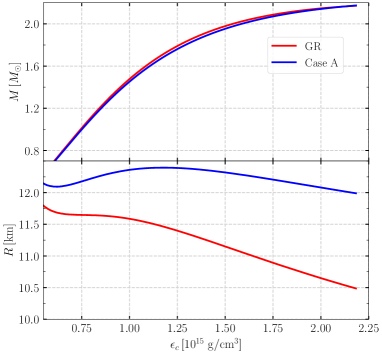
As shown in Fig. 2, the mass and radius of model UU are plotted against the central density $\epsilon_{c}$. The Case A and GR lines represent the background equations calculated by the Case A and TOV schemes, respectively (see Table 1). We can see that the masses computed in the Case A formulation can approximate well the GR solutions. The Case A formulation has absolute percentage differences $5$–$17\%$ for the radius of model UU. Note that the percentage difference of the stellar radii depends on the value of central density and the different EOS models. Detailed percentage differences of the stellar radii are illustrated in Appendix B of Tang and Lin [10].

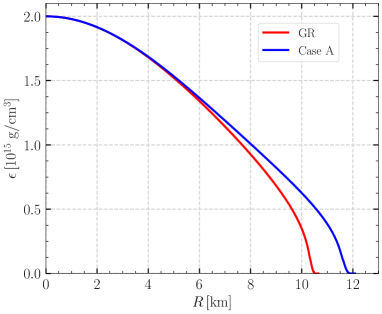
The energy density profiles of the GR and Case A schemes with central density $\epsilon=2.0\times 10^{15}\rm g\,cm^{-3}$ for model UU is shown in Fig. 3. Compared with the GR solution, the Case A solution has a noticeable deviation only in the outer region of the surface. The total mass of the star is mainly determined by the high-density inner region. The above results may explain the fact that the total mass computed in the Case A formulation approximates well the GR solutions, though the radius has a large deviation.

Note that the rest-mass density $\rho$ appears in the background and perturbation equations in N and N+lapse schemes; the total energy density $\epsilon$ and rest-mass density $\rho$ exhibit the background equations in Case A and Case A+lapse schemes, but the rest-mass density $\rho$ appears in the perturbation equations. To compare with the results of Lai [31], we use the energy density $\epsilon$ to obtain the mass-radius relation, as well as to solve perturbation equations. The difference between Case A and GR is apparent, though much smaller than the difference between Newtonian gravity and GR. Case A potential has captured some main effects from the full GR. As we will see, the perturbation results will be even closer to that of GR than the background results.

Lai [31] investigated $f$ and $g$ mode frequencies of EOS models AU and UU with a given mass $M=1.4\,M_{\odot}$¹¹1Lai [31] also calculated models UT and UU2. However, the maximum mass of the model UT does not accord with the new observation results [51, 52]. Also the model UU2 only considers the free $\mathrm{n},\mathrm{p},\mathrm{e}$ ($V_{0}=V_{2}=0$). We will not include the two EOSs in our calculations.. They found that the $f$-mode properties are very similar, due to the fact that the two EOSs have similar bulk properties ($V_{0}$) for the nuclear matter. However, the properties of the $g$-mode are very different from models AU and UU. From the bottom right panel of Fig. 1, we find that the value of $(c_{\mathrm{s}}^{2}-c_{\mathrm{e}}^{2})/c_{\mathrm{s}}^{2}$ is different with increase of the energy density. These differences reflect the sensitive dependence of $g$-mode on the nuclear matter’s symmetry energy ($V_{2}$).

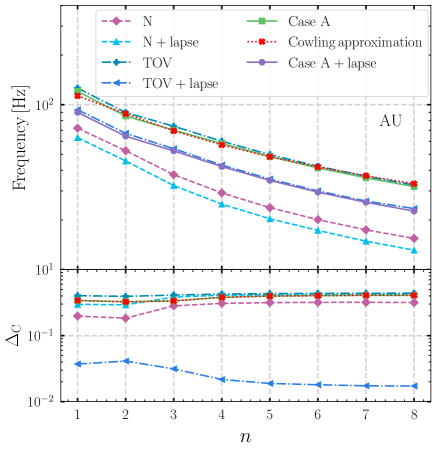
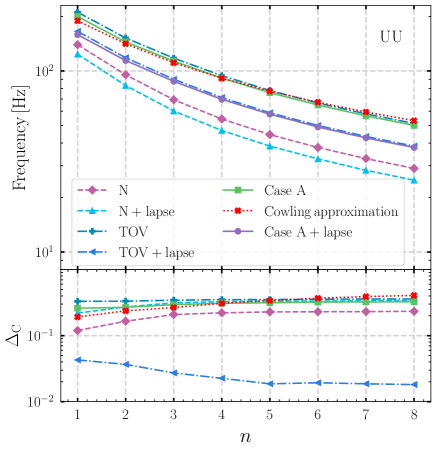
In our study, we extend calculations in Lai [31] by computing the $g$-mode. We use the stars with a fixed mass $M=1.98\,M_{\odot}$ as an example. In the upper panel of Fig. 4, we plot the frequencies of the first eight quadrupolar $g$-mode for the EOS AU. The results computed by all perturbation schemes are represented by different color lines in Fig. 4. The lower panel of Fig. 4 shows the absolute fraction difference $\Delta_{\rm C}$ defined by

where $f$ is the frequency of $g$-mode obtained by our perturbation schemes in Table 1. According to the numerical results of non-radial oscillation ($f$-mode) in Tang and Lin [10], the Case A+lapse scheme can approximate to about a few percents for a given mass $M=1.4\,M_{\odot}$ in full GR. Hence, we use the results of Case A+lapse as the baseline in the case of the composition gradient. In particular, we found that the TOV+lapse scheme can give a good approximation to the $g$-mode frequencies to a few percent levels. Besides, the absolute percentage difference $\Delta_{\rm C}$ of the TOV+lapse scheme decreases with increasing nodes. We also plot the results of frequencies of $g$-mode and the absolute percentage difference $\Delta_{\rm C}$ for the EOS UU in Fig. 5. We seen similar properties of $g$-mode, as the EOS AU in Fig. 4.

In this subsection, we study the effect of discontinuities at high density on the oscillation spectrum of a NS. We consider a simple polytropic EOS of the form [21, 22, 24]

where the discontinuity of amplitude $\Delta\epsilon$ is located at a mass-energy density $\epsilon_{\rm d}$. We study the properties of $g$-modes with density discontinuity using the pseudo-Newtonian gravity schemes in Table 1.

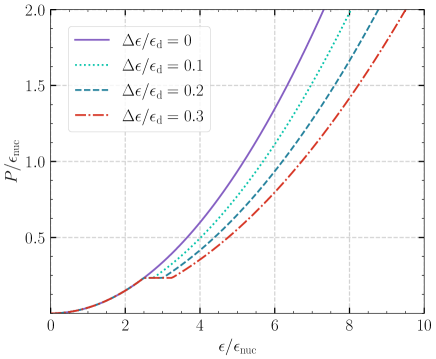
Now we have five parameters for a NS: the central density $\epsilon_{c}$, the discontinuity of amplitude $\Delta\epsilon$, the critical density $\epsilon_{\rm d}$, the polytropic index $\gamma$, and $K$. To compared with the results of non-radial oscillating relativistic stars in the full theory [i.e. without the relativistic Cowling approximation, 24], we adopt the same parameters as Miniutti et al. [24]: the polytropic index $\gamma=2$, $K=180\ \rm km^{2}$ for the NSs without discontinuity, and $K(1+\Delta\epsilon/\epsilon_{\rm{d}})^{2}=180\ \rm km^{2}$ for the case with a discontinuity. Some examples of this EOS are illustrated in Fig. 6.

In performing the calculation, boundary conditions must be specified at the locations of the density discontinuities. Finn [21] analyzed the jump conditions of the perturbation variables with the Cowling approximation in Newtonian gravity. Since the density is discontinuous, the perturbation variables are discontinuous as well, and the differential equations (28–31) require jump conditions in the discontinuity density, denoted as [$\rho$]

To compare with the results of Miniutti et al. [24], we use the energy density $\epsilon$ to solve perturbation equations.

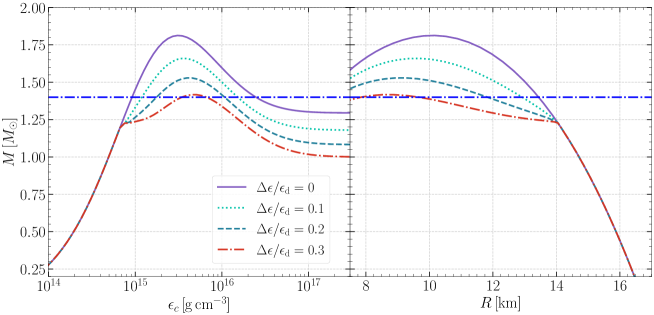
In the left panel of Fig. 7, we show the mass $M$ versus central density $\epsilon_{c}$ for each value of $\Delta\epsilon/\epsilon_{\rm{d}}$. As $\Delta\epsilon/\epsilon_{\rm{d}}$ gets larger, the maximum mass decreases, and the stable region $\mathrm{d}M/\rm d\epsilon_{c}>0$ becomes narrower and moves to a high-density region. In this work, we study only stable NS models with $\rm dM/\rm d\epsilon_{c}>0$. In our analysis, we fix the mass of a NS to $M=1.4\,M_{\odot}$ as an example. In the right panel of Fig. 7, we plot the mass-radius relation for NSs with and without density discontinuity. In both cases, we set the polytropic index $\gamma=2$. Comparing to the same EOS for $\epsilon<\epsilon_{\rm{d}}$, we adopt $K=180\ \rm km^{2}$ for the NS models without discontinuity, and $K(1+\Delta\epsilon/\epsilon_{\rm{d}})^{2}=180\ \rm km^{2}$ for the NS models with discontinuity. We find that the maximum mass is lower for the model with a discontinuity. Because the softening of EOS affected by the discontinuity. NSs with a discontinuity are more compact than those without discontinuity for a fixed mass.

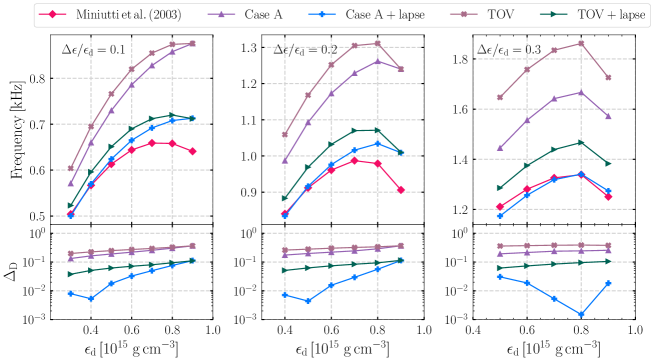
Now we will focus on the $\ell=2$ non-radial oscillation modes. In particular, we consider the quadrupolar fundamental $f$-mode and gravity $g$-mode. The frequency versus density $\epsilon_{\rm{d}}$ for the fixed mass $M=1.4\,M_{\odot}$ is shown in the top panel of Fig. 8. The results computed by the four different perturbation schemes are represented by different color lines in Fig. 8. The GR curves in the upper panel correspond to the results of full perturbation theory in GR [24]. Additionally, the absolute fraction difference $\Delta_{\rm D}$ defined by

is shown in the bottom panel of Fig. 8. The frequency of $f$-mode of the Case A+lapse scheme decreases with increasing density $\epsilon_{\rm d}$, which is similar to the GR results in trend. Again, the Case A+lapse scheme is quite accurate for the frequency of the $f$-mode. For the $\Delta\epsilon/\epsilon_{\rm{d}}=0.3$, the Case A+lapse scheme is not as good as that of the $\Delta\epsilon/\epsilon_{\rm{d}}=0.1,0.2$ cases, but it is still the best among the four perturbation schemes. Tang and Lin [10] calculated $f$-mode using Newtonian, Newtonian+lapse, Case A, and Case A+lapse schemes. They found that the Case A+lapse scheme performs much better and can reasonably approximate the $f$-mode frequency.

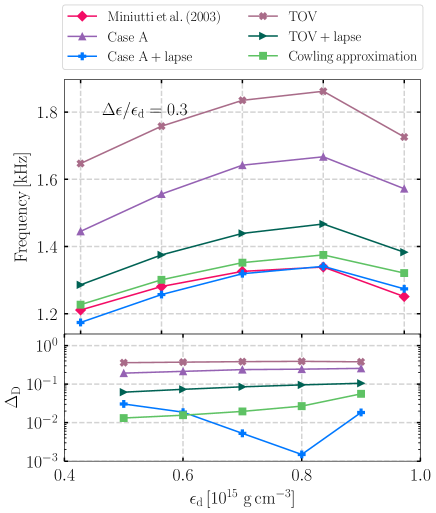
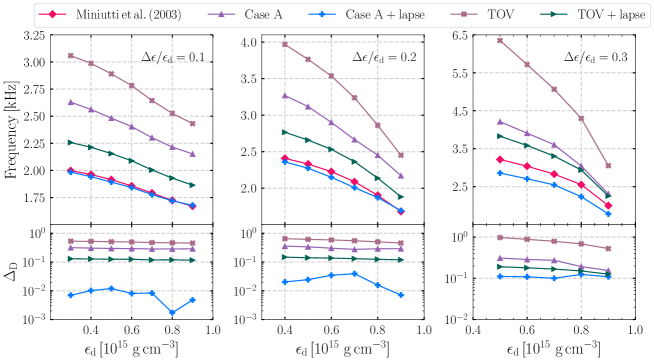
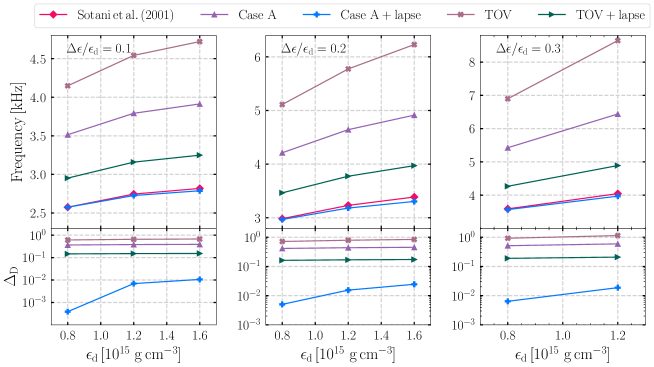
In the top panel of Fig. 9, we show the frequency of $g$-mode as a function of the density $\epsilon_{\rm d}$ for the four schemes and the results of Miniutti et al. [24]. We also plot the results of $\Delta_{\rm D}$ for the four schemes at the bottom of Fig. 9. In particular, we find that the Case A+lapse scheme can approximate the $g$-mode frequency of GR reasonably well [24]. The percentage difference $\Delta_{\rm D}$ of $g$-mode of the Case A+lapse scheme decreases with increasing $\Delta\epsilon/\epsilon_{\rm{d}}$. The Case A+lapse scheme provides the best approximation to the frequencies of $f$ and $g$ modes. For the same central density and discontinuity density, the radius of density discontinuity $R_{\rm{d}}$ is larger than the radius $R$ of the Newtonian star. Hence, we ignore the N and N+lapse schemes of discontinuity $g$-mode in this work. Numerical results of the different schemes are given in Tables 3 and 4.

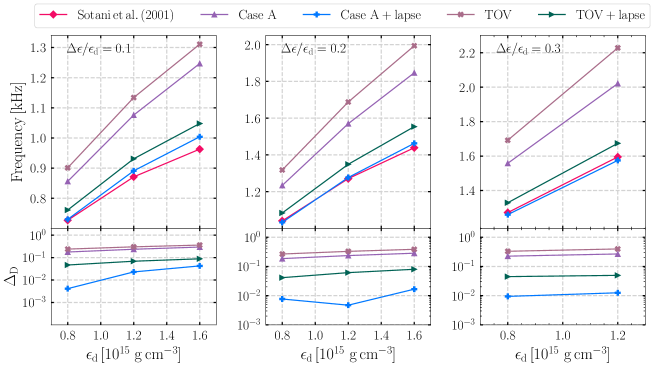
To prove that the pseudo-Newtonian treatments can approximate well the GR solutions, we also calculate the $f$ and $g$ modes of mass $M=1.2\,M_{\odot}$ for the different schemes. Detailed numerical results of the different schemes are given in Fig. 10, Fig. 11, as well as in Tables 5 and 6. We find that the pseudo-Newtonian gravity can accurately describe the oscillation of the relativistic NSs constructed from an EOS with a first-order phase transition.

For a given density $\epsilon_{\rm d}$ and $\Delta\epsilon/\epsilon_{\rm d}$, we show our numerical results for the frequencies of $f$ and $g$ modes with four schemes and the GR scheme, where the GR results were calculated by Miniutti et al. [24], Sotani et al. [23]. They integrated the equations describing the polar, non-radial perturbations of a non-rotating star as formulated by Lindblom and Detweiler [53] and Detweiler and Lindblom [54].

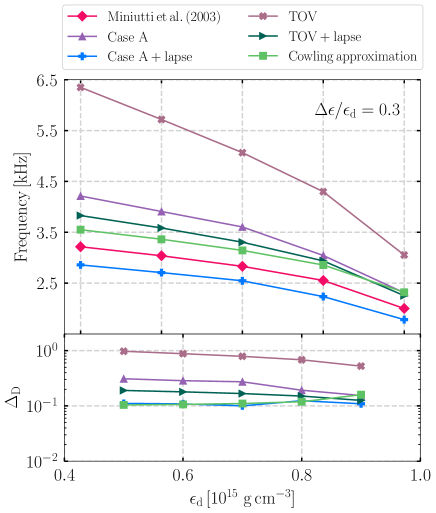
Finally, Sotani et al. [23] used the Cowling approximation to calculate the $f$ and $g$ modes and compared them to the results obtained from full GR. The results computed by the different perturbation schemes are represented by different colored lines in Fig. 12 and Fig. 13. We can see that the Case A+lapse scheme provides the best approximation to the frequency of $g$-mode when the central density increases.