Geometric and Dynamic Properties of Entangled Polymer Chains in Athermal Solvents: A Coarse-Grained Molecular Dynamics Study

Two length scales, a geometric entanglement length, $N_{e}$, and a dynamic critical entanglement length, $N_{c}$, are commonly used to describe entangled polymer melts [8]. The relationship between $N_{c}$ and $N_{e}$ has been studied by de Gennes, Kavassalis and Richard P. Wool, and a constant ratio between $N_{c}$ and $N_{e}$ has been estimated to be between 9/4 to 27/4 for isotropic melt of flexible polymer chains [12, 14, 17]. In this work, we hope to establish this constant ratio through molecular dynamics simulations and verify whether it holds for fully flexible chains in the pure melt and in athermal solvents.

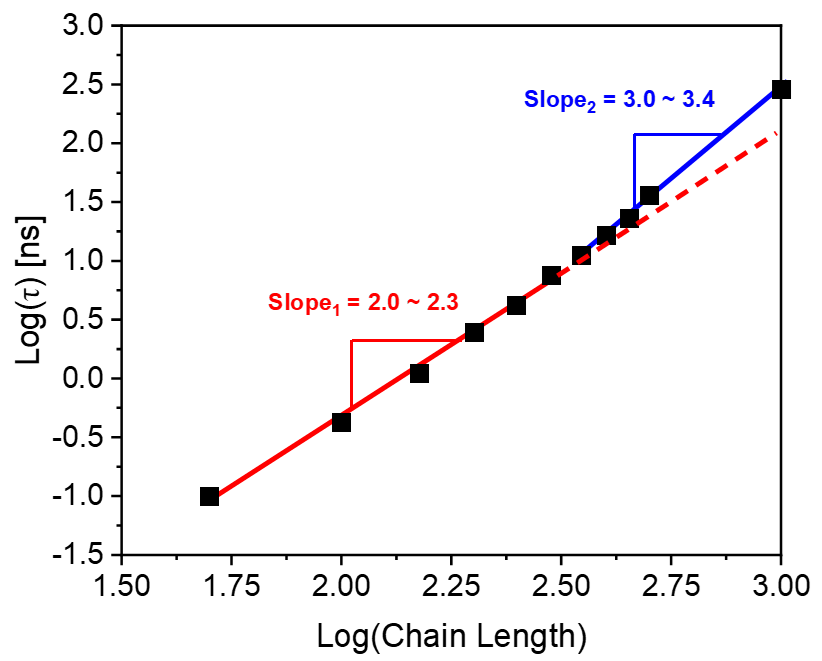
We generated models of monodisperse polymer melts with varying chain lengths, ranging from 100 to 1000 monomers per chain to cover the unentangled to entangled range. To determine the entanglement length, we used the Z1 method developed by Martin Kröger[35, 36, 37], which yielded a constant value of $N_{e}\cong 58$, consistent with the previous literatures [38, 39]. To calculate $N_{c}$, we computed the relaxation time for each model by analyzing the autocorrelation function of the end-to-end vector. The resulting relaxation time is plotted in Fig. 2, with the red and blue lines representing the unentangled and entangled states, respectively. Our analysis reveals a critical chain length $N_{c}$ above which the proportionality constant between the logarithmic relaxation time of the melt and that of the chain length changes from $2.0\sim 2.3$ to $3.0\sim 3.4$. The critical length $N_{c}$ was approximately 316 based on the figure, and the unentangled and entangled regions were consistent with the Rouse and tube models, respectively. Thus, the ratio of the critical dynamical entanglement length $N_{c}$ over that of the geometric entanglement length $N_{e}$ equals to 5.45. This result lies in the range of 9/4 to 27/4 as given by the geometric analysis of Wool [17].

To ensure the accuracy of our simulation model for fully flexible polymer chains in athermal solvents, we first validated our coarse-grained model by simulating the scaling laws for the mean square end-to-end distance $<R_{ee}^{2}>$ and the entanglement length $N_{e}$ at varying polymer volume fractions $\Phi$. The scaling law for $<R_{ee}^{2}>$ at concentrations well above the over lapping concentration $\Phi^{*}$, proposed by de Gennes, is given by equation (4), as follows [40]:

$<R_{ee}^{2}>\sim N^{1.0}\Phi^{-0.25}$       (4)

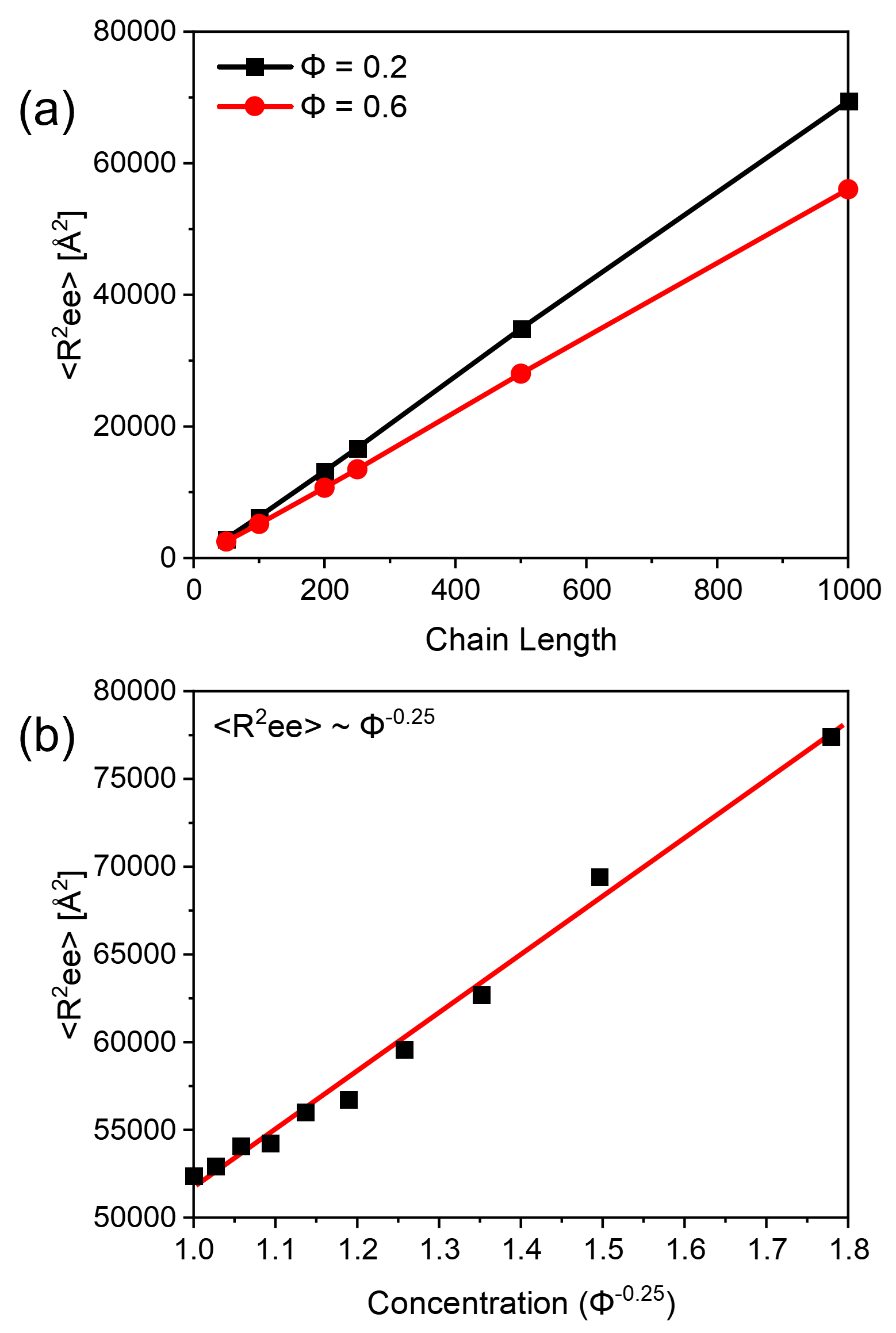
Here $N$ represents the polymer chain length and $\Phi$ is the polymer volume fraction. We investigated the dependence of dependence of $<R_{ee}^{2}>$ on chain length and polymer concentration by MD simulations. Six models of monodisperse polymer chains were generated at $N=50,100,200,250,500$ and $1000$,with ” fixed polymer concentrations at $\Phi$ = 0.2 and 0.6 for each model. Additionally, ten models of monodispersed polymer chains were generated at $N=1000$, but varying polymer volume fractions from 0.1 to 1.0 at constant intervals of 0.1 to explore concentration dependence. All simulation range corresponds to the heavily overlapped systems as they are well above the critical concentration for chain overlap, $\Phi^{*}_{m}ax=0.068$ when $N=50$. We plotted the calculated values of $<R_{ee}^{2}>$ as a function of $N$ and $\Phi^{-0.25}$, in Figures 3(a)-(b), respectively. The data points represent the simulation values, while the lines were obtained by linear fitting of equation (4). The excellent agreement between the calculated values to the fitted lines given by equation (4) shows that our model can successfully describe the concentrated polymer solutions in athermal solvents.

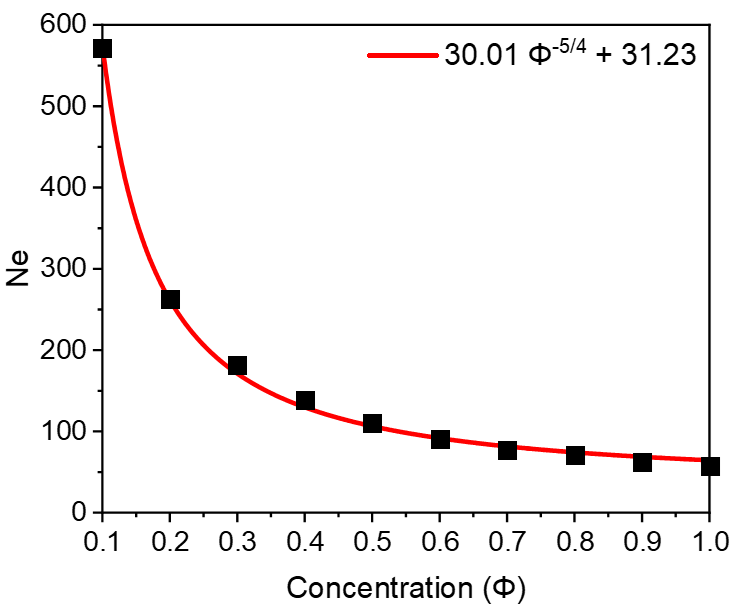
For the entanglement length, using the Z1 method, we calculated the entanglement length $N_{e}$ of $N=1000$ models at different concentrations and plotted the results in Fig. 4. The data points represent the simulated results, and the continuous line represents the fitting of $N_{e}=A\Phi^{-1.25}+B$, where $A$ and $B$ are fitting constants. Whilst the scaling exponent agrees with the literature findings of $N_{e}\sim\Phi^{-5/4}$ for flexible polymer chains in good solvent systems [12], a non-zero constant $B$ was observed in this study. This is because that polymer chains are unentangled at concentrations below the overlapping concentration $\Phi^{*}$.

After demonstrating the accuracy of our coarse-grained models in predicting the geometric scaling laws for concentrated polymer solutions in athermal solvents, we proceeded to simulate the dynamic relaxation behavior of these polymer solutions of monodisperse polymer chains at $N=1000$. We computed the relaxation time constant by analyzing the auto-correlation function of the end-to-end vector. Fig. 5 (a) plots the simulated logarithmic relaxation time versus logarithmic polymer concentrations, with the scattered points representing the simulations and the continuous lines fitted by least square linear fitting. The best fit to the data shows a slope change at a critical concentration $\Phi_{c}=0.3$.

From the scaling relationship established in Fig. 4, we can deduce this corresponds to $N_{e}=182$. Assuming this corresponds to the long-lived entanglement effect, we may deduce the dynamic critical entanglement length $N_{c}=1000$, giving a ratio of $N_{c}/N_{e}=5.49=5\sim 6$. This ratio is nearly the same as that simulated for the pure melt system presented in the previous section. Therefore, we may conclude that both the pure melt and fully flexible polymer chains in athermal solvents show similar ratios between geometric and dynamic entanglement lengths.

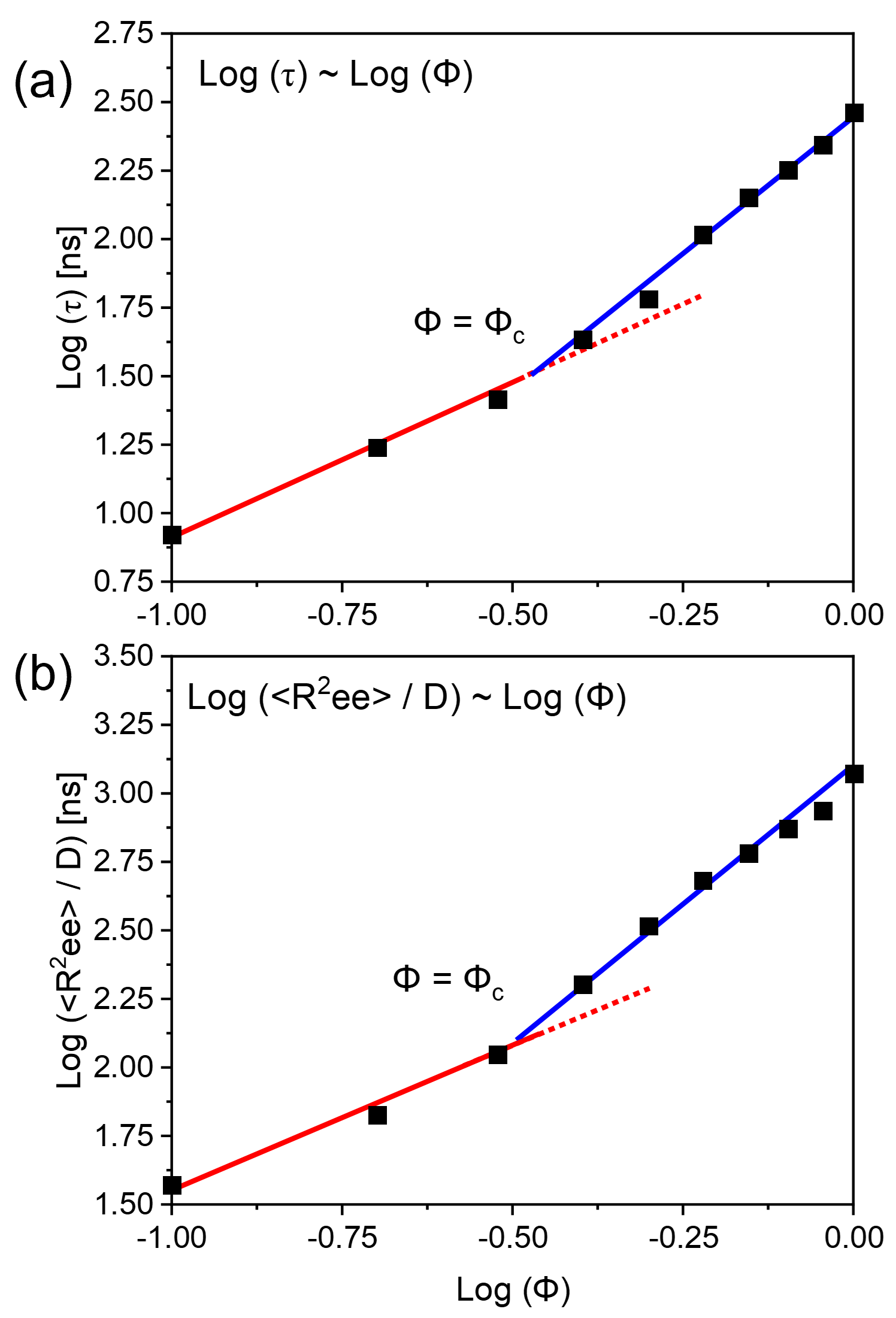
To further validate our analysis, we computed the relaxation time constant of the polymer solution by computing the diffusion time constant. The relaxation time corresponds to the time required for a polymer chain displacement over a length scale equals to that of the radius of gyration or mean end-to-end distance. The simulated results are plotted in Fig. 5(b). Like Fig. 5(a), the fitted lines also show a slope change at a critical concentration $\Phi_{c}=0.3$, and the values of the two slopes are identical to those in Fig. 5(a). This further shows the accuracy and the consistency of our simulation results.

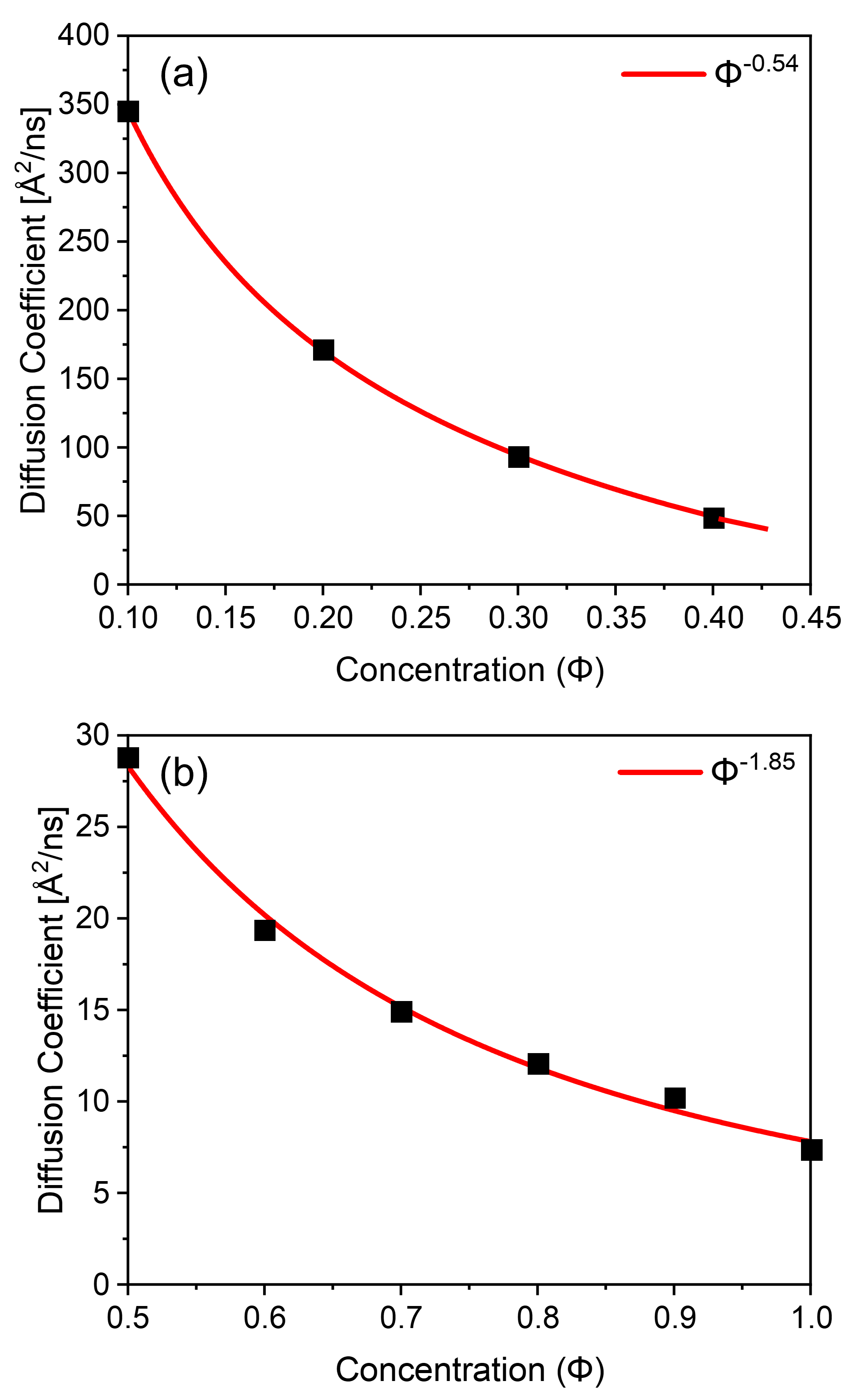
Figs. 6(a)-(b) illustrate the scaling relationships between diffusion coefficient and polymer concentration below and above the critical concentration for polymer chains in athermal solvents, respectively. These plots demonstrate excellent agreement between the calculated results and the literature scaling relations for unentangled and entangled polymer solutions [6, 7, 12], highlighting the ability of our model to accurately simulate the dynamics of polymer solutions. Our simulations of dynamic responses, in terms of scaling relations of diffusivity and relaxation time constant, have uncovered a new critical concentration $\Phi_{c}$, above which a long-lived entanglement effect becomes significant. Importantly, this critical concentration is significantly larger than the critical concentration for chain overlap. We propose that $\Phi_{c}$ should be regarded as a new parameter to quantify the dynamical state of entangled polymers in athermal solvents.

Polymer chains in athermal solvents are strongly influenced both by the solvents and adjacent chains. The size of a target polymer chain becomes swelled by the solvents and follows the law of self-avoidance walk (SAW) in dilute solutions. In concentrated polymer solutions, the screening effect of proximity chains causes the chains to exhibit the Gaussian scaling in the whole. Such screening effect implicates that the swelling effects are limited to the local scale. The local environment of a chain can be described by packing length, which is defined by Milner as the closest distance between to backbone moieties on different strands. A larger packing length means there are more solvent molecules and fewer adjacent polymer chains around a target polymer chain. Milner’s definition enables the packing length to be readily evaluated from the radial distribution function (RDF), and accurate values of the packing lengths $p$ for flexible polymers of different architectures were obtained accordingly [41, 42]. The scaling relations between the packing length and polymer concentration can be derived following the analysis by Y.H. Lin, who stipulates that for all flexible polymers the number of entanglement strands coexisting in the volume penetrated by one entangled strands remains constant [25], i.e.,

$p^{3}\sim N_{e}$          (5)

Here $p$ is the packing length, and $N_{e}$ is the entanglement length. By substituting $N_{e}\sim\Phi^{-5/4}$ to equation (5), the packing length is shown to scale with the polymer concentration as follows:

$p\sim\Phi^{-5/12}$         (6)

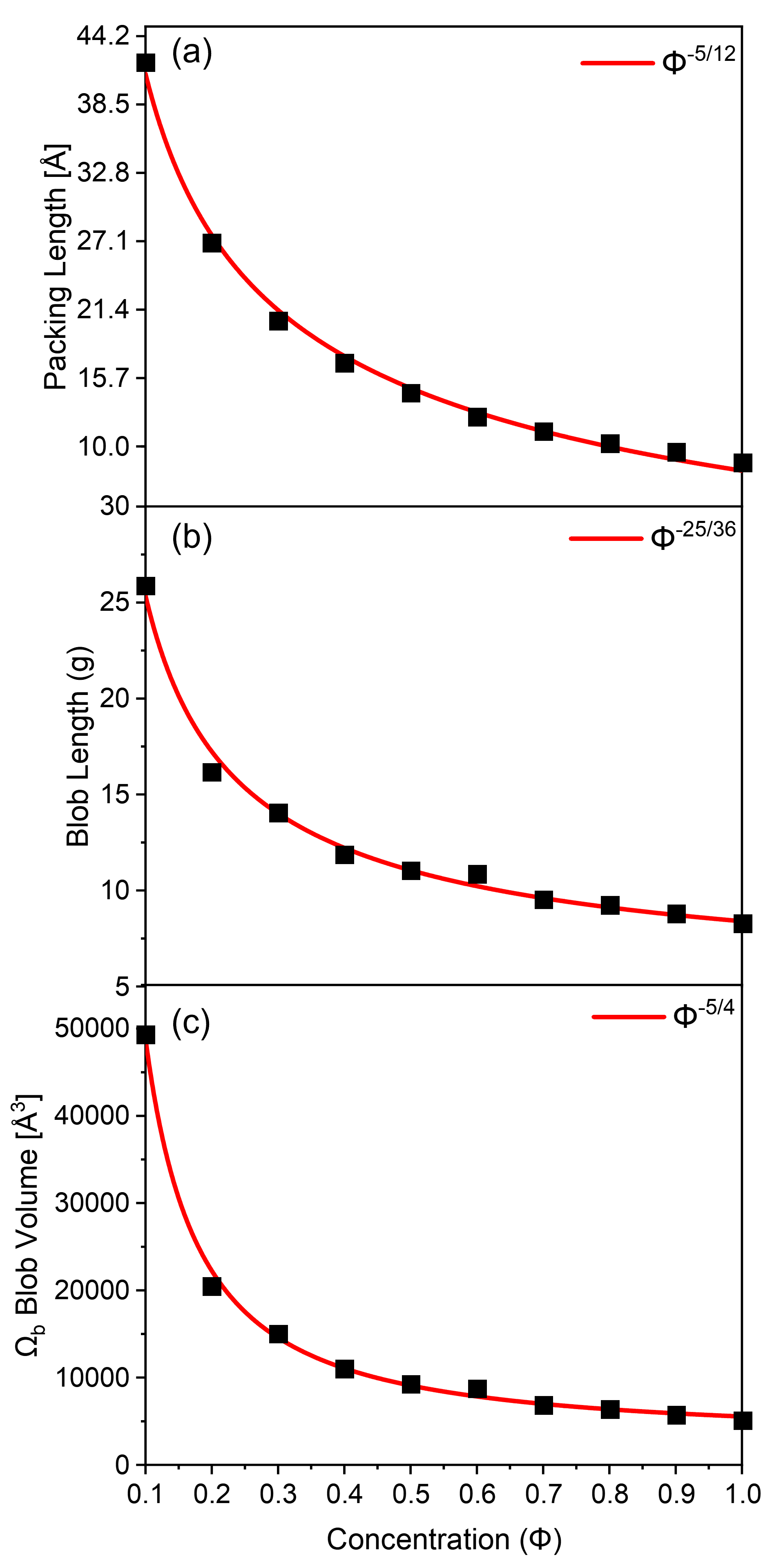
The packing length of polymer chains at different polymer concentrations was calculated using the radial distribution function (RDF) method proposed by Milner, and the result was plotted together with that predicted using equation (6) in Fig. 7(a). The agreement between the simulation and the scaling prediction is excellent.

To capture the local swelling effect in our model, we proposed a hypothesis that the polymer chain can be viewed as a series of connected swelling blobs, each with a diameter of $\xi$ and a length of $g$. The length of each blob, $g$, can be described by the correlation function of bond vectors. A larger $g$ corresponds to a stiffer chain, as it indicates a stronger correlation between bond vectors. We assumed that the correlation between chain segments in different blobs is lost due to the screening effect, while within a blob, the chain segment cannot effectively perceive the presence of other chains, resulting in swelling by the athermal solvents. By assuming the blob size scales linearly with the packing size $p$, we find:

$\xi\sim\Phi^{-5/12}$         (7)

And the coil diameter scales with the correlation length $g$ by:

$\xi\sim g^{3/5}$          (8)

Combine equations (7) and (8), we arrived at the concentration scaling expression for the length $g$ as follows:

$g\sim\Phi^{-25/36}$        (9)

Thus, the blob volume $\Omega_{b}$ is:

$\Omega_{b}\sim\xi^{3}\sim\Phi^{-5/4}$      (10)

We plotted the scaling equations for $g$ and $\Omega_{b}$ together with the simulated data in Figs. 7(b)-(c), and observed excellent agreement.

Our hypothesis, based on the swelling concept introduced previously, was that the elastic properties of the polymer chains could be altered, such that the plateau modulus of polymer chains $G$ in athermal solvents may not follow that by the classical Lin-Noolandi ansatz: $G\sim\Phi/N_{e}$. We have demonstrated that swelling of the chains inside the swelling blobs are stiffer as they exhibited larger correlation function $g$. In the meantime, the local swelling also leads to the formation of larger blob volumes, which render the chains softer. By taking these two factors into account, we obtained a modified scaling equation for the plateau modulus as follows:

$G\sim\frac{\Phi}{\left(N_{e}/g\right)\Omega_{b}}\sim\frac{\Phi g}{N_{e}\Omega_{b}}$       (11)

In addition, as described earlier (see Fig. 4), the scaling relation for $N_{e}$ should account for the non-entangling condition for dilute solutions, i.e., $N_{e}=A\Phi^{-1.25}+B$. Combining these together, we arrived at a new scaling expression for $G$ as $G\sim\Phi^{2.28}$. This expression agrees well with the previously reported experimental findings for concentrated polymer solutions in good solvent systems [15, 16, 3]. On the other hand, substitution of $N_{e}=A\Phi^{-5/4}+B$ into the classical Lin-Noolandi ansatz, we found that the scaling relation for $G$ as $G\sim\Phi^{1.69}$. This unexpected scaling exponent differs from previous literature reports [26], we attribute the discrepancy to the non-negligible $B$, which had been previously ignored.

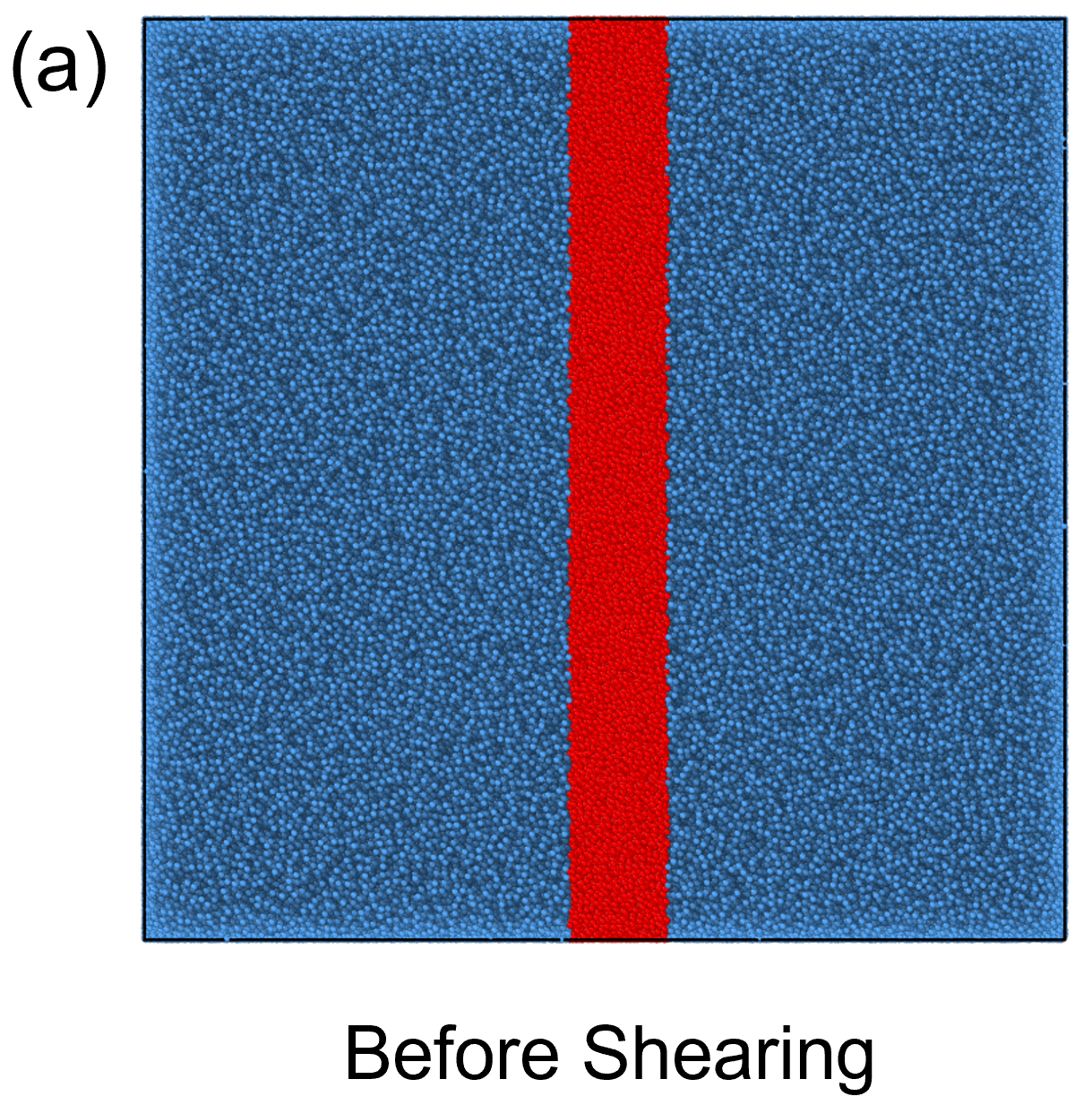
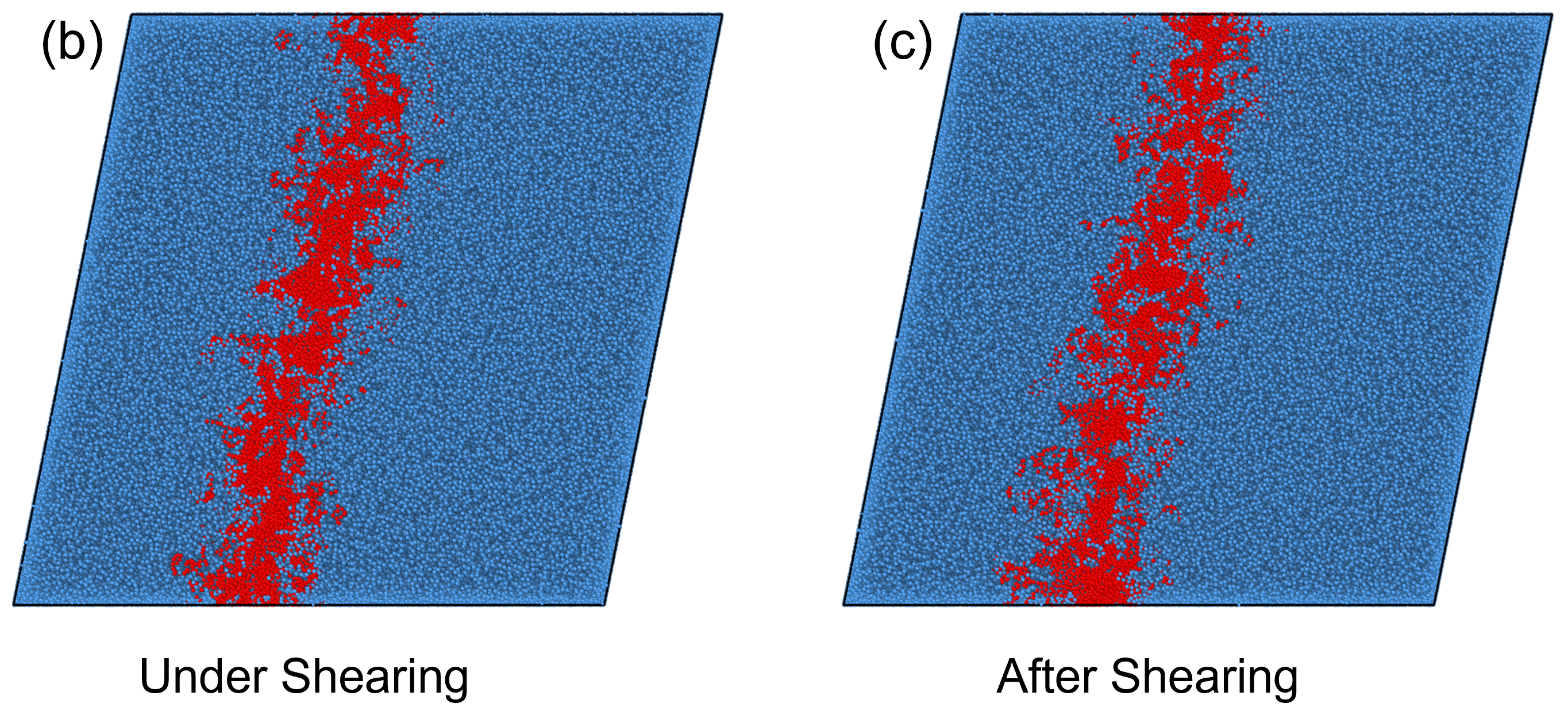
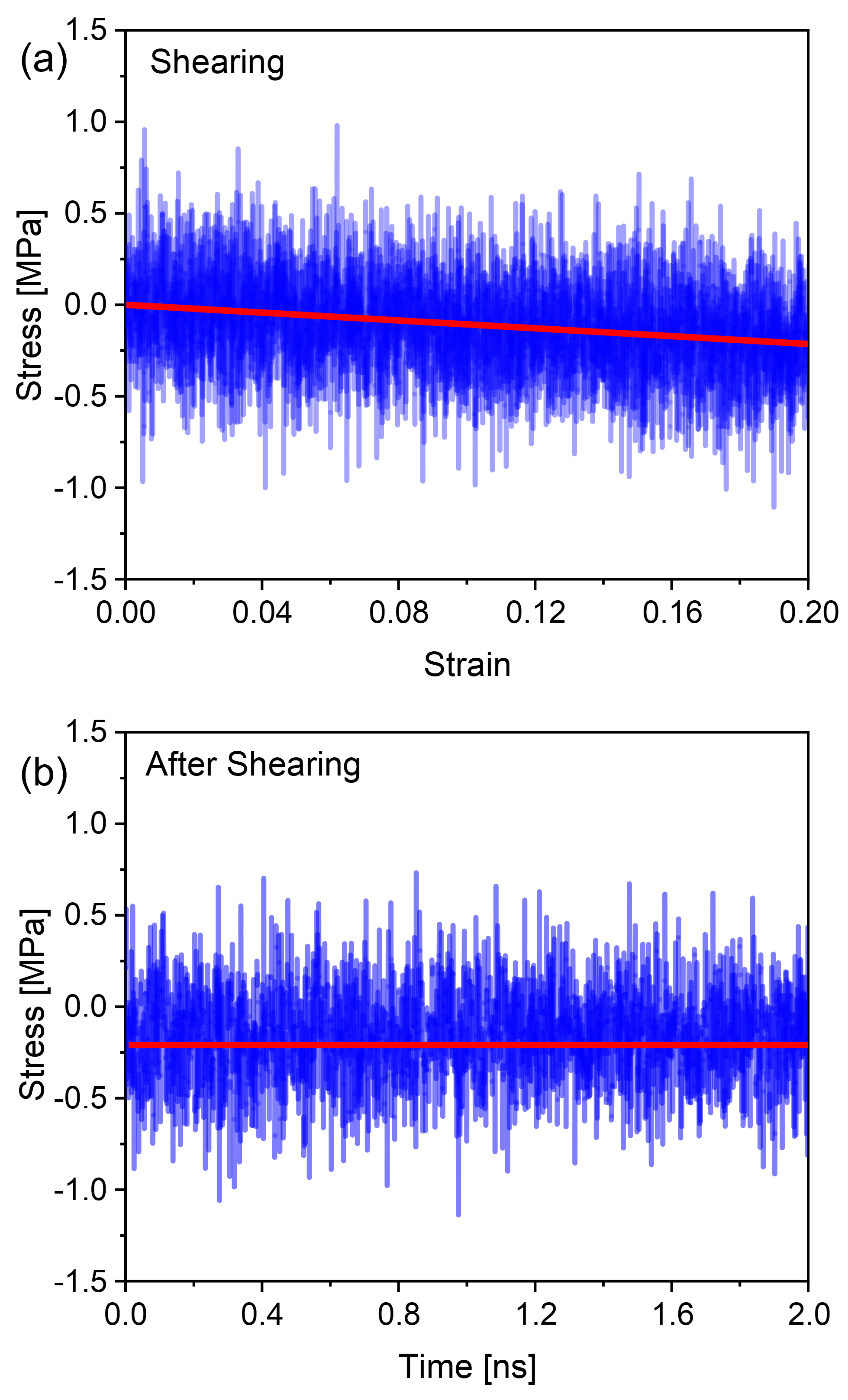
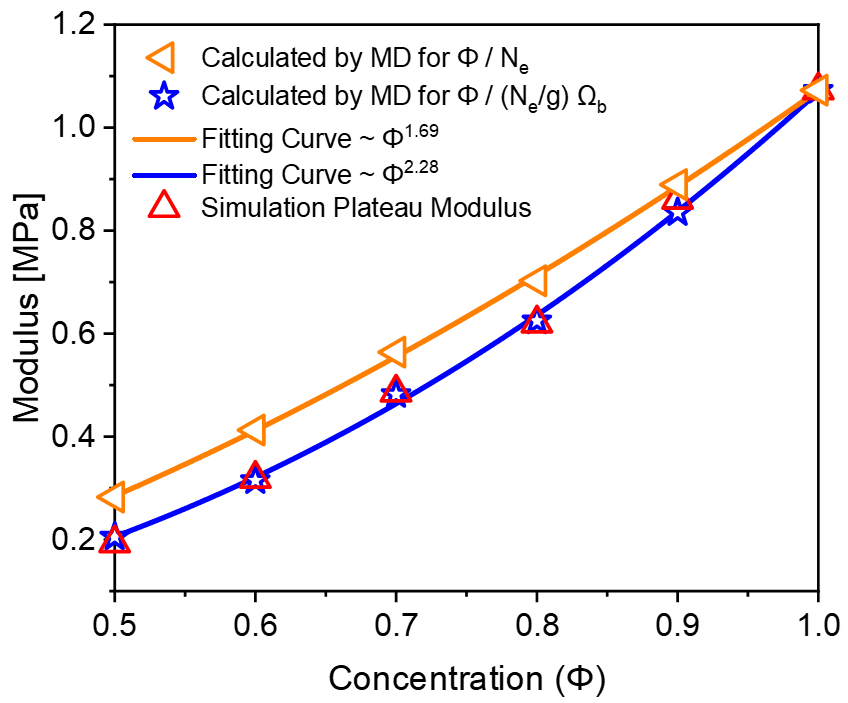
To investigate this numerically, we simulated the plateau moduli as a function of polymer concentration under simple shear deformation. Initially, we constructed a large-scale model box that was larger than the $<R_{ee}>$ of the chains, as shown in Fig. 8(a), to ensure the conformation of the polymers was not restricted by size. To simulate the shear progress, we deformed the box under a stable velocity along the $X$-direction[43, 44, 45, 46]. Figs. 8(b) shows the stress-strain relationship in shear process, for a better observation, the beads in the middle of the system were colored in red. It can be observed that the system exhibited a uniform velocity field, the maximum shear strain was set to 0.2. After the shearing deformation, the system was relaxed at the fixed maximum strain, seen in Fig. 8(c), the chains in the system did not recover during the relaxation process. To further ensure the deformation was elastic, the stress evolution of the system during and after shearing are plotted in Fig. 9(a)-(b). From Fig. 9(a), the stress is linearly dependent on strain in the process of shearing, while in Fig. 9(b), when the system is fixed at the maximum strain, no stress relaxation is observed. These results suggest that the system was elastically deformed under the shear deformation. We computed the plateau modulus of the polymer chains at concentrations where the long-lived entanglements are important, i.e., for [$\Phi$ = 0.5, 0.6, 0.7, 0.8, 0.9, 1.0], and plotted the data in Fig. 10 along with the classical Lin-Noolandi ansatz and equation (11).

The orange and blue data points respectively represent the modulus calculated from the MD simulation of classical Lin-Noolandi ansatz and equation (11), while the red triangles represent the simulated modulus values from the shear simulation. Orange and blue curves show the fitting results of $G\sim\Phi/N_{e}$ and equation (11), resulting in $G\sim\Phi^{1.69}$ and $G\sim\Phi^{2.28}$, respectively. Our results show the simulated values deviate from the classical Lin-Noolandi ansatz but matches well with equation (11). Both equation (11) and direct numerical modelling show excellent agreement with the concentration scaling law $G\sim\Phi^{2.28}$. This new scaling relationship matches well with the experimental results $G\sim\Phi^{2.0\sim 2.3}$ [14, 15, 16, 26, 3], suggesting that large-scale MD simulations are important to study the underlying mechanisms for entangled polymer systems.