Generative Time Series Forecasting with Diffusion, Denoise, and Disentanglement
Abstract
Time series forecasting has been a widely explored task of great importance in many applications. However, it is common that real-world time series data are recorded in a short time period, which results in a big gap between the deep model and the limited and noisy time series. In this work, we propose to address the time series forecasting problem with generative modeling and propose a bidirectional variational auto-encoder (BVAE) equipped with diffusion, denoise, and disentanglement, namely D3VAE. Specifically, a coupled diffusion probabilistic model is proposed to augment the time series data without increasing the aleatoric uncertainty and implement a more tractable inference process with BVAE. To ensure the generated series move toward the true target, we further propose to adapt and integrate the multiscale denoising score matching into the diffusion process for time series forecasting. In addition, to enhance the interpretability and stability of the prediction, we treat the latent variable in a multivariate manner and disentangle them on top of minimizing total correlation. Extensive experiments on synthetic and real-world data show that D3VAE outperforms competitive algorithms with remarkable margins. Our implementation is available at https://github.com/PaddlePaddle/PaddleSpatial/tree/main/research/D3VAE.
1 Introduction
Time series forecasting is of great importance for risk-averse and decision-making. Traditional RNN-based methods capture temporal dependencies of the time series to predict the future. Long short-term memories (LSTMs) and gated recurrent units (GRUs) [108, 35, 32, 80] introduce the gate functions into the cell structure to handle long-term dependencies effectively. The models based on convolutional neural networks (CNNs) capture complex inner patterns of the time series through convolutional operations [60, 8, 7]. Recently, the Transformer-based models have shown great performance in time series forecasting [104, 109, 55, 61] with the help of multi-head self-attention. However, one big issue of neural networks in time series forecasting is the uncertainty [31, 1] resulting from the properties of the deep structure. The models based on vector autoregression (VAR) [12, 24, 51] try to model the distribution of time series from hidden states, which could provide more reliability to the prediction, while the performance is not satisfactory [58].
Interpretable representation learning is another merit of time series forecasting. Variational auto-encoders (VAEs) have shown not only the superiority in modeling latent distributions of the data and reducing the gradient noise [75, 54, 63, 89] but also the interpretability of time series forecasting [26, 27]. However, the interpretability of VAEs might be inferior due to the entangled latent variables. There have been efforts to learn representation disentangling [50, 6, 39], which show that the well-disentangled representation can improve the performance and robustness of the algorithm.
Moreover, real-world time series are often noisy and recorded in a short time period, which may result in overfitting and generalization issues [30, 93, 110, 81]111The detailed literature review can be found in Appendix A.. To this end, we address the time series forecasting problem with generative modeling. Specifically, we propose a bidirectional variational auto-encoder (BVAE) equipped with diffusion, denoise, and disentanglement, namely D3VAE. More specifically, we first propose a coupled diffusion probabilistic model to remedy the limitation of time series data by augmenting the input time series, as well as the output time series, inspired by the forward process of the diffusion model [85, 41, 70, 74]. Besides, we adapt the Nouveau VAE [89] to the time series forecasting task and develop a BVAE as a substitute for the reverse process of the diffusion model. In this way, the expressiveness of the diffusion model plus the tractability of the VAE can be leveraged together for generative time series forecasting. Though the merit of generalizability is helpful, the diffused samples might be corrupted, which results in a generative model moving toward the noisy target. Therefore, we further develop a scaled denoising score-matching network for cleaning diffused target time series. In addition, we disentangle the latent variables of the time series by assuming that different disentangled dimensions of the latent variables correspond to different temporal patterns (such as trend, seasonality, etc.). Our contributions can be summarized as follows:
-
•
We propose a coupled diffusion probabilistic model aiming to reduce the aleatoric uncertainty of the time series and improve the generalization capability of the generative model.
-
•
We integrate the multiscale denoising score matching into the coupled diffusion process to improve the accuracy of generated results.
-
•
We disentangle the latent variables of the generative model to improve the interpretability for time series forecasting.
-
•
Extensive experiments on synthetic and real-world datasets demonstrate that D3VAE outperforms competitive baselines with satisfactory margins.
2 Methodology
2.1 Generative Time Series Forecasting
Problem Formulation. Given an input multivariate time series and the corresponding target time series (). We assume that can be generated from latent variables that can be drawn from the Gaussian distribution . The latent distribution can be further formulated as where denotes a nonlinear function. Then, the data density of the target series is given by:
| (1) |
where denotes a parameterized function. The target time series can be obtained directly by sampling from .

In our problem setting, time series forecasting is to learn the representation that captures useful signals of , and map the low dimensional to the latent space with high expressiveness. The framework overview of D3VAE is demonstrated in Fig. 1. Before diving into the detailed techniques, we first introduce a preliminary proposition.
Proposition 1.
Given a time series and its inherent noise , we have the decomposition: , where is the ideal time series data without noise. and are independent of each other. Let , the estimated target series can be generated with the distribution where is the ideal part of and is the estimation noise. Without loss of generality, can be fully captured by the model. That is, where is the ideal part of ground truth target series . In addition, can be decomposed as ( denotes the noise of ). Therefore, the error between ground truth and prediction, i.e., , can be deemed as the combination of aleatoric uncertainty and epistemic uncertainty.
2.2 Coupled Diffusion Probabilistic Model
The diffusion probabilistic model (diffusion model for brevity) is a family of latent variable models aiming to generate high-quality samples. To equip the generative time series forecasting model with high expressiveness, a coupled forward process is developed to augment the input series and target series synchronously. Besides, in the forecasting task, more tractable and accurate prediction is expected. To achieve this, we propose a bidirectional variational auto-encoder (BVAE) to take the place of the reverse process in the diffusion model. We present the technical details in the following two parts, respectively.
2.2.1 Coupled Diffusion Process
The forward diffusion process is fixed to a Markov chain that gradually adds Gaussian noise to the data [85, 41]. To diffuse the input and output series, we propose a coupled diffusion process, which is demonstrated in Fig. 2. Specifically, given the input , the approximate posterior can be obtained as
| (2) |
where a uniformly increasing variance schedule is employed to control the level of noise to be added. Then, let and , we have
| (3) |
Furthermore, according to Proposition 1 we decompose as . Then, with Eq. 3, the diffused can be decomposed as follows:
| (4) |
where denotes the standard Gaussian noise of . As can be determined when the variance schedule is known, the ideal part is also determined in the diffusion process. Let and , then, according to Proposition 1 and Eq. 4, we have
| (5) |
where denotes the generated noise of . To relieve the effect of aleatoric uncertainty resulting from time series data, we further apply the diffusion process to the target series . In particular, a scale parameter is adopted, such that and . Then, according to Proposition 1, we can obtain the following decomposition (similar to Eq. 4):
| (6) |
Consequently, we have . Afterward, we can draw the following conclusions with Proposition 1 and Eqs. 5 and 6. The proofs can be found in Appendix B.

Lemma 1.
, there exists a probabilistic model to guarantee that , where .
Lemma 2.
With the coupled diffusion process, the difference between diffusion noise and generation noise will be reduced, i.e., .
Therefore, the uncertainty raised by the generative model and the inherent data noise can be reduced through the coupled diffusion process. In addition, the diffusion process simultaneously augments the input series and the target series, which can improve the generalization capability for (esp. short) time series forecasting.
2.2.2 Bidirectional Variational Auto-Encoder
Traditionally, in the diffusion model, a reverse process is adopted to generate high-quality samples [85, 41]. However, for the generative time series forecasting problem, not only the expressiveness but also the supervision of the ground truths should be considered. In this work, we employ a more efficient generative model, i.e., bidirectional variational auto-encoder (BVAE) [89], to take the place of the reverse process of the diffusion model. The architecture of BVAE is described in Fig. 1 where is treated in a multivariate fashion () and . Then, is determined in accordance with the number of residual blocks in the encoder, as well as the decoder. Another merit of BVAE is that it opens an interface to integrate the disentanglement for improving model interpretability (refer to Section 2.4).
2.3 Scaled Denoising Score Matching for Diffused Time Series Cleaning
Although the time series data can be augmented with the aforementioned coupled diffusion probabilistic model, the generative distribution tends to move toward the diffused target series which has been corrupted [65, 87]. To further “clean” the generated target series, we employ the Denoising Score Matching (DSM) to accelerate the de-uncertainty process without sacrificing the model flexibility. DSM [90, 65] was proposed to link Denoising Auto-Encoder (DAE) [91] to Score Matching (SM) [43]. Let denote the generated target series, then we have the objective
| (7) |
where is the joint density of pairs of corrupted and clean samples , is derivative of the log density of a single noise kernel, which is dedicated to replacing the Parzen density estimator: in score matching, and is the energy function. In the particular case of Gaussian noise, . Thus, we have
| (8) |
Then, for the diffused target series at step , we can obtain
| (9) |
To scale the noise of different levels [65], a monotonically decreasing series of fixed values (refer to the aforementioned variance schedule in Section 2.2) is adopted. Therefore, the objective of the multi-scaled DSM is
| (10) |
where and . With Eq. 10, we can ensure that the gradient has the right magnitude by setting .
In the generative time series forecasting setting, the generated samples will be tested without applying the diffusion process. To further denoise the generated target series , we apply a single-step gradient denoising jump [78]:
| (11) |
The generated results tend to possess a larger distribution space than the true target, and the noisy term in Eq. 11 approximates the noise between the generated target series and the “cleaned” target series. Therefore, can be treated as the estimated uncertainty of the prediction.
2.4 Disentangling Latent Variables for Interpretation
The interpretability of the time series forecasting model is of great importance for many downstream tasks [88, 38, 44]. Through disentangling the latent variables of the generative model, not only the interpretability but also the reliability of the prediction can be further enhanced [64].
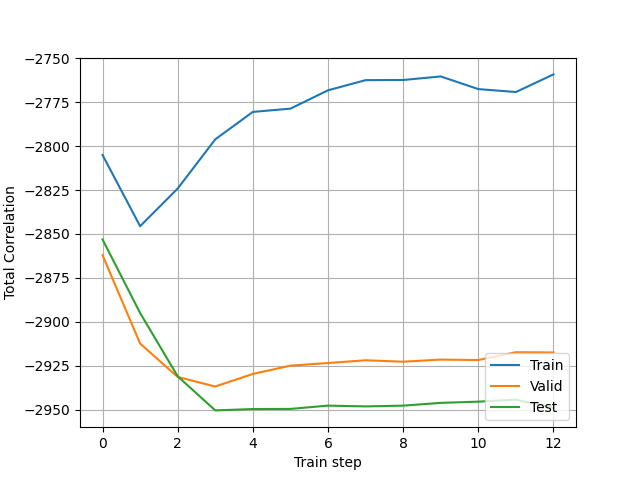
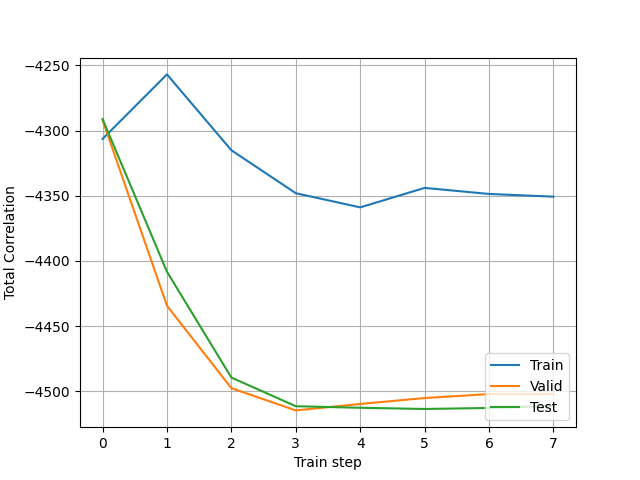
To disentangle the latent variables , we attempt to minimize the Total Correlation (TC) [94, 50], which is a popular metric to measure dependencies among multiple random variables,
| (12) |
where denotes the number of factors of that need to be disentangled. Lower TC generally means better disentanglement if the latent variables preserve useful information. However, a very low TC can still be obtained when the latent variables carry no meaningful signals. Through the bidirectional structure of BVAE, such issues can be tackled without too much effort. As shown in Fig. 1, the signals are disseminated in both the encoder and decoder, such that rich semantics are aggregated into the latent variables. Furthermore, to alleviate the effect of potential irregular values, we average the total correlations of , then the loss w.r.t. the TC score of BVAE can be obtained:
| (13) |
Algorithm 1 Training Procedure. 1: repeat 2: 3: Randomly choose and with Eqs. 4 and 6, 4: 5: Generate the latent variable with BVAE, 6: Sample and calculate 7: Calculate DSM loss with Eq. 10 8: Calculate total correlation of with Eq. 13 9: Construct the total loss with Eq. 14 10: 11: until Convergence
Algorithm 2 Forecasting Procedure. 1: Input: 2: Sample 3: Generate 4: Output: and the estimated uncertainty with Eq. 11
2.5 Training and Forecasting
Training Objective. To reduce the effect of uncertainty, the coupled diffusion equipped with the denoising network is proposed without sacrificing generalizability. Then we disentangle the latent variables of the generative model by minimizing the TC of the latent variables. Finally, we reconstruct the loss with several trade-off parameters, and with Eqs. 10, 11 and 13 we have
| (14) |
where calculates the mean square error (MSE) between and . We minimize the above objective to learn the generative model accordingly.
Algorithms. Algorithm 1 displays the complete training procedure of D3VAE with the loss function in Eq. 14. For inference, as described in Algorithm 2, given the input series , the target series can be generated directly from the distribution which is conditioned on the latent states drawn from the distribution .
3 Experiments
3.1 Experiment Settings
Datasets. We generate two synthetic datasets suggested by [23],
where and (), , denotes the dimensionality and is the number of time points, are two constants. We set to generate D1, and for D2, and for both D1 and D2.
| Model | D3VAE | NVAE | -TCVAE | f-VAE | DeepAR | TimeGrad | GP-copula | VAE | |
|---|---|---|---|---|---|---|---|---|---|
| D1 | 8 | ||||||||
| 16 | |||||||||
| D2 | 8 | ||||||||
| 16 | |||||||||
| Model | D3VAE | NVAE | -TCVAE | f-VAE | DeepAR | TimeGrad | GP-copula | VAE | |
|---|---|---|---|---|---|---|---|---|---|
| Traffic | 8 | ||||||||
| 16 | |||||||||
| Electricity | 8 | ||||||||
| 16 | |||||||||
| Weather | 8 | ||||||||
| 16 | |||||||||
| ETTm1 | 8 | ||||||||
| 16 | |||||||||
| ETTh1 | 8 | ||||||||
| 16 | |||||||||
| Wind | 8 | ||||||||
| 16 | |||||||||
Six real-world datasets with diverse spatiotemporal dynamics are selected, including Traffic [58], Electricity222https://archive.ics.uci.edu/ml/datasets/ElectricityLoadDiagrams20112014, Weather333https://www.bgc-jena.mpg.de/wetter/, Wind (Wind Power) 444This dataset is published at https://github.com/PaddlePaddle/PaddleSpatial/tree/main/paddlespatial/datasets/WindPower. , and ETTs [109] (ETTm1 and ETTh1). To highlight the uncertainty in short time series scenarios, for each dataset, we slice a subset from the starting point to make sure that each sliced dataset contains at most 1000 time points. Subsequently, we obtained -Traffic, -Electricity, -Weather, -Wind, -ETTm1, and -ETTh1. The statistical descriptions of the real-world datasets can be found in Section C.1. All datasets are split chronologically and adopt the same train/validation/test ratios, i.e., 7:1:2.
Baselines. We compare D3VAE with one GP (Gaussian Process) based method (GP-copula [76]), two auto-regressive methods (DeepAR [77] and TimeGrad [74]), and four VAE-based methods, i.e., vanilla VAE, NVAE [89], factor-VAE (f-VAE for short) [50] and -TCVAE [15].
Implementation Details. An input--predict- window is applied to roll the train, validation, and test sets with stride one time-step, respectively, and this setting is adopted for all datasets. Hereinafter, the last dimension of the multivariate time series is selected as the target variable by default.
We use the Adam optimizer with an initial learning rate of . The batch size is , and the training is set to epochs at most equipped with early stopping. The number of disentanglement factors is chosen from , and is set to range from to with different diffusion steps , then is set to . The trade-off hyperparameters are set as for ETTs, and for others. All the experiments were carried out on a Linux machine with a single NVIDIA P40 GPU. The experiments are repeated five times, and the average and variance of the predictions are reported. We use the Continuous Ranked Probability Score (CRPS) [68] and Mean Squared Error (MSE) as the evaluation metrics. For both metrics, the lower, the better. In particular, CRPS is used to evaluate the similarity of two distributions and is equivalent to Mean Absolute Error (MAE) when two distributions are discrete.
3.2 Main Results
Two different prediction lengths, i.e., (), are evaluated. The results of longer prediction lengths are available in Appendix D.
Toy Datasets. In Table 1, we can observe that D3VAE achieves SOTA performance most of the time, and achieves competitive CRPS in D2 for prediction length 16. Besides, VAEs outperform VARs and GP on D1, but VARs achieve better performance on D2, which demonstrates the advantage of VARs in learning complex temporal dependencies.
Real-World Datasets. As for the experiments on real-world data, D3VAE achieves consistent SOTA performance except for the prediction length 16 on the Wind dataset (Table 2). Particularly, under the input-8-predict-8 setting, D3VAE can provide remarkable improvements in Traffic, Electricity, Wind, ETTm1, ETTh1 and Weather w.r.t. MSE reduction (90%, 71%, 48%, 43%, 40% and 28%). Regarding the CRPS reduction, D3VAE achieves a 73% reduction in Traffic, 31% in Wind, and 27% in Electricity under the input-8-predict-8 setting, and a 70% reduction in Traffic, 18% in Electricity, and 7% in Weather under the input-16-predict-16 setting. Overall, D3VAE gains the averaged 43% MSE reduction and 23% CRPS reduction among the above settings. More results under longer prediction-length settings and on full datasets can be found in Section D.1.
Uncertainty Estimation. The uncertainty can be assessed by estimating the noise of the outcome series when doing the prediction (see Section 2.3). Through scale parameter , the generated distribution space can be adjusted accordingly (results on the effect of can be found in Appendix D.3). The showcases in Fig. 3 demonstrate the uncertainty estimation of the yielded series in the Traffic dataset, where the last six dimensions are treated as target variables. We can find that noise estimation can quantify the uncertainty effectively. For example, the estimated uncertainty grows rapidly when extreme values are encountered.






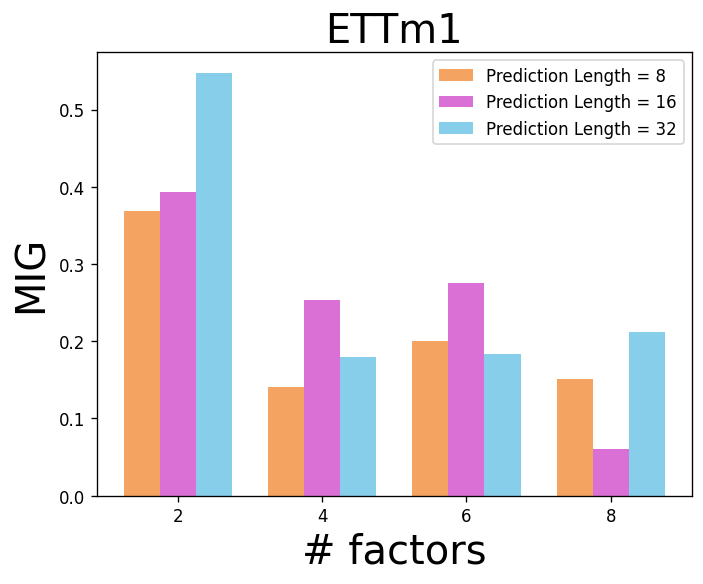
Disentanglement Evaluation. For time series forecasting, it is difficult to label disentangled factors by hand, thus we take different dimensions of as the factors to be disentangled: (). We build a classifier to discriminate whether an instance belongs to class such that the disentanglement quality can be assessed by evaluating the classification performance. Besides, we adopt the Mutual Information Gap (MIG) [15] as a metric to evaluate the disentanglement more straightforwardly. Due to the space limit, the evaluation of disentanglement with different factors can be found in Appendix E.
| Dataset | Traffic | Electricity | ||
|---|---|---|---|---|
| 16 | 32 | 16 | 32 | |
| D3VAE | ||||
| D3VAE | ||||
| D3VAE | ||||
| D3VAE-CDM | ||||
| D3VAE-CDM-DSM | ||||
| D3VAE | ||||
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6275ac07-c899-4b33-ab10-9f1a7e7f5398/end6.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6275ac07-c899-4b33-ab10-9f1a7e7f5398/step5.png)
3.3 Model Analysis
Ablation Study of the Coupled Diffusion and Denoising Network. To evaluate the effectiveness of the coupled diffusion model (CDM), we compare the full versioned D3VAE with its three variants: i) D3VAE, i.e. D3VAE without diffused , ii) D3VAE, i.e. D3VAE without diffused , and iii) D3VAE-CDM, i.e. D3VAE without any diffusion. Besides, the performance of D3VAE without denoising score matching (DSM) is also reported when the target series is not diffused, which are denoted as D3VAE and D3VAE-CDM-DSM. The ablation study is carried out on Traffic and Electricity datasets under input-16-predict-16 and input-32-predict-32. In Table 3, we can find that the diffusion process can effectively augment the input or the target. Moreover, when the target is not diffused, the denoising network would be deficient since the noise level of the target cannot be estimated by then.
Variance Schedule and The Number of Diffusion Steps . To reduce the effect of the uncertainty while preserving the informative temporal patterns, the extent of the diffusion should be configured properly. Too small a variance schedule or inadequate diffusion steps will lead to a meaningless diffusion process. Otherwise, the diffusion could be out of control 555 An illustrative showcase can be found in Appendix F. . Here we analyze the effect of the variance schedule and the number of diffusion steps . We set and change the value of in the range of , and ranges from to . As shown in Fig. 4, we can see that the prediction performance can be improved if proper and are employed.
4 Discussion
Sampling for Generative Time Series Forecasting.
The Langevin dynamics has been widely applied to the sampling of energy-based models (EBMs) [101, 21, 103],
| (15) |
where , denotes the number of sampling steps, and is a constant. With and being properly configured, high-quality samples can be generated. The Langevin dynamics has been successfully applied to applications in computer vision [56, 102], and natural language processing [20].
We employ a single-step gradient denoising jump in this work to generate the target series. The experiments that were carried out demonstrate the effectiveness of such single-step sampling. We conduct an extra empirical study to investigate whether it is worth taking more sampling steps for further performance improvement of time series forecasting. We showcase the prediction results under different sampling strategies in Fig. 5. By omitting the additive noise in Langevin dynamics, we employ the multi-step denoising for D3VAE to generate the target series and plot the generated results in Fig. 5(a). Then, with the standard Langevin dynamics, we can implement a generative procedure instead of denoising and compare the generated target series with different (see Figs. 5(b), 5(c) and 5(d)). We can observe that more sampling steps might not be helpful in improving prediction performance for generative time series forecasting (Fig. 5(a)). Besides, larger sampling steps would lead to high computational complexity. On the other hand, different configurations of Langevin dynamics (with varying ) cannot bring indispensable benefits for time series forecasting (Figs. 5(b), 5(c) and 5(d)).




Limitations.
With the coupled diffusion probabilistic model, although the aleatoric uncertainty of the time series can be reduced, a new bias is brought into the series to mimic the distribution of the input and target.
However, as a common issue in VAEs that any introduced bias in the input will result in bias in the generated output [92], the diffusion steps and variance schedule need to be chosen cautiously, such that this model can be applied to different time series tasks smoothly.
The proposed model is devised for general time series forecasting, it should be used properly to avoid the potential negative societal impacts, such as illegal applications.
In time series predictive analysis, disentanglement of the latent variables has been very important for interpreting the prediction to provide more reliance. Due to the lack of prior knowledge of the entangled factors in generative time series forecasting, only unsupervised disentanglement learning can be done, which has been proven theoretically feasible for time series [64]. Despite this, for boarder applications of disentanglement and better performance, it is still worth exploring how to label the factors of time series in the future. Moreover, because of the uniqueness of time series data, it is also a promising direction to explore more generative and sampling methods for the time series generation task.
5 Conclusion
In this work, we propose a generative model with the bidirectional VAE as the backbone. To further improve the generalizability, we devise a coupled diffusion probabilistic model for time series forecasting. Then a scaled denoising network is developed to guarantee the prediction accuracy. Afterward, the latent variables are further disentangled for better model interpretability. Extensive experiments on synthetic data and real-world data validate that our proposed generative model achieves SOTA performance compared to existing competitive generative models.
Acknowledgement
We thank Longyuan Power Group Corp. Ltd. for supporting this work.
References
- [1] Moloud Abdar, Farhad Pourpanah, Sadiq Hussain, Dana Rezazadegan, Li Liu, Mohammad Ghavamzadeh, Paul Fieguth, Xiaochun Cao, Abbas Khosravi, U Rajendra Acharya, et al. A review of uncertainty quantification in deep learning: Techniques, applications and challenges. Information Fusion, 76:243–297, 2021.
- [2] Marco Ancona, Enea Ceolini, Cengiz Öztireli, and Markus Gross. Towards better understanding of gradient-based attribution methods for deep neural networks. In International Conference on Learning Representations, 2018.
- [3] Adebiyi A Ariyo, Adewumi O Adewumi, and Charles K Ayo. Stock price prediction using the ARIMA model. In UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, pages 106–112. IEEE, 2014.
- [4] Shaojie Bai, J Zico Kolter, and Vladlen Koltun. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv preprint arXiv:1803.01271, 2018.
- [5] Mauricio Barahona and Chi-Sang Poon. Detection of nonlinear dynamics in short, noisy time series. Nature, 381(6579):215–217, 1996.
- [6] Yoshua Bengio, Aaron Courville, and Pascal Vincent. Representation learning: A review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(8):1798–1828, 2013.
- [7] Mikolaj Binkowski, Gautier Marti, and Philippe Donnat. Autoregressive convolutional neural networks for asynchronous time series. In International Conference on Machine Learning, pages 580–589. PMLR, 2018.
- [8] Anastasia Borovykh, Sander Bohte, and Cornelis W Oosterlee. Conditional time series forecasting with convolutional neural networks. STAT, 1050:16, 2017.
- [9] George EP Box and Gwilym M Jenkins. Some recent advances in forecasting and control. Journal of the Royal Statistical Society. Series C (Applied Statistics), 17(2):91–109, 1968.
- [10] Sofiane Brahim-Belhouari and Amine Bermak. Gaussian process for nonstationary time series prediction. Computational Statistics & Data Analysis, 47(4):705–712, 2004.
- [11] Defu Cao, Yujing Wang, Juanyong Duan, Ce Zhang, Xia Zhu, Congrui Huang, Yunhai Tong, Bixiong Xu, Jing Bai, Jie Tong, et al. Spectral temporal graph neural network for multivariate time-series forecasting. Advances in Neural Information Processing Systems, 33:17766–17778, 2020.
- [12] Li-Juan Cao and Francis Eng Hock Tay. Support vector machine with adaptive parameters in financial time series forecasting. IEEE Transactions on Neural Networks, 14(6):1506–1518, 2003.
- [13] Shiyu Chang, Yang Zhang, Wei Han, Mo Yu, Xiaoxiao Guo, Wei Tan, Xiaodong Cui, Michael Witbrock, Mark A Hasegawa-Johnson, and Thomas S Huang. Dilated recurrent neural networks. Advances in Neural Information Processing Systems, 30, 2017.
- [14] Sotirios P Chatzis. Recurrent latent variable conditional heteroscedasticity. In IEEE International Conference on Acoustics, Speech and Signal Processing, pages 2711–2715. IEEE, 2017.
- [15] Ricky TQ Chen, Xuechen Li, Roger B Grosse, and David K Duvenaud. Isolating sources of disentanglement in variational autoencoders. Advances in Neural Information Processing Systems, 31, 2018.
- [16] Junyoung Chung, Kyle Kastner, Laurent Dinh, Kratarth Goel, Aaron C Courville, and Yoshua Bengio. A recurrent latent variable model for sequential data. Advances in Neural Information Processing Systems, 28, 2015.
- [17] Hoang Anh Dau, Anthony Bagnall, Kaveh Kamgar, Chin-Chia Michael Yeh, Yan Zhu, Shaghayegh Gharghabi, Chotirat Ann Ratanamahatana, and Eamonn Keogh. The UCR time series archive. IEEE/CAA Journal of Automatica Sinica, 6(6):1293–1305, 2019.
- [18] Emmanuel de Bézenac, Syama Sundar Rangapuram, Konstantinos Benidis, Michael Bohlke-Schneider, Richard Kurle, Lorenzo Stella, Hilaf Hasson, Patrick Gallinari, and Tim Januschowski. Normalizing kalman filters for multivariate time series analysis. Advances in Neural Information Processing Systems, 33:2995–3007, 2020.
- [19] Ankur Debnath, Govind Waghmare, Hardik Wadhwa, Siddhartha Asthana, and Ankur Arora. Exploring generative data augmentation in multivariate time series forecasting: Opportunities and challenges. Solar-Energy, 137:52–560, 2021.
- [20] Yuntian Deng, Anton Bakhtin, Myle Ott, Arthur Szlam, and Marc’Aurelio Ranzato. Residual energy-based models for text generation. In International Conference on Learning Representations, 2019.
- [21] Yilun Du and Igor Mordatch. Implicit generation and modeling with energy based models. Advances in Neural Information Processing Systems, 32, 2019.
- [22] Stephen Ellner and Peter Turchin. Chaos in a noisy world: New methods and evidence from time-series analysis. The American Naturalist, 145(3):343–375, 1995.
- [23] Amirreza Farnoosh, Bahar Azari, and Sarah Ostadabbas. Deep switching auto-regressive factorization: Application to time series forecasting. arXiv preprint arXiv:2009.05135, 2020.
- [24] Konstantinos Fokianos, Anders Rahbek, and Dag Tjøstheim. Poisson autoregression. Journal of the American Statistical Association, 104(488):1430–1439, 2009.
- [25] Germain Forestier, François Petitjean, Hoang Anh Dau, Geoffrey I Webb, and Eamonn Keogh. Generating synthetic time series to augment sparse datasets. In IEEE International Conference on Data Mining, pages 865–870. IEEE, 2017.
- [26] Vincent Fortuin, Dmitry Baranchuk, Gunnar Rätsch, and Stephan Mandt. GP-VAE: Deep probabilistic time series imputation. In International Conference on Artificial Intelligence and Statistics, pages 1651–1661. PMLR, 2020.
- [27] Vincent Fortuin, Matthias Hüser, Francesco Locatello, Heiko Strathmann, and Gunnar Rätsch. SOM-VAE: Interpretable discrete representation learning on time series. In International Conference on Learning Representations, 2019.
- [28] WR Foster, F Collopy, and LH Ungar. Neural network forecasting of short, noisy time series. Computers & Chemical Engineering, 16(4):293–297, 1992.
- [29] Marco Fraccaro, Simon Kamronn, Ulrich Paquet, and Ole Winther. A disentangled recognition and nonlinear dynamics model for unsupervised learning. Advances in Neural Information Processing Systems, 30, 2017.
- [30] John Cristian Borges Gamboa. Deep learning for time-series analysis. arXiv preprint arXiv:1701.01887, 2017.
- [31] Jakob Gawlikowski, Cedrique Rovile Njieutcheu Tassi, Mohsin Ali, Jongseok Lee, Matthias Humt, Jianxiang Feng, Anna Kruspe, Rudolph Triebel, Peter Jung, Ribana Roscher, et al. A survey of uncertainty in deep neural networks. arXiv preprint arXiv:2107.03342, 2021.
- [32] Felix A Gers, Nicol N Schraudolph, and Jürgen Schmidhuber. Learning precise timing with LSTM recurrent networks. Journal of Machine Learning Research, 3(Aug):115–143, 2002.
- [33] C Lee Giles, Steve Lawrence, and Ah Chung Tsoi. Noisy time series prediction using recurrent neural networks and grammatical inference. Machine Learning, 44(1):161–183, 2001.
- [34] Laurent Girin, Simon Leglaive, Xiaoyu Bie, Julien Diard, Thomas Hueber, and Xavier Alameda-Pineda. Dynamical variational autoencoders: A comprehensive review. arXiv preprint arXiv:2008.12595, 2020.
- [35] Klaus Greff, Rupesh K Srivastava, Jan Koutník, Bas R Steunebrink, and Jürgen Schmidhuber. LSTM: A search space odyssey. IEEE Transactions on Neural Networks and Learning Systems, 28(10):2222–2232, 2016.
- [36] Vinayaka Gude, Steven Corns, and Suzanna Long. Flood prediction and uncertainty estimation using deep learning. Water, 12(3):884, 2020.
- [37] Shengnan Guo, Youfang Lin, Ning Feng, Chao Song, and Huaiyu Wan. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In AAAI Conference on Artificial Intelligence, volume 33, pages 922–929, 2019.
- [38] Michaela Hardt, Alvin Rajkomar, Gerardo Flores, Andrew Dai, Michael Howell, Greg Corrado, Claire Cui, and Moritz Hardt. Explaining an increase in predicted risk for clinical alerts. In ACM Conference on Health, Inference, and Learning, pages 80–89, 2020.
- [39] Irina Higgins, Loic Matthey, Arka Pal, Christopher Burgess, Xavier Glorot, Matthew Botvinick, Shakir Mohamed, and Alexander Lerchner. beta-VAE: Learning basic visual concepts with a constrained variational framework. 2016.
- [40] Steven Craig Hillmer and George C Tiao. An ARIMA-model-based approach to seasonal adjustment. Journal of the American Statistical Association, 77(377):63–70, 1982.
- [41] Jonathan Ho, Ajay Jain, and Pieter Abbeel. Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems, 33:6840–6851, 2020.
- [42] Siu Lau Ho and Min Xie. The use of ARIMA models for reliability forecasting and analysis. Computers & Industrial Engineering, 35(1-2):213–216, 1998.
- [43] Aapo Hyvärinen, Jarmo Hurri, and Patrik O Hoyer. Estimation of non-normalized statistical models. In Natural Image Statistics, pages 419–426. Springer, 2009.
- [44] Aya Abdelsalam Ismail, Mohamed Gunady, Hector Corrada Bravo, and Soheil Feizi. Benchmarking deep learning interpretability in time series predictions. Advances in Neural Information Processing Systems, 33:6441–6452, 2020.
- [45] Aya Abdelsalam Ismail, Mohamed Gunady, Luiz Pessoa, Hector Corrada Bravo, and Soheil Feizi. Input-cell attention reduces vanishing saliency of recurrent neural networks. Advances in Neural Information Processing Systems, 32, 2019.
- [46] Hassan Ismail Fawaz, Germain Forestier, Jonathan Weber, Lhassane Idoumghar, and Pierre-Alain Muller. Deep learning for time series classification: a review. Data Mining and Knowledge Discovery, 33(4):917–963, 2019.
- [47] Dulakshi SK Karunasinghe and Shie-Yui Liong. Chaotic time series prediction with a global model: Artificial neural network. Journal of Hydrology, 323(1-4):92–105, 2006.
- [48] Alex Kendall and Yarin Gal. What uncertainties do we need in bayesian deep learning for computer vision? Advances in Neural Information Processing Systems, 30, 2017.
- [49] Been Kim, Martin Wattenberg, Justin Gilmer, Carrie Cai, James Wexler, Fernanda Viegas, et al. Interpretability beyond feature attribution: Quantitative testing with concept activation vectors (TCAV). In International Conference on Machine Learning, pages 2668–2677. PMLR, 2018.
- [50] Hyunjik Kim and Andriy Mnih. Disentangling by factorising. In International Conference on Machine Learning, pages 2649–2658. PMLR, 2018.
- [51] Kyoung-jae Kim. Financial time series forecasting using support vector machines. Neurocomputing, 55(1-2):307–319, 2003.
- [52] Pieter-Jan Kindermans, Sara Hooker, Julius Adebayo, Maximilian Alber, Kristof T Schütt, Sven Dähne, Dumitru Erhan, and Been Kim. The (un) reliability of saliency methods. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning, pages 267–280. Springer, 2019.
- [53] Diederik P Kingma and Max Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.
- [54] Durk P Kingma, Tim Salimans, Rafal Jozefowicz, Xi Chen, Ilya Sutskever, and Max Welling. Improved variational inference with inverse autoregressive flow. Advances in Neural Information Processing Systems, 29, 2016.
- [55] Nikita Kitaev, Łukasz Kaiser, and Anselm Levskaya. Reformer: The efficient transformer. arXiv preprint arXiv:2001.04451, 2020.
- [56] Rithesh Kumar, Sherjil Ozair, Anirudh Goyal, Aaron Courville, and Yoshua Bengio. Maximum entropy generators for energy-based models. arXiv preprint arXiv:1901.08508, 2019.
- [57] Naoto Kunitomo and Seisho Sato. A robust-filtering method for noisy non-stationary multivariate time series with econometric applications. Japanese Journal of Statistics and Data Science, 4(1):373–410, 2021.
- [58] Guokun Lai, Wei-Cheng Chang, Yiming Yang, and Hanxiao Liu. Modeling long-and short-term temporal patterns with deep neural networks. In International ACM SIGIR Conference on Research & Development in Information Retrieval, pages 95–104, 2018.
- [59] Brenden M Lake, Tomer D Ullman, Joshua B Tenenbaum, and Samuel J Gershman. Building machines that learn and think like people. Behavioral and Brain Sciences, 40, 2017.
- [60] Colin Lea, Rene Vidal, Austin Reiter, and Gregory D Hager. Temporal convolutional networks: A unified approach to action segmentation. In European Conference on Computer Vision, pages 47–54. Springer, 2016.
- [61] Shiyang Li, Xiaoyong Jin, Yao Xuan, Xiyou Zhou, Wenhu Chen, Yu-Xiang Wang, and Xifeng Yan. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. Advances in Neural Information Processing Systems, 32, 2019.
- [62] Yaguang Li, Rose Yu, Cyrus Shahabi, and Yan Liu. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. In International Conference on Learning Representations, 2018.
- [63] Yingzhen Li and Richard E Turner. Rényi divergence variational inference. Advances in Neural Information Processing Systems, 29, 2016.
- [64] Yuening Li, Zhengzhang Chen, Daochen Zha, Mengnan Du, Denghui Zhang, Haifeng Chen, and Xia Hu. Learning disentangled representations for time series. arXiv preprint arXiv:2105.08179, 2021.
- [65] Zengyi Li, Yubei Chen, and Friedrich T Sommer. Learning energy-based models in high-dimensional spaces with multi-scale denoising score matching. arXiv preprint arXiv:1910.07762, 2019.
- [66] Chi-Jie Lu, Tian-Shyug Lee, and Chih-Chou Chiu. Financial time series forecasting using independent component analysis and support vector regression. Decision Support Systems, 47(2):115–125, 2009.
- [67] Danielle C Maddix, Yuyang Wang, and Alex Smola. Deep factors with Gaussian processes for forecasting. arXiv preprint arXiv:1812.00098, 2018.
- [68] James E Matheson and Robert L Winkler. Scoring rules for continuous probability distributions. Management Science, 22(10):1087–1096, 1976.
- [69] Nam Nguyen and Brian Quanz. Temporal latent auto-encoder: A method for probabilistic multivariate time series forecasting. In AAAI Conference on Artificial Intelligence, volume 35, pages 9117–9125, 2021.
- [70] Alexander Quinn Nichol and Prafulla Dhariwal. Improved denoising diffusion probabilistic models. In International Conference on Machine Learning, pages 8162–8171. PMLR, 2021.
- [71] Fotios Petropoulos, Rob J Hyndman, and Christoph Bergmeir. Exploring the sources of uncertainty: Why does bagging for time series forecasting work? European Journal of Operational Research, 268(2):545–554, 2018.
- [72] Yao Qin, Dongjin Song, Haifeng Chen, Wei Cheng, Guofei Jiang, and Garrison W Cottrell. A dual-stage attention-based recurrent neural network for time series prediction. In International Joint Conference on Artificial Intelligence, 2017.
- [73] Syama Sundar Rangapuram, Matthias W Seeger, Jan Gasthaus, Lorenzo Stella, Yuyang Wang, and Tim Januschowski. Deep state space models for time series forecasting. Advances in Neural Information Processing Systems, 31, 2018.
- [74] Kashif Rasul, Calvin Seward, Ingmar Schuster, and Roland Vollgraf. Autoregressive denoising diffusion models for multivariate probabilistic time series forecasting. In International Conference on Machine Learning, pages 8857–8868. PMLR, 2021.
- [75] Geoffrey Roeder, Yuhuai Wu, and David K Duvenaud. Sticking the landing: Simple, lower-variance gradient estimators for variational inference. Advances in Neural Information Processing Systems, 30, 2017.
- [76] David Salinas, Michael Bohlke-Schneider, Laurent Callot, Roberto Medico, and Jan Gasthaus. High-dimensional multivariate forecasting with low-rank Gaussian copula processes. Advances in Neural Information Processing Systems, 32, 2019.
- [77] David Salinas, Valentin Flunkert, Jan Gasthaus, and Tim Januschowski. DeepAR: probabilistic forecasting with autoregressive recurrent networks. International Journal of Forecasting, 36(3):1181–1191, 2020.
- [78] Saeed Saremi, Aapo Hyvärinen, et al. Neural empirical Bayes. Journal of Machine Learning Research, 2019.
- [79] Rajat Sen, Hsiang-Fu Yu, and Inderjit S Dhillon. Think globally, act locally: A deep neural network approach to high-dimensional time series forecasting. Advances in Neural Information Processing Systems, 32, 2019.
- [80] Alex Sherstinsky. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Physica D: Nonlinear Phenomena, 404:132306, 2020.
- [81] Qiquan Shi, Jiaming Yin, Jiajun Cai, Andrzej Cichocki, Tatsuya Yokota, Lei Chen, Mingxuan Yuan, and Jia Zeng. Block hankel tensor ARIMA for multiple short time series forecasting. In AAAI Conference on Artificial Intelligence, volume 34, pages 5758–5766, 2020.
- [82] Shun-Yao Shih, Fan-Keng Sun, and Hung-yi Lee. Temporal pattern attention for multivariate time series forecasting. Machine Learning, 108(8):1421–1441, 2019.
- [83] Sameer Singh. Noisy time-series prediction using pattern recognition techniques. Computational Intelligence, 16(1):114–133, 2000.
- [84] Slawek Smyl and Karthik Kuber. Data preprocessing and augmentation for multiple short time series forecasting with recurrent neural networks. In International Symposium on Forecasting, 2016.
- [85] Jascha Sohl-Dickstein, Eric Weiss, Niru Maheswaranathan, and Surya Ganguli. Deep unsupervised learning using nonequilibrium thermodynamics. In International Conference on Machine Learning, pages 2256–2265. PMLR, 2015.
- [86] Huan Song, Deepta Rajan, Jayaraman J Thiagarajan, and Andreas Spanias. Attend and diagnose: Clinical time series analysis using attention models. In AAAI Conference on Artificial Intelligence, 2018.
- [87] Yang Song and Stefano Ermon. Generative modeling by estimating gradients of the data distribution. Advances in Neural Information Processing Systems, 32, 2019.
- [88] Sana Tonekaboni, Shalmali Joshi, Kieran Campbell, David K Duvenaud, and Anna Goldenberg. What went wrong and when? instance-wise feature importance for time-series black-box models. Advances in Neural Information Processing Systems, 33:799–809, 2020.
- [89] Arash Vahdat and Jan Kautz. NVAE: A deep hierarchical variational autoencoder. Advances in Neural Information Processing Systems, 33:19667–19679, 2020.
- [90] Pascal Vincent. A connection between score matching and denoising autoencoders. Neural Computation, 23(7):1661–1674, 2011.
- [91] Pascal Vincent, Hugo Larochelle, Isabelle Lajoie, Yoshua Bengio, Pierre-Antoine Manzagol, and Léon Bottou. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. Journal of Machine Learning Research, 11(12), 2010.
- [92] Julius Von Kügelgen, Yash Sharma, Luigi Gresele, Wieland Brendel, Bernhard Schölkopf, Michel Besserve, and Francesco Locatello. Self-supervised learning with data augmentations provably isolates content from style. Advances in Neural Information Processing Systems, 34, 2021.
- [93] Juntao Wang, Wun Kwan Yam, Kin Long Fong, Siew Ann Cheong, and KY Wong. Gaussian process kernels for noisy time series: Application to housing price prediction. In International Conference on Neural Information Processing, pages 78–89. Springer, 2018.
- [94] Satosi Watanabe. Information theoretical analysis of multivariate correlation. Ibm Journal of Research and Development, 4(1):66–82, 1960.
- [95] Ruofeng Wen, Kari Torkkola, Balakrishnan Narayanaswamy, and Dhruv Madeka. A multi-horizon quantile recurrent forecaster. arXiv preprint arXiv:1711.11053, 2017.
- [96] Mike West. Bayesian forecasting of multivariate time series: scalability, structure uncertainty and decisions. Annals of the Institute of Statistical Mathematics, 72(1):1–31, 2020.
- [97] Bingzhe Wu, Jintang Li, Chengbin Hou, Guoji Fu, Yatao Bian, Liang Chen, and Junzhou Huang. Recent advances in reliable deep graph learning: Adversarial attack, inherent noise, and distribution shift. arXiv preprint arXiv:2202.07114, 2022.
- [98] Mike Wu, Michael Hughes, Sonali Parbhoo, Maurizio Zazzi, Volker Roth, and Finale Doshi-Velez. Beyond sparsity: Tree regularization of deep models for interpretability. In AAAI Conference on Artificial Intelligence, volume 32, 2018.
- [99] Neo Wu, Bradley Green, Xue Ben, and Shawn O’Banion. Deep transformer models for time series forecasting: The influenza prevalence case. arXiv preprint arXiv:2001.08317, 2020.
- [100] Zonghan Wu, Shirui Pan, Guodong Long, Jing Jiang, and Chengqi Zhang. Graph wavenet for deep spatial-temporal graph modeling. In International Joint Conference on Artificial Intelligence, pages 1907–1913, 2019.
- [101] Jianwen Xie, Yang Lu, Song-Chun Zhu, and Yingnian Wu. A theory of generative convnet. In International Conference on Machine Learning, pages 2635–2644. PMLR, 2016.
- [102] Jianwen Xie, Yifei Xu, Zilong Zheng, Song-Chun Zhu, and Ying Nian Wu. Generative pointnet: Deep energy-based learning on unordered point sets for 3d generation, reconstruction and classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 14976–14985, 2021.
- [103] Jianwen Xie, Song-Chun Zhu, and Ying Nian Wu. Learning energy-based spatial-temporal generative convnets for dynamic patterns. IEEE transactions on pattern analysis and machine intelligence, 43(2):516–531, 2019.
- [104] Jiehui Xu, Jianmin Wang, Mingsheng Long, et al. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Advances in Neural Information Processing Systems, 34, 2021.
- [105] Tijin Yan, Hongwei Zhang, Tong Zhou, Yufeng Zhan, and Yuanqing Xia. ScoreGrad: Multivariate probabilistic time series forecasting with continuous energy-based generative models. arXiv preprint arXiv:2106.10121, 2021.
- [106] Jinsung Yoon, Daniel Jarrett, and Mihaela Van der Schaar. Time-series generative adversarial networks. Advances in Neural Information Processing Systems, 32, 2019.
- [107] Bing Yu, Haoteng Yin, and Zhanxing Zhu. Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting. In International Joint Conference on Artificial Intelligence, pages 3634–3640, 2018.
- [108] Yong Yu, Xiaosheng Si, Changhua Hu, and Jianxun Zhang. A review of recurrent neural networks: LSTM cells and network architectures. Neural Computation, 31(7):1235–1270, 2019.
- [109] Haoyi Zhou, Shanghang Zhang, Jieqi Peng, Shuai Zhang, Jianxin Li, Hui Xiong, and Wancai Zhang. Informer: Beyond efficient transformer for long sequence time-series forecasting. In AAAI Conference on Artificial Intelligence, 2021.
- [110] Yong Zou, Reik V Donner, Norbert Marwan, Jonathan F Donges, and Jürgen Kurths. Complex network approaches to nonlinear time series analysis. Physics Reports, 787:1–97, 2019.
Appendix A Related Work
A.1 Time Series Forecasting
We first briefly review the related literature of time series forecasting (TSF) methods as below. Complex temporal patterns can be manifested over short- and long-term as the time series evolves across time. To leverage the time evolution nature, existing statistical models, such as ARIMA [9] and Gaussian process regression [10] have been well established and applied to many downstream tasks [40, 42, 3]. Recurrent neural network (RNN) models are also introduced to model temporal dependencies for TSF in a sequence-to-sequence paradigm [35, 13, 95, 58, 67, 73, 77]. Besides, temporal attention [72, 86, 82] and causal convolution [4, 8, 79] are further explored to model the intrinsic temporal dependencies. Recent Transformer-based models have strengthened the capability of exploring hidden intricate temporal patterns for long-term TSF [104, 61, 99, 109]. On the other hand, the multivariate nature of TSF is another topic many works have been focusing on. These works treat a collection of time series as a unified entity and mine the inter-series correlations with different techniques, such as probabilistic models [77, 73], matrix/tensor factorization [79, 81], convolution neural networks (CNNs) [4, 58], and graph neural networks (GNNs) [37, 62, 107, 100, 11].
To improve the reliability and performance of TSF, instead of modeling the raw data, there exist works inferring the underlying distribution of the time series data with generative models [106, 18]. Many studies have employed a variational auto-encoder (VAE) to model the probabilistic distribution of sequential data [29, 34, 16, 14, 69]. For example, VRNN [16] employs the VAE to each hidden state of RNN such that the variability of highly structured sequential data can be captured. To yield predictive distribution for multivariate TSF, TLAE [69] implements nonlinear transformation by replacing matrix factorization with encoder-decoder architecture and temporal deep temporal latent model. Another line of generative methods for TSF focus on energy-based models (EBMs), such as TimeGrad [74] and ScoreGrad [105]. EBMs do not restrict the tractability of the normalizing constants [105]. Though flexible, the unknown normalizing constant makes the training of EBMs particularly difficult.
This paper focuses on TSF with VAE-based models. Besides, as many real-world time series data are relatively short and small [84], a coupled probabilistic diffusion model is proposed to augment the input series, as well as the output series, simultaneously, such that the distribution space can be enlarged without increasing the aleatoric uncertainty [48]. Moreover, to guarantee the generated target series moving toward the true target, a multi-scaled score-matching denoising network is plugged in for accurate future series prediction. To our knowledge, this is the first work focusing on generative TSF with the diffusion model and denoising techniques.
A.2 Time Series Augmentation
Both the traditional methods and deep learning methods can deteriorate when limited time series data are encountered. Generating synthetic time series is commonly adopted for augmenting short time series [17, 25, 106]. Transforming the original time series by cropping, flipping, and warping [46, 19] is another approach dedicated to TSF when the training data is limited. Whereas the synthetic time series may not respect the original feature relationship across time, and the transformation methods do not change the distribution space. Thus, the overfitting issues cannot be avoided. Incorporating the probabilistic diffusion model for TSF differentiates our work from existing time series augmentation methods.
A.3 Uncertainty Estimation and Denoising for Time Series Forecasting
There exist works aiming to estimate the uncertainty [48] for time series forecasting [71, 96, 36] by epistemic uncertainty. Nevertheless, the inevitable aleatoric uncertainty of time series is often ignored, which may stem from error-prone data measurement, collection, and so forth [97]. Another line of studies focuses on detecting noise in time series data [66] or devising suitable models for noise alleviation [33]. However, none of the existing works attempts to quantify the aleatoric uncertainty, which further differentiates our work from priors.
It is necessary to relieve the effect of noise in real-world time series data [22]. [5, 57] propose to preprocess the time series with smoothing and filtering techniques. However, such preprocessing methods can only be applied to the noise raised by the irregular data of time series. Neural networks are also introduced to denoise the time series [28, 83, 33, 47], while these deep networks can only deal with specific types of time series as well.
A.4 Interpretability of Time Series Forecasting
A number of works put effort into explaining the deep neural networks [98, 49, 2] to make the prediction more interpretable, but these methods often lack reliability when the explanation is sensitive to factors that do not contribute to the prediction [52]. Several works have been proposed to increase the reliability of TSF tasks [44, 45]. For multivariate time series, the interpretability of the representations can be improved by mapping the time series into latent space [27]. Besides, recent works have been proposed to disentangle the latent variables to identify the independent factors of the data, which can further lead to improved interpretability of the representation and higher performance [39, 59, 50]. The disentangled VAE has been applied to time series to benefit the generated results [64]. However, the choice of the latent variables is crucial for the disentanglement of time series data. We devise a bidirectional VAE (BVAE) and take the dimensions of each latent variable as the factors to be disentangled.
Appendix B Proofs of Lemma 1 and Lemma 2
With the coupled diffusion process and Eqs. 5 and 6, as well as Proposition 1, introduced in the main text, the diffused target series and generated target series can be decomposed as and . Then, we can draw the following two conclusions:
Lemma 1.
, there exists a probabilistic model to guarantee that , where .
Proof.
According to Proposition 1, can be fully captured by the model. That is, where is the ideal part of ground truth target series . And, with Eq. 6 (in the main text), . Therefore, when . ∎
Lemma 2.
With the coupled diffusion process, the difference between diffusion noise and generation noise will be reduced, i.e., .
Proof.
According to Proposition 1, the noise of consists of the estimation noise and residual noise , i.e., where and are independent of each other, then . Let , we have
which leads to . Moreover, both and are Gaussian noises, when , , we have . ∎
| Datasets | # Dims. | Full Data | Sliced Data | Target Variable | Time Interval | ||
|---|---|---|---|---|---|---|---|
| Time Span | # Points | Pct. of Full Data | # Points | ||||
| Traffic | 862 | 2015-2016 | 17544 | 5% | 877 | Sensor 862 | 1 hour |
| Electricity | 321 | 2011-2014 | 18381 | 3% | 551 | MT_321 | 10 mins |
| Weather | 21 | 2020-2021 | 36761 | 2% | 735 | CO2 (ppm) | 10 mins |
| ETTm1 | 7 | 2016-2018 | 69680 | 1% | 697 | OT | 15 mins |
| ETTh1 | 7 | 2016-2018 | 17420 | 5% | 871 | OT | 1 hour |
| Wind | 7 | 2020-2021 | 45550 | 2% | 911 | wind_power | 15 mins |
Appendix C Extra Implementation Details
C.1 Experimental Settings
Datasets Description. The main descriptive statistics of the real-world datasets adopted in the experiments of this work are demonstrated in Table 4.
Input Representation. We adopt the embedding method introduced in [109] and feed it to an RNN to extract the temporal dependency. Then we concatenate them as follows:
where is the raw time series data and denotes the embedding operation. Here, we use a two-layer gated recurrent unit (GRU), and the dimensionality of the hidden state and embeddings are and , respectively.
Diffusion Process Configuration. Besides, the diffusion process is configured to be and for the Weather dataset, and for the ETTh1 dataset, and for the Wind dataset, and and for the other datasets.
C.2 Implementation Details of Baselines
We select previous state-of-the-art generative models as our baselines in the experiments on synthetic and real-world datasets. Specifically, 1) GP-copula [76] is a method based on the Gaussian process, which is devoted to high-dimensional multivariate time series, 2) DeepAR [77] combines traditional auto-regressive models with RNNs by modeling a probabilistic distribution in an auto-encoder fashion, 3) TimeGrad [74] is an auto-regressive model for multivariate probabilistic time series forecasting with the help of an energy-based model, 4) Vanilla VAE (VAE for short) [53] is a classical statistical variational inference method on top of auto-encoder, 5) NVAE [89] is a deep hierarchical VAE built for image generation using depth-wise separable convolutions and batch normalization, 6) factor-VAE (f-VAE for short) [50] disentangles the latent variables by encouraging the distribution of representations to be factorial and independent across dimensions, and 7) -TCVAE [15] learns the disentangled representations with total correlation variational auto-encoder algorithm.

To train DeepAR, TimeGrad, and GP-copula in accordance with their original settings, the batch is constructed without shuffling the samples. The instances (sampled with the input--predict- rolling window and , as illustrated in Fig. 6) are fed to the training procedure of these three baselines in chronological order. Besides, these three baselines employ the cumulative distribution function (CDF) for training, so the CDF needs to be reverted to the real distribution for testing.
For f-VAE, -TCVAE, and VAE, since the dimensionality of different time series varies, we design a preprocess block to map the original time series into a tensor with the fix-sized dimensionality, which can further suit the VAEs well. The preprocess block consists of three nonlinear layers with the sizes of the hidden states: . For NVAE, we keep the original settings suggested in [89] and use Gaussian distribution as the prior. All the baselines are trained using early stopping, and the patience is set to 5.
| Model | D3VAE | NVAE | -TCVAE | f-VAE | DeepAR | TimeGrad | GP-copula | VAE | |
|---|---|---|---|---|---|---|---|---|---|
| Traffic | 8 | ||||||||
| 16 | |||||||||
| 32 | |||||||||
| 64 | |||||||||
| Electricity | 8 | ||||||||
| 16 | |||||||||
| 32 | |||||||||
| Weather | 8 | ||||||||
| 16 | |||||||||
| 32 | |||||||||
| 64 | |||||||||
| ETTm1 | 8 | ||||||||
| 16 | |||||||||
| 32 | |||||||||
| ETTh1 | 8 | ||||||||
| 16 | |||||||||
| 32 | |||||||||
| 64 | |||||||||
| Wind | 8 | ||||||||
| 16 | |||||||||
| 32 | |||||||||
| 64 | |||||||||
| Model | D3VAE | NVAE | -TCVAE | f-VAE | DeepAR | TimeGrad | GP-copula | VAE | |
|---|---|---|---|---|---|---|---|---|---|
| Electricity | 16 | ||||||||
| 32 | |||||||||
| ETTm1 | 16 | ||||||||
| 32 | |||||||||
Appendix D Supplementary Experimental Results
D.1 Comparisons of Predictive Performance for TSF Under Different Settings
Longer-Term Time Series Forecasting. To further inspect the performance of our method, we additionally conduct more experiments for longer-term time series forecasting. In particular, by configuring the output length with 32 and 64666The length of the input time series is the same as the output time series., we compare D3VAE to other baselines in terms of MSE and CRPS, and the results (including short-term and long-term) are reported in Table 5. We can conclude that D3VAE also outperforms the competitive baselines consistently under the longer-term forecasting settings.
Time Series Forecasting in Full Datasets. Moreover, we evaluate the predictive performance for time series forecasting in two “full-version” datasets, i.e. 100%-Electricity and 100%-ETTm1. The split of train/validation/test is 7:1:2 which is the same as the main experiments. The comparisons in terms of MSE and CRPS can be found in Table 6. With sufficient data, compared to previous state-of-the-art generative models, the MSE and CRPS reductions of our method are also satisfactory under different settings (including input-16-predict-16 and input-32-predict-32). For example, in the Electricity dataset, compared to the second best results, D3VAE achieves 52% (0.680 0.330) and 54% (0.727 0.336) MSE reductions, and 34% (0.675 0.445) and 36% (0.692 0.444) CRPS reductions, under input-16-predict-16 and input-32-predict-32 settings, respectively.


























D.2 Case Study
D.3 The Effect of Scale Parameter
We demonstrate the forecasting results with different values of on Electricity and Traffic datasets, and the results are plotted in Figs. 11 and 11. It can be depicted that larger or smaller would lead to deviated prediction, which is far from the ground truth. Therefore, the value of does affect the prediction performance, which should be tuned properly.
| Length | Metric | Percentage of Full Electricity Data | ||||||
|---|---|---|---|---|---|---|---|---|
| 100% | 80% | 60% | 40% | 20% | 10% | 5% | ||
| 8 | MSE | |||||||
| CRPS | ||||||||
| 16 | MSE | |||||||
| CRPS | ||||||||
| 32 | MSE | |||||||
| CRPS | ||||||||
| Length | Metric | Percentage of Full Traffic Data | ||||||
|---|---|---|---|---|---|---|---|---|
| 100% | 80% | 60% | 40% | 20% | 10% | 5% | ||
| 8 | MSE | |||||||
| CRPS | ||||||||
| 16 | MSE | |||||||
| CRPS | ||||||||
| 32 | MSE | |||||||
| CRPS | ||||||||
D.4 Sensitivity Analysis of Trade-off Parameters in Reconstruction Loss
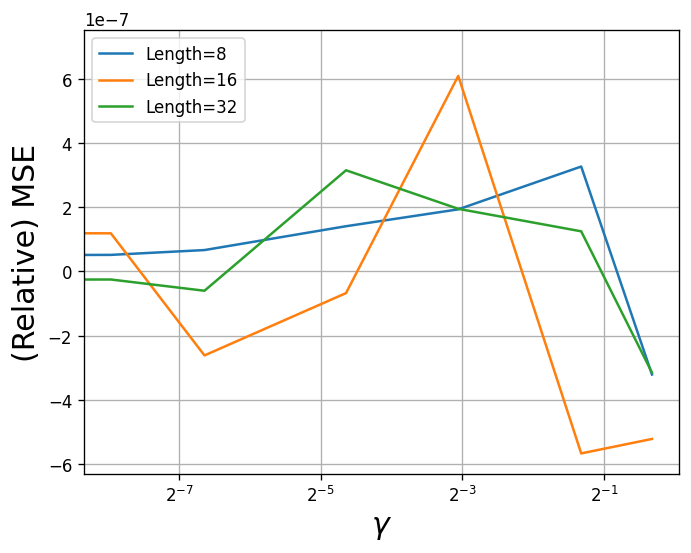
To examine the effect of the trade-off hyperparameters in loss , we plot the mean square error (MSE) against different values of trade-off parameters, i.e., , and , in the Traffic dataset. Note that the relative value of MSE is plotted to ensure the difference is distinguishable. This experiment is conducted under different settings: input-8-predict-8, input-16-predict-16, and input-32-predict-32. For , the value ranges from to , ranges from to , and ranges from to . The results are shown in Fig. 11. We can see that the model’s performance varies slightly as the trade-off parameters take different values, which shows that our model is robust enough against different trade-off parameters.
D.5 Scalability Analysis of Varying Time Series Length and Dataset Size
We additionally investigate the scalability of D3VAE against different lengths of the time series and varying amounts of available data. The experiments are conducted on the Electricity and Traffic datasets, and the results are reported in Sections D.3 and D.3, respectively. We can observe that the predictive performance of D3VAE is relatively stable under different settings. In particular, the longer the target series to predict, the worse performance might be obtained. Besides, when the amount of available data is shrunk, D3VAE performs more stable than expected. Note that on the 20%-Electricity dataset, the performance of D3VAE is much worse than other subsets of the Electricity dataset, mainly because the sliced 20%-Electricity dataset involves more irregular values.
# factors = 2



# factors = 4


# factors = 6



# factors = 8



# factors = 10


# factors = 12



Appendix E Disentanglement for Time Series Forecasting
Fig. 13 illustrates the disentanglement of latent variable for time series forecasting. It is difficult to choose suitable disentanglement factors under the unsupervised learning of disentanglement. Therefore, we attempt to inspect the TSF performance against different numbers of factors to be disentangled. We implement a simple classifier as a discriminator to further evaluate the disentanglement quality in Fig. 12 (and Algorithm 3 demonstrates the training procedure of the discriminator). To be specific, we take different dimensions of as the factors to be disentangled: (), then an instance consisting of factor and label is constructed. We shuffle these examples for each and attempt to classify them with a discriminator, then the disentanglement can be evaluated by measuring the loss of the discriminator. The learning curve of the discriminator can be leveraged to assess the disentanglement, and the discriminator is implemented by an MLP with six nonlinear layers and 100 hidden states. The results of prediction, discriminator loss, and the total correlation w.r.t. different numbers of factors are plotted in Fig. 12, respectively. As shown in Fig. 12, the number of factors does affect the prediction performance, as well as the disentanglement quality. On the other hand, the learning curves can be converged when different factors are adopted, which validates that the disentanglement of the latent factors is of high quality.




In addition to the above method evaluating the disentanglement indirectly, we adopt another metric named Mutual Information Gap (MIG) [15] to evaluate the quality of disentanglement in a more straightforward way. Specifically, for a latent variable , the mutual information between , and a factor can be calculated by
| (16) |
where denotes the sample of and is the support set of . Then, for
| (17) |
where means the second max value of , then the MIG of can be obtained as
| (18) |
We evaluate the quality of disentanglement in terms of MIG on ETTm1 and ETTh1 datasets, respectively, which can be seen in Fig. 14. From Figs. 14(a) and 14(b), when the weight of disentanglement (i.e., in Eq. 14 of the main text) grows, the disentangled factors are of higher quality. In other words, the latent variables can be disentangled with the help of the disentanglement module in D3VAE. In addition, we examine the changes in MIG against different numbers of factors. We can observe that the difficulty of disentanglement climbs up as the number of factors increases.
T = 10
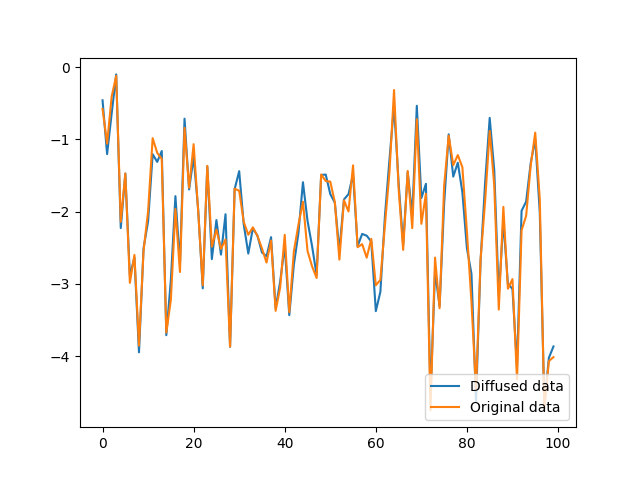



T = 50




T = 100




T = 200




T = 400




T = 600




T = 800




T = 900




Appendix F Model Inspection: Coupled Diffusion Process
To gain more insights into the coupled diffusion process, we demonstrate how a time series can be diffused under different settings in terms of variance schedule and the max number of diffusion steps . The examples are illustrated in Fig. 15. It can be seen that when larger diffusion steps or a wider variance schedule is employed, the diffused series deviates far from the original data gradually, which may result in the loss of useful signals, like, temporal dependencies. Therefore, it is important to choose a suitable variance schedule and diffusion steps to ensure that the distribution space is deviated enough without losing useful signals.
Appendix G Necessity of Data Augmentation for Time Series Forecasting
Limited data would result in overfitting and poor performance. To demonstrate the necessity of enlarging the size of data for time series forecasting when deep models are employed, we implement a two-layer RNN and evaluate how many time points are required to ensure the generalization ability. A synthetic dataset is adopted for this demonstration.
According to [23], we generate a toy time series dataset with time points in which each point is a -dimension variable:
where , , , , and . An input-8-predict-8 window is utilized to roll this synthetic dataset. We split this synthetic dataset into training and test sets with a ratio of 7:3. We train the RNN in 100 epochs at most, and the MSE loss of training and testing are plotted in Fig. 16. It can be seen that the inflection points of the loss curves move back gradually and disappear as increasing the size of the dataset. Besides, with fewer time points, like, 400, the model can be overfitted more easily.






‘