Generalized Transport Characterizations for Short Oceanic Internal Waves in a Sea of Long Waves

In the limit of small nonlinearity, one develops a perturbation expansion in the nonlinearity strengh, which leads under certain assumptions to the wave turbulence kinetic equation. The derivation of the resonant kinetic equation is well understood and studied, see Zakharov et al. (1992); Nazarenko (2011). Taking nonresonant interactions leads to a different version of the kinetic equation with the frequency delta functions being replaced by a Lorenzian, see Lvov et al. (1997, 2012). This derivation also hinges on the assessment that fourth order cumulants are a subleading term compared to the product of two double correlators (Deng and Hani, 2021). For the three-wave Hamiltonian (13), the kinetic equation is Eq. (LABEL:BroadenedKineticEquation), describing general internal waves interacting in both rotating and non-rotating environments:

	$\displaystyle\frac{\partial}{\partial t}n_{{\textbf{p}}}=\displaystyle\int\int d{\textbf{p}}_{1}d{\textbf{p}}_{2}$	$\displaystyle\Big{(}\mid V_{{\textbf{p}}_{1},{\textbf{p}}_{2}}^{{\textbf{p}}}\mid^{2}\delta({\textbf{p}}-{\textbf{p}}_{1}-{\textbf{p}}_{2}){\mathcal{L}}(\Delta\sigma_{p12},\Gamma_{p12})[n_{{\textbf{p}}_{1}}n_{{\textbf{p}}_{2}}-n_{{\textbf{p}}}[n_{{\textbf{p}}_{1}}+n_{{\textbf{p}}_{2}}]]$
		$\displaystyle\left.-\mid V_{{\textbf{p}}_{2},{\textbf{p}}}^{{\textbf{p}}_{1}}\mid^{2}\delta({\textbf{p}}-{\textbf{p}}_{1}+{\textbf{p}}_{2}){\mathcal{L}}(\Delta\sigma_{12p},\Gamma_{p12})[n_{{\textbf{p}}_{2}}n_{{\textbf{p}}}-n_{{\textbf{p}}_{1}}[n_{{\textbf{p}}_{2}}+n_{{\textbf{p}}}]]\right.$
		$\displaystyle-\mid V_{{\textbf{p}},{\textbf{p}}_{1}}^{{\textbf{p}}_{2}}\mid^{2}\delta({\textbf{p}}+{\textbf{p}}_{1}-{\textbf{p}}_{2}){\mathcal{L}}(\Delta\sigma_{2p1},\Gamma_{p12})[n_{{\textbf{p}}}n_{{\textbf{p}}_{1}}-n_{{\textbf{p}}_{2}}[n_{{\textbf{p}}}+n_{{\textbf{p}}_{1}}]]\Big{)}.$

where Laurencian $\mathcal{L}$ is given by ${\mathcal{L}}=\frac{\Gamma_{p12}}{(\Delta\sigma)^{2}+\Gamma_{p12}^{2}},$ and $\Delta\sigma_{p12}=\sigma_{p}-\sigma_{p_{1}}-\sigma_{p_{2}}$ represents the distance from the resonant surface. The resonant manifold is defined by

	$\displaystyle\sigma$	$\displaystyle=$	$\displaystyle\sigma_{1}+\sigma_{2};\;\;\;\;\;\;\;\;\;\;\;\bf{p}=\bf{p}_{1}+\bf{p}_{2}$
	$\displaystyle\sigma$	$\displaystyle=$	$\displaystyle\sigma_{1}-\sigma_{2};\;\;\;\;\;\;\;\;\bf{p}=\bf{p}_{1}-\bf{p}_{2}$
	$\displaystyle\sigma$	$\displaystyle=$	$\displaystyle\sigma_{2}-\sigma_{1};\;\;\;\;\;\;\bf{p}=\bf{p}_{2}-\bf{p}_{1}\$		(16)

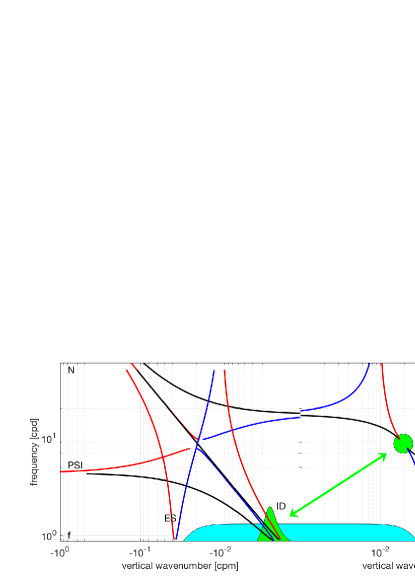
and appears in figure 1. In wave turbulence theory of internal waves the importance of special extreme scale separated triads was recognized in McComas and Bretherton (1977). These extreme-scale separated limits are called Induced Diffusion (ID), Elastic Scattering (ES) and Parametric Subharmonic Instability (PSI). For an explanation of these triads see, as well, McComas and Müller (1981a).

The total resonance width associated with a specific triad is given by $\Gamma_{p12}=\gamma_{p}+\gamma_{1}+\gamma_{2},$ and the equation for the individual resonance widths is given by

	$\displaystyle\gamma_{p}=\displaystyle\int\int d{\textbf{p}}_{1}d{\textbf{p}}_{2}$	$\displaystyle\Big{(}\mid V_{{\textbf{p}}_{1},{\textbf{p}}_{2}}^{{\textbf{p}}}\mid^{2}\delta({\textbf{p}}-{\textbf{p}}_{1}-{\textbf{p}}_{2}){\mathcal{L}}(\sigma-\sigma_{1}-\sigma_{2})[n_{{\textbf{p}}_{1}}+n_{{\textbf{p}}_{2}}]$
		$\displaystyle\left.+\mid V_{{\textbf{p}}_{2},{\textbf{p}}}^{{\textbf{p}}_{1}}\mid^{2}\delta({\textbf{p}}-{\textbf{p}}_{1}+{\textbf{p}}_{2}){\mathcal{L}}(\sigma-\sigma_{1}+\sigma_{2})[n_{{\textbf{p}}_{2}}-n_{{\textbf{p}}_{1}}]\right.$
		$\displaystyle+\mid V_{{\textbf{p}},{\textbf{p}}_{1}}^{{\textbf{p}}_{2}}\mid^{2}\delta({\textbf{p}}+{\textbf{p}}_{1}-{\textbf{p}}_{2}){\mathcal{L}}(\sigma+\sigma_{1}-\sigma_{2})[n_{{\textbf{p}}_{1}}-n_{{\textbf{p}}_{2}}]\Big{)}.$

Physically this $\gamma_{p}$ represents the fast time scale of decay of a narrow perturbation to the otherwise stationary spectrum (Lvov et al., 1997; Polzin and Lvov, 2017). It coincides with Langevin rates estimated by Pomphrey et al. (1980) and the decay rate of McComas (1977)’s spike experiments. The replacement of the frequency conserving delta function by the Lorentzian takes into account not only resonant, but also near-resonant and nonresonant interactions. Nonresonant interactions appear as a result of the Lorentzian decaying slowly. The role of the nonresonant interactions have to be investigated separately for each particular problem. The detailed investigation that will be presented elsewhere, show that for the case of internal waves and the Garrett and Munk spectrum, the nonresonant interactions leads to the Doppler defect, noticed in Polzin and Lvov (2017).

Following McComas and Bretherton (1977) for the resonant kinetic equation, we start from (LABEL:BroadenedKineticEquation) and pick off the interactions having p nearly parallel to ${\textbf{p}}_{1}$ with ${\textbf{p}}_{2}$ small, or nearly parallel to ${\textbf{p}}_{2}$ with ${\textbf{p}}_{1}$ small , which selects the ID class triads. For a sufficiently red spectrum, this permits discarding the small $n_{\textbf{p}}n_{{\textbf{p}}1}$ ($n_{\textbf{p}}n_{{\textbf{p}}2}$, respectively) terms. We then rewrite (LABEL:BroadenedKineticEquation) as

$$\frac{\partial n_{{\textbf{p}}}}{\partial t}=\int d{\textbf{q}}\left({\cal B}({\textbf{p}})-{\cal B}({\textbf{p}}+{\textbf{q}})\right)\simeq-\int d{\textbf{q}}\ \ \left({\textbf{q}}\cdot\frac{\partial}{\partial{\textbf{p}}}\right){\cal B}({\textbf{p}}),$$

(18)

where we introduced

$${\cal B}({\textbf{p}})=8\pi\int|V_{{\textbf{p}}_{1},{\textbf{q}}}^{{\textbf{p}}}|^{2}\,n_{q}(n_{{\textbf{p}}1}-n_{\textbf{p}})\,\delta_{{{\textbf{p}}-{\textbf{p}}_{1}-{\textbf{q}}}}\,{\cal L}({\sigma_{{\textbf{p}}}-\sigma_{{{\textbf{p}}_{1}}}-\sigma_{{{\textbf{q}}}}})d{\textbf{p}}_{1},$$

and expanded the difference $\left({\cal B}({\textbf{p}})-{\cal B}({\textbf{p}}+{\textbf{q}})\right)$ in a Taylor series using q to represent the small difference in wavenumber between the two high frequency waves. Expanding the difference $n_{{\textbf{p}}_{1}}-n_{\textbf{p}}$ for small q gives

$\displaystyle{\cal B}({\textbf{p}})\simeq-8\pi\left({\textbf{q}}\cdot\frac{\partial n_{\textbf{p}}}{\partial{\textbf{p}}}\right)\,\int|V_{{\textbf{p}}_{1},{\textbf{q}}}^{{\textbf{p}}}|^{2}\,n_{q}\delta_{{{\textbf{p}}-{\textbf{p}}_{1}-{\textbf{q}}}}\,{\cal L}({\sigma_{{\textbf{p}}}-\sigma_{{{\textbf{p}}_{1}}}-\sigma_{{{\textbf{q}}}}})d{\textbf{p}}_{1}.$

(19)

Combining (18) with (19) we obtain

	$\displaystyle\frac{\partial n_{{\textbf{p}}}}{\partial t}$	$\displaystyle=$	$\displaystyle\frac{\partial}{\partial p_{i}}D_{ij}({\textbf{p}},{\textbf{q}})\frac{\partial}{\partial p_{j}}n_{{\textbf{p}}},$
	$\displaystyle D_{ij}({\textbf{p}},{\textbf{q}})$	$\displaystyle=$	$\displaystyle 8\pi\int d{\textbf{q}}\left(q_{i}q_{j}\right)|V_{{\textbf{p}}_{1},{\textbf{q}}}^{{\textbf{p}}}|^{2}\,n_{q}\,\delta_{{{\textbf{p}}-{\textbf{p}}_{1}-{\textbf{q}}}}\,{\cal L}({\sigma_{{\textbf{p}}}-\sigma_{{{\textbf{p}}_{1}}}-\sigma_{{{\textbf{q}}}}})d{\textbf{p}}_{1}.$		(20)

This is a Fokker-Planck diffusion equation describing the diffusion of wave action in the system dominated by nonlocal in wavenumber interactions. Comparison between the Fokker-Planck equation (20) obtained here, and the similar Fokker-Planck equation (obtained using WKB theory (Section 3.2.4 below) will lead to critical insights into the spectral energy transfers in internal wave systems and ultimately to the parametrization of the energy supply to internal wave breaking processes.

To study interactions between long and short waves we start at (7) and make a Reynolds decomposition in wave amplitude:

$\displaystyle\Pi\rightarrow\Pi_{0}+\Pi+\pi^{\prime},\ \ \ \ \phi=\Phi+\phi^{\prime},\ \ \ \ \psi=\Psi+\psi^{\prime}\ .$

(21)

Here the large amplitude waves are represented with $\Pi,\Phi,\Psi$ and small amplitude waves are given by $\phi^{\prime}$, $\pi^{\prime}$ and $\psi^{\prime}$. Given the potentials $\Phi$ and $\phi$, the corresponding velocities are

$${\cal U}=\nabla\Phi+\nabla^{\perp}\Psi,\ \ \ u^{\prime}=\nabla\phi^{\prime}+\nabla^{\perp}\psi^{\prime}.$$

To simplify the presentation we will utilize the non-rotating approximation ($f=0$) in which $(\nabla^{\perp}\Psi,\nabla^{\perp}\psi)\rightarrow 0$. The case of rotating ocean $f\neq 0$ is presented in Appendix.

We substitute the Reynolds decomposition (21) into the equations of motion (1) and subtract equations for the large amplitude waves. The result is given by

	$\displaystyle\dot{\pi}^{\prime}+\nabla\cdot\left((\Pi_{0}+\Pi+\pi^{\prime})\nabla\Phi\right)+\nabla\left(\pi^{\prime}\Phi\right)=0,$
	$\displaystyle\dot{\phi}^{\prime}+\frac{|\nabla\phi^{\prime}|^{2}}{2}+\nabla\phi^{\prime}\cdot\nabla\Phi+\frac{g}{\rho_{0}^{2}}\int\int d\rho^{\prime}d\rho^{{}^{\prime\prime}}\pi^{\prime}=0.$
			(22)

In these equations $\Pi$ and $\Phi$ are given time-space dependent functions representing the large amplitude waves.

These equations are also Hamilton’s equations,

$$\frac{\partial\pi^{\prime}}{\partial t}=\frac{\delta{\cal H}}{\delta\phi^{\prime}}\,,\qquad\frac{\partial\phi^{\prime}}{\partial t}=-\frac{\delta{\cal H}}{\delta\pi^{\prime}}\,,$$

(23)

with the time-dependent Hamiltonian given by ²²2This Hamiltonian may be obtained by substituting (21) to (8).

$\displaystyle{\cal H}=\frac{1}{2}\int d{\bf{r}}\left(\left(\Pi_{0}+\Pi+\pi^{\prime}\right)\,\left|\nabla\phi^{\prime}\right|^{2}+2\pi^{\prime}\nabla\phi^{\prime}\cdot\nabla\Phi-g\left|\int^{\rho}d\hat{\rho}\frac{\pi^{\prime}}{\hat{\rho}}\right|^{2}\right)\,.$

(24)

There are two types of terms here - those that will ultimately describe a sea of interacting small scale waves and those that will describe the influence of large amplitude large scale waves on the small scale waves. In our previous efforts (Lvov and Tabak, 2001, 2004; Lvov et al., 2010; Polzin and Lvov, 2011, 2017) these terms are comingled. Comparing (8) and (24), we see that (24) contains additional terms $\Pi$$|\nabla\phi^{\prime}|^{2}$ and $\pi^{\prime}\nabla\phi^{\prime}\cdot\nabla\Phi$ that are explicit representations of what will be scale separated interactions. The term $\pi^{\prime}\nabla\phi^{\prime}\cdot\nabla\Phi$ describes the advection of the small-scale internal field by the given large-scale large amplitude field. The term $\Pi$$|\nabla\phi^{\prime}|^{2}$ represents a coupling of small scales to large through changes in the stratification by the large scale wave. The term $\pi^{\prime}|\nabla\phi^{\prime}|^{2}$ will represent interactions local in wavenumber.

We now express the space-dependent variables $\pi^{\prime}({\textbf{r}}),\Pi({\textbf{r}}),\phi^{\prime}({\textbf{r}})$ and $\Phi({\textbf{r}})$ in terms of their Fourier images $\pi^{\prime}({\textbf{p}}),\Pi({\textbf{p}}),\phi^{\prime}({\textbf{p}})$ via (9), make the Boussinesq approximation $\frac{\Pi}{\rho}\simeq\frac{\Pi}{\rho_{0}}$ and use $\int d{\textbf{p}}e^{i{\textbf{p}}\cdot{\textbf{r}}}=(2\pi)^{3}\delta({\textbf{p}})$ to obtain

	$\displaystyle{\cal H}$	$\displaystyle=$	$\displaystyle{\cal H}_{\rm linear}+{\cal H}_{\rm nonlinear},$
	$\displaystyle{\cal H}_{\rm linear}$	$\displaystyle=$	$\displaystyle\frac{1}{2}\int d{\textbf{p}}\left(\Pi_{0}|{\bf k}|^{2}|\phi^{\prime}_{{\textbf{p}}}|^{2}-\frac{g}{\rho_{0}^{2}}\frac{|\phi^{\prime}_{{\textbf{p}}}|^{2}}{m^{2}}\right),$
	$\displaystyle{\cal H}_{\rm nonlinear}$	$\displaystyle=$	$\displaystyle{\cal H}_{\rm local}+{\cal H}_{\rm sweeping}+{\cal H}_{\rm density},$

	$\displaystyle{\cal H}_{\rm local}$	$\displaystyle=$	$\displaystyle-{\bf\frac{1}{2(2\pi)^{\frac{3}{2}}}}\int d{\textbf{p}}_{1}d{\textbf{p}}_{2}d{\textbf{p}}_{3}\delta({\textbf{p}}_{1}+{\textbf{p}}_{2}+{\textbf{p}}_{3}){\textbf{k}}_{2}\cdot{\textbf{k}}_{3}\pi^{\prime}_{{\textbf{p}}_{1}}\phi^{\prime}_{{\textbf{p}}_{2}}\phi^{\prime}_{{\textbf{p}}_{3}},$
	$\displaystyle{\cal H}_{\rm sweeping}$	$\displaystyle=$	$\displaystyle-{\bf\frac{1}{2(2\pi)^{\frac{3}{2}}}}\int d{\textbf{p}}_{1}d{\textbf{p}}_{2}d{\textbf{p}}_{3}\delta({\textbf{p}}_{1}+{\textbf{p}}_{2}+{\textbf{p}}_{3})2{\textbf{k}}_{1}\cdot{\textbf{k}}_{2}\Phi_{{\textbf{p}}_{1}}\phi^{\prime}_{{\textbf{p}}_{2}}\pi^{\prime}_{{\textbf{p}}_{3}},$
	$\displaystyle{\cal H}_{\rm density}$	$\displaystyle=$	$\displaystyle-{\bf\frac{1}{2(2\pi)^{\frac{3}{2}}}}\int d{\textbf{p}}_{1}d{\textbf{p}}_{2}d{\textbf{p}}_{3}\delta({\textbf{p}}_{1}+{\textbf{p}}_{2}+{\textbf{p}}_{3}){\textbf{k}}_{2}\cdot{\textbf{k}}_{3}\Pi_{{\textbf{p}}_{1}}\phi^{\prime}_{{\textbf{p}}_{2}}\phi^{\prime}_{{\textbf{p}}_{3}}.$

The Hamiltonian ${\cal H}_{\rm nonlinear}$ is the sum of three terms:

• •

  ${\cal H}_{\rm local}$ represents small amplitudes interacting with small amplitudes. We will call this term “local” interactions in anticipation of making a scale separation between large amplitude large scale and small amplitude small scale waves in sections 3.1.2 and3.1.3.

• •

  ${\cal H}_{\rm density}$ is the term that describes the variations of stratification that small amplitude waves experience due to the compression and rarification of isopycnals associated with the large amplitude waves. We will refer to this term as a density term.

• •

  ${\cal H}_{\rm sweeping}$ is the term that describes the advection (sweeping) of small amplitude waves by large amplitude waves. In the future, we refer to this term as a sweeping term.

The main focus of this manuscript is to investigate how the density and sweeping terms affect the overall spectral energy density.

Following the traditional wave turbulence approach, we make a transformation to the wave-action variables that represent wave amplitude and phase:

	$\displaystyle\phi^{\prime}_{\bf p}=\frac{iN\sqrt{\sigma_{\textbf{p}}}}{\sqrt{2g}|{\bf k}|}\left(a_{\textbf{p}}-a^{*}_{-{\textbf{p}}}\right)\,,\ \ \ \pi^{\prime}_{\textbf{p}}=\frac{\sqrt{g}|{\bf k}|}{\sqrt{2\sigma_{\textbf{p}}}N}\left(a_{\textbf{p}}+a^{*}_{-{\textbf{p}}}\right)\,.$
			(27)

We substitute (27) into ${\cal H}_{\rm sweeping}$ of (LABEL:FourierHam), and obtain

	$\displaystyle{\cal H}_{\rm sweeping}$	$\displaystyle=$	$\displaystyle-{\bf\frac{1}{2(2\pi)^{\frac{3}{2}}}}\int d{\textbf{p}}_{1}d{\textbf{p}}_{2}d{\textbf{p}}_{3}\delta({\textbf{p}}_{1}+{\textbf{p}}_{2}+{\textbf{p}}_{3})2{\textbf{k}}_{1}\cdot{\textbf{k}}_{2}\Phi_{{\textbf{p}}_{1}}\frac{iN\sqrt{\sigma_{{\textbf{p}}_{2}}}}{\sqrt{2g}|{\bf k}_{2}|}\frac{\sqrt{g}|{\bf k}_{3}|}{\sqrt{2\sigma_{{\textbf{p}}_{3}}}N}$
			$\displaystyle\hskip 113.81102pt\times\left(a_{{\textbf{p}}_{2}}-a^{*}_{-{\textbf{p}}_{2}}\right)\left(a_{{\textbf{p}}_{3}}+a^{*}_{-{\textbf{p}}_{3}}\right)\,.$

The next step is algebraically trivial but conceptually fundamental. We invoke an extreme scale separated limit in which the two small amplitude waves have similar frequency and horizontal wavenumber magnitude. No condition is required on the vertical wavenumber. This conditioning retains both the induced diffusion (ID) and Bragg scattering (ES) branches of the resonant manifold, figure 1.

In this scale separated limit of the internal wave problem, $\sigma_{{\textbf{p}}_{2}}\cong\sigma_{{\textbf{p}}_{3}}$ and $|{\bf k}_{2}|\cong|{\bf k}_{3}|$. Beyond the obvious algebraic simplifications, upon expanding the brackets we find terms of the type $a_{{\textbf{p}}_{2}}a_{{\textbf{p}}_{3}}$, $a^{*}_{-{\textbf{p}}_{2}}a^{*}_{-{\textbf{p}}_{3}}$ and $a_{{\textbf{p}}_{2}}a^{*}_{-{\textbf{p}}_{3}}$, $a^{*}_{-{\textbf{p}}_{2}}a_{-{\textbf{p}}_{3}}$. In what follows we neglect the $a_{{\textbf{p}}_{2}}a_{{\textbf{p}}_{3}}$ and $a^{*}_{-{\textbf{p}}_{2}}a^{*}_{-{\textbf{p}}_{3}}$ terms and retain the $a_{{\textbf{p}}_{2}}a^{*}_{-{\textbf{p}}_{3}}$, $a^{*}_{-{\textbf{p}}_{2}}a_{-{\textbf{p}}_{3}}$ terms, since the former terms are nonresonant, while the latter may be in the resonance for some wave numbers. The discarded terms lead to a process when one lower-frequency wave decays into two high-frequency waves and thus the frequencies do not sum to zero. Such decay is a nonresonant process, so we can remove these terms at the onset.

After relabelling subscripts, in which $2\to 1$ and $3\to 2$, we obtain

	$\displaystyle{\cal H}_{\rm sweeping}$	$\displaystyle=$	$\displaystyle\int d{\textbf{p}}_{1}d{\textbf{p}}_{2}A_{\rm sweeping}({\textbf{p}}_{1},{\textbf{p}}_{2})a_{{\textbf{p}}_{1}}a^{*}_{{\textbf{p}}_{2}},$		(29)
		$\displaystyle{\rm with}$
	$\displaystyle A_{\rm sweeping}({\textbf{p}}_{1},{\textbf{p}}_{2})$	$\displaystyle=$	$\displaystyle-\frac{1}{2}i\left({{\textbf{k}}_{1}-{\textbf{k}}_{2}}\right)\cdot\left({\textbf{k}}_{1}+{\textbf{k}}_{2}\right)\Phi_{{\textbf{p}}_{1}-{\textbf{p}}_{2}}\;.$

In the limit of large vertical background scales, (3.1.2) describes a quasi-coherent translation of small scale small amplitude waves by the large scale background. At $1/2$ the vertical scale of ${\textbf{p}}_{1}$ and ${\textbf{p}}_{2}$, (3.1.2) describes a Bragg Scattering process. This is distinct from ’local’ interactions as the large amplitude wave has a much larger horizontal scale.

We now can repeat the same steps for the density Hamiltonian. We substitute (27) into the ${\cal H}_{\rm density}$ of (LABEL:FourierHam), use $\sigma_{{\textbf{p}}_{2}}\cong\sigma_{{\textbf{p}}_{3}}$ and $|{\bf k}_{2}|\cong|{\bf k}_{3}|$, relable subscripts and obtain

	$\displaystyle{\cal H}_{\rm density}$	$\displaystyle=$	$\displaystyle\int d{\textbf{p}}_{1}d{\textbf{p}}_{2}A_{\rm density}({\textbf{p}}_{1},{\textbf{p}}_{2})a_{{\textbf{p}}_{1}}a^{*}_{{\textbf{p}}_{2}},$		(30)
		$\displaystyle{\rm with}$
	$\displaystyle A_{\rm density}({\textbf{p}}_{1},{\textbf{p}}_{2})$	$\displaystyle=$	$\displaystyle\frac{1}{2\Pi_{0}}\Pi_{{\textbf{p}}_{2}-{\textbf{p}}_{1}}\sqrt{\sigma_{{\textbf{p}}_{1}}\sigma_{{\textbf{p}}_{2}}}\;.$

In the limit of large vertical background scales, (30) describes the modulation of the background stratification. At $1/2$ the vertical scale of ${\textbf{p}}_{1}$ and ${\textbf{p}}_{2}$, (30) describes a Bragg Scattering process. This is distinct from ’local’ interactions as the large amplitude wave has a much larger horizontal scale.

Let us neglect the local interaction term ${\cal H}_{\rm local}$ in Hamiltonian (LABEL:FourierHam). Then the Hamiltonian (LABEL:FourierHam) of small amplitude small horizontal scale internal waves $a_{\textbf{p}}$ superimposed into a field of large amplitude large horizontal scale internal waves given by space-time-dependent $\Pi$ and $\Phi$ are given by a form that is quadratic in the small-scale variables $a_{{\textbf{p}}}$

	$\displaystyle{\cal H}$	$\displaystyle=$	$\displaystyle\int d{\textbf{p}}_{1}d{\textbf{p}}_{2}A({\textbf{p}}_{1},{\textbf{p}}_{2})a_{{\textbf{p}}_{1}}a^{*}_{{\textbf{p}}_{2}},$		(31)
		$\displaystyle{\rm with}$
	$\displaystyle A({\textbf{p}}_{1},{\textbf{p}}_{2})$	$\displaystyle=$	$\displaystyle\sigma_{\textbf{p}}\delta({\textbf{p}}_{1}-{\textbf{p}}_{2})+A_{\rm sweeping}({\textbf{p}}_{1},{\textbf{p}}_{2})+A_{\rm density}({\textbf{p}}_{1},{\textbf{p}}_{2}),$

where $A_{\rm sweeping}({\textbf{p}}_{1},{\textbf{p}}_{2})$ and $A_{\rm density}({\textbf{p}}_{1},{\textbf{p}}_{2})$ are given in (3.1.2) and (30). The $A({\textbf{p}}_{1},{\textbf{p}}_{2})$ are time dependent and depend upon the phases of the external field.

In the spatially homogeneous wave turbulence of Section 2.2 we used wave action density $n_{\textbf{p}}$ and a linear dispersion relation $\sigma_{\textbf{p}}$, both being a function of a wave number p. In the case when there is a slowly varying large scale background, i.e. a system where spatial inhomogeneity is present, the properties of wave action and the dispersion relation will depend on the position in space. Then it makes sense to introduce an additional parameter, a position vector r in wave action and linear dispersion relation. The theory for this spatial dependence is developed in Gershgorin et al. (2009) using a Gabor transform to represent the envelope structure describing the spatial localization and carrier frequency. The leading order balance in Gershgorin et al. (2009) leads to action and phase conservation along ray paths. The balance on the envelope scale implies phase modulation, for which we direct the reader to the appendix of Cohen and Lee (1990) for clarity. Associated with the envelope structure is a residual circulation Bühler and McIntyre (2005). The potential for the wave packet to interact with its envelope structure is possible Bühler and McIntyre (2005); Dosser and Sutherland (2011) but would require a modification of the uniform potential vorticity statement (6). It is at this stage that one might also want to consider the potential for nonlinear wave steepening effects associated with ${\cal H}_{\rm local}$ to counter the dispersion of ray characteristics as a precursor to the description of solitary wave dynamics.

The familiar statement of action conservation that we are after is obtained in Gershgorin et al. (2009) by assuming the scale of the envelope structure is large in comparison to the inverse wavenumber of the small scale wave, i.e. the wave packet contains many oscillations. The result required here can be obtained more simply by using a Wigner transform alone to define the space-time dependent wave action spectral density:

$\displaystyle n_{{\textbf{p}},{\textbf{r}}}\equiv\int e^{i{\textbf{q}}\cdot{\textbf{r}}}\langle a_{{\textbf{p}}+{\textbf{q}}/2}a_{{\textbf{p}}-{\textbf{q}}/2}^{*}\rangle d{\textbf{q}}\;,$

(32)

in which the transform variable q is a difference between two large wave numbers ${\textbf{p}}_{1}$ and ${\textbf{p}}_{2}$, ${\textbf{q}}={\textbf{p}}_{1}-{\textbf{p}}_{2}$ and the field variables $a$ are evaluated at ${\textbf{p}}\pm{\textbf{q}}/2$. We similarly introduce the space-dependent intrinsic frequency $\omega_{{\textbf{p}},{\textbf{r}}}$

$\displaystyle\omega_{{\textbf{p}},{\textbf{r}}}=\int e^{i{\textbf{r}}\cdot{\textbf{q}}}A({{\textbf{p}}+{\textbf{q}}/2,{\textbf{p}}-{\textbf{q}}/2})d{\textbf{q}},$

(33)

This is a generalization of our “traditional” wave action (14) which allows for slow variations of the background. It will incorporate the large vertical scale contributions of ${\cal H}_{{\rm sweeping}}$ and ${\cal H}_{{\rm density}}$.

To derive the transport equation, we take definition (32), differentiate it with respect to time, use Hamilton’s equation of motion (12), with the Hamiltonian (31). The spatial dependence is then made explicit by representing $A({\textbf{p}}_{1},{\textbf{p}}_{2})$ and $a({\textbf{p}}_{1})a^{\ast}({\textbf{p}}_{2})$ with their corresponding Fourier transforms. After an inspired change of variables (Lvov and Rubenchik, 1977; Gershgorin et al., 2009) that maps the ID portion of the resonant manifold, one obtains an intermediary expression:

$$i\frac{\partial n_{{\textbf{p}},{\textbf{r}}}}{\partial t}=\int\frac{d{\textbf{r}}^{\prime}d{\textbf{r}}^{\prime\prime}}{(2\pi)^{6}}dq^{\prime}dq^{\prime\prime}e^{iq^{\prime}\cdot({\textbf{r}}-{\textbf{r}}^{\prime})+iq^{\prime\prime}\cdot({\textbf{r}}-{\textbf{r}}^{\prime\prime})}\mbox{$\left[\rule{0.0pt}{17.07164pt}\right.$}\omega_{{\textbf{p}}+\frac{q^{\prime\prime}}{2}}({\textbf{r}}^{\prime})n_{{\textbf{p}}-\frac{q^{\prime}}{2}}({\textbf{r}}^{\prime\prime})-\omega_{{\textbf{p}}-\frac{q^{\prime\prime}}{2}}({\textbf{r}}^{\prime})n_{{\textbf{p}}+\frac{q^{\prime}}{2}}({\textbf{r}}^{\prime\prime})\mbox{$\left.\rule{0.0pt}{17.07164pt}\right]$}$$

(34)

After expanding $\omega$ and $n$ in Taylor series with respect to p and truncating higher order terms, one ultimately arrive at the action balance:

	$\displaystyle\frac{\partial n_{{\textbf{p}},{\textbf{r}}}}{\partial t}+\nabla_{\textbf{p}}\sigma_{{\textbf{p}},{\textbf{r}}}\cdot\nabla_{{\textbf{r}}}n_{{\textbf{p}},{\textbf{r}}}-\nabla_{\textbf{r}}\sigma_{{\textbf{p}},{\textbf{r}}}\cdot\nabla_{{\textbf{p}}}n_{{\textbf{p}},{\textbf{r}}}=0,$
			(35)

or alternately

	$\displaystyle\frac{\partial n_{{\textbf{p}},{\textbf{r}}}}{\partial t}+\nabla_{{\textbf{r}}}\cdot\mbox{$\left[\rule{0.0pt}{17.07164pt}\right.$}n_{{\textbf{p}},{\textbf{r}}}\nabla_{{\textbf{p}}}\sigma_{{\textbf{p}},{\textbf{r}}}\mbox{$\left.\rule{0.0pt}{17.07164pt}\right]$}-\nabla_{{\textbf{p}}}\cdot\mbox{$\left[\rule{0.0pt}{17.07164pt}\right.$}n_{{\textbf{p}},{\textbf{r}}}\nabla_{{\textbf{r}}}\sigma_{{\textbf{p}},{\textbf{r}}}\mbox{$\left.\rule{0.0pt}{17.07164pt}\right]$}=0.$
			(36)

Integration of (36) over wavenumber provides a connection to the space-time variational formulations found in Witham (1974), Chapters 11.7 and 14. The Bragg scattering process residing in the scale-separated Hamiltonian (3.1.2) has been eliminated by using the Wigner transform and Taylor series expansion that serendipitously exploits the symmetries associated with the ID resonance.

We now take the expression for $A_{{\textbf{p}}_{1},{\textbf{p}}_{2}}$ from (31) and substitute it into (33) for the space-dependent linear dispersion relation. The result is given by:

$\displaystyle\omega_{{\textbf{p}},{\textbf{r}}}=\sigma_{\textbf{p}}-{\textbf{k}}\cdot{\cal U}({\textbf{r}})+\sigma_{\textbf{p}}\frac{\Pi({\textbf{r}})}{2\Pi_{0}},$

(37)

where ${\textbf{p}}=({\bf k},m)$ is the wavevector, ${\cal U}({\textbf{r}})$ is the time-dependent horizontal velocity of the external large-scale wavefield and $\Pi({\textbf{r}})$ is the time dependent stratification of the external wavefield. Here the $\sigma_{\textbf{p}}$ term was produced by the term proportional to $\delta({\textbf{p}}_{1}-{\textbf{p}}_{2})$, ${\textbf{k}}\cdot{\cal U}$ comes from the sweeping term in the Hamiltonian and $\sigma_{\textbf{p}}\Pi/2\Pi_{0}$ comes from density term in the Hamiltonian. The frequency $\sigma_{\textbf{p}}$ is given by (11) using $f=0$. For a high-frequency wave in a rotating ocean, $\cal{U}$ is replaced by $\nabla\Phi+\nabla^{\perp}\Psi$. The derivation for $f\neq 0$ appears in the Appendix.

The transport equation (35) or its alternative formulation (36) with the space-time dependent linear dispersion relationship (37) is a fundamental result expressing wave action conservation that provides the basis for the analyses to follow.

The action balance (35) can be simply solved by the method of characteristics. The characteristics of (35), also called rays, are defined by

$\displaystyle\dot{\textbf{r}}(t)$

$\displaystyle\equiv$

$\displaystyle\nabla_{\textbf{p}}\sigma_{{\textbf{p}},{\textbf{r}}},\ \ \dot{\textbf{p}}(t)\equiv-\nabla_{\textbf{r}}\sigma_{{\textbf{p}},{\textbf{r}}}\;.$

(38)

Equations (38) imply that wave action spectral density is conserved along these characteristics:

$\displaystyle\frac{\partial n_{{\textbf{p}},{\textbf{r}}}}{\partial t}+\dot{\textbf{r}}\cdot\nabla_{{\textbf{r}}}n_{{\textbf{p}},{\textbf{r}}}+\dot{\textbf{p}}\cdot\nabla_{{\textbf{p}}}n_{{\textbf{p}},{\textbf{r}}}=0.$

(39)

This is the classical representation for the conservation of action spectral density along ray trajectories. A derivation for a general Hamiltonian set is presented in Gershgorin et al. (2009), here the derivation is specifically for internal waves in the scale separated limit. Integration over wavenumber provides the space-time result presented in Witham (1974). This result often appears as an analogy to Louiville’s theorem for the conservation of the phase volume of particles without justification. Note that it is the balance of first-order terms in a Taylor series expansion of (34).

In what follows we derive a combined advective-diffusive transport equation for the action balance (35) by generalizing an approach found in Nazarenko et al. (2001). There are strong parallels here to the discussion of Taylor (1921) that appear in the appendix of McComas and Bretherton (1977): The illuminating analogy with particle dispersion in Taylor (1921) is to substitute wavenumber p for the Lagrangian particle position r and obtain a quantitative approach for discussing the migration and dispersion of wave packets in the spectral domain following ray trajectories. Having said this, it should be intuitively obvious that, since particle dispersion in r has little to do with resonance, neither should the issue of dispersion of p in phase space be intrinsically tied to resonance! Yet, an emphasis on the resonant paradigm is the interpretive context pursued in (McComas and Bretherton, 1977; Nazarenko et al., 2001). A second key departure is that our motivation stems from the fact that the GM76 spectrum is a no-flux solution to the Fokker-Planck equation (20). We acknowledge the oceanographic literature in this regard and so are focused upon the issue of a mean drift of wave packets to high wavenumber that is accessible in ray-tracing simulations (e.g. Henyey et al., 1986) but not explicitly represented in (20). To underscore the distinction, the existence of a mean drift implies relative dispersion (e.g. Bennett (1984)) rather than the issue of absolute dispersion addressed in Taylor (1921).

The very first step in our derivation is to specify a wave-packet ensemble mean drift and departures from the mean drift. This decomposition is an improvement on the arguments presented in McComas and Bretherton (1977) and Nazarenko et al. (2001). Our limited knowledge of the ray literature does not permit us from commenting on the originality of our interpretation. It is, however, crucial in understanding intrinsic differences between the kinetic equation and ray theory. Given the nature of our understanding, the issue assuredly carries over to other physical problems such as the interaction of near-inertial waves with lower frequency flows, (e.g. Young and Jelloul, 1997; Kafiabad et al., 2019; Dong et al., 2020) surface gravity wave interaction with lower frequency flows (Villas Boas and Young, 2020) and Rossby wave - Rossby wave interactions Nazarenko (2011).

We represent the wave action of a single wave packet as a sum of a spatially homogeneous part $\overline{n}$ and small “wiggles” $\tilde{n}$:

$\displaystyle n_{{\textbf{p}},{\textbf{r}}}=\overline{n}_{\textbf{p}}+\tilde{n}_{{\textbf{p}},{\textbf{r}}};\ \ \ n_{\textbf{p}}=\int d{\textbf{r}}\;n_{{\textbf{p}},{\textbf{r}}};\ \ \ \int d{\textbf{r}}\;\tilde{n}_{{\textbf{p}},{\textbf{r}}}=0,$

(40)

and acknowledge the presence of a mean drift in the spectral domain by adding zero:

$\displaystyle\dot{{\textbf{p}}}=\dot{{\textbf{p}}}-\langle\dot{{\textbf{p}}}\rangle+\langle\dot{{\textbf{p}}}\rangle\;,$

(41)

in which $\langle\dots\rangle$ is an ensemble average for a system with spatially homogenous statistics, so that $\langle\dots\rangle$ is independent of r. The mean drift arises due to inhomogeneities of the ray path statistics in the spectral domain. Please note that the dimensions of $\overline{n}_{\textbf{p}}$ and $n_{{\textbf{p}}}$ are different.

Starting from the flux form of the action balance (36), we substitute (40), (41), invoke an ensemble average and integrate over r to obtain

$\displaystyle\frac{\partial\langle n_{{\textbf{p}}}\rangle}{\partial t}=-\int d{\textbf{r}}\langle\nabla_{\textbf{p}}\cdot[\dot{{\textbf{p}}}-\langle\dot{{\textbf{p}}}\rangle]n_{{\textbf{p}},{\textbf{r}}}\rangle-\nabla_{\textbf{p}}\cdot[\langle\dot{{\textbf{p}}}\rangle\langle n_{{\textbf{p}}}\rangle].$

(42)

Closure of this equation depends upon writing $n_{{\textbf{p}},{\textbf{r}}}$ in terms of $n_{{\textbf{p}}}$. At this juncture, we invoke that property that wave action spectral density does not change along trajectories:

	$\displaystyle n_{{\textbf{p}},{\textbf{r}}}\equiv n({\textbf{p}}(t),{\textbf{r}}(t),t)=n({\textbf{p}}(t-T),{\textbf{r}}(t-T),t-T)$
	$\displaystyle=\overline{n}\Big{[}{\textbf{p}}(t)-\int\limits_{t-T}^{t}\dot{p}(t^{\prime})dt^{\prime};\;t-T\Big{]}+\tilde{n}\Big{[}{\textbf{p}}(t)-\int\limits_{t-T}^{t}\dot{p}(t^{\prime})dt^{\prime};\;{\textbf{r}}(t)-\int\limits_{t-\tau}^{t}\dot{\textbf{r}}(t^{\prime})dt^{\prime};\;t-T\Big{]}$

We then execute a Taylor series expansion of $\overline{n}$,

	$\displaystyle n({\textbf{p}}(t-\tau),{\textbf{r}}(t-\tau),t-\tau)\simeq\overline{n}({\textbf{p}}(t);\;t-T)-\nabla_{p}\overline{n}({\textbf{p}}(t);\;t-T)\cdot\int\limits_{t-T}^{t}\dot{{\textbf{p}}}(t^{\prime})dt^{\prime}+\tilde{n}(\dots)\;,$
			(44)

substitute, add zero once again, and using the definition of ensemble averaging $\langle\dots\rangle$

$\displaystyle\Big{\langle}\nabla_{{\textbf{p}}}[\dot{{\textbf{p}}}-\big{\langle}\dot{{\textbf{p}}}\big{\rangle}]\overline{n}({\textbf{p}}(t),t-\tau)\Big{\rangle}$

$\displaystyle\cong$

$\displaystyle\nabla_{{\textbf{p}}}\big{\langle}\dot{{\textbf{p}}}-\big{\langle}\dot{{\textbf{p}}}\big{\rangle}\big{\rangle}\big{\langle}\overline{n}({\textbf{p}}(t),t-\tau)\rangle=0$

and

	$\displaystyle\Big{\langle}\nabla_{{\textbf{p}}}[\dot{{\textbf{p}}}-\big{\langle}\dot{{\textbf{p}}}\big{\rangle}]\int\limits_{t-\tau}^{t}\big{\langle}\dot{{\textbf{p}}}\big{\rangle}dt^{\prime}\cdot\nabla_{{\textbf{p}}}\overline{n}({\textbf{p}}(t),t-\tau)\Big{\rangle}$	$\displaystyle\cong$	$\displaystyle\nabla_{{\textbf{p}}}\big{\langle}\dot{{\textbf{p}}}-\big{\langle}\dot{{\textbf{p}}}\big{\rangle}\big{\rangle}\int\limits_{t-\tau}^{t}\big{\langle}\dot{{\textbf{p}}}\big{\rangle}dt^{\prime}\cdot\nabla_{{\textbf{p}}}\big{\langle}\overline{n}({\textbf{p}}(t),t-\tau)\big{\rangle}$		(45)
		$\displaystyle=$	$\displaystyle 0$

as $\langle\dot{{\textbf{p}}}-\langle\dot{{\textbf{p}}}\rangle\rangle\equiv 0$ and neglect an initial transient term

$\displaystyle\langle\nabla_{{\textbf{p}}}[\dot{{\textbf{p}}}(t)-\langle\dot{{\textbf{p}}}\rangle]\tilde{n}({\textbf{p}}(t-\tau),{\textbf{r}}(t-\tau),t-\tau)\rangle$

(46)

so that (42) becomes

$\displaystyle\frac{\partial\langle n_{{\textbf{p}}}\rangle}{\partial t}=-\nabla_{\textbf{p}}\cdot\int\limits_{t-\tau}^{t}\langle[\dot{{\textbf{p}}}(t)-\langle\dot{{\textbf{p}}}\rangle][\dot{{\textbf{p}}}(t^{\prime}-\tau)-\langle\dot{{\textbf{p}}}\rangle]\rangle dt^{\prime}\nabla_{\textbf{p}}\langle n_{{\textbf{p}}}\rangle-\nabla_{\textbf{p}}\langle\dot{{\textbf{p}}}\rangle\langle n_{{\textbf{p}}}\rangle,$

(47)

We introduce the auto-lag covariance matrix

$\displaystyle{\cal C}_{ij}({\textbf{p}},t,t^{\prime})=\Big{\langle}\Big{[}\dot{\textbf{p}}({\textbf{r}}(t))-\langle\dot{\textbf{p}}({\textbf{r}}(t))\rangle\Big{]}_{i}\Big{[}\dot{\textbf{p}}({\textbf{r}}(t^{\prime}))-\langle\dot{\textbf{p}}({\textbf{r}}(t^{\prime}))\rangle\Big{]}_{j}\Big{\rangle}.$

(48)

The final result is then

$\displaystyle\frac{\partial\langle n_{{\textbf{p}}}\rangle}{\partial t}=-\nabla_{{\textbf{p}}_{i}}\cdot\int\limits^{t}_{t-\tau}{\cal C}_{ij}({\textbf{p}},t,t^{\prime})dt^{\prime}\cdot\nabla_{{\textbf{p}}_{j}}\langle n_{\textbf{p}}\rangle\;\;-\;\;\nabla_{{\textbf{p}}_{i}}\langle\dot{\textbf{p}}_{i}\rangle\langle n_{\textbf{p}}\rangle.$

(49)