Generalized Ribaucour-type surfaces
Abstract
In this work we generalize the surfaces studied in [8], we define the generalization of Ribaucour-type surfaces (in short, GRT-surfaces). We obtain present a representation for GRT-surfaces with prescribed Gauss map which depends on two holomorphic functions and a real function . We give explicit examples of GRT-surfaces. Also, we use this representation to classify the GRT-surfaces of rotation.
Keywords.
Generalitation of Ribaucour-type surfaces, generalized Weingarten surfaces, prescribed normal Gauss map.
Introduction: Let be an oriented surface with normal Gauss map , functions given by and , , where denotes the Euclidean scalar product in , are called support function and quadratic distance function, respectively. Geometrically, measures the signed distance from the origin to and measures the squared distance from the origin to . Let , a sphere with center and radius is called the middle sphere.
In 1888, Appell [5] studied a class of surfaces oriented in associated with area-preserving sphere transformations. Later, Ferreira and Roitman [3] showed that these surfaces satisfy the Weingarten relation, .
In 1907, Tzitzeica [9] studied hyperbolic surfaces oriented so that there is a nonzero constant for which .
In [1], the authors motivated by the works [5] and [9] defined generalized Weingarten surfaces as surfaces that satisfy a relation of the form , where are differentiable functions that do not depend on the parameterization of . In particular, they studied the class of surfaces that satisfy the relation . Called Special Generalized Weingartem Surfaces depending on the support function and the distance function (in short, EDSGW-surfaces), these surfaces have the geometric property that all medium spheres pass through the origin. The authors obtained a Weierstrass-like representation of EDSGW-surfaces depending on two homomorphic functions. In [6], the authors classified isothermic EDSGW-surfaces in relation to the third fundamental shape parameterized by plane curvature lines. Also in [4], it is shown that EDSGW-surfaces are in correspondence with the surface class in where the Gaussian curvature and the extrinsic curvature satisfy .
Martínez and Roitman, in [2] showed what appears to be the first example found for the second case of the problem posed by Élie Cartan in his classic book about external differential systems and their applications to Differential Geometry. Such examples are given by a class of Weingarten surfaces that satisfy the relation , Ribaucour surface calls, these surfaces have the geometric property that all the medial spheres intercept a fixed sphere along a large circle.
In [10], the authors define a surface class called Ribaucour surface of harmonic type (in short, HR-surface) if it satisfies , where is a nonzero real constant, a harmonic function with respect to the third fundamental form. These surfaces generalize Ribaucour surfaces studied in [2].
Motivated by [8], we define be a surface with Gauss map is called a surface of type Ribaucour generalized or abbreviated GRT-Surface. There is a harmonic map with respect to the third fundamental form and a function such that for all the sphere with center and radius , tangents a fixed sphere. In this case satisfies the following relation generalized Weingarten
We obtain present a representation for GRT-surfaces with prescribed Gauss map which depends on two holomorphic functions and a real function . We give explicit examples of GRT-surfaces. Also, we use this representation to classify the GRT-surfaces of rotation.
1 Preliminaries
In this section we fix the notation used in this work, a surface on , its normal Gaussian map, and an open subset of .
Let , a parameterization of a surface and , normal Gaussian map. Considering as a base of , where , further we can write vector , , as
The coefficients are called Christoffel symbols.
Definition 1.1.
Let be a local parameterization of with map of Gauss , matrix , such that
is called the Weingarten matrix of .
Lemma 1.2.
Let be the normal Gaussian map given by (2) such that the metric is Euclidean conformal. Christoffel’s symbols for metric are given by
For e different.
Remark.
Let the inner product be defined by , where and are holomorphic functions. If are holomorphic functions, then
| (1) |
where
Below we present some important results studied in [8].
Theorem 1.3.
Let , an orientable surface with non-zero Gauss-Kronecker curvature. Then there is a differentiable function and a holomorphic function such that normal Gauss map is given by
| (2) |
the coefficients of the fundamental form are
| (3) |
is locally parameterized by
| (4) |
In this case is the support function. Furthermore, the Weingarten matrix is given by where
where are Christoffel’s symbols of and the fundamental forms and of , in local coordinates, are given by
furthermore,
| (5) |
| (6) |
called quadratic distance function and support function, respectively.
2 GRT-surfaces
In this chapter, we introduce a few classes of surfaces called surfaces. of generalized Ribaucour type and we call it GRT-surfaces, we show a local parameterization of this class of surfaces and characterize the case where such surfaces are rotating.
Definition 2.1.
Let be a surface with Gauss map is called a surface of type Ribaucour generalized or abbreviated GRT-Surface. There is a harmonic map with respect to the third fundamental form and a function such that for all the sphere with center and radius , tangents a fixed sphere. In this case satisfies the following relation generalized Weingarten
| (7) |
Remark.
Lemma 2.2.
Consider holomorphic functions and , with , where is a Riemann surface. Taking the local parameters and such that , the matrix
Using the metric given by (3), we have
| (8) |
Here , furthermore, trace of give for
Proof.
Let , the derivatives of are given by:
Using the previous expressions and (1) we have
where . Similarly, knowing that , we obtain
It is
So we can write
Thus,
therefore,
∎
Theorem 2.3.
Let be given by (4), and , harmonic with respect to third fundamental form then is a TRG-surface if and only if
| (9) |
Proof.
The following theorem allows to obtain a class of GRT-surfaces.
Theorem 2.4.
Let be a Riemann surface and be an immersion such that the Gauss-kronecker curvature is non-zero. Let and , with a holomorphic function and . Then is given by (4) and is a TRG-surface with , where . Furthermore, let be a holomorphic function and , then is locally parameterized by
| (11) |
with .
Proof.
Let where be a real function and , in this case we have,
Substituting the above derivatives in (9) we have the following equivalence
The following examples are GRT-surfaces for some holomorphic functions and with , using (11) we have






The following results will be used to classify the GRT-surfaces given by (11).
Lemma 2.5.
Proof.
If is rotational, without loss of generality, we can assume that the axis of rotation is the axis. This way, the sections orthogonal to the axis of rotation determine in spheres dimensional centered on this axis. Note that along these spheres both and the angle between and are constant. Given that
We conclude that and are constant along these spheres. Taking as the inverse of the stereographic projection we get,
so that,
which says that is constant as one traverses the orthogonal sections, therefore is constant along the spheres dimensional centered at the origin, therefore is a function radial.
Let be a radial function, we write , for a differentiable function. Let and denote the derivative of with respect to as . Thus, and taking as the inverse of the stereographic projection we have,
If is constant then
Which means that the sections orthogonal to the axis determine in spheres dimensional centered on this axis, so that is of rotation . ∎
Theorem 2.6.
Let be a GRT-surface given by (11), connected, where is a real function and . Then is rotational if and only if, there are constants , such that can be locally parameterized by
and
Proof.
From Theorem 2.4, we have that is locally parameterized by
where are holomorphic functions, is not constant and remembering that , and . The Cauchy-Riemann equations guarantee us that , with , thus Thus, by the lemma 2.5 we have that is rotational if and only if
so that , and . In this conditions,
follow or result. ∎
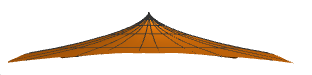
The following figures are examples of rotating GRT-surfaces for some functions and constants and .
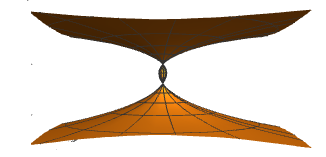
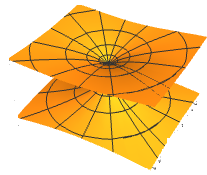

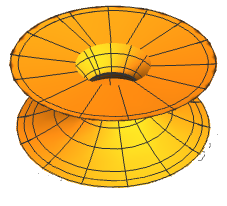
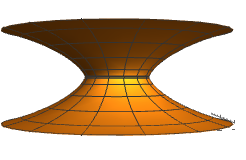

Bibliografía
- [1] A.V. Corro, D.G. Dias, Classes of generalized Weingarten surfaces in the Euclidean 3-space,Adv.Geom. 2016;16(1)45–55
- [2] A. Martinez, P. Roitman, A class of surfaces related to a problem posed by Élie Cartan, Ann.Mat. Pura Appl,195,513–527
- [3] W. Ferreira, P. Roitman, Area preserving transformations in twodimensional space forms and classical differential geometry, Israel J.Mat,190,325–348
- [4] A.V. Corro, R. Pina, M. Souza, Classes of Weingarten surfaces in , HOUSTON JOURNAL OF MATHEMATICS, v. 46, p. 651-664, 2020.
- [5] P. Appell,, Surfaces telles que lórigine se projette sur chaque normale au milieu des centres de courbure principaux., Amer. J. Math. 10(1888),175–186. MR1505475 JFM 19.0825.01
- [6] A.V. Corro, C.M. Riveros, D.G. Dias, A class of generalized special Weingarten surfaces, International Journal of Mathematics Vol. 30, No. 14 (2019) 1950075
- [7] A.V. Corro, K. Tenenblat, Ribaucour transformations revisited., Comm. Anal. Geom. 12(2004), 1055–1082. MR2103311 (2005j:53063) Zbl 1090.53055
- [8] A.V. Corro, M.J.C. Mendez, Ribaucour-type Surfaces, arXiv:2012.02132 [math.DG].
- [9] G. Tzitzéica, Sur une nouvelle classe de surfaces., Rend. Circ. Mat. Palermo 25 (1908), 180–187. JFM 39.0685.05
- [10] A.V. Corro, C.M. Riveros, K. Fernandes Ribaucour surfaces of harmonic type International Journal of Mathematics Vol. 33, No. 1 (2022) 2250006