Generalized Laplacian Regularized Framelet Graph Neural Networks
Abstract
Graph neural networks (GNNs) have achieved remarkable results for various graph learning tasks. However, one of the recent challenges for GNNs is to adapt to different types of graph inputs, such as heterophilic graph datasets in which linked nodes are more likely to contain a different class of labels and features. Accordingly, an ideal GNN model should adaptively accommodate all types of graph datasets with different labeling distributions. In this paper, we tackle this challenge by proposing a regularization framework on graph framelet with the regularizer induced from graph -Laplacian. By adjusting the value of , the -Laplacian based regularizer restricts the solution space of graph framelet into the desirable region based on the graph homophilic features. We propose an algorithm to effectively solve a more generalized regularization problem and prove that the algorithm imposes a (-Laplacian based) spectral convolution and diagonal scaling operation to the framelet filtered node features. Furthermore, we analyze the denoising power of the proposed model and compare it with the predefined framelet denoising regularizer. Finally, we conduct empirical studies to show the prediction power of the proposed model in both homophily undirect and heterophily direct graphs with and without noises. Our proposed model shows significant improvements compared to multiple baselines, and this suggests the effectiveness of combining graph framelet and -Laplacian.
Highlight
-
•
We define two types of new GNN layers by introducing -Laplacian regularizers to both decomposed and reconstructed framelets.
-
•
We provide an iterative algorithm to fit the proposed models and explore an alternative algorithm developed from the F-norm Locality Preserving Projection (LPP).
-
•
We prove that our algorithm provides a sequence of spectral graph convolutions and diagonal scaling over framelet-filtered graph signals and this further explains the interaction between -Laplacian regularizer and framelet.
-
•
We link the proposed -Laplacian regularizer with the previous work of framelet regularizer to illustrate the denoising power of our model.
-
•
We test the model on homophilic (undirected) and heterophilic (directed) graphs. To our best knowledge, we are the first to explore the possibility of applying the framelet GCN for directed graphs
1 Introduction
Graph neural networks (GNNs) have demonstrated remarkable ability for graph learning tasks (Bronstein et al, 2017; Wu et al, 2020; Zhang et al, 2022; Zhou et al, 2020). The input to GNNs is the so-called graph data which records useful features and structural information among data. Such data are widely seen in many fields, such as biomedical science (Ahmedt-Aristizabal et al, 2021), social networks (Fan et al, 2019), and recommend systems (Wu et al, 2022). GNN models can be broadly categorized into spectral and spatial methods. The spatial methods such as MPNN (Gilmer et al, 2017), GAT (Veličković et al, 2018) and GIN (Xu et al, 2018a) utilize the message passing mechanism to propagate node feature information based on their neighbours (Scarselli et al, 2009). On the other hand, the spectral methods including ChebyNet (Defferrard et al, 2016), GCN (Kipf and Welling, 2017) and BernNet (He et al, 2021) are derived from the classic convolutional networks, treating the input graph data as signals (i.e., a function with the domain of graph nodes) (Ortega et al, 2018), and filtering signals in the Fourier domain (Bruna et al, 2014; Defferrard et al, 2016). Among various spectral-based GNNs, the graph framelets GCN (Zheng et al, 2022), which is constructed on a type of wavelet frame analogized from the identical concept defined on manifold (Dong, 2017), further separates the input signal by predefined low-pass and high-pass filtering functions and resulting a convolution-type model as in the studies (Chen et al, 2022a; Zheng et al, 2021b, 2022). The graph framelet shows great flexibility in terms of controlling both low and high-frequency information with robustness to noise and thus in general possesses high prediction power in multiple graph learning tasks (Chen et al, 2022a; Yang et al, 2022; Zheng et al, 2021b; Zhou et al, 2021a, b; Zou et al, 2022).
Along with the path of developing more advanced models, one of the major challenges in GNN is identified from the aspect of data consistency. For example, many GNN models (Xu et al, 2018a; Wu et al, 2020; Zhu et al, 2020b; Wu et al, 2021; Liu et al, 2022) are designed based on the homophily assumption i.e., nodes with similar features or labels are often linked with each other. Such phenomenon can be commonly observed in citation networks (Ciotti et al, 2016) which have been widely used as benchmarks in GNNs empirical studies. However, the homophily assumption may not always hold, and its opposite, i.e. Heterophily, can be observed quite often in many real-world datasets in which the linked nodes are more likely to contain different class labels and features (Zheng et al, 2021a). For example, in online transaction networks, fraudsters are more likely to link to customers instead of other fraudsters (Pandit et al, 2007). The GNNs designed under homophilic assumption are deemed unsuitable for heterophilic graphs. It is evident from their significant performance degradation (Zheng et al, 2021a). The reason is that the class of heterophilic graphs contains heterogeneous instances and hence the signals should be sharpened rather than smoothed out. An ideal framework for learning on graphs should be able to accommodate both homophilic and heterophilic scenarios.
One of the active aspects to resolve the GNN adaption challenge is by regularizing the solution of GNNs via the perspective of optimization. The work done by Zhu et al (2021) unified most of state-of-the-art GNNs as an optimization framework. Furthermore, one of the recent works (Fu et al, 2022) considered assigning an adjustable -Laplacian regularizer to the (discrete) graph regularization problem that is conventionally treated as a way of producing GNN outcomes (i.e., Laplacian smoothing). In view of the fact that the classic graph Laplacian regularizer measures the graph signal energy along edges under metric, it would be beneficial if GNN could be adapted to heterophilic graphs under metric (). Given that metric is more robust to high-frequency signals, a higher model discriminative power is preserved. The early work (Hu et al, 2018) has demonstrated the advantage of adopting metric in the Locality Preserving Projection (LPP) model. In addition, the recently proposed -Laplacian GNN (Fu et al, 2022) adaptively modifies aggregation weights by exploiting the variance of node embeddings on edges measured by the graph gradient. With a further investigation on the application of -Laplacian, Luo et al (2010) suggested an efficient gradient descent optimization strategy to construct the -Laplacian embedding space that guarantees convergence to viable local solutions. Although the -Laplacian based optimization scheme has been successfully lodged in basic GNN model (Fu et al, 2022), whether it can be further incorporated with more advanced GNN model (i.e., graph framelets) with higher prediction power and flexibility is still unclear. Specifically, one may be interested in identifying whether the advantage of deploying -Laplacian in GNN still remains in graph framelet or what is the exact functionality of -Laplacian interacting with the feature representations generated both low and high pass framelet domains. In addition, as graph framelets have shown great potential in terms of the graph noise reduction (Zheng et al, 2022; Yang et al, 2022; Zou et al, 2022), whether the inclusion of -Laplacian regularizer could enhance/dilute such power remains unclear. These research gaps inspire us to incorporate -Laplacian into graph framelets and explore further for the underlying relationship between them.
Since the -Laplacian regularized optimization problem lacks a closed-form solution, except for when (Zhou and Schölkopf, 2005), an iterative algorithm is suggested to estimate the solution and each iteration can be analogized to a GNN layer (Zhou et al, 2021a)). The solution of such an algorithm is defined by the first-order condition of the optimization problem. As a result, one can relate this to the implicit layer approach (Chen et al, 2022b; Zhang et al, 2003) which has the potential of avoiding over-smoothing issues since the adjusted node feature will be re-injected in each iteration step. By adjusting the value of , both -Laplacian GNN and the algorithm are capable of producing learning outcomes with different discriminative levels and thus able to handle both homophilic and heterophilic graphs. Similar work has been done by Frecon et al (2022) which presents a framework based on the Bregman layer to fulfill the bi-level optimization formulations. To reap the benefit of -Laplacian regularization in the framelet domain, in this paper, we propose two -Laplacian Regularized Framelet GCN models which are named -Laplacian Undecimated Framelet GCN (pL-UFG) and -Laplacian Fourier Undecimated Framelet GCN (pL-fUFG). In these models, the -Laplacian regularization can be applied on either the framelet domain or the well-known framelet Fourier domain. The -Laplacian-based regularizer incurs a penalty to both low and high-frequency domains created by framelet, producing flexible models that are capable of adapting different types of graph inputs (i.e., homophily and heterophily, direct and undirect). We summarize our contributions as follows:
-
•
We define two types of new GNN layers by introducing -Laplacian regularizers to both decomposed and reconstructed framelets. This paves the way for introducing more general Bregman divergence regularization in the graph framelet framework;
-
•
We propose an iterative algorithm to fit the proposed models and explore an alternative algorithm developed from the F-norm LPP;
-
•
We prove that the iteration of the proposed algorithm provides a sequence of spectral graph convolutions and diagonal scaling over framelet-filtered graph signals, this gives an deeper explanation of how -Laplacian regularizer interacts with the framelet.
-
•
We connect the proposed -Laplacian regularizer to the previously studied framelet regularizer to illustrate the denoising power of the proposed model.
-
•
We investigate the performance of the new models on graph learning tasks for both homophilic (undirected) graphs and heterophilic (directed) graphs. To our best knowledge, we are the first to explore the possibility of applying the framelet GCN for directed graphs. The experiment results demonstrate the effectiveness of pL-UFG and pL-fUFG on real-world node classification tasks with strong robustness.
The rest of the paper is organized as follows. In Section 2, we introduce the -Laplacian operator and regularized GNN, followed by a review of recent studies on regularized graph neural networks, which include implicit layers and graph homophily. In Section 3, we introduce the fundamental properties of graph framelet and propose the -Laplacian regularized framelet models. Furthermore, we develop an algorithm to solve the regularization problem that is more general than -Laplacian regularization. We also provide theoretical analysis to show how the -Laplacian based regularizer interacts with the graph framelet. By the end of Section 3 a brief discussion on the denoising power of the proposed model is presented. Lastly, we present the experimental results and analysis in Section 5. Finally, this paper is concluded in Section 6.
2 Preliminaries
This section provides an in-depth exploration of the fundamental concepts, encompassing graphs, graph framelets, and regularized graph neural networks. For the sake of reader comprehension and ease of following the intended ideas, each newly introduced model and definition will be accompanied by a succinct review of its developmental history.
2.1 Basic Notations
Let denote a weighted graph, where and represent the node set and the edge set, respectively. is the feature matrix for with as its rows, and is the weight matrix on edges with if and otherwise. For undirected graphs, we have which means that is a symmetric matrix. For directed graphs, it is likely that which means that may not be a symmetric matrix. In most cases, the weight matrix is the graph adjacency matrix, i.e., with elements if and otherwise. Furthermore, let denote the set of neighbours of node and denote the diagonal degree matrix with for . The normalized graph Laplacian is defined as . Lastly, for any vector , we use to denote its L2-norm, and similarly for any matrix , is used to denote its Frobenius norm.
2.2 Consistency in Graphs
Generally speaking, most GNN frameworks are designed under the homophily assumption in which the labels of nodes and neighbours in the graph are mostly identical. The recent work by Zhu et al (2020a) emphasises that the general topology GNN fails to obtain outstanding results on the graphs with different class labels and dissimilar features in their connected nodes, which we call heterophilic or low homophilic graphs. The definition of homophilic and heterophilic graphs are given by:
Definition 2.1 (Homophily and Heterophily (Fu et al, 2022)).
The homophily or heterophily of a network is used to define the relationship between labels of connected nodes. The level of homophily of a graph can be measured by , where denotes the number of neighbours of that share the same label as such that . corresponds to strong homophily while indicates strong heterophily. We say that a graph is a homophilic (heterophilic) graph if it has strong homophily (heterophily).
2.3 -Laplacian Operator
The first paper that explores the notation of graph -Laplacian and utilizes it in the regularization problem in graph structure data can be traced back to the work (Zhou and Schölkopf, 2005), in which the regularization scheme was further explored to build a flexible GNN learning model in the study (Fu et al, 2022). In this paper, we refer to the notation similar to the one used in the paper (Fu et al, 2022) to define the graph -Laplacian operator. We first define the graph gradient as follows:
Definition 2.2 (Graph Gradient).
Let and be the function space on nodes and edges, respectively. Given a graph and a function , the graph gradient is an operator : defined as for all ,
where and are the signal vectors on nodes and , i.e., the rows of .
Without confusion, we will simply denote as for convenience. For , . The graph gradient of at a vertex , , is defined as and its Frobenius norm is given by which measures the variation of around node . Note that we have two explanations for the notation : one as a graph gradient (over edges) and one as node gradient (over nodes). The meaning can be inferred from its context in the rest of the paper. We also provide the definition of graph divergence, analogous to the Laplacian operator in continuous setting, which is the divergence of the gradient of a continuous function.
Definition 2.3 (Graph Divergence).
Given a graph and a function , , the graph divergence is an operator which satisfies:
| (1) |
Furthermore, the graph divergence can be computed by:
| (2) |
Given the above definitions on graph gradient and divergence, we reach the definition of the graph -Laplacian.
Definition 2.4 (-Laplacian operator (Fu et al, 2022)).
Given a graph and a multiple channel signal function , the graph -Laplacian is an operator , defined by:
| (3) |
where is element-wise power over the node gradient .
Remark 1.
Clearly, when we have , Eq. (3) recovers the classic graph Laplacian. When , we can analogize Eq. (3) as a curvature operator defined on the nodes of the graph, because when , we have Eq. (3) as . This aligns with the definition of mean curvature operator defined on the continuous domain. Furthermore, we note that the -Laplacian operator is linear when , while in general for , the -Laplacian is a non-linear operator since .
Definition 2.5 (-eigenvector and -eigenvalue).
Let for . With some abuse of the notation, we call () a -eigenvector of if where is the associated -eigenvalue.
Note that in above definition, we use the fact that acting on all nodes gives a vector in . Let for . One (Fu et al, 2022) can show that -Laplacian can be decomposed as for some diagonal matrix .
2.4 Graph Framelets
Framelet is a type of wavelet frame. The study by Sweldens (1998) is the first to present a wavelet with a lifting scheme that provides a foundation in the research of wavelet transform on graphs. With the increase of computational power, Hammond et al (2011) proposed a framework for the wavelet transformation on graphs and employed Chebyshev polynomials to make approximations on wavelets. Dong (2017) further developed tight framelets on graphs. The new design has been applied for graph learning tasks (Zheng et al, 2021b) with great performance enhancement against the classic GNNs. The recent studies show that framelet can naturally decompose the graph signal and re-aggregate them effectively, achieving a significant result on graph noise reduction (Zhou et al, 2021a) with the use of a double term regularizer on the framelet coefficients. Combing with singular value decomposition (SVD), the framelets have been made applicable to directed graphs (Zou et al, 2022).
A simple method of building more versatile and stable framelet families was suggested by Yang et al (2022) which is known as Quasi-Framelets. In this study, we will introduce graph framelets using the same architecture described in the paper (Yang et al, 2022). We begin by defining the filtering functions for Quasi-Framelets:
Definition 2.6 (Filtering functions for Quasi-Framelets).
We call a set of positive filtering functions defined on , , Quasi-Framelet scaling functions if the following identity condition is satisfied:
| (4) |
such that descends from 1 to 0 and ascends from 0 to 1 as frequency increases over the spectral domain .
Particularly aims to regulate the highest frequency while to regulate the lowest frequency, and the rest to regulate other frequencies in between.
Consider a graph with its normalized graph Laplacian . Let have the eigen-decomposition where is the orthogonal spectral bases with its spectra in increasing order. For a given set of Quasi-Framelet functions defined on and a given level (), define the following Quasi-Framelet signal transformation matrices
| (5) | ||||
| (6) | ||||
| (7) | ||||
Note that in the above definition, is called the coarsest scale level which is the smallest satisfying . Denote by as the stacked matrix. It can be proved that , thus providing a signal decomposition and reconstruction process based on . We call this graph Framelet transformation.
In order to alleviate the computational cost imposed by eigendecomposition for the graph Laplacians, the framelet transformation matrices can be approximated by Chebyshev polynomials. Empirically, the implementation of the Chebyshev polynomials with a fixed degree , is sufficient to approximate . In the sequel, we will simplify the notation by using instead of . Then the Quasi-Framelet transformation matrices are defined in Eqs. (6) - (7) can be approximated by,
| (8) | ||||
| (9) | ||||
| (10) | ||||
Remark 1: The approximated transformation matrices defined in Eqs. (8)-(10) simply depend on the graph Laplacian. For directed graphs, we directly take in the Laplacian normalized by the out degrees in our experiments. We observe this strategy leads to improved performance in general.
For a graph signal , the framelet (graph) convolution similar to the spectral graph convolution that can be defined as
| (11) |
where is the learnable network filter. We also call the framelet coefficients of in Fourier domain. The signal then will be filtered in its spectral-domain according to learnable filter .
2.5 Regularized Graph Neural Network
In reality, graph data normally have large, noisy and complex structures (Leskovec and Faloutsos, 2006; He and Kempe, 2015). This brings the challenge of choosing a suitable neural network for fitting the data. It is well known that one of the common computational issues for most classic GNNs is over-smoothing which can be quantified by Dirichlet energy that converges to zero as the number of layers increases. This observation leads to an investigation into the so-called implicit layers on regularized graph neural networks.
The first paper to consider GNNs layer as a regularized signal smoothing process is done by Zhu et al (2021), in which the classic GNN layers are interpreted as the solution of the regularized optimization problem, with certain approximation strategies to avoid matrix inversion in the closed-form solution. The regularized layer also can be linked to the implicit layer (Zhang et al, 2003), more specific examples are given by Zhu et al (2021). In general, given the node features, the output of the GNN layer can be written as the solution for the following optimization problem
| (12) |
where is the graph signal. Eq. (12) defines the layer output as the solution for the (layer) optimization problem with a regularization term , which is able to enforce smoothness of a graph signal. The closed form solution is given by . It is computationally inefficient because of matrix inversion. However, we can rearrange it to and interpret it as a fixed point solution to . The latter is then the implicit layer in GNN at layer . Such an iteration is motivated by the recurrent GNNs as shown in several recent works (Gu et al, 2020; Liu et al, 2021a; Park et al, 2021). Different from explicit GNNs, the output features of a general implicit GNN are directly modeled as the solution of a well defined implicit function, e.g., the first order condition from an optimization problem. Denote the rows of by () in column shape. It is well known that the regularization term (12) is
which is the so-called graph Dirichlet energy (Zhou and Schölkopf, 2005). As proposed in the work (Zhou and Schölkopf, 2005), one can replace the graph Laplacian matrix in the above equation to the pre-defined graph -Laplacian, then the -Laplacian based energy denoted as can be defined as (for any ):
| (13) |
where we adopt the definition of element-wise -norm as in paper (Fu et al, 2022). Finally, the regularization problem becomes
| (14) |
With strong generalizability of the regularization form in Eq. (14), it is natural to consider to deploy Eq. 14 to multi-scale graph neural networks (i.e., graph framelets) to explore whether the benefits of allocating -Laplacian based regularizer still remains and how the changes of within included regularizer interacts with the feature propagation process via each individual filtered domains. In the next section, we will accordingly proposed our model and provide detailed discussion and analysis on it.
3 The Proposed Models
In this section, we show our proposed models: -Laplacian Framelet GNN (pL-UFG) and -Laplacian Fourier Undecimated Framelet GNN (pL-fUFG) models. In addition, we introduce a more general regularization framework and describe the algorithms of our proposed models.
3.1 -Laplacian Undecimated Framelet GNN (pL-UFG)
Instead of simply taking the convolution result as the framelet layer output (derived in Eq. (11)), we apply the -Laplacian regularization on the framelet reconstructed signal by imposing the following optimization to define the new layer,
| (15) |
where . In which we recall that the first term in the above equation is the -Laplacian based energy defined in Eq. (13). measures the total signals’ variation throughout the graph-based format of -Laplacian. The second term dictates that optimal should not deviate excessively from the framelet reconstructed signal for the input signal . Each component of the network filter in the frequency domain is applied to the framelet coefficients . We call the model in Eq.(15) pL-UFG2.
One possible variant to model (15) is to apply the regularization individually on the reconstruction at each scale level, i.e., for all the , define
| (16) |
We name the model with the propagation in the above equation as pL-UFG1. In our experiment, we note that pL-UFG1 performs better than pL-UFG2.
3.2 -Laplacian Fourier Undecimated Framelet GNN (pL-fUFG)
In pL-fUFG, we take a strategy of regularizing the framelet coefficients. Informed by earlier experience, we consider the following optimization problem for each framelet transformation in Fourier domain. For each framelet transformation defined in Eqs. (9)-(10), define
| (17) |
Then the final layer output is defined by the reconstruction as follows
| (18) |
Or we can only aggregate all the regularized and filtered framelet coefficients in the following way
| (19) |
With the form of both pL-UFG and pL-fUFG, in the next section we show an even more generalized regularization framework by incorporating -Laplacian with graph framelets.
3.3 More General Regularization

For convenience, we write the graph gradient for multiple channel signals as
or simply if no confusion. For an undirected graph we have . With this notation, we can re-write the -Laplacian regularizer in (13) (the element-wise -norm) in the following.
| (20) | ||||
where stands for the node that is connected to node and is the node gradient vector for each node and is the vector -norm. In fact, measures the variation of in the neighbourhood of each node . Next, we generalize the regularizer by considering any positive convex function as
| (21) |
It is clear when , we recover the -Laplacian regularizer. In image processing field, several penalty functions have been proposed in the literature. For example, is known in the context of Tikhonov regularization (Li et al, 2022; Belkin et al, 2004; Assis et al, 2021). When (i.e. ), it is the classic total variation regularization. When , it is referred as the regularized total variation. An example work can be found in the work (Cheng and Wang, 2020). The case of corresponds to the non linear diffusion (Oka and Yamada, 2023).
In pL-UFG and pL-fUFG, we use to denote and respectively, as then we propose the generalized -Laplacian regularization models as
| (22) |
3.4 The Algorithm
We derive an iterative algorithm for solving the generalized -Laplacian regularization problem (22), presented as the following theorem.
Theorem 3.1.
For a given positive convex function , define
and denote the matrices , and
. Then the solution to problem (22) can be solved by the following message passing process
| (23) |
with an initial value, e.g., .
Here , and are calculated according to the current features . When , from Eq. (23) we can have the algorithm for solving pL-UFG and pL-fUFG.
Proof: Define as the objective function in Eq. (22), consider a node feature in , then we have
Setting gives the following first order condition:
This equation defines the message passing on each node from its neighbour nodes . With the definition of , and , it can be turned into the iterative formula in Eq. (23). This completes the proof.
Remark 2.
When , the objective function is not differentiable in some extreme cases for example the neighbor node signals are the same and with the same degrees. In these rare cases, the first order condition cannot be applied in the above proof. However in practice, we suggest the following alternative iterative algorithm to solve the optimization problem. In fact, we can split the terms in as
| (24) |
At iteration , we take as the new edge weights, then the next iterate is defined as the solution to optimize the Dirichlet energy with the new weights, i.e.,
Thus one step of the classic GCN can be applied in the iteration to solve the -Laplacian regularized problem (14).
3.5 Interaction between -Laplacian and Framelets
In this section, we present some theoretical support on how the -Laplacian regularizer interact with the framelets in the model. Specifically, we show that the proposed algorithm in Eq. (23) provides a sequence of (-Laplacian-based) spectral graph convolutions and diagonal scaling of the node features over the framelet filtered graph signals.This is indicated by the following analysis.
First considering the iteration Eq. (23) with initial values or without loss of generality333In our practical algorithm we choose , this will gives with a diagonal matrix ., we have
The result depends on the key operations for , where
| (25) | |||
| (26) |
where has absorbed and into defined in Theorem 3.1, i.e., .
Denote
To introduce the following analysis, define the relevant matrices , and (the Kronecker sum) with the column vector
Now, recall that the definition of the classic -Laplacian is:
| (27) |
Our purpose is to show that our generalized algorithm Eq. (3.5) above can be implemented as the linear combination of the classic -Laplacian filtering. First, based on Fu et al (2022), the operator Eq. (27) in the original -Laplacian message passing algorithm can be written in detailed matrix form as follows
| (28) |
where the matrix has elements
and the diagonal matrix has diagonal element defined as
Eq. (28) shows that the operation can be represented as the product of a matrix (still denoted as ) and the signal matrix .
Noting that , multiplying diagonal matrix on both sides of Eq. (28) and taking out give
As is diagonal, we can re-write the above equality as
Given that is the Kronecker sum of the vector and its transpose, if we still use as its diagonal matrix, then we have
| (29) |
This demonstrates that the key terms in our generalized algorithm is in linear form of -Laplacian operator . As demonstrated in the research Fu et al (2022), the operator approximately performs spectral graph convolution. Hence we can conclude that the generalized -Laplacian iterations (23) indeed performs a sequence of graph spectral convolutions (see Lemma 1 below) and gradient-based diagonal transformation (i.e., node feature scaling) over the framelet filtered graph signals.
Lemma 1.
Remark 3.
Eq. (3.5) indicates that the -Laplacian regularizer provides graph spectral convolution on top of the framelet filtering, which produces a second layer of filtering conceptually and hence restricts the solution space further. See Fig. 1 for the illustration. Interestingly, the combination of -Laplacian regularization and framelet offers a more adaptive smoothness that suites both homophilic and heterophilic data as shown in our experiments.
Remark 4.
In terms of asymptotic behavior of Eq. (3.5), one can show roughly that the elements in are between 0 and 1, which converges to zero if is too large. Therefore a large annihilates the first term in Eq. (3.5) but leaves the second term and partial sum from the third. A larger value of seems to speed up this convergence further, resulting shortening the time for finding the solution. However, it is a model selection problem for generalizability. Moreover, the inclusion of the source term guarantees to supply certain amount of variations of the node features from both low and high frequency domains of the graph framelet and it has been shown such inclusion can help the model escape from over-smoothing issue (Chien et al, 2021).
Remark 5.
Compared to GPRGNN (Chien et al, 2021) in which the model outcome is obtained by
where is learnable generalized Page rank coefficients, as we have shown in Eq. (3.5), our proposed algorithm defined in Eq. (23) provides a mixed (spectral convolution and diagonal scaling) to the framelet graph signal outputs and thus further directs the solution space of framelet to a reasonably defined region. Furthermore, due to the utilization of the Chebyshev polynomial in framelet, the computational complexity for the first filtering is not high, which is helpful in terms of defining the provably corrected space for the second operation. This shows the efficiency of incorporating framelet in -Laplacian based regularization.
4 Discussions on the Proposed Model
In this section, we conduct comprehensive discussions for our proposed models. We note that we will mainly focused on exploring the property of the generalized -Laplacian based framelet GNN (Eq. (22)) and the iterative algorithm in Eq. (23), although we may also show some conclusions of pL-UFG and pL-fUFG as well. Specifically, in Section 4.1 we discuss the denoising power of our proposed model. Section 4.2 analyzes the model’s computational complexity. Section 4.3 provides a comparison between the -Laplacian regularizer with other regularizers that are applied to GNNs via different learning tasks. Finally, the section is concluded (Section 4.4) by illustrating the limitation of the model and potential aspects for future studies.
4.1 Discussion on the Denoising Power
The denoising power of framelet has been developed in the study(Dong, 2017) and empirically studied by the past works Dong (2017); Zhou et al (2021a); Yang et al (2022). Let be the input node feature matrix with noise . In works (Dong, 2017; Zhou et al, 2021a), a framelet-based regularizer was proposed to resolve the optimization problem which can be described as:
| (30) |
where is some fidelity function that takes different forms for different applications. For any graph signal , the graph -norm , where is the degree of the -th node with respect to . is a linear transformation generated from discrete transformations, for example, the graph Fourier transforms or the Framelet transforms. Thus, the regularizer assigns a higher penalty to the node with a larger number of neighbours. Specifically, considering the functional as the framelet transformation, then the first term in Eq. (30) can be written as:
| (31) |
where . Replacing the -Laplacian regularizer in Eq. (15) by the framelet regularizer defined in the above Eq. (31) we have:
| (32) |
Followed by the work in the research (Dong, 2017), the framelet regularizer-based denoising problem in Eq. (30) is associated with the variational regularization problem that can be generally described in the form similar to Eq. (15) where the variational term is utilized for regularizing the framelet objective function. Simply by replacing the input of the first term in Eq. (32) by and omitting node degree information, we have:
| (33) |
Therefore our proposed model naturally is equipped with denoising capability and the corresponding (denoising) regularizing term aligns with the denoising regularizer developed in the paper (Zhou and Schölkopf, 2005) without nodes degree information. However, the work in the study (Zhou and Schölkopf, 2005) only handles and . Whereas our -Laplacian framelet model covers the values of . This allows more flexibility and effectiveness in the model.
Furthermore, the major difference between most wavelet frame models and the classic variational models is the choice of the underlying transformation (i.e., applied to the graph signal) that maps the data to the transformed domain that can be sparsely approximated. Given both -Laplacian (i.e., Eq. (15)) and framelet regularizers (i.e., Eq. (31)) target on the graph signal that is produced from the sparse and tight framelet transformation (Chebyshev polynomials), this further illustrates the equivalence between two denoising regularizers. Please refer to (Dong, 2017) for more details.
4.2 Discussion on the Computational Complexity
In this section, we briefly discuss the computational complexity of our proposed model, specific to the generalized model defined in Eq. (22) with its results that can be approximated by the algorithm presented in Eq. (23). The primary computational cost of our model stems from the generation of the framelet decomposition matrices () or the framelet transformation applied to the node features. We acknowledge that generating involves a high computational complexity, as transitional framelet methods typically employ eigen-decomposition of the graph Laplacian for this purpose. Consequently, the framelet transform itself exhibits a time complexity of and a space complexity of for a graph with nodes and -dimensional features. Notably, the constants , , and are independent of the graph data. Existing literature (Zheng et al, 2021b) has demonstrated that when the input graph contains fewer than nodes (with fixed feature dimension), the computational time for framelet convolution is comparable to that of graph attention networks with 8 attention heads (Veličković et al, 2018). As the graph’s node size increases, the performance of graph attention networks degrades rapidly, while graph framelets maintain faster computation. However, our application of Chebyshev polynomials to approximate significantly reduces the associated computational cost compared to traditional methods. Additionally, we acknowledge that the inclusion of the -Laplacian based implicit layer introduces additional computational cost to the original framelet model, primarily arising from the computation of the norm of the graph gradient, denoted as . Considering the example of the Euclidean norm, the computational cost for scales as , where and represent the number of nodes and feature dimension, respectively. Thus, even when accounting for the computation of the implicit layer, the overall cost of our proposed method remains comparable to that of the framelet model.
4.3 Comparison with Other Regularizers and Potential Application Scenarios
As we have illustrated in Section 3.3, with the assistance from different form of the regularizers, GNNs performance could be enhanced via different learning tasks. In this discussion, we position our study within the wider research landscape that investigates various regularizers to enhance the performance of Graph Neural Networks (GNNs) across different learning tasks. We earlier discussed the denoising power of the pL-UFG in Section 4.1, establishing that it can be expressed in terms of a denoising formulation. This is comparable to the approach from Ma et al (2021), who used a different regularizer term to highlight the denoising capabilities of GNNs. They showed that their regularizer can effectively reduce noise and enhance the robustness of GNN models.
Our study, however, emphasizes the unique advantages that the -Laplacian brings, a theme also echoed in the works by Liu et al (2010) and Candès et al (2011). Both studies incorporated the -norm as a regularization term in robust principal component analysis (RPCA), showcasing its ability to recover low-rank matrices even in the presence of significant noise. Furthermore, the study by Liu et al (2021b) reinforces the benefits of the -norm in preserving discontinuity and enhancing local smoothness. Characterized by its heavy-tail property, the -norm imposes less penalty on large values, thereby making it effective in handling data with substantial corruption or outliers.
Furthermore, in terms of the potential practical implementations, one can deploy our method into various aspects. For example, the -Laplacian based regularizer can be used in image processing and computer vision applications, where it can help to smooth out noisy or jagged images while preserving important features. In addition, we note that, as we implement our graph learning method via an optimization (regularization) framework, this suggests any potential practical implementations (such as graph generation (Ho et al, 2020), graph based time series forecasting (Wen et al, 2023)) of GNNs can also be deployed under our proposed methods with a higher flexibility power.
4.4 Limitation and Potential Future Studies
While outstanding properties have been presented from our proposed model, the exploration of how the -Laplacian based regularization framework can be deployed to various types of graphs (i.e., dynamic or spatio-temporal) is still wanted. In fact, one may require the corresponding GNNs to be able to capture the pattern of the evolution (i.e., combing GNN with LSTM or Transformer (Manessi et al, 2020)) of the graph when the input graph is dynamic. We note that such a requirement is beyond the capability of the current model. However, as the -Laplacian based regularizer restricts the solution of the graph framelet, it would be interesting to make the quantity of learnable throughout the training process. We leave this to future work.
Moreover, followed by the idea of making value as a learnable parameter in the model, one can also explore assigning different values of to different frequency domains of framelet. It has been verified that the low-frequency domain of framelet induces a smoothing effect on the graph signal whereas the sharpening effect is produced from the high-frequency domain (Han et al, 2022). Therefore, one may prefer to obtain a relatively large quantity of to the low-frequency domain to enhance the smoothing effect of the framelet when the input graph is highly homophily, as one prefers to predict identical labels for connected nodes. On the other hand, a smaller value of is wanted for a high-frequency domain to further sharpen the differences between node features (i.e., ) so that distinguished labels can be produced from the model when the input graph is heterophilic. Moreover, as the -Laplacian-based implicit layers are allocated before the framelet reconstruction, it would be interesting to explore how such implicit layers can affect the signal reconstruction of the framelet.
5 Experiments
In this section, we present empirical studies on pL-UFG and pL-fUFG on real-world node classification tasks with both heterophilic and homophilic graphs. We also test the robustness of the proposed models against noise. Both two experiments are presented with detailed discussions on their results. In addition, we discuss by adjusting the quantity of the in our proposed model, the so-called ablation study is automatically conducted in our experiments. The code for our experiment can be accessed via https://github.com/superca729/pL-UFG. Lastly, it is worth noting that our proposed method has the potential to be applied to the graph learning task other than node classification such as graph level classification (pooling) (Zheng et al, 2021b) and link prediction (Lin and Gao, 2023). Although we have yet to delve into these tasks, we believe that by assigning some simple manipulations to our methods, such as deploying the readout function for graph pooling or computing the log-likelihood for graph link prediction, our method is capable of handling these tasks. Similarly, our model could be beneficial in community detection tasks by possibly identifying clusters of similar characteristics or behaviors. We leave these promising research aspects to our future work.
5.1 Datasets, Baseline Models and the Parameter Setting
Datasets. We use both homophilic and heterophilic graphs from https://www.pyg.org/ to assess pL-UFG and pL-fUFG, including benchmark heterophilic datasets: Chameleon, Squirrel, Actor, Wisconsin, Texas, Cornell, and homophilic datasets: Cora, CiteSeer, PubMed, Computers, Photos, CS, Physics. In our experiments, homophilic graphs are undirected and heterophilic graphs are directed (where we observe an improved performance when direction information is provided). We included the summary statistics of the included datasets together with their homophily index and split ratio in Table 1
Baseline models. We consider eight baseline models for comparison:
-
•
MLP: standard feedward multiple layer perceptron.
-
•
GCN (Kipf and Welling, 2017): GCN is the first of its kind to implement linear approximation to spectral graph convolutions.
-
•
SGC (Wu et al, 2019): SGC reduces GCNs’ complexity by removing nonlinearities and collapsing weight matrices between consecutive layers.
-
•
GAT (Veličković et al, 2018): GAT is a graph neural network that applies the attention mechanism on node feature to learn edge weight.
-
•
JKNet (Xu et al, 2018b): JKNet can flexibly leverage different neighbourhood ranges to enable better structure-aware representation for each node.
-
•
APPNP (Gasteiger et al, 2019): APPNP combines GNN with personalized PageRank to separate the neural network from the propagation scheme.
-
•
GPRGNN (Chien et al, 2021): GPRGNN architecture that adaptively learns the GPR (General Pagerank) weights so as to jointly optimize node feature and topological information extraction, regardless the level of homophily on a graph.
-
•
-GNN (Fu et al, 2022): -GNN is -Laplacian based GNN model, whose message-passing mechanism is derived from a discrete regularization framework.
-
•
UFG (Zheng et al, 2021b): UFG is a type of GNNs based on framelet transforms, the framelet decomposition can naturally aggregate the graph features into low-pass and high-pass spectra.
The test results are reproduced using code that runs in our machine, which might be different from the reported results. In addition, compared to -GNN, the extra time and space complexity induced from our algorithm is .
Hyperparameter tuning. We use grid search for tuning hyperparameters. We test for PGNN, pL-UFG and pL-fUFG. The learning rate is chosen from {0.01, 0.005}. We consider the number of iterations in -Laplacian message passing from after 10 warming-up steps. For homophilic datasets, we tune and for heterophilic graphs . The framelet type is fixed as Linear (see (Yang et al, 2022)) and the level is set to 1. The dilation scale , and for , the degree of Chebyshev polynomial approximation to all ’s in (15)-(18), is drawn from {2, 3, 7}. It is worth noting that in graph framelets, the Chebyshev polynomial is utilized for approximating the spectral filtering of the Laplacian eigenvalues. Thus, a -degree polynomial approximates -hop neighbouring information of each node of the graph. Therefore, when the input graph is heterophilic, one may require to be relatively larger as node labels tend to be different between directly connected (1-hop) nodes. The number of epochs is set to 200, the same as the baseline model(Fu et al, 2022).
| Datasets | Class | Feature | Node | Edge | Train/Valid/Test | |
|---|---|---|---|---|---|---|
| Cora | 7 | 1433 | 2708 | 5278 | 20%/10%/70% | 0.825 |
| CiteSeer | 6 | 3703 | 3327 | 4552 | 20%/10%/70% | 0.717 |
| PubMed | 3 | 500 | 19717 | 44324 | 20%/10%/70% | 0.792 |
| Computers | 10 | 767 | 13381 | 245778 | 20%/10%/70% | 0.802 |
| Photo | 8 | 745 | 7487 | 119043 | 20%/10%/70% | 0.849 |
| CS | 15 | 6805 | 18333 | 81894 | 20%/10%/70% | 0.832 |
| Physics | 5 | 8415 | 34493 | 247962 | 20%/10%/70% | 0.915 |
| Chameleon | 5 | 2325 | 2277 | 31371 | 60%/20%/20% | 0.247 |
| Squirrel | 5 | 2089 | 5201 | 198353 | 60%/20%/20% | 0.216 |
| Actor | 5 | 932 | 7600 | 26659 | 60%/20%/20% | 0.221 |
| Wisconsin | 5 | 251 | 499 | 1703 | 60%/20%/20% | 0.150 |
| Texas | 5 | 1703 | 183 | 279 | 60%/20%/20% | 0.097 |
| Cornell | 5 | 1703 | 183 | 277 | 60%/20%/20% | 0.386 |
5.2 Experiment Results and Discussion
Node Classification Tables 2 and 3 summarize the results on homophilic and heterophilic datasets. The values after are standard deviations. The top three results are highlighted in First, Second, and Third. From the experiment results, we observe that pL-UFG and pL-fUFG achieve competitive performances against the baselines in most of the homophily and heterophily benchmarks. For the models’ performance on homophily undirect graphs, Table 2 shows that pL-UFG21.5 has the top accuracy in Cora, Photos and CS. For Citeseer, pL-UFG12.0, pL-UFG22.0 and pL-fUFG2.0 have the best performance. In terms of the performance on heterophily direct graphs (Table 3), we observe that both of our two models are capable of generating the highest accuracy in all benchmark datasets except Actor where the top performance was generated from MLP. However, we note that for Actor, our pL-UFG11.0 achieves almost identical outcomes compared to those of MLP.
Aligned with our theoretical prediction in Remark 4 from the experiment, we discover that the value of the trade-off term for pL-UFG and pL-fUFG is significantly higher than that in pGNN, indicating that framelet has a major impact on the performance of the model. The performance of pL-UFG, pL-fUFG and others on heterophilic graphs are shown in Table 3. pL-UFG and pL-fUFG both can outperform MLP and other state-of-the-art GNNs under a low homophilic rate. In terms of denoising capacity, pL-UFG and pL-fUFG are far better than the baseline models. Figs. 6 and 7 show that both pL-UFG and pL-fUFG produce the top accuracies across different noise levels.
Discussion for . To enable GNN model to better adapt to the heterophilic graphs, an ideal GNN model shall induce a relatively high variation in terms of the node feature generated from it. Therefore, compared to the models with , the model regularized with regularizer imposes a lesser penalty and thus produces outputs with a higher variation. This is supported by the empirical observation from Table 3 in which the highest prediction accuracy for heterophilic graphs are usually achieved by our model with .
Discussion for = 1. Here we specifically focus on in our models. Recall that when , the -Laplacian operator acts on the graph signal is . Based on Remark 1, when , is equivalent to the mean curvature operator defined on the embedded surface. In analogy to differential geometry, points that curvature can not be properly defined are so-called singular points. Thus one can similarly conclude that when a graph contains a singular node (i.e., the graph is crumpled (Burda et al, 2001)) then both and its corresponding can not be properly defined. Furthermore, one can easily check that, when , the regularization term produces a higher penalty than its counterparts. This is because, when , whereas . Clearly, we have unless all of the nodes in the graph are singular nodes, or in the graph in which there is only one non-singular point while the rest nodes are singular.
5.3 Visualization on the Effect of
Based on the claim we made in previous sections, increasing the value of leads our model to exhibit a stronger smoothing effect on the node features, thereby making it more suitable for homophilic graphs. Conversely, when is small, the model preserves distinct node features, making it a better fit for heterophilic graphs. To validate this idea, we visualize the changes in relative positions (distances) between node features for (the minimum value) and (the maximum value). We specifically selected the Cora and Actor datasets and employed Isomap (Tenenbaum et al, 2000) to map both the initial node features and the node features generated by our model to , while preserving their distances. The results are depicted in Figure 2 and 3.
From both Figure 2 and 3, it can be observed that when , the sharpening effect induced by our model causes the node features to become more distinct from each other. Under the Isomap projection, the nodes are scattered apart compared to the input features. Conversely, when a relatively large value of is assigned, the model exhibits a stronger smoothing effect, resulting in all nodes being aggregated towards the center in the Isomap visualization. These observations provide direct support for our main claim regarding the proposed model.


| Method | Cora | CiteSeer | PubMed | Computers | Photos | CS | Physics |
|---|---|---|---|---|---|---|---|
| MLP | |||||||
| GCN | |||||||
| SGC | OOM | OOM | |||||
| GAT | |||||||
| JKNet | |||||||
| APPNP | |||||||
| GPRGNN | |||||||
| UFG | |||||||
| PGNN1.0 | |||||||
| PGNN1.5 | |||||||
| PGNN2.0 | |||||||
| PGNN2.5 | |||||||
| pL-UFG11.0 | |||||||
| pL-UFG11.5 | |||||||
| pL-UFG12.0 | |||||||
| pL-UFG12.5 | |||||||
| pL-UFG21.0 | |||||||
| pL-UFG21.5 | |||||||
| pL-UFG22.0 | 76.120.82 | ||||||
| pL-UFG22.5 | |||||||
| pL-fUFG1.0 | |||||||
| pL-fUFG1.5 | 94.980.23 | ||||||
| pL-fUFG2.0 | |||||||
| pL-fUFG2.5 |
| Method | Chameleon | Squirrel | Actor | Wisconsin | Texas | Cornell |
|---|---|---|---|---|---|---|
| MLP | ||||||
| GCN | ||||||
| SGC | ||||||
| GAT | ||||||
| JKNet | ||||||
| APPNP | ||||||
| GPRGNN | ||||||
| UFG | ||||||
| PGNN1.0 | ||||||
| PGNN1.5 | ||||||
| PGNN2.0 | ||||||
| PGNN2.5 | ||||||
| pL-UFG11.0 | ||||||
| pL-UFG11.5 | ||||||
| pL-UFG12.0 | ||||||
| pL-UFG12.5 | ||||||
| pL-UFG21.0 | ||||||
| pL-UFG21.5 | ||||||
| pL-UFG22.0 | ||||||
| pL-UFG22.5 | ||||||
| pL-fUFG1.0 | ||||||
| pL-fUFG1.5 | ||||||
| pL-fUFG2.0 | ||||||
| pL-fUFG2.5 |
5.4 Experiments on Denoising Capacity
Followed by the discussion in Section 4.1, in this section we evaluate our proposed models’ (pL-UFG and pL-fUFG) denoising capacity on both homophilic (Cora) and heterophilic (Chameleon) graphs. Since the node features of the included datasets are in binary, we randomly assign binary noise with different proportions of the node features (i.e., ). From Fig. 6 and 7 we see that pL-UFG defined in Eq. (16) outperforms other baselines and showed the strongest robustness to the contaminated datasets. This is expected based on our discussion on the denoising power in Section 4.1 and the formulation of our models (defined in Eqs. (15), (16) and (17)). The denoising capacity of our proposed model is sourced from two parts including the sparse approximation of the framelet decomposition and reconstruction, i.e., and , and variational regularizer (Dong, 2017). Compared to pL-UFG1 defined in Eq. (15), pL-UFG2 assigns the denoising operators, , and , to the node inputs that is reconstructed from both sparsely decomposed low and high-frequency domains so that the denoising operators target on the original graph inputs at different scales and hence naturally result in a better model denoising performance. In addition, without taking the reconstruction in the first place, the term in pL-fUFG is less sparse than the pL-UFG2 counterpart. Thus regularizing with the same , the effect from insufficient eliminated noise from pL-fUFG will lead pL-fUFG to an incorrect (respect to pL-UFG2) solution space which can not be recovered by the additional reconstruction using , and this is the potential reason for observing an outperforming result from pL-UFG2 compared to other proposed models.
In addition to the above experiment, here we show how the results of how the quantity of affect the denoising power of the proposed model, while keeping all other parameters constant. The results of the changes of the denoising power are included in Fig. 4 (homophilic graph) and 5 (heterophilic graph).
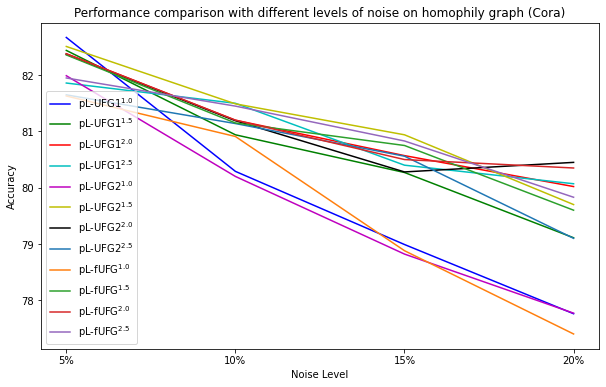

Based on the observations from the results, it appears that the performance of different values of varies under different noise rates. For the homophilic graph, the performance of pL-UFG21.5 and pL-UFG22.0 seems to be relatively stable across different noise rates, while the performance of other values of fluctuates more. For the heterophilic graph, the performance of pL-UFG12.5 and pL-UFG22.5 appears to be relatively stable across different noise rates, while the performance of other values of fluctuates more.
We also note that these observations on the fluctuations of the results are expected, as we have shown that the denoising process of our proposed model can be presented as:
| (34) |
where is the set of indices of all framelet decomposed frequency domains. It is not hard to verify that once a larger quantity of is assigned, the penalty on the node feature difference () becomes to be greater. Therefore, a stronger denoising power is induced. In terms of different graph types, when the input graph is heterophily, in most of the cases, the connected nodes tend to have distinct features, after assigning noise to those features, if the feature difference becomes larger, a higher quantity of is preferred. In the meanwhile, adding noise for the heterophilic graph could also make the feature difference becomes smaller, in this case a large quantity of may not be appropriate, this explains why most of lines in Fig. 5 are with large fluctuations. Similar reasoning can be applied to the case of the denoising performance of our model for homophilic graphs, we omit it here.
5.5 Regarding to Ablation Study
It is worth noting that one of the advantages of assigning an adjustable -Laplacian-based regularizer is on the convenience of conducting the ablation study. As the key principle of ablation study is to test whether a new component (in our case the regularizer) in a proposed method can always add advantages over baseline model counterparts regardless of the newly involved parameters. This suggests that the ablation study of our method are naturally conducted to compare our models with the regularizers with the underlying networks via both the node classification tasks and the model denoising power test. It is not hard to observed that in most of cases, regardless of the change of , our proposed model kept outperforming baseline models. However, as our proposed model was driven from an regularization framework, another potential parameter that we note could affect the model performance is the quantity of . Based on Eq. (22), an increase of the quantity of leads to a increase of model’s convexity, as a consequence, could guide model more closed to the global optima when . Another observation to is we found that a smaller value of together with a relatively bigger value of are more suitable for homophily/heterophilic graphs, this implies that seems to have an opposite effect on model’s adaption power compared to . However, to quantify the effect of via a suitable measure (i.e., potentially Dirichlet energy (Han et al, 2022)) is out of the scope of this paper, we leave it to future discussions.


6 Conclusion and Further work
This paper showcases the application of -Laplacian Graph Neural Networks (GNN) in conjunction with framelet graphs. The incorporation of -Laplacian regularization brings remarkable flexibility, enabling effective adaptation to both homophilic undirected and heterophilic directed graphs, thereby significantly enhancing the predictive capabilities of the model. To validate the efficacy of our proposed model, we conducted extensive numerical experiments on diverse graph datasets, demonstrating its superiority over baseline methods. Notably, our model exhibits robustness against noise perturbation, even under high noise levels. These promising findings highlight the tremendous potential of our approach and warrant further investigations in several directions. For instance, delving into the intriguing mathematical properties of our model, including weak and strong convergence, analyzing the behavior of (Dirichlet) energy, and establishing connections with non-linear diffusion equations, opens up fascinating avenues for future research.
References
- Ahmedt-Aristizabal et al (2021) Ahmedt-Aristizabal D, Armin MA, Denman S, Fookes C, Petersson L (2021) Graph-based deep learning for medical diagnosis and analysis: past, present and future. Sensors 21(14):4758
- Assis et al (2021) Assis AD, Torres LC, Araújo LR, Hanriot VM, Braga AP (2021) Neural networks regularization with graph-based local resampling. IEEE Access 9:50727–50737
- Belkin et al (2004) Belkin M, Matveeva I, Niyogi P (2004) Tikhonov regularization and semi-supervised learning on large graphs. In: 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, IEEE, vol 3, pp iii–1000
- Bozorgnia et al (2019) Bozorgnia F, Mohammadi SA, Vejchodskỳ T (2019) The first eigenvalue and eigenfunction of a nonlinear elliptic system. Applied Numerical Mathematics 145:159–174
- Bronstein et al (2017) Bronstein MM, Bruna J, LeCun Y, Szlam A, Vandergheynst P (2017) Geometric deep learning: going beyond Euclidean data. IEEE Signal Processing Magazine 34(4):18–42
- Bruna et al (2014) Bruna J, Zaremba W, Szlam A, LeCun Y (2014) Spectral networks and locally connected networks on graphs. In: Proceedings of International Conference on Learning Representations
- Burda et al (2001) Burda Z, Correia J, Krzywicki A (2001) Statistical ensemble of scale-free random graphs. Physical Review E 64(4):046118
- Candès et al (2011) Candès EJ, Li X, Ma Y, Wright J (2011) Robust principal component analysis? Journal of the ACM (JACM) 58(3):1–37
- Chen et al (2022a) Chen J, Wang Y, Bodnar C, Liò P, Wang YG (2022a) Dirichlet energy enhancement of graph neural networks by framelet augmentation. https://yuguangwanggithubio/papers/EEConvpdf
- Chen et al (2022b) Chen Q, Wang Y, Wang Y, Yang J, Lin Z (2022b) Optimization-induced graph implicit nonlinear diffusion. In: Proceedings of the 39th International Conference on Machine Learning
- Cheng and Wang (2020) Cheng T, Wang B (2020) Graph and total variation regularized low-rank representation for hyperspectral anomaly detection. IEEE Transactions on Geoscience and Remote Sensing 58(1):391–406, DOI 10.1109/TGRS.2019.2936609
- Chien et al (2021) Chien E, Peng J, Li P, Milenkovic O (2021) Adaptive universal generalized pagerank graph neural network. In: Proceedings of International Conference on Learning Representations
- Ciotti et al (2016) Ciotti V, Bonaventura M, Nicosia V, Panzarasa P, Latora V (2016) Homophily and missing links in citation networks. EPJ Data Science 5:1–14
- Defferrard et al (2016) Defferrard M, Bresson X, Vandergheynst P (2016) Convolutional neural networks on graphs with fast localized spectral filtering. Advances in Neural Information Processing Systems 29
- Dong (2017) Dong B (2017) Sparse representation on graphs by tight wavelet frames and applications. Applied and Computational Harmonic Analysis 42(3):452–479, DOI 10.1016/j.acha.2015.09.005
- Fan et al (2019) Fan W, Ma Y, Li Q, He Y, Zhao E, Tang J, Yin D (2019) Graph neural networks for social recommendation. In: Proceedings of WWW, pp 417–426
- Frecon et al (2022) Frecon J, Gasso G, Pontil M, Salzo S (2022) Bregman neural networks. In: International Conference on Machine Learning, PMLR, pp 6779–6792
- Fu et al (2022) Fu G, Zhao P, Bian Y (2022) -Laplacian based graph neural networks. In: Proceedings of the 39th International Conference on Machine Learning, PMLR, vol 162, pp 6878–6917
- Gasteiger et al (2019) Gasteiger J, Bojchevski A, Günnemann S (2019) Predict then propagate: Graph neural networks meet personalized pagerank. In: Proceedings of International Conference on Learning Representations
- Gilmer et al (2017) Gilmer J, Schoenholz SS, Riley PF, Vinyals O, Dahl GE (2017) Neural message passing for quantum chemistry. In: International Conference on Machine Learning, PMLR, pp 1263–1272
- Gu et al (2020) Gu F, Chang H, Zhu W, Sojoudi S, El Ghaoui L (2020) Implicit graph neural networks. In: Advances in Neural Information Processing Systems
- Hammond et al (2011) Hammond DK, Vandergheynst P, Gribonval R (2011) Wavelets on graphs via spectral graph theory. Applied and Computational Harmonic Analysis (2):129–150
- Han et al (2022) Han A, Shi D, Shao Z, Gao J (2022) Generalized energy and gradient flow via graph framelets. arXiv:221004124
- He et al (2021) He M, Wei Z, Xu H, et al (2021) Bernnet: Learning arbitrary graph spectral filters via bernstein approximation. Advances in Neural Information Processing Systems 34:14239–14251
- He and Kempe (2015) He X, Kempe D (2015) Stability of influence maximization. In: Proceedings of the 20th ACM International Conference on Knowledge Discovery and Data Mining, p 1256–1265
- Ho et al (2020) Ho J, Jain A, Abbeel P (2020) Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems 33:6840–6851
- Hu et al (2018) Hu X, Sun Y, Gao J, Hu Y, Yin B (2018) Locality preserving projection based on F-norm. In: Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, pp 1330–1337
- Kipf and Welling (2017) Kipf TN, Welling M (2017) Semi-supervised classification with graph convolutional networks. In: Proceedings of International Conference on Learning Representations
- Leskovec and Faloutsos (2006) Leskovec J, Faloutsos C (2006) Sampling from large graphs. In: Proceedings of the 12th ACM International Conference on Knowledge Discovery and Data Mining, p 631–636, DOI 10.1145/1150402.1150479
- Li et al (2022) Li J, Lin S, Blanchet J, Nguyen VA (2022) Tikhonov regularization is optimal transport robust under martingale constraints. 2210.01413
- Lin and Gao (2023) Lin L, Gao J (2023) A magnetic framelet-based convolutional neural network for directed graphs. In: ICASSP 2023 - 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp 1–5, DOI 10.1109/ICASSP49357.2023.10097148
- Liu et al (2022) Liu A, Li B, Li T, Zhou P, Wang R (2022) An-gcn: An anonymous graph convolutional network against edge-perturbing attacks. IEEE Transactions on Neural Networks and Learning Systems pp 1–15, DOI 10.1109/TNNLS.2022.3172296
- Liu et al (2010) Liu G, Lin Z, Yu Y (2010) Robust subspace segmentation by low-rank representation. In: Proceedings of the 27th international conference on machine learning (ICML-10), pp 663–670
- Liu et al (2021a) Liu J, Kawaguchi K, Hooi B, Wang Y, Xiao X (2021a) Eignn: Efficient infinite-depth graph neural networks. In: Advances in Neural Information Processing Systems
- Liu et al (2021b) Liu X, Jin W, Ma Y, Li Y, Liu H, Wang Y, Yan M, Tang J (2021b) Elastic graph neural networks. In: International Conference on Machine Learning, PMLR, pp 6837–6849
- Luo et al (2010) Luo D, Huang H, Ding CHQ, Nie F (2010) On the eigenvectors of -Laplacian. Machine Learning 81(1):37–51
- Ly (2005) Ly I (2005) The first eigenvalue for the p-laplacian operator. JIPAM J Inequal Pure Appl Math 6:91
- Ma et al (2021) Ma Y, Liu X, Zhao T, Liu Y, Tang J, Shah N (2021) A unified view on graph neural networks as graph signal denoising. URL https://openreview.net/forum?id=MD3D5UbTcb1
- Manessi et al (2020) Manessi F, Rozza A, Manzo M (2020) Dynamic graph convolutional networks. Pattern Recognition 97:107000
- Oka and Yamada (2023) Oka T, Yamada T (2023) Topology optimization method with nonlinear diffusion. Computer Methods in Applied Mechanics and Engineering 408:115940, DOI https://doi.org/10.1016/j.cma.2023.115940, URL https://www.sciencedirect.com/science/article/pii/S0045782523000634
- Ortega et al (2018) Ortega A, Frossard P, Kovacević J, Moura JMF, Vandergheynst P (2018) Graph signal processing: Overview, challenges, and applications. Proceedings of the IEEE 106(5):808–828
- Pandit et al (2007) Pandit S, Chau DH, Wang S, Faloutsos C (2007) Netprobe: a fast and scalable system for fraud detection in online auction networks. In: Proceedings of the 16th international conference on World Wide Web, pp 201–210
- Park et al (2021) Park J, Choo J, Park J (2021) Convergent graph solvers. In: Proceedings of International Conference on Learning Representations
- Scarselli et al (2009) Scarselli F, Gori M, Tsoi AC, Hagenbuchner M, Monfardini G (2009) The graph neural network model. IEEE Transactions on Neural Networks 20(1):61–80
- Sweldens (1998) Sweldens W (1998) The lifting scheme: A construction of second generation wavelets. SIAM Journal on Mathematical Analysis 29(2):511–546, DOI 10.1137/S0036141095289051, https://doi.org/10.1137/S0036141095289051
- Tenenbaum et al (2000) Tenenbaum JB, Silva Vd, Langford JC (2000) A global geometric framework for nonlinear dimensionality reduction. science 290(5500):2319–2323
- Veličković et al (2018) Veličković P, Cucurull G, Casanova A, Romero A, Lio P, Bengio Y (2018) Graph attention networks. In: Proceedings of International Conference on Learning Representations
- Wen et al (2023) Wen H, Lin Y, Xia Y, Wan H, Zimmermann R, Liang Y (2023) Diffstg: Probabilistic spatio-temporal graph forecasting with denoising diffusion models. arXiv preprint arXiv:230113629
- Wu et al (2019) Wu F, Zhang T, Souza AHd, Fifty C, Yu T, Weinberger KQ (2019) Simplifying graph convolutional networks. In: Proceedings of International Conference on Machine Learning
- Wu et al (2021) Wu J, Sun J, Sun H, Sun G (2021) Performance analysis of graph neural network frameworks. In: Proceedings of the IEEE International Symposium on Performance Analysis of Systems and Software, pp 118–127, DOI 10.1109/ISPASS51385.2021.00029
- Wu et al (2022) Wu S, Sun F, Zhang W, Xie X, Cui B (2022) Graph neural networks in recommender systems: a survey. ACM Computing Surveys to appear
- Wu et al (2020) Wu Z, Pan S, Chen F, Long G, Zhang C, Yu PS (2020) A comprehensive survey on graph neural networks. IEEE Transactions on Neural Networks and Learning Systems 32(1):4–24
- Xu et al (2018a) Xu K, Hu W, Leskovec J, Jegelka S (2018a) How powerful are graph neural networks? In: Proceedings of International Conference on Learning Representations
- Xu et al (2018b) Xu K, Li C, Tian Y, Sonobe T, Kawarabayashi Ki, Jegelka S (2018b) Representation learning on graphs with jumping knowledge networks. In: Proceedings of International Conference on Machine Learning
- Yang et al (2022) Yang M, Zheng X, Yin J, Gao J (2022) Quasi-Framelets: Another improvement to graph neural networks. arXiv:220104728 2201.04728
- Zhang et al (2003) Zhang Q, Gu Y, Mateusz M, Baktashmotlagh M, Eriksson A (2003) Implicitly defined layers in neural networks. arxiv200301822
- Zhang et al (2022) Zhang Z, Cui P, Zhu W (2022) Deep learning on graphs: A survey. IEEE Transactions on Knowledge and Data Engineering 34(1):249–270, DOI 10.1109/TKDE.2020.2981333
- Zheng et al (2021a) Zheng X, Liu Y, Pan S, Zhang M, Jin D, Yu PS (2021a) Graph neural networks for graphs with heterophily: A survey. In: Proceedings of the AAAI Conference on Artificial Intelligence
- Zheng et al (2021b) Zheng X, Zhou B, Gao J, Wang YG, Lio P, Li M, Montufar G (2021b) How framelets enhance graph neural networks. In: Proceedings of International Conference on Machine Learning
- Zheng et al (2022) Zheng X, Zhou B, Wang YG, Zhuang X (2022) Decimated framelet system on graphs and fast g-framelet transforms. Journal of Machine Learning Research 23:18–1
- Zhou et al (2021a) Zhou B, Li R, Zheng X, Wang YG, Gao J (2021a) Graph denoising with framelet regularizer. arXiv:211103264
- Zhou et al (2021b) Zhou B, Liu X, Liu Y, Huang Y, Lio P, Wang Y (2021b) Spectral transform forms scalable transformer. arXiv:211107602
- Zhou and Schölkopf (2005) Zhou D, Schölkopf B (2005) Regularization on discrete spaces. In: The 27th DAGM Symposium,, August 31 - September 2, 2005, Vienna, Austria, vol 3663, pp 361–368
- Zhou et al (2020) Zhou J, Cui G, Hu S, Zhang Z, Yang C, Liu Z, Wang L, Li C, Sun M (2020) Graph neural networks: A review of methods and applications. AI Open 1:57–81
- Zhu et al (2020a) Zhu J, Yan Y, Zhao L, Heimann M, Akoglu L, Koutra D (2020a) Beyond homophily in graph neural networks: Current limitations and effective designs. In: Advances in Neural Information Processing Systems, vol 33, pp 7793–7804
- Zhu et al (2021) Zhu M, Wang X, Shi C, Ji H, Cui P (2021) Interpreting and unifying graph neural networks with an optimization framework. In: Proceedings of WWW
- Zhu et al (2020b) Zhu S, Pan S, Zhou C, Wu J, Cao Y, Wang B (2020b) Graph geometry interaction learning. Advances in Neural Information Processing Systems 33:7548–7558
- Zou et al (2022) Zou C, Han A, Lin L, Gao J (2022) A simple yet effective SVD-GCN for directed graphs. arxiv220509335