Generalized Kramers-Wanier Duality from Bilinear Phase Map

In this work, we propose a generalization of KW transformation, which is denoted as Bilinear Phase Map (BPM). The BPM is characterized by a matrix of $\mathbb{Z}_{2}$ numbers. Notably, the matrix not only captures all the essential information of original KW duality in its plain linear algebra properties, but also engenders a wider array of exotic phases and phase transitions. For general BPMs, we present a systematic approach to address ground state degeneracy and the loss of unitarity by considering more twisted boundary conditions, and also derive general non-invertible fusion rules, all by simply examining the linear algebra features of its matrix.

As an application, we construct two new BPMs in (1+1)D, denoted as $\mathcal{N}_{\text{3-KW}}$ and $\mathcal{N}_{\text{4-KW}}$, which are associated with three-site-interacting and four-site-interacting Ising spin chain respectively [73, 74, 75, 76, 77, 78, 79, 80, 81]. Notably, for self-dual systems, we prove $\mathcal{N}_{\text{4-KW}}$ is anomalous while $\mathcal{N}_{\text{3-KW}}$ is anomaly-free, allowing an SPT phase to exist. We also find a generalized Kennedy-Tasaki (KT) duality [82, 83, 84, 85, 86, 87, 88, 89, 90, 23, 91, 92, 93] between this SPT phase and an SSB phase. Based on these results, we propose one web of duality in Fig. 1 connecting gapped phases and another web in Fig. 2 between related phase transitions.

Let us consider a closed spin-1/2 chain with $L$ sites. On each site $i$ sits a spin-1/2 variable $s_{i}\in\{0,1\}$. We also consider the $\mathbb{Z}_{2}$ symmetry generated by $U=\prod_{j}X_{j}$, which flips all spins, namely $s_{j}\to s_{j}+1$. The KW transformation is realized by gauging the $\mathbb{Z}_{2}$ symmetry for the entire Hilbert space. On the (1+1)D lattice, the $\mathbb{Z}_{2}$ gauge field is defined as dual spins $\{\hat{s}_{i-\frac{1}{2}}\}$ on the link. Therefore, the spins $\{s_{i}\}$ on the original lattice are mapped to dual spins $\{\hat{s}_{i-\frac{1}{2}}\}$ under KW transformation. In addition, we use $(-1)^{\hat{u}}$ to denote the eigenvalue of the dual symmetry $\hat{U}:=\prod_{i=1}^{L}\hat{X}_{i-\frac{1}{2}}$, and $\hat{t}$ to denote the boundary condition ${\hat{s}_{i-\frac{1}{2}+L}}={\hat{s}_{i-\frac{1}{2}}+\hat{t}}$.

The KW transformation is realized by an operator $\mathcal{N}$ that maps the basis state to a state of the gauge field spins,

The exponents in (1) are reminiscent of the minimal coupling of the gauge fields. The boundary terms in the exponents are chosen to give the correct mapping of symmetry-twist sectors.

The KW duality is particularly useful in understanding the physics of 1D spin chains with the same global $\mathbb{Z}_{2}$ symmetry, such as the Hamiltonian

Note that if we consider periodic boundary condition (PBC), namely $\hat{t}=0$, Eq. (1) can be written in a more compact form after shifting $\hat{s}_{j-\frac{1}{2}}$ to $\hat{s}_{j}$ as

where ${\bf\it A}$ is a $\mathbb{Z}_{2}$ valued $L\times L$ matrix,

A crucial feature is that the rank of ${\bf\it A}^{\text{T}}$ is $L-1$, and it has a non-trivial kernel

The kernel is the root of several key properties of the KW duality. First, we have

That is, the duality mapping does not distinguish $\ket{\{s_{i}\}}$ and $\ket{\{s_{i}+1\}}$. Both states are mapped to the same state of the dual spins $\hat{s}_{i}$. Therefore, if we start from a system with an SSB phase with two ground states $\ket{\{s_{i}\}}$ and $\ket{\{s_{i}+1\}}$, the KW duality will map them to the same state. For the same reason, the KW duality maps the states in the odd sector of the $\mathbb{Z}_{2}$ symmetry (i.e., $\ket{\{s_{i}\}}-\ket{\{s_{i}+1\}}$) to zero. Hence, the kernel leads to a loss of unitarity of the KW duality.

Similarly, since we also have

That is, the state mapped to by the KW duality is always in the even sector of dual $\mathbb{Z}_{2}$ operation defined by the kernel $\hat{s}_{i}\to\hat{s}_{i}+a_{i}$.

Another feature associated with the kernel is the collection of states that are mapped into the paramagnetic state $\ket{\{\hat{s}_{i}\}}=\ket{\rightarrow\rightarrow\dots}$. To start, by definition of the mapping, it is always true that $\ket{{\bf\it 0}}\equiv\ket{\{s_{i}=0\}}$ is mapped into $\ket{\rightarrow\rightarrow\dots}$ because $\sum_{j,k=1}^{L}s_{j}A_{jk}=0$. It then follows that $\ket{\{0+a_{i}\}}=\ket{\{1,1,\dots\}}$ satisfies the same condition, and is mapped to the paramagnetic state.

Finally, the boundary condition terms $s_{L}\hat{t}$ can be understood in the context of the phase map too. It is simply making the replacement

where $\hat{{\bf\it t}}=(0,\dots,0,1)$ for the twisted boundary condition. The reason why this term works is that it distinguishes the $\mathbb{Z}_{2}$ dual two states $\ket{\{s_{i}\}}$ and $\ket{\{s_{i}+a_{i}\}}$, i.e., $\hat{{\bf\it t}}\cdot{{\bf\it s}}\neq\hat{{\bf\it t}}\cdot({{\bf\it s}}+{{\bf\it a}})$, so the problem of ${\bf\it A}$ being rank $L-1$ and hence the map being non-unitary is resolved. Based on this, we can actually introduce other general $\hat{{\bf\it t}}$ with odd number of element $1$ that achieves the same purpose. Physically, such $\hat{{\bf\it t}}$’s correspond to twisting the spins odd times on the chain. That is, the kernel defines the twisted boundary condition that recovers the unitarity of KW duality.

This is exactly the problem solved by the Bilinear Phase Map construction: for each generalized KW duality, one simply needs to analyze its corresponding matrix ${\bf\it A}$ to straightforwardly derive these properties of the generalized duality.

We consider a generalized KW duality map under PBC described by BPM as

where ${\bf\it A}$ can be any $L\times L$ matrix defined on a ring with $L$ sites and each element is $\mathbb{Z}_{2}$ value, namely $A_{jk}=0,1$. In practice, we are more interested in ${\bf\it A}$ with reasonable properties such as translational invariance and locality. The properties of the corresponding BPM can be then easily read out from linear algebra of ${\bf\it A}$, as summarized in the Table 1.

Suppose the matrix ${\bf\it A}^{\text{T}}$ have $N$ linearly independent kernel vectors:

Then the BPM duality mapping does not distinguish state $\ket{\{s_{i}\}}$ and $\ket{\{s_{i}+b^{m}_{i}\}}$ due to

which shows explicitly that the mapping is not unitary. Moreover, the group $G$ generated by $U_{m}:\{s_{i}\}\to\{s_{i}+b^{m}_{i}\}$ will be mapped to the identity group acting on the dual spins under BPM.

This motivates us to consider the Hamiltonian invariant under $G$ since the Hamiltonian for $\hat{s}_{i}$ after BPM naturally commutes with identity. In particular, if the $\{s_{i}\}$-system is in $G$-SSB phase with $2^{N}$ degenerate ground state (these states are $\ket{{\bf\it 0}}$, $\ket{{\bf\it 0}+{\bf\it b}^{1}}$, $\ket{{\bf\it 0}+{\bf\it b}^{2}}$, $\ket{{\bf\it 0}+{\bf\it b}^{1}+{\bf\it b}^{2}}$ , …), the dual system is in the trivial or SPT phase with a unique ground state.

Recovering the unitarity can be achieved by additional terms ${\bf\it\hat{t}}\cdot{\bf\it s}$ to the BPM to distinguish the kernel states $\ket{\{s_{i}={b}^{m}_{i}\}}$ and the state $\ket{\{s_{i}=0\}}$ (several terms with different ${\bf\it\hat{t}}$’s may be needed if there are several kernels).

Finally, the fusion rule of BPM and its conjugation can be directly computed by

In particular, when the matrices ${\bf\it A}$ and ${\bf\it A}^{T}$ are related by translation over $n$ sites

we can further calculate the fusion of two BPMs:

where $T$ is the translation operator: $T\ket{\{s_{i}\}}=\ket{\{s^{\prime}_{i}=s_{i-1}\}}$ [94, 26].

When $h=\infty$, this system is in a trivially gapped phase with a paramagnetic ground state $\ket{\rightarrow\rightarrow\cdots}$. When $h=0$, this system has SSB ground states that we need to understand.

Similar to the usual two-site Ising model with the transverse field, these two phases can be related by a generalized KW duality [73], under PBC given by

Its BPM matrix is

Then the properties of symmetry and SSB ground state degeneracy can be directly derived from the expression of ${\bf\it A}_{\text{3-KW}}$. The associated ${\bf\it A}_{\text{3-KW}}^{T}$ matrix has a two dimension kernel space generated by

which shows that the system has a $(\mathbb{Z}_{2})^{2}$ symmetry:

In operator form, they are written as

which satisfies the algebra with translation $TU_{A}T^{-1}=U_{G},T^{2}U_{G}T^{-2}=U_{A}$. The states can be organized into eigenstates of $U_{A/G}$ with eigenvalue $(-1)^{u_{A/G}}=\pm 1$, i.e. $u_{A/G}=0,1$.

From the all spin-up state, this $(\mathbb{Z}_{2})^{2}$ symmetry can generate all ground states of SSB phases as $\ket{{\bf\it 0}}$, $\ket{{\bf\it 0}+{\bf\it b}^{1}}$, $\ket{{\bf\it 0}+{\bf\it b}^{2}}$, $\ket{{\bf\it 0}+{\bf\it b}^{1}+{\bf\it b}^{2}}$:

and all these ground states are mapped to $|\rightarrow\rightarrow\cdots\rangle$ by $N_{\text{3-KW}}$ under PBC.

Moreover, one can directly check this BPM induces the following transformation of Pauli operators

and map the transverse field $h$ in eq. (15) to $1/h$. Thus the dual model also has a $(\mathbb{Z}_{2})^{2}$ symmetry generated by

Likewise, the dual Hilbert space can also be organized into four symmetry sectors labeled by $(\hat{u}_{A},\hat{u}_{G})\in\{0,1\}^{2}$. By acting the products of operators on a general state, we further find the fusion rules under PBC ¹¹1Unlike the conventional KW duality, the translation and its square, in this case, are not reduced to identity in the low energy limit, as they satisfy the nontrivial algebra with $(\mathbb{Z}_{2})^{2}$ symmetry operators.:

Now, let us discuss the unitarity problem of BPM by introducing boundary spins $(\hat{t}_{A},\hat{t}_{G})\in\{0,1\}^{2}$ in $\{\hat{s}_{i}\}$-system, which corresponds to the untwisted/twisted boundary conditions of $(\mathbb{Z}_{2})^{2}$ symmetry [96, 97, 97, 98, 99]:

Then we can modify the BPM as follows:

This modified BPM can distinguish four SSB ground states, satisfying that $s_{j-2}+s_{j-1}+s_{j}=0$. The BPM maps them to the same state

that is the paramagnetic state $|\rightarrow\rightarrow\cdots\rangle$ with a phase $(-1)^{\hat{t}_{A}s_{L-1}+\hat{t}_{G}s_{L}}$. When $\hat{t}_{A}=\hat{t}_{G}=0$, this phase is trivial and only linear combination $\sum^{4}_{i=1}\ket{\text{GS}}_{i}$ with $u_{1}=u_{2}=0$ survives. But when $\hat{t}_{A}=1$ and $\hat{t}_{G}=0$, two ground states with $s_{1}=1$ will have additional $-1$ sign after mapping. Then only linear combination $(\ket{\text{GS}}_{1}+\ket{\text{GS}}_{4}-\ket{\text{GS}}_{2}-\ket{\text{GS}}_{3})$ survives under BPM duality. This combination has symmetry charge $u_{A}=u_{G}=1$. On the other hand, when $\hat{t}_{A}=0$ and $\hat{t}_{G}=1$, two ground states with $s_{L}=1$ will have additional $-1$ sign after mapping. Only linear combination $(\ket{\text{GS}}_{1}-\ket{\text{GS}}_{4}+\ket{\text{GS}}_{2}-\ket{\text{GS}}_{3})$ survives under BPM, which has symmetry charge $u_{A}=0,u_{G}=1$. This statement above is also consistent with symmetry-twisted sector mapping in the appendix.

Now, since there are SPT, trivially gapped and SSB phases, we can construct a web of duality connecting them, which is summarized in Fig. 1.

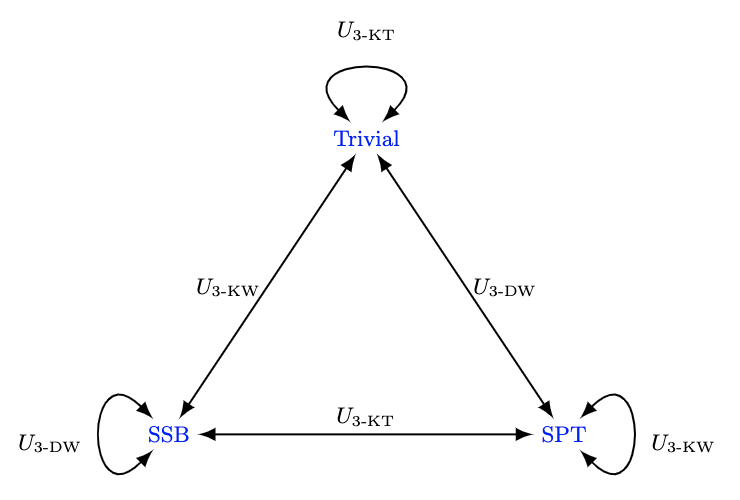
Here $U_{\text{3-KT}}$ is a generalized Kennedy-Tasaki transformation [23, 91]:

Moreover, such a web of duality can also connect phase transitions between two different gapped phases, as shown in Fig. 2. These duality-related three phase transitions have the same center charge $c=1$.

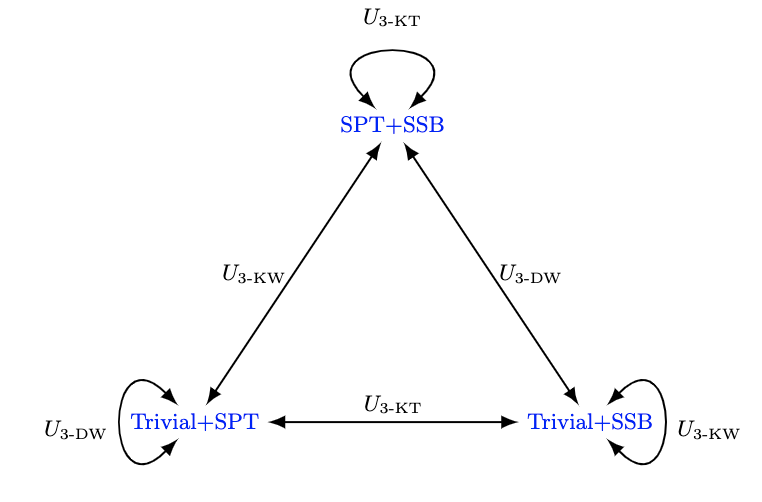
Lastly, we have constructed another BPM duality example that connects $H=-\sum X_{i}$ and $H=-\sum Z_{i}Z_{i+1}Z_{i+2}Z_{i+3}$ in the appendix. Interestingly, on self-dual points, this duality becomes an anomalous symmetry, which guarantees the self-dual theory must be either a first-order or continuous phase transition.