Generalized effective-potential Landau theory for a tunable state-dependent hexagonal optical lattice

Graphene has a profound impact in condensed matter physics owing its linear band dispersion around the Dirac point graphene1 ; graphene2 . In solids, many properties of the electrons, such as the effective mass, the velocity and their interactions, are rigidly determined by the sample itself Creating-D , and it is hardly changed. Consequently, it restricts the potential application of graphene. In recent years, stimulated by the extraordinary properties of graphene, the emulation of graphene-like physics in artificial hexagonal or hexagonal-like lattices systems (artificial graphene) is booming Artificial-graph . In progress of the engineering novel optical lattices engineering-OL , ultracold atoms in hexagonal-like optical lattices provide an avenue to exploring the novel phenomenon which hardly exists in graphene Creating-D ; hexagonal1 ; hexagonal2 ; hexagonal3 ; hexagonal4 ; hexagonal5 ; hexagonal6 ; hexagonal7 ; hexagonal8 .

In ultracold systems, bosons in the state-dependent hexagonal optical lattice is the first realization of an artificial graphene system hexagonal1 . Here the site-offset energy between two sublattice is dependent on the lattice depth and the value of the effective magnetic quantum number $m$ of bosons, moreover its strength can be easily tuned. In this novel optical lattice, the phase diagrams of the single-component quantum gas with various values of $m$ have been numerically studied using cluster Gutzwiller method hexagonal-Gutzwiller . Furthermore, the numerical results indicate that the phase diagrams strongly depend on the values of $m$. However, there is still a lack of analytical results for the phase diagrams of Bose gas in state-dependent hexagonal optical lattice.

So far, the phase diagrams of ultracold bosons in complex optical lattice (such as hexagonal, Kagomé optical lattice, and optical superlattice induced by dipolar interaction) could have been obtained by several analytical methods, including mean-field theory SC1 , random-phase approximation RPA , strong-coupling expansion (SCE) method SC1 ; SC2 ; SC3 , and the generalized Green’s function method GGF1 ; GGF2 , the generalized effective-potential Landau theory (GEPLT) wang ; zhi-4 ; zhi-5 . Although the effect of high-order corrections is more obvious in a system with small coordination number, there are still only two analytical methods, i.e., SCE method and GEPLT, which are easy to calculate the high-order corrections of the phase boundaries.

There are some technical issues zhi-4 in the former GEPLT wang ; wei , but fortunately these issues are clarified in our previous work zhi-4 . We have revealed that the clarified GEPLT is extremely well for obtaining the phase diagrams of ultracold bosons in two different type bipartite superlattices zhi-4 ; zhi-5 : one is a bipartite superlattice caused by superlattice structure, and the other one is a bipartite superlattice induced by dipolar interaction (induced bipartite superlattice). More specifically, the phase boundaries of the third-order corrections obtained by the clarified GEPLT are in excellent agreement with the quantum Monte Carlo (QMC) simulations in bipartite superlattice zhi-4 . In induced bipartite superlattice, the third-order results obtained by the clarified GEPLT are better than the third-order SCE calculations for weak nearest-neighbor repulsion zhi-4 and these results are also in complete agreement with QMC calculations for second-order phase transition zhi-5 .

In this paper, with the help of GEPLT, we can study the phase diagrams of single-component quantum gas with different $m$, i.e., $m=0$, $m=0.02$ and $m=0.1$, in state-dependent hexagonal optical lattice. In our previous work zhi-4 , the phase boundaries of the bosons in the normal bipartite superlattice, in which the site-offset energy $\epsilon$ is independent on the trapping lattice depth, have been analytically calculated by the GEPLT. Compared with QMC simulations of this system, we find that our third-order analytical calculations are in excellent agreement with QMC simulations zhi-4 . Therefore, we are sure that the GEPLT will be a high-accuracy analytical method for studying the phase diagrams of ultracold bosons in a state-dependent hexagonal optical lattice, in which the site-offset energy $\epsilon$ is dependent on lattice depth and $m$.

The state-dependent hexagonal optical lattice has been realized in the experiment hexagonal1 , and the total trapping potential hexagonal1 ; hexagonal-Gutzwiller ; bbm-Gutzwiller reads

$$V(\textbf{r})=-V_{0}\left[V_{\rm{Hex}}+V_{\rm{pol}}\right],$$

(1)

where $V_{0}$ is the corresponding lattice depth. Here the state-independent potential reads

$$V_{\rm{Hex}}=6-2\sum_{i}\cos(\mathbf{b}_{i}\mathbf{r}),$$

(2)

and state-dependent potential for $|F,m_{F}\rangle$ state reads

$$V_{\rm{Hex}}=\sqrt{3}(-1)^{F}m_{F}cos\alpha\,\eta\sum_{i}\sin(\mathbf{b}_{i}\mathbf{r}),$$

(3)

with $\mathbf{b}_{1}=2\pi/\lambda(\sqrt{3},0,0)$, $\mathbf{b}_{2}=\pi/\lambda(-\sqrt{3},3,0)$ and $\mathbf{b}_{3}=\pi/\lambda(-\sqrt{3},-3,0)$, where $\alpha$ is the angle between the quantization axis (or orientation of homogeneous magnetic field $\mathbf{B}$) and lattice plane, and $\eta=0.13$ is dimensionless proportionality factor hexagonal-Gutzwiller . Here we can define a effective magnetic quantum number $m=(-1)^{F+1}m_{F}cos\alpha$ hexagonal-Gutzwiller , and it is clear that the ranging of $m$ can continuously be adjusted from $-m_{F}$ to $m_{F}$. In Ref. hexagonal1 , the wavelength of the lattice laser beams is chosen as $\lambda=830$ nm, and the corresponding lattice constant is $a=2\lambda/(3\sqrt{3})$.

In Dirk-Sören Lühmann et al.’s work hexagonal-Gutzwiller , the optimal Wannier functions are determined in such a way that the amplitudes of processes beyond the Hubbard model are minimized. By choosing this optimal Wannier functions, the corresponding Hamiltonian of the state-dependent hexagonal optical lattice can read hexagonal-Gutzwiller

$$\hat{H}=-J\!\sum_{\langle i,j\rangle}\!\hat{a}_{i}^{\dagger}\hat{a}_{j}+\!\frac{1}{2}\sum_{i}\!U_{i}\hat{n}_{i}(\hat{n}_{i}-1)+\sum_{i}(\epsilon_{i}-\mu)\hat{n}_{i},$$

(4)

where $J$ is the nearest-neighbor tunneling, $\hat{a}_{i}$ ($\hat{a}_{i}^{\dagger}$) is the boson annihilation(creation) operator at site $i$, $\hat{n}_{i}=\hat{a}_{i}^{\dagger}\hat{a}_{i}$ is the particle-number operator on $i$-th site, $U_{i}$ denotes the on-site repulsion at site $i$, $\mu$ is the chemical potential, and $\epsilon_{i}$ is the site-offset energy($\epsilon_{A}=0$ and $\epsilon_{B}=\epsilon$ for sublattice A and B). Since only the site-offset energy $\epsilon$ is approximately linearly dependent on the parameter $m$ hexagonal-Gutzwiller , but the other interactions are weak dependent on $m$, i.e., $J(m)\approx J$ and $U_{A}(m)\approx U_{B}(m)\approx U$ (see the Figs. 8 in the ref. hexagonal-Gutzwiller ), and therefore the phase boundaries in the ref. hexagonal-Gutzwiller can be obtained by using cluster Gutzwiller method to study the standard Hubbard model, in which the on-site repulsions $U_{A}$ and $U_{B}$ are assumed to be equal.

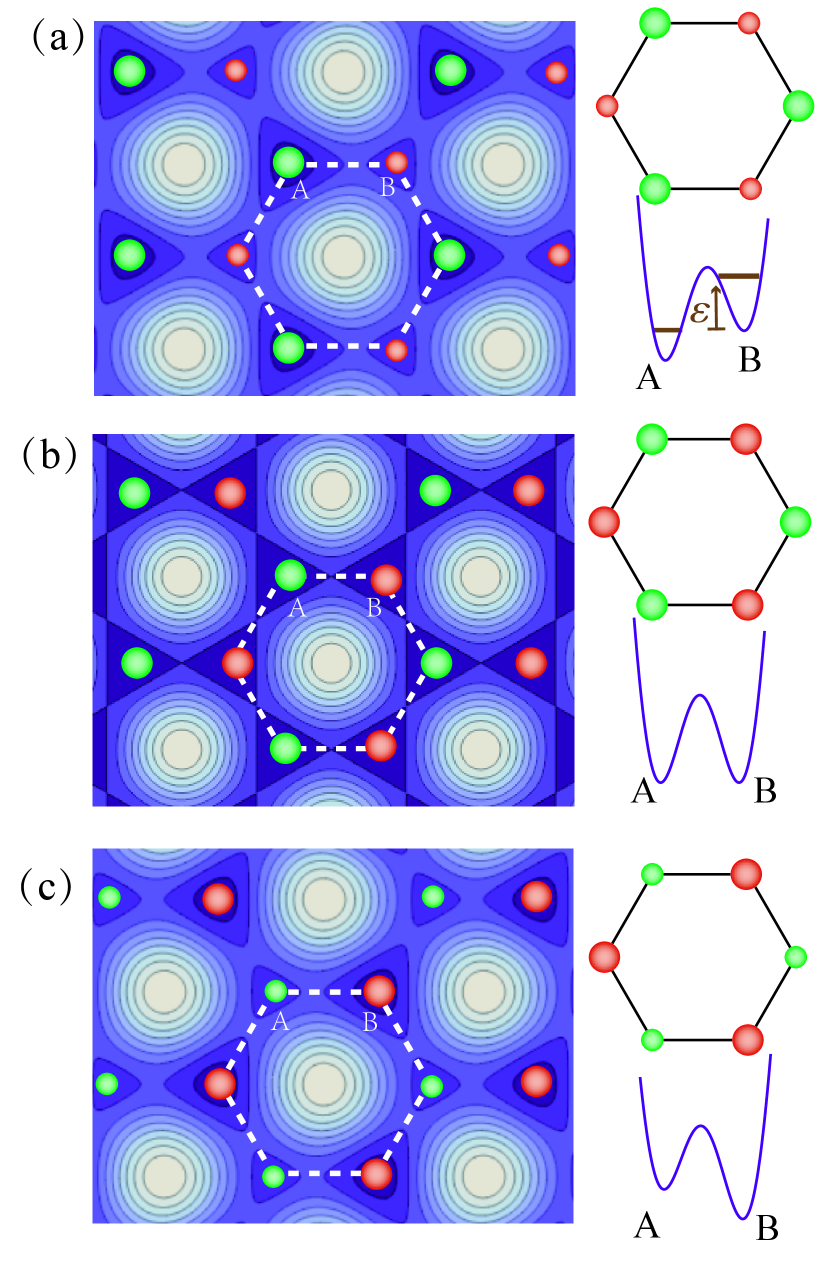
Before calculating the phase diagrams, we would like to discuss the possible ground states of the systems in the atomic limit ($J=0$). In this limit, the ground states are determined by the competing between the on-site interaction $U$ and the site-offset energy $\epsilon$. If the Mott lobe $(n_{A},n_{B})$ with the imbalance $\Delta n=n_{A}-n_{B}$ and the fixed filling $\rho=(n_{A}+n_{B})/2$ is in existence, $\epsilon$ needs to meet the constraint $\Delta n-1<\epsilon/U<\Delta n+1$ obtained by solving the inequations $E_{n_{A}+1,n_{B}-1}>E_{n_{A},n_{B}}<E_{n_{A}-1,n_{B}+1}$, where $n_{B}$ is nonzero. In the case of $n_{B}=0$, the Mott lobe $(1,0)$, i.e., $\Delta n=1$, can always exist in the systems with $\epsilon/U>0$. The site-offset energies $\epsilon(m=0)/U$, $\epsilon(m=0.02)/U$ and $\epsilon(m=0.1)/U$ as a function of the variational trapping lattice depth $V_{0}$ are shown in Fig. 2, respectively. In the deep lattice depth, due to the $\epsilon(m=0.02)/U$ in the range of $(0,1)$, therefore the $\Delta n$ for the Mott lobes $(n_{A},n_{B})$ can take two values $\Delta n=0$ and $\Delta n=1$. For the similar reason, the $\Delta n$ can take three values, i.e., $\Delta n=1$, $\Delta n=2$, and $\Delta n=3$ in the system with $m=0.1$, where we have $2<\epsilon(m=0.1)/U<3$. Taking $m=0.02$ as an example, we will analyse the chemical potential width of the Mott lobes $(n_{A},n_{B})$. In the Mott lobes $(n,n)$ [$(n,n-1)$], the chemical potential should satisfy constraint inequations $E_{n,n-1}\geq E_{n,n}\leq E_{n+1,n}$ ($E_{n-1,n-1}\geq E_{n,n-1}\leq E_{n,n}$), i.e., $\epsilon+U(n-1)\leq\mu\leq Un$ [$U(n-1)\leq\mu\leq\epsilon+U(n-1)$], where the $E_{n,n}$ is the eigenvale of the $\hat{H}(J=0)$. More specifically, the chemical potential widths of the Mott lobes $(1,0)$, $(1,1)$, $(2,1)$, $(2,2)$, $(3,2)$ and $(3,3)$ are $0\leq\mu\leq\epsilon$, $\epsilon\leq\mu\leq U$, $U\leq\mu\leq\epsilon+U$, $\epsilon+U\leq\mu\leq 2U$, $2U\leq\mu\leq\epsilon+2U$, and $\epsilon+2U\leq\mu\leq 3U$, respectively.

We can make a reasonable assumption that the features of the Mott lobes obtained in the limit $J=0$ will not change when we keep $J/U\ll 1$. Hence, the region of Mott lobes $(n,n)$ will expand with increasing the value of $J/U$ (or decreasing the value of the lattice depth) in the deep lattice ($J/U\ll 1$), owing the fact that $\epsilon$ is decreasing with increasing the value of $J/U$. This feature of Mott lobes $(n,n)$ is in contrast to the feature of Mott lobes $(n,n)$ in normal superlattice system in which the $\epsilon$ is constant (do not change with the lattice depth), and this feature has clearly been shown in Fig.  4(b) [or see the Fig. 9(b) in ref. hexagonal-Gutzwiller ].

As mentioned above, the features of the Mott lobes have been revealed in the atomic limit ($J=0$). At below, we will introduce the GEPLT to study the phase boundaries of single-component quantum gas in state-dependent hexagonal optical lattice, in which the site-offset energy $\epsilon$ is dependent on lattice depth $V_{0}$ and effective magnetic quantum number $m$. In our previous work zhi-4 , we have revealed that the GEPLT is good enough to obtain phase boundaries of bipartite superlattice with the fixed site-offset energy $\Delta\mu$ which is independent on $V_{0}$. By mapping $\mu\rightarrow\mu+\epsilon$ and $\epsilon\rightarrow\Delta\mu$, then the forms of the Hamiltonian in state-dependent hexagonal optical lattice and the normal bipartite superlattice are the same. Thus, we can directly use the GEPLT, which is established in normal bipartite superlattice system with the fixed site-offset energy $\Delta\mu$, to study the phase diagrams of the state-dependent hexagonal systems. Immediately, we can obtain the first three orders of the phase boundaries $J^{(n)}_{c}$ of single-component quantum gas in state-dependent hexagonal optical lattice, which read

$$J^{(1)}_{c}=\sqrt{\alpha_{2AA}^{(0)}\alpha_{2BB}^{(0)}}/\alpha_{2AB}^{(1)},$$

(5)

$$J^{(2)}_{c}=\frac{2\sqrt{\alpha_{2AA}^{(0)}\alpha_{2BB}^{(0)}}\alpha_{2AB}^{(1)}}{\alpha_{2AA}^{(0)}\alpha_{2BB}^{(2)}+\alpha_{2BB}^{(0)}\alpha_{2AA}^{(2)}},$$

(6)

$$J^{(3)}_{c}=\frac{\alpha_{2AA}^{(0)}\alpha_{2BB}^{(2)}+\alpha_{2BB}^{(0)}\alpha_{2AA}^{(2)}}{2\sqrt{\alpha_{2AA}^{(0)}\alpha_{2BB}^{(0)}}\alpha_{2AB}^{(3)}},$$

(7)

where $\alpha^{(n)}_{2ij}$ are perturbative coefficients for state-dependent hexagonal systems. With the help of Raylieigh-Schrödinger perturbation expansion, we can easily calculate the values of these perturbative coefficients $\alpha^{(n)}_{2ij}$. The specific process of calculating the perturbative coefficients $\alpha^{(n)}_{2ij}$ have been clearly demonstrated santos ; zhi-1 ; wang ; zhi-5 .

With the help of the phase boundaries in Eqs. (5)-(7), we can analytically obtain the first three orders of the phase boundaries with effective magnetic quantum number $m=0$, $m=0.02$ and $m=0.1$, respectively.

From the Fig. 4, it is easy to find that our analytical results are consistent with cluster Gutzwiller simulations for effective magnetic quantum number $m=0$ and $m=0.02$. In the case of $m=0.1$, our analytical results are in good accord with cluster Gutzwiller calculations in the Mott lobe $(2,0)$ for the large interval, and only in small interval $\mu/U\in(1.04,1.15)$, there are some deviations between our analytical results and cluster Gutzwiller simulations hexagonal-Gutzwiller . Moreover, it is interesting that the Mott phase $(2,1)$ forms a island in contrast to a normal lobe in the parameter space. In order to obtain the outline of the Mott island, we need to consider at least the contributions of third-order corrections, the first two orders of the calculations do not have ability to obtain this interesting Mott island [See Fig. 4(c)]. One of the possible reasons why there are some deviations between our results and cluster Gutzwiller calculations for the Mott island $(2,1)$ and Mott lobe $(2,0)$ in small interval $\mu/U\in(1.04,1.15)$ is that the type of phase transitions from Mott island or lobe to superfluid is dependent on $\mu$. This interesting phenomenon has been revealed in the bipartite lattice system caused by dipolar interaction Ohgoe . More specifically, the phase transition is maybe a fist-order or weak fist-order phase transition for Mott lobe $(2,0)$ [Mott island $(2,1)$] with small (large) $\mu$, but the phase transition is second-order phase transition in the other regions.

In order to study the deviations of the tips of Mott phases obtained by these two methods, we also reveal the universal $\epsilon/U$-$J/U$ phase diagrams, in which each point $(\epsilon/U,J/U)$ represents the tip of the Mott phase in $J-\mu-U$ phase diagrams for the fixed $\epsilon/U$. From the Fig. 5, it is clear that the values of the tips obtained by our analytical method are perfectly consistent with cluster Gutzwiller simulations, the relative deviations of our third-order results and cluster Gutzwiller calculations are less than $9\%$($5\%$) for Mott insulator with (half-)integer filling.

The phase diagrams of single-component Bose gas with various values of $m$ in the state-dependent hexagonal optical have been revealed by using the GEPLT. In the case of $m=0.02$, we reveal that the Mott lobes $(n,n)$ will abnormally expand with increasing $J/U$ in deep lattice. The reason why there exists such abnormally expanding phenomenon is that the site-offset energy $\epsilon$ decreases with increasing $J/U$. Furthermore, this interesting phenomenon can be detected in this novel lattice with a harmonic confinement by using in situ imaging techniques Ott . In the case of $m=0.1$, we find that our third-order analytical results can well demonstrate that the outline form of the Mott phase $(2,1)$ is island. More generally, the first three orders of the corrections have also been calculated analytically, and our third-order analytical results are in good agreement with the numerical solutions obtained by cluster Gutzwiller method. Besides, the values $J_{c}/U$ of the tips in the Mott phases as a function of the site-offset energy $\epsilon/U$ have also been calculated analytically. Compared to cluster Gutzwiller simulations, the relative deviations of these tips of our third-order results are less than $9\%$ ($5\%$) for Mott insulator with (half-)integer filling. Thus, the GEPLT as an accurate analytical method, which is easy to obtain higher orders hopping corrections, has tremendous potential especially for studying the second-order quantum phase transition of ultracold bosons in lattices with small coordination numbers, for example, artificial hexagonal-like lattices systems.