General Chaotic Behaviors of Heavy ion Collisions at Intermediate Energy Based on Dynamical Transport Model

Entropy is an important thermodynamic quantity. The variation of its’ magnitude reflects the confusion in the microscopic state of a system, or the equilibrium of the system under certain macroscopic condition. And thus the entropy production in the HICs has attracted considerable attention in both nuclear physics and nonlinear dynamics [12,29]. In 1981, Bertsch and Cugnon[30] studied quantitatively the entropy production in the collision of ${}^{40}Ca+^{40}Ca$ at incident energy $E=800MeV$ within cascade model and concluded that the generation of the entropy is closely related to the formation of clusters. In Ref.[31], based on the fireball model, the authors investigated the same issue and speculated that the amount of the entropy production is not the same during the various stage of nuclear reactions and pointed out that there is barely entropy generation in the final stage, expansion stage, since the density of the particle has become to be so small, thus they seldom collide and the Liouville’s theorem guarantees that the density of particles in phase space remains constant in the absence of collisions. However, S. Das Gupta et. al. [32] developed a microscopic model for treating the fragmentation of nuclear matter in which both hard collision and propagation of nucleons are treated. They argued that the mean field can lead to fragmentation of nuclear matter and increase of the entropy simultaneously. Therefore, the mechanism responsible for, and the significance of, the entropy generation in HICs have been a matter of much disputed issue in nuclear physics[29]. Here we want to observe the variation of the entropy in the real nuclear reaction instead of the schematic model.

The entropy for a Fermi system is defined by[31]

$$S=-\int d\gamma[{f\ln(f)-(1-f)\ln(1-f)}],~{}~{}~{}~{}~{}~{}~{}~{}d\gamma=g\frac{d{\vec{r}}d{\vec{p}}}{(2\pi\hbar)^{3}}$$

$(6)$

where $f=f({\vec{r}},{\vec{p}})$ stands for the occupation probability of nucleon in a phase space volume of $h^{3}$ and $g=4$ is the degeneration of the spin-isospin degree of freedom. In order to avoid the complicated integration which is very time-consuming, we turn to calculate the time evolution of the coarse-grained entropy, namely, the so-called generalized entropy (GE) defined in Ref.[32] and adopt the ansantz used in Ref.[33]. Specifically, the available phase space is broken up into cells of volume $\beta h^{3}$ with $\beta$ being an adjustable parameter. Then the entropy becomes

$$S=-4\beta\sum_{i}[n_{i}\ln(n_{i})-(1-n_{i})\ln{(1-n_{i})}],~{}~{}~{}~{}~{}~{}n_{i}=\frac{N}{4R\beta}$$

$(7)$

where $N$ is the number of nucleons in a cell of volume $\beta h^{3}$ and $R$ the number of runs in our numerical simulation. $n_{i}$ indicates the occupation probability of a phase space of volume $h^{3}$. However, it is still not easy to perform the calculation of Eq.(7) in the six dimension space, in particular for a nucleus with large numbers of nucleons. Moreover, there is an uncertainty in the amount of $S$ which stems from the adjustability of the parameters, $\beta$, $R$ and the size of cells. Fortunately, Ref.[32] has proved that the trend of the variation of GE does not depend sensitively on the size of cells although the magnitude of entropy is determined significantly by the volume of a cell. Coincidentally, our main concerning focus mainly on the tendency of GE variation reflecting the chaotic behavior of the system. Therefore, we calculate the generation of GE in the central collision of ${}^{40}Ca+^{40}Ca$ at incident energy 800 MeV/u and the results are depicted in the Fig.1. It shows that the value of the entropy is saturated at $4.0-4.4$, which is a reasonable value quoted in Ref.[30] for 10 events or 800 nucleons. In the left panel of the Fig.1 the curves from bottom to top correspond respectively to the magnitude of mesh side-length in six dimension space, (a) $\Delta r=35fm$ , $\Delta p=0.29GeV/c$, (b) $\Delta r=24fm$ , $\Delta p=0.19GeV/c$, (c) $\Delta r=17fm$, $\Delta p=0.15GeV/c$ and (d) $\Delta r=14fm$, $\Delta p=0.12GeV/c$ with $\beta=0.8$ in each cases. Here the $\Delta r=max\{\Delta x,\Delta y,\Delta z\}$ and $\Delta p=max\{\Delta p_{x},\Delta p_{y},\Delta p_{z}\}$ are the largest side length of the mesh in coordinate and momentum, respectively. In the actual calculations, $\Delta x\neq\Delta y\neq\Delta z$ since the spread velocity of nucleons is not the same in different direction at a given time. The division of the momentum space is alike in coordinates space. Comparing the behavior of each curve we can learn that the sensitivity of the variation of the GE to the mesh size since the function $n_{i}\ln(n_{i})$ depends sensitively on the value of the distribution $n_{i}$, as has illustrated in the Fig.1 of Ref.[30]. The left panel in our Fig.1 shows that the magnitude of the entropy tends to saturation with decrease of the size of the cell. Of course, It can be expected that the location and the magnitude of the peak of $S$ will vary with the size of cells if we keep the size going down so that the most cells would be empty. But we are not going to do so because we have come to a reasonable range in the case (d) with the $S\approx 4.0\sim 4.4$ which is consistent well with the value given in Ref.[30]. We also notice that the increment $\Delta S\approx 0.1\sim 0.2$ produced in the expansion stage of the reaction[33] has been confirmed in our calculation.

Fig.1

Our results, obtained by using IQMD and the lattice method, demonstrate dynamically the production of the GE during the whole reaction process, i.e., the rapid increase in the stage of the collision phase and the slow growth in the expansion stage of the reaction. We can easily exhibit further the generation of GE in the coordinate space and the momentum space, separately, shown in the right panel of the Fig.1 obtained with any model parameter involved unchanged in the previous calculations. It is clearly seen that the GE grows much substantially in the momentum space (dash curve) than that in the position space (solid curve) in the compressed stage of the reaction where the bombarding energy converts rapidly into the thermal energy. In order to visualize the thermalization of the reaction process, we explore the averaged transverse momentum transfer(TMT) of the colliding system as has done in Ref.[34]. To this end it is needed first to determine the reaction plane by defining a vector

$${\vec{Q}}=\sum^{M}_{\mu}\omega{\vec{p}}^{t}_{\mu}$$

$(8)$

where ${\mu}$ is a particle index and $\omega_{\mu}=+1$ for nucleons with longitudinal momentum $p_{z}\geq 0$ and $\omega_{\mu}=-1$ for $p_{z}<0$. $M$ is the number of the nucleons with rapidity in the range of $-1.5\leq Y\equiv\frac{1}{2}\ln(\frac{E+p_{z}}{E-p_{z}})\leq 1.5$. The momentum of nucleon $\nu$ projected on the reaction plane, $p^{X}_{\nu}={\vec{p}}^{t}_{\nu}\frac{{\vec{Q}}_{\nu}}{|{\vec{Q}}_{\nu}|}$, can be used to estimated the average transverse momentum transfer in the reaction. Where ${\vec{Q}}_{\nu}={\vec{Q}}-{\vec{p}}^{t}_{\nu}$ and ${\vec{p}}^{t}_{\nu}=p_{x}(\nu){\vec{i}}+p_{y}(\nu){\vec{j}}$. The variation of averaged values $<P^{X}>$ for per particle in each event with respect to the time is plotted in Fig.2. It shows that the average transverse momentum transfer increases rapidly up to its summit at $t^{TMT}\simeq 16(fm/c)$ and then become nearly an constant. This indicate the relaxation time reflected by transverse momentum transfer is approximately consistent with that of the GE rapidly increase, $t^{GE}_{rap}\approx\ 22fm/c$, in the momentum space showing by Fig.1,comparing to the whole reaction time. The subtle differences between $t^{TMT}$ and $t^{GE}_{rap}$ can be explained by the statistical error in the calculations for their averaged values according to the different mathematical expressions. This approximate coincidence confirms further the conclusion drawn in Ref.[34] that the transverse momentum transfer should be viewed as a convenient tool which is complementary to entropy analysis and allow us to estimate the degree of thermalization of the reaction process.

Fig.2

Compared the rate of GE productions in different spaces, we can see that the transverse momentum transfer of the nucleons is much rapid than the diffusion of the nucleons in spatial space. And thus the change of GE in momentum space is faster than that in the position space since the increase rate of the GE is proportional to the rate of particle spread out. To be more precise, the increase of GE in the collision stage mainly comes from the thermalization of the colliding system, while the generation of GE in the expansion stage of the reaction stems mainly from the diffusion of the composite system.

It is worth to notice that the GE decrease slightly in the momentum space due to the reduce of the density in the momentum space with time, while it increases continuously in position space with respect to time in the expansion stage of the reaction. Nevertheless, the total amount of the GE is still increase slowly in the phase space showing by the curve (d) in the left panel of Fig.1. This behavior indicates that the expanding of the region in position space is partly compensated by the shrinking of the velocity distribution into a smaller region in the momentum space as the matter cools.

As has pointed out by Schuster[35] that the entropy increases not only due to the increase of the particle number, but also due to the dynamical fluctuations. We consider a multifractal description of that fluctuation and focus on the information dimension as a characterization of the entropy of the system. Fractal geometry is also a new science which devotes to answer the question how the microscopic behavior is related to what we observe on the macroscopic scale. According to the Fractal theory the information dimension $D_{I}$ is defined in[36]

$$D_{I}=-\lim_{\delta\to 0}\frac{S}{ln(\delta)}$$

$(9)$

with $\delta$ being the size of each cell.

In the Fig.3 we show the result for the central collision of ${}^{40}Ca+^{40}Ca$ at incident energy $E=800MeV/u$ at time $t=100fm/c$ when the generalized entropy has come to a plateau. In this figure the straight line is the fitted results with our computed results indicated by the scattering points and the extracted information dimension is $D_{I}=0.484$. $D_{I}$ is not an integer meaning the existence of the self-similarity in the distribution of the available phase space.

Fig.3

In 1999, Y.G. Ma introduced a method [37] to diagnose a nuclear liquid gas phase transition by multiplicity entropy(ME),

$$H=k_{b}\sum_{i}p_{i}\ln(p_{i}),$$

$(10)$

which determines the critical point by finding the maximum value of multiplicity entropy in a certain state of the system. In this definition $k_{b}$ is Boltzmann constant and the probability distribution $p_{i}$ is the ratio of the number of ‘i‘ particle produced by $N_{i}$ to the total number of particles produced by $N$, i.e. $p_{i}=N_{i}/N$ and $\sum_{i=1}^{N}p_{i}=1$. He used the ME to study the phase transition of nuclei in the framework of the isospin dependent lattice gas model and molecular dynamical model, and concluded for the first time that the maximum of the ME indicates that the system comes at a largest fluctuation/stochasticity/chaoticity in the event space. It is naturally making sense to check such behavior of the ME and compare it with the GE in the given reaction system under exactly the same incident conditions. Our calculated results for the ME for the reaction system considered here is presented in the left panel of Fig.4.

Fig.4

This figure shows that the maximum of the ME appears at the time $t^{ME}_{Max}\approx 16fm/c$, and the multiplicity reaches its’ maximum value at about $t^{Nimf}_{Max}\approx 22fm/c$ showing in the right panel of the Fig.4. The discrepancy between $t^{ME}_{Max}$ and $t^{Nimf}_{Max}$ is mainly caused by their different mathematical expressions since they are obtained by the analysis of the same set of simulation results. Therefore, the appearance of ME maximum reflects the formation of primary fragments and a phase transition from two colliding nuclei to multiple clusters, i. e. the multifragmentation phase transition. In the terminology of nonlinear dynamics, it is a transition from order to disorder of the nucleon motion involved in the reaction.

Comparing the behavior of the variations of the GE shown in the Fig.1 and the ME in Fig.4, we can see that both kinds of entropies have a common feature that they increase rapidly in the compress stage of the reaction. But there is a slight difference in time when the two kinds of entropies reach their respective maximum. This can be understood with the help of the behavior of the transverse momentum transfer which increase rapidly with time in this reaction stage, shown in the Fig.2. Meanwhile, in our calculation the clusters are constructed by using the coalescence model[38], which requires that the distance in phase space between nucleons belonging to one cluster must be less than $P_{0}$ and $R_{0}$ simultaneously. Specifically, $P_{0}=350MeV/c$ and $R_{0}=0.3fm$ here. In other words, the distance between nucleons belonging to different clusters must be greater than P0 and R0. However, in the calculations for the generalized entropy performed before the size of the lattice cells, e. g. $\Delta r=14fm$, $\Delta p=120MeV/c$ for the curve (d) in Fig.1, is not exactly equal to the values of $P_{0}$ and $R_{0}$. Namely, the nucleons located in one lattice cell may belong to different clusters and vice versa. Therefore, the time when the maximum of the multifragmentation entropy reached is not exactly same as that when the generalized entropy reaches its’ maximum. In our numerical results $t^{ME}_{Max}<t^{GE}_{rap}$. Anyway, the production of both types of the entropy is responsible for the increase in the disorder or the chaoticity of nucleons motion.

Intermittency is a manifestation of the scale invariance of a physical system or a nonlinear dynamical process and the randomness of underlying scaling law. According to nonlinear dynamics theory [39], the emergence of the intermittency during the spatial-temporal evolution of a dynamics system is considered as a indicative sign of chaotic behavior, similar to the period-doubling bifurcation. The original idea of the studying intermittency in nuclear collisions came from the work of Bialas and Peschanski [40] who looked at the rapidity distribution of produced particles in cosmic ray experiments. They proposed using scaled factorial moments of the rapidity distribution to study the possible appearance of intermittent behavior in such collisions and evidence for non-Poissonian fluctuations. The greatest merit of this method is that the factorial moments filter out the statistical fluctuation and retain only dynamical fluctuation which is just the most essential concern of the chaotic dynamics. The intermittent behaviour and the self-similarity pattern of the fluctuations in the charge distribution in the breakup of ${}^{197}Au+^{179}Au$ at energy $E=1GeV/u$ in a nuclear emulsion[41] have been explained by scaled factorial moment method based on the percolation model[40,41,42] and by the microcanonical model[42,43]. For the purpose of finding the critical phase transition signal, references [42,44,45] have studied the normal and factorial moments of fragment distribution in heavy ion collisions near the Fermi energy by quantum and classical dynamics models respectively and pointed out that the intermittency signal is most obvious near the critical phase transition point. As a typical signal of nonlinear dynamics and self-similarity of complex systems, here we quantitatively investigate the general performance of the factorial moments in our nuclear collisions.

The factorial moment defined by Bialas and Peschanski[40] is

$$F_{q}=M^{q-1}\frac{\sum^{M}_{m=1}n_{m}(n_{m}-1)...(n_{m}-q+1)}{N(N-1)...(N-q+1)}$$

$(11)$

Where the range $\Delta A$ of the distribution of fragment mass $A$ is divided into $M$ bins with each of interval $\delta A=\frac{\Delta A}{M}$. $N=\sum^{M}_{m=1}n_{m}$ is the total number of fragments with $n_{m}$ being the number of the fragments in bin $m$. The factorial moment for the central collision of ${}^{40}Ca+^{40}Ca$ at incident energies $E=800MeV$ is plotted in Fig.5. Where the results are obtained in the simulation of our colliding system for 1000 events.

Each curve corresponding to different $q$ in the Fig.5 looks roughly like a straight line indicating a power-like increase of the factorial moment with decreasing bins length. The slops of these fitted lines, $\alpha_{q}$, termed as the intermittency exponent[40,43], can be express as

$$F_{q}\propto(\delta Z)^{-\alpha_{q}}.$$

$(12)$

This is just the typical characteristics of the self-similarity[46] emerged at all scales in the distribution. The fractal dimension can be derived from the formula

$$d_{q}=\alpha_{q}/(q-1)).$$

$(13)$

Both the intermittency exponent $\alpha_{q}$ and fractal dimension $d_{q}$ for various $q$ are listed in Table I.

Table 1: the intermittency exponent and fractal dimension q 2 3 4 5 6 $\alpha_{q}$ 0.524 1.138 1.765 2.393 3.022 $d_{q}$ 0.524 0.569 0.588 0.598 0.604

As showing by the table I the fractal dimension $d_{q}$ is not integral indicating that there still is fractal structure in the fragmentation pattern though the incident energy is much higher than Fermi energy and the collision between nucleons more violence comparing to that considered Ref.[44-47]. Besides, there are a few characteristics worthy of our attention: (1) The factorial moment exponents increase with their order ’q’ indicating that the phase space structure of multifragmentation is a multifractal structure; (2) it is impossible to infer that whether the fragmentation process of the colliding system is a prompt fragmentation or sequent decay[42] due to the dimensions being neither constant nor directly proportional to $q$.

We have actually completed the calculations and analyses of the factorial moments for the colliding system considered here at different incident energies varying from $E=50MeV$ to $E=800MeV$. The results are similar to that showing in the Fig.5 except the magnitudes of the intermittency exponents increasing with the incident energy. Since the second factorial moment relate to the the mean value $<n_{m}>$ and the variance $\sigma_{m}$ of the multiplicity distribution in the $m$th bin, explicitly, $F_{2}=1+\frac{\sum_{m}(\sigma^{2}_{m}-<n_{m}>)}{\sum_{m}<n_{m}>^{2}}$, and hence we only plot the variation of the slop of $F_{2}$, i.e.,$\alpha_{2}$, as a function of the incident energy in Fig. 6.

Fig.6

This figure shows that the intermittency exponents increases monotonically with the incident energy though the rate of the increase varying with the energy.

It is generally believed that nuclear fragmentation occurs near the critical point of liquid-gas phase transition of nuclear matter based intensively on the studies both experimentally and theoretically. According to Fishers[48,49,50] semi-phenomenological droplet model for equilibrium liquid-gas transitions in infinite systems, the fragment mass distribution should be a power law multiplied by an exponential whose argument goes to zero at the critical point:

$$Y(A)=q_{0}A^{-\tau}\exp{\{A\Delta\mu-c_{0}\epsilon A^{\sigma}/T\}}$$

$(14)$

where A is the mass of the drop, $\Delta\mu$ is the difference of the chemical potentials of the gas and liquid phases, $\sigma$ is the surface tension. At the critical point $\Delta\mu$, $c_{0}$ and $\sigma$ go to zero and we are left with a simple power law,

$$Y(A)=q_{0}A^{-\tau}$$

$(15)$

For infinite systems in equilibrium the value of the exponent $\tau$ lies in $2<\tau<3$.

Ones have found that the power-law distribution exists universally in natural and social phenomena such as the distribution of citation of scientific papers[51]. At present there is no definite answer to the question about the dynamical mechanism of power-law distribution. The critical phase transition is one of the various speculated mechanisms. The existing studies have pointed out that the power-law distribution is a necessary condition for the critical phase transition, but is not a sufficient condition for a system being in equilibrium. In particular, the power-law behaviour can be observed in the non-equilibrium phase transition in the self-organized critical phase transitions which is a process of entropy reduction and ordering. In the context of nonlinear complex systems, the power-law distribution can be used as the evidence of the critical state of self-organizing systems[52], that is, a sign of the transition from steady state to chaotic state. Therefore, it is equally important for us to understand the dynamics mechanism of heavy ion collisions in nuclear physics and the generation mechanism of power-law distribution in nonlinear dynamics.

Here, again, we simulate the colliding system, ${}^{40}Ca+^{40}Ca$, due to its simplicity to explore the general features of the distribution of the intermediate mass fragments(IMF) in the final state of this reaction. The distributions of the fragments with masses in the range of $2<A\leq 10$ have been analyzed for the incident energies varying from $E=50MeV$ to $E=800MeV$ and the power law behaviors in these distributions have been checked. In Fig.7 we give the IMFs distribution( isolated square points ) and the fitted results(straight lines) at $E=100MeV$(up panel) and $E=800MeV$ (down panel). The resulting power law exponents are $\tau=2.17$ for $E=100MeV$ and $\tau=5.02$ for $E=800MeV$, respectively. In order to test the reliability of our fittings, we sample a set of 100000 data according to the standard power-law distribution function, $Y(x)\sim x^{-\tau}$ with $\tau$ taken as the corresponding fitted values, and compare the complement cumulative distribution functions(CCDF) of these standard models with that of our fitted data, so as to obtain the Kolmogorov Smirnov(KS) statistic[53], which is simply the maximum relative distance between the CCDFs of the models and the fitted data,

$$D=Sup[\frac{|S(x)-P(x)|}{\sqrt{P(x)*(1.0-P(x))}}].$$

$(16)$

Here $S(x)$ and $P(x)$ are the CCDFs of the data and the power-law model, respectively. The comparison is, as an example, presented in Fig.8 for $E=100MeV$ and the estimated $D=0.14$.

Fig.7

Fig.8

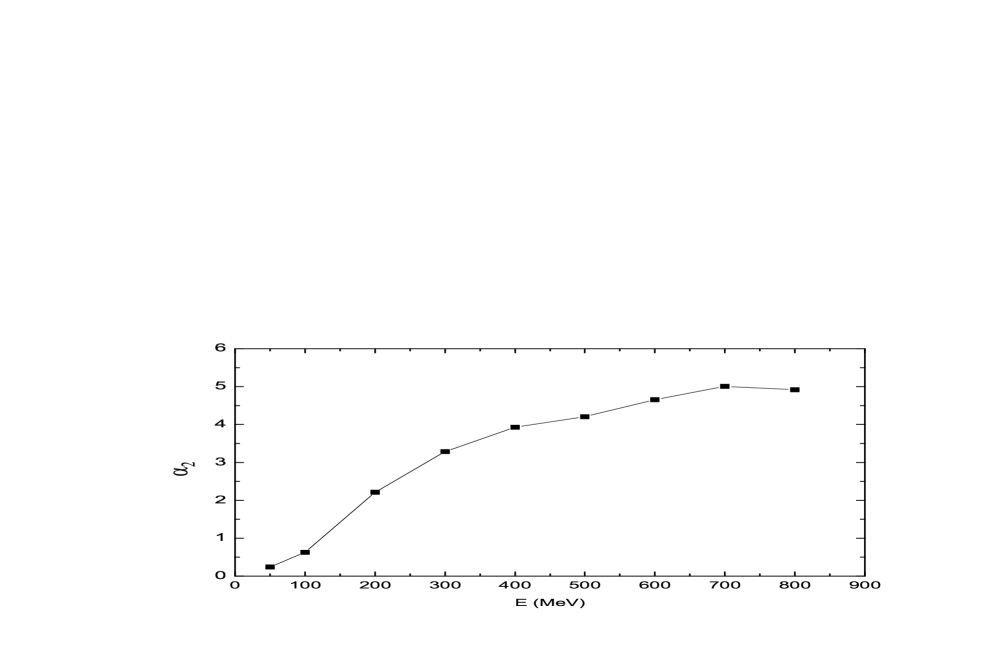
The variation of the power-law index(left pannel) and the KS statistic(right pannel) for the colliding system at various incident energies from 50MeV to 800MeV are depicted in Fig.9. It shows that the fitted power-law index and the corresponding KS statistics go up with the increase of the bombarding energy and the latter indicates the distribution come from our numerical fittings become more inconsistent with the their corresponding standard power-law distributions in the course of energy increasing. It should be especially pointed out here that our conclusion on the power-law distribution is obtained under the premise of a given collision system(40 nucleons), fixed fragment mass interval($2<A\leq 10$) and the number of simulation events(1000 runs) in the whole energy range considered to obverse the general characteristics of the nonlinear dynamics. Therefore, our calculation results are not enough to exact the most appropriate power law exponents, i.e., the minimum index. Such study is currently under way.

Fig.9

In order to exmine intuitively the difference of the multifragmentation of the colliding systems at various incident energy, we plot the largest fragments at different incident energies and analyze the normalized variance of the masses of the largest fragments(NVM), which is an alternative signal for testing the gas-liquid phase transition, proposed in Ref.[54]. The definition of NVM is

$$\sigma_{NVM}=\frac{<A_{MAX}^{2}>-<A_{MAX}>^{2}}{<A_{MAX}>}$$

$(17)$

where $A_{MAX}$ is the mass of the largest fragment and the symbol $<.>$ stand for the average over an ensemble of events at a given energy. The study of Ref.[54] have pointed out that there will be a maximum of the NVM in the critical region of a phase transition system. For our reaction, the changes of the NVM with increase of the incident energy are plotted in the left panel of Fig.10 and the maximum of the NVM emerges at $E=100MeV$ perspicuously. The average number of the largest fragments continues to decline with the increase of incident energy, showing in the right panel of Fig.10. Taking the appearances of this figure and Fig.9 together, we can learn that the characteristics of critical phase transition are the most obvious near $E=100MeV$ in the collision system and the energy region considered in this paper.

Fig.10