Galactic structure dependence of cloud-cloud collisions driven star formation in the barred galaxy NGC 3627

As an SFR tracer, we used the H$\alpha$ image provided by the PHANGS-MUSE project (Emsellem et al., 2022), which has the same resolution as the CO(2–1) data. The PHANGS-MUSE project provides fully calibrated data cubes and maps of 19 nearby galaxies including NGC 3627. From their data archive, we retrieved H$\alpha$ and H$\beta$ maps at $1.^{\prime\prime}05$ resolution. Note that [NII] lines around H$\alpha$ are fitted separately and that these maps are already corrected for the Milky Way foreground extinction. The observed flux ratio of H$\alpha$ to H$\beta$ is used to correct for internal extinction to the H$\alpha$ emission. We adopted parameters in Table 2 of Calzetti (2001) for this calculation, and excluded pixels where signal-to-noise ratio (S/N) $<3$ for either of the two emissions. If the calculated extinction becomes negative, no correction is applied. The median values of correction are 0.72 mag.

The $\Sigma_{\rm SFR}^{\rm ap}$ is derived as

where $L_{\rm H\alpha}^{\rm ap}$ is the attenuation corrected H$\alpha$ luminosity in the aperture, and $A_{\rm ap}$ is the deprojected area of the aperture. The coefficient of $5.37\times 10^{-42}~{}M_{\odot}~{}\rm yr^{-1}~{}erg^{-1}~{}s$ is the conversion factor from H$\alpha$ luminosity to the SFR obtained by Murphy et al. (2011). They adopted Kroupa IMF (Kroupa, 2001).

Because NGC 3627 is classified as a low-ionization nuclear emission-line region (LINER)/type 2 Seyfert galaxy (e.g., Ho et al., 1997; Filho et al., 2000), most of the H$\alpha$ emission in the center contains contamination from the AGN. Using the BPT diagram, i.e., $\rm[OIII]/H\beta$ versus $\rm[NII]/H\alpha$ diagram, most of the H$\alpha$ there were flagged as AGN (Emsellem et al., 2022; Groves et al., 2023). Therefore, the center region defined in Figure 2(a) is not used in this study because of the large uncertainties of the SFR.

We adopted the definition of the center, bar, and the bar-end regions by Maeda et al. (2023). Figure 2 shows the definition as black rectangles. Maeda et al. (2023) defined a rectangle to enclose the elliptical stellar bar defined based on Spitzer 3.6 $\mu$m by Herrera-Endoqui et al. (2015) and then divided the rectangle into five equal boxes. The position angle of the bar is $160^{\circ}$. The length and width of the black rectangle are 8.0 and 1.5 kpc, respectively. Among the five defined boxes, the central box is referred to as the “center,” the two ends as “bar-ends,” and the boxes between them as the “bar”. The length of the rectangle was set to 1.25 times the major axis of the elliptical stellar bar to ensure that the SFR peak at the edge of the ellipse and surrounding region are included as the bar-end region. The size of the center region is approximately four times the effective radius of the bulge (Salo et al., 2015), encompassing majority of the bulge light. Notably, most of the emissions flagged as AGN in the BPT diagram (Emsellem et al., 2022; Groves et al., 2023) are located within this center region.

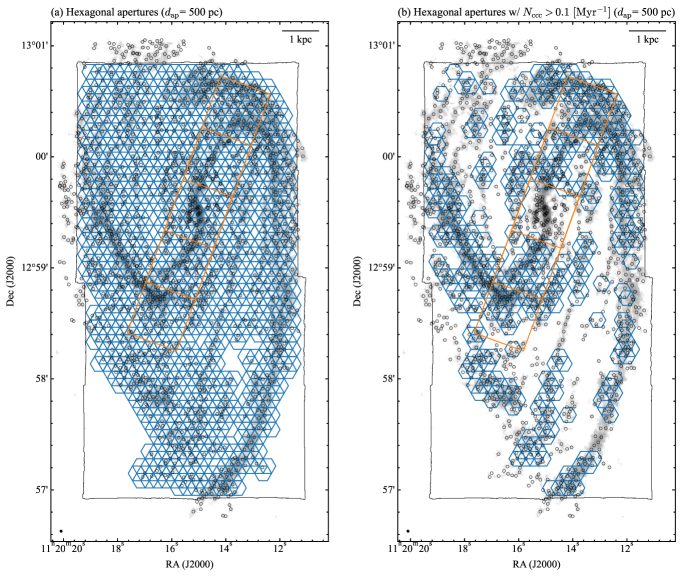
In this study, hexagonal apertures with a size (diameter) of $d_{\rm ap}=500~{}\rm pc$ were positioned to cover all the GMCs in the FoV of the H$\alpha$ image as shown in Figure 5(a). The centers of these apertures were spaced at intervals of $d_{\rm ap}/2=250~{}\rm pc$, representing a form of Nyquist sampling that minimizes arbitrariness in the aperture setting. The total number of apertures is 1157. The size of the aperture is roughly comparable to the width of the dust lane in the bar and arm region.

After excluding 157 apertures that contained only one GMC, we calculated the $v_{\rm col}$, $\nu_{\rm CCC}$, $N_{\rm CCC}$, $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$. To extract regions where the CCC-driven star formation is considered to be dominated, we then identified apertures with $N_{\rm CCC}\geq 0.1~{}\rm Myr^{-1}$ as regions where CCCs are considered to occur frequently. The apertures in the center region were excluded from the analysis due to the inability to estimate $\Sigma_{\rm SFR}$ accurately because of the LINER activity (see Section 3.2). As a result, 406 apertures were extracted from a total of 1157 apertures. Figure 5(b) illustrates the apertures used in our analysis, showing that apertures on the bar, bar-end, and spiral arms were selected. The number of apertures in the bar-end and bar region are 51 and 54, respectively. This figure shows that regions with strong CO(2–1) emissions generally correspond to regions where CCCs are frequent in NGC 3627. The dependencies of our results on the $d_{\rm ap}$ and the aperture extraction criterion are discussed in Section 5.1.

Table 1 shows the median values of the physical properties within the apertures ($d_{\rm ap}=500~{}\rm pc$) with $N_{\rm CCC}>0.1~{}\rm Myr^{-1}$ in each region. The scatter is defined as the distance from the 25th percentile to the 75th percentile (the so-called “interquartile range”, IQR). In this table, “Disk” refers to the subgroup of 301 apertures other than the bar-end and bar regions. Most of the apertures classified as “disk” are located within the spiral arms, although some are in the inter-arm regions as well. Similar to Figures 3(c)-(d), the $\bar{M}_{\rm GMC}$ and ensemble mean GMC surface density in the aperture, $\bar{\Sigma}_{\rm GMC}$, are the highest in the bar-end region. The $\Sigma_{\rm SFR}^{\rm ap}$ derived from H$\alpha$ emission in the bar-end region is about 6 times higher than that in the disk region.

Figure 5(a) shows the distribution of the collision velocity, $v_{\rm col}$. The median $v_{\rm col}$ in NGC 3627 is 19.4 $\rm km~{}s^{-1}$. We find that the $v_{\rm col}$ in the bar region is higher, with a median of 44.4 $\rm km~{}s^{-1}$, compared to a median of 21.0 $\rm km~{}s^{-1}$ in the bar-end region. The calculated $\nu_{\rm CCC}$ and $N_{\rm CCC}$ are also higher in the bar region compared to the bar-end region. This is primarily due to the difference in the $v_{\rm col}$ because there is no significant difference in the $n_{\rm GMC}$ between the bar and bar-end regions. The collision timescale for a GMC, $t_{\rm CCC}$, is the inverse of the $\nu_{\rm CCC}$, which is 27.3, 9.89, and 21.7 Myr in the disk, bar, and bar-end regions, respectively.

Figure 5(b) and (c) show the distribution of the total mass of stars formed per CCC, $m^{\star}_{\rm CCC}$, and the SFE per CCC in the aperture, $\epsilon_{\rm CCC}$, respectively. In NGC 3627, the median $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ are $10^{4.30}~{}M_{\odot}$ and $0.73~{}\%$, respectively. Moreover, the median $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ are lower in the bar region, at $10^{3.84}~{}M_{\odot}$ and $0.18~{}\%$, and higher in the bar-end region, at $10^{4.89}~{}M_{\odot}$ and $1.10~{}\%$, compared to $10^{4.28}~{}M_{\odot}$ and $0.75~{}\%$ in the disk region. These findings suggest that star formation activity driven by CCCs is suppressed in the bar region and enhanced in the bar-end region relative to the disk region in NGC 3627. We observe that both $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ decrease along the bar from the bar-end toward the center, with $m^{\star}_{\rm CCC}$ declining from $\sim 10^{5.5}~{}M_{\odot}$ to $\sim 10^{3.5}~{}M_{\odot}$ and $\epsilon_{\rm CCC}$ decreasing from $\sim$10% to $\sim$0.01%.

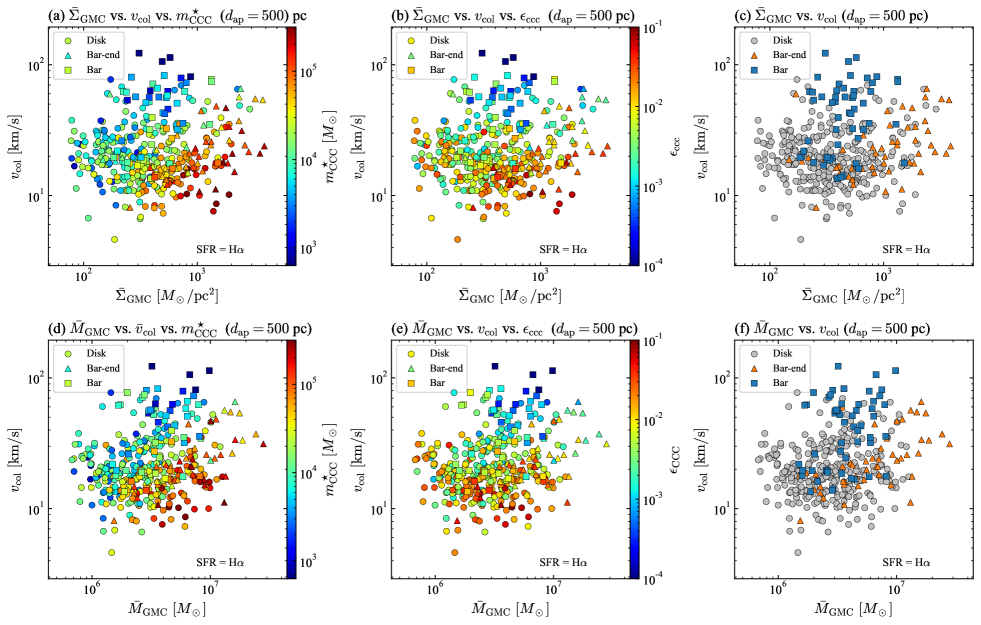
This section explores the connections between the SFR and SFE of the colliding GMC, collision velocity and GMC mass (or surface density), and galactic structures. Figure 6(a) shows the dependence of $m^{\star}_{\rm CCC}$ on $v_{\rm col}$ and $\bar{\Sigma}_{\rm GMC}$. The $m^{\star}_{\rm CCC}$ decreases with both increasing $v_{\rm col}$ and decreasing $\bar{\Sigma}_{\rm GMC}$. When $v_{\rm col}$ exceeds $50~{}\rm km~{}s^{-1}$ and $\bar{\Sigma}_{\rm GMC}$ is below $300~{}M_{\odot}~{}\rm pc^{-2}$, $m^{\star}_{\rm CCC}$ generally remains under $10^{4}~{}M_{\odot}$. Figure 6(b) shows dependence of $\epsilon_{\rm CCC}$ on $v_{\rm col}$ and $\bar{\Sigma}_{\rm GMC}$. Similar to $m^{\star}_{\rm CCC}$, the $v_{\rm col}$ dependence of $\epsilon_{\rm CCC}$ is clearly seen, while the $\bar{\Sigma}_{\rm GMC}$ dependence is weaker than that seen for $m^{\star}_{\rm CCC}$. Note that, due to the calculation method, $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ inherently tend to decrease as $v_{\rm col}$ increases. Specifically, $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ are calculated using Equations (3),(5) and (6), which inherently results in a tendency to be inversely proportional to $v_{\rm col}$.

Figure 6(c) shows the distribution of disk, bar-end, and bar apertures in the parameter space of $v_{\rm col}$ and $\bar{\Sigma}_{\rm GMC}$. When comparing the bar and bar-end regions, apertures in the bar tend to exhibit lower $\bar{\Sigma}_{\rm GMC}$ and higher $v_{\rm col}$ (see also Table 1). This distribution difference leads to lower $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ in the bar, contrasting to higher $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ in the bar-end region.

Figures 6(d) and (e) are the same as panels (a) and (b) but for the dependence on $v_{\rm col}$ and $\bar{M}_{\rm GMC}$. Similar to panel (a), $m^{\star}_{\rm CCC}$ decreases with decreasing $\bar{M}_{\rm GMC}$. However, the dependence of $\epsilon_{\rm CCC}$ on $\bar{M}_{\rm GMC}$ at a fixed $v_{\rm col}$ is not observed.

To clarify the structural differences within the parameter space of $v_{\rm col}$ and $\bar{\Sigma}_{\rm GMC}$($\bar{M}_{\rm GMC}$), we performed a fitting assuming that $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ are proportional to a product of powers of $v_{\rm col}$ and $\bar{\Sigma}_{\rm GMC}$ ($\bar{M}_{\rm GMC}$). We used the curve_fit function in Python’s SciPy package, which applies non-linear least squares to fit a function to the data. Figure 7 shows the fitting results, with coefficient values provided in Table 3. As shown in Figure 6(a) and (b), both $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ decrease with both increasing $v_{\rm col}$ and decreasing $\bar{\Sigma}_{\rm GMC}$:

As shown in Figure 6(d) and (e), $m^{\star}_{\rm CCC}$ depends on mass, whereas $\epsilon_{\rm CCC}$ is mass independent:

Figure 7 clearly show that the different structures have different distributions in the parameter space, with higher $\bar{\Sigma}_{\rm GMC}$ ($\bar{M}_{\rm GMC}$) in the bar-end regions and higher $v_{\rm col}$ in the bar regions compared to the disk region, leading to differences in star-forming activity across these structures.

Once again, note that the dependence of $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ inherently results in a tendency to be inversely proportional to $v_{\rm col}$ by definition. However, the fact that the best-fit power of $v_{\rm col}$ is less than $-1$ indicates that $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ exhibit a stronger dependence on $v_{\rm col}$ than what is expected from the definition. This result may suggest that $v_{\rm col}$ is physically important for suppressing star formation. Although $\epsilon_{\rm CCC}$ inherently tends to be inversely proportional to $\bar{M}_{\rm GMC}$, since it is calculated as $m^{\star}_{\rm CCC}/\bar{M}_{\rm GMC}$ (Equation (6)), dependence on $\bar{M}_{\rm GMC}$ does not exhibit. This is because $m^{\star}_{\rm CCC}$ is proportional to $\bar{M}_{\rm GMC}$, which effectively cancels out the dependence of $\bar{M}_{\rm GMC}$ on $\epsilon_{\rm CCC}$.

This subsection discusses the uncertainties in our results as presented in Section 4. The results of our study under different conditions are summarized in Tables 2 and 3. While detailed analyses are provided below, our findings summarize that aperture size (Section 5.1.1) and the choice of SFR tracer (Section 5.1.3) contribute most to the uncertainties in our results. Nevertheless, our conclusions remain robust that structural differences within the parameter space of $v_{\rm col}$ and $M_{\rm GMC}$ ($\Sigma_{\rm GMC}$), with higher $M_{\rm GMC}$ ($\Sigma_{\rm GMC}$) in the bar-end and higher $v_{\rm col}$ in the bar compared to the disk, lead to higher star formation activity in the bar-end and lower activity in the bar.

Although $m^{\star}_{\rm CCC}$ and $\epsilon_{\rm CCC}$ inherently tend to decrease as $v_{\rm col}$ increases in this study (Section 2), recent sub-pc scale CCC simulations show the $m^{\star}_{\rm CCC}$ decreases with increasing $v_{\rm col}$ (Takahira et al., 2014, 2018; Sakre et al., 2023).Takahira et al. (2014) and Takahira et al. (2018) conducted sub-parsec resolution simulations of CCCs between two clouds with collision speeds ranging from 3 to 30 $\rm km~{}s^{-1}$, finding that higher collision velocities can shorten the gas accretion phase, thereby suppressing core growth and massive star formation. Consequently, the slope of the core mass function becomes steeper with increasing collision velocity, and the total mass of the cores formed decreases. Similar suppression effects are seen in magnetohydrodynamic simulations (Sakre et al., 2023).

Takahira et al. (2018) further indicates that the number of massive cores tends to increase with the mass of the colliding cloud at a fixed collision velocity, which is qualitatively consistent with our results. There are two possible reasons for this increase. First, if the radius increases with mass, the collision duration becomes longer, allowing more time for gas to accrete onto the cores. Second, if the density increases with mass, the amount of surrounding gas available for core accretion also increases. The latter effect may be significant in NGC 3627, because no correlation is seen between $\bar{M}_{\rm GMC}$ and $\bar{R}_{\rm GMC}$ within the extracted apertures.

Given the uncertainties in our results (Section 5.1), it remains unclear how $\epsilon_{\rm CCC}$ depends on mass or surface density. Previous studies proposed the CCCs are responsible for the correlation between efficiency and cloud mass (e.g., Scoville et al., 1986; Ikuta & Sofue, 1997; Tan, 2000). However, in the simulation by (Takahira et al., 2018), increasing the mass or surface density tends to increase the number of high-mass cores, but it does not seem to increase $\epsilon_{\rm CCC}$.

Note that other simulations suggest star formation activity driven by CCC also depends on the angle between the magnetic field direction and the collision axis (e.g., Inoue & Inutsuka, 2009; Sakre et al., 2021). Sakre et al. (2021) found that when the two axes are nearly parallel, the converging gas flow toward the collision front is stronger, promoting the formation of massive cores. This dependence is expected to be explored in future studies of CCCs in the Milky Way.

Our results support the scenario that variations in the collision velocity and mass (or density) of colliding GMCs across different galactic structures may explain the observed differences in SFE on a kpc scale. The different structures have different distributions in the parameter space of $v_{\rm col}$ and $\bar{\Sigma}_{\rm GMC}$ ($\bar{M}_{\rm GMC}$), with higher $\bar{\Sigma}_{\rm GMC}$ ($\bar{M}_{\rm GMC}$) in the bar-end regions and higher $v_{\rm col}$ in the bar regions compared to the disk region, leading to differences in star-forming activity across these structures.

The different distributions in the parameter space of $v_{\rm col}$ and $\bar{\Sigma}_{\rm GMC}$ ($\bar{M}_{\rm GMC}$) by structures are interpreted as follows. The non-axisymmetric gravitational bar potential increases noncircular gas motion in the bar-end and bar region, and the crossing of cloud orbits is thought to be an environment in which molecular cloud collisions occur frequently. In the bar-end regions, gas accumulates not only because of the stagnation of the gas in the elongated elliptical orbit but also because of the inflow of the gas rotating in the disk (e.g., Downes et al., 1996), resulting in high $\bar{\Sigma}_{\rm GMC}$ ($\bar{M}_{\rm GMC}$) (e.g., Renaud et al., 2015). In the bar region, the $v_{\rm col}$ becomes high due to the violent noncircular, streaming motions caused by the bar potential. Parsec-scale hydrodynamical simulations of barred galaxies found the collision velocity of the GMCs in the bar regions is larger than in the arm regions due to the bar potential (Fujimoto et al., 2014b, a, 2020), which is consistent with our results. Furthermore, a part of the gas that fell into the center would have overshot and sprayed into the dust lane (e.g., Sormani et al., 2019), which could be one factor contributing to the increase in the $v_{\rm col}$.

Previous CO observations on a kpc scale towards nearby barred galaxies showed that the velocity width in bar regions was larger than in arm and bar-end regions and that there was a negative correlation between velocity width and SFE on a kpc scale (e.g., Yajima et al., 2019; Maeda et al., 2023). This result may reflect the negative correlation between the $\epsilon_{\rm CCC}$ and $v_{\rm col}$.

Compared to the CCC study in NGC 1300 (Maeda et al., 2021), the correlation between collision velocity, GMC mass, and star formation activity is qualitatively consistent with our findings in NGC 3627. However, NGC 3627 exhibits larger values for GMC mass, collision velocity, and collision frequency than NGC 1300. The typical values in the bar of NGC 3627 are $10^{6.5}~{}M_{\odot}$, $44~{}\rm km~{}s^{-1}$, and $101~{}\rm Gyr^{-1}$, while in the bar of NGC 1300, they are $10^{5.5}M_{\odot}$, $20~{}\rm km~{}s^{-1}$, and $25~{}\rm Gyr^{-1}$. The higher collision velocity in NGC 3627 may be attributed to its stronger bar potential, as the stellar surface density derived from WISE 3.4$\mu$m data (Leroy et al., 2019) is about five times higher in the bar of NGC 3627 ($\sim 600~{}M_{\odot}\rm pc^{-2}$) than that in NGC 1300 ($\sim 130~{}M_{\odot}~{}\rm pc^{-2}$). On a kpc scale, the gas surface density in NGC 3627 ($\sim 100~{}M_{\odot}~{}\rm pc^{-2}$) is also one order of magnitude higher than that in NGC 1300 ($\sim 10~{}M_{\odot}~{}\rm pc^{-2}$), leading to significantly larger GMC mass and surface density in NGC 3627. Due to the lower GMC number density and collision velocity in NGC 1300, the collision frequency is also lower. These comparisons suggest that CCC properties may vary depending on the characteristics of the host galaxy such as morphology, stellar mass, and gas mass. Investigating the correlation between CCC properties and these factors will be an important direction for future research.

Sun et al. (2022) estimated the GMC collision timescale ($t_{\rm CCC}$) for 80 PHANGS galaxies, reporting a typical value of 91 Myr—about three times longer than the 27 Myr observed in NGC 3627. Several factors could explain this discrepancy. First, since $t_{\rm CCC}$ in Sun et al. (2022) was calculated across all regions with molecular gas detection, it likely includes many regions where CCC is not the dominant star formation mechanism, potentially resulting in a larger $t_{\rm CCC}$. Second, the difference could arise from the methods used to calculate the collision velocity. While our study assumes random motion, Sun et al. (2022) adopted the shear-induced collision model (Tan, 2000), which assumes CCCs occur only when clouds catch up with others in adjacent circular orbits due to orbital shear. This method may overestimate $t_{\rm CCC}$ since streaming motions and intersections were not considered. Finally, NGC 3627 may be a unique disk galaxy among the 80 PHANGS galaxies, with a short collision timescale due to its high gas surface density and high GMC number density compared to other galaxies, as mentioned above. It has been suggested that a high gas surface density on a kpc scale is essential for CCC-driven star formation to dominate (e.g., Komugi et al., 2006).