Furstenberg set problem and exceptional set estimate in prime fields: dimension two implies higher dimensions

Shengwen Gan Department of Mathematics
University of Wisconsin-Madison
Madison, WI-53706, USA [email protected]

Abstract.

We study Furstenberg set problem, and exceptional set estimate for Marstrand’s orthogonal projection in prime fields for all dimensions. We define the Furstenberg index $\mathbf{F}(s,t;n,k)$ and the Marstrand index $\mathbf{M}(a,s;n,k)$ .

It is shown that the two-dimensional result for Furstenberg set problem implies all higher dimensional results.

Key words and phrases:

Furstenberg problem

2020 Mathematics Subject Classification:

28A75, 28A78

1. Introduction

We study the Furstenberg set problem, as well as the exceptional set estimate in prime fields. The main novelty of this paper is that we prove, for these two problems, the two-dimensional result implies all higher dimensional results. In common sense, high dimensional version is harder than low dimensional version. For example, a closely related problem—Kakeya conjecture is known for dimension two but wide open for dimension bigger than two. Hence, it is surprising that for these two problems in prime fields, all higher dimensional results can be deduced from the two dimensional result.

1.1. Background

We first introduce the two problems—Furstenberg set problem and exceptional set estimate in Euclidean space.

1.1.1. Furstenberg set problem

The Furstenberg set problem was originally considered by Wolff [16] in $\mathbb{R}^{2}$ . Fix $s\in(0,1],t\in(0,2]$ . We say $E\subset\mathbb{R}^{2}$ is a $(s,t)$ -set in $\mathbb{R}^{2}$ , if $E$ is of the form

E=\bigcup_{\ell\in\mathcal{L}}Y(\ell),

where $\mathcal{L}\subset A(1,2)$ is a set of lines with $\dim\mathcal{L}=t$ and for each $\ell\in\mathcal{L}$ there exists $Y(\ell)\subset\ell$ with $\dim Y(\ell)=s$ . ( $\dim$ will always mean Hausdorff dimension.) Furstenberg set problem asks about the optimal lower bound on the Hausdorff dimension of $(s,t)$ -sets, i.e.,

\inf_{E\textup{~{}is~{}a~{}}(s,t)\textup{-set}}\dim(E).

Recently, Ren and Wang [15] resolved the Furstenberg set problem by proving

(1)

\inf_{E\textup{~{}is~{}a~{}}(s,t)\textup{-set}}\dim(E)=\min\{s+t,\frac{3}{2}s+\frac{1}{2}t,s+1\}.

For more reference and the history on this problem, we refer to [15], [13].

Furstenberg set problem was also considered in higher dimensions, see for example [5], [1], [7]. It can be formulated similarly as follows.

Fix integers $1\leq k<n$ . Fix $s\in[0,k],t\in[0,(k+1)(n-k)]$ . We say $E\subset\mathbb{R}^{n}$ is a $(s,t;n,k)$ -set in $\mathbb{R}^{n}$ , if $E$ is of the form

E=\bigcup_{V\in\mathcal{V}}Y(V),

where $\mathcal{V}\subset A(k,n)$ is a set of $k$ -planes with $\dim\mathcal{V}=t$ and for each $V\in\mathcal{V}$ there exists $Y(V)\subset V$ with $\dim Y(V)=s$ . Furstenberg set problem in $\mathbb{R}^{n}$ for $k$ -planes asks to compute

\inf_{E\textup{~{}is~{}a~{}}(s,t;n,k)\textup{-set}}\dim(E).

The Furstenberg set problems in higher dimensions remains wide open.

1.1.2. Exceptional set estimate

Next, we introduce the problem of exceptional set estimate. We first introduce this problem over $\mathbb{R}$ . The projection theory dates back to Marstrand [8], who showed that if $A$ is a Borel set in $\mathbb{R}^{2}$ , then the projection of $A$ onto almost every one-dimensional subspace has Hausdorff dimension $\min\{1,\dim A\}$ . This was generalized to $\mathbb{R}^{n}$ by Mattila [9] who showed that if $A$ is a Borel set in $\mathbb{R}^{n}$ , then the projection of $A$ onto almost every $k$ -dimensional subspace has Hausdorff dimension $\min\{k,\dim A\}$ .

One can consider a refined version of the Marstrand’s projection problem, which is known as the exceptional set estimate.

For $V\in G(k,\mathbb{R}^{n})$ , we use $\pi_{V}:\mathbb{R}^{n}\rightarrow V$ to denote the orthogonal projection. For $A\subset\mathbb{R}^{n}$ and $s>0$ , we define the exceptional set

E_{s}(A;n,k):=\{V\in G(k,\mathbb{R}^{n}):\dim(\pi_{V}(A))<s\}.

The exceptional set estimate is about finding optimal upper bound of $\dim(E_{s}(A;n,k))$ (in terms of $\dim A,s,n,k$ ), i.e.,

\sup_{A\subset\mathbb{R}^{n},\dim(A)=a}\dim(E_{s}(A;n,k)).

Many progress have been made on this problem, see for example [6], [2], [14], [12], [13].

In $\mathbb{R}^{2}$ , D. Oberlin [10] conjectured that for $0<s\leq\min\{1,a\}$ and $A\subset\mathbb{R}^{2}$ with $\dim A=a$ , one has the following exceptional set estimate

(2)

\dim(E_{s}(A;2,1))\leq\max\{2s-a,0\}.

This conjecture was proved by Ren and Wang in [15].

1.2. The problems in prime fields

In the rest of the paper, we only look at prime fields. Let $p$ be a prime and $\mathbb{F}_{p}$ be the prime field with $p$ elements. Throughout the paper, $A\lessapprox B$ means $A\leq C(\log p)^{C}B$ for some large constant $C$ (independent of $p$ ). $A\approx B$ means both $A\lessapprox B$ and $B\lessapprox A$ . $A\lesssim B$ means $A\leq CB$ for a large constant $C$ (independent of $p$ ). $A\sim B$ means both $A\lesssim B$ and $B\lesssim A$ .

1.2.1. Furstenberg set problem

Definition 1 ( $(s,t;n,k)$ -set).

Fix integers $1\leq k<n$ , and numbers $0\leq s\leq k$ , $0\leq t\leq(k+1)(n-k)$ . Let $0<\lambda\leq 1$ . We say $E$ is a $(s,t;n,k;\lambda)$ -Furstenberg set (over $\mathbb{F}_{p}$ ), if $E$ is a subset of $\mathbb{F}_{p}^{n}$ of form

E=\bigcup_{V\in\mathcal{V}}Y(V).

Here, $\mathcal{V}\subset A(k,\mathbb{F}_{p}^{n})$ is a set of $k$ -planes with $\#\mathcal{V}\geq\lambda p^{t}$ ; for each $V\in\mathcal{V}$ , $Y(V)$ is a subset of $V$ with $\#Y(V)\geq\lambda p^{s}$ .

Remark 2.

We remark that $s,t,n,k$ are important parameters, while $\lambda$ is not. Since $\lambda$ is not an important parameter, from now on, we will drop $\lambda$ from notation and simply call $(s,t;n,k;\lambda)$ -set as $(s,t;n,k)$ -set, thinking of $\lambda$ as a constant in $(0,1]$ .

We make the following definition.

Definition 3.

We say $(s,t;n,k)$ is admissible, if $1\leq k<n$ are integers and $0\leq s\leq k$ , $0\leq t\leq(k+1)(n-k)$ .

The Furstenberg set problem can be formulated as:

Question 1.

Suppose $(s,t;n,k)$ is admissible. Find the largest $\mathbf{F}(s,t;n,k)$ , so that

(3)

\inf_{E:\ (s,t;n,k)\textup{-set}}\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t;n,k)-\varepsilon}

holds for any $\varepsilon>0$ .

The $\gtrsim_{\varepsilon}$ in the above inequality is actually $\gtrsim_{s,t,n,k,\varepsilon}$ . We just view $s,t,n,k$ as fixed parameters, so we simplify it to $\lesssim_{\varepsilon}$ . The crucial point is that the implicit constant in $\gtrsim$ or $\lesssim$ throughout this paper never depends on $p$ , but can depend on any other fixed parameters. We are interested in the behaviour as $p$ goes to infinity, so the goal is to find the index $\mathbf{F}(s,t;n,k)$ for fixed $(s,t;n,k)$ .

We see the problem consists of two parts: for fixed $(s,t;n,k)$ ,

(1)

(Lower bound) show for any $(s,t;n,k)$ -set $E$ , we have $\#E\gtrsim p^{\mathbf{F}(s,t;n,k)-\varepsilon}$ ;
(2)

(Upper bound) show the existence of a $(s,t;n,k)$ -set $E$ , such that $\#E\lesssim p^{\mathbf{F}(s,t;n,k)}$ .

Based on the Ren-Wang’s result (1), it is reasonable to make the conjecture in $\mathbb{F}_{p}^{2}$ .

Conjecture 4.

Fix $s\in(0,1],t\in(0,2]$ . Then for any $(s,t;2,1)$ -set $E$ over $\mathbb{F}_{p}$ , we have

\#E\gtrsim_{\varepsilon}p^{\min\{s+t,\frac{3}{2}s+\frac{1}{2}t,s+1\}-\varepsilon},

for any $\varepsilon>0$ .

Remark 5.

It is crucial to use prime field $\mathbb{F}_{p}$ . Otherwise, the conjecture fails. Consider the problem in $\mathbb{F}_{p}^{2}$ , where $q=p^{2}$ is the square of a prime. We choose the set of lines $\mathcal{V}=\{y=ax+b:a,b\in\mathbb{F}_{p}\}$ , so $\#\mathcal{V}=q$ and hence $t=1$ . For each line $V:y=ax+b$ in $\mathcal{V}$ , define $Y(V):=\{(x,ax+b):x\in\mathbb{F}_{p}\}$ , so $\#Y(V)=p=q^{\frac{1}{2}}$ and hence $s=\frac{1}{2}$ . One can calculate $\#\big{(}\bigcup_{V\in\mathcal{V}}Y(V)\big{)}=p^{2}=q$ . However, $\min\{s+t,\frac{3}{2}s+\frac{1}{2}t,s+1\}=\frac{5}{4}$ .

Usually, people believe the problem in finite field is easier than in Euclidean space. However, Conjecture 4 remains open, while Euclidean version have been resolved.

In the paper, we explicitly find the function $\mathbf{F}(s,t;n,k)$ . The definition for $\mathbf{F}(s,t;n,k)$ is tricky, so we postpone it later in Definition 11. The following are main results.

Theorem 6 (Upper bound).

Suppose $(s,t;n,k)$ is admissible. Then for any prime $p$ , there exits a $(s,t;n,k)$ -set $E$ over $\mathbb{F}_{p}$ , such that

\#E\lesssim p^{\mathbf{F}(s,t;n,k)}.

Theorem 7 (Lower bound).

Suppose $(s,t;n,k)$ is admissible. If we assume Conjecture 4 holds, then for any $(s,t;n,k)$ -set $E$ over $\mathbb{F}_{p}$ , we have

\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t;n,k)-\varepsilon},

for any $\varepsilon>0$ .

1.2.2. Exceptional set estimate

We also study the exceptional set estimate in prime fields in all dimensions. We show that the two-dimensional result for Furstenberg set problem implies all higher dimensional results for exceptional set estimates.

To define the projection in $\mathbb{F}_{p}^{n}$ , we first consider an equivalent definition of projection in $\mathbb{R}^{n}$ .

Recall $\pi_{V}:\mathbb{R}^{n}\rightarrow V$ is the orthogonal projection. For $V\in G(k,\mathbb{R}^{n})$ , we also define the map

\pi_{V}^{*}:\mathbb{R}^{n}\rightarrow A(k,\mathbb{R}^{n})

as $\pi^{*}_{V}(x):=x+V$ . We see that $\pi_{V}^{*}(x)$ is the unique $k$ -plane in $A(k,\mathbb{R}^{n})$ that is parallel to $V$ and passes through $x$ . It is not hard to see that $\pi_{V}$ and $\pi^{*}_{V^{\perp}}$ are the same things. This motivates the definition of projections in $\mathbb{F}_{p}^{n}$ . We will still use the notations $E_{s}(A;n,k),\pi_{V}^{*}$ for $\mathbb{F}_{p}^{n}$ (which have been used for $\mathbb{R}^{n}$ in previous subsection). This will not cause any confusion.

Definition 8 (Exceptional set).

For $V\in G(m,\mathbb{F}_{p}^{n})$ , define

\pi_{V}^{*}:\mathbb{F}_{p}^{n}\rightarrow A(m,\mathbb{F}_{p}^{n})

as $\pi_{V}^{*}(x):=x+V$ .

Suppose $A\subset\mathbb{F}_{p}^{n}$ . Let $s>0$ . We define

E_{s}(A;n,k):=\{V\in G(n-k,\mathbb{F}_{p}^{n}):\#\pi_{V}^{*}(A)<p^{s}\}.

(We remark that $E_{s}(A;n,k)$ also depends on $p$ , but for simplicity, we drop $p$ from the notation.)

We explicitly find the function $\mathbf{M}(a,s;n,k)$ , whose definition is tricky and therefore postponed to Definition 14. We state the following results.

Theorem 9 (Lower bound).

Fix $1\leq k<n$ , $a\in(0,n]$ and $0<s$ . Then for $p$ large enough, there exists $A\subset\mathbb{F}_{p}^{n}$ with $\#A\gtrsim p^{a}$ , such that

(4)

\#E_{s}(A;n,k)\gtrsim p^{\mathbf{M}(a,s;n,k)}.

Theorem 10 (Upper bound).

Assume Conjecture 4 holds. Fix $1\leq k<n$ , $a\in(0,n]$ and $0<s$ . If $p$ is large enough, then for any $A\subset\mathbb{F}_{p}^{n}$ with $\#A\gtrsim p^{a}$ , we have

(5)

\#E_{s-\varepsilon}(A;n,k)\lesssim_{\varepsilon}p^{\varepsilon+\mathbf{M}(a,s;n,k)},

for any $\varepsilon>0$ .

1.3. Strategy of the proof

The proof of Theorem 6 and Theorem 9 is by constructing examples. The proof of Theorem 7 and Theorem 10 is by a sequence of pigeonholing arguments and induction on both $n$ and $k$ . We explain the idea of the proof of Theorem 7.

We consider the case $(n,k)=(3,1)$ . Suppose for any $(s^{\prime},t^{\prime};2,1)$ -set $E^{\prime}$ , we have $\#E^{\prime}\gtrsim p^{\mathbf{F}(s^{\prime},t^{\prime};2,1)}$ . The goal is to prove for any $(s,t;3,1)$ -set $E$ , $\#E\gtrsim p^{\mathbf{F}(s,t;3,1)}$ . We will carefully analyze the structure of $E$ and find subsets of $E$ which are $(s^{\prime},t^{\prime};2,1)$ -set. Then we use the estimate for those $(s^{\prime},t^{\prime};2,1)$ -sets.

Write $E=\bigcup_{L\in\mathcal{L}}Y(L)$ , where $\mathcal{L}\subset A(1,\mathbb{F}_{p}^{3})$ with $\#\mathcal{L}=p^{t}$ and $Y(L)\subset L$ with $\#Y(L)=p^{s}$ . Project $\mathcal{L}$ to $\mathbb{F}_{p}^{2}$ , and partition $\mathcal{L}$ according to their images. For each $W\in A(1,\mathbb{F}_{p}^{2})$ , define $\mathcal{L}_{W}$ to be the set of those $L\in\mathcal{L}$ whose image under the projection $\mathbb{F}_{p}^{3}\rightarrow\mathbb{F}_{p}^{2}$ is $W$ . We may assume all the lines in $\mathcal{L}$ are not parallel to $(0,0,1)$ (by throwing away a small portion of $\mathcal{L}$ ). We obtain the partition

\mathcal{L}=\bigsqcup_{W\in A(1,\mathbb{F}_{p}^{2})}\mathcal{L}_{W}.

By pigeonholing, we can find $\mathcal{W}\subset A(1,\mathbb{F}_{p}^{2})$ so that $\#\mathcal{L}_{W}$ are comparable for all $W\in\mathcal{W}$ . Moreover, denoting $\#\mathcal{W}=p^{t_{1}}$ , $\#\mathcal{L}_{W}=p^{t_{2}}$ , we may assume $t_{1}+t_{2}=t$ .

Next, we look at

E_{W}:=\bigcup_{L\in\mathcal{L}_{W}}Y(L).

This is a $(s,t_{2};2,1)$ -set in $W\times\mathbb{F}_{p}\cong\mathbb{F}_{p}^{2}$ . By hypothesis, we have

\#E_{W}\gtrsim p^{\mathbf{F}(s,t_{2};2,1)}.

We write

E_{W}=\bigsqcup_{\xi\in W}E_{W}\cap(\xi\times\mathbb{F}_{p}).

By pigeonholing on $\#E_{W}\cap(\xi\times\mathbb{F}_{p})$ , we may assume there is a subset $\Xi_{W}\subset W$ so that $\#E_{W}\cap(\xi\times\mathbb{F}_{p})$ are comparable for $\xi\in\Xi_{W}$ . Moreover, denoting $\#\Xi=p^{s_{1}}$ , $\#E_{W}\cap(\xi\times\mathbb{F}_{p})=p^{s_{2}}$ , we may assume

s_{1}+s_{2}\geq\mathbf{F}(s,t_{2};2,1).

Also, we may assume $s_{1},s_{2}$ are the same for all $W\in\mathcal{W}$ by doing another pigeonholing on $W$ . We can also assume a strong condition on $s_{1}$ : $s_{1}\geq s$ . But we do not expand the discussion here.

It turns out that the worst scenario for $E_{W}$ is when

E_{W}=\Xi_{W}\times\{1,\dots,p^{s_{2}}\}.

This will be made precise in the latter sections, so we do not expand the discussion here.

Now, we have

E\supset(\bigcup_{W\in\mathcal{W}}\Xi_{W})\times\{1,\dots,p^{s_{2}}\}.

Note that $\bigcup_{W\in\mathcal{W}}\Xi_{W}$ is a $(s_{1},t_{1};2,1)$ -set. Hence

\#E\gtrsim p^{\mathbf{F}(s_{1},t_{1};2,1)+s_{2}}.

The problem boils down to the following linear programming problem: suppose

(6)

\begin{cases}t_{1}+t_{2}=t,\\ s_{1}+s_{2}\geq\mathbf{F}(s,t_{2};2,1),\\ s_{1}\geq s.\end{cases}

Show that

\mathbf{F}(s_{1},t_{1};2,1)+s_{2}\geq\mathbf{F}(s,t;3,1).

The proof of the last inequality will be done by brutal force.

1.4. Structure of the paper

In Section 2, we define $\mathbf{F}(s,t;n,k),\mathbf{M}(a,s;n,k)$ and prove some fundamental lemmas. In Section 3, we prove Theorem 6. In Section 4 and 5, we prove Theorem 7. In Section 6, we prove Theorem 9. In Section 7 and 8, we prove Theorem 10.

Acknowledgement. The author would like to thank Larry Guth, Bochen Liu, Hong Wang and Shukun Wu for some helpful communications.

2. Preliminary

2.1. Definition of $\mathbf{F}(s,t;n,k)$ and $\mathbf{M}(a,s;n,k)$

Now, we make clear the mysterious $\mathbf{F}$ and $\mathbf{M}$ that appeared in Theorem 6, 7, 9, 10.

Definition 11 (Furstenberg index).

Suppose $(s,t;n,k)$ is admissible, we define $\mathbf{F}(s,t;n,k)$ as follows.

(a) If $s=0$ , define

(7)

\mathbf{F}(0,t;n,k)=\max\{0,t-k(n-k)\}.

(b) If $s>0$ , write $s=d+\sigma$ where $d\in\mathbb{N},\sigma\in(0,1]$ . If also $t\in[0,(k-d-1)(n-k)]$ , define

(8)

\mathbf{F}(s,t;n,k)=s.

If we are not in Case (a) and (b), then $s\in(0,k]$ and $t\in((k-d-1)(n-k),(k+1)(n-k)]$ , we write

(9)

\begin{cases}s=d+\sigma\\ t=(k-d-1)(n-k)+(d+2)m+\tau,\end{cases}

where $d\in\{0,\dots,k-1\}$ , $\sigma\in(0,1]$ , $m\in\{0,\dots,n-k-1\}$ , $\tau\in(0,d+2]$ .

(10)

\begin{split}\mathbf{F}(s,t;n,k)&=d+m+\min\{\sigma+\tau,\frac{3}{2}\sigma+\frac{1}{2}\tau,\sigma+1\}\\ &=s+m+\min\{\tau,\frac{1}{2}(\sigma+\tau),1\}.\end{split}

(d) If $\tau\in(2,d+2]$ , define

(11)

\mathbf{F}(s,t;n,k)=s+m+1(=s+m+\min\{\tau,\frac{1}{2}(\sigma+\tau),1\}).

Remark 12.

Through this definition, we can calculate $\mathbf{F}(s,t;2,1)=\min\{s+t,\frac{3}{2}s+\frac{1}{2}t,s+1\}$ for $s\in(0,1],t\in[0,2]$ . One sees that Conjecture 4 is equivalent to saying that $\inf_{E:\ (s,t;2,1)\textup{-set}}\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t;2,1)-\varepsilon}$ .

The following is a construction of $(s,t;2,1)$ -set, which provides evidence on why Conjecture 4 should be reasonable.

Proposition 13.

For $0\leq t\leq 2$ , there exists a $(0,t;2,1)$ -set $E$ such that

(12)

\#E\lesssim p^{\max\{0,t-1\}}.

For $0<s\leq 1,0\leq t\leq 2$ . there exists a $(s,t;2,1;\frac{1}{2})$ -set $E$ such that

(13)

\#E\lesssim p^{\min\{s+t,\frac{3}{2}s+\frac{1}{2}t,s+1\}}.

Proof.

When $s=0$ , we construct $E=\bigcup_{L\in\mathcal{L}}Y(L)$ as follows. If $t\leq 1$ , choose $\mathcal{L}$ to be a set of $p^{t}$ lines passing through $(0,0)$ and $Y(L)=(0,0)$ . Then $\#E=1=p^{0}$ . If $t>1$ , we choose $p^{t-1}$ points $E$ on $\mathbb{F}_{p}\times\{0\}$ , and for each $x\in E$ , we choose $p-1$ lines through $x$ that are not parallel to $\mathbb{F}_{p}\times\{0\}$ . If the line $L$ is through $x\in E$ , then we let $Y(L)=x$ . We see that $E$ is a $(0,t;2,1;\frac{1}{2})$ -set with cardinality $p^{t-1}$ . (Here, $p^{t-1}$ should actually be the integer $\lceil p^{t-1}\rceil$ , but we still write it as $p^{t-1}$ for simplicity, thinking of it as an integer. Same convention applies in the whole paper.)

Consider the case when $s>0$ . There are three terms in the “min” on the RHS of (13). We note that: when $t\leq s$ , minimum achieves at $s+t$ ; when $s\leq t\leq 2-s$ , minimum achieves at $\frac{3}{2}s+\frac{1}{2}t$ ; when $2-s\leq t$ , minimum achieves at $s+1$ .

(1)

If $E=\bigcup_{L\in\mathcal{L}}Y(L)$ is a $(s,t;2,1;\frac{1}{2})$ -set, then $\#E\leq\sum_{L\in\mathcal{L}}\#Y(L)\leq p^{s+t}$ .
(2)

Choose $\mathcal{L}$ to be a set of $\frac{1}{2}p^{t}$ lines that are not parallel to the line $\mathbb{F}_{p}\times\{0\}$ . Let $Y(L)=L\cap(\mathbb{F}_{p}\times\{1,2,\dots,p^{s}\})$ . Then $E$ is a $(s,t;2,1;\frac{1}{2})$ -set with $E=\bigcup_{L\in\mathcal{L}}Y(L)\subset\mathbb{F}_{p}\times\{1,\dots,p^{s}\}$ . Therefore, $\#E\leq p^{s+1}$ .
(3)

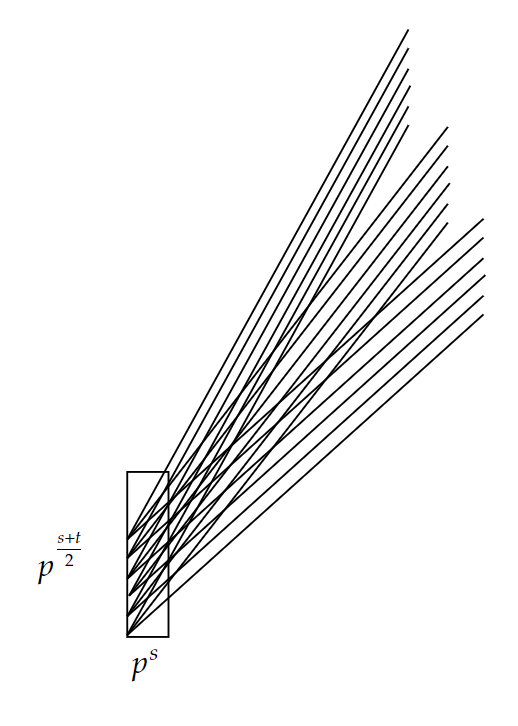
It remains to consider the case when $s+t\leq 2,s\leq t$ . This example is of Szemerédi-Trotter type. The heuristic is shown in Figure 1, where we have $\sim p^{\frac{t-s}{2}}$ directions and for each direction, there are $\sim p^{\frac{t+s}{2}}$ lines. We also have a rectangle of size $\sim p^{s}\times p^{\frac{s+t}{2}}$ . The rectangle intersects each line $L$ at $\sim p^{s}$ points, which is defined to be $Y(L)$ . We also see $E=\bigcup_{L}Y(L)$ is contained in the rectangle. Therefore, $\#E\lesssim p^{\frac{3}{2}s+\frac{1}{2}t}$ .

Let $\mathcal{L}=\{y=ax+b:a=1,\dots,p^{\frac{t-s}{2}},b=1,\dots,p^{\frac{s+t}{2}}\}$ . Here, we view $a,b$ as elements in $\mathbb{F}_{p}$ , and hence $y=ax+b$ as a line in $\mathbb{F}_{p}^{2}$ . For each $L\in\mathcal{L}$ , let $Y(L)=\{(x,y)\in L:x=1,\dots,\frac{1}{2}p^{s}\}$ . We see that $E=\bigcup_{L\in\mathcal{L}}Y(L)$ is contained in $\{(x,y):x=1,\dots,\frac{1}{2}p^{s},y=1,\dots,2p^{\frac{s+t}{2}}\}$ . Therefore, $\#E\lesssim p^{\frac{3}{2}s+\frac{1}{2}t}$ .

∎

Next, we define the index for Marstrand’s orthogonal projection.

Definition 14 (Marstrand index).

Let $1\leq k<n$ be integers. Let $a\in(0,n],s>0$ . We make the following definition for $\mathbf{M}(a,s;n,k)$ . We write $a=m+\beta,s=l+\gamma$ where $m,l\in\mathbb{N}$ and $\beta,\gamma\in(0,1]$ . For convenience, we call such expression of $a,s$ canonical.

Type 1: If $s>\min\{a,k\}$ , define

(14)

\displaystyle\mathbf{M}(a,s;n,k)=k(n-k).

Type 2: If $s\leq\min\{a,k\}$ , $l+1\leq m\leq n+l-k$ and $\gamma\in(\beta,1]$ , define

(15)

\displaystyle\mathbf{M}(a,s;n,k)=k(n-k)-(m-l)(k-l)+\max\{2\gamma-(\beta+1),0\}.

Type 3: If $s\leq\min\{a,k\}$ , $l\leq m\leq n+l-k-1$ and $\gamma\in(0,\beta]$ , define

(16)

\displaystyle\mathbf{M}(a,s;n,k)=k(n-k)-(m+1-l)(k-l)+\max\{2\gamma-\beta,0\}.

Type 4: If $s\leq a-(n-k)$ , define

(17)

\displaystyle\mathbf{M}(a,s;n,k)=-\infty.

Remark 15.

$\mathbf{M}(a,s;n,k)=-\infty$ corresponds to the case when exceptional set is empty. We remark that in the Euclidean setting, the empty set is assumed to have dimension $-\infty$ , in order to satisfy a Fubini-type heuristic $\dim(A\times B)=\dim A\times\dim B$ .

One can check, when $(n,k)=(2,1)$ ,

(18)

\mathbf{M}(a,s;2,1)=\begin{cases}1&s>\min\{1,a\}\\ \max\{0,2s-a\}&a-1<s\leq\min\{1,a\}\\ -\infty&s\leq a-1.\end{cases}

We discuss a construction of exceptional set.

Proposition 16.

Let $a\in(0,2]$ , $s\in(\frac{a}{2},\min\{1,a\}]$ . Then for $p$ large enough, there exists $A\subset\mathbb{F}_{p}^{2}$ with $\#A\gtrsim p^{a}$ , such that

\#E_{s}(A;2,1)\gtrsim p^{2s-a}.

Proof.

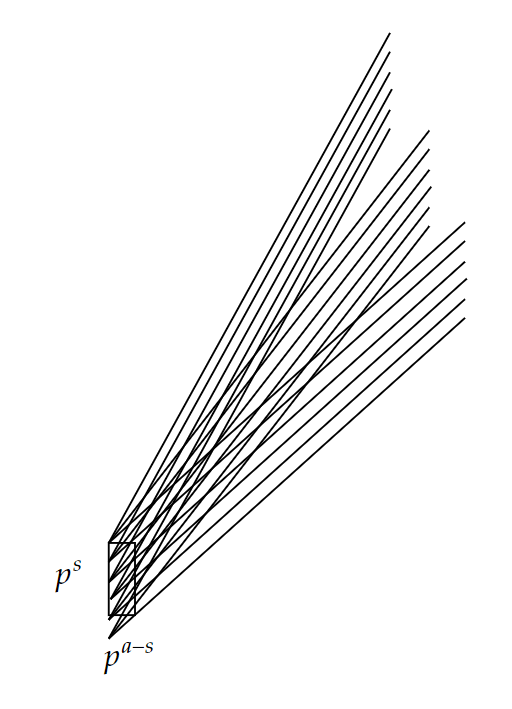
The heuristic is shown in Figure 2. Our set $A$ is the lattice points in the rectangle of size $\frac{1}{5}p^{a-s}\times\frac{1}{5}p^{s}$ . For any slope $k\in[1,p^{2s-a}]$ , we are able to find $<p^{s}$ lines with slope $k$ to cover $A$ . Hence, this slope- $k$ direction belongs to the exceptional set.

Consider the set $A=\{(x,y):|x|\leq\frac{1}{5}p^{a-s},|y|\leq\frac{1}{5}p^{s}\}\subset\mathbb{F}_{p}^{2}$ . For $k,m\in\mathbb{F}_{p}$ , we use $\ell_{k,m}$ to denote the line $y=kx+m$ . We claim that for each $|k|\leq\frac{1}{5}p^{2s-a}$ ,

\pi_{\ell_{k,0}}^{*}(A)\subset\{\ell_{k,m}:|m|<\frac{1}{2}p^{s}\}.

Note that if $(x,y)\in A$ and $|k|\leq\frac{1}{5}p^{2s-a}$ , then $|y-kx|\leq\frac{1}{2}p^{s}$ , which means there exists $|m|<\frac{1}{2}p^{s}$ such that $(x,y)\in\ell_{k,m}$ . Hence, $\#\pi_{\ell_{k,0}}^{*}(A)<p^{s}$ . This means $E_{s}(A;2,1)\supset\{\ell_{k,0}:|k|\leq\frac{1}{5}p^{2s-a}\}$ .

We see that $\#A\gtrsim p^{a}$ , and $E_{s}(A;2,1)$ has cardinality $\gtrsim p^{2s-a}$ . ∎

2.2. Useful lemmas

We prove several useful lemmas, which will be used in the later proof. We suggest the reader to skip this part in the first reading.

Lemma 17.

Suppose $G(k,\mathbb{F}_{p}^{n})$ is the set of $k$ -dimensional subspaces in $\mathbb{F}_{p}^{n}$ , $A(k,\mathbb{F}_{p}^{n})$ is the set of $k$ -planes in $\mathbb{F}_{p}^{n}$ . We have:

(1)

$\#G(k,\mathbb{F}_{p}^{n})\sim p^{k(n-k)}$ ;
(2)

$\#A(k,\mathbb{F}_{p}^{n})\sim p^{(k+1)(n-k)}$ ;
(3)

Fix integers $l,k$ with $l+k\geq n$ . Let $W_{0}\in A(l,\mathbb{F}_{p}^{n})$ . Then $\#\{V\in A(k,\mathbb{F}_{p}^{n}):V\cap W_{0}\textup{~{}is~{}a~{}}(l+k-n)\textup{-plane}\}\gtrsim p^{(k+1)(n-k)}$ .

Proof.

(1) and (2) are fundamental. We prove (3). $V\cap W_{0}$ is a $(l+k-n)$ -plane means $V$ intersects $W_{0}$ transversely. (3) agrees with the intuition in $\mathbb{R}^{n}$ , since generic $V\in A(k,\mathbb{R}^{n})$ intersect $W_{0}$ transversely. Noting (2), we see that it suffices to prove

(19)

\#\{V\in A(k,\mathbb{F}_{p}^{n}):V\cap W_{0}\textup{~{}is~{}a~{}}r\textup{-plane}\}\lesssim p^{(k+1)(n-k)-1},

for $r>l+k-n$ . The proof of (19) is as follows. Choose a $r$ -plane $L$ in $W_{0}$ . There are $\#G(r,\mathbb{F}_{p}^{l})\sim p^{(r+1)(l-r)}$ choices for $L$ . If $V\cap W_{0}=L$ , then $V\supset L$ . We have $\leq\#\{V\in A(k,\mathbb{F}_{p}^{n}):V\supset L\}=\#G(k-r,\mathbb{F}_{p}^{n-r})\sim p^{(k-r)(n-k)}$ choices for $V$ such that $V\cap W_{0}=L$ . The two estimates give (19). ∎

Lemma 18.

Let $0\leq l\leq n$ , $1\leq k,m\leq n$ be integers satisfying $n-k\geq m-l$ and $l\leq k,m$ . If $W\in G(m,\mathbb{F}_{p}^{n})$ , then

\#\{V\in G(n-k,\mathbb{F}_{p}^{n}):\#(\pi^{*}_{V}(W))\leq p^{l}\}\sim p^{k(n-k)-(k-l)(m-l)}.

Proof.

By definition

\displaystyle\{V\in G(n-k,\mathbb{F}_{p}^{n}):\#(\pi_{V}^{*}(W))\leq p^{l}\}

\displaystyle=\{V\in G(n-k,\mathbb{F}_{p}^{n}):\#(V\cap W)\geq\#W/p^{l}=p^{m-l}\},

The latter set is

\bigcup_{j\geq m-l}\bigcup_{U\in G(j,W)}\{V\in G(n-k,\mathbb{F}_{p}^{n}):V\supset U\}.

It suffices to show for $j\geq m-l$ ,

(20)

\#\bigcup_{U\in G(j,W)}\{V\in G(n-k,\mathbb{F}_{p}^{n}):V\supset U\}\sim p^{k(n-k)-(k+j-m)j}.

On the one hand, the LHS is

(21)

\begin{split}&\leq\sum_{U\in G(j,W)}\#\{V\in G(n-k,n):V\supset U\}=\#G(j,\mathbb{F}_{p}^{m})\#G(n-k-j,\mathbb{F}_{p}^{n-j})\\ &\sim p^{j(m-j)}p^{(n-k-j)k}=p^{k(n-k)-(k+j-m)j}.\end{split}

On the other hand, for fixed $U\in G(j,W)$ , we have

(22)

\begin{split}&\{V\in G(n-k,\mathbb{F}_{p}^{n}):V\cap W=U\}\\ \supset&\{V\in G(n-k,\mathbb{F}_{p}^{n}):V\supset U\}\setminus\bigcup_{j+1\leq j^{\prime}\leq n-k}\bigcup_{U^{\prime}\in G(j^{\prime},W),U^{\prime}\supset U}\{V\in G(n-k,\mathbb{F}_{p}^{n}):V\supset U^{\prime}\}\end{split}

One can check $\#\{V\in G(n-k,\mathbb{F}_{p}^{n}):V\supset U\}=\#G(n-k-j,\mathbb{F}_{p}^{n-j})=p^{k(n-k-j)}$ . $\bigcup_{j+1\leq j^{\prime}\leq n-k}\bigcup_{U^{\prime}\in G(j^{\prime},W),U^{\prime}\supset U}\{V\in G(n-k,\mathbb{F}_{p}^{n}):V\supset U^{\prime}\}$ has cardinality

(23)

\begin{split}&\leq\sum_{j+1\leq j^{\prime}\leq n-k}\#G(j^{\prime}-j,\mathbb{F}_{p}^{m-j})\#G(n-k-j^{\prime},n-j^{\prime})\\ &\sim\sum_{j+1\leq j^{\prime}\leq n-k}p^{(j^{\prime}-j)(m-j^{\prime})+(n-k-j^{\prime})k}\\ &=\sum_{j+1\leq j^{\prime}\leq n-k}p^{k(n-k-j)+(j^{\prime}-j)(m-k-j^{\prime})}\\ &\lesssim p^{k(n-k-j)-1}.\end{split}

In the last line, we use $(j^{\prime}-j)(m-k-j^{\prime})\leq m-k-j-1\leq m-k-(m-l)-1\leq-1$ . Therefore,

\#\{V\in G(n-k,\mathbb{F}_{p}^{n}):V\cap W=U\}\sim p^{k(n-k-j)}.

We can bound the left hand side of (20) by

\geq\#\bigsqcup_{U\in G(j,W)}\{V\in G(n-k,\mathbb{F}_{p}^{n}):V\cap W=U\}\sim p^{j(m-j)+k(n-k-j)}=p^{k(n-k)-(k+j-m)j}.

∎

Lemma 19.

Suppose $(s,t;n,k)$ is admissible, then

\mathbf{F}(s,t;n,k)\geq s+\max\{0,t-k(n-k)\}.

Proof.

It is easy to check $\mathbf{F}(s,t;n,k)\geq s$ , so we just need to check $\mathbf{F}(s,t;n,k)\geq s+t-k(n-k)$ . We check four cases as in Definition 11.

(a) If $s=0$ , this is true by definition.

(b) If $s>0$ , write $s=d+\sigma.$ If $t\in[0,(k-d-1)(n-k)]$ , then

\mathbf{F}(s,t;n,k)=s\geq s+t-k(n-k).

\mathbf{F}(s,t;n,k)=s+m+\min\{\tau,\frac{1}{2}(\sigma+\tau),1\}.

To show it is $\geq s+t-k(n-k)$ is equivalent to show

(d+1)(n-k-m)+\min\{\tau,\frac{1}{2}\sigma+\frac{1}{2}\tau,1\}\geq\tau.

Since $(d+1)(n-k-m)\geq 1\geq\frac{1}{2}\tau$ and $\min\{\tau,\frac{1}{2}\sigma+\frac{1}{2}\tau,1\}\geq\frac{1}{2}\tau$ , it is proved.

(d) In the final case, we have

\mathbf{F}(s,t;n,k)=s+m+1.

To show it is $\geq s+t-k(n-k)$ is equivalent to show

(d+1)(n-k-m)+1\geq\tau.

This is true since $(d+1)(n-k-m)\geq d+1$ and $\tau\leq d+2$ . ∎

Lemma 20.

Suppose $(s,t_{1}+t_{2};n,k)$ is admissible, $t_{1},t_{2}\geq 0$ . Then

\mathbf{F}(s,t_{1}+t_{2};n,k)\leq t_{1}+\mathbf{F}(s,t_{2};n,k).

Proof.

This is equivalent to showing that for fixed $s,n,k$ , the map $t\mapsto\mathbf{F}(s,t;n,k)$ is Lipschitz with Lipschitz constant $\leq 1$ . We sketch the proof. First, it is not hard to show $t\mapsto\mathbf{F}(s,t;n,k)$ is continuous. Since $\mathbf{F}(s,t;n,k)$ is piecewise defined, we check each formula of $\mathbf{F}(s,t;n,k)$ . We see the derivative on $t$ is $\leq 1$ . ∎

$\mathbf{F}(s,t;n,k)$ is continuous in $t$ , but not in $s$ . Nevertheless, we can still say something about $s$ .

Lemma 21.

$\mathbf{F}(s,t;n,k)$ is locally left-Lipschitz in $s$ . In other words, if we write $s=d+\sigma$ ( $d\in\mathbb{N},\sigma\in(0,1]$ ), we have

\mathbf{F}(s-\theta,t;n,k)\geq\mathbf{F}(s,t;n,k)-O(\theta)

for any $0\leq\theta<\sigma$ .

Proof.

We just note that $s\mapsto\mathbf{F}(s,t;n,k)$ is defined piecewise for $s$ in left-open intervals of form $(d,d+1]$ where $d\in\mathbb{N}$ . Moreover, $s\mapsto\mathbf{F}(s,t;n,k)$ is Lipschitz in each of these left-open intervals. ∎

The next results are for the Marstrand index.

Lemma 22.

Each pair $(a,s)$ satisfying $a\in(0,n],s>0$ belongs to exactly one of the four types in Definition 14.

Proof.

To show this, we just need to prove for a fixed $a\in(0,n]$ , the ranges of $s$ determined by four cases form a partition of $(0,\infty)$ . Type 1 corresponds to $s\in(\min\{a,k\},\infty)$ . Type 4 corresponds to $s\in(0,a-(n-k)]$ . Note that $a-(n-k)\leq\min\{a,k\}$ , so we just need to show the ranges of $s$ determined by Type 2 and Type 3 from a partition of $(a-(n-k),\min\{a,k\}]$ . Since the ranges of $s$ determined by Type2 and Type 3 are disjoint, we just need to show

\{s:s\textup{~{}satisfies~{}Type~{}}2\}\bigcup\{s:s\textup{~{}satisfies~{}Type~{}}3\}=(a-(n-k),\min\{a,k\}].

We first show “ $\subset"$ . Suppose $s$ satisfies the condition in Type 2. We want to show $s>a-(n-k)$ , which is equivalent to $m<n+l-k+\gamma-\beta$ . This is true since $m\leq n+l-k$ and $\gamma>\beta$ . Suppose $s$ satisfies condition in Type 3. Again, we want to show $m<n+l-k+\gamma-\beta$ . This is true since $m\leq n+l-k-1$ and $\gamma-\beta>-\beta\geq-1$ .

Next, we show “ $\supset$ ”. Suppose $s=l+\gamma\in(a-(n-k),\min\{a,k\}]$ . $s>a-(n-k)$ implies

m<n+l-k+\gamma-\beta.

$s\leq a$ implies

m\geq l+\gamma-\beta.

If $\gamma\in(\beta,1]$ , then $l+1\leq m\leq n+l-k$ . Hence, $s$ satisfies the condition in Type 2. If $\gamma\in(0,\beta]$ , then $l\leq m\leq n+l-k-1$ . Hence, $s$ satisfies the condition in Type 3. ∎

Lemma 23.

For $(a,s,n,k)$ and $(a-\theta,s-\theta;n,k)$ that are in the domain of $\mathbf{M}$ and $\theta\geq 0$ , we have

\mathbf{M}(a-\theta,s-\theta;n,k)\leq\mathbf{M}(a,s;n,k).

Proof.

Let $a=m+\beta,s=l+\gamma$ be the canonical expression. We just check four types as in Definition 14.

Type 1: If $s>\min\{a,k\}$ , then

\mathbf{M}(a-\theta,s-\theta;n,k)\leq k\leq\mathbf{M}(a,s;n,k).

Type 4: If $s\leq a-(n-k)$ , then we have $\mathbf{M}(a-\theta,s-\theta;n,k)=\mathbf{M}(a,s;n,k)=-\infty$ .

Type 2: Suppose $(a,s;n,k)$ is of Type 2.

If $\theta<\beta$ .

	$\displaystyle\mathbf{M}(a-\theta,s-\theta;n,k)=k(n-k)-(m-l)(k-l)+\max\{2(\gamma-\theta)-(\beta-\theta+1),0\}$
	$\displaystyle\leq k(n-k)-(m-l)(k-l)+\max\{2\gamma-(\beta+1),0\}=\mathbf{M}(a,s;n,k).$

If $\beta\leq\theta<\gamma$ , then $a-\theta=(m-1)+(1+\beta-\theta),s-\theta=l+(\gamma-\theta)$ . So, $(a-\theta,s-\theta;n,k)$ is of Type 3. We have the same estimate:

	$\displaystyle\mathbf{M}(a-\theta,s-\theta;n,k)=k(n-k)-(m-l)(k-l)+\max\{2(\gamma-\theta)-(\beta-\theta+1),0\}$
	$\displaystyle\leq k(n-k)-(m-l)(k-l)+\max\{2\gamma-(\beta+1),0\}=\mathbf{M}(a,s;n,k).$

Note that the integer part $(m,l)$ is reduced to $(n-1,l)$ , so we can keep doing the iteration.

Type 3: This is similar to Type 2, so we just omit the proof.

∎

Lemma 24.

Suppose $a-(n-k)<s\leq\min\{k,a\}$ . Write $a=m+\beta,s=l+\gamma$ as in Definition 14. Then

\mathbf{M}(a,s;n,k)\leq k(n-k)-(m-l)(k-l)+\max\{2\gamma-(\beta+1),0\},

and

\mathbf{M}(a,s;n,k)\geq k(n-k)-(m+1-l)(k-l)+\max\{2\gamma-\beta,0\}.

Proof.

The proof is simply by checking when $(a,s;n,k)$ is of Type 2 or Type 3. ∎

We also show two easy results about exceptional set estimate.

Lemma 25.

Recall Definition 14. Suppose we are in Type 1: $s>\min\{k,a\}$ . Then there exists $A\subset\mathbb{F}_{p}^{n}$ with $\#A\sim p^{a}$ , such that

\#E_{s}(A;n,k)\gtrsim p^{k(n-k)}.

Proof.

We just choose $A$ to be any set with cardinality $p^{a}$ . One can check by definition that $E_{s}(A;n,k)=G(k,\mathbb{F}_{p}^{n})$ . ∎

Lemma 26.

Recall Definition 14. Suppose we are in Type 4: $s\leq a-(n-k)$ . Then for any $A\subset\mathbb{F}_{p}^{n}$ with $\#A\geq p^{a}$ , we have

\#E_{s}(A;n,k)=0.

Proof.

If $V\in E_{s}(A;n,k)$ , then

p^{a}=\#A=\sum_{L\in\pi_{V}^{*}(A)}\#(L\cap A)\leq\#\pi_{V}^{*}(A)\cdot\#V<p^{s+n-k},

a contradiction! Therefore, $E_{s}(A;n,k)=\emptyset$ . ∎

3. Furstenberg set problem: upper bound

In this section, we prove Theorem 6. In other words, we will construct a $(s,t;n,k)$ -set $E=\bigcup_{V\in\mathcal{V}}Y(V)$ , such that

\#E\lesssim_{s,t,n,k}p^{\mathbf{F}(s,t;n,k)}.

3.1. Two special cases

To get familiar with $\mathbf{F}(s,t;n,k)$ , we discuss two special cases: $s=k$ ; $k=1$ .

When $s=k$ , we can morally view $Y(V)$ as $V$ . Therefore, a $(k,t;n,k)$ -set is of form

E=\bigcup_{V\in\mathcal{V}}V.

Estimating the size of $E$ is known as the “union of $k$ -planes problem”. It has been resolved in finite fields by R. Oberlin [11]. The Euclidean version was resolved by the author in [3].

When $k=1$ , this is the Furstenberg set problem for lines. To construct a $(s,t;n,1)$ -set

E=\bigcup_{L\in\mathcal{L}}Y(L)

with size as small as possible, we hope the lines in $\mathcal{L}$ are compressed in low dimensional space. Write $t=2m+\beta$ , where $0\leq m\leq n-2$ is an integer and $\beta\in(0,2]$ . Since $t\leq 2(m+1)$ , we can make $\mathcal{L}$ contained in $\mathbb{F}_{p}^{m+2}$ . Therefore, our goal becomes to construct a small $(s,t;m+2,1)$ -set. The trick is to take Cartesian product of a $(s,\beta;2,1)$ -set with $\mathbb{F}_{p}^{m}$ . Let $E^{\prime}\subset\mathbb{F}_{p}^{2}$ be a $(s,\beta;2,1)$ -set and $E^{\prime}$ has the form

E^{\prime}=\bigcup_{L^{\prime}\in\mathcal{L}^{\prime}}Y(L^{\prime}).

We will construct a $(s,t;m+2,1)$ -set $E$ based on $E^{\prime}$ . Let $\pi_{\mathbb{F}_{p}^{2}}:\mathbb{F}_{p}^{m+2}\rightarrow\mathbb{F}_{p}^{2}$ be the projection onto the first two coordinates. Define $\mathcal{L}$ to be the set of lines $L$ in $\mathbb{F}_{p}^{m+2}$ such that $\pi_{\mathbb{F}_{p}^{2}}(L)$ is a line in $\mathcal{L}^{\prime}$ . Then, $\#\mathcal{L}\sim\#G(1,\mathbb{F}_{p}^{m+1})\cdot\#\mathcal{L}^{\prime}\sim p^{2m+\beta}=p^{t}$ . If $L\in\mathcal{L}$ , then $L^{\prime}=\pi_{\mathbb{F}_{p}^{2}}(L)\in\mathcal{L}^{\prime}$ . We define $Y(L):=L\cap\pi_{\mathbb{F}_{p}^{2}}^{-1}(Y(L^{\prime}))$ . We see that $\#Y(L)=\#Y(L^{\prime})\sim p^{s}$ , so

E=\bigcup_{L\in\mathcal{L}}Y(L)

is a $(s,t;m+2,1)$ -set. Also, since $E\subset E^{\prime}\times\mathbb{F}_{p}^{m}$ , we have

\#E\leq\#E^{\prime}\cdot p^{m}\lesssim p^{m+\min\{s+\beta,\frac{3}{2}s+\frac{1}{2}\beta,s+1\}}

By checking Definition 11, one exactly sees that

m+\min\{s+\beta,\frac{3}{2}s+\frac{1}{2}\beta,s+1\}=\mathbf{F}(s,t;m+2,1)=\mathbf{F}(s,t;n,1).

3.2. Proof of Theorem 6

For admissible $(s,t;n,k)$ , we will construct a $(s,t;n,k)$ -set

E=\bigcup_{V\in\mathcal{V}}Y(V)

such that

\#E\gtrsim p^{\mathbf{F}(s,t;n,k)}.

Case (a): $s=0$

If $t\leq k(n-k)$ , we choose $\mathcal{V}$ to be $p^{t}$ $k$ -planes pass through the origin $\mathbf{0}^{n}$ , and $Y(V)=\{\mathbf{0}^{n}\}$ . Then $\#E\leq 1=p^{0}$ . Here, $\mathbf{0}^{n}$ means $(\underbrace{0,\dots,0}_{n\textup{~{}times~{}}})$ .

If $t\geq k(n-k)$ , we choose $p^{t-k(n-k)}$ points $X$ in $\mathbb{F}_{p}^{n-k}$ . For each such point $x\in X$ , we choose $\sim p^{k(n-k)}$ $k$ -planes that pass through $x$ , and require the $k$ -planes to be transverse to $\mathbb{F}_{p}^{n-k}$ . We obtain $\sim p^{t}$ $k$ -planes which is $\mathcal{V}$ . If $V$ pass through $x\in X$ , we set $Y(V)=\{x\}$ . We see that $\#E=\#X\leq p^{t-k(n-k)}$ .

Case (b): $s>0,t\in[0,(k-d-1)(n-k)]$

We write $s=d+\sigma$ , where $d\in\{0,\dots,k-1\},\sigma\in(0,1]$ . The construction is similar to Case (a). We choose $\sim p^{t}$ many $k$ -planes that contain $\mathbb{F}_{p}^{d+1}$ . This is doable since

\#\{V\in A(k,\mathbb{F}_{p}^{n}):V\supset L\}=\#G(k-d-1,\mathbb{F}_{p}^{n-d-1})\sim p^{(k-d-1)(n-k)}.

Let $\mathcal{V}$ be these $k$ -planes. Fix $Y\subset\mathbb{F}_{p}^{d+1}$ with $\#Y=p^{s}$ . For each $V\in\mathcal{V}$ , let $Y(V)=Y$ . We see that $\#E=\#Y=p^{s}$ .

Case (c): $s\in(0,k],t\in((k-d-1)(n-k),(k+1)(n-k)]$

We write

(24)

\begin{cases}s=d+\sigma\\ t=(k-d-1)(n-k)+(d+2)m+\tau,\end{cases}

where $d\in\{0,\dots,k-1\}$ , $\sigma\in(0,1]$ , $m\in\{0,\dots,n-k-1\}$ , $\tau\in[0,2]$ . We remark that here we allow $\tau=0$ , though we assumed $\tau>$ in the canonical expression. Allowing $\tau=0$ will produce the example in Case (d).

We write $\mathbb{F}_{p}^{n}=\mathbb{F}_{p}^{n-k+d+1}\times\mathbb{F}_{p}^{k-d-1}$ . Note that $\gtrsim 1$ fraction of $k$ -planes intersect $\mathbb{F}_{p}^{n-k+d+1}$ at a $(d+1)$ -plane. Heuristically speaking, to make $\#E$ as small as possible, we would like $E$ to be a subset of $\mathbb{F}_{p}^{n-k+d+1}\times\mathbf{0}^{k-d-1}$ . For simplicity, we write $\mathbb{F}_{p}^{n-k+d+1}\times\mathbf{0}^{k-d-1}$ as $\mathbb{F}_{p}^{n-k+d+1}$ , thinking of it as a subspace of $\mathbb{F}_{p}^{n}$ . This will not cause any ambiguity.

Note that for each $W\in A(d+1,\mathbb{F}_{p}^{n-k+d+1})$ , the cardinality of

\{V\in A(k,\mathbb{F}_{p}^{n}):V\supset W,V\textup{~{}is~{}transverse~{}to~{}}\mathbb{F}_{p}^{n-k+d+1}\}

is $\sim\#G(k-d-1,\mathbb{F}_{p}^{n-k})\sim p^{(k-d-1)(n-k)}$ . We just need to find $\mathcal{W}\subset A(d+1,\mathbb{F}_{p}^{n-k+d+1})$ with $\#\mathcal{W}\sim p^{t-(k-d-1)(n-k)}=p^{(d+2)m+\tau}$ , and for each $W\in\mathcal{W}$ , to find $Y(W)\subset W$ with $\#Y(W)\sim p^{s}$ , such that

(25)

\#\bigcup_{W\in\mathcal{W}}Y(W)\lesssim p^{\mathbf{F}(s,t;n,k)}.

If this is done, then we let $\mathcal{V}$ be those $k$ -planes $V$ that contain some $W\in\mathcal{W}$ , and $Y(V)=Y(W)$ if $V\supset W$ . We see that $\#\mathcal{V}\sim\#\{W\}\cdot p^{(k-d-1)(n-k)}\sim p^{t}$ , and hence $E=\bigcup_{V\in\mathcal{V}}Y(V)$ is a $(s,t;n,k)$ -set. Also, we have the upper bound

\#E=\#\bigcup_{W\in\mathcal{W}}Y(W)\lesssim p^{\mathbf{F}(s,t;n,k)}.

It suffices to find a $(s,(d+2)m+\tau;n-k+d+1,d+1)$ -set $E_{1}=\bigcup_{W\in\mathcal{W}}Y(W)$ such that (25) holds. Note that $\#A(d+1,\mathbb{F}_{p}^{m+d+2})\sim p^{(d+2)(m+1)}$ and $(d+2)m+\tau\leq(d+2)(m+1)$ . We will construct the $(d+1)$ -planes $\mathcal{W}$ so that they lie in $\mathbb{F}_{p}^{m+d+2}$ . It suffices to find a $(s,(d+2)m+\tau;m+d+2,d+1)$ -set $E_{1}=\bigcup_{W\in\mathcal{W}}Y(W)$ such that (25) holds.

We write $\mathbb{F}_{p}^{m+d+2}=\mathbb{F}_{p}^{d+2}\times\mathbb{F}_{p}^{m}=\mathbb{F}_{p}^{2}\times\mathbb{F}_{p}^{d}\times\mathbb{F}_{p}^{m}$ . We first choose a $(\sigma,\tau;2,1)$ -set $E_{2}=\bigcup_{L\in\mathcal{L}}Y(L)$ in $\mathbb{F}_{p}^{2}$ , such that

\#E_{2}\lesssim p^{\min\{\sigma+\tau,\frac{3}{2}\sigma+\frac{1}{2}\tau,\sigma+1\}}.

The existence of $E_{2}$ was shown in Proposition 13.

Next, we define $\mathcal{U}:=\{L\times\mathbb{F}_{p}^{d}:L\in\mathcal{L}\}$ which is a subset of $A(d+1,\mathbb{F}_{p}^{d+2})$ . And for each $U=L\times\mathbb{F}_{p}^{d}\in\mathcal{U}$ , define $Y(U)=Y(L)\times\mathbb{F}_{p}^{d}$ . We see that $\#\mathcal{U}=\#\mathcal{L}\sim p^{\tau}$ , $\#Y(U)=\#Y(L)\cdot p^{d}\sim p^{\sigma+d}=p^{s}$ . We also see that $E_{3}:=\bigcup_{U\in\mathcal{U}}Y(U)$ is contained in $E_{2}\times\mathbb{F}_{p}^{d}$ , and hence

\#E_{3}\lesssim p^{d+\min\{\sigma+\tau,\frac{3}{2}\sigma+\frac{1}{2}\tau,\sigma+1\}}.

Finally, we define $\mathcal{W}$ . For each $U\in\mathcal{U}$ , consider the $(m+d+1)$ -plane $U\times\mathbb{F}_{p}^{m}$ . Let $\pi_{U}:U\times\mathbb{F}_{p}^{m}\rightarrow U$ be the projection (naturally defined). We let $\mathcal{W}_{U}$ be the set of $(d+1)$ -planes $W$ contained in $U\times\mathbb{F}_{p}^{m}$ such that $\pi_{U}(W)=U$ . Note that $\gtrsim 1$ fraction of the $(d+1)$ -planes in $U\times\mathbb{F}_{p}^{m}$ lie in $\mathcal{W}_{U}$ , so $\#\mathcal{W}_{U}\sim\#A(d+1,\mathbb{F}_{p}^{m+d+1})\sim p^{(d+2)m}$ .

We define $\mathcal{W}=\bigcup_{U\in\mathcal{U}}\mathcal{W}_{U}$ (actually this is a disjoint union). For $W\in\mathcal{W}_{U}$ , define $Y(W)=W\cap\pi_{U}^{-1}(Y(U))$ . We see that $\#\mathcal{W}\sim\#\mathcal{U}\cdot p^{(d+2)m}\sim p^{(d+2)m+\tau}$ , and $\#Y(W)=\#Y(U)\sim p^{s}$ . Hence, $E_{1}=\bigcup_{W\in\mathcal{W}}Y(W)$ is a $(s,(d+2)m+\tau;m+d+2,d+1)$ -set. Since $E_{1}\subset E_{3}\times\mathbb{F}_{p}^{m}$ , we have

\#E_{1}\leq\#E_{3}\cdot p^{m}\lesssim p^{d+m+\min\{\sigma+\tau,\frac{3}{2}\sigma+\frac{1}{2}\tau,\sigma+1\}}.

The construction is done.

Case (d)

We still use (24), but the range of $\tau$ is $\tau\in(2,d+2]$ . Note the worst case is when $\tau=d+2$ . What we need to do is, for

(26)

\begin{cases}s=d+\sigma\\ t=(k-d-1)(n-k)+(d+2)(m+1),\end{cases}

construct a $(s,t;n,k)$ -set $E$ such that

\#E\lesssim p^{s+m+1}.

The trick is to still use the construction in Case (c), with $\tau$ replaced by $0$ and $m$ replaced by $m+1$ . Therefore, we can construct a $(s,t;n,k)$ -set $E$ such that

\#E\lesssim p^{d+m+1+\min\{\sigma+0,\frac{3}{2}\sigma+\frac{1}{2}0,\sigma+1\}=p^{d+m+1+\sigma}=p^{s+m+1}}.

4. Furstenberg set problem: Lower bound I

To get more familiar with the problem, we first prove two special cases of Theorem 7: $s=0$ ; $t=0$ .

Proposition 27.

If $E$ is a $(0,t;n,k)$ -set, then

\#E\gtrsim p^{\mathbf{F}(0,t;n,k)}=p^{\max\{0,t-k(n-k)\}}.

Proof.

Suppose $E=\bigcup_{V\in\mathcal{V}}Y(V)$ . Note that each $x\in E$ can lie in at most $\#G(k,\mathbb{F}_{p}^{n})\sim p^{k(n-k)}$ different $V$ . We have

\#E\cdot p^{k(n-k)}\geq\sum_{V\in\mathcal{V}}\#Y(V)\gtrsim p^{t}.

Hence, $\#E\gtrsim p^{t-k(n-k)}$ . Also, trivially, $\#E\geq 1$ . ∎

Proposition 28.

If $E$ is a $(s,0;n,k)$ -set, then

\#E\gtrsim p^{\mathbf{F}(s,0;n,k)}=p^{s}.

Proof.

By the definition of $(s,0;n,k)$ -set, $\#E\geq\#Y(V)\gtrsim p^{s}$ . ∎

In this section, we prove Theorem 7 for $(n,k)=(k+1,k)$ . The proof is by induction on $k$ . The goal of this section is to prove the following result.

Proposition 29.

Let $k\in\mathbb{N}$ and $k\geq 2$ . Suppose for admissible $(s,t;k,k-1)$ , we know

(27)

\inf_{E:\ (s,t;k,k-1)\textup{-set}}\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t;k,k-1)-\varepsilon}

for any $\varepsilon>0$ . Then for admissible $(s,t;k+1,k)$ , we have

(28)

\inf_{E:\ (s,t;k+1,k)\textup{-set}}\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t;k+1,k)-\varepsilon},

for any $\varepsilon>0$ .

We first prove the following lemma.

Lemma 30.

Assume (27) holds. Suppose $(s,t;k+1,k)$ is admissible. Then for any $(s,t;k+1,k)$ -set $E$ , there exist numbers $t_{1},t_{2},s_{1},s_{2},u,v$ , such that

(29)

\begin{cases}1\leq p^{t_{1}}\leq p^{k-1},1\leq p^{t_{2}}\leq p^{2};\\ 1\leq p^{s_{1}}\leq p,1\leq p^{s_{2}}\leq p^{s};\\ p^{s_{1}}\lesssim p^{u}\leq p,1\leq p^{v}\leq p;\end{cases}

and

(30)

\begin{cases}p^{t_{1}+t_{2}}\gtrapprox p^{t};\\ p^{s_{1}+s_{2}}\gtrapprox p^{s};\\ p^{u+v}\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},t_{2};2,1)-\varepsilon};\end{cases}

and

(31)

\#E\gtrsim_{\varepsilon}p^{u+\max\{\mathbf{F}(s_{2},t_{1}+v;k,k-1),s_{2}+v\}-\varepsilon}.

Proof.

We will do several steps of pigeonholing, which lead to the parameters $t_{1},t_{2},s_{1},s_{2},u,v$ .

By the definition of $(s,t;k+1,k)$ -set, we write

E=\bigcup_{V\in\mathcal{V}}Y(V),

where $\mathcal{V}\subset A(k,\mathbb{F}_{p}^{k+1})$ with $\#\mathcal{V}\sim p^{t}$ , and $Y(V)\subset V$ with $\#Y(V)\sim p^{s}$ .

The strategy is to find a subset of $\mathcal{V}$ , and a subset of $Y(V)$ for each $V$ , still denoted by $\mathcal{V}$ , $Y(V)$ , so that the new $\mathcal{V},Y(V)$ satisfy certain uniformity. This is done by a sequence of pigeonhole arguments.

By properly choosing the coordinate, we can assume $\gtrsim 1$ fraction of the $k$ -planes in $\mathcal{V}$ are not parallel to $\mathbb{F}_{p}^{k}$ . Throwing away some $V\in\mathcal{V}$ , we can just assume all the $k$ -planes in $\mathcal{V}$ are not parallel to $\mathbb{F}_{p}^{k}$ .

Now, we partition $\mathcal{V}$ according to $G(k-1,\mathbb{F}_{p}^{k}\times\mathbf{0})$ . Since each $V\in\mathcal{V}$ is not parallel to $\mathbb{F}_{p}^{k}$ and the ambient space is $\mathbb{F}_{p}^{k+1}$ , $V$ must intersect $\mathbb{F}_{p}^{k}\times\mathbf{0}$ at a $(k-1)$ -plane. For each $W\in G(k-1,\mathbb{F}_{p}^{k}\times\mathbf{0})$ , we define $\mathcal{V}_{W}$ to be the set of $V\in\mathcal{V}$ such that $V\cap\mathbb{F}_{p}^{k}$ is parallel to $W$ . We obtain a partition

\mathcal{V}=\bigsqcup_{W\in G(k-1,\mathbb{F}_{p}^{k}\times\mathbf{0})}\mathcal{V}_{W}.

First pigeonholing. We assume there exists $\mathcal{W}\subset G(k-1,\mathbb{F}_{p}^{k}\times\mathbf{0})$ with $\#\mathcal{W}\sim p^{t_{1}}$ such that for each $W\in\mathcal{W}$ , $\#\mathcal{V}_{W}\sim p^{t_{2}}$ . Here, $1\leq p^{t_{1}}\leq p^{k-1},1\leq p^{t_{2}}\leq p^{2}$ are dyadic numbers and

(32)

p^{t_{1}}p^{t_{2}}\gtrapprox p^{t}.

(Recall $A\gtrapprox B$ means $A\gtrsim(\log p)^{C}B$ .) We still use $\mathcal{V}$ to denote $\bigcup_{W\in\mathcal{W}}\mathcal{V}_{W}$ . And we see that

\#\mathcal{V}\gtrapprox p^{t}.

Second pigeonholing. By properly choosing the coordinate and throw away $\lesssim 1$ fraction of $W$ in $\mathcal{W}$ , we can assume each $W$ in $\mathcal{W}$ satisfies $W\cap(\mathbb{F}_{p}\times\mathbf{0}^{k})=\mathbf{0}^{k+1}$ . Denote $\widetilde{\mathbb{F}_{p}^{2}}=\mathbb{F}_{p}\times\mathbf{0}^{k-1}\times\mathbb{F}_{p}$ . If $V\in\mathcal{V}_{W}$ and $W\in\mathcal{W}$ , then $V\cap\widetilde{\mathbb{F}_{p}^{2}}$ is a line. We denote it by $\ell_{V}:=V\cap\widetilde{\mathbb{F}_{p}^{2}}$ . Note that $\ell_{V}$ is not parallel to the first coordinate in $\widetilde{\mathbb{F}_{p}^{2}}$ .

For a fixed $V\in\mathcal{V}_{W}$ , we do a Fubini-type argument. Write

V=\bigsqcup_{x\in\ell_{V}}(x+W).

Noting that $\#Y(V)\sim p^{s}$ , by pigeonholing, we find a subset $Y(\ell_{V})\subset\ell_{V}$ , so that $\#Y(\ell_{V})\sim s_{1}(V)$ , and for each $x\in Y(\ell_{V})$ , $\#Y(V)\cap(x+W)\sim s_{2}(V)$ . Here, $1\leq p^{s_{1}(V)}\leq p,1\leq p^{s_{2}(V)}\leq p^{s}$ are dyadic numbers and satisfy

p^{s_{1}(V)}\cdot p^{s_{2}(V)}\gtrapprox p^{s}.

By throwing away some horizontal slices of $Y(V)$ , we can assume

Y(V)=\bigsqcup_{x\in Y(\ell_{V})}\bigg{(}Y(V)\cap(x+W)\bigg{)}.

For the new $Y(V)$ , we still have

\#Y(V)\gtrapprox p^{s}.

For convenience, given $V\in\mathcal{V}_{W}$ and $x\in\ell_{V}$ , we denote

Y(V,x):=Y(V)\cap(x+W).

$Y(V,x)$ is called the horizontal $x$ -slice. (Note that there is no confusion, since $V$ uniquely determines $W$ .) Thus, we have

(33)

Y(V)=\bigsqcup_{x\in Y(\ell_{V})}Y(V,x).

Third pigeonholing. For each $W\in\mathcal{W}$ , we can find dyadic numbers $p^{s_{1}(W)},p^{s_{2}(W)}$ so that $\gtrapprox 1$ fraction of $V$ in $\mathcal{V}(W)$ satisfy $p^{s_{1}(V)}=p^{s_{1}(W)},p^{s_{2}(V)}=p^{s_{2}(W)}$ .

Fourth pigeonholing. There exist dyadic numbers $p^{s_{1}},p^{s_{2}}$ such that $\gtrapprox 1$ fraction of $W$ in $\mathcal{W}$ satisfy $p^{s_{1}(W)}=p^{s_{1}}$ and $p^{s_{2}(W)}=p^{s_{2}}$ .

We summarize what we have done so far. We can redefine $\mathcal{W}$ , $\mathcal{V}_{W}$ and $\mathcal{V}$ , so that $\mathcal{V}=\bigcup_{W\in\mathcal{W}}\mathcal{V}_{W}$ and the following uniformity holds.

\#\mathcal{W}\gtrapprox p^{t_{1}}.

\#\mathcal{V}_{W}\gtrapprox p^{t_{2}},\textup{~{}for~{}}W\in\mathcal{W}.

For $W\in\mathcal{W}$ and each $V\in\mathcal{V}_{W}$ ,

(34)

Y(V)=\bigsqcup_{x\in Y(\ell_{V})}Y(V,x),

with $\#Y(\ell_{V})\sim p^{s_{1}}$ and for each $x\in Y(\ell_{V})$ , $\#Y(V,x)\sim p^{s_{2}}$ .

Fix a $W\in\mathcal{W}$ . We want to estimate $\bigcup_{V\in\mathcal{V}_{W}}Y(\ell_{V})(\subset\widetilde{\mathbb{F}_{p}^{2}})$ . This is some sort of Furstenberg set in two-dimensional space. Also, an important preperty is that each $\ell_{V}$ is not parallel to the first coordinate. We will exploit some “quasi-product” structure of this set.

Lemma 31.

Assume Conjecture 4 holds. Suppose $E=\bigcup_{\ell\in\mathcal{L}}Y(\ell)$ is a $(s_{1},t_{2};2,1)$ -set. Also, we assume each $\ell\in\mathcal{L}$ is not parallel to $\mathbb{F}_{p}\times\mathbf{0}$ . Then there exist dyadic numbers $p^{u},p^{v}$ such that

p^{s_{1}}\lesssim p^{u}\lesssim p,

1\leq p^{v}\leq p,

and

p^{u}p^{v}\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},t_{2};2,1)-\varepsilon}.

for any $\varepsilon>0$ . Also, $E$ contains a subset of form

\bigsqcup_{\xi\in\Xi}Y_{\xi},

where $\Xi\subset\mathbf{0}\times\mathbb{F}_{p}$ with $\#\Xi\sim p^{u}$ , and $Y_{\xi}\subset E\cap\bigg{(}\xi+(\mathbb{F}_{p}\times\mathbf{0})\bigg{)}$ with $\#Y_{\xi}\sim p^{v}$ .

Proof.

For $\xi\in\mathbf{0}\times\mathbb{F}_{p}$ , define $E(\xi):=E\cap\bigg{(}\xi+(\mathbb{F}_{p}\times\mathbf{0})\bigg{)}$ . By pigeonholing on horizontal slices of $E$ , we can find $\Xi\subset\mathbf{0}\times\mathbb{F}_{p}$ so that for all $\xi\in\Xi$ , $E(\xi)$ have comparable cardinality. We may denote $\#\Xi\sim p^{u},\#E(\xi)\sim p^{v}$ for two dyadic numbers $p^{u},p^{v}\geq 1$ . We can also assume $p^{u}p^{v}\gtrapprox\#E$ . Hence, assuming Conjecture 4, we have

p^{u}p^{v}\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},t_{2};2,1)-\varepsilon}.

However, we still need the condition $p^{u}\gtrsim p^{s_{1}}$ . This is handled by the following trick. We will conduct an algorithm to find a sequence $E=E_{1}\supset E_{2}\supset\cdots\supset E_{m}$ , and disjoint subsets $\Xi_{1},\Xi_{2}\cdots,\Xi_{m}$ of $\mathbf{0}\times\mathbb{F}_{p}$ . To start with, let $E_{1}=E$ . By pigeonholing, we can find $\Xi_{1}\subset\mathbf{0}\times\mathbb{F}_{p}$ , such that $\#\Xi_{1}\sim p^{u_{1}}$ , $\#E(\xi)\sim p^{v_{1}}$ for each $\xi\in\Xi$ , and

p^{u_{1}}p^{v_{1}}\gtrsim_{\varepsilon}\#E_{1}\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},t_{2};2,1)-\varepsilon}.

Suppose we have defined $E_{i},\Xi_{i}$ for $1\leq i\leq j-1$ . If $\sum_{i=1}^{j-1}p^{u_{i}}\ll p^{s_{1}}$ , then we define

E_{j}:=E\setminus\bigcup_{1\leq i\leq j-1}\bigsqcup_{\xi\in\Xi_{i}}E(\xi).

Since each $\ell\in\mathcal{L}$ is not parallel to $\mathbb{F}_{p}\times\mathbf{0}$ , we see that $E_{j}$ is still a $(s_{1},t_{2};2,1)$ -set. By the same pigeonholing, we find $\Xi_{j}\subset(\mathbf{0}\times\mathbb{F}_{p})\setminus\bigcup_{1\leq i\leq j-1}\Xi_{i}$ , so that $\#\Xi_{j}\sim p^{u_{j}}$ , $\#E(\xi)\sim p^{v_{j}}$ for each $\xi\in\Xi_{j}$ , and

p^{u_{j}}p^{v_{j}}\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},t_{2};2,1)-\varepsilon}.

If $\sum_{i=1}^{j-1}p^{u_{i}}\gtrsim p^{s_{1}}$ , then we stop and let $m=j-1$ .

The algorithm will stop in finite steps. Denote $\Xi:=\bigcup_{1\leq i\leq m}\Xi_{i}$ . Let $p^{u},p^{v}$ be dyadic numbers so that $p^{v}=\min_{1\leq i\leq m}p^{v_{i}}$ , $p^{u}\sim\#\Xi$ . For each $\xi\in\Xi$ , let $Y_{\xi}$ be a subset of $E(\xi)$ with $\#Y_{\xi}\sim p^{v}$ . This is doable, since $\#E(\xi)\gtrsim p^{v}$ if $\xi\in\Xi$ . One can check

p^{u}p^{v}\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},t_{2};2,1)-\varepsilon}.

This is proved in the following way. Suppose $p^{v}=p^{v_{i}}$ , then

p^{u}p^{v}=p^{u}p^{v_{i}}\geq p^{u_{i}}p^{v_{i}}\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},t_{1};2,1)-\varepsilon}.

Also, one can check

p^{u}=\sum_{i=1}^{m}p^{u_{i}}\gtrsim p^{s_{1}}.

∎

Return back to $\widetilde{E}_{W}:=\bigcup_{V\in\mathcal{V}_{W}}Y(\ell_{V})$ (which lie in $\widetilde{\mathbb{F}_{p}^{2}}=\mathbb{F}_{p}\times\mathbf{0}^{k-1}\times\mathbb{F}_{p}$ ). Recall $\#\mathcal{V}_{W}\gtrapprox p^{t_{2}}$ and $\#Y(\ell_{V})\sim p^{s_{1}}$ . We see that $\widetilde{E}_{W}$ is a $(s_{1},(t_{2}-\varepsilon)_{+};2,1)$ -set, for any $\varepsilon>0$ . Here, $(t_{2}-\varepsilon)_{+}=\max\{t_{2}-\varepsilon,0\}$ .

By Lemma 31, there exist dyadic numbers $p^{u(W)},p^{v(W)}$ , so that $\widetilde{E}_{W}$ contains a subset of form

\bigsqcup_{\xi\in\Xi_{W}}Y_{W}(\rho_{\xi}).

Here, $\Xi_{W}\subset\mathbf{0}^{k}\times\mathbb{F}_{p}$ with $\#\Xi_{W}\sim p^{u(W)}$ ; $\rho_{\xi}:=\xi+(\mathbb{F}_{p}\times\mathbf{0}^{k})$ and $Y_{W}(\rho_{\xi})\subset\rho_{\xi}$ with $\#Y_{W}(\rho_{\xi})\sim p^{v(W)}$ . We also have

p^{u(W)}\gtrsim p^{s_{1}}.

p^{u(W)}p^{v(W)}\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},(t_{2}-\varepsilon)_{+};2,1)-\varepsilon}.

By pigeonholing on $(u(W),v(W))$ again, we can throw away some $W\in\mathcal{W}$ so that the cardinality of $\mathcal{W}$ is still $\gtrapprox p^{t_{1}}$ , and assume there exist $u,v$ such that

(u(W),v(W))=(u,v),\ \textup{~{}for~{}all~{}}W\in\mathcal{W},

and

p^{u}\gtrsim p^{s_{1}}.

p^{u}p^{v}\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},(t_{2}-\varepsilon)_{+};2,1)-\varepsilon}.

By Lemma 20,

p^{u}p^{v}\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},t_{2};2,1)-\varepsilon}.

Finally, we are about to estimate the lower bound of the cardinality of $E=\bigcup_{W\in\mathcal{W}}\bigcup_{V\in\mathcal{V}_{W}}Y(V).$ This $E$ is not the original one, but the one after pigeonholing. Recall (34), we have

(35)

\begin{split}\bigcup_{V\in\mathcal{V}_{W}}Y(V)&=\bigcup_{V\in\mathcal{V}_{W}}\bigsqcup_{x\in Y(\ell_{V})}Y(V,x)\\ &=\bigcup_{x\in\widetilde{E}_{W}}\bigg{(}\bigcup_{V:V\in\mathcal{V}_{W},x\in Y(\ell_{V})}Y(V,x)\bigg{)}.\end{split}

We define

Y(W,x):=\bigcup_{V:V\in\mathcal{V}_{W},x\in Y(\ell_{V})}Y(V,x).

Then $Y(W,x)$ is contained in the $(k-1)$ -plane $x+W$ .

If $x\in\widetilde{E}_{W}$ , then

\#Y(W,x)\gtrsim p^{s_{2}}.

Recall that

\widetilde{E}_{W}\supset\bigsqcup_{\xi\in\Xi_{W}}Y_{W}(\rho_{\xi}).

We have

\bigcup_{V\in\mathcal{V}_{W}}Y(V)\supset\bigcup_{\xi\in\Xi_{W}}\bigcup_{x\in Y_{W}(\rho_{\xi})}Y(W,x).

The reader can check, for fixed $\xi\in\Xi_{W}$ , $\bigcup_{x\in Y_{W}(\rho_{\xi})}Y(W,x)$ lies in $\mathbb{F}_{p}^{k}\times\{\xi\}$ .

Now we see that

E\supset\bigcup_{W\in\mathcal{W}}\bigcup_{\xi\in\Xi_{W}}\bigcup_{x\in Y_{W}(\rho_{\xi})}Y(W,x).

We want to estimate the lower bound of the right hand side. Intuitively, one can imagine the worst case is when $\Xi_{W}$ are morally the same for all $W\in\mathcal{W}$ ; otherwise we may translate them to the same $(k+1)$ -th coordinate so that their union becomes smaller. For example, if we have sets $A_{i}\times\{\xi_{i}\}\subset\mathbb{F}_{p}^{k}\times\mathbb{F}_{p}$ ( $i\in I$ ). Then $\bigcup_{i\in I}A_{i}\times\{\xi_{i}\}$ is the smallest when all the $\xi_{i}$ are the same.

Let us return to the estimate of

E^{\prime}:=\bigcup_{W\in\mathcal{W}}\bigcup_{\xi\in\Xi_{W}}\bigcup_{x\in Y_{W}(\rho_{\xi})}Y(W,x).

There are two lower bounds. The first lower bound is obtained from a fixed $W$ . We have

\#E^{\prime}\geq\bigcup_{\xi\in\Xi_{W}}\bigcup_{x\in Y_{W}(\rho_{\xi})}Y(W,x)\gtrsim p^{u}p^{v}p^{s_{2}}.

For the second lower bound, we will estimate $E^{\prime}$ on each $\xi$ -slice. We define the $\xi$ -slice of $E^{\prime}$ by

E^{\prime}_{\xi}:=E^{\prime}\cap(\mathbb{F}_{p}^{k}\times\{\xi\})=\bigcup_{W:W\in\mathcal{W},\xi\in\Xi_{W}}\bigcup_{x\in Y_{W}(\rho_{\xi})}Y(W,x).

We will see that $E^{\prime}_{\xi}$ is some sort of $(s_{2},t_{\xi};k,k-1)$ -set. Define

p^{t_{\xi}}:=\#\{(W,x):W\in\mathcal{W},\xi\in\Xi_{W},x\in Y_{W}(\rho_{\xi})\}.

We note two bounds for $t_{\xi}$ :

(36)

p^{t_{\xi}}\leq\#\mathcal{W}\cdot\#Y_{W}(\rho_{\xi})\lesssim p^{t_{1}}p^{v};

(37)

\sum_{\xi\in\mathbf{0}^{k}\times\mathbb{F}_{p}}p^{t_{\xi}}=\sum_{W\in\mathcal{W}}\#\Xi_{W}\cdot\#Y_{W}(\rho_{\xi})\gtrapprox p^{t_{1}}p^{u}p^{v}.

We used that $p^{t_{1}}\gtrsim\#\mathcal{W}\gtrapprox p^{t_{1}}$ , $\#\Xi_{W}\sim p^{u}$ , $\#Y_{W}(\rho_{\xi})\sim p^{v}$ .

And note that $Y(W,x)$ is a subset of the line $x+W$ such that $\#Y(W,x)\gtrsim p^{s_{2}}$ . Therefore, $E_{\xi}^{\prime}$ is a $(s_{2},t_{\xi};k,k-1)$ -set. By (27), we have

\#E^{\prime}_{\xi}\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{2},t_{\xi};k,k-1)-\varepsilon}.

Therefore,

\#E\gtrsim_{\varepsilon}\sum_{\xi\in\mathbf{0}^{k}\times\mathbb{F}_{p}}p^{\mathbf{F}(s_{2},t_{\xi};k,k-1)-\varepsilon}.

We claim that the right hand side is

\gtrapprox p^{u}p^{\mathbf{F}(s_{2},t_{1}+v;k,k-1)-\varepsilon}.

By pigeonholing, we can find a dyadic number $p^{t_{\circ}}\lesssim p^{t_{1}}p^{v}$ and $\Xi_{\circ}\subset\mathbf{0}^{k}\times\mathbb{F}_{p}$ , so that $2p^{t_{\circ}}\geq p^{t_{\xi}}\geq p^{t_{\circ}}$ for $\xi\in\Xi_{\circ}$ and

\#\Xi_{\circ}\cdot p^{t_{\circ}}\gtrapprox p^{t_{1}}p^{u}p^{v}.

Hence,

\#\Xi_{\circ}\gtrapprox p^{u}p^{t_{1}+v-t_{\circ}}.

We can estimate

\#E\gtrsim_{\varepsilon}\sum_{\xi\in\Xi_{\circ}}p^{\mathbf{F}(s_{2},t_{\xi};k,k-1)-\varepsilon}\geq\#\Xi_{\circ}\cdot p^{\mathbf{F}(s_{2},t_{\circ};k,k-1)-\varepsilon}\gtrapprox p^{u}p^{\mathbf{F}(s_{2},t_{\circ};k,k-1)+t_{1}+v-t_{\circ}-\varepsilon}.

By Lemma 20, we have

\#E\gtrapprox_{\varepsilon}p^{u+\mathbf{F}(s_{2},t_{1}+v;k,k-1)-\varepsilon}.

∎

The next lemma is a recursive inequality of $\mathbf{F}(s,t;k+1,k)$ , which can be used to bound the right hand side of (31).

Lemma 32.

Suppose $(s,t;k+1,k)$ is admissible. Suppose there exist numbers $t_{1},t_{2},s_{1},s_{2},u,v$ , such that

(38)

\begin{cases}t_{1}\in[0,k-1],t_{2}\in[0,2];\\ s_{1}\in[0,1],s_{2}\in[0,s];\\ u\in[s_{1},1],v\in[0,1];\end{cases}

and

(39)

\begin{cases}t_{1}+t_{2}\geq t;\\ s_{1}+s_{2}\geq s;\\ u+v\geq\mathbf{F}(s_{1},t_{2};2,1);\end{cases}

Then,

(40)

u+\max\{\mathbf{F}(s_{2},t_{1}+v;k,k-1),s_{2}+v\}\geq\mathbf{F}(s,t;k+1,k).

Let us quickly see how Lemma 30 and Lemma 32 combined to prove Proposition 29.

Proof of Proposition 29 assuming Lemma 30 and Lemma 32.

If $s=0$ or $t=0$ , by Proposition 27 or 28, we are done. So, we suppose $s,t>0$ .

Fix $0<\varepsilon<\min\{\sigma/2,t/2,1/2\}$ , where $s=d+\sigma$ with $d\in\mathbb{N},\sigma\in(0,1]$ . We just need to prove

(41)

\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t;k+1,k)-C\varepsilon}

for any $(s,t;k+1,k)$ -set $E$ . Here, $C$ is a large number.

We only need to prove for large enough $p$ , since for small $p$ we can choose the constant to be large.

Suppose (27) holds. Then in particular, Conjecture 4 also holds. If $E$ is a $(s,t;k+1,k)$ -set, by Lemma 30, there exist numbers $t_{1},t_{2},s_{1},s_{2},u,v$ , such that

(42)

\begin{cases}t_{1}\in[0,k-1],t_{2}\in[0,2];\\ s_{1}\in[0,1],s_{2}\in[0,s];\\ u\in[s_{1}-\varepsilon,1],v\in[0,1];\end{cases}

and

(43)

\begin{cases}t_{1}+t_{2}\geq t-\varepsilon;\\ s_{1}+s_{2}\geq s-\varepsilon;\\ u+v\geq\mathbf{F}(s_{1},t_{2};2,1)-\varepsilon;\end{cases}

and

(44)

\#E\gtrsim_{\varepsilon}p^{u+\max\{\mathbf{F}(s_{2},t_{1}+v;k,k-1),s_{2}+v\}-\varepsilon}.

Here, we used the fact that when $p$ is large enough (depending on $\varepsilon$ ), then $p^{t_{1}+t_{2}}\gtrapprox p^{t}$ implies $t_{1}+t_{2}\geq t-\varepsilon$ . Also, by our assumption. $t-\varepsilon,s-\varepsilon>0$ . Let $t^{\prime}=t-\varepsilon$ . $s^{\prime}=s-\varepsilon$ .

Since $\mathbf{F}(s_{1},t_{2};2,1)\leq 2$ , we can find $u\leq u^{\prime}\leq\min\{u+\varepsilon,1\}$ and $v\leq v^{\prime}\leq\min\{v+\varepsilon,1\}$ , so that $u^{\prime}\geq s_{1}$ , $u^{\prime}+v^{\prime}\geq\mathbf{F}(s_{1},t_{2};2,1)$ . Now we have

(45)

\begin{cases}t_{1}\in[0,k-1],t_{2}\in[0,2];\\ s_{1}\in[0,1],s_{2}\in[0,s];\\ u^{\prime}\in[s_{1},1],v^{\prime}\in[0,1];\end{cases}

and

(46)

\begin{cases}t_{1}+t_{2}\geq t^{\prime};\\ s_{1}+s_{2}\geq s^{\prime};\\ u^{\prime}+v^{\prime}\geq\mathbf{F}(s_{1},t_{2};2,1);\end{cases}

and

(47)

\#E\gtrsim p^{u+\max\{\mathbf{F}(s_{2},t_{1}+v;k,k-1),s_{2}+v\}-\varepsilon}\geq p^{u^{\prime}+\max\{\mathbf{F}(s_{2},t_{1}+v^{\prime};k,k-1),s_{2}+v^{\prime}\}-O(\varepsilon)}.

In the last inequality, we used Lemma 20.

Finally, by Lemma 32, we have

u^{\prime}+\max\{\mathbf{F}(s_{2},t_{1}+v^{\prime};k,k-1),s_{2}+v^{\prime}\}\geq\mathbf{F}(s^{\prime},t^{\prime};k+1,k)\geq\mathbf{F}(s,t;n,k)-O(\varepsilon).

The last inequality is by Proposition 21 and 20.

In summary, we finish the proof of

\#E\gtrsim p^{\mathbf{F}(s,t;k+1,k)-C\varepsilon}.

∎

It remains to prove Lemma 32. It can be reduced to the following lemma, with “ $\geq$ ” in (39) all replaced by “ $=$ ”.

Lemma 33.

Suppose $(s,t;k+1,k)$ is admissible. Suppose there exist numbers $t_{1},t_{2},s_{1},s_{2},u,v$ , such that

(48)

\begin{cases}t_{1}\in[0,k-1],t_{2}\in[0,2];\\ s_{1}\in[0,1],s_{2}\in[0,s];\\ u\in[s_{1},1],v\in[0,1];\end{cases}

and

(49)

\begin{cases}t_{1}+t_{2}=t;\\ s_{1}+s_{2}=s;\\ u+v=\mathbf{F}(s_{1},t_{2};2,1);\end{cases}

Then,

(50)

u+\max\{\mathbf{F}(s_{2},t_{1}+v;k,k-1),s_{2}+v\}\geq\mathbf{F}(s,t;k+1,k).

We show that Lemma 33 implies Lemma 32.

Proof of Lemma 32 assuming Lemma 33.

The idea is to slightly modify $s_{1},s_{2},t_{1},t_{2},u,v$ so that the “ $\geq$ ” in (39) become “ $=$ ”, and then we can apply Lemma 33.

For $i=1,2$ , we can find $t_{i}^{\prime}\in[0,t_{i}],s^{\prime}_{i}\in[0,s_{i}]$ , so that $t_{1}^{\prime}+t_{2}^{\prime}=t,s_{1}^{\prime}+s_{2}^{\prime}=s$ . It is slightly trickier to modify $u,v$ . Noting that $u+v\geq\mathbf{F}(s_{1},t_{2};2,1)\geq\mathbf{F}(s_{1}^{\prime},t_{2}^{\prime};2,1)\geq s_{1}^{\prime}$ , we can find $u^{\prime}\in[s_{1}^{\prime},u],v^{\prime}\in[0,v]$ so that $u^{\prime}+v^{\prime}=\mathbf{F}(s_{1}^{\prime},t_{2}^{\prime};2,1)$ . Now we can apply Lemma 33 to the numbers $t_{1}^{\prime},t_{2}^{\prime},s_{1}^{\prime},s_{2}^{\prime},u^{\prime},v^{\prime}$ . We obtain

u^{\prime}+\max\{\mathbf{F}(s^{\prime}_{2},t^{\prime}_{1}+v^{\prime};k,k-1),s^{\prime}_{2}+v^{\prime}\}\geq\mathbf{F}(s,t;k+1,k).

Since the new numbers are smaller than the old numbers and by using the monotonicity of $\mathbf{F}(\cdot,\cdot;n,k)$ , we have

u+\max\{\mathbf{F}(s_{2},t_{1}+v;k,k-1),s_{2}+v\}\geq\mathbf{F}(s,t;k+1,k).

∎

It remains to prove Lemma 33.

Proof of Lemma 33.

For convenience, we recall the definition of Furstenberg index in the special case $(n,k)=(k+1,k)$ .

(a) If $s=0$ ,

\mathbf{F}(0,t;k+1,k)=\max\{0,t-k\}.

(b) If $s>0$ , write $s=d+\sigma$ . If also $t\in[0,k-d-1]$ ,

\mathbf{F}(s,t;k+1,k)=s.

If we are not in Case (a) and (b), then $s\in(0,k]$ and $t\in(k-d-1,k+1]$ , we write

\begin{cases}s=d+\sigma\\ t=k-d-1+\tau,\end{cases}

where $d\in\{0,\dots,k-1\}$ , $\sigma\in(0,1]$ , $\tau\in(0,d+2]$ .

\mathbf{F}(s,t;k+1,k)=d+\min\{\sigma+\tau,\frac{3}{2}\sigma+\frac{1}{2}\tau,\sigma+1\}

(d) If $\tau\in(2,d+2]$ ,

\mathbf{F}(s,t;k+1,k)=s+1.

Let us denote

\mathbf{F}:=u+\max\{\mathbf{F}(s_{2},t_{1}+v;k,k-1),s_{2}+v\}.

Our goal is to prove

\mathbf{F}\geq\mathbf{F}(s,t;k+1,k).

When $s=0$ , then $s_{1}=s_{2}=0$ . We want to prove $\mathbf{F}\geq\max\{0,t-k\}$ . Trivially, $\mathbf{F}\geq 0$ . Also,

\mathbf{F}\geq u+\mathbf{F}(0,t_{1}+v;k,k-1)\geq u+t_{1}+v-(k-1).

Using $u+v=\mathbf{F}(s_{1},t_{2};2,1)\geq t_{2}-1$ and $t_{1}+t_{2}=t$ , we obtain

\mathbf{F}\geq t-k.

When $t\in[0,k-d-1]$ , we have

\mathbf{F}\geq u+s_{2}+v=s_{2}+\mathbf{F}(s_{1},t_{2};2,1)\geq s_{2}+s_{1}=s=\mathbf{F}(s,t;k+1,k).

So we consider $s>0$ and $t>k-d-1$ . Write

\begin{cases}s=d+\sigma\\ t=k-d-1+\tau,\end{cases}

where $d\in\{0,\dots,k-1\}$ , $\sigma\in(0,1]$ , $\tau\in(0,d+2]$ . In this case,

\mathbf{F}(s,t;k+1,k)=d+\min\{\sigma+\tau,\frac{3}{2}\sigma+\frac{1}{2}\tau,\sigma+1\}.

We just need to show either $\mathbf{F}\geq d+\sigma+\tau$ , or $\mathbf{F}\geq d+\frac{3}{2}\sigma+\frac{1}{2}\tau$ , or $\mathbf{F}\geq d+\sigma+1$ .

We first analyze $\mathbf{F}(s_{2},t_{1}+v;k,k-1)$ . This is done by discussing the values of $(s_{2},t_{1}+v)$ .

Case (a): $s_{2}=0$ By definition, we have $\mathbf{F}(s_{2},t_{1}+v;k,k-1)=\max\{0,t_{1}+v-(k-1)\}$ . Since $s_{1}+s_{2}=s=d+\sigma$ and $s_{1}\leq 1$ , we have $d=0,s_{1}=\sigma$ . We have

\mathbf{F}\geq u+\max\{t_{1}+v-(k-1),v\}.

Recall $u+v\geq\mathbf{F}(\sigma,t_{2};2,1),t_{1}+t_{2}=t=k-1+\tau$ . We have

\mathbf{F}\geq\mathbf{F}(\sigma,t_{2};2,1)+\max\{\tau-t_{2},0\}.

If $t_{2}\geq\tau$ , then $\mathbf{F}(\sigma,t_{2};2,1)\geq\mathbf{F}(\sigma,\tau;2,1)$ . If $t_{2}\leq\tau$ , then $\mathbf{F}(\sigma,t_{2};2,1)+\tau-t_{2}\geq\mathbf{F}(\sigma,\tau;2,1)$ , by Lemma 20. Therefore, we have

\mathbf{F}\geq\mathbf{F}(\sigma,\tau;2,1)=\min\{\sigma+\tau,\frac{3}{2}\sigma+\frac{1}{2}\tau,\sigma+1\}=\mathbf{F}(s,t;k+1,k).

The last inequality is because $d=0$ .

Case (b) $t_{1}+v\leq k-d-2$ We have

\mathbf{F}\geq u+v+s_{2}\geq\mathbf{F}(s_{1},t_{2};2,1)+s_{2}.

Subcase (b.0): $s_{1}=0$ In this case, $\mathbf{F}(s_{1},t_{2};2,1)=\max\{0,t_{2}-1\}$ , $s_{2}=d+\sigma$ . We have

\mathbf{F}\geq\max\{0,t_{2}-1\}+d+\sigma\geq d+\sigma+\tau.

The last inequality is because

t_{2}=t-t_{1}\geq(k-d-1+\tau)-(k-d-2-v)\geq 1+\tau.

Subcase (b.1): $\mathbf{F}(s_{1},t_{2};2,1)=s_{1}+t_{2}$ We have

\mathbf{F}\geq s_{1}+t_{2}+s_{2}=s+t_{2}\geq d+\sigma+\tau.

since $t_{2}\geq 1+\tau$ .

Subcase (b.2): $\mathbf{F}(s_{1},t_{2};2,1)=\frac{3}{2}s_{1}+\frac{1}{2}t_{2}$ We have

\mathbf{F}\geq\frac{1}{2}(s_{1}+t_{2})+d+\sigma\geq d+\frac{3}{2}\sigma+\frac{1}{2}\tau.

Since $t_{2}\geq 1+\tau\geq\sigma+\tau.$

Subcase (b.3): $\mathbf{F}(s_{1},t_{2};2,1)=s_{1}+1$ We have

\mathbf{F}\geq s+1=d+\sigma+1.

Case (c): $s_{2}>0$ , $k-d-2<t_{1}+v\leq k-d$ We write $t_{1}+v=k-d-2+\tau^{\prime}$ for $\tau^{\prime}\in(0,2]$ . Since $t_{1}+t_{2}=k-d-1+\tau$ , we have $\tau^{\prime}=1+\tau+v-t_{2}$ .

Subcase (c.I): $s_{1}<\sigma$ We have $s_{2}=s-s_{1}=d+(\sigma-s_{1})$ . We have

(51)

\begin{split}\mathbf{F}(s_{2},t_{1}+v;k,k-1)=\mathbf{F}(d+(\sigma-s_{1}),t_{1}+v;k,k-1)\\ =d+\min\{\sigma-s_{1}+\tau^{\prime},\frac{3}{2}(\sigma-s_{1})+\frac{1}{2}\tau^{\prime},(\sigma-s_{1})+1\}.\end{split}

Subsubcase (c.I.1): $\mathbf{F}(s_{2},t_{1}+v;k,k-1)=s_{2}+\tau^{\prime}$ We have

(52)

\begin{split}\mathbf{F}&\geq u+\max\{s_{2}+\tau^{\prime},s_{2}+v\}\\ &=u+s_{2}+\max\{\tau^{\prime},v\}.\end{split}

Subsubsubcase (c.I.1.0): $s_{1}=0$ Then $u+v=\mathbf{F}(0,t_{2};2,1)=\max\{0,t_{2}-1\}$ . We have

\mathbf{F}\geq u+s_{2}+\tau^{\prime}=u+v+s_{2}+1+\tau-t_{2}\geq s_{2}+\tau=s+\tau.

Subsubsubcase (c.I.1.1): $u+v=\mathbf{F}(s_{1},t_{2};2,1)=s_{1}+t_{2}$ We have

\mathbf{F}\geq u+s_{2}+\tau^{\prime}=u+s_{2}+1+\tau+v-t_{2}=s+\tau+1.

Subsubsubcase (c.I.1.2): $u+v=\mathbf{F}(s_{1},t_{2};2,1)=\frac{3}{2}s_{1}+\frac{1}{2}t_{2}$ We have

\mathbf{F}\geq\frac{3}{2}s_{1}+\frac{1}{2}t_{2}+s_{2}+1+\tau-t_{2}=s+\frac{1}{2}(s_{1}+t_{2})+1+\tau-t_{2}\geq s+1+\tau-\frac{1}{2}t_{2}.

We also have

\mathbf{F}\geq u+v+s_{2}\geq s+\frac{1}{2}t_{2}.

Combining together gives

\mathbf{F}\geq s+\frac{1}{2}(1+\tau)\geq d+\frac{3}{2}\sigma+\frac{1}{2}\tau.

Subsubsubcase (c.I.1.3): $u+v=\mathbf{F}(s_{1},t_{2};2,1)=s_{1}+1$ We have

\mathbf{F}\geq u+v+s_{2}\geq s+1.

SubSubcase (c.I.2): $\mathbf{F}(s_{2},t_{1}+v;k,k-1)=d+\frac{3}{2}(\sigma-s_{1})+\frac{1}{2}\tau^{\prime}=s_{2}+\frac{1}{2}(\sigma-s_{1}+\tau^{\prime})$ We have

\mathbf{F}\geq u+s_{2}+\max\{\frac{1}{2}(\sigma-s_{1}+\tau^{\prime}),v\}=u+s_{2}+\max\{\frac{1}{2}(\sigma+1+\tau+v-t_{2}-s_{1}),v\}.

Subsubsubcase (c,I.2.0): $s_{1}=0$ Then $u+v=\max\{0,t_{2}-1\}$ . We have

\mathbf{F}\geq\frac{1}{2}u+s_{2}+\frac{1}{2}(u+v+\sigma+1+\tau-t_{2}-s_{1})\geq s_{2}+\frac{1}{2}(\sigma+\tau-s_{1})=d+\frac{3}{2}\sigma+\frac{1}{2}\tau.

Subsubsubcase (c.I.2.1): $u+v=s_{1}+t_{2}$ We have

\mathbf{F}\geq\frac{1}{2}u+s_{2}+\frac{1}{2}(\sigma+\tau+1)\geq d+\frac{3}{2}\sigma+\frac{1}{2}\tau.

Here, we used $u\geq s_{1},1\geq s_{1}$ .

Subsubsubcase (c.I.2.2): $u+v=\frac{3}{2}s_{1}+\frac{1}{2}t_{2}$ We have

\mathbf{F}\geq\frac{1}{2}u+s_{2}+\frac{1}{2}(\sigma+1+\tau)+\frac{1}{4}(s_{1}-t_{2})

To prove $\mathbf{F}\geq d+\frac{3}{2}\sigma+\frac{1}{2}\tau$ , it suffices to prove

\frac{1}{2}(u+1)+\frac{1}{4}(s_{1}-t_{2})\geq s_{1}.

This is true since $u+1\geq u+v=\frac{3}{2}s_{1}+\frac{1}{2}t_{2}$ .

Subsubsubcase (c.I.2.3): $u+v=s_{1}+1$

\mathbf{F}\geq u+v+s_{2}=s+1.

Subsubcase (c.I.3): $\mathbf{F}(s_{2},t_{1}+v;k,k-1)=s_{2}+1$ We have

\mathbf{F}\geq u+s_{2}+1\geq s_{1}+s_{2}+1=s+1.

Subcase (c.II): $s_{1}\geq\sigma$ We write $s_{2}=(d-1)+(\sigma+1-s_{1})$ . We have

	$\displaystyle\mathbf{F}(s_{2},t_{1}+v;k,k-1)$	$\displaystyle=d-1+\min\{\sigma+1-s_{1}+\tau^{\prime},\frac{3}{2}(\sigma-s_{1}+1)+\frac{1}{2}\tau^{\prime},\sigma-s_{1}+2\}$
		$\displaystyle=d+\min\{\sigma-s_{1}+\tau^{\prime},\frac{3}{2}(\sigma-s_{1})+\frac{1}{2}\tau^{\prime}+\frac{1}{2},\sigma-s_{1}+1\}$
		$\displaystyle\geq d+\min\{\sigma-s_{1}+\tau^{\prime},\frac{3}{2}(\sigma-s_{1})+\frac{1}{2}\tau^{\prime},\sigma-s_{1}+1\}$

The discussion is the same as Subcase (c.I), since we did not use the condition $s_{1}<\sigma$ .

Subcase (d): $t_{1}+v>k-d$ We have

\mathbf{F}(s_{2},t_{1}+v;k,k-1)=s_{2}+1.

Therefore,

\mathbf{F}\geq u+s_{2}+1\geq s_{1}+s_{2}+1=s+1.

∎

5. Furstenberg set problem: Lower bound II

Proposition 34.

Let $n,k\in\mathbb{N}$ and $n\geq k+2$ . Suppose for any $n^{\prime}=k+1,\dots,n-1$ and admissible $(s,t;n^{\prime},k)$ , we know

(53)

\inf_{E:\ (s,t;n^{\prime},k)\textup{-set}}\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t;n^{\prime},k)-\varepsilon},

for any $\varepsilon>0$ . Then for admissible $(s,t;n,k)$ , we know

(54)

\inf_{E:\ (s,t;n,k)\textup{-set}}\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t;n,k)-\varepsilon},

for any $\varepsilon>0$ .

We prove the following lemma.

Lemma 35.

Assume (53) holds. Suppose $(s,t;n,k)$ is admissible and $n\geq k+2$ . Then for any $(s,t;n,k)$ -set $E$ , there exist numbers $t_{1},t_{2},s_{1},s_{2}$ , such that

(55)

\begin{cases}1\leq p^{t_{1}}\leq p^{(k+1)(n-k-1)},1\leq p^{t_{2}}\leq p^{k+1};\\ p^{s}\lesssim p^{s_{1}}\leq p^{k},1\leq p^{s_{2}}\leq p;\end{cases}

and

(56)

\begin{cases}p^{t_{1}+t_{2}}\gtrapprox p^{t};\\ p^{s_{1}+s_{2}}\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t_{2};n-1,k)-\varepsilon};\end{cases}

and

(57)

\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},t_{1};n-1,k)+s_{2}-\varepsilon}.

Proof.

We will do several steps of pigeonholing, which lead to the parameters $t_{1},t_{2},s_{1},s_{2},u,v$ .

By the definition of $(s,t;n,k)$ -set, we write

E=\bigcup_{V\in\mathcal{V}}Y(V),

where $\mathcal{V}\subset A(k,\mathbb{F}_{p}^{n})$ with $\#\mathcal{V}\sim p^{t}$ , and $Y(V)\subset V$ with $\#Y(V)\sim p^{s}$ .

By properly choosing the coordinate, we can assume $\gtrsim 1$ fraction of the $k$ -planes in $\mathcal{V}$ are not parallel to the $n$ -th axis $\mathbf{0}^{n-1}\times\mathbb{F}_{p}$ . Throwing away some $V\in\mathcal{V}$ , we can just assume all the $k$ -planes in $\mathcal{V}$ are not parallel to $\mathbf{0}^{n-1}\times\mathbb{F}_{p}$ with $\mathcal{V}$ still satisfying $\#\mathcal{V}\gtrsim p^{t}$ . Because of this, we see that for any $V\in\mathcal{V}$ , the projection of $V$ onto $\mathbb{F}_{p}^{n-1}\times\mathbf{0}$ , denoted by $\pi_{\mathbb{F}_{p}^{n-1}}(V)$ is a $k$ -plane in $\mathbb{F}_{p}^{n-1}\times\mathbf{0}$ .

Now, we partition $\mathcal{V}$ according to $A(k,\mathbb{F}_{p}^{n-1}\times\mathbf{0})$ . For each $W\in A(k,\mathbb{F}_{p}^{n-1}\times\mathbf{0})$ , we define $\mathcal{V}_{W}$ to be the set of $V\in\mathcal{V}$ such that $\pi_{\mathbb{F}_{p}^{n-1}}(V)=W$ . We obtain a partition

\mathcal{V}=\bigsqcup_{W\in A(k,\mathbb{F}_{p}^{n-1}\times\mathbf{0})}\mathcal{V}_{W}.

First pigeonholing. We assume there exists $\mathcal{W}\subset A(k,\mathbb{F}_{p}^{n-1}\times\mathbf{0})$ with $\#\mathcal{W}\sim p^{t_{1}}$ such that for each $W\in\mathcal{W}$ , $\#\mathcal{V}_{W}\sim p^{t_{2}}$ . Here, $1\leq p^{t_{1}}\leq p^{(k+1)(n-k-1)},1\leq p^{t_{2}}\leq p^{k+1}$ are dyadic numbers and

(58)

p^{t_{1}}p^{t_{2}}\gtrapprox p^{t}.

The upper bound for $t_{1},t_{2}$ is because $\#A(k,\mathbb{F}_{p}^{n-1}\times\mathbf{0})\lesssim p^{(k+1)(n-k-1)}$ , and $\#\mathcal{V}_{W}\leq\#A(k,W\times\mathbb{F}_{p})\lesssim p^{k+1}$ . We still use $\mathcal{V}$ to denote $\bigcup_{W\in\mathcal{W}}\mathcal{V}_{W}$ . And we see that

\#\mathcal{V}\gtrapprox p^{t}.

Fix a $W\in\mathcal{W}$ . We want to estimate $\bigcup_{V\in\mathcal{V}_{W}}Y(V)(\subset W\times\mathbb{F}_{p}\cong\mathbb{F}_{p}^{k+1})$ . This is some sort of Furstenberg set for $k$ -planes in $(k+1)$ -dimensional space. Also, an important preperty is that each $V\in\mathcal{V}_{W}$ is not parallel to the last coordinate. Therefore, any line parallel to $\mathbf{0}^{n-1}\times\mathbb{F}_{p}$ will intersect $V$ at a single point. We will exploit some “quasi-product” structure of this set.

Lemma 36.

Assume (53) holds for $n^{\prime}=k+1$ . Suppose $E=\bigcup_{V\in\mathcal{V}}Y(V)$ is a $(s,t_{2};k,k+1)$ -set. Also, we assume each $V\in\mathcal{V}$ intersects $\mathbf{0}^{k}\times\mathbb{F}_{p}$ at a single point. Then there exist dyadic numbers $p^{s_{1}},p^{s_{2}}$ such that

p^{s}\lesssim p^{s_{1}}\leq p^{k},

1\leq p^{s_{2}}\leq p,

and

p^{s_{1}}p^{s_{2}}\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t_{2};k+1,k)-\varepsilon},

for any $\varepsilon>0$ . Also, $E$ contains a subset of form

\bigsqcup_{\xi\in\Xi}Y_{\xi},

where $\Xi\subset\mathbb{F}_{p}^{k}\times\mathbf{0}$ with $\#\Xi\sim p^{s_{1}}$ , and $Y_{\xi}\subset E\cap\bigg{(}\xi+(\mathbf{0}^{k}\times\mathbb{F}_{p})\bigg{)}$ with $\#Y_{\xi}\sim p^{s_{2}}$ .

Proof.

For $\xi\in\mathbb{F}_{p}^{k}\times\mathbf{0}$ , define $E(\xi):=E\cap\bigg{(}\xi+(\mathbf{0}^{k}\times\mathbb{F}_{p})\bigg{)}$ . By pigeonholing on vertical slices of $E$ , we can find $\Xi\subset\mathbb{F}_{p}^{k}\times\mathbf{0}$ so that for all $\xi\in\Xi$ , $E(\xi)$ have comparable cardinality. We may denote $\#\Xi\sim p^{s_{1}},\#E(\xi)\sim p^{s_{2}}$ for two dyadic numbers $p^{s_{1}},p^{s_{2}}\geq 1$ . We can also assume $p^{s_{1}}p^{s_{2}}\gtrapprox\#E$ . Hence, assuming (53) holds for $n^{\prime}=k+1$ , we have

p^{s_{1}}p^{s_{2}}\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t_{2};k+1,k)-\varepsilon}.

However, we still need the condition $p^{s_{1}}\gtrsim p^{s}$ . This is handled by the same trick as in the proof of Lemma 31. We will conduct an algorithm to find a sequence $E=E_{1}\supset E_{2}\supset\cdots\supset E_{m}$ , and disjoint subsets $\Xi_{1},\Xi_{2}\cdots,\Xi_{m}$ of $\mathbb{F}_{p}^{k}\times\mathbf{0}$ . To start with, let $E_{1}=E$ . By pigeonholing, we can find $\Xi_{1}\subset\mathbb{F}_{p}^{k}\times\mathbf{0}$ , such that $\#\Xi_{1}\sim p^{u_{1}}$ , $\#E(\xi)\sim p^{v_{1}}$ for each $\xi\in\Xi$ , and

p^{u_{1}}p^{v_{1}}\gtrsim_{\varepsilon}\#E_{1}\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t_{2};2,1)-\varepsilon}.

Suppose we have defined $E_{i},\Xi_{i}$ for $1\leq i\leq j-1$ . If $\sum_{i=1}^{j-1}p^{u_{i}}\ll p^{s}$ , then we define

E_{j}:=E\setminus\bigcup_{1\leq i\leq j-1}\bigsqcup_{\xi\in\Xi_{i}}E(\xi).

Since each $V\in\mathcal{V}$ intersect $\xi+(\mathbf{0}^{k}\times\mathbb{F}_{p})$ (and hence $E(\xi)$ ) at a single point, we see that $E_{j}$ is still a $(s,t_{2};2,1)$ -set. By the same pigeonholing, we find $\Xi_{j}\subset(\mathbb{F}_{p}^{k}\times\mathbf{0})\setminus\bigcup_{1\leq i\leq j-1}\Xi_{i}$ , so that $\#\Xi_{j}\sim p^{u_{j}}$ , $\#E(\xi)\sim p^{v_{j}}$ for each $\xi\in\Xi_{j}$ , and

p^{u_{j}}p^{v_{j}}\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t_{2};2,1)-\varepsilon}.

If $\sum_{i=1}^{j-1}p^{u_{i}}\gtrsim p^{s}$ , then we stop and let $m=j-1$ .

The algorithm will stop in finite steps. Denote $\Xi:=\bigcup_{1\leq i\leq m}\Xi_{i}$ . Let $p^{s_{1}},p^{s_{2}}$ be dyadic numbers so that $p^{s_{2}}=\min_{1\leq i\leq m}p^{v_{i}}$ , $p^{s_{1}}\sim\#\Xi$ . For each $\xi\in\Xi$ , let $Y_{\xi}$ be a subset of $E(\xi)$ with $\#Y_{\xi}\sim p^{s_{2}}$ . This is doable, since $\#E(\xi)\gtrsim p^{s_{2}}$ if $\xi\in\Xi$ . One can check

p^{s_{1}}p^{s_{2}}\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t_{2};2,1)-\varepsilon}.

This is proved in the following way. Suppose $p^{s_{2}}=p^{v_{i}}$ , then

p^{s_{1}}p^{s_{2}}=p^{s_{1}}p^{v_{i}}\geq p^{u_{i}}p^{v_{i}}\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t_{1};2,1)-\varepsilon}.

Also, one can check

p^{s_{1}}=\sum_{i=1}^{m}p^{u_{i}}\gtrsim p^{s}.

∎

Return back to $E_{W}:=\bigcup_{V\in\mathcal{V}_{W}}Y(V)$ (which lie in $W\times\mathbb{F}_{p}\cong\mathbb{F}_{p}^{k+1}$ ). Recall $\#\mathcal{V}_{W}\gtrapprox p^{t_{2}}$ and $\#Y(V)\sim p^{s}$ . We see that $E_{W}$ is a $(s,(t_{2}-\varepsilon)_{+};k+1,k)$ -set.

By Lemma 36, there exist dyadic numbers $p^{s_{1}(W)},p^{s_{2}(W)}$ , so that $E_{W}$ contains a subset of form

\bigsqcup_{\xi\in\Xi_{W}}Y_{W}(\rho_{\xi}).

Here, $\Xi_{W}\subset W(\subset\mathbb{F}_{p}^{n-1}\times\mathbf{0})$ with $\#\Xi_{W}\sim p^{s_{1}(W)}$ ; $\rho_{\xi}:=\xi+(\mathbf{0}^{n-1}\times\mathbb{F}_{p})$ and $Y_{W}(\rho_{\xi})\subset\rho_{\xi}$ with $\#Y_{W}(\rho_{\xi})\sim p^{s_{2}(W)}$ . We also have

p^{s_{1}(W)}\gtrsim p^{s}.

p^{s_{1}(W)}p^{s_{2}(W)}\gtrsim_{\varepsilon}p^{\mathbf{F}(s,(t_{2}-\varepsilon)_{+};k+1,k)-\varepsilon}.

By pigeonholing on $(s_{1}(W),s_{2}(W))$ again, we can throw away some $W\in\mathcal{W}$ so that the cardinality of $\mathcal{W}$ is still $\gtrapprox p^{t_{1}}$ , and assume there exist $s_{1},s_{2}$ such that

(s_{1}(W),s_{2}(W))=(s_{1},s_{2}),\ \textup{~{}for~{}all~{}}W\in\mathcal{W},

and

p^{s_{1}}\gtrsim p^{s}.

p^{s_{1}}p^{s_{2}}\gtrsim_{\varepsilon}p^{\mathbf{F}(s,(t_{2}-\varepsilon)_{+};2,1)-\varepsilon}.

By Lemma 20, we have

p^{s_{1}}p^{s_{2}}\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t_{2};2,1)-\varepsilon}.

(59)

\begin{split}E=\bigcup_{W\in\mathcal{W}}E_{W}&\supset\bigcup_{W\in\mathcal{W}}\bigcup_{\xi\in\Xi_{W}}Y_{W}(\rho_{\xi}).\end{split}

Since $\#Y_{W}(\rho_{\xi})\sim p^{s_{2}}$ , we see that

\#E\gtrsim\#(\bigcup_{W\in\mathcal{W}}\Xi_{W})\cdot p^{s_{2}}.

Since $\bigcup_{W\in\mathcal{W}}\Xi_{W}$ is a $(s_{1},t_{1};n-1,k)$ -set, by (53), we have

\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},t_{1};n-1,k)-\varepsilon}p^{s_{2}}.

∎

The next lemma is a recursive inequality of $\mathbf{F}(s,t;n,k)$ , which can be used to bound the right hand side of (57).

Lemma 37.

Suppose $(s,t;n,k)$ is admissible and $n\geq k+2$ . Suppose there exist numbers $t_{1},t_{2},s_{1}$ , such that

(60)

\begin{cases}t_{1}\in[0,(k+1)(n-k-1)];\\ t_{2}\in[0,k+1];\\ s_{1}\in[s,k];\end{cases}

and

(61)

t_{1}+t_{2}=t;

Then,

(62)

\mathbf{F}(s_{1},t_{1};n-1,k)+\max\{\mathbf{F}(s,t_{2};k+1,k)-s_{1},0\}\geq\mathbf{F}(s,t;n,k).

Let us quickly see how Lemma 35 and Lemma 37 combined to prove Proposition 34.

Proof of Proposition 34 assuming Lemma 35 and Lemma 37.

If $s=0$ or $t=0$ , by Proposition 27 or 28, we are done. So, we suppose $s,t>0$ .

Fix $0<\varepsilon<\min\{\sigma/2,t/2,1/2\}$ , where $s=d+\sigma$ with $d\in\mathbb{N},\sigma\in(0,1]$ . We just need to prove

(63)

\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t;n,k)-C\varepsilon}

for any $(s,t;n,k)$ -set $E$ . Here, $C$ is a large number.

We only need to prove for large enough $p$ , since for small $p$ we can choose the constant to be large.

Suppose (53) holds. If $E$ is a $(s,t;n,k)$ -set, by Lemma 35, there exist numbers $t_{1},t_{2},s_{1},s_{2}$ , such that

(64)

\begin{cases}t_{1}\in[0,(k+1)(n-k-1)],t_{2}\in[0,k+1];\\ s_{1}\in[s-\varepsilon,k],s_{2}\in[0,1];\end{cases}

and

(65)

\begin{cases}t_{1}+t_{2}\geq t-\varepsilon;\\ s_{1}+s_{2}\geq\mathbf{F}(s,t_{2};k+1,k)-\varepsilon;\end{cases}

and

(66)

\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s_{1},t_{1};n-1,k)+s_{2}-\varepsilon}\geq p^{\mathbf{F}(s_{1},t_{1};n-1,k)+\max\{\mathbf{F}(s,t_{2};k+1,k)-s_{1},0\}-2\varepsilon}.

Let $t^{\prime}=t-\varepsilon$ which is $>0$ by assumption. Choose $0\leq t_{i}^{\prime}\leq t_{i}$ for $i=1,2$ , so that $t_{1}^{\prime}+t_{2}^{\prime}=t^{\prime}$ . Choose $s_{1}\leq s_{1}^{\prime}\leq s_{1}+\varepsilon$ , so that $s_{1}^{\prime}\in[s,k]$ . Then $t^{\prime},t_{1}^{\prime},t_{2}^{\prime},s_{1}^{\prime}$ satisfy the condition in Lemma 37, we obtain

\mathbf{F}(s_{1}^{\prime},t_{1}^{\prime};n-1,k)+\max\{\mathbf{F}(s,t_{2}^{\prime};k+1,k)-s_{1},0\}\geq\mathbf{F}(s,t^{\prime};n,k).

By monotonicity of $t\mapsto\mathbf{F}(s,t;n,k)$ , Lemma 20 and Lemma 21, we have

\#E\gtrsim_{\varepsilon}p^{\mathbf{F}(s,t;n,k)-C\varepsilon}.

∎

It remains to prove Lemma 37.

Proof of Lemma 37.

When $s=0$ , we have $\mathbf{F}(0,t;n,k)=\max\{0,t-k(n-k)\}$ . By Lemma 19, we have

\mathbf{F}(s_{1},t_{1};n-1,k)+\mathbf{F}(0,t_{2};k+1,k)-s_{1}\geq s_{1}+t_{1}-k(n-k-1)+t_{2}-k-s_{1}=t-k(n-k).

When $s>0$ , write $s=d+\sigma$ . If also $t\leq(k-d-1)(n-k)$ , then

\mathbf{F}(s,t;n,k)=s.

By Lemma 19,

\mathbf{F}(s_{1},t_{1};n-1,k)+\mathbf{F}(s,t_{2};k+1,k)-s_{1}\geq s_{1}+s-s_{1}=s.

So we consider $s>0$ and $t>(k-d-1)(n-k)$ . Denote

\mathbf{F}:=\mathbf{F}(s_{1},t_{1};n-1,k)+\max\{\mathbf{F}(s,t_{2};k+1,k)-s_{1},0\}.

We have both

(67)

\mathbf{F}\geq\mathbf{F}(s,t_{2};k+1,k)+\mathbf{F}(s_{1},t_{1};n-1,k)-s_{1}.

and

(68)

\mathbf{F}\geq\mathbf{F}(s_{1},t_{1};n-1,k).

Write the canonical expression

(69)

\begin{cases}s=d+\sigma\\ t=(k-d-1)(n-k)+(d+2)m+\tau,\end{cases}

where $d\in\{0,\dots,k-1\}$ , $\sigma\in(0,1]$ , $m\in\{0,\dots,n-k-1\}$ , $\tau\in(0,d+2]$ . We have

\mathbf{F}(s,t;n,k)=s+m+\min\{\tau,\frac{1}{2}(\sigma+\tau),1\}.

Next, we analyze $\mathbf{F}(s,t_{2};k+1,k)$ .

Case (1): $t_{2}\leq k-d-1$ We use

\mathbf{F}\geq\mathbf{F}(s_{1},t_{1};n-1,k)\geq\mathbf{F}(s,t_{1};n-1,k).

Since $t_{2}\leq k-d-1$ , we have

t_{1}\geq(k-d-1)(n-k-1)+(d+2)m+\tau.

Therefore,

\mathbf{F}\geq\mathbf{F}(s,(k-d-1)(n-k-1)+(d+2)m+\tau;n-1,k)=s+m+\min\{\tau,\frac{1}{2}(\sigma+\tau),1\}.

Therefore,

\mathbf{F}\geq\mathbf{F}(s,t;n,k).

Case (2): $t_{2}>k-d-1$ We write $t_{2}=k-d-1+\tau_{2}$ , where $\tau_{2}\in(0,d+2]$ . We have

\mathbf{F}(s,t_{2};k+1,k)=s+\min\{\tau_{2},\frac{1}{2}(\sigma+\tau_{2}),1\}.

Since $s_{1}\geq s$ , write

s_{1}=d+\sigma_{1},

with $\sigma_{1}\geq\sigma$ .

Subcase (2.1): $\sigma_{1}\in[\sigma,1]$ We have

t_{1}=t-t_{2}=(k-d-1)(n-k-1)+(d+2)m+\tau-\tau_{2}.

Subsubcase (2.1.1): $\tau-\tau_{2}>0$ We have the canonical expression for $(s_{1},t_{1})$ :

\begin{cases}s_{1}=d+\sigma_{1},\\ t_{1}=t-t_{2}=(k-d-1)(n-k-1)+(d+2)m+\tau-\tau_{2}.\end{cases}

Therefore,

\mathbf{F}(s_{1},t_{1};n-1,k)=s_{1}+m+\min\{\tau-\tau_{2},\frac{1}{2}(\sigma_{1}+\tau-\tau_{2}),1\}.

Therefore,

\mathbf{F}\geq s+m+\min\{\tau_{2},\frac{1}{2}(\sigma+\tau_{2}),1\}+\min\{\tau-\tau_{2},\frac{1}{2}(\sigma+\tau-\tau_{2}),1\}.

We just need to show

\min\{\tau_{2},\frac{1}{2}(\sigma+\tau_{2}),1\}+\min\{\tau-\tau_{2},\frac{1}{2}(\sigma+\tau-\tau_{2}),1\}\geq\min\{\tau,\frac{1}{2}(\sigma+\tau),1\}.

To show $\min_{i}a_{i}+\min_{j}b_{j}\geq\min_{k}c_{k}$ , it suffices to show $\forall i,j,\exists k$ , s.t. $a_{i}+b_{j}\geq c_{k}$ . We can check:

$\bullet$ $\tau_{2}+\tau-\tau_{2}\geq\tau$ .

$\bullet$ $\tau_{2}+\frac{1}{2}(\sigma+\tau-\tau_{2})\geq\frac{1}{2}(\sigma+\tau)$ .

$\bullet$ $\frac{1}{2}(\sigma+\tau_{2})+\tau-\tau_{2}\geq\frac{1}{2}(\sigma+\tau).$

$\bullet$ $\frac{1}{2}(\sigma+\tau_{2})+\frac{1}{2}(\sigma+\tau-\tau_{2})\geq\frac{1}{2}(\sigma+\tau)$ .

Subsubcase (2.1.2): $\tau-\tau_{2}\leq 0,m\geq 1$ We write $t_{1}=(k-d-1)(n-k-1)+(d+2)(m-1)+d+2+\tau-\tau_{2}$ . We have

\mathbf{F}(s_{1},t_{1};n-1,k)=s_{1}+m-1+\min\{\tau-\tau_{2}+d+2,\frac{1}{2}(\sigma_{1}+\tau-\tau_{2}+d+2),1\}.

Therefore,

\mathbf{F}\geq s+m-1+\min\{\tau_{2},\frac{1}{2}(\sigma+\tau_{2}),1\}+\min\{\tau-\tau_{2}+d+2,\frac{1}{2}(\sigma_{1}+\tau-\tau_{2}+d+2),1\}.

We just need to prove

\min\{\tau_{2},\frac{1}{2}(\sigma+\tau_{2}),1\}+\min\{\tau-\tau_{2}+d+1,\frac{1}{2}(\sigma+\tau-\tau_{2}+d),0\}\geq\min\{\tau,\frac{1}{2}(\sigma+\tau),1\}.

This is not hard to verify by noting $\tau\leq\tau_{2}\leq d+2$ .

$\bullet$ $\tau_{2}+\tau-\tau_{2}+d+1\geq\tau$ .

$\bullet$ $\tau_{2}+\frac{1}{2}(\sigma+\tau-\tau_{2}+d)\geq\frac{1}{2}(\sigma+\tau)$ .

$\bullet$ $\tau_{2}+0\geq\tau$ .

$\bullet$ $\frac{1}{2}(\sigma+\tau_{2})+\tau-\tau_{2}+d+1\geq\tau+d+1-\frac{1}{2}\tau_{2}\geq\tau$ .

$\bullet$ $\frac{1}{2}(\sigma+\tau_{2})+\frac{1}{2}(\sigma+\tau-\tau_{2}+d)\geq\frac{1}{2}(\sigma+\tau)$ .

$\bullet$ $\frac{1}{2}(\sigma+\tau_{2})+0\geq\frac{1}{2}(\sigma+\tau)$ .

$\bullet$ $1+\tau-\tau_{2}+d+1\geq\tau$ .

$\bullet$ $1+\frac{1}{2}(\sigma+\tau-\tau_{2}+d)\geq\frac{1}{2}(\sigma+\tau)$ .

$\bullet$ $1+0\geq 1$ .

Subsubcase (2.1.3): $\tau-\tau_{2}\leq 0,m=0$ We have $t_{1}\leq(k-d-1)(n-k-1)$ , so

\mathbf{F}(s_{1},t_{1};n-1,k)=s_{1}.

Therefore,

\mathbf{F}\geq\mathbf{F}(s,t_{2};k+1,k)=s+\min\{\tau_{2},\frac{1}{2}(\sigma+\tau_{2}),1\}.

Also, $\mathbf{F}(s,t;n,k)=s+\min\{\tau,\frac{1}{2}(\sigma+\tau),1\}$ . We see that $\mathbf{F}\geq\mathbf{F}(s,t;n,k)$ since $\tau_{2}\geq\tau$ .

Subcase(2.2): $\sigma_{1}>1$ Write $s_{1}=(d+\Delta)+(\sigma_{1}-\Delta),$ where $\Delta\in\mathbb{N}^{+}$ so that $\sigma_{1}-\Delta\in(0,1]$ . We have

	$\displaystyle t_{1}$	$\displaystyle=(k-d-1)(n-k-1)+(d+2)m+\tau-\tau_{2}$
		$\displaystyle=(k-d-\Delta-1)(n-k-1)+(d+2)m+\tau-\tau_{2}+\Delta(n-k-1)$
		$\displaystyle=(k-d-\Delta-1)(n-k-1)+(d+2)m_{1}+\tau_{1}.$

Here, the last line is the canonical expression for $t_{1}$ (see (9)), in which $0\leq m_{1}\leq n-k-2$ , $\tau_{1}\in(0,d+\Delta+2]$ .

If $(d+2)m+\tau-\tau_{2}\leq 0$ , then $m=0,\tau_{2}\geq\tau$ . By the same reasoning as in Subsubcase (2.1.3), we have $\mathbf{F}\geq\mathbf{F}(s,t;n,k)$ .

Hence, we can assume $(d+2)m+\tau-\tau_{2}>0$ We have

\mathbf{F}(s_{1},t_{1};n-1,k)=s_{1}+m_{1}+\min\{\tau_{1},\frac{1}{2}(\sigma_{1}-\Delta+\tau_{1}),1\}.

Since $(d+2)m+\tau-\tau_{2}\leq(d+2)m_{1}+\tau_{1}$ and $\tau,\tau_{1},\tau_{2}\in(0,d+2]$ , we have $m_{1}\geq m-1$ . If $m_{1}\geq m+1$ , then $\mathbf{F}\geq\mathbf{F}(s_{1},t_{1};n-1,k)\geq s+m+1\geq\mathbf{F}(s,t;n,k)$ . We only need to consider two cases: $m_{1}=m,m_{1}=m-1$ .

We have

\mathbf{F}\geq s+\min\{\tau_{2},\frac{1}{2}(\sigma+\tau_{2}),1\}+m_{1}+\min\{\tau_{1},\frac{1}{2}(\sigma_{1}-\Delta+\tau_{1}),1\}.

Subsubcase (2.2.1): When $m_{1}=m,\tau_{1}=\tau-\tau_{2}+\Delta(n-k-1)$ We have

\mathbf{F}\geq s+m+\min\{\tau_{2},\frac{1}{2}(\sigma+\tau_{2}),1\}+\min\{(\tau-\tau_{2})\vee 0,\frac{1}{2}(\sigma+\tau-\tau_{2}),1\},

where we used $\tau_{1}\geq(\tau-\tau_{2})\vee 0,$ and $\sigma_{1}-\Delta+\tau_{1}\geq\sigma-\Delta+\tau-\tau_{2}+\Delta(n-k-1)\geq\sigma+\tau-\tau_{2}$ .

We just need to check

\min\{\tau_{2},\frac{1}{2}(\sigma+\tau_{2}),1\}+\min\{(\tau-\tau_{2})\vee 0,\frac{1}{2}(\sigma+\tau-\tau_{2}),1\}\geq\min\{\tau,\frac{1}{2}(\sigma+\tau),1\}.

A less obvious case will be $\frac{1}{2}(\sigma+\tau_{2})+(\tau-\tau_{2})\vee 0\geq\frac{1}{2}(\sigma+\tau_{2})+\frac{1}{2}(\tau-\tau_{2})\geq\frac{1}{2}(\sigma+\tau)$ . We leave out the verification of other cases.

Subsubcase (2.2.2): When $m_{1}=m-1,\tau_{1}=\tau-\tau_{2}+d+2+\Delta(n-k-1)$ Since $n\geq k+2$ , we have

\mathbf{F}\geq s+m-1+\min\{\tau_{2},\frac{1}{2}(\sigma+\tau_{2}),1\}+\min\{\tau-\tau_{2}+d+2+\Delta,\frac{1}{2}(\sigma+\tau-\tau_{2}+d+2),1\}.

Since $\tau_{1}\leq d+2$ , we have $\tau_{2}\geq\tau$ . Note that

\min\{\tau-\tau_{2}+d+2+\Delta,\frac{1}{2}(\sigma+\tau-\tau_{2}+d+2),1\}-1\geq\min\{(\tau-\tau_{2}+1)\vee 0,\frac{1}{2}(\sigma+\tau-\tau_{2}),0\}.

We just need to prove

\min\{\tau_{2},\frac{1}{2}(\sigma+\tau_{2}),1\}+\min\{(\tau-\tau_{2}+1)\vee 0,\frac{1}{2}(\sigma+\tau-\tau_{2}),0\}\geq\min\{\tau,\frac{1}{2}(\sigma+\tau),1\}.

This is not hard to verify by noting $\tau_{2}\geq\tau$ . A less obvious case is $\frac{1}{2}(\sigma+\tau_{2})+(\tau-\tau_{2}+1)\vee 0\geq\frac{1}{2}(\sigma+\tau_{2})+\frac{1}{2}(\tau-\tau_{2}+1)\geq\frac{1}{2}(\sigma+\tau)$ .

∎

Proof of Theorem 7.

Finally, we see that Theorem 7 can be obtained from Proposition 29 and Proposition 34 using induction on $(n,k)$ . ∎

6. Exceptional set estimate: lower bound

We prove Theorem 9 in this section. The result in this section has been studied by the author [4] under the Euclidean setting, the statement there is slightly different from this paper. We still provide the details for the finite field setting, though they are essentially the same.

Proof of Theorem 9.

Recall that $(n,k)=(2,1)$ and $\frac{a}{2}<s\leq\min\{1,a\}$ was considered in Proposition 16. We denote $\mathbf{A}_{s,a}\subset\mathbb{F}_{p}^{2}$ to be the set constructed there which satisfies $\#\mathbf{A}_{s,a}\gtrsim p^{a}$ , and

E_{s}(\mathbf{A}_{s,a};2,1)\gtrsim p^{2s-a}.

Next, we prove for general $(n,k)$ . Note that Type 1 and Type 4 are easy, so we consider Type 2 and Type 3. Recall the canonical expression as in Definition 14: $a=m+\beta,s=l+\gamma$ .

Type 2 We have $l+1\leq m\leq n+l-k$ . For $\gamma$ , we only use $\gamma>\beta$ . We first show the existence of $A$ with $\#A\sim p^{a}$ such that $\#E_{s}(A;n,k)\gtrsim p^{k(n-k)-(m-l)(k-l)}$ .

Choose $A=\mathbb{F}_{p}^{m}\times I\times\mathbf{0}^{n-m-1}$ , where $I\subset\mathbb{F}_{p}$ has cardinality $p^{\beta}$ . For simplicity, we just write $A=\mathbb{F}_{p}^{m}\times I$ . We want to find those $V\in G(n-k,\mathbb{F}_{p}^{n})$ such that $\#(\pi_{V}^{*}(A))<p^{l+\gamma}$ . We note that if $V$ satisfies $\#\pi_{V}^{*}(\mathbb{F}_{p}^{m})\leq p^{l}$ , then $\#\pi_{V}^{*}(\mathbb{F}_{p}^{m}\times I)\leq p^{l+\beta}<p^{l+\gamma}$ , which means $V\in E_{s}(A;n,k)$ . This shows that

E_{s}(A;n,k)\supset\{V\in G(n-k,n):\#\pi_{V}^{*}(\mathbb{F}_{p}^{m})\leq p^{l}\}.

By Lemma 18, the right hand side has cardinality $\sim p^{k(n-k)-(k-l)(m-l)}$ .

Type 3, $\gamma\in(\frac{\beta}{2},\beta]$ We have $n-m-1\geq k-l,\gamma>\frac{\beta}{2}$ . We show the existence of $A$ with $\#A\sim p^{a}$ such that $\#E_{s}(A;n,k)\gtrsim p^{k(n-k)-(m+1-l)(k-l)+2\gamma-\beta}$ .

We choose $A=\mathbf{A}_{\gamma,\beta}\times\mathbb{F}_{p}^{m}\times\mathbf{0}^{n-m-2}$ , where $\mathbf{A}_{\gamma,\beta}\subset\mathbb{F}_{p}^{2}$ is such that $\#\mathbf{A}_{\gamma,\beta}\sim p^{\beta}$ and $\#E_{\gamma}(\mathbf{A}_{\gamma,\beta};2,1)\gtrsim p^{2\gamma-\beta}$ . We will use $\mathbb{F}_{p}^{2}$ to denote $\mathbb{F}_{p}^{2}\times\mathbf{0}^{n-2}$ . We use $\mathbb{F}_{p}^{m}$ to denote $\mathbf{0}^{2}\times\mathbb{F}_{p}^{m}\times\mathbf{0}^{n-m-2}$ . We use $\theta$ to denote the lines in $G(1,\mathbb{F}_{p}^{2})$ . Define

\mathcal{U}_{\theta}=\{V\in G(n-k,\mathbb{F}_{p}^{n}):\#(\pi^{*}_{V}(\theta\oplus\mathbb{F}_{p}^{m}))\leq p^{l},\#(\pi_{V}^{*}(\mathbb{F}_{p}^{m}))=p^{l},\#(\pi_{V}^{*}(\mathbb{F}_{p}^{2}\times\mathbb{F}_{p}^{m}))=p^{l+1}\},

\mathcal{V}_{\theta}=\{V\in G(n-k,\mathbb{F}_{p}^{n}):\#(\pi_{V}^{*}(\theta\oplus\mathbb{F}_{p}^{m}))\leq p^{l}\},

\mathcal{W}_{\theta}=\{V\in\mathcal{V}_{\theta}:\#(\pi_{V}^{*}(\mathbb{F}_{p}^{m}))\leq p^{l-1}\}\cup\{V\in\mathcal{V}_{\theta}:\#(\pi_{V}^{*}(\mathbb{F}_{p}^{2}\times\mathbb{F}_{p}^{m})\leq p^{l}\}.

It is not hard to see $\mathcal{U}_{\theta}=\mathcal{V}_{\theta}\setminus\mathcal{W}_{\theta}$ .

Let $\mathbf{E}_{\gamma,\beta}:=E_{\gamma}(\mathbf{A}_{\gamma,\beta};2,1)=\{\theta\in G(1,\mathbb{F}_{p}^{2}):\#(\pi_{\theta}^{*}(\mathbf{A}_{\gamma,\beta}))<p^{\gamma}\}$ . We claim that if $\theta\in\mathbf{E}_{\gamma,\beta}$ , then $\mathcal{V}_{\theta}\subset E_{l+\gamma}(A)$ . In other words, $V\in\mathcal{V}_{\theta}$ satisfies $\#(\pi_{V}^{*}(A))<p^{l+\gamma}$ . We first note that by definition $\mathbf{A}_{\gamma,\beta}\subset\bigcup_{L\in\pi_{\theta}^{*}(\mathbf{A}_{\gamma,\beta})}L$ , so

A=\mathbf{A}_{\gamma,\beta}\times\mathbb{F}_{p}^{m}\subset(\bigcup_{L\in\pi_{\theta}^{*}(\mathbf{A}_{\gamma,\beta})}L)\times\mathbb{F}_{p}^{m}=(\bigcup_{L\in\pi_{\theta}^{*}(\mathbf{A}_{\gamma,\beta})}L\times\mathbb{F}_{p}^{m}).

Therefore,

\#(\pi_{V}^{*}(A))\leq\#(\pi_{\theta}^{*}(\mathbf{A}_{\gamma,\beta}))\cdot\#(\pi_{V}^{*}(\theta\oplus\mathbb{F}_{p}^{m}))<p^{\gamma+l}.

We see that $E_{l+\gamma}(A;n,k)\supset\bigcup_{\theta\in\mathbf{E}_{\gamma,\beta}}\mathcal{V}_{\theta}.$ $\mathcal{V}_{\theta}$ may intersect with each other, so we delete a tiny portion $\mathcal{W}_{\theta}$ from $\mathcal{V}_{\theta}$ , so that the remaining part $\mathcal{U}_{\theta}=\mathcal{V}_{\theta}\setminus\mathcal{W}_{\theta}$ are disjoint with each other. Then we have

E_{l+\gamma}(A;n,k)\supset\bigsqcup_{\theta\in\mathbf{E}_{\gamma,\beta}}\mathcal{U}_{\theta}.

To make the argument precise, we first apply Lemma 18 to see

\#\mathcal{V}_{\theta}\sim p^{k(n-k)-(m+1-l)(k-l)}.

To calculate $\#\mathcal{W}_{\theta}$ , we apply Lemma 18 again to see

\#\{V\in G(n-k,n):\dim(\pi_{V}^{*}(\mathbb{F}_{p}^{m}))\leq p^{l-1}\}\sim p^{k(n-k)-(m-l+1)(k-l+1)},

and

\#\{V\in G(n-k,n):\dim(\pi_{V}^{*}(\mathbb{F}_{p}^{2}\times\mathbb{F}_{p}^{m}))\leq p^{l}\}\sim p^{k(n-k)-(m+2-l)(k-l)}.

Therefore, $\#\mathcal{W}_{\theta}\ll\#\mathcal{V}_{\theta}$ (when $p$ is large enough) and hence

\#\mathcal{U}_{\theta}\sim\#\mathcal{V}_{\theta}\sim p^{k(n-k)-(m+1-l)(k-l)}.

Next we show $\mathcal{U}_{\theta}\cap\mathcal{U}_{\theta^{\prime}}=\emptyset$ for $\theta\neq\theta^{\prime}$ . By contradiction, suppose $V\in\mathcal{U}_{\theta}\cap\mathcal{U}_{\theta^{\prime}}$ . By definition, $V$ satisfies

	$\displaystyle\#(\pi_{V}^{*}(\theta\oplus\mathbb{F}_{p}^{m}))\leq p^{l},$
	$\displaystyle\#(\pi_{V}^{*}(\theta^{\prime}\oplus\mathbb{F}_{p}^{m}))\leq p^{l},$
	$\displaystyle\#(\pi_{V}^{*}(\mathbb{F}_{p}^{m}))=p^{l},$
	$\displaystyle\#(\pi_{V}^{*}(\mathbb{F}_{p}^{2}\times\mathbb{F}_{p}^{m}))=p^{l+1}.$

The first and third conditions imply $\pi_{V}^{*}(\theta)\subset\pi_{V}^{*}(\mathbb{F}_{p}^{m})$ . Similarly, the second and third conditions imply $\pi_{V}^{*}(\theta^{\prime})\subset\pi_{V}^{*}(\mathbb{F}_{p}^{m})$ . Noting that $\textup{span}\{\theta,\theta^{\prime}\}=\mathbb{F}_{p}^{2}$ , we have

\pi_{V}^{*}(\mathbb{F}_{p}^{2}\times\mathbb{F}_{p}^{m})\subset\pi_{V}^{*}(\mathbb{F}_{p}^{m}),

which has cardinality $=p^{l}$ , contradicting the fourth condition.

We have shown that $E_{l+\gamma}(A;n,k)\supset\bigsqcup_{\theta\in\mathbf{E}_{\gamma,\beta}}\mathcal{U}_{\theta}$ , which has cardinality $\#\mathbf{E}_{\gamma,\beta}\cdot\#\mathcal{U}_{\theta}$

\gtrsim p^{2\gamma-\beta+k(n-k)-(m+1-l)(k-l)}.

Type 2, $\gamma\in(\frac{\beta+1}{2},1]$ The trick is to write $a=(m-1)+(\beta+1)=:m^{\prime}+\beta^{\prime}$ . Note that $l\leq m^{\prime}\leq n+l-k-1$ and $\gamma>\frac{\beta^{\prime}}{2}$ . We apply the construction in “Type 3, $\gamma\in(\frac{\beta}{2},\beta]$ ”, where we only used $\gamma>\frac{\beta}{2}$ . We obtain a $A$ with $\#A\sim p^{a}$ such that

\#E_{s}(A;n,k)\gtrsim p^{k(n-k)-(m^{\prime}+1-l)(k-l)+2\gamma-\beta^{\prime}}=p^{k(n-k)-(m-l)(k-l)+2\gamma-(\beta+1)}.

Type 3, $\gamma\in(0,\frac{\beta}{2}]$ The trick is to make $a$ bigger. We write $a=m+\beta\leq(m+1)+0=:m^{\prime}+\beta^{\prime}$ . One can check $l+1\leq m^{\prime}\leq n+l-k$ and $\gamma>\beta^{\prime}$ . We apply the construction in Type 2 with $(m^{\prime},\beta^{\prime})$ . We find $A^{\prime}$ with $\#A^{\prime}\sim p^{m+1}$ such that

\#E_{s}(A^{\prime};n,k)\gtrsim p^{k(n-k)-(m+1-l)(k-l)}.

Choosing any subset $A\subset A^{\prime}$ with $\#A\sim p^{a}$ , we get

\#E_{s}(A;n,k)\geq\#E_{s}(A^{\prime};n,k)\gtrsim p^{k(n-k)-(m+1-l)(k-l)}.

∎

7. Exceptional set estimate: Upper bound I

We prove the following proposition in this section.

Proposition 38.

Assume Conjecture 4 holds. For $0<a\leq k+1$ and $0<s$ , and $A\subset\mathbb{F}_{p}^{k+1}$ with $\#A\gtrsim p^{a}$ , we have

(70)

\#E_{s-\varepsilon}(A;k+1,k)\lesssim_{\varepsilon}p^{\varepsilon+\mathbf{M}(a,s;k+1,k)},

for any $\varepsilon>0$ .

It is proved by using the following lemma.

Lemma 39.

Assume Conjecture 4 holds. Fix $0<\varepsilon_{0}<1/100$ . Let $0<a\leq k+1,s>0$ and $\sigma\geq 0$ . Suppose the parameters satisfy $\mathbf{M}(a,s;k+1,k)+\varepsilon_{0}\leq k$ and $a-s+\varepsilon_{0}\leq\sigma\leq a$ . Let $A\subset\mathbb{F}_{p}^{k+1}$ with $\#A=p^{k+1}$ . Define

\mathcal{V}:=\{L\in A(1,\mathbb{F}_{p}^{k+1}):p^{\sigma}\leq\#(L\cap A)\}.

Then

\#\mathcal{V}\lesssim_{\varepsilon_{0}}p^{\mathbf{M}(a,s;k+1,k)+a-\sigma+\varepsilon_{0}}.

Remark 40.

The implicit constant in $\lesssim_{\varepsilon_{0}}$ can be made independent of $\sigma$ , since we can apply the lemma to $\sigma\in\varepsilon_{0}^{2}\cdot\mathbb{N}$ which consists $O(\varepsilon_{0}^{-2})$ values.

Proof.

The proof of this part is by Furstenberg estimate. As in Definition 14, write

(71)

\begin{cases}a=m+\beta\\ s=l+\gamma.\end{cases}

There are four cases.

Type 1: When $s>\min\{a,k\}$ ,

\mathbf{M}(a,s;k+1,k)=k.

Type 2: When $s\leq\min\{a,k\}$ and $m=l+1,\gamma\in(\beta,1]$ ,

\displaystyle\mathbf{M}(a,s;k+1,k)=l+\max\{2\gamma-(\beta+1),0\}.

Type 3: When $s\leq\min\{a,k\}$ and $m=l,\gamma\in(0,\beta]$ ,

\displaystyle\mathbf{M}(a,s;k+1,k)=l+\max\{2\gamma-\beta,0\}.

Type 4: When $s\leq a-1$ ,

\mathbf{M}(a,s;k+1,k)=-\infty.

Type 1 is trivial, since $\#\mathcal{V}\leq p^{k}$ is always true. Type 4 is also easy, since in this case we have $\sigma\geq a-s+\varepsilon_{0}\geq 1+\varepsilon_{0}$ , and hence $\mathcal{V}=\emptyset$ . We only need to consider Type 2 and Type 3.

Suppose $\#\mathcal{V}=p^{t}$ , we want to show

t\leq\mathbf{M}(a,s;k+1,k)+a-\sigma+\varepsilon_{0}.

We write $t=2w+\tau$ , where $w\in\{0,\dots,k-1\}$ , $\tau\in(0,2]$ .

For convenience, we define

(72)

R(\beta,\gamma):=\begin{cases}\max\{2\gamma-(\beta+1),0\}&m=l+1,\gamma\in(\beta,1]\\ \max\{2\gamma-\beta,0\}&m=l,\gamma\in(0,\beta].\end{cases}

Then $\mathbf{M}(a,s;k+1,k)=l+R(\beta,\gamma)$ in the case of Type 2 or Type 3.

Note that $A$ contains a $(\sigma,t;k+1,1)$ -Furstenberg set $\bigcup_{L\in\mathcal{V}}(L\cap A)$ . Since Conjecture 4 holds, by Theorem 7, we have the lower bound:

(73)

a+\eta_{0}\geq\mathbf{F}(\sigma,t;k+1,1)=w+\min\{\sigma+\tau,\frac{3}{2}\sigma+\frac{1}{2}\tau,\sigma+1\},

for any $\eta_{0}>0$ when $p$ is big enough depending on $\eta_{0}$ . We choose $\eta_{0}$ such that $\eta_{0}<\varepsilon_{0}/2$

From (73), there are three possible cases.

(1) $a+\eta_{0}\geq w+\sigma+\tau$ .

This implies $t=2w+\tau\leq a+w-\sigma+\eta_{0}$ . Our goal is to show $t\leq\mathbf{M}(a,s;k+1,k)+a-\sigma+\varepsilon_{0}$ , so we just need to show

\mathbf{M}(a,s;k+1,k)\geq w.

We also know

a\geq w+\sigma+\tau-\eta_{0}\geq w+\tau+a-s+\varepsilon_{0}-\eta_{0}\geq w+\tau+a-s+\varepsilon_{0}/2,

which implies

s\geq w+\tau+\varepsilon_{0}/2.

Since $s\leq l+1$ and $w\in\mathbb{N}$ , we have $w\leq l$ . Therefore, with the condition that $\mathbf{M}(a,s;k+1,k)\geq l$ , we see that

\mathbf{M}(a,s;k+1,k)\geq w.

(2) $a+\eta_{0}\geq\sigma+1+w$ .

In this case, $a\geq\sigma+1+w-\eta_{0}\geq a-s+w+1+\varepsilon_{0}-\eta_{0}$ , which implies

s\geq w+1+\varepsilon_{0}/2.

Since $s\leq l+1$ and $w\in\mathbb{N}$ , we get $w\leq l-1$ .

Now we want to prove $t\leq\mathbf{M}(a,s;k+1,k)+a-\sigma+\varepsilon_{0}$ . If this is not true, then by contradiction, we assume

2w+\tau=t>\mathbf{M}(a,s;k+1,k)+a-\sigma+\varepsilon_{0}.

This will imply

l-1+\tau\geq w+\tau>\mathbf{M}(a,s;k+1,k)+a-\sigma-w+\varepsilon_{0}\geq\mathbf{M}(a,s;k+1,k)+1+\varepsilon_{0}-\eta_{0}\geq l+1,

which is a contradiction, as $\tau\leq 2$ .

(3) $a+\eta_{0}\geq w+\frac{3}{2}\sigma+\frac{1}{2}\tau$ .

This is equivalent to $t\leq 2a-3\sigma+2\eta_{0}$ . We hope to prove

t\leq\mathbf{M}(a,s;k+1,k)+a-\sigma+\varepsilon_{0}.

We just need to prove

2a-3\sigma\leq\mathbf{M}(a,s;k+1,k)+a-\sigma,

since $2\eta_{0}<\varepsilon_{0}$ .

This is equivalent to

a\leq\mathbf{M}(a,s;k+1,k)+2\sigma.

We plug in $a=m+\beta,s=l+\gamma,\mathbf{M}(a,s;k+1,k)=l+R(\beta,\gamma),\sigma\geq(m+\beta)-(l+\gamma)+\varepsilon_{0}$ . Then it suffices to prove

m+\beta\leq l+R(\beta,\gamma)+2(m+\beta)-2(l+\gamma)+2\varepsilon_{0}.

This inequality is equivalent to

2\gamma-(\beta+m-l)\leq R(\beta,\gamma)+2\varepsilon_{0},

This is easy to verify by checking either in case $m=l+1,\gamma\in(\beta,1]$ or in case $m=l,\gamma\in(0,\beta]$ . ∎

Proof of Proposition 38.

We will use the lemma that we just proved. We show that, if $A\subset\mathbb{F}_{p}^{k+1}$ with $\#A\gtrsim p^{a}$ , $E\subset G(1,\mathbb{F}_{p}^{k+1})$ with $\#E>C_{\varepsilon}p^{\varepsilon+\mathbf{M}(a,s;k+1,k)}$ , and $p$ is big enough, then there exists $V\in E$ such that

\#\pi_{V}^{*}(A)>p^{s-\varepsilon}.

Since $\#E\leq p^{k}$ , we have

\varepsilon+\mathbf{M}(a,s;k+1,k)\leq k.

For each $V\in E$ and dyadic number $1\leq\mu\leq p$ , define

\mathbb{L}_{V,\mu}:=\{L\in A(1,\mathbb{F}_{p}^{k+1}):L\parallel V,\mu\leq\#(A\cap L)<2\mu\}.

We see that $\{\mathbb{L}_{V,\mu}\}_{\mu}$ form a partition of the of lines that are parallel to $V$ .

We choose $\varepsilon_{0}\ll\varepsilon$ , for example, $\varepsilon_{0}=\varepsilon^{2}$ . We will estimate the cardinality of the set $\bigcup_{V\in E}\mathbb{L}_{V,\mu}$ for $\mu\geq p^{a-s+\varepsilon_{0}}$ . We write $\mu=p^{\sigma}$ with $a\geq\sigma\geq a-s+\varepsilon_{0}$ . By Lemma 39, we have

\#\bigcup_{V\in E}\mathbb{L}_{V,\mu}\lesssim_{\varepsilon}p^{\mathbf{M}(a,s;k+1,k)+a-\sigma+\varepsilon_{0}}.

If we define

E_{\mu}:=\{V\in E:\#\mathbb{L}_{V,\mu}>p^{a-\sigma-\varepsilon_{0}}\},

then

\#E_{\mu}\lesssim_{\varepsilon}p^{\mathbf{M}(a,s;k+1,k)+2\varepsilon_{0}}.

Summing over dyadic $\mu\geq p^{a-s+\varepsilon_{0}}$ , we have

\#\bigcup_{\mu\geq p^{a-s+\varepsilon_{0}}}E_{\mu}\lesssim_{\varepsilon}p^{\mathbf{M}(a,s;k+1,k)+3\varepsilon_{0}}.

Therefore, $\#E>\#\bigcup_{\mu\geq p^{a-s+\varepsilon_{0}}}E_{\mu}$ when $p$ is large enough. We can find $V\in E\setminus\bigcup_{\mu\geq p^{a-s+\varepsilon_{0}}}E_{\mu}$ . In other words, there exists $V\in E$ , such that for any $\mu=p^{\sigma}\geq p^{a-s+\varepsilon_{0}}$ ,

\#\mathbb{L}_{V,\mu}\leq p^{a-\sigma-\varepsilon_{0}}.

Now, we do the estimate. We have

\#A=\sum_{\mu<p^{a-s+\varepsilon_{0}}}\sum_{L\in\mathbb{L}_{V,\mu}}\#(A\cap L)+\sum_{\mu\geq p^{a-s+\varepsilon_{0}}}\sum_{L\in\mathbb{L}_{V,\mu}}\#(A\cap L).

Note that

\sum_{\mu\geq p^{a-s+\varepsilon_{0}}}\sum_{L\in\mathbb{L}_{V,\mu}}\#(A\cap L)\leq\sum_{\mu\geq p^{a-s+\varepsilon_{0}}}2\mu\cdot\#\mathbb{L}_{V,\mu}\leq 2\sum_{\mu\geq p^{a-s+\varepsilon_{0}}}p^{a-\varepsilon_{0}}\leq\frac{1}{2}\#A.

In the last inequality, we are summing over $O(\log p)$ terms and we assume $p$ is big enough.

We have

\frac{1}{2}\#A\leq\sum_{\mu<p^{a-s+\varepsilon_{0}}}\sum_{L\in\mathbb{L}_{V,\mu}}\#(A\cap L)<2p^{a-s+\varepsilon_{0}}\#\pi_{V}^{*}(A).

This implies $\#\pi_{V}^{*}(A)\gtrsim p^{s-\varepsilon_{0}}>p^{s-\varepsilon}$ .

∎

8. Exceptional set estimate: Upper bound II

The goal of this section is to prove the following proposition.

Proposition 41.

Let $n,k\in\mathbb{N}$ and $n\geq k+2$ . Suppose for any $n^{\prime}=k+1,\dots,n-1$ and $a\in(0,n^{\prime}],s>0$ , we have

(74)

\sup_{A\subset\mathbb{F}_{p}^{n^{\prime}},\#A\sim p^{a}}\#E_{s-\varepsilon}(A;n^{\prime},k)\lesssim_{\varepsilon}p^{\varepsilon+\mathbf{M}(a,s;n^{\prime},k)},

for any $\varepsilon>0$ . Then for $a\in(0,n],s>0$ , we have

\sup_{A\subset\mathbb{F}_{p}^{n},\#A\sim p^{a}}\#E_{s-\varepsilon}(A;n,k)\lesssim_{\varepsilon}p^{\varepsilon+\mathbf{M}(a,s;n,k)},

for any $\varepsilon>0$ .

We prove the following lemma.

Lemma 42.

Assume (74) holds. Suppose $n,k\in\mathbb{N}$ , $n\geq k+2$ , $a\in(0,n]$ , $s>0$ and $s\in(a-(n-k),\min\{a,k\}]$ . Then for any $A\subset\mathbb{F}_{p}^{n}$ with $\#A\sim p^{a}$ , there exist numbers $a_{1},s_{1}$ , such that

(75)

\begin{cases}p^{\max\{0,a-1\}}\leq p^{a_{1}}\leq p^{\min\{n-1,a\}};\\ 1\leq p^{s_{1}}\leq p^{s};\end{cases}

and

(76)

\#E_{s-\varepsilon}(A;n,k)\lesssim_{\varepsilon}p^{\varepsilon+\mathbf{M}(a_{1},s_{1};n-1,k)+\mathbf{M}(s_{1}+a-a_{1},s;k+1,k)}.

Proof.

We will do several steps of pigeonholing, which lead to the parameters $s_{1},a_{1}$ . For convenience, we denote $\mathcal{V}:=E_{s-\varepsilon}(A;n,k)$ .

By properly choosing the coordinate, we can assume $\gtrsim 1$ fraction of the $(n-k)$ -planes in $\mathcal{V}$ intersect $\mathbb{F}_{p}^{n-1}\times\mathbf{0}$ transversely (at a $(n-k-1)$ -plane). Since we are going to find upper bound for $\#\mathcal{V}$ , we can just assume all the planes in $\mathcal{V}$ intersect $\mathbb{F}_{p}^{n-1}\times\mathbf{0}$ at a $(n-k-1)$ -plane.

For each $W\in G(n-k-1,\mathbb{F}_{p}^{n-1}\times\mathbf{0})$ , we define $\mathcal{V}_{W}:=\{V\in\mathcal{V}:V\cap(\mathbb{F}_{p}^{n-1}\times\mathbf{0})=W\}$ . By pigeonholing, there exits $\mathcal{W}\subset G(n-k-1,\mathbb{F}_{p}^{n-1}\times\mathbf{0})$ with $\#\mathcal{W}\sim p^{t_{1}}$ such that for each $W\in\mathcal{W}$ , $\#\mathcal{V}_{W}\sim p^{t_{2}}$ . Here, $p^{t_{1}},p^{t_{2}}\geq 1$ are dyadic numbers so that

p^{t_{1}+t_{2}}\gtrapprox\#\mathcal{V}.

By pigeonholing on $\#A\cap(\mathbb{F}_{p}^{n-1}\times\xi)$ for $\xi\in\mathbb{F}_{p}$ , we can find a dyadic number $1\leq p^{a_{1}}\leq p^{a}$ and $\Xi_{1}\subset\mathbb{F}_{p}$ so that $\#A\cap(\mathbb{F}_{p}^{n-1}\times\xi)\sim p^{a_{1}}$ for any $\xi\in\Xi_{1}$ and

p^{a_{1}}\cdot\#\Xi_{1}\gtrapprox p^{a}.

Since $\#\Xi_{1}\leq p$ , we also have $p^{a_{1}}\gtrapprox p^{a-1}$ .

For each $\xi\in\Xi_{1}$ , we consider the slice $\mathbb{F}_{p}^{n-1}\times\xi$ . We denote $A_{\xi}:=A\cap(\mathbb{F}_{p}^{n-1}\times\xi)$ . There exists a dyadic number $1\leq p^{s_{1}(\xi)}\leq p^{s-\varepsilon}$ , such that

\#\pi_{W}^{*}(A_{\xi})\sim p^{s_{1}(\xi)},

for $\gtrapprox\#\mathcal{W}\sim p^{t_{1}}$ many $W\in\mathcal{W}$ . Here, $s_{1}(\xi)\leq s-\varepsilon$ is because $\#\pi_{W}^{*}(A_{\xi})\leq\#\pi_{V}^{*}(A)<p^{s-\varepsilon}$ for $V\in\mathcal{V}_{W}$ .

We see that $E_{s_{1}(\xi)+\varepsilon^{2}/2}(A_{\xi};n-1,k)$ contains a $\gtrapprox 1$ portion of $\mathcal{W}$ when $p$ is large enough depending on $\varepsilon$ . We can use (74) for the quadruple $(a_{1},s_{1}(\xi)+\varepsilon^{2};n-1,k)$ to obtain

p^{t_{1}}\lessapprox\#E_{s_{1}(\xi)+\varepsilon^{2}/2}(A_{\xi};n-1,k)\lesssim_{\varepsilon}p^{\varepsilon^{2}/2+\mathbf{M}(a_{1},s_{1}(\xi)+\varepsilon^{2};n-1,k)}.

By pigeonholing on $s_{1}(\xi)$ , we can find $\Xi\subset\Xi_{1}$ such that

s_{1}(\xi)=s_{1},

for all $\xi\in\Xi$ . And,

\#\Xi\gtrapprox\#\Xi_{1}\gtrapprox p^{a-a_{1}}.

Next, we note that

\sum_{W\in\mathcal{W}}\sum_{\xi\in\Xi}\#\pi_{W}^{*}(A_{\xi})\gtrapprox\#\mathcal{W}\cdot\#\Xi\cdot p^{s_{1}}.

By pigeonholing, there exists $W\in\mathcal{W}$ such that

\sum_{\xi\in\Xi}\#\pi_{W}^{*}(A_{\xi})\gtrapprox\#\Xi\cdot p^{s_{1}}\gtrapprox p^{a-a_{1}+s_{1}}.

We fix this $W$ and study the behavior of $\mathcal{V}_{W}$ . Without loss of generality, we can assume $W=\mathbb{F}_{p}^{n-1-k}\times\mathbf{0}^{k}\times\mathbf{0}$ . For $V\in\mathcal{V}_{W}$ , then $V\supset W$ . We see that $V$ is of form $V=\mathbb{F}_{p}^{n-1-k}\times\ell_{V}$ , where $\ell_{V}\in G(1,\mathbf{0}^{n-1-k}\times\mathbb{F}_{p}^{k+1})$ . Since $V\cap\mathbb{F}_{p}^{n-1}\times\mathbf{0}=W$ , we have that $\ell_{V}$ is not parallel to $\mathbb{F}_{p}^{n-1}\times\mathbf{0}$ .

Next, we project everything onto $\mathbf{0}^{n-1-k}\times\mathbb{F}_{p}^{k+1}$ . For $x=(x_{1},\dots,x_{n})\in\mathbb{F}_{p}^{n}$ , we define

\pi_{\mathbb{F}_{p}^{k+1}}(x):=(0,\dots,0,x_{n-k},x_{n-k+1},\dots,x_{n}).

One can also check that $\pi_{W}^{*}(x)=\pi_{\mathbb{F}_{p}^{k+1}}(x)+W$ .

Define $B_{\xi}=\pi_{\mathbb{F}_{p}^{k+1}}(A_{\xi})$ . We see that $B_{\xi}$ is a subset of $\mathbf{0}^{n-1-k}\times\mathbb{F}_{p}^{k+1}$ and $\#B_{\xi}=\#\pi_{W}^{*}(A_{\xi})$ .

The next important observation is that for any $A\subset\mathbb{F}_{p}^{n}$ , $V=\mathbb{F}_{p}^{n-1-k}\times\ell_{V}\in\mathcal{V}_{W}$ , one has

\#\pi_{V}^{*}(A)=\#\pi_{\ell_{V}}^{*}(\pi_{\mathbb{F}_{p}^{k+1}}(A)).

This is not hard to verify once writing down the definition.

We can now do the estimate. By definition, $\#\pi_{V}^{*}(A)<p^{s-\varepsilon}$ for $V\in\mathcal{V}_{W}$ . Therefore,

p^{s-\varepsilon}>\#\pi_{\ell_{V}}^{*}(\pi_{\mathbb{F}_{p}^{k+1}}(A)).

This means that

\{\ell_{V}:V\in\mathcal{V}_{W}\}\subset E_{s-\varepsilon}(\pi_{\mathbb{F}_{p}^{k+1}}(A);k+1,k).

Also, note that

\#\pi_{\mathbb{F}_{p}^{k+1}}(A)\geq\#\pi_{\mathbb{F}_{p}^{k+1}}(\bigcup_{\xi\in\Xi}A_{\xi})=\#\pi^{*}_{W}(\bigcup_{\xi\in\Xi}A_{\xi})=\sum_{\xi\in\Xi}\#\pi_{W}^{*}(A_{\xi})\gtrapprox p^{a-a_{1}+s_{1}}.

By (74) with $n^{\prime}=k+1$ , we get

p^{t_{2}}\lessapprox\#\mathcal{V}_{W}\leq\#E_{s-\varepsilon}(\pi_{\mathbb{F}_{p}^{k+1}}(A);k+1,k)\lesssim_{\varepsilon}p^{\varepsilon/3+\mathbf{M}(a-a_{1}+s_{1}-\varepsilon^{2},s-\varepsilon/2;k+1,k)}.

(It is crucial that we use $s-\varepsilon/2$ instead of $s$ on the right hand side.)

Combining with the upper bound of $p^{t_{1}}$ , we get

\#\mathcal{V}\lessapprox p^{t_{1}+t_{2}}\lesssim_{\varepsilon}p^{\varepsilon/2+\mathbf{M}(a_{1},s_{1}+\varepsilon^{2};n-1,k)+\mathbf{M}(a-a_{1}+s_{1}-\varepsilon^{2},s-\varepsilon/2;k+1,k)}.

Let $s_{1}^{\prime}=s_{1}+2\varepsilon^{2}$ . Since $s_{1}\leq s-\varepsilon$ , we have $s_{1}^{\prime}\leq s$ .

Recall $3\varepsilon^{2}<\varepsilon/2$ and note $\mathbf{M}(a,s;n,k)$ is decreasing in $a$ . By Lemma 23, we have

\mathbf{M}(a-a_{1}+s_{1}^{\prime}-3\varepsilon^{2},s-\varepsilon/2;k+1,k)\leq\mathbf{M}(a-a_{1}+s_{1}^{\prime},s;k+1,k).

Therefore, under the new $s_{1}^{\prime}$ , we have

\#\mathcal{V}\lesssim_{\varepsilon}p^{\varepsilon+\mathbf{M}(a_{1},s_{1}^{\prime}-\varepsilon^{2};n-1,k)+\mathbf{M}(a-a_{1}+s_{1}^{\prime},s;k+1,k)}.

Next, we want to slightly increase $a_{1}$ to $a_{1}^{\prime}$ so that $p^{\min\{0,a-1\}}\leq p^{a_{1}^{\prime}}$ . By the condition $p^{\min\{0,a-1\}}\lessapprox p^{a_{1}}$ , we have $p^{\min\{0,a-1\}}\leq p^{a_{1}+\varepsilon^{2}}$ when $p$ is large enough. We just need to let $a_{1}^{\prime}=\min\{a_{1}+\varepsilon^{2},\min\{0,a-1\}\}$ . Noting $a_{1}^{\prime}\leq a_{1}+\varepsilon^{2}$ and by Lemma 23 again, we have

\mathbf{M}(a_{1},s_{1}^{\prime}-\varepsilon^{2};n-1,k)\leq\mathbf{M}(a_{1}^{\prime}-\varepsilon^{2},s_{1}^{\prime}-\varepsilon^{2};n-1,k)\leq\mathbf{M}(a_{1}^{\prime},s_{1}^{\prime};n-1,k)

We still use $s_{1},a_{1}$ for $s_{1}^{\prime},a_{1}^{\prime}$ . We obtain

\#\mathcal{V}\lesssim_{\varepsilon}p^{\varepsilon+\mathbf{M}(a_{1},s_{1};n-1,k)+\mathbf{M}(a-a_{1}+s_{1},s;k+1,k)}.

∎

Lemma 43.

Suppose $n,k\in\mathbb{N}$ , $n\geq k+2$ , $a\in(0,n]$ , $s>0$ and $s\in(a-(n-k),\min\{a,k\}]$ . Suppose there exist numbers $a_{1},s_{1}$ , such that

(77)

\begin{cases}\max\{0,a-1\}\leq a_{1}\leq\min\{n-1,a\};\\ 0\leq s_{1}\leq s.\end{cases}

Then

(78)

\mathbf{M}(a_{1},s_{1};n-1,k)+\mathbf{M}(s_{1}+a-a_{1},s;k+1,k)\leq\mathbf{M}(a,s;n,k).

Proof.

Write $a=m+\beta,s=l+\gamma$ ; $a_{1}=m_{1}+\beta_{1},s_{1}=l_{1}+\gamma_{1}$ in the canonical expressions. Since $a-1\leq a_{1}\leq a$ , there are only two choices for $m_{1}$ : $m_{1}=m$ or $m_{1}=m-1$ . Since $s_{1}\leq s$ , we have $l_{1}\leq l$ .

Case 1: $m_{1}=m,l_{1}\leq l-1$

By Lemma 24,

\mathbf{M}(a_{1},s_{1};n-1,k)\leq k(n-1-k)-(m-l+1)(k-l+1)+\max\{2\gamma_{1}-(\beta_{1}+1),0\}.

Trivially,

\mathbf{M}(s_{1}+a-a_{1},s;k+1,k)\leq k.

Also, by Lemma 24,

\mathbf{M}(a,s;n,k)\geq k(n-k)-(m+1-l)(k-l).

It suffices to prove

\max\{2\gamma_{1}-\beta_{1}-1,0\}\leq m+1-l.

Just need to note $m\geq l$ and $2\gamma_{1}\leq 2$ .

Case 2: $m_{1}=m,l_{1}=l$

Case 2.1: $\gamma>\beta,\gamma_{1}>\beta_{1}$

Since $s\leq a$ and $\gamma>\beta$ , we have $m\geq l+1$ . Hence,

\begin{split}\mathbf{M}(a_{1},s_{1};n-1,k)&=\mathbf{M}(m+\beta_{1},l+\gamma_{1};n-1,k)\\ &=k(n-1-k)-(m-l)(k-l)+\max\{2\gamma_{1}-(\beta_{1}+1),0\}.\end{split}

Next we estimate $\mathbf{M}(s_{1}+a-a_{1},s;k+1,k)=\mathbf{M}(l+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)$ . We claim we have

(79)

\mathbf{M}(l+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)\leq\begin{cases}k-(k-l)+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}&\gamma_{1}+\beta-\beta_{1}\geq\gamma;\\ k&\gamma_{1}+\beta-\beta_{1}<\gamma.\end{cases}

We just consider when $\gamma_{1}+\beta-\beta_{1}\geq\gamma$ . We note $\gamma_{1}+\beta-\beta_{1}\in(0,2)$ . If $\gamma_{1}+\beta-\beta_{1}\in(0,1]$ , then we use Type 3 in Definition 14, which gives the desired formula. If $\gamma_{1}+\beta-\beta_{1}\in(1,2]$ , we use Type 2, which gives $\mathbf{M}(l+1+(\gamma_{1}+\beta-\beta_{1}-1),l+\gamma;k+1,k)=k-(k-l)+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}$ , which is the same.

We also have $\mathbf{M}(a,s;n,k)=k(n-k)-(m-l)(k-l)+\max\{2\gamma-(\beta+1),0\}$ .

When $\gamma_{1}+\beta-\beta_{1}<\gamma$ , we just need to prove

\max\{2\gamma_{1}-(\beta_{1}+1),0\}\leq\max\{2\gamma-(\beta+1),0\},

which is easy to verify, since $\gamma_{1}\leq\gamma$ and $\gamma_{1}+\beta-\beta_{1}<\gamma$ .

When $\gamma_{1}+\beta-\beta_{1}\geq\gamma$ , we just need to prove

\max\{2\gamma_{1}-(\beta_{1}+1),0\}+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}\leq 1+\max\{2\gamma-(\beta+1),0\}.

Just need to check three scenarios:

(1) $2\gamma_{1}-(\beta_{1}+1)\leq 1$ , since $\gamma_{1}\leq 1$ .

(2) $2\gamma-(\gamma_{1}+\beta-\beta_{1})\leq 1+2\gamma-(\beta+1)$ , since $\gamma_{1}>\beta_{1}$ .

(3) Their sum $2\gamma_{1}-(\beta_{1}+1)+2\gamma-(\gamma_{1}+\beta-\beta_{1})=2\gamma+\gamma_{1}-(\beta+1)\leq 1+2\gamma-(\beta+1)$ .

Case 2.2: $\gamma>\beta,\gamma_{1}\leq\beta_{1}$

In this case, by Lemma 24,

\mathbf{M}(a_{1},s_{1};n-1,k)\leq k(n-1-k)-(m+1-l)(k-l)+\max\{2\gamma_{1}-\beta_{1},0\}.

\mathbf{M}(l+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)\leq k.

\mathbf{M}(a,s;n,k)=k(n-k)-(m-l)(k-l)+\max\{2\gamma-(\beta+1),0\}.

It suffices to prove

\max\{2\gamma_{1}-\beta_{1},0\}\leq 1+\max\{2\gamma-(\beta+1),0\}.

We just use $2\gamma_{1}-\beta_{1}\leq 1$ , since $\gamma_{1}\leq\beta_{1}$ .

Case 2.3: $\gamma\leq\beta,\gamma_{1}>\beta_{1}$

\mathbf{M}(a_{1},s_{1};n-1,k)\leq k(n-1-k)-(m-l)(k-l)+\max\{2\gamma_{1}-(\beta_{1}+1),0\}.

(We use $\leq$ instead of $=$ , since when $m=l$ , $\mathbf{M}(a_{1},s_{1};n-1,k)=k(n-1-k)$ .)

Since $\gamma_{1}+\beta-\beta_{1}>\gamma$ ,

\mathbf{M}(l+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)\leq k-(k-l)+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}.

Also, we have

\mathbf{M}(a,s;n,k)=k(n-k)-(m+1-l)(k-l)+\max\{2\gamma-\beta,0\}.

It suffices to prove

\max\{2\gamma_{1}-(\beta_{1}+1),0\}+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}\leq\max\{2\gamma-\beta,0\}.

(1) $2\gamma_{1}-(\beta_{1}+1)\leq 2\gamma-\beta$ , since $s_{1}\leq s$ implies $\gamma_{1}\leq\gamma$ , and $\beta\leq 1$ .

(2) $2\gamma-(\gamma_{1}+\beta-\beta_{1})\leq 2\gamma-\beta$ , since $\gamma_{1}>\beta_{1}$ .

(3) $2\gamma_{1}-(\beta_{1}+1)+2\gamma-(\gamma_{1}+\beta-\beta_{1})=2\gamma+\gamma_{1}-(\beta+1)\leq 2\gamma-\beta$ , since $\gamma_{1}\leq 1$ .

Case 2.4: $\gamma\leq\beta,\gamma_{1}\leq\beta_{1}$

\mathbf{M}(a_{1},s_{1};n-1,k)=k(n-1-k)-(m+1-l)(k-l)+\max\{2\gamma_{1}-\beta_{1},0\}.

\mathbf{M}(l+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)=\begin{cases}k&\gamma>\gamma_{1}+\beta-\beta_{1}\\ k-(k-l)+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}&\gamma\leq\gamma_{1}+\beta-\beta_{1}.\end{cases}

\mathbf{M}(a,s;n,k)=k(n-k)-(m+1-l)(k-l)+\max\{2\gamma-\beta,0\}.

When $\gamma>\gamma_{1}+\beta-\beta_{1}$ , it suffices to show

\max\{2\gamma_{1}-\beta_{1},0\}\leq\max\{2\gamma-\beta,0\}.

This is true by noting $\gamma_{1}\leq\gamma$ and $\gamma>\gamma_{1}+\beta-\beta_{1}$ .

When $\gamma\leq\gamma_{1}+\beta-\beta_{1}$ , it suffices to show

\max\{2\gamma_{1}-\beta_{1},0\}+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}\leq 1+\max\{2\gamma-\beta,0\}.

(1) $2\gamma_{1}-\beta_{1}\leq 1+2\gamma-\beta$ , since $\gamma_{1}\leq\gamma$ and $\beta\leq 1$ .

(2) $2\gamma-(\gamma_{1}+\beta-\beta_{1})\leq 1+2\gamma-\beta$ , since $\beta_{1}\leq 1$ .

(3) $2\gamma_{1}-\beta_{1}+2\gamma-(\gamma_{1}+\beta-\beta_{1})=\gamma_{1}-\beta+2\gamma\leq 1+2\gamma-\beta$ , since $\gamma_{1}\leq 1$ .

Case 3: $m_{1}=m-1,l_{1}\leq l-2$ The proof is similar to Case 1. By Lemma 24,

\mathbf{M}(a_{1},s_{1};n-1,k)\leq k(n-1-k)-(m-l)(k-l+2)+\max\{2\gamma_{1}-(\beta_{1}+1),0\}.

Trivially,

\mathbf{M}(s_{1}+a-a_{1},s;k+1,k)\leq k.

Also, by Lemma 24,

\mathbf{M}(a,s;n,k)\geq k(n-k)-(m-l)(k-l+1).

It suffices to prove

\max\{2\gamma_{1}-\beta_{1}-1,0\}\leq m-l.

Just need to note $m-l\geq 1$ and $2\gamma_{1}\leq 2$ .

Case 4: $m_{1}=m-1,l_{1}=l-1$

Case 4.1: $\gamma>\beta,\gamma_{1}>\beta_{1}$

Since $s\leq a$ and $\gamma>\beta$ , we have $m\geq l+1$ . Hence,

\begin{split}\mathbf{M}(a_{1},s_{1};n-1,k)&=\mathbf{M}(m-1+\beta_{1},l-1+\gamma_{1};n-1,k)\\ &=k(n-1-k)-(m-l)(k-l+1)+\max\{2\gamma_{1}-(\beta_{1}+1),0\}.\end{split}

Next we estimate $\mathbf{M}(s_{1}+a-a_{1},s;k+1,k)=\mathbf{M}(l+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)$ . As is Case 2.1,

(80)

\mathbf{M}(l+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)\leq\begin{cases}k-(k-l)+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}&\gamma_{1}+\beta-\beta_{1}\geq\gamma;\\ k&\gamma_{1}+\beta-\beta_{1}<\gamma.\end{cases}

We also have $\mathbf{M}(a,s;n,k)=k(n-k)-(m-l)(k-l)+\max\{2\gamma-(\beta+1),0\}$ .

When $\gamma_{1}+\beta-\beta_{1}<\gamma$ , we just need to prove

\max\{2\gamma_{1}-(\beta_{1}+1),0\}\leq 1+\max\{2\gamma-(\beta+1),0\},

which is easy to verify,since $\gamma_{1}\leq 1$ and $\gamma_{1}+\beta-\beta_{1}<\gamma$ .

When $\gamma_{1}+\beta-\beta_{1}\geq\gamma$ , we just need to prove

\max\{2\gamma_{1}-(\beta_{1}+1),0\}+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}\leq 2+\max\{2\gamma-(\beta+1),0\}.

Just need to check three scenarios:

(1) $2\gamma_{1}-(\beta_{1}+1)\leq 2$ , since $\gamma_{1}\leq 1$ .

(2) $2\gamma-(\gamma_{1}+\beta-\beta_{1})\leq 2$ , since $\gamma_{1}+\beta-\beta_{1}\geq\gamma\geq 0$ .

(3) $2\gamma_{1}-(\beta_{1}+1)+2\gamma-(\gamma_{1}+\beta-\beta_{1})=2\gamma+\gamma_{1}-(\beta+1)\leq 2+2\gamma-(\beta+1)$ , since $\gamma_{1}\leq 1$ .

Case 4.2: $\gamma>\beta,\gamma_{1}\leq\beta_{1}$

In this case,

\mathbf{M}(a_{1},s_{1};n-1,k)\leq k(n-1-k)-(m+1-l)(k-l+1)+\max\{2\gamma_{1}-\beta_{1},0\}.

\mathbf{M}(l+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)\leq k.

\mathbf{M}(a,s;n,k)=k(n-k)-(m-l)(k-l)+\max\{2\gamma-(\beta+1),0\}.

It suffices to prove

\max\{2\gamma_{1}-\beta_{1},0\}\leq 1+\max\{2\gamma-(\beta+1),0\}.

We just use $2\gamma_{1}-\beta_{1}\leq 1$ , since $\gamma_{1}\leq\beta_{1}$ .

Case 4.3: $\gamma\leq\beta,\gamma_{1}>\beta_{1}$

\mathbf{M}(a_{1},s_{1};n-1,k)\leq\begin{cases}k(n-1-k)-(m-l)(k-l+1)+\max\{2\gamma_{1}-(\beta_{1}+1),0\}&m>l\\ k(n-1-k)&m=l.\end{cases}

Since $\gamma_{1}+\beta-\beta_{1}>\gamma$ ,

\mathbf{M}(l+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)\leq k-(k-l)+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}.

Also, we can assume $\gamma_{1}+\beta-\beta_{1}\leq\gamma+1$ ; otherwise, it $=-\infty$ .

Also, we have

\mathbf{M}(a,s;n,k)=k(n-k)-(m+1-l)(k-l)+\max\{2\gamma-\beta,0\}.

When $m=l$ , we just need to prove

\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}\leq\max\{2\gamma-\beta,0\}.

It is easy to verify $2\gamma-(\gamma_{1}+\beta-\beta_{1})\leq 2\gamma-\beta$ .

When $m>l$ , it suffices to prove

\max\{2\gamma_{1}-(\beta_{1}+1),0\}+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}\leq 1+\max\{2\gamma-\beta,0\}.

(1) $2\gamma_{1}-(\beta_{1}+1)\leq 1+2\gamma-\beta$ , since $\gamma_{1}+\beta-\beta_{1}\leq\gamma+1$ and $\gamma_{1}\leq 1$ .

(2) $2\gamma-(\gamma_{1}+\beta-\beta_{1})\leq 1+2\gamma-\beta$ , since $\gamma_{1}>\beta_{1}$ .

(3) $2\gamma_{1}-(\beta_{1}+1)+2\gamma-(\gamma_{1}+\beta-\beta_{1})=2\gamma+\gamma_{1}-(\beta+1)\leq 2\gamma-\beta$ , since $\gamma_{1}\leq 1$ .

Case 4.4: $\gamma\leq\beta,\gamma_{1}\leq\beta_{1}$

\mathbf{M}(a_{1},s_{1};n-1,k)=k(n-1-k)-(m+1-l)(k-l+1)+\max\{2\gamma_{1}-\beta_{1},0\}.

\mathbf{M}(l+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)\leq\begin{cases}k&\gamma>\gamma_{1}+\beta-\beta_{1}\\ k-(k-l)+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}&\gamma\leq\gamma_{1}+\beta-\beta_{1}.\end{cases}

We can also assume $\gamma_{1}+\beta-\beta_{1}\leq\gamma+1$ ; otherwise, it $=-\infty$ .

\mathbf{M}(a,s;n,k)=k(n-k)-(m+1-l)(k-l)+\max\{2\gamma-\beta,0\}.

When $\gamma>\gamma_{1}+\beta-\beta_{1}$ , it suffices to show

\max\{2\gamma_{1}-\beta_{1},0\}\leq 1+\max\{2\gamma-\beta,0\}.

This is true by noting $\gamma_{1}\leq 1$ and $\gamma>\gamma_{1}+\beta-\beta_{1}$ .

When $\gamma\leq\gamma_{1}+\beta-\beta_{1}$ , it suffices to show

\max\{2\gamma_{1}-\beta_{1},0\}+\max\{2\gamma-(\gamma_{1}+\beta-\beta_{1}),0\}\leq 2+\max\{2\gamma-\beta,0\}.

(1) $2\gamma_{1}-\beta_{1}\leq 2+2\gamma-\beta$ , since $\gamma_{1}+\beta-\beta_{1}\leq\gamma+1$ , $\gamma_{1}\leq 1$ .

(2) $2\gamma-(\gamma_{1}+\beta-\beta_{1})\leq 2+2\gamma-\beta$ , since $\beta_{1}\leq 1$ .

(3) $2\gamma_{1}-\beta_{1}+2\gamma-(\gamma_{1}+\beta-\beta_{1})=\gamma_{1}-\beta+2\gamma\leq 2+2\gamma-\beta$ , since $\gamma_{1}\leq 1$ .

Case 5: $m_{1}=m-1,l_{1}=l$

Case 5.1: $\gamma>\beta,\gamma_{1}>\beta_{1}$

In this case, we have

\mathbf{M}(m-1+\beta_{1},l+\gamma_{1};n-1,k)\leq k(n-1-k)-(m-1-l)(k-l)+\max\{2\gamma_{1}-(\beta_{1}+1),0\}.

\mathbf{M}(l+1+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)\leq k-(k-l)+\max\{2\gamma-(1+\gamma_{1}+\beta-\beta_{1}),0\}.

We assume

(81)

\gamma>\gamma_{1}+\beta-\beta_{1},

otherwise this is $-\infty$ .

We also have $\mathbf{M}(a,s;n,k)=k(n-k)-(m-l)(k-l)+\max\{2\gamma-(\beta+1),0\}$ . We just need to prove

\max\{2\gamma_{1}-(\beta_{1}+1),0\}+\max\{2\gamma-(1+\gamma_{1}+\beta-\beta_{1}),0\}\leq\max\{2\gamma-(\beta+1),0\}.

Check three scenarios:

(1) $2\gamma_{1}-(\beta_{1}+1)\leq 2\gamma-(\beta+1)$ , since $\gamma>\gamma_{1}+\beta-\beta_{1}$ and $\gamma_{1}\leq\gamma$ (since $s_{1}\leq s$ ).

(2) $2\gamma-(1+\gamma_{1}+\beta-\beta_{1})\leq 2\gamma-(\beta+1)$ , since $\gamma_{1}>\beta_{1}$ .

(3) $2\gamma_{1}-(\beta_{1}+1)+2\gamma-(1+\gamma_{1}+\beta-\beta_{1})=2\gamma+\gamma_{1}-(\beta+2)\leq 2\gamma-(\beta+1)$ , since $\gamma_{1}\leq 1$ .

Case 5.2: $\gamma>\beta,\gamma_{1}\leq\beta_{1}$

In this case, by discussing $m=l$ or $m>l$ , we have

\mathbf{M}(a_{1},s_{1};n-1,k)\leq k(n-1-k)-(m-l)(k-l)+\max\{2\gamma_{1}-\beta_{1},0\}.

\mathbf{M}(l+1+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)\leq k-(k-l)+\max\{2\gamma-(1+\gamma_{1}+\beta-\beta_{1}),0\}.

\mathbf{M}(a,s;n,k)=k(n-k)-(m-l)(k-l)+\max\{2\gamma-(\beta+1),0\}.

It suffices to prove

\max\{2\gamma_{1}-\beta_{1},0\}+\max\{2\gamma-(1+\gamma_{1}+\beta-\beta_{1}),0\}\leq 1+\max\{2\gamma-(\beta+1),0\}.

(1) $2\gamma_{1}-\beta_{1}\leq 1$ , since $\gamma_{1}\leq\beta_{1}$ .

(2) $2\gamma-(1+\gamma_{1}+\beta-\beta_{1})\leq 2\gamma-\beta$ , since $\beta_{1}\leq 1$ .

(3) $2\gamma+\gamma_{1}-(1+\beta)\leq 2\gamma-\beta$ , since $\gamma_{1}\leq 1$ .

Case 5.3: $\gamma\leq\beta,\gamma_{1}>\beta_{1}$

\mathbf{M}(l+1+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)=-\infty.

There is nothing to do.

Case 5.4: $\gamma\leq\beta,\gamma_{1}\leq\beta_{1}$

\mathbf{M}(a_{1},s_{1};n-1,k)\leq k(n-1-k)-(m-l)(k-l)+\max\{2\gamma_{1}-\beta_{1},0\}.

\mathbf{M}(l+1+\gamma_{1}+\beta-\beta_{1},l+\gamma;k+1,k)\leq k-(k-l)+\max\{2\gamma-(1+\gamma_{1}+\beta-\beta_{1}),0\}.

We assume

(82)

\gamma>\gamma_{1}+\beta-\beta_{1},

otherwise this is $-\infty.$

\mathbf{M}(a,s;n,k)=k(n-k)-(m+1-l)(k-l)+\max\{2\gamma-\beta,0\}.

It suffices to show

\max\{2\gamma_{1}-\beta_{1},0\}+\max\{2\gamma-(1+\gamma_{1}+\beta-\beta_{1}),0\}\leq\max\{2\gamma-\beta,0\}.

(1) $2\gamma_{1}-\beta_{1}\leq 2\gamma-\beta$ , since $\gamma>\gamma_{1}+\beta-\beta_{1}$ and $\gamma_{1}\leq\gamma$ .

(2) $2\gamma-(1+\gamma_{1}+\beta-\beta_{1})\leq 2\gamma-\beta$ , since $\beta_{1}\leq 1$ .

(3) $2\gamma+\gamma_{1}-\beta-1\leq 2\gamma-\beta$ , since $\gamma_{1}\leq 1$ . ∎

Proof of Proposition 41.

We just combine Lemma 42 and Lemma 43. ∎

Proof of Theorem 10.

Finally, we see that Theorem 10 can be obtained from Proposition 38 and Proposition 41 by induction on $(n,k)$ . ∎

References

[1] D. Dabrowski, T. Orponen, and M. Villa. Integrability of orthogonal projections, and applications to Furstenberg sets. Advances in Mathematics, 407:108567, 2022.
[2] K. J. Falconer. Hausdorff dimension and the exceptional set of projections. Mathematika, 29(1):109–115, 1982.
[3] S. Gan. Hausdorff dimension of unions of $k$ -planes. arXiv preprint arXiv:2305.14544, 2023.
[4] S. Gan. Exceptional set estimate through Brascamp-Lieb inequality. International Mathematics Research Notices, 2024(9):7944–7971, 2024.
[5] K. Héra, T. Keleti, and A. Máthé. Hausdorff dimension of unions of affine subspaces and of Furstenberg-type sets. Journal of Fractal Geometry, 6(3):263–284, 2019.
[6] R. Kaufman. On Hausdorff dimension of projections. Mathematika, 15(2):153–155, 1968.
[7] L. Li and B. Liu. Orthogonal projection, dual furstenberg problem, and discretized sum-product. arXiv preprint arXiv:2403.15784, 2024.
[8] J. M. Marstrand. Some fundamental geometrical properties of plane sets of fractional dimensions. Proceedings of the London Mathematical Society, 3(1):257–302, 1954.
[9] P. Mattila. Hausdorff dimension, orthogonal projections and intersections with planes. Annales Fennici Mathematici, 1(2):227–244, 1975.
[10] D. M. Oberlin. Restricted Radon transforms and projections of planar sets. Canadian Mathematical Bulletin, 55(4):815–820, 2012.
[11] R. Oberlin. Unions of lines in ${F}^{n}$ . Mathematika, 62(3):738–752, 2016.
[12] T. Orponen and P. Shmerkin. On the Hausdorff dimension of Furstenberg sets and orthogonal projections in the plane. Duke Mathematical Journal, 172(18):3559–3632, 2023.
[13] T. Orponen and P. Shmerkin. Projections, Furstenberg sets, and the ${ABC}$ sum-product problem. arXiv preprint arXiv:2301.10199, 2023.
[14] Y. Peres and W. Schlag. Smoothness of projections, Bernoulli convolutions, and the dimension of exceptions. Duke Mathematical Journal, 2000.
[15] K. Ren and H. Wang. Furstenberg sets estimate in the plane. arXiv preprint arXiv:2308.08819, 2023.
[16] T. Wolff. Recent work connected with the Kakeya problem. Prospects in mathematics (Princeton, NJ, 1996), 2(129-162):4, 1999.

Furstenberg set problem and exceptional set estimate in prime fields: dimension two implies higher dimensions

Abstract.

Key words and phrases:

2020 Mathematics Subject Classification:

1. Introduction

1.1. Background

1.1.1. Furstenberg set problem

1.1.2. Exceptional set estimate

1.2. The problems in prime fields

1.2.1. Furstenberg set problem

Definition 1 ((s,t;n,k)(s,t;n,k)-set).

Remark 2.

Definition 3.

Question 1.

Conjecture 4.

Remark 5.

Theorem 6 (Upper bound).

Theorem 7 (Lower bound).

1.2.2. Exceptional set estimate

Definition 8 (Exceptional set).

Theorem 9 (Lower bound).

Theorem 10 (Upper bound).

1.3. Strategy of the proof

1.4. Structure of the paper

2. Preliminary

2.1. Definition of 𝐅​(s,t;n,k)\mathbf{F}(s,t;n,k) and 𝐌​(a,s;n,k)\mathbf{M}(a,s;n,k)

Definition 11 (Furstenberg index).

Remark 12.

Proposition 13.

Proof.

Definition 14 (Marstrand index).

Remark 15.

Proposition 16.

Proof.

2.2. Useful lemmas

Lemma 17.

Proof.

Lemma 18.

Proof.

Lemma 19.

Proof.

Lemma 20.

Proof.

Lemma 21.

Proof.

Lemma 22.

Proof.

Lemma 23.

Proof.

Lemma 24.

Proof.

Lemma 25.

Proof.

Lemma 26.

Proof.

3. Furstenberg set problem: upper bound

3.1. Two special cases

3.2. Proof of Theorem 6

4. Furstenberg set problem: Lower bound I

Proposition 27.

Proof.

Proposition 28.

Proof.

Proposition 29.

Lemma 30.

Proof.

Lemma 31.

Proof.

Lemma 32.

Proof of Proposition 29 assuming Lemma 30 and Lemma 32.

Lemma 33.

Proof of Lemma 32 assuming Lemma 33.

Proof of Lemma 33.

5. Furstenberg set problem: Lower bound II

Proposition 34.

Lemma 35.

Proof.

Lemma 36.

Proof.

Lemma 37.

Definition 1 ( $(s,t;n,k)$ -set).

2.1. Definition of $\mathbf{F}(s,t;n,k)$ and $\mathbf{M}(a,s;n,k)$