Fully-heavy tetraquark states and their evidences in the LHC observations

Searching for genuine exotic hadrons beyond the conventional quark model has been one of the most important initiatives since the establishment of the nonrelativistic constituent quark model in 1964 GellMann:1964nj ; Zweig:1981pd . Benefited from great progresses in experiment, many candidates of exotic hadrons have been found since the discovery of $X(3872)$ by Belle in 2003 Choi:2003ue . Recent reviews of the status of experimental and theoretical studies can be found in Refs. Liu:2019zoy ; Esposito:2016noz ; Olsen:2017bmm ; Lebed:2016hpi ; Chen:2016qju ; Ali:2017jda ; Guo:2017jvc . While many observed candidates have been found located in the vicinity of $S$-wave open thresholds, no signals for overall-color-singlet multiquark states have been indisputably established due to difficulties of distinguishing them from hadronic molecules Guo:2017jvc . Recently, the tetraquarks of all-heavy systems, such as $cc\bar{c}\bar{c}$ and $bb\bar{b}\bar{b}$, have received considerable attention. Since the light quark degrees of freedom cannot be exchanged between two heavy mesons at leading order, the color interactions between the heavy quarks (antiquarks) should be dominant at short distance and they may favor to form genuine color-singlet tetraquark configurations rather than loosely bound hadronic molecules. Furthermore, such exotic states may have masses and decay modes significantly different from other conventional states, thus, can be established in experiment.

Early theoretical studies of the full-heavy tetraquark states can be found in the literature Ader:1981db ; Iwasaki:1975pv ; Zouzou:1986qh ; Heller:1985cb ; Lloyd:2003yc ; Barnea:2006sd . A revival of this topic driven by the experimental progresses can be found by the intensive publications recently Wang:2017jtz ; Karliner:2016zzc ; Berezhnoy:2011xn ; Bai:2016int ; Anwar:2017toa ; Esposito:2018cwh ; Chen:2016jxd ; Wu:2016vtq ; Hughes:2017xie ; Richard:2018yrm ; Debastiani:2017msn ; Wang:2018poa ; Richard:2017vry ; Vijande:2009kj ; Deng:2020iqw ; Ohlsson ; Wang:2019rdo ; Bedolla:2019zwg ; Chen:2020lgj ; Chen:2018cqz ; Liu:2019zuc . Physicists are very concerned with the stability of the tetraquark $cc\bar{c}\bar{c}$ ($T_{(4c)}$) and $bb\bar{b}\bar{b}$ ($T_{(4b)}$) states. If the $T_{(4c)}$ or $T_{(4b)}$ states have relatively smaller masses below the thresholds of heavy charmonium or bottomonium pairs Wang:2017jtz ; Karliner:2016zzc ; Berezhnoy:2011xn ; Bai:2016int ; Anwar:2017toa ; Esposito:2018cwh ; Debastiani:2017msn ; Wang:2018poa , they may become “stable” because no direct decays into heavy quarkonium pairs through quark rearrangements would be allowed. However, some studies showed that stable bound tetraquark states made of $cc\bar{c}\bar{c}$ or $bb\bar{b}\bar{b}$ may not exist Wu:2016vtq ; Lloyd:2003yc ; Ader:1981db ; Hughes:2017xie ; Richard:2018yrm ; Richard:2017vry ; Liu:2019zuc ; Deng:2020iqw ; Wang:2019rdo ; Chen:2016jxd ; Chen:2018cqz because the the predicted masses are large enough for them to decay into heavy quarkonium pairs. Due to these very controversial issues, experimental evidence for such exotic objects would be crucial for our understanding of the underlying dynamics.

In 2020, the LHCb Collaboration reported their results on the observations of $T_{(4c)}$ states LHCexp . In the di-$J/\psi$ invariant mass spectrum, a broad structure above $J/\psi J/\psi$ threshold ranging from 6.2 to 6.8 GeV and a narrower resonance $X(6900)$ were observed with more than 5 $\sigma$ of significance level. There are also some vague structures around 7.2 GeV to be confirmed. Later in 2022, $X(6900)$ was confirmed in the same final state by both the ATLAS ATLASexp and CMS CMSexp collaborations. Some signal of $X(6900)$ was also seen in the $J/\psi\psi(2S)$ channel by the ATLAS Collaboration ATLASexp . In addition, in the lower mass region the CMS measurements show that a clear resonance $X(6600)$ together with a small shoulder structure around $6.2-6.4$ GeV lies in the di-$J/\psi$ spectrum CMSexp . These clear structures may be evidences for genuine tetraquark $T_{(4c)}$ states, they can also set up experimental constraints on theoretical models of which the successful interpretations and most importantly the early predictions should bring a lot of insights to the underlying dynamics. Stimulated by the newly observed structures in the di-$J/\psi$ invariant mass spectrum, the study of full-heavy tetraquark states has been a hot topic in the last two years Dong:2022sef ; Chen:2022mcr ; Faustov:2022mvs ; Niu:2022cug ; Wang:2022yes ; An:2022qpt ; Biloshytskyi:2022dmo ; Wang:2022jmb ; Gong:2022hgd ; Wu:2022qwd ; Zhuang:2021pci ; Yan:2021glh ; Wang:2021mma ; Majarshin:2021hex ; Wang:2021kfv ; Yang:2021hrb ; Huang:2021vtb ; Goncalves:2021ytq ; Liu:2020tqy ; Wang:2020tpt ; Wan:2020fsk ; Gong:2020bmg ; Cao:2020gul ; Guo:2020pvt ; Zhu:2020xni ; Zhang:2020xtb ; Feng:2020riv ; Ma:2020kwb ; Dong:2020nwy ; Wang:2020dlo ; Karliner:2020dta ; Wang:2020wrp ; Giron:2020wpx ; Wang:2020gmd ; Chen:2020xwe ; Wang:2020ols ; Yang:2020rih ; Niu:2022vqp ; Liang:2022rew ; Liang:2021fzr ; Dong:2021lkh ; Li:2021ygk ; Ke:2021iyh ; Yang:2020wkh ; Weng:2020jao ; Zhao:2020nwy ; Zhou:2022xpd ; Kuang:2023vac ; Zhao:2020jvl ; Becchi:2020mjz ; Becchi:2020uvq ; Chen:2022sbf .

In Refs. Liu:2019zuc ; Liu:2021rtn we adopted a nonrelativistic potential quark model (NRPQM), which is based on the Hamiltonian proposed by the Cornell model Eichten:1978tg , for the study of fully-heavy tetraquark system. The masses of the $1S$-wave fully-heavy tetraquark states were predicted there and we found that the $1S$-wave $T_{(4c)}$ masses should be above the two-charmonium thresholds within a commonly accepted parameter space Liu:2019zuc . This turns out to be consistent with the structure $X(6600)$. The predicted masses of the $2S$-wave $T_{(4c)}$ states are comparable with the narrow structure $X(6900)$. Later studies by Refs. Wang:2019rdo ; Wang:2021kfv ; Lu:2020cns ; Li:2021ygk ; Zhao:2020jvl turn out to agree with our predictions.

In this work we carry out a systematic study of the fall-apart decays of the $1S$-, $2S$- and $1P$-wave $T_{(4Q)}$ states in the NRPQM framework. The $1S$-, $2S$- and $1P$-wave $T_{(4Q)}$ ($Q=c,b$) states are calculated in the same framework. Thus, it allows us to obtain a self-consistent treatment for the mass spectrum and decay properties. We will show that some of these structures observed at LHC may arise from the $S$- and $P$-wave $T_{(4c)}$ states. To proceed, we first give a brief introduction to our model and method.

Apart from the linear confinement, Coulomb type potential, and spin-spin interaction potential for calculating the $S$-wave tetraquark states in the Hamiltonian Liu:2019zuc , we include the spin-orbit and tensor potentials here to deal with the first orbital ($1P$) excitation,

$$\begin{split}V^{LS}_{ij}=&-\frac{\alpha_{ij}}{16}\frac{{\mbox{\boldmath$\lambda$\unboldmath}}_{i}\cdot{\mbox{\boldmath$\lambda$\unboldmath}}_{j}}{r_{ij}^{3}}\bigg{(}\frac{1}{m_{i}^{2}}+\frac{1}{m_{j}^{2}}+\frac{4}{m_{i}m_{j}}\bigg{)}\bigg{\{}\mathbf{L}_{ij}\cdot(\mathbf{S}_{i}+\mathbf{S}_{j})\bigg{\}}\\ &-\frac{\alpha_{ij}}{16}\frac{{\mbox{\boldmath$\lambda$\unboldmath}}_{i}\cdot{\mbox{\boldmath$\lambda$\unboldmath}}_{j}}{r_{ij}^{3}}\bigg{(}\frac{1}{m_{i}^{2}}-\frac{1}{m_{j}^{2}}\bigg{)}\bigg{\{}\mathbf{L}_{ij}\cdot(\mathbf{S}_{i}-\mathbf{S}_{j})\bigg{\}},\end{split}$$

(1)

$$V^{T}_{ij}=-\frac{\alpha_{ij}}{4}({\mbox{\boldmath$\lambda$\unboldmath}}_{i}\cdot{\mbox{\boldmath$\lambda$\unboldmath}}_{j})\frac{1}{m_{i}m_{j}r_{ij}^{3}}\Bigg{\{}\frac{3(\mathbf{S}_{i}\cdot\mathbf{r}_{ij})(\mathbf{S}_{j}\cdot\mathbf{r}_{ij})}{r_{ij}^{2}}-\mathbf{S}_{i}\cdot\mathbf{S}_{j}\Bigg{\}},$$

(2)

where $r_{ij}\equiv|\mathbf{r}_{i}-\mathbf{r}_{j}|$ is the distance between the $i$th and $j$th quarks, $\mathbf{S}_{i}$ stands for the spin of the $i$-th quark, and $\mathbf{L}_{ij}$ stands for the relative orbital angular momentum between the $i$-th and $j$-th quark. If the interaction occurs between two quarks or antiquarks, operator $\mbox{\boldmath$\lambda$\unboldmath}_{i}\cdot\mbox{\boldmath$\lambda$\unboldmath}_{j}$ is defined as $\mbox{\boldmath$\lambda$\unboldmath}_{i}\cdot\mbox{\boldmath$\lambda$\unboldmath}_{j}\equiv\sum_{a=1}^{8}\lambda_{i}^{a}\lambda_{j}^{a}$, while if the interaction occurs between a quark and antiquark, we have $\mbox{\boldmath$\lambda$\unboldmath}_{i}\cdot\mbox{\boldmath$\lambda$\unboldmath}_{j}\equiv\sum_{a=1}^{8}-\lambda_{i}^{a}\lambda_{j}^{a*}$, where $\lambda^{a*}$ is the complex conjugate of the Gell-Mann matrix $\lambda^{a}$. The parameters $b_{ij}$ and $\alpha_{ij}$ denote the confinement potential strength and the strong coupling for the OGE potential, respectively. The same model parameters, $m_{c}/m_{b}=1.483/4.852$ GeV, ${\alpha_{cc}}/{\alpha_{bb}}=0.5461/0.4311$, ${\sigma_{cc}}/{\sigma_{bb}}=1.1384/2.3200$ GeV, and $b_{cc/bb}=0.1425$ GeV², are adopted by fitting the $c\bar{c}$ and $b\bar{b}$ spectra as in Refs. Deng:2016stx ; Liu:2019zuc .

For $T_{(4Q)}$, there are two kinds of color structures, $(6\bar{6})_{c}$ and $(3\bar{3})_{c}$. As shown in Fig. 1, the relative Jacobi coordinate between these two charm quarks (two anticharm quarks) is defined by $\mbox{\boldmath$\xi$\unboldmath}_{1}=(\textbf{r}_{1}-\textbf{r}_{2})/\sqrt{2}$ ($\mbox{\boldmath$\xi$\unboldmath}_{2}=(\textbf{r}_{3}-\textbf{r}_{4})/\sqrt{2}$), while the relative Jacobi coordinate between $Q_{1}Q_{2}$ and $\bar{Q}_{3}\bar{Q}_{4}$ is defined by $\mbox{\boldmath$\xi$\unboldmath}_{3}=(\textbf{r}_{1}+\textbf{r}_{2})/2-(\textbf{r}_{3}+\textbf{r}_{4})/2$. Thus, there are three spatial excitation modes which are denoted as $\xi_{1}$, $\xi_{2}$, and $\xi_{3}$. Their wave functions are defined as $\phi(\xi_{i})$ ($i=1,2,3$). According to the requirements of symmetry, there will be four $1S$ configurations, 12 $2S$ configurations, and 20 $1P$ configurations in the $L-S$ coupling scheme, which are listed in Table 1. Apart from the conventional quantum numbers, i.e., $J^{PC}=0^{-+},\ 1^{--},\ 2^{-\pm},\ 3^{--}$, the $P$-wave states can access exotic quantum numbers, i.e., $J^{PC}=0^{--},\ 1^{-+}$.

To solve the Schrödinger equation, we expand the radial part $R_{n_{\xi_{i}}l_{\xi_{i}}}(\mathbf{\xi_{i}})$ of spatial wave function $\phi(\xi_{i})$ with a series of harmonic oscillator functions Liu:2019vtx :

$$R_{n_{\xi_{i}}l_{\xi_{i}}}(\xi_{i})=\sum_{\ell=1}^{n}\mathcal{C}_{\xi_{i}\ell}~{}\phi_{n_{\xi_{i}}l_{\xi_{i}}}(d_{\xi_{i}\ell},\xi_{i}),$$

(3)

with

$\displaystyle\phi_{n_{\xi_{i}}l_{\xi_{i}}}(d_{\xi_{i}\ell},\mbox{\boldmath$\xi$\unboldmath}_{i})$

$\displaystyle=\left(\frac{1}{d_{\xi_{i}\ell}}\right)^{\frac{3}{2}}\Bigg{[}\frac{2^{l_{\xi_{i}}+2}}{(2l_{\xi_{i}}+1)!!\sqrt{\pi}}\Bigg{]}^{\frac{1}{2}}\left(\frac{\xi_{i}}{d_{\xi_{i}\ell}}\right)^{l_{\xi_{i}}}e^{-\frac{1}{2}\left(\frac{\xi_{i}}{d_{\xi_{i}\ell}}\right)^{2}}.$

(4)

The parameter $d_{\xi\ell}$ can be related to the harmonic oscillator frequency $\omega_{\xi\ell}$ with $1/d^{2}_{\xi\ell}=M_{\xi}\omega_{\xi\ell}$. For $T_{(4Q)}$ the reduced masses $M_{\xi_{i}}=m_{Q}$. On the other hand, the harmonic oscillator frequency $\omega_{\xi_{i}\ell}$ can be related to the harmonic oscillator stiffness factor $K_{\ell}$ with $\omega_{\xi_{i}\ell}=\sqrt{3K_{\ell}/M_{\xi_{i}}}$. Then, one has $d_{\xi_{i}\ell}=d_{\ell}=(3m_{Q}K_{\ell})^{-1/4}$. The oscillator length $d_{\ell}$ is set to be

$$d_{\ell}=d_{1}a^{\ell-1}\ \ \ (\ell=1,...,n),$$

(5)

where $n$ is the number of harmonic oscillator functions, and $a$ is the ratio coefficient. There are three parameters $\{d_{1},d_{n},n\}$ to be determined through the variation method. It is found that with the parameter sets {0.068 fm, 2.711 fm, 15} and {0.050 fm, 2.016 fm, 15} for the $cc\bar{c}\bar{c}$ and $bb\bar{b}\bar{b}$ systems, we can obtain stable solutions.

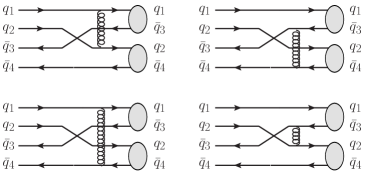
By using the spectrum obtained from NRPQM, we further evaluate the fall-apart decays of the $T_{(4Q)}$ states in a quark-exchange model Barnes:2000hu . The interactions $V_{ij}$ between inner quarks of final hadrons $B$ and $C$ may be the sources of the fall-apart decays of a $T_{(4Q)}$ state via the quark rearrangement. The decay amplitude $\mathcal{M}(A\to BC)$ of $T_{(4Q)}$ state is described by:

$$\mathcal{M}(A\to BC)=-\sqrt{(2\pi)^{3}}\sqrt{8M_{A}E_{B}E_{C}}\left\langle BC|\underset{i<j}{\sum}V_{ij}|A\right\rangle,$$

(6)

where $A$ stands for the initial tetraquark state, $BC$ stands for the final hadron pair. $M_{A}$ is the mass of the initial state, and $E_{B}$ and $E_{C}$ are the energies of the final states $B$ and $C$, respectively. The decay width $\Gamma$ of $A\to BC$ can be described by:

$\displaystyle\Gamma$

$\displaystyle=$

$\displaystyle\frac{1}{2J_{A}+1}\frac{|\boldsymbol{p}|}{8\pi M_{A}^{2}}\left|\mathcal{M}(A\to BC)\right|^{2},$

(7)

where $|\boldsymbol{p}|$ is magnitude of the momentum for the final states $B$ and $C$. The potentials $V_{ij}$ ($ij\neq 13,24$ or $ij\neq 14,23$) between inner quarks of final hadrons $B$ and $C$, as shown in Fig. 3, are taken the same as our mass calculations. The calculation of the decay amplitude for a $T_{(4Q)}$ state is indeed a tedious task, some details are given in the appendix. This model has been developed and applied to the study of the hidden-charm decay properties for the multiquark states in the literature Wang:2019spc ; Xiao:2019spy ; Wang:2020prk ; Han:2022fup ; Liu:2022hbk , and a lot of inspiring results are obtained. For simplicity, the wave functions of the $A,B,C$ hadron states are parametrized out in a single harmonic oscillator form by fitting the wave functions calculated from our potential model Liu:2019vtx ; Liu:2020lpw ; Liu:2021rtn . The harmonic oscillator parameters for the final meson states and initial tetraquark states are collected in Tables 4 and  5 of the appendix, respectively.