From “Thumbs Up” to “10 out of 10”: Reconsidering Scalar Feedback in Interactive Reinforcement Learning
Abstract
Learning from human feedback is an effective way to improve robotic learning in exploration-heavy tasks. Compared to the wide application of binary human feedback, scalar human feedback has been used less because it is believed to be noisy and unstable. In this paper, we compare scalar and binary feedback, and demonstrate that scalar feedback benefits learning when properly handled. We collected binary or scalar feedback respectively from two groups of crowdworkers on a robot task. We found that when considering how consistently a participant labeled the same data, scalar feedback led to less consistency than binary feedback; however, the difference vanishes if small mismatches are allowed. Additionally, scalar and binary feedback show no significant differences in their correlations with key Reinforcement Learning targets. We then introduce Stabilizing TEacher Assessment DYnamics (STEADY) to improve learning from scalar feedback. Based on the idea that scalar feedback is muti-distributional, STEADY re-constructs underlying positive and negative feedback distributions and re-scales scalar feedback based on feedback statistics. We show that models trained with scalar feedback + STEADY outperform baselines, including binary feedback and raw scalar feedback, in a robot reaching task with non-expert human feedback. Our results show that both binary feedback and scalar feedback are dynamic, and scalar feedback is a promising signal for use in interactive Reinforcement Learning.
I Introduction
Interactive Reinforcement Learning is a method that reduces data needs and improves learning efficiency by having a human-in-the-loop providing evaluative feedback to an agent during learning. Evaluative feedback is natural for non-experts to provide, and can take the form of either binary feedback, in which feedback can only be either “good” or “bad”, or scalar feedback, which takes a value from a scale of values (e.g., “1-10”, “A-F”, or “0-5 stars”). In theory, both of these types of feedback can contain useful information. However, only binary feedback has been widely used in prior work since it is easy to separate into positive and negative, and limiting people to only two options can reduce noise.
Despite these advantages, allowing only binary feedback reduces information in the signal such as the intensity of preferences. Scalar feedback, on the other hand, is also naturally used in daily life (e.g., movie rating and product evaluation) but encodes information beyond that in binary feedback, such as ranking and magnitude, through a wider range of possible values. However, scalar feedback is more difficult to apply to RL; it is likely to have minor differences while evaluating the same data and is more difficult to separate into good and bad. Furthermore, users are unlikely to scale their feedback such that it can be interpreted directly as a reward. For example, on a scale of 10, the distance from 5 to 7 may be perceived as different from the distance from 3 to 5 although they are numerically the same. These difficulties have led to prior work categorizing scalar feedback as non-optimal [1, 2] and have led researchers to underestimate the potential of scalar feedback in interactive RL.

In this work, we conduct a study of scalar and binary feedback with 90 online participants evaluating a robot performing a manipulation task, and show that scalar feedback has the potential to improve learning when properly handled. We show that human teachers can be inconsistent when giving both scalar and binary feedback even in a task (reaching to and pressing a button) that is among the most easy-to-understand tasks a robot might do. We study the correlation of scalar and binary feedback with interactive RL training targets, and fail to find a significant difference between scalar and binary feedback, although we find that scalar feedback has more variation. Given that these results suggest that scalar feedback is not necessarily worse for learning if we can address the scaling problem [3] and noise, we present Stabilizing TEacher Assessment DYnamics (STEADY), an unsupervised feedback filter. The key insight of STEADY is to use a multi-distributional model for scalar feedback, re-normalizing noisy scalar feedback to confidence scores (i.e. more precise magnitudes) and recovering positive/negative labels. This enables binary-feedback-based learning algorithms to learn effectively from information-rich scalar feedback and results in a significant improvement over binary feedback. We demonstrate that models trained with scalar feedback + STEADY outperform models trained with binary feedback on a robot learning task.

To the best of our knowledge, this is the first work that quantifies feedback dynamics in binary feedback and scalar feedback, indicating that feedback dynamics within individuals and between participants should be taken into consideration while using both binary feedback and scalar feedback. STEADY is the first algorithm that enables binary-feedback-based algorithms to learn from scalar rewards even when those rewards do not have a clear division into positive and negative. This work bridges the research of learning from binary feedback and scalar feedback, and demonstrates the potential of scalar feedback as a teaching signal.
II Background
Interactive information in various forms from humans is widely used in prior work: as reward or feedback to shape learned policies [4, 5, 6, 7, 8]; as signals, such as state visiting counts, prediction errors, and actions-states, to perform inverse reinforcement learning [9, 10, 11, 12]; as demonstrations to enable imitation learning or behavior cloning [13, 14]; and as preferences, which indicate preferable actions or trajectories [15, 3]. Three representative methods are Policy Shaping [7, 8], TAMER [4, 5], and COACH [16]. In policy shaping, people give binary feedback on a robot’s behaviors to indicate whether it is correct and thus shape the policies learned from environmental rewards. In TAMER, a human’s feedback is used as a reward signal to train a policy. COACH also uses human feedback as a reward signal, but instead of direct rewards, COACH replaces advantaged rewards with human feedback, arguing that scalar feedback better matches the advantage function than the reward function. Although TAMER and COACH theoretically can use scalar feedback, they have primarily been evaluated with binary feedback or trinary feedback (e.g. -1, +1, +4 in [16]). According to [17], the accuracy of human feedback can significantly impact learning efficiency with algorithms that expect binary feedback. Throughout the body of prior work, there is a strong focus on using binary feedback to improve learning, with limited exploration of scalar feedback. Our work provides the research community with a more explicit understanding of the differences between scalar and binary feedback and proposes a method that enables existing binary-feedback interactive RL algorithms to use scalar feedback.
Another area of related work characterizes the dynamics of how humans provide feedback to learning agents, both robots and other humans. For example, human reward signals correspond with both past actions and future rewards [18], the contingency of robot feedback has an impact on participants’ tutoring behaviors [19], and temporal details are critical information for researchers to comprehend human expectations of joint attention [20]. From the view of robots, research has shown that robots’ action style [21] or deceptive feedback [22] can affect participants. Education research has also shown that teacher feedback is not only related to the objective truth but also affected by human personalities, emotions, and characteristics, many of which may change over time and manifested through values (e.g. [23] and [24]).
Moreover, teaching a robot not only concerns teaching behaviors, but also learning (since human teachers can learn to teach better), which has been shown to involve emotions that change over time [25]. Furthermore, users learn to how to teach the robot during the interaction process [26], which may change their feedback as they become more familiar with the system. Thus, feedback is not a static value, even in what appears to the learning agent as the same state. Instead, feedback varies with individuals’ emotions, personalities, and expectations about the future as well as the type and contingency of robots’ behavior. Our work contributes to this literature with a direct comparison of feedback dynamics for binary and scalar feedback in a realistic robot reaching task and guidelines for using scalar feedback.
III Methodology
We conducted an online user study to investigate binary and scalar feedback consistency over time and between users (Figure 2). Two groups of participants were asked to evaluate the robot’s performance while the robot was completing a button-pressing task. The robot performed six trajectories twice, allowing us to detect changes in feedback by comparing the difference in feedback between the two sessions. All users saw the same trajectories, allowing us to detect variation in feedback between users on the same task with the same feedback type. We showed how feedback correlates to the training targets of different algorithms. These results, and the data collected, motivate and enable the development and evaluation of our STEADY algorithm.
III-A Robot Task
Participants evaluated the robot’s performance on a button-pressing task. The robot is a humanoid robot with a 7-degree-of-freedom Kinova Jaco arm with a Robotiq gripper. A RealSense camera on the robot’s head is used to identify the button’s location and return the button’s depth. In the task, the robot’s goal is to navigate to the button’s location and press the green button. The robot’s observation is the current position of the gripper and the position of the button. The robot’s actions are going in one direction (left, right, backward, forward, or down). The move distance for each action is not deterministic (about 4 to 5 centimeters) due to noise in the manipulation pipeline of the robot.
We used a relatively simple task to reduce the cognitive load on solving the task and thus reduce feedback dynamics from confusion over the task. While this is not a highly-complex task from the perspective of the robot learning literature, we used a relatively high-resolution representation (700 states, 3500 state-action pairs) and allowed the robot to have movement noise. It is comparable to tasks used in interactive RL with real robots [16, 27, 28, 29], where training time needs to be limited, and is easily understandable by non-expert users.
III-B Experimental Setup
During the study, participants were asked to watch the robot performing the task and to give evaluative feedback, either by clicking a button that said good or bad or by selecting a number between zero and ten. We did not use a range for scalar feedback that contains negative values since scales with no negative values are frequently used in daily life and including negative values naturally biases users toward separating scalar feedback into positive and negative, which would unfairly benefit scalar feedback in this experiment. We generated the videos by recording the robot’s behaviors in performing the task. The robot’s behavior was sampled from a partially-trained Q-Learning model. The model is trained by objective rewards. The robot received 0.4 to 0.5 rewards (based on distance) if it moved toward the button, -0.4 to -0.5 rewards if it moved away from the button, +10 if the robot successfully pressed the button, and -1 reward if it went down at the wrong location. Videos were divided into clips. There were 200 video clips in total, each 3 seconds long (about 10 minutes total) with the first 100 and second 100 clips identical to each other; each clip represented one action performed by the robot; clips are in sequential order of a trajectory; each 100 clips consisted of six trajectories (three successes, three failures). No indication was given to participants that the two 100-clip “sessions” were the same. To validate that participants would not notice the duplications, we conducted a pilot study by recruiting three robot experts from a robotic lab. We asked if they were aware that all clips were repeated once. All of them answered no.
III-C Online Participant Recruitment
The study was approved by the university review board and conducted online through Amazon Mechanical Turk (AMT). In order to reflect the feedback abilities of non-expert crowdworkers, we did not set worker requirements to only collect data from top workers with AMT Masters Qualification or workers with backgrounds. However, we did use filters to filter out click bots (HIT Approval Rate 95% and Number of HITs Approved 50). A total of 90 AMT crowdworkers were recruited, divided evenly between two groups (45 participants per group). One group of workers was asked to give binary feedback and the other group of workers was asked to give scalar feedback. All workers received the same compensation and viewed the same content.
III-D Experimental Procedure
Participants were redirected to the experiment website from the Amazon Mechanical Turk (AMT) website after they clicked the accept & work button, where they viewed a welcome page and filled out a consent form to ensure that they were qualified for our study. After completing the consent documents, participants were shown how the robot performs the task by watching a short video and reading a short instruction to ensure that they had a consistent understanding of the task goals. The demonstration video shows a human performing the task instead of a robot arm to avoid biasing their feedback to the robot. After the demonstration video, the participant started the study. They watched 200 video clips about the robot performing the button-pressing task. After watching one video clip, the participants gave feedback by clicking the button with the corresponding value, which caused the page to jump to the next clip. The webpage displayed the thank you page once all clips had been evaluated and provided them a validation code, ending the study. The validation code is used to redeem their compensations via the AMT platform.
III-E Hypotheses
H1. Human binary feedback changes less in the second session than scalar feedback From prior work, we expect that binary feedback is noise-reduced and scalar feedback tends to be unstable, but none of the prior work has closely examined it. To test this, we compare feedback between the first and second sessions with regards to self-agreement, feedback patterns, and bias in values.
H2. Human feedback patterns tend to be different. We expect that human feedback patterns, especially scalar feedback patterns, are statistically significantly different from each other between users. The uniqueness of the feedback pattern explains why learning from multiple people is a common issue in Interactive RL.


H3. Scalar feedback is less well correlated with a fully trained policy than binary feedback. A significant concern with scalar feedback is that its noisiness and inconsistency decrease its usefulness for reinforcement learning.
IV User Study Results
We show the overview of all feedback we collected during the human study in Figure 3. Participants have diverse feedback patterns, but there are observable agreements in two sessions, and consistency between participants within the same group. We investigate both the consistent and diverse aspects of feedback in this section. According to the average time per assignment provided by AMT, total study times on average were 29:22 minutes in the binary and 29:56 minutes in the scalar feedback condition. The study websites and the instructions are near-identical. This suggests that asking participants to give scalar feedback did not substantially increase the participant’s effort, likely because scalar feedback is common in daily life.
Using Shapiro-Wilk tests, we determined that the results do not from a normal distribution. Therefore, we applied Kruskal-Wallis H Tests and Wilcoxon Rank-Sum Tests to our results to test our hypotheses. For the scenarios that we performed Wilcoxon Rank-Sum Test multiple times, we used Holm-Sidak method to correct the p-values.
IV-A Analysis of H1: Did participants give consistent feedback in the two sessions?
Self-agreement on values.
To answer the question of whether participants are self-consistent, we calculated the agreement of their first and second feedback sessions (Figure 4). Each point in Figure 4 represents the percentage of self-agreed feedback for one participant. Two scalar feedback values are considered to agree with each other if the difference between them is less than a threshold. Using Kruskal-Wallis H Test, we found a significant difference in results . The average self-agreed feedback percentage rates over 45 participants are 76.3% for binary feedback, 25.2% for scalar feedback with a threshold of 0, 58.2% with a threshold of 1, and 77.7% with a threshold of 2. If exact matches are required, binary feedback is significantly more self-consistent than scalar feedback ( for threshold and ), which supports H1. However, when we increase the threshold of agreement, the self-consistency of scalar feedback improves, and by a threshold of the difference with binary feedback vanishes ().
Feedback pattern changed in the second session
By comparing the averages in the two sessions, we found that most participants (74 out of 90) had a bias in their feedback in the second session as compared to the first. We defined bias as a difference in the averages of the two sessions greater than 0.5 for scalar feedback or 0.05 for binary feedback (i.e. their average feedback changed by more than about 10%). More than half of the participants (23 binary, 25 scalar) were positively biased, while only 16 participants were non-biased (12 binary, 4 scalar). This might be because the task is relatively simple and participants expected the robot to perform well on the task. To study whether participants had significantly changed feedback-giving patterns during the interaction, we performed a Wilcoxon Rank-Sum test over each participant’s first 100 feedback and second 100 feedback, and corrected p-values by using the Holm-Sidak method. After correction, 15 out of 45 participants that gave binary feedback and 27 out of 45 participants that gave scalar feedback gave significantly different feedback () in the two sessions. This supports H1, and also suggests that scalar feedback is more sensitive to changes in feedback.

IV-B Analysis of H2: Were participants’ feedback consistent with each other?
Participants rarely agreed with each other exactly
Figure 5(a) shows the average feedback values of each participant, which cover a large range. Some participants preferred high-value feedback, while the majority gave balanced-value feedback, which is consistent with the conclusion in prior work [30]. Using Kruskal-Wallis H test, we compared individual feedback within the group that gives the same type of feedback. We found a significant difference () within the group where participants were asked to give binary feedback, and a significant difference () within the group where participants were asked to give scalar feedback. To investigate the uniqueness of participants’ feedback patterns, we performed a Wilcoxon Rank-Sum test for each participant and paired them with other participants within their groups (i.e. for each participant, we performed a Wilcoxon Rank-Sum test 44 times) and corrected the p-values with a step-down method using Holm-Sidak adjustments. The results of the Wilcoxon Rank-Sum tests are shown in Figure 5(b). For participants that gave binary feedback, their feedback patterns on average had a significant difference with 25.58 participants (58.1%). For participants that gave scalar feedback, their feedback patterns on average had a significant difference with 37.13 participants (84.4%). That is, even correcting for the large number of tests, participants’ feedback patterns were drawn from different distributions for most pairs of participants, supporting H2.
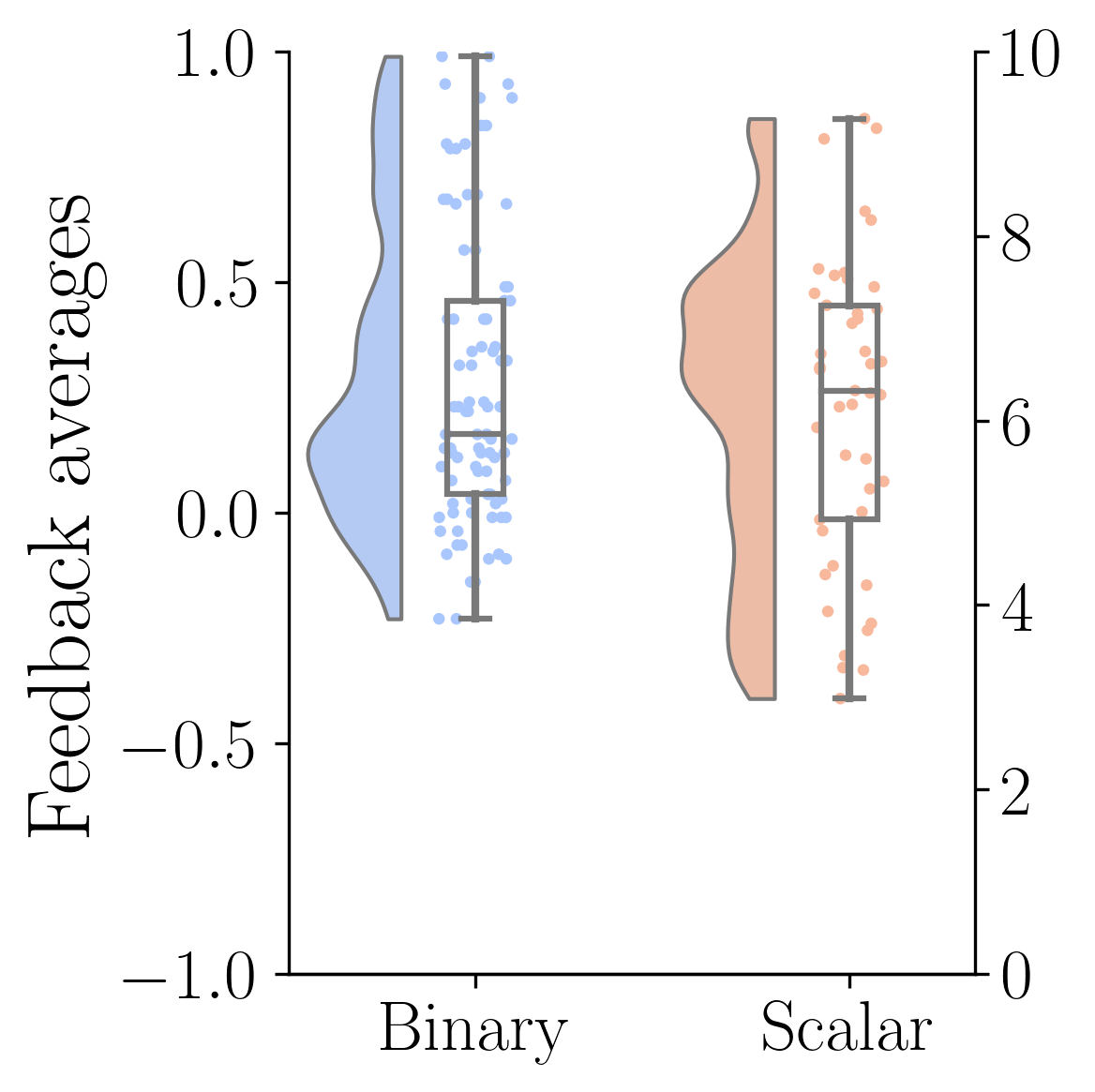


IV-C Analysis of H3: How do scalar and binary feedback correlate with the learning algorithm’s learning targets?
To improve learning, Interactive RL uses human feedback to estimate internal elements of RL algorithms [1]; different Interactive RL algorithms correspond feedback with a different part of the learning problem. We calculated the Spearman’s Rank correlation between the feedback values and the training targets used in several key Interactive RL algorithms: advantaged rewards (COACH [16]), normalized Q-values (TAMER [4], and action rankings (Policy Shaping [8]), using a standard MDP formulation with states , actions , and value functions and . The advantaged rewards were computed by using the advantage function: . The normalized Q-values were computed based on the equation: . The action ranking assigned the rank to each action based on the magnitude of . The results are shown in Figure 6. Using Wilcoxon Rank-Sum test, no significance has been found in these results (feedback-normalized Q-Values , feedback-action ranking , and feedback-advantage rewards ), so H3 is not supported.
V Stabilizing Teacher Assessment Dynamics
The user study results suggest that scalar feedback is as good as binary feedback, but noise needs to be mitigated. In previous work using scalar feedback, scalar feedback is limited to a small range (e.g., COACH [16] is evaluated with scalar feedback with a range of ), and must contain a negative range [4, 31, 7] to prevent algorithms from performing poorly. To address these issues and to confirm that scalar feedback has advantages for learning, we present Stabilizing TEacher Assessment DYnamics (STEADY) to reduce the noise in scalar feedback and extend the use of scalar feedback by enabling binary-feedback-based methods to learn from scalar feedback.

V-A STEADY
Our key intuitions are: First, human evaluations often involve associating certain qualities with certain ranges. These are subject to variation, and each range can be viewed as one distribution. Second, since some robot behaviors are more preferred than others, feedback distributions can be separated into at least two classes, preferable (positive) and non-preferable (negative). Based on the key intuitions, STEADY re-constructs feedback distributions, labels scalar feedback with binary labels, and remaps the magnitude of the feedback in a more algorithmically useful way based on feedback statistics.
Initialization In an online learning setting, the robot needs to learn from human feedback in real time and update its policy. The feedback distributions thus also need to be updated after new feedback is added. Since there is no pre-labeled scalar feedback, we use a heuristic method to initialize the distributions. For the first feedback, a midpoint method is used, which classifies the feedback above the average value as positive and otherwise negative. In this work, we set .
Distribution distance The distance used is Wasserstein distance [32, 33]. The Wasserstein distance between the positive distributions and the negative distribution is:
| (1) |
where is the set of (probability) distributions on whose marginals are and .

Confidence Degree We use an inferred magnitude, which we refer to as the confidence degree to describe the intensity of feedback. The confidence degree can be used to improve learning by directly replacing raw scalar feedback with confidence degree binary label. The confidence degree of feedback is the degree to which deviates from the center of its classified distribution, in the direction away from or towards the other distribution. Thus, there are two different cases for the confidence degree, which are visualized in Figure 7. For feedback and its classified distribution , the confidence degree of increase weight cases is given by:
| (2) |
In decrease weight cases, the confidence degree is given by:
| (3) |
where is the mean of the distribution and is the non-classified distribution.
Overlap Reduction To differentiate the positive and negative distributions, we introduce a compensation mechanism. If feedback is in three-sigma areas of both distributions, STEADY pops the minimal feedback of the positive distribution and adds it into the negative distribution and vice versa unless is minimal/maximal feedback. This reduces the overlap area and differentiates the two distributions by moving outliers between the two distributions.
STEADY Algorithm 1 describes the overview of STEADY. After initialization, STEADY updates the distributions by adding new feedback to the distribution that maximizes the . We introduce an overlap reduction mechanism to differentiate the distributions, and provide improved magnitudes (effectively a measure of confidence in the label) from the constructed distributions.
Multiple Distribution Extension We use STEADY in a two-distributional case, but STEADY can be easily extended to -distributional scenarios by selecting -th percentiles instead of maximum and minimum and maximizing the distance described in Equation 4 instead of Equation 1. The distance among distributions is:
| (4) |
where is adjacent to , and is adjacent to .
V-B Scalar Feedback with STEADY
We validated that STEADY enables learning from scalar feedback by training the robot to perform the button-pressing task using collected human feedback. We use TAMER[4] as our learning algorithm. Human feedback is used as reward signal. Since the robot did not take any environmental rewards as input and had been initialized to be the same, the only factor that impacts learning is human feedback.
V-B1 Baselines
We have four baselines to compare the performance with scalar feedback + STEADY: Binary feedback; Raw scalar feedback; Scalar feedback with a midpoint classifier; Scalar feedback with a sliding window classifier. Additionally, we included the environmental reward (the same used to train the oracle) to show the ceiling performance. Raw scalar feedback was pre-processed by subtracting the midpoint value of the range (i.e. five) since TAMER performs poorly with scalar feedback without a negative range. The Midpoint Classifier converts scalar feedback to binary by converting a scalar feedback value greater than five to positive and less or equal to five to negative. Using the sliding window method, feedback higher than the mean of received feedback within a window is treated as positive feedback, while feedback less or equal to the mean is treated as negative feedback. We used a window size of 20, which was empirically derived from a series of experiments with window sizes from 1 to 200.
V-B2 Trained Models
For each baseline, we trained 45 models. Each model is a TAMER agent trained by one participant’s feedback. Thus, there are models in total. We initialized the models to the same state (completely untrained). Each transition (state-action-feedback tuple) is only learned once for each model and fed to the models in the same order. After finishing training, we applied the trained models to the robot and performed the button-pressing task. For each model, we ran it 10 times on the robot to evaluate real-world performance while reducing the random noise in the results.
V-B3 Model Performance
We use returned environmental rewards to measure the performance of the models. The maximum return reward can be 14, and the minimum can be -50; because the models were tested on the real robot, randomness in the results comes from noise in robot movement. The performance is shown in Figure 8. The Kruskal-Wallis H test shows that the choice of the baselines has a significant impact on the trained agents’ performance (). Post-hoc analysis with the Wilcoxon Rank-Sum test shows that the models trained with STEADY have a higher average return rewards than the models trained with the binary feedback (), a higher average return rewards than the models trained with the raw scalar feedback (), higher than the models trained with midpoint classifier (), and higher than the models trained with sliding window (). STEADY enables learning from scalar feedback and models with STEADY have a higher average return reward than all baselines using human feedback including binary feedback.
VI Discussion & Conclusion
The results above demonstrate that scalar feedback is not inherently worse than binary feedback as a teaching signal even without stabilization. Scalar feedback does change more than binary feedback, but tolerating small variations removes the effect. Furthermore, the average time per assignment provided by AMT suggests that for crowdworkers, giving scalar feedback does not put an extra time burden on participants. Our results show that human feedback patterns in both scalar and binary feedback, but especially scalar feedback patterns, tend to be different in statistically distinguishable ways. This explains why learning from multiple participants is likely to be difficult and suggests that learning agents may be able to differentiate between teachers based on their individual feedback patterns. In addition, our results show that scalar feedback with stabilization can be leveraged to improve learning. That is, scalar feedback with STEADY achieves significantly better performance than binary feedback and other baseline methods. This conclusion should be able to extend to more complex tasks and other algorithms that have been shown to work with binary feedback since STEADY does not require changing any part of the learning algorithms and only filters human feedback.
One limitation of our work is that the experiments were relatively short-term and only repeated each clip once. We are aware that human teachers were learning and adapting during teaching in the short term, but we did not address long-term feedback dynamics. Repeating the robot behaviors only once was necessary to prevent participants from becoming aware that clips were repeating, but this limits our ability to understand the full range of possible changes in feedback dynamics. Future work could investigate longer-term changes in feedback and new methods for stabilizing dynamics over long periods of time.
Overall, our work suggests that HRI and interactive RL practitioners should give scalar feedback more attention, including developing new learning algorithms to utilize the additional information, finding new methods to collect more accurate scalar feedback, and considering using scalar feedback and binary feedback together. STEADY provides a bridge between algorithms that are designed and validated with binary feedback and the next generation of algorithms that can appropriately leverage scalar feedback. Future studies can build on these results and more fully leverage the scalar information that is available from human teachers.
References
- [1] C. Arzate Cruz and T. Igarashi, “A survey on interactive reinforcement learning: design principles and open challenges,” in Proc. of the 2020 ACM designing interactive Sys. Conf., 2020, pp. 1195–1209.
- [2] J. Leike, D. Krueger, T. Everitt, M. Martic, V. Maini, and S. Legg, “Scalable agent alignment via reward modeling: a research direction,” 2018. [Online]. Available: https://arxiv.org/abs/1811.07871
- [3] B. Ibarz, J. Leike, T. Pohlen, G. Irving, S. Legg, and D. Amodei, “Reward learning from human preferences and demonstrations in atari,” in Adv. in neural information processing Sys., 2018, pp. 8011–8023.
- [4] W. B. Knox and P. Stone, “Tamer: Training an agent manually via evaluative reinforcement,” in 2008 7th IEEE Intl. Conf. on Development and Learning. IEEE, 2008, pp. 292–297.
- [5] ——, “Interactively shaping agents via human reinforcement: The TAMER framework,” in Proceedings of the fifth Intl. Conf. on Knowledge capture, 2009, pp. 9–16.
- [6] A. L. Thomaz, G. Hoffman, and C. Breazeal, “Real-time interactive reinforcement learning for robots,” in AAAI 2005 workshop on human comprehensible machine learning, 2005.
- [7] T. Cederborg, I. Grover, C. L. Isbell, and A. L. Thomaz, “Policy shaping with human teachers,” in Twenty-Fourth Intl. Joint Conf. on Artificial Intelligence, 2015.
- [8] S. Griffith, K. Subramanian, J. Scholz, C. L. Isbell, and A. L. Thomaz, “Policy shaping: Integrating human feedback with reinforcement learning,” in Adv. in neural information processing Sys., 2013, pp. 2625–2633.
- [9] K. Gregor, D. J. Rezende, and D. Wierstra, “Variational intrinsic control,” arXiv preprint arXiv:1611.07507, 2016.
- [10] D. Pathak, P. Agrawal, A. A. Efros, and T. Darrell, “Curiosity-driven exploration by self-supervised prediction,” in Intl. Conf. on Machine Learning. PMLR, 2017, pp. 2778–2787.
- [11] M. G. Bellemare, S. Srinivasan, G. Ostrovski, T. Schaul, D. Saxton, and R. Munos, “Unifying count-based exploration and intrinsic motivation,” arXiv preprint arXiv:1606.01868, 2016.
- [12] R. Wang, S. S. Du, L. F. Yang, and R. Salakhutdinov, “On reward-free reinforcement learning with linear function approximation,” arXiv preprint arXiv:2006.11274, 2020.
- [13] T. Hester, M. Vecerik, O. Pietquin, M. Lanctot, T. Schaul, B. Piot, D. Horgan, J. Quan, A. Sendonaris, G. Dulac-Arnold et al., “Deep q-learning from demonstrations,” arXiv preprint arXiv:1704.03732, 2017.
- [14] J. Ho and S. Ermon, “Generative adversarial imitation learning,” arXiv preprint arXiv:1606.03476, 2016.
- [15] P. F. Christiano, J. Leike, T. Brown, M. Martic, S. Legg, and D. Amodei, “Deep reinforcement learning from human preferences,” in Adv. in Neural Information Processing Sys., 2017, pp. 4299–4307.
- [16] J. MacGlashan, M. K. Ho, R. Loftin, B. Peng, G. Wang, D. L. Roberts, M. E. Taylor, and M. L. Littman, “Interactive learning from policy-dependent human feedback,” in Proc. of the 34th Intl. Conf. on Machine Learning, ser. Proc. of Machine Learning Research, D. Precup and Y. W. Teh, Eds., vol. 70. PMLR, 06–11 Aug 2017, pp. 2285–2294.
- [17] T. A. K. Faulkner, E. S. Short, and A. L. Thomaz, “Interactive reinforcement learning with inaccurate feedback,” in 2020 IEEE Intl. Conf. on Robotics and Automation (ICRA). IEEE, 2020, pp. 7498–7504.
- [18] A. L. Thomaz, C. Breazeal et al., “Reinforcement learning with human teachers: Evidence of feedback and guidance with implications for learning performance,” in Aaai, vol. 6. Boston, MA, 2006, pp. 1000–1005.
- [19] K. Fischer, K. Lohan, J. Saunders, C. Nehaniv, B. Wrede, and K. Rohlfing, “The impact of the contingency of robot feedback on HRI,” in 2013 Intl. Conf. on Collaboration Technologies and Sys. (CTS). IEEE, 2013, pp. 210–217.
- [20] C. Yu, M. Scheutz, and P. Schermerhorn, “Investigating multimodal real-time patterns of joint attention in an hri word learning task,” in 2010 5th ACM/IEEE Intl. Conf. on Human-Robot Interaction (HRI). IEEE, 2010, pp. 309–316.
- [21] S. Zafari, I. Schwaninger, M. Hirschmanner, C. Schmidbauer, A. Weiss, and S. T. Koeszegi, ““You Are Doing so Great!”–The Effect of a Robot’s Interaction Style on Self-Efficacy in HRI,” in 2019 28th IEEE Intl. Conf. on Robot and Human Interactive Communication (RO-MAN). IEEE, 2019, pp. 1–7.
- [22] J. Shim and R. C. Arkin, “Other-oriented Robot Deception: How can a robot’s deceptive feedback help humans in HRI?” in Intl. Conf. on Social Robotics. Springer, 2016, pp. 222–232.
- [23] A. C. Butler, J. D. Karpicke, and H. L. Roediger III, “The effect of type and timing of feedback on learning from multiple-choice tests.” J. of Experimental Psychology: Applied, vol. 13, no. 4, p. 273, 2007.
- [24] R. A. Magill, “The influence of augmented feedback on skill learning depends on characteristics of the skill and the learner,” Quest, vol. 46, no. 3, pp. 314–327, 1994.
- [25] R. W. Picard, E. Vyzas, and J. Healey, “Toward machine emotional intelligence: Analysis of affective physiological state,” IEEE Trans. on pattern analysis and machine intelligence, vol. 23, no. 10, pp. 1175–1191, 2001.
- [26] E. S. Kim, D. Leyzberg, K. M. Tsui, and B. Scassellati, “How people talk when teaching a robot,” in Proc. of the 4th ACM/IEEE Intl. Conf. on Human robot interaction, 2009, pp. 23–30.
- [27] T. Kessler Faulkner, R. A. Gutierrez, E. S. Short, G. Hoffman, and A. L. Thomaz, “Active attention-modified policy shaping: socially interactive agents track,” in Proc. of the 18th Intl. Conf. on Autonomous Agents and MultiAgent Sys. Intl. Foundation for Autonomous Agents and Multiagent Sys., 2019, pp. 728–736.
- [28] Y. Cui, Q. Zhang, A. Allievi, P. Stone, S. Niekum, and W. B. Knox, “The empathic framework for task learning from implicit human feedback,” arXiv preprint arXiv:2009.13649, 2020.
- [29] B. Liu, E. Robertson, S. Grigsby, and S. Mazumder, “Self-initiated open world learning for autonomous AI agents,” CoRR, vol. abs/2110.11385, 2021.
- [30] S. Sidana, M. Trofimov, O. Horodnytskyi, C. Laclau, Y. Maximov, and M.-R. Amini, “User preference and embedding learning with implicit feedback for recommender sys.” Data Mining and Knowledge Discovery, vol. 35, no. 2, pp. 568–592, 2021.
- [31] R. Arakawa, S. Kobayashi, Y. Unno, Y. Tsuboi, and S.-i. Maeda, “Dqn-tamer: Human-in-the-loop reinforcement learning with intractable feedback,” arXiv preprint arXiv:1810.11748, 2018.
- [32] L. V. Kantorovich, “Mathematical methods of organizing and planning production,” Management science, vol. 6, no. 4, pp. 366–422, 1960.
- [33] A. Ramdas, N. García Trillos, and M. Cuturi, “On wasserstein two-sample testing and related families of nonparametric tests,” Entropy, vol. 19, no. 2, p. 47, 2017.