From latent ferroelectricity to hyperferroelectricity in alkali lead halide perovskites
Abstract
Using first principles calculations we show that several alkali lead halides potentially present collective ferroelectric polarization. This should occur at least at the nanoscale; it could be detected macroscopically provided it is not concealed by lattice vibrations in the temperature range of stability of the cubic perovskite phase. For potassium lead halides and for alkali lead fluorides, remarkably, the ferroelectric behavior turns hyper-ferroelectric, suggesting a more robust ferroelectric polarization in spite of depolarization potentials induced by charge accumulation on surfaces or interfaces.
Ferroelectricity arises from cooperative polar distortions that stabilise a non-centrosymmetric crystalline structure. An electric field beyond a given threshold can collectively flip the dipole moments associated with the local distortions, which leads to hysteresis in the polarization/electric field curve. When thermal fluctuations are sufficient to destroy long range correlations between the orientation of local dipoles, the crystal becomes paraelectric, keeping however an enhanced dielectric susceptibility in a given range of electric fields. While oxide perovskites have been largely studied for their ferroelectric or paraelectric behaviorDawber et al. (2005); Ghosez and Triscone (2011), halide perovskites are mostly studied in recent years for photovoltaic applications, in particular hybrid organic-inorganic ones. In the latter, the A cation in the ABX3 perovskite structure is a small organic molecule whose dipole moment, if aligned in a periodic arrangement, can produce ferroelectricityFrost et al. (2014a).
Early experiments conducted at room temperature showed that the orientations of the molecular cations correspond to a paraelectric phase for CH3NH3PbI3Fan et al. (2015) (methylammonium lead iodide, or MAPbI3). TheoreticallyEven et al. (2016), dipole orientations are shown to be random in the high temperature cubic phase. But the structural phase transition from the high temperature cubic to room temperature tetragonal phase of CH3NH3PbI3 is almost impossible to properly simulate by using ab initio molecular dynamics, due to the limitations of computational ressources. When lowering the temperature, the orthorhombic phase is usually obtained by these methods before the long-range correlations characteristic of the tetragonal phase can be characterized. Recent experiments have shown that MAPbI3 (unlike MAPbBr3) is pyroelectric in its tetragonal phase, at room temperature and ferroelectricity was further demonstrated at T=204 K by showing an hysteresis loop in the polarization versus electric field curveRakita et al. (2017). Similar results have been obtained for layered perovskites.Zhang et al. (2019)
Focusing on the dipole of the organic moiety has somewhat concealed the contribution of the inorganic framework to the polarization. However, CsPbF3 is an example of an alkali halide perovskite with a polar, ferroelectric, ground state Berastegui et al. (2001); Smith et al. (2015), and also CsPbI3 presents polar instabilities in some of its phases Marronnier et al. (2017, 2018a); Sutton et al. (2018), including the cubic, high temperature, perovskite phase. This phase, or the tetragonal one, are stabilized at room temperature in the form of quantum dotsSwarnkar et al. (2016) or thin filmsWang et al. (2019), producing highly efficient solar cells, but the room temperature ground state is, in reality, a non-perovskite structureMarronnier et al. (2018a); Sutton et al. (2018).
Concerning polar distortions, the lack of inversion symmetry in the distorted structure, together with strong spin-orbit coupling, leads to the Rashba-effect that could reduce the recombination rateZheng et al. (2015); exciton binding energy could be very low as a consequence of large dielectric screening associated to the ionic contribution to the dielectric constant Even et al. (2014); Miyata et al. (2015). The role of these two propositions on carrier dynamics has been downplayed because, for the former, first principles calculations show that the influence of the Rashba effect on recombination is weaker than initially expected, both in hybrid Zhang et al. (2018a, b) and inorganic Marronnier et al. (2019) halide perovskites; for the latter hypothesis, the calculated ionic contribution to the dielectric constantMarronnier et al. (2018b) is large but not huge. A third scenario, proposed by MiyataMiyata and Zhu (2018), involves polar nanodomains surrounding a ferroelectric large polaron, which could provide a much more effective screening and a potential barrier hindering charge recombination. Several works have discussed the possible role of ferroelectric distortionsFrost et al. (2014b); Chen et al. (2015), highly anharmonic polar modes leading to dipolar random fluctuations larger than stochastic dipolar molecular rotationsKatan et al. (2018) competing with octahedral rotationsSmith et al. (2015); Radha et al. (2018) in halide perovskites, but a detailed knowledge of internal electric fields and polarization in these materials is still missing and it is necessary in order to develop further any model relying on a supposed ferroelectricity.
In this paper we focus on inorganic alkali lead halide perovskites, keeping Pb in the ABX3 structure because lead’s lone pair seems to be instrumental in stabilizing a polar ground stateSmith et al. (2015); we show that all the cubic perovskite phases of APbX3 compounds studied here (A=Cs, Rb, K ; B=I, Br, Cl, F) present a ferroelectric behavior, to various degrees, reaching in some cases the hyperferroelectricGarrity et al. (2014) regime; when ferroelectricity, or hyperferroelectricity, is wiped out by thermal fluctuations (which is apparently the case for the -phase of CsPbI3 in its stability domain) the material is paraelectric, or hyperparaelectric, but conserves the internal polar distortions typical of normal, or hyper, ferroelectrics, now showing up as dynamical fluctuations of local dipole moments.
Our approach is based on Density Functional Theory (DFT) calculations of four crucial quantities along the distortion pattern of a soft polar phonon: the Kohn-Sham total energy , the unit cell volume , the polarization , and the dielectric constant in the high frequency limit . The dielectric constant is obtained with Density Functional Perturbation TheoryBaroni et al. (2001) and the polarization is obtained with the Berry phase approachResta (1994). We used the Quantum-Espresso packageGiannozzi et al. (2009) for the calculation of the four ingredients of the modelTec .
We describe the atomic displacements along the soft phonon previously described for CsPbI3Marronnier et al. (2017) with a parameter, : we define for the centrosymmetric structure (with space group ) and for the distorted minimum energy configuration. Intermediate configurations are obtained by linear interpolation between symmetric and asymmetric structures. We fit with a 6th order polynomial with even powers of , as in our previous studies of CsPbI3Marronnier et al. (2017, 2018a). For the fitting of polarization we use an odd polynomial of fifth degree, for the susceptibility an even combination of Chebyshev polynomials up to 8th degree.
All twelve APbX3 compounds present the same double well profile of the total energy, U(), around the symmetric structure previously described for CsPbI3 (see Fig. 1a). The energy barriers of the double well range from 9 meV for CsPbBr3 to 326 meV for KPbF3 (Fig. 1b). The displacement along one of the three degenerate soft polar phonons (we choose the direction) leads to a tetrahedral distortion and a slight volume expansion for all compounds except the three fluorides, which contract (Fig. 1c); this feature underlines a possible coupling between optical and acoustic phonons.
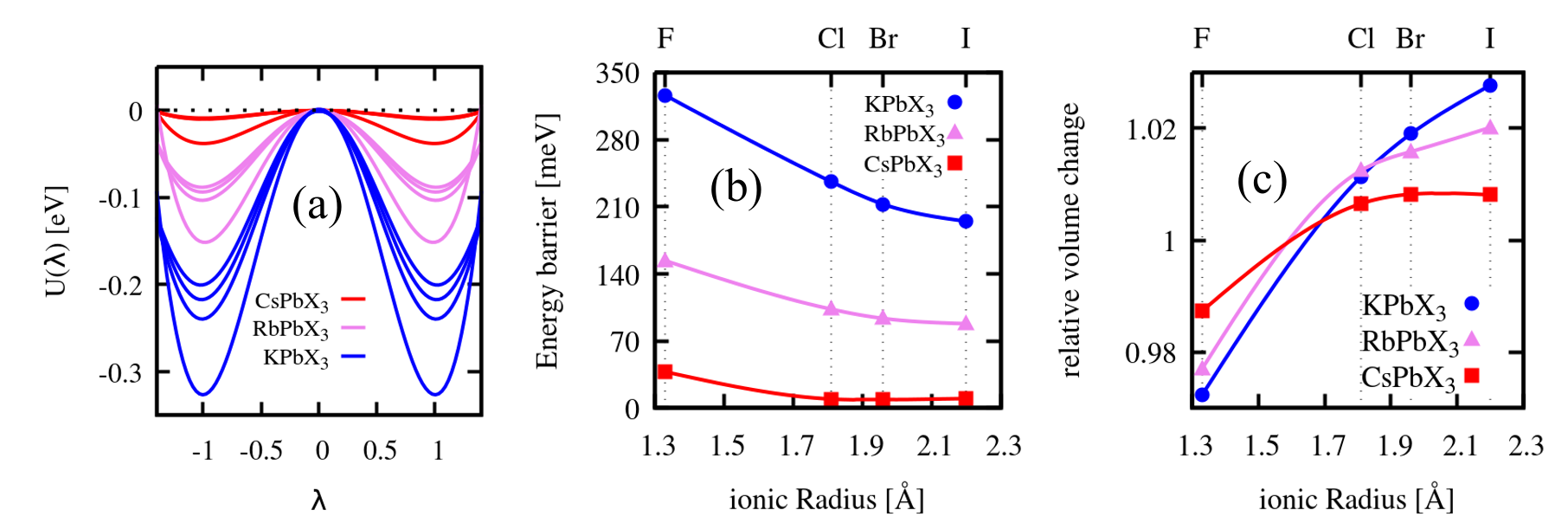
Coupling between polar and non polar distortions may affect the nature of the ferroelectric behavior and the presence of a soft polar phonon does not mean automatically ferroelectricity. A deeper understanding can be gained by studying the electric equation of state, relating the electric field and either the polarization P or the electric dispacement D. We consider the electric energy functional espressionStengel et al. (2009) for a solid in an external electric field E, as proposed in Ref. Adhikari and Fu, 2019:
| (1) |
where we assumed atomic units, substituting for the dielectric constant of free space.
In addition to the total energy U and the volume, , the espression contains also the polarization P and the electronic susceptibility , which we both calculated for various , , and fitted them with polynomials. From these ingredients we can obtain the electric field by solving the second degree equation minimizing the electric energy functional Adhikari and Fu (2019) and, with it, obtain the parametric P-E and D-E curves, i.e., the electric equation of state.
Let us consider first the three iodides: the parametric P-E (or D-E) curves shown in Fig. 2a-c present the typical S-shape associated to the hysteresis in ferroelectric materials, confirming the potential ferroelectric behavior of these cubic perovskite phases. We use the red/green/blue colors to distinguish the locally stable, locally unstable and globally stable regions, respectively, which correspond to values where and (locally stable), (locally unstable) and and (globally stable). The shape of the curves evolves from CsPbI3 to KPbI3, widening progressively the range of electric fields spanned by the unstable region.
The Kohn-Sham total energy double well profile, as well as the volume, polarization and dielectric constant, are obtained with calculations at zero field (E=0) and within short circuit boundary conditions (SCDC), which means that the electric field vanishes at the hypothetical surface of an infinite bulk described within periodic boundary conditions. Experimentally, this corresponds to a macroscopic sample where the surfaces are kept at the same potential. Conversely, in several experimental situations implementing open circuit boundary conditions (OCBC), charges accumulate at the surface and induce a depolarization field which counters the buildup of polarization inside the sample. In practice, the polar ground state is at least partially destroyed by the depolarization field. This effect can be predicted by inspecting the electric energy in OCBCAdhikari and Fu (2019):
| (2) |
which will show a double well instability only if the depolarization field is not sufficient to destroy the bulk polarization. In panels d-f of Fig. 2 we show the electric energy in OCBC alongside with the P(E) and D(E) curves previously discussed. The electric energy in OCBC presents a single minimum for CsPbI3 and RbPbI3, but has still a (very shallow) double well profile for KPbI3. This double well is the signature of what has been called a hyperferroelectric Garrity et al. (2014): a material which is able to keep a bulk ferroelectric polarization in spite of the depolarization field induced by surface charge accumulation.

In a similar way we can analyse the trend while varying the halogen atom. For the sake of illustration we show in Fig. 3 caesium lead halides, where the evolution from iodide to fluoride is stronger. Starting from CsPbI3, where the ferroelectric behavior stands on a shallow double well for U() whose energy barrier is only on the order of 10 meV (see Fig. 1a-b), we end up with CsPbF3, with a barrier almost four times larger and whose already discussed ferroelectricitySmith et al. (2015) we show to be, in reality, hyperferroelectricity. In between them, CsPbBr3 and CsPbCl3 behave very similarly to CsPbI3.

The hyperferroelectric behavior manifests itself not only in the double well shape of the electric energy in OCBC, but also in the shape of the D-E curves (electric displacement electric field), qualitatively very similar to the P-E curves. In normal dielectrics the derivative of the electric displacement the electric field (i.e., the static dielectric constant, ) is positive, including when the external electric field vanishes ; at the ferroelectric transition, however, the dielectric constant diverges and, for a proper ferroelectric, becomes multivalued (hence comes hysteresis); at the crossing of the D=0 axis (in the unstable region) it becomes negative . If we could progressively tune the shape of the D-E curve from a normal ferroelectric towards a hyperferroelectric, would at some point vanish and become positive in the hyperferroelectric state. We consider then in the unstable region as a measure of the strength of the ferroelectric polarization, neglecting here the role of lattice vibration, which will eventually determine whether the material is (hyper-)ferroelectric or (hyper-)paraelectric. We use this parameter to follow the trends in the ferroelectricity of alkali lead halides. In Fig. 4 we show the value of for the twelve alkali lead halides considered in this paper.
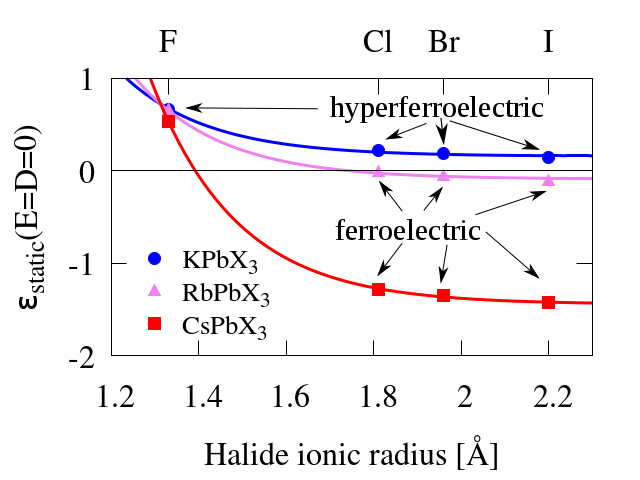
These reults reveal, first, that the trends with alkali substitution, observed in Fig 2 for the iodides, is maintained for bromides and clorides. Second, all alkali lead fluorides considered here are hyperferroelectric. Third, all potassium lead halides, too, present hyperferroelectric behavior.
Most of these compounds are found experimentally with the cubic perovskite structure only at relatively high temperatures: CsPbI3 -phase is stable only above 373∘CMarronnier et al. (2018a); Sutton et al. (2018), CsPbCl3 assumes the cubic perovskite structure above 47∘CMøller (1959) and according to dielectric measurements is not ferroelectric, although Raman measurements show soft phonon modesHirotsu (1970). CsPbBr3 becomes cubic only above 130∘CMøller (1959); Hirotsu et al. (1974). The fluoride CsPbF3, conversely, is in the symmetry at room temperature, transforming to rhombohedral below -83∘C. As far as rubidium compounds are concerned, the bromide has a perovskite structure only above 290∘CTang et al. (2019) and the fluoride above 217∘CYamane et al. (2008). We could not find reports on solid phases of potassium triiodides, except from a citation of KPbI3 as occuring in NH4CdCl3-type structure ( symmetry)Zandbergen et al. (1979)
This tendency to lose the cubic perovskite structure below a certain temperature can be interpreted in terms of the so called Goldschmidt tolerance factor, useful to assess the tendency of an ABX3 compound to stabilize in the cubic perovskite structure. Assuming Shannon radiirad the three alkali lead iodides have tolerance factors ranging from 0.75 (for potassium) to 0.85 (for caesium), somewhere at the lower limit to form perovskite structure. A tolerance factor smaller than one indicates that octahedral tilt rotations can lower the energy of the system, and this explains why several of the compounds considered in this paper have an orthorhombic non-perovskite low temperature ground state and, after intermediate phases, switch to the cubic perovskite structure only at sufficiently high temperature. A mechanism for the transition, as recently shownBechtel et al. (2019), is due to the temperature evolution of the distribution of tilting angles, which from bimodal at low temperature switches to a single peak at the transitioin to the cubic phase. It has been suggested that octahedral rotations and ferroelectric distortions are mutually exclusiveRadha et al. (2018). The competition between these two mechanisms depends also on how the respective double well depths vary with volume expansion. A full understanding of this point would need a thorough study of thermal expansion including anharmonic effects in these materials, however a simpler check is worthwhile: we calculated the depth of the potential well for the ferroelectric distortion at a few negative pressures for CsPbI3 and CsPbF3. The results, summarized in Table 1, show that thermal expansion does not affect the crucial features of the energy landscape governing ferroelectricity in these materials.
| Halide | P (kbar) | ||||
|---|---|---|---|---|---|
| CsPbI3 | 0 | -5.7% (-4.8%) | 10 | 10 | -1.43 |
| -5 | -3.4% (-1.8%) | 8 | 20 | -1.05 | |
| -10 | -0.3% (+2.1%) | -1 | 36 | -0.88 | |
| CsPbF3 | 0 | -2.4% (-3.7%) | 38 | 38 | 0.54 |
| -20 | +1.6% (+2.2%) | 25 | 33 | 0.57 | |
| -25 | +3.0% (+4.8%) | 6 | 36 | 0.95 |
Independently from the issue of the stability of the cubic phase for each of the considered compounds, we remind that doping hybrid perovskite solar cells with Cs, Rb and, recently, also K was shown to be beneficial for the stability and performance of halide perovskite solar cells. In particular, potassium doping was shown to improve luminescenceAbdi-Jalebi et al. (2018), reduce hysteresisTang et al. (2017), improve stability and reduce ion migration Nam et al. (2017), by decorating surfaces and grain boundaries. Apart from reducing the band gap and inducing potential beneficial elastic effects —doping with K tends to shrink the lattice parameter—, we suggest that potassium could enhance charge separation thanks to a local hyperferroelectric polarization, possibly stabilizing polar nanodomains responsibles for the large ferroelectric polaron mechanismMiyata and Zhu (2018).
We might expect a ferroelectric behavior similar to alkali lead halides in analogous compounds where lead is substituted by other elements in the same column of the periodic table, like Sn, Ge or SiRadha et al. (2018), suggesting further experimental studies on the phase stability of these materials. Finally, we remind that the soft polar phonons which are at the origin of the ferroelectric distortion may also cause a dynamical Rashba effect in CsPbI3Marronnier et al. (2019), supporting the possibility of an electric field control of the spin texture in alkali lead halide thin films.
In conclusion, using first principles calculations we have shown that several alkali lead halides potentially present collective ferroelectric polarization. This should occur at least at the nanoscale; it could be detected macroscopically provided it is not concealed by lattice vibrations in the temperature range of stability of the cubic perovskite phase. For potassium lead halides and for alkali lead fluorides, remarkably, the ferroelectric behavior turns hyperferroelectric, suggesting a more robust ferroelectric polarization in spite of depolarization potentials induced by charge accumulation on surfaces or interfaces.
I Acknowledgements
This work was granted access to the HPC resources of TGCC under the allocation 2018A0010906018 made by GENCI and under the allocation by CEA-DEN.
References
- Dawber et al. (2005) M. Dawber, K. M. Rabe, and J. F. Scott, Rev. Mod. Phys. 77, 1083 (2005).
- Ghosez and Triscone (2011) P. Ghosez and J.-M. Triscone, Nature Mater. 10, 269 (2011).
- Frost et al. (2014a) J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde, and A. Walsh, Nano Letters 14, 2584 (2014a), pMID: 24684284, https://doi.org/10.1021/nl500390f .
- Fan et al. (2015) Z. Fan, J. Xiao, K. Sun, L. Chen, Y. Hu, J. Ouyang, K. P. Ong, K. Zeng, and J. Wang, The Journal of Physical Chemistry Letters 6, 1155 (2015), pMID: 26262965, https://doi.org/10.1021/acs.jpclett.5b00389 .
- Even et al. (2016) J. Even, M. Carignano, and C. Katan, Nanoscale 8, 6222 (2016).
- Rakita et al. (2017) Y. Rakita, O. Bar-Elli, E. Meirzadeh, H. Kaslasi, Y. Peleg, G. Hodes, I. Lubomirsky, D. Oron, D. Ehre, and D. Cahen, Proceedings of the National Academy of Sciences 114, E5504 (2017), https://www.pnas.org/content/114/28/E5504.full.pdf .
- Zhang et al. (2019) Q. Zhang, A. Solanki, K. Parida, D. Giovanni, M. Li, T. L. C. Jansen, M. S. Pshenichnikov, and T. C. Sum, ACS Applied Materials & Interfaces 11, 13523 (2019), https://doi.org/10.1021/acsami.8b21579 .
- Berastegui et al. (2001) P. Berastegui, S. Hull, and S.-G. Eriksson, Journal of Physics: Condensed Matter 13, 5077 (2001).
- Smith et al. (2015) E. H. Smith, N. A. Benedek, and C. J. Fennie, Inorganic Chemistry 54, 8536 (2015), pMID: 26295352, https://doi.org/10.1021/acs.inorgchem.5b01213 .
- Marronnier et al. (2017) A. Marronnier, H. Lee, B. Geffroy, J. Even, Y. Bonnassieux, and G. Roma, The Journal of Physical Chemistry Letters 8, 2659 (2017), http://dx.doi.org/10.1021/acs.jpclett.7b00807 .
- Marronnier et al. (2018a) A. Marronnier, G. Roma, S. Boyer-Richard, L. Pedesseau, J.-M. Jancu, Y. Bonnassieux, C. Katan, C. C. Stoumpos, M. G. Kanatzidis, and J. Even, ACS Nano 12, 3477 (2018a), https://doi.org/10.1021/acsnano.8b00267 .
- Sutton et al. (2018) R. J. Sutton, M. R. Filip, A. A. Haghighirad, N. Sakai, B. Wenger, F. Giustino, and H. J. Snaith, ACS Energy Letters 3, 1787 (2018), https://doi.org/10.1021/acsenergylett.8b00672 .
- Swarnkar et al. (2016) A. Swarnkar, A. R. Marshall, E. M. Sanehira, B. D. Chernomordik, D. T. Moore, J. A. Christians, T. Chakrabarti, and J. M. Luther, Science 354, 92 (2016), https://science.sciencemag.org/content/354/6308/92.full.pdf .
- Wang et al. (2019) Y. Wang, M. I. Dar, L. K. Ono, T. Zhang, M. Kan, Y. Li, L. Zhang, X. Wang, Y. Yang, X. Gao, Y. Qi, M. Grätzel, and Y. Zhao, Science 365, 591 (2019), https://science.sciencemag.org/content/365/6453/591.full.pdf .
- Zheng et al. (2015) F. Zheng, L. Z. Tan, S. Liu, and A. M. Rappe, Nano Lett. 15, 7794 (2015).
- Even et al. (2014) J. Even, L. Pedesseau, and C. Katan, The Journal of Physical Chemistry C 118, 11566 (2014), https://doi.org/10.1021/jp503337a .
- Miyata et al. (2015) A. Miyata, A. Mitioglu, P. Plochocka, O. Portugal, J. T. Wang, S. D. Stranks, and H. J. H. J. S. J. Nicholas, Nature Physics 11, 582 (2015).
- Zhang et al. (2018a) X. Zhang, J.-X. Shen, and C. G. Van de Walle, J. Phys. Chem. Lett. 9, 2903 (2018a), https://doi.org/10.1021/acs.jpclett.8b01004 .
- Zhang et al. (2018b) X. Zhang, J.-X. Shen, W. Wang, and C. G. Van de Walle, ACS Energy Lett. 3, 2329 (2018b), https://doi.org/10.1021/acsenergylett.8b01297 .
- Marronnier et al. (2019) A. Marronnier, G. Roma, M. A. Carignano, Y. Bonnassieux, C. Katan, J. Even, E. Mosconi, and F. De Angelis, J. Phys. Chem. C 123, 291 (2019).
- Marronnier et al. (2018b) A. Marronnier, H. Lee, H. Lee, M. Kim, C. Eypert, J.-P. Gaston, G. Roma, D. Tondelier, B. Geffroy, and Y. Bonnassieux, Solar Energy Materials and Solar Cells 178, 179 (2018b).
- Miyata and Zhu (2018) K. Miyata and X.-Y. Zhu, Nat. Mater. 17, 379 (2018).
- Frost et al. (2014b) J. M. Frost, K. T. Butler, and A. Walsh, APL Materials 2, 081506 (2014b), https://doi.org/10.1063/1.4890246 .
- Chen et al. (2015) B. Chen, J. Shi, X. Zheng, Y. Zhou, K. Zhu, and S. Priya, J. Mater. Chem. A 3, 7699 (2015).
- Katan et al. (2018) C. Katan, A. D. Mohite, and J. Even, Nature Materials 17, 377 (2018).
- Radha et al. (2018) S. K. Radha, C. Bhandari, and W. R. L. Lambrecht, Phys. Rev. Materials 2, 063605 (2018).
- Garrity et al. (2014) K. F. Garrity, K. M. Rabe, and D. Vanderbilt, Phys. Rev. Lett. 112, 127601 (2014).
- Baroni et al. (2001) S. Baroni, S. de Gironcoli, A. Dal Corso, and P. Giannozzi, Rev. Mod. Phys. 73, 515 (2001).
- Resta (1994) R. Resta, Rev. Mod. Phys. 66, 899 (1994).
- Giannozzi et al. (2009) P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari, and R. M. Wentzcovitch, Journal of Physics: Condensed Matter 21, 395502 (2009).
- (31) Calculations were performed with Quantum-Espresso within the local density approximation (LDA). We used scalar relativistic norm conserving pseudopotentials with 14 valence electrons for Pb and 9 for all alkali atoms, as for previous works on CsPbI3. An energy cutoff of 100 Rydberg, k-point mesh of size 888 and strict threshold for forces (10-4 Ryd/Bohr) were used. The Berry phase calculations of the polarization were performed as an integral over a path in reciprocal space containing 20 k-points in the relevant (kx) direction, averaged over a 88 mesh in the kykz plane.
- (32) We use Shannon ionic radii, assuming oxidation state +1,+2 and -1 for alkali, lead and halogens respectively. The coordination number is 6 for lead and the halogens and 12 for alkali atoms.
- Stengel et al. (2009) M. Stengel, N. A. Spaldin, and D. Vanderbilt, Nature Physics 5, 304 (2009).
- Adhikari and Fu (2019) R. Adhikari and H. Fu, Phys. Rev. B 99, 104101 (2019).
- Møller (1959) C. K. Møller, Mat. Fys. Medd . Dan . Vid. Sels. 32 (1959), n.2.
- Hirotsu (1970) S. Hirotsu, J. Phys. Soc. Japan 31, 552 (1970).
- Hirotsu et al. (1974) S. Hirotsu, J. Harada, M. Iizumi, and K. Gesi, J. Phys. Soc. Japan 37, 1393 (1974).
- Tang et al. (2019) B. Tang, Y. Hu, H. Dong, L. Sun, B. Zhao, X. Jiang, and L. Zhang, Angewandte Chemie International Edition 58, 16134 (2019), https://onlinelibrary.wiley.com/doi/pdf/10.1002/anie.201910617 .
- Yamane et al. (2008) Y. Yamane, K. Yamada, and K. Inoue, Sol. State Ionics 179, 605 (2008).
- Zandbergen et al. (1979) H. W. Zandbergen, G. C. Verschoor, and D. J. W. Ijdo, Acta Cryst. B35, 1425 (1979).
- Bechtel et al. (2019) J. S. Bechtel, J. C. Thomas, and A. Van der Ven, Phys. Rev. Materials 3, 113605 (2019).
- Abdi-Jalebi et al. (2018) M. Abdi-Jalebi, Z. Andaji-Garmaroudi, S. Cacovich, C. Stavrakas, B. Philippe, J. M. Richter, M. Alsari, E. P. Booker, E. M. Hutter, A. J. Pearson, S. Lilliu, T. J. Savenije, H. Rensmo, G. Divitini, C. Ducati, R. H. Friend, and S. D. Stranks, Nature 555, 497 (2018).
- Tang et al. (2017) Z. Tang, T. Bessho, F. Awai, T. Kinoshita, M. M. Maitani, R. Jono, T. N. Murakami, H. Wang, T. Kubo, S. Uchida, and H. Segawa, Scientific Reports 7, 12183 (2017).
- Nam et al. (2017) J. K. Nam, S. U. Chai, W. Cha, Y. J. Choi, W. Kim, M. S. Jung, J. Kwon, D. Kim, and J. H. Park, Nano Letters 17, 2028 (2017), pMID: 28170276, https://doi.org/10.1021/acs.nanolett.7b00050 .