Freehand Sketch Generation from Mechanical Components

Zhichao Liao [email protected] 0009-0004-9125-9428 Tsinghua Shenzhen International Graduate School, Tsinghua UniversityShenzhenChina , Di Huang [email protected] 0009-0009-7336-161X Tsinghua Shenzhen International Graduate School, Tsinghua UniversityShenzhenChina , Heming Fang [email protected] 0009-0001-0902-0441 State Key Laboratory of Fluid Power & Mechatronic Systems, Zhejiang UniversityHangzhouChina , Yue Ma [email protected] 0009-0000-5485-4237 Tsinghua Shenzhen International Graduate School, Tsinghua UniversityShenzhenChina , Fengyuan Piao [email protected] 0009-0005-6688-8916 Tsinghua Shenzhen International Graduate School, Tsinghua UniversityShenzhenChina , Xinghui Li [email protected] 0009-0009-9813-6259 Tsinghua Shenzhen International Graduate School, Tsinghua UniversityShenzhenChina , Long Zeng [email protected] 0000-0002-3090-6319 Tsinghua Shenzhen International Graduate School, Tsinghua UniversityShenzhenChina and Pingfa Feng [email protected] 0000-0002-8090-1508 Tsinghua Shenzhen International Graduate School, Tsinghua UniversityShenzhenChina

(2024)

Abstract.

Drawing freehand sketches of mechanical components on multimedia devices for AI-based engineering modeling has become a new trend. However, its development is being impeded because existing works cannot produce suitable sketches for data-driven research. These works either generate sketches lacking a freehand style or utilize generative models not originally designed for this task resulting in poor effectiveness. To address this issue, we design a two-stage generative framework mimicking the human sketching behavior pattern, called MSFormer, which is the first time to produce humanoid freehand sketches tailored for mechanical components. The first stage employs Open CASCADE technology to obtain multi-view contour sketches from mechanical components, filtering perturbing signals for the ensuing generation process. Meanwhile, we design a view selector to simulate viewpoint selection tasks during human sketching for picking out information-rich sketches. The second stage translates contour sketches into freehand sketches by a transformer-based generator. To retain essential modeling features as much as possible and rationalize stroke distribution, we introduce a novel edge-constraint stroke initialization. Furthermore, we utilize a CLIP vision encoder and a new loss function incorporating the Hausdorff distance to enhance the generalizability and robustness of the model. Extensive experiments demonstrate that our approach achieves state-of-the-art performance for generating freehand sketches in the mechanical domain. Project page: https://mcfreeskegen.github.io/.

Freehand Sketch; Generative Model; Mechanical Components

^†^†journalyear: 2024^†^†copyright: rightsretained^†^†conference: Proceedings of the 32nd ACM International Conference on Multimedia; October 28-November 1, 2024; Melbourne, VIC, Australia^†^†booktitle: Proceedings of the 32nd ACM International Conference on Multimedia (MM ’24), October 28-November 1, 2024, Melbourne, VIC, Australia^†^†doi: 10.1145/3664647.3681046^†^†isbn: 979-8-4007-0686-8/24/10^†^†ccs: Computing methodologies Computer vision

Refer to caption — Figure 1. Various mechanical freehand sketches generated by ours and other approaches. Our method produces sketches from mechanical components while maintaining a freehand style and their essential modeling features, e.g., pulley grooves, through holes on the bush, and gear teeth.

1. Introduction

Nowadays, with the vigorous development of multimedia technology, a new mechanical modeling approach has gradually emerged, known as freehand sketch modeling (Li et al., 2022, 2020b) . Different from traditional mechanical modeling paradigms (Zeng et al., 2012) , freehand sketch modeling on multimedia devices does not require users to undergo prior training with CAD tools. In the process of freehand sketch modeling for mechanical components, engineers can utilize sketches to achieve tasks such as component sketch recognition, components fine-grained retrieval based on sketches (Zeng et al., 2019) , and three-dimensional reconstruction from sketches to components. Modeling in this way greatly improves modeling efficiency. However, limited by the lack of appropriate freehand sketches for these data-driven studies in the sketch community, the development of freehand sketch modeling for mechanical components is hindered. It is worth emphasizing that manual sketching and collecting mechanical sketches is a time-consuming and resource-demanding endeavor. To address the bottleneck, we propose a novel two-stage generative model to produce freehand sketches from mechanical components automatically.

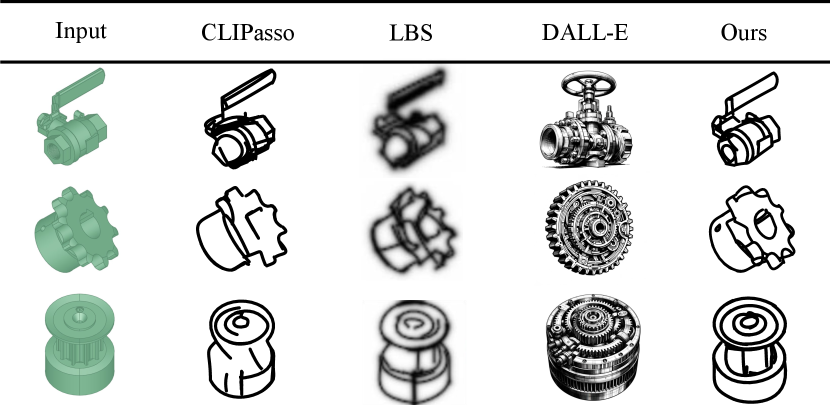
To meet the requirements of information richness and accuracy for modeling, we expect that freehand sketches used for mechanical modeling maintain a style of hand-drawn while preserving essential model information as much as possible. Previous works that generate engineering sketches (Manda et al., 2021; Han et al., 2020; Para et al., 2021; Seff et al., 2020; Willis et al., 2021) , primarily focus on perspective and geometric features of models. As a result, their sketches lack a hand-drawn style, making them unsuitable as the solution of data generation for freehand sketch modeling. Existing data-driven freehand sketch generation methods (Ge et al., 2020; Liu et al., 2020a; Zhang et al., 2015; Tong et al., 2021; Bhunia et al., 2022; Cao et al., 2019; Luhman and Luhman, 2020; Wang et al., 2022; Ribeiro et al., 2020; Lin et al., 2020) also fall short in this task because they require the existence and availability of relevant datasets. While CLIPasso (Vinker et al., 2022) and LBS (Lee et al., 2023) can produce abstract sketches without additional datasets, as shown in Figure 1 , their results for mechanical components are afflicted by issues such as losing features, line distortions, and random strokes. In contrast, we propose a mechanical vector sketch generation technique that excels in maintaining precise and abundant modeling features and a freehand style without additional sketch datasets.

Our method, the first time to generate freehand sketches for mechanical components, employs a novel two-stage architecture. It mimics the human sketching behavior pattern which commences with selecting optimal viewpoints, followed by hand-sketching. In Stage-One, we generate multi-perspective contour sketches from mechanical components via Open CASCADE, removing irrelevant information for engineering modeling which may also mislead stroke distribution in generated sketches. To select information-rich sketches, we devise a view selector to simulate the viewpoint choices made by engineers during sketching. Stage-Two translates regular contour sketches into humanoid freehand sketches by a transformer-based generator. It is trained by sketches created by a guidance sketch generator that utilizes our innovative edge-constraint initialization to retain more modeling features. Our inference process relies on trained weights to stably produce sketches defined as a set of Bézier curves. Additionally, we employ a CLIP vision encoder combining a pretrained vision transformer (Dosovitskiy et al., 2020) ViT-B/32 model of CLIP (Radford et al., 2021) with an adapter (Gao et al., 2024) , which utilizes a self-attention mechanism (Vaswani et al., 2017) to establish global relations among graph blocks, enhancing the capture of overall features. It fortifies the method’s generalization capability for unseen models during training and inputs with geometric transformation (equivariance). Furthermore, our proposed new guidance loss, incorporating the Hausdorff distance, considers not only the spatial positions but also the boundary features and structural relationships between shapes. It improves model’s ability to capture global information leading to better equivariance. Finally, we evaluate our method both quantitatively and qualitatively on the collected mechanical component dataset, which demonstrates the superiority of our proposed framework. We also conduct ablation experiments on key modules to validate their effectiveness.

In summary, our contributions are the following:

•

As far as our knowledge goes, this is the first time to produce freehand sketches tailored for mechanical components. To address this task, we imitate the human sketching behavior pattern to design a novel two-stage sketch generation framework.
•

We introduce an innovative edge-constraint initialization method to optimize strokes of guidance sketches, ensuring that outcomes retain essential modeling features and rationalize stroke distribution.
•

We utilize an encoder constituted by CLIP ViT-B/32 model and an adapter to improve the generalization and equivariance of the model. Furthermore, we propose a novel Hausdorff distance-based guidance loss to capture global features of sketches, enhancing the method’s equivariance.
•

Extensive quantitative and qualitative experiments demonstrate that our approach can achieve state-of-the-art performance compared to previous methods.

2. Related Work

Due to little research on freehand sketch generation from mechanical components, there is a review of mainstream generation methods relevant to our work in the sketch community.

Traditional Generation Method In the early stages of sketch research, sketches from 3D models were predominantly produced via traditional edge extraction methodologies (Sobel et al., 1968; Canny, 1986; Winnemöller et al., 2012; Prewitt et al., 1970; Marr, 1977; Manda et al., 2021) . Among them, Occluding contours (Marr, 1977) which detects the occluding boundaries between foreground objects and the background to obtain contours, is the foundation of non-photorealistic 3D computer graphics. Progressions in occluding contours (Marr, 1977) have catalyzed advancements in contour generation, starting with Suggestive contours (DeCarlo et al., 2023) , and continuing with Ridge-valley lines (Ohtake et al., 2004) and kinds of other approaches (Judd et al., 2007; Manda et al., 2021) . A comprehensive overview (DeCarlo, 2012) is available in existing contour generalizations. Similarly to the results of generating contours, Han et al. (Han et al., 2020) present an approach to generate line drawings from 3D models based on modeling information. Building upon previous work that solely focused on outlines of models, CAD2Sketch (Hähnlein et al., 2022) addresses the challenge of representing line solidity and transparency in results, which also incorporates certain drawing styles. However, all of these traditional approaches lack a freehand style like ours.

Learning Based Methods Coupled with deep learning (Huang et al., 2024b; Ma et al., 2024a, 2022b, 2022a, 2023, b; Yue Ma, 2024) , sketch generation approaches (Ge et al., 2020; Liu et al., 2020a; Zhang et al., 2015; Tong et al., 2021; Bhunia et al., 2022; Cao et al., 2019; Para et al., 2021; Ye et al., 2019) have been further developed. Combining the advantage of traditional edge extraction approaches for 3D models and deep learning, Neural Contours (Liu et al., 2020a) employs a dual-branch structure to leverage edge maps as a substitution for sketches. SketchGen (Para et al., 2021) , SketchGraphs (Seff et al., 2020) , and CurveGen and TurtleGen (Willis et al., 2021) produce engineering sketches for Computer-Aided Design. However, such approaches generate sketches that only emphasize the perspective and geometric features of models, which align more closely with regular outlines, the results do not contain a freehand style. Generative adversarial networks (GANs) (Goodfellow et al., 2014) provide new possibilities for adding a freehand style to sketches (Ge et al., 2020; Liu et al., 2020b; Manushree et al., 2021; Li et al., 2020a; Wang et al., 2020) . These approaches are based on pixel-level sketch generation, which is fundamentally different from how humans draw sketches by pens, resulting in unsuitability for freehand sketch modeling. Therefore, sketches are preferred to be treated as continuous stroke sequences. Recently, Sketch-RNN (Ha and Eck, 2017) based on recurrent neural networks (RNNs) (Zaremba et al., 2014) and variational autoencoders (VAEs) (Kingma and Welling, 2013) , reinforcement learning (Xie et al., 2013; Zheng et al., 2018; Ganin et al., 2018) , diffusion models (Huang et al., 2024a; Luhman and Luhman, 2020; Wang et al., 2022) are explored for generating sketches. However, they perform poorly in generating mechanical sketches with a freehand style due to the lack of relevant training datasets. Following the integration of Transformer (Vaswani et al., 2017) architectures into the sketch generation, the sketch community has witnessed the emergence of innovative models (Willis et al., 2021; Ribeiro et al., 2020; Lin et al., 2020) . CLIPasso (Vinker et al., 2022) provides a powerful image to abstract sketch model based on CLIP (Radford et al., 2021) to generate vector sketches, but this method will take a long time to generate a single sketch. More critically, CLIPasso (Vinker et al., 2022) initializes strokes by sampling randomly, and optimizes strokes by using an optimizer for thousands of steps rather than based on pre-trained weights, leading to numerical instability. Despite LBS (Lee et al., 2023) being an improvement over Clipasso (Vinker et al., 2022) , it performs unsatisfactorily in generalization capability for inputs unseen or transformed. Compared to many previous approaches, our proposed generative model can produce vector sketches based on mechanical components, persevering key modeling features and a freehand style, greatly meeting the development needs of freehand sketch modeling.

3. Method

We first elaborate on problem setting in section 3.1 . Then, we introduce our sketch generation process that presents Stage-One (CSG) and Stage-Two (FSG) of MSFormer in sections 3.2 and 3.3 .

3.1. Problem Setting

Given a mechanical component, our goal is to produce a freehand sketch. As depicted in Figure 2 , it is carried out by stages: contour sketch generator and freehand sketch generator. We describe an mechanical component as $\mathcal{M}\in{\Delta}^{3}$ , where ${\Delta}^{3}$ represents 3D homogeneous physical space. Each point on model corresponds to a coordinate $({x}_{i},{y}_{i},{z}_{i})\in\mathbb{R}^{3}$ , where $\mathbb{R}$ is information dimension. Through an affine transformation, a 3D model is transformed into 2D contour sketches $\mathcal{C}\in{\Delta}^{2}$ , which consists of a series of black curves expressed by pixel coordinates $({x}_{i},{y}_{i})\in\mathbb{R}^{2}$ . In the gradual optimization process of Stage-Two, process sketches $\{\mathcal{P}_{i}\}_{i=1}^{K}$ are guided by guidance sketches $\{\mathcal{G}_{i}\}_{i=1}^{K}$ , K is the number of sketches. Deriving from features of contour sketch $\mathcal{C}$ and guidance sketches $\{\mathcal{G}_{i}\}_{i=1}^{K}$ , our model produces an ultimate output freehand sketch $\mathcal{S}$ , which is defined as a set of n two-dimensional Bézier curves $\{s_{1},s_{2},\ldots,s_{n}\}$ . Each of curve strokes is composed by four control points ${s}_{i}=\{(x_{1},y_{1})^{(i)},(x_{2},y_{2})^{(i)},(x_{3},y_{3})^{(i)},(x_{4},y_{4})^{(i)}\}\in\mathbb{R}^{8},\forall i\in n$ .

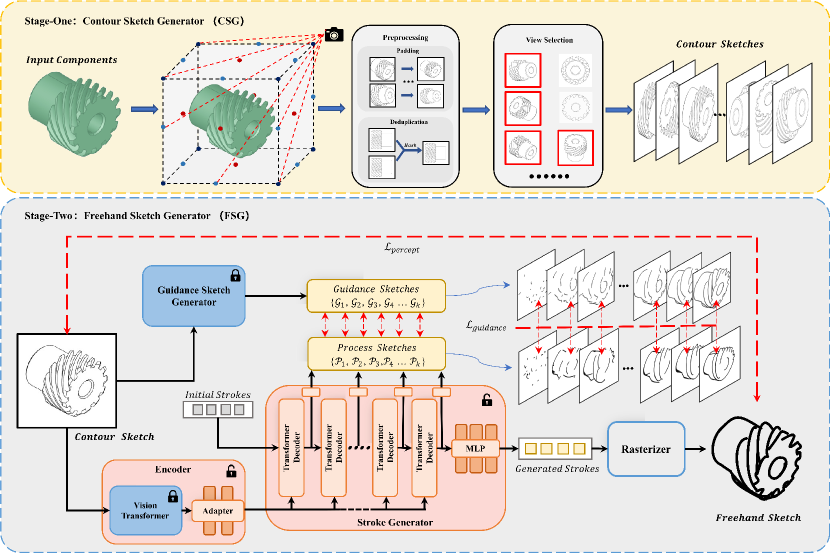
3.2. Stage-One: Contour Sketch Generator

Contour Sketch Generator (CSG), called Stage-One, is designed for filtering noise (colors, shadows, textures, etc.) and simulating the viewpoint selection during human sketching to obtain recognizable and informative contour sketches from mechanical components. Previous methods optimize sketches using details such as the distribution of different colors and variations in texture. However, mechanical components typically exhibit monotonic colors and subtle texture changes. We experimentally observe that referencing this information within components not only fails to aid inference but also introduces biases in final output stroke sequences, resulting in the loss of critical features. As a result, when generating mechanical sketches, the main focus is on utilizing the contours of components to create modeling features.

Modeling engineers generally choose specific perspectives for sketching rather than random ones, such as three-view (Front/Top/ Right views), isometric view (pairwise angles between all three projected principal axes are equal), etc. As shown in Figure 2 Stage-One, we can imagine placing a mechanical component within a cube and selecting centers of the six faces, midpoints of the twelve edges, and eight vertices of the cube as 26 viewpoints. Subsequently, we use PythonOCC (Paviot, 2018) , a Python wrapper for the CAD-Kernel OpenCASCADE, to infer engineering modeling information and render regular contour sketches of the model from these 26 viewpoints.

Generated contour sketches are not directly suitable for subsequent processes. By padding, we ensure all sketches are presented in appropriate proportions. Given that most mechanical components exhibit symmetry, the same sketch may be rendered from different perspectives. We utilize ImageHash technology for deduplication. Additionally, not all of generated sketches are useful and information-rich for freehand sketch modeling. For instance, some viewpoints of mechanical components may represent simple or misleading geometric shapes that are not recognizable nor effective for freehand sketch modeling. Therefore, we design a viewpoint selector based on ICNet (Zhao et al., 2018) , which is trained by excellent viewpoint sketches picked out by modeling experts, to simulate the viewpoint selection task engineers face during sketching, as shown in Figure 2 . Through viewpoint selection, we obtained several of the most informative and representative optimal contour sketches for each mechanical component. The detailed procedure of Stage-One is outlined in Algorithm 1.

Algorithm 1 Stage-One: Contour Sketch Generation

Input: Mechanical components

Output Contour Sketches of mechanical components

1:procedure cad_to_contours

I\leftarrow

Read a mechanical component in STEP format

3: Set OCC to HLR mode and enable anti-aliasing

V1\leftarrow

Acquire contour sketches of

I

from the 26 built-in viewpoints in OCC

V2\leftarrow

Center the object in

V1

and maintain a margin from edges of the picture

V3\leftarrow

Remove duplicates from sketches in

V2

using the

ImageHash

library

O\leftarrow

Filter the top

N

contours with the most information from

V3

using an image complexity estimator

3.3. Stage-Two: Freehand Sketch Generator

Stage-Two, in Figure 2 , comprises the Freehand Sketch Generator (FSG), which aims to generate freehand sketches based on regular contour sketches obtained from Stage-One. To achieve this goal, we design a transformers-based (Ribeiro et al., 2020; Liu et al., 2021; Lee et al., 2023) generator trained by guidance sketches, which stably generates freehand sketches with precise geometric modeling information. Our generative model does not require additional datasets for training. All training data are derived from the excellent procedural sketches produced by the guidance sketch generator.

Generative Process As illustrated in Figure 2 , freehand sketch generator consists of four components: an encoder, a stroke generator, a guidance sketch generator, and a differentiable rasterizer. Our encoder utilizes CLIP ViT-B/32 (Radford et al., 2021) and an adapter to extract essential vision and semantic information from input. Although, in previous works, CLIPasso (Vinker et al., 2022) performs strongly in creating abstract sketches, it initializes strokes by sampling randomly and uses an optimizer for thousands of steps to optimize sketches, resulting in a high diversity of outputs and numerical instability. To a ensure stable generation of sketches, we design a training-based stroke generator that employs improved CLIPasso (Vinker et al., 2022) from the guidance sketch generator as ideal guidance. It allows us to infer high-quality sketches stably by utilizing pre-trained weights. Our stroke generator consists of eight transformer decoder layers and two MLP decoder layers. During training, to guarantee the stroke generator learns features better, process sketches $\{\mathcal{P}_{i}\}_{i=1}^{K}$ (K=8 in this paper) extracted from each intermediate layer are guided by guidance sketches $\{\mathcal{P}_{i}\}_{i=1}^{K}$ generated at the corresponding intermediate step of the optimization process in the guidance sketch generator. In the inference phase, the stroke generator optimizes initial strokes generated from trainable parameters into a set of n Bezier curves $\{s_{1},s_{2},\ldots,s_{n}\}$ . These strokes are then fed into the differentiable rasterizer $\mathcal{R}$ to produce a vector sketch $\mathcal{S}=\mathcal{R}(s_{1},\ldots,s_{n})=\mathcal{R}(\{(x_{j},y_{j})^{(1)}\}_{j=1}^{4},\ldots,\{(x_{j},y_{j})^{(n)}\}_{j=1}^{4})$ .

Edge-constraint Initialization The quality of guidance sketches plays a pivotal role in determining our outcomes’ quality. Original CLIPasso (Vinker et al., 2022) initializes strokes via stochastic sampling from the saliency map. It could lead to the failure to accurately capture features, as well as the aggregation of initial strokes in localized areas, resulting in generated stroke clutter. To address these issues, as shown in Figure 3 , we modify the mechanism for initializing strokes in our guidance sketch generator. We segment contour sketches using SAM (Kirillov et al., 2023) and based on segmentation results accurately place the initial stroke on the edges of component’s features to constraint stroke locations. It ensures guidance generator not only generates precise geometric modeling information but also optimizes the distribution of strokes. Initialization comparison to original CLIPasso (Vinker et al., 2022) is provided in the .

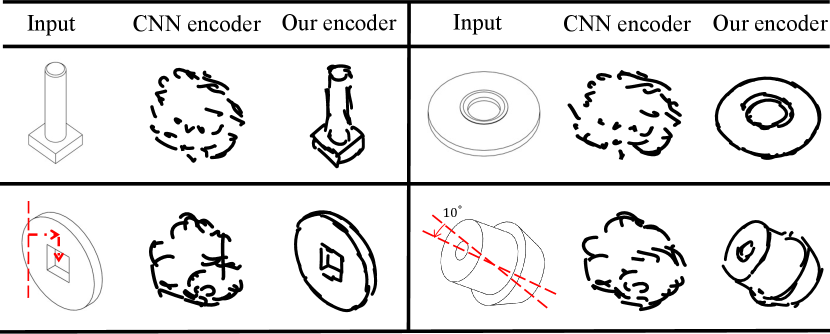
Encoder FSG requires an encoder to capture features. Previous works for similar tasks predominantly employ a CNN encoder that solely relies on local receptive fields to capture features, making it susceptible to local variations and resulting in poor robustness for inputs unseen or transformed. While vision transformer (ViT) uses a self-attention mechanism (Vaswani et al., 2017) to establish global relationships between features. It enables the model to attend to overall information in inputs, unconstrained by fixed posture or shape. Therefore, we utilize ViT-B/32 model of CLIP (Radford et al., 2021) to encode semantic understanding of visual depictions, which is trained on 400 million image-text pairs. And we combine it with an adapter that consists of two fully connected layers to fine-tune based on training data. As shown in Figure 7 and Table 1 , our encoder substantially improves the robustness to unseen models during training and the equivariance.

Loss Function During training, we employ CLIP-based perceptual loss to quantify the resemblance between generated freehand sketch $\mathcal{S}$ and contour sketch $\mathcal{C}$ considering both geometric and semantic differences (Vinker et al., 2022; Radford et al., 2021) . For synthesis of a sketch that is semantically similar to the given contour sketch, the goal is to constrict the distance in the embedding space of the CLIP model represented by $CLIP(x)$ , defined as:

(1)

\mathcal{L}_{semantic}=\phi(CLIP(C),CLIP(S)),

where $\phi$ represents the cosine proximity of the CLIP embeddings, i.e., $\phi(x,y)=1-\cos(x,y)$ . Beyond this, the geometric similarity is measured by contrasting low-level features of output sketch and input contour, as follows:

(2)

\mathcal{L}_{geometric}=\sum_{i=3,4}dist(CLIP_{i}(C),CLIP_{i}(S)),

where $dist$ represents the $\mathcal{L}_{2}$ norm, explicitly, $dist(x,y)=\|x-y\|_{2}^{2}$ , and $CLIP_{i}$ is the $i$ -th layer CLIP encoder activation. As recommended by (Vinker et al., 2022), we use layers 3 and 4 of the ResNet101 CLIP model. Finally, the perceptual loss is given by:

(3)

\mathcal{L}_{percept}=\mathcal{L}_{geometric}+\beta_{s}\mathcal{L}_{semantic},

where $\beta_{s}$ is set to 0.1.

In the process of optimizing the stroke generator, a guidance loss is employed to quantify the resemblance between guidance sketches $\mathcal{G}$ and process sketches $\mathcal{P}$ . Firstly, we introduce the Jonker-Volgenant algorithm (Kuhn, 1955) to ensure that guidance loss is invariant to arrangement of each stroke’s order, which is extensively utilized in assignment problems. The mathematical expression is as follows:

(4)

\mathcal{L}_{JK}=\sum_{k=1}^{K}\mathop{\min}_{\alpha}\sum_{i=1}^{n}\mathcal{L}_{1}(g_{k}^{(i)},p_{k}^{\alpha(i)}),

where $\mathcal{L}_{1}$ is the manhattan distance, $n$ is the number of strokes in the sketch. $p_{k}^{(i)}$ is the $i$ -th stroke of the sketch from the $k$ -th middle process layer (with a total of $K$ layers), and $g_{k}^{(i)}$ is the guidance stroke corresponding to $p_{k}^{\alpha(i)}$ , $\alpha$ is an arrangement of stroke indices.

Additionally, we innovatively integrate bidirectional Hausdorff distance into the guidance loss, which serves as a metric quantifying the similarity between two non-empty point sets that our strokes can be considered as. It aids the model in achieving more precise matching of guidance sketch edges and maintaining structural relationships between shapes during training, thereby capturing more global features and enhancing the model’s robustness to input with transformations. Experiment evaluation can be seen in section 4.5 , The specific mathematical expression is as follows:

(5)

\mathcal{\delta}_{H}=\max\{\tilde{\delta}_{H}(\mathcal{G},\mathcal{P}),\tilde{\delta}_{H}(\mathcal{P},\mathcal{G})\},

where $\mathcal{P}=\{p_{1},\ldots,p_{n}\}$ is the process sketch from each layer and $\mathcal{G}=\{g_{1},\ldots,g_{n}\}$ is the guidance sketch corresponding to $\mathcal{P}$ . $g_{i}$ and $p_{i}$ represent the strokes that constitute corresponding sketch. Both $\mathcal{P}$ and $\mathcal{G}$ are sets containing n 8-dimensional vectors. $\tilde{\delta}_{H}(\mathcal{G},\mathcal{P})$ signifies the one-sided Hausdorff distance from set $\mathcal{G}$ to set $\mathcal{P}$ :

(6)

\tilde{\delta}_{H}(\mathcal{G},\mathcal{P})=\underset{g\in\mathcal{G}}{\max}\{\underset{p\in\mathcal{P}}{\min}\|g-p\|\},

where $\|\cdot\|$ is the Euclidean distance. Similarly, $\tilde{\delta}_{H}(\mathcal{P},\mathcal{G})$ represents the unidirectional Hausdorff distance from set $\mathcal{P}$ to set $\mathcal{G}$ :

(7)

\tilde{\delta}_{H}(\mathcal{P},\mathcal{G})=\underset{p\in\mathcal{P}}{\max}\{\underset{g\in\mathcal{G}}{\min}\|p-g\|\}.

The guidance loss is as follows:

(8)

\mathcal{L}_{guidance}=\mathcal{L}_{JK}+\beta_{h}\delta_{H},

where $\beta_{h}$ is set to 0.8.

Our final loss function is as follows:

(9)

\mathcal{L}_{total}=\mathcal{L}_{percept}+\mathcal{L}_{guidance}.

4. Experiments

4.1. Experimental Setup

Dataset We collect mechanical components in STEP format from TraceParts (Tra, 2001) databases, encompassing various categories. On the collected dataset, we employ hashing techniques for deduplication ensuring the uniqueness of models. Additionally, we remove models with poor quality, which are excessively simplistic or intricate, as well as exceptionally rare instances. Following this, we classify these models based on ICS (ICS, 2015) into 24 main categories. Ultimately, we obtain a clean dataset consisting of 926 models for experiments.

Implementation Details All experiments are conducted on the Ubuntu 20.04 operating system. Our hardware specifications include an Intel Xeon Gold 6326 CPU, 32GB RAM, and an NVIDIA GeForce RTX 4090. The batch size is set to 32. Contour sketches from Stage-one are processed to a size of 224 × 224 pixels. Detailed information about experiments is provided in the Appendix.

4.2. Qualitative Evaluation

Due to the absence of research on the same task, we intend to compare our approach from two perspectives, which involve approaches designed for generating engineering sketches and existing state-of-the-art freehand sketches generative methods.

Sketches of mechanical components In Figure 4 , we contrast our method with Han et al. (Han et al., 2020) and Manda et al. (Manda et al., 2021) , using our collected components as inputs. Han et al. (Han et al., 2020) use PythonOCC (Paviot, 2018) to produce view drawings, while Manda et al. (Manda et al., 2021) create sketches through image-based edge extraction techniques. Although their results preserve plentiful engineering features, it is apparent that their outcomes resembling extracted outlines from models lack the style of freehand, which limits applicability in freehand sketch modeling. In contrast, our approach almost retains essential information of mechanical components equivalent to their results, such as through holes, gear tooth, slots, and overall recognizable features, while our results also demonstrate an excellent freehand style.

Sketch with a freehand style We compare our method with excellent freehand sketch generative methods like CLIPasso (Vinker et al., 2022) and LBS (Lee et al., 2023) . Moreover, we present a contrast with DALL-E (Ramesh et al., 2021) , which is a mainstream large-model-based image generation approach. As shown in Figure 5 , all results are produced by 25 strokes using our collected dataset. In the first example, CLIPasso’s (Vinker et al., 2022) result exhibits significant disorganized strokes, and LBS (Lee et al., 2023) almost completely covers the handle of valve with numerous strokes, leading to inaccurate representation of features. In the second and third examples, results by CLIPasso (Vinker et al., 2022) lose key features, such as the gear hole and the pulley grooves. For LBS (Lee et al., 2023) , unexpected stroke connections appear between modeling features and its stroke distribution is chaotic. In contrast, our strokes accurately and clearly are distributed over the features of components. These differences are attributed to the fact that CLIPasso (Vinker et al., 2022) initializes strokes via sampling randomly from the saliency map resulting in features that may not always be captured. Although LBS (Lee et al., 2023) modifies initialization of CLIPasso (Vinker et al., 2022) , it initializes strokes still relying on saliency maps influenced by noise information like monotonous colors and textures in mechanical components. Our method addresses this issue by introducing a novel edge-constraint initialization, which accurately places initial strokes on feature edges. Additionally, as LBS reported that its transformer-based model uses a CNN encoder. So its robustness comparison to our method will be similar to the results in Figure 7 . In contrast to DALL-E (Ramesh et al., 2021) , we employ inputs consistent with previous experiments coupled with the prompt (”Create a pure white background abstract freehand sketch of input in 25 strokes”) as the final inputs. It is evident that the large-model-based sketch generation method is still inadequate for our task.

Table 1. Quantitative comparison results by metrics. ”-T” means test by transformed inputs. ”-U” means test by unseen inputs.

	Simple				Moderate				Complex
Method	FID↓	GS↓	Prec↑	Rec↑	FID↓	GS↓	Prec↑	Rec↑	FID↓	GS↓	Prec↑	Rec↑
CLIPasso (Vinker et al., 2022)	10.28	5.70	0.44	0.79	12.03	7.40	0.35	0.72	13.43	9.91	0.30	0.69
LBS (Lee et al., 2023)	9.46	5.29	0.45	0.81	11.57	7.03	0.32	0.71	12.71	8.78	0.31	0.66
Ours	6.80	3.37	0.53	0.87	7.07	3.96	0.47	0.83	7.27	4.52	0.42	0.81
Ours(VIT-B/32+adapter) -T	7.01	3.98	0.48	0.83	7.25	6.08	0.38	0.72	7.42	6.51	0.32	0.70
Ours(CNN) -T	17.46	28.10	0.18	0.56	19.44	63.14	0.13	0.37	25.13	79.44	0.11	0.25
Ours(VIT-B/32+adapter) -U	8.60	4.10	0.44	0.81	10.68	6.20	0.33	0.68	13.44	7.24	0.31	0.63
Ours(CNN) -U	18.85	30.33	0.19	0.51	20.78	70.66	0.11	0.40	27.54	87.54	0.10	0.20

4.3. Quantitative Evaluation

Metrics Evaluation We rasterize vector sketches into images and utilize evaluation metrics for image generation to assess the quality of generated sketches. FID (Fréchet Inception Distance) (Heusel et al., 2017) quantifies the dissimilarity between generated sketches and standard data by evaluating the mean and variance of sketch features, which are extracted from Inception-V3 (Szegedy et al., 2016) pre-trained on ImageNet (Krizhevsky et al., 2012) . GS (Geometry Score) (Khrulkov and Oseledets, 2018) is used to contrast the geometric information of data manifold between generated sketches and standard ones. Additionally, we apply the improved precision and recall (Kynkäänniemi et al., 2019) as supplementary metrics following other generative works (Nichol and Dhariwal, 2021) . In this experiment, we employ model outlines processed by PythonOCC (Paviot, 2018) as standard data, which encapsulate the most comprehensive engineering information. The lower FID and GS scores and higher Prec and Rec scores indicate a greater degree of consistency in preserving modeling features between the generated sketches and the standard data. As shown in Table 1 , we classify generated sketches into three levels based on the number of strokes ( $NoS$ ) : Simple ( $16\leq NoS\textless 24$ strokes), Moderate ( $24\leq NoS\textless 32$ strokes), and Complex ( $32\leq NoS\textless 40$ strokes). The first part of Table 1 showcases comparisons between our approach and other competitors, revealing superior FID, GS, Precision, and Recall scores across all three complexity levels. Consistent with the conclusions of qualitative evaluation, our approach retains more precise modeling features while generating freehand sketches. Additional metrics evaluation (standard data employ human-drawn sketches) is provided in the Appendix.

User Study We randomly select 592 mechanical components from 15 main categories in collected dataset as the test dataset utilized in user study. We compare results produced by Han et al. (Han et al., 2020) , Manda et al. (Manda et al., 2021) , CLIPasso (Vinker et al., 2022) , LBS (Lee et al., 2023) and our method (the last three methods create sketches in 25 strokes). We invite 47 mechanical modeling researchers and ask them to score sketches based on two aspects: engineering information and the freehand style. Scores range from 0 to 5, with higher scores indicating better performance in creating features and possessing a hand-drawn style. Finally, we compute average scores for all components in each method. As shown in Table 2 , the result of user study indicates that our method achieves the highest style score and overall score. These reveal our results have a human-prefer freehand style and a better comprehensive performance in balancing information with style.

Table 2. User study results. ”Information” is the engineering information content score , ”Style” denotes the score of freehand style, and ”Overall” is the average of these two scores.

Method	Information↑	Style↑	Overall↑
Han et al.(Han et al., 2020)	4.20	0.84	2.52
Manda et al. (Manda et al., 2021)	4.04	1.21	2.63
CLIPasso (Vinker et al., 2022)	2.71	3.81	3.26
LBS (Lee et al., 2023)	2.94	3.76	3.35
Ours	3.80	3.84	3.82

4.4. Performance of the Model

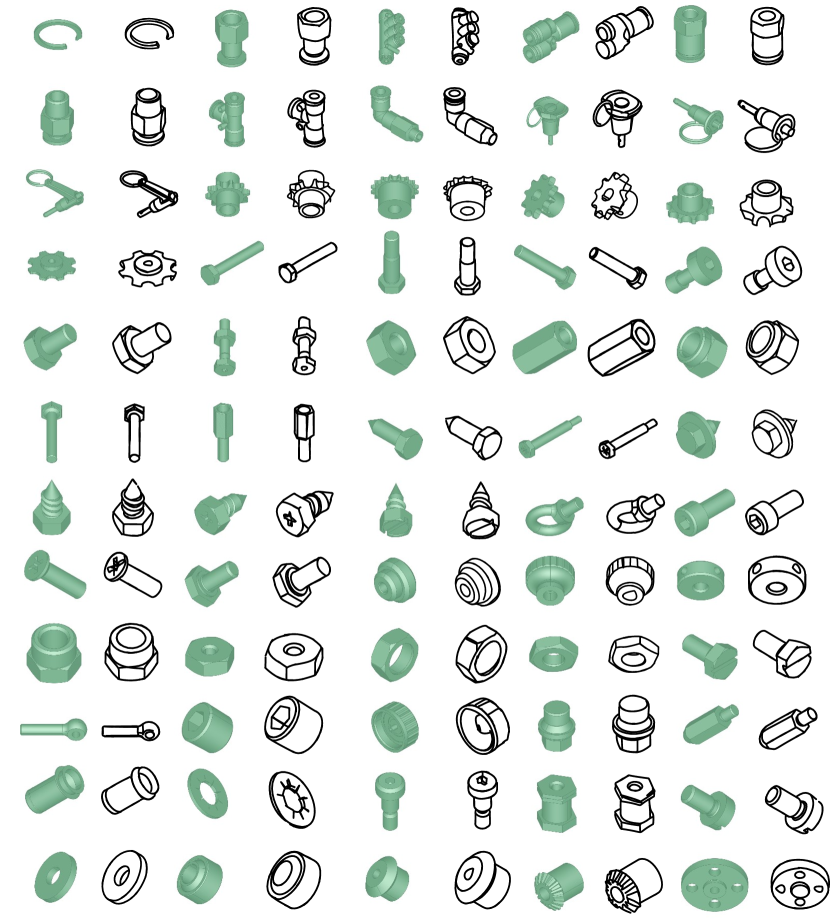
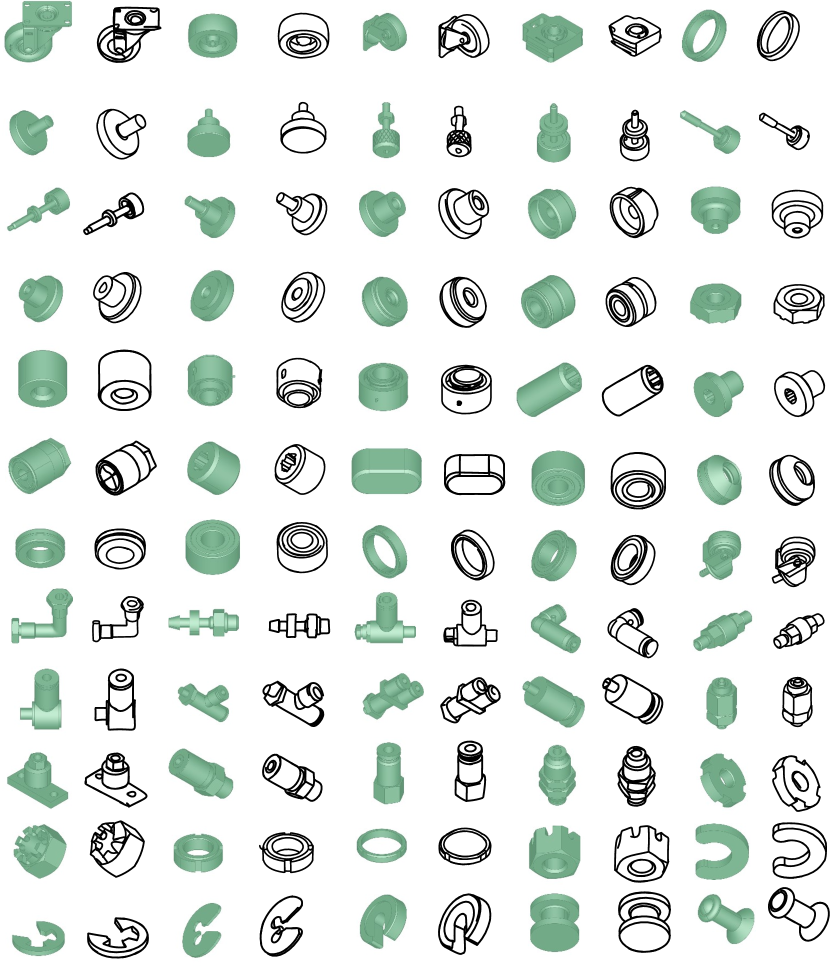
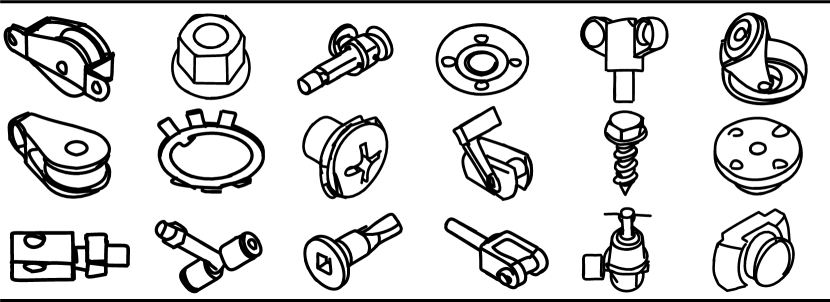
Different from traditional sketch generation methods, our generative model does not require additional sketch datasets. All training sketches are produced from our guidance sketch generator, which is optimized via CLIP (Radford et al., 2021) , a model pre-trained on four billion text-image pairs, producing high-quality guidance sketches. Benefiting from the guidance sketch generation process not being limited to specific categories, our method demonstrates robustness across a wide variety of mechanical components. In Figures 1 and 6 , we showcase excellent generation results for various mechanical components. More qualitative results are provided in Appendix.

Table 3. Ablation Study with metrics evaluation. S-O : Stage-One, E-I : Guidance sketches generated by edge-constraint initialization , L-H: Training using

\mathcal{L}_{Hausdorff}

. ”-T” means test by transformed inputs.

. Simple Moderate Complex Model S-O I-O L-H FID↓ GS↓ Prec↑ Rec↑ FID↓ GS↓ Prec↑ Rec↑ FID↓ GS↓ Prec↑ Rec↑ Ours ✓ ✓ 9.01 4.73 0.45 0.81 10.57 6.79 0.39 0.75 11.11 7.20 0.31 0.68 Ours ✓ ✓ 7.69 4.38 0.47 0.82 8.28 5.08 0.40 0.78 8.62 6.43 0.33 0.70 Ours ✓ ✓ ✓ 6.80 3.37 0.53 0.87 7.07 3.96 0.47 0.83 7.27 4.52 0.42 0.81 Ours -T ✓ ✓ 9.42 5.38 0.40 0.74 10.23 7.34 0.32 0.65 11.04 8.77 0.21 0.63 Ours -T ✓ ✓ ✓ 7.01 3.98 0.48 0.83 7.25 5.28 0.38 0.72 7.42 6.51 0.32 0.70

Previous works like (Lee et al., 2023) predominantly employ a CNN encoder that uses fixed-size convolution kernels and pooling layers to extract local features. It leads to the neglect of global information, resulting in poor robustness. To address this issue, we utilize a CLIP ViT-B/32 combined with an adapter as our encoder. Qualitative and quantitative comparative experiments are designed to demonstrate the efficacy of our encoder. In the first row of Figure 7 , we employ models which are similar-category, but unseen in training as test inputs. Compared to the method using a CNN encoder (ResNeXt18 (Xie et al., 2017) is used in this experiment), which only produces chaotic and shapeless strokes, the method with our encoder creates sketches with recognizable overall contours and essential features. In the second row, we apply contour sketches seen in training as inputs, each of which is transformed to the right and downward by 5 pixels and rotated counterclockwise by 10°. It can be observed that the method with our encoder still accurately infers component sketches, whereas the one using a CNN encoder fails to generate recognizable features. The quantitative comparison results are presented in the second part of Table 1 . Consistent with our expectations, the method with our encoder performs better in terms of evaluation metrics. It showcases that our encoder fortifies the encoding robustness for unseen and transformed inputs, enhancing the generalization and equivariance of the model.

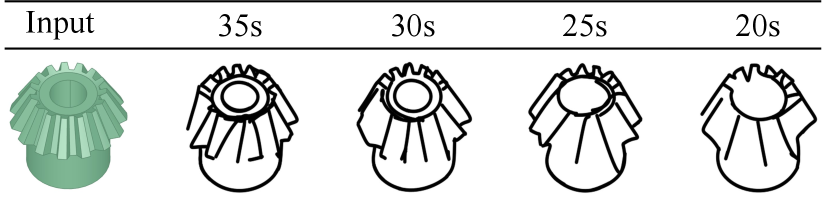
Abstraction is an important characteristic of freehand sketches. Our method effectively achieves it by individually training the stroke generator on different levels of abstraction sketches datasets. As shown in Figure 8 , we respectively present the generated sketches from an input gear component using 35, 30, 25, and 20 strokes. As the number of strokes decreases, the abstraction level of gear sketches increases. Our method constrains strokes to create the essence of the gear. Iconic characteristics of a gear such as the general contour, teeth, and tooth spaces can be maintained, even though some minor details like through-holes may be removed.

4.5. Ablation Study

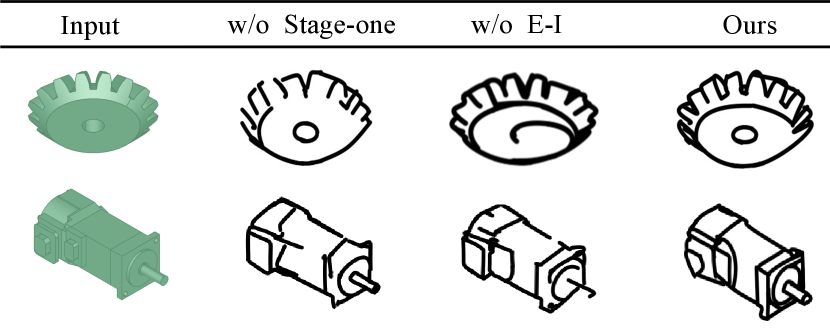
Stage-One As shown in Figure 9 , the results of the method lacking Stage-One are susceptible to issues such as producing unstructured features and line distortions in qualitative ablation experiment. Excellent metric scores in Table 3 demonstrate our complete framework can create richer and more accurate modeling information. This improvement is attributed to Stage-One, which filters out noise information such as color, texture, and shadows, mitigating their interference with the generation process.

Edge-constraint Initialization In order to verify whether edge-constraint initialization can make precise geometric modeling features, we remove the optimized mechanism in the initial process. Comparison in Figure 9 clearly demonstrates that sketches generated with edge-constraint initialization(E-I) exhibit better performance in details generation and more reasonable stroke distribution. These benefit from E-I ensuring that initial strokes are accurately distributed on the edges of model features. Similarly, we utilized quantitative metrics to measure the generation performance. As shown in Table 3 , sketches generated after initialization optimization achieve improvements in metrics such as FID, GS, and so on.

Hausdorff distance Loss Hausdorff distance is a metric used to measure the distance between two shapes, considering not only the spatial positions but also the structural relationships between shapes. By learning shape invariance and semantic features, the model can more accurately match shapes with different transformations and morphologies, aiding in the model’s equivariance. The ablation experimental result is depicted in Table 3 . It is evident that all the quantitative metrics for our method training with Hausdorff distance become better on the transformed test dataset.

5. Conclusion and Future Work

This paper proposes a novel two-stage framework, which is the first time to generate freehand sketches for mechanical components. We mimic the human sketching behavior pattern that produces optimal-view contour sketches in Stage-One and then translate them into freehand sketches in Stage-Two. To retain abundant and precise modeling features, we introduce an innovative edge-constraint initialization. Additionally, we utilize a CLIP vision encoder and propose a Hausdorff distance-based guidance loss to improve the robustness of the model. Our approach aims to promote research on data-driven algorithms in the freehand sketch domain. Extensive experiments demonstrate that our approach performs superiorly compared to state-of-the-art methods.

Through experiments, we discover that we would better utilize a comprehensive model rather than direct inference to obtain desirable outcomes for unseen models with significant geometric differences. In future work, we will explore methods to address this issue, further enhancing the model’s generalizability.

Acknowledgements.

This work is partially supported by National Key Research and Development Program of China (2022YFB3303101). We thank Chaoran Zhang, Fuhao Li, Hao Zhang, and Duc Vu Minh for their valuable advice, which helped to improve this work. (Chaoran Zhang, Fuhao Li, and Hao Zhang are members of the Tsinghua IMMV Lab.) We also thank Newdim for providing data support.

References

(1)
Tra (2001) 2001. TraceParts. https://www.traceparts.com/en.
ICS (2015) 2015. International Classification for Standards. https://www.iso.org/publication/PUB100033.html.
Bhunia et al. (2022) Ankan Kumar Bhunia, Salman Khan, Hisham Cholakkal, Rao Muhammad Anwer, Fahad Shahbaz Khan, Jorma Laaksonen, and Michael Felsberg. 2022. Doodleformer: Creative sketch drawing with transformers. In European Conference on Computer Vision. Springer, 338–355.
Canny (1986) John Canny. 1986. A computational approach to edge detection. IEEE Transactions on pattern analysis and machine intelligence 6 (1986), 679–698.
Cao et al. (2019) Nan Cao, Xin Yan, Yang Shi, and Chaoran Chen. 2019. AI-sketcher: a deep generative model for producing high-quality sketches. In Proceedings of the AAAI conference on artificial intelligence, Vol. 33. 2564–2571.
DeCarlo (2012) Doug DeCarlo. 2012. Depicting 3D shape using lines. Human Vision and Electronic Imaging XVII 8291 (2012), 361–376.
DeCarlo et al. (2023) Doug DeCarlo, Adam Finkelstein, Szymon Rusinkiewicz, and Anthony Santella. 2023. Suggestive contours for conveying shape. In Seminal Graphics Papers: Pushing the Boundaries, Volume 2. 401–408.
Dosovitskiy et al. (2020) Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, et al. 2020. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929 (2020).
Ganin et al. (2018) Yaroslav Ganin, Tejas Kulkarni, Igor Babuschkin, S. M. Ali Eslami, and Oriol Vinyals. 2018. Synthesizing Programs for Images using Reinforced Adversarial Learning. In Proceedings of the 35th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 80), Jennifer Dy and Andreas Krause (Eds.). PMLR, 1666–1675. https://proceedings.mlr.press/v80/ganin18a.html
Gao et al. (2024) Peng Gao, Shijie Geng, Renrui Zhang, Teli Ma, Rongyao Fang, Yongfeng Zhang, Hongsheng Li, and Yu Qiao. 2024. Clip-adapter: Better vision-language models with feature adapters. International Journal of Computer Vision 132, 2 (2024), 581–595.
Ge et al. (2020) Songwei Ge, Vedanuj Goswami, C. Lawrence Zitnick, and Devi Parikh. 2020. Creative Sketch Generation. arXiv:2011.10039 [cs.CV]
Goodfellow et al. (2014) Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. 2014. Generative adversarial nets. Advances in neural information processing systems 27 (2014).
Ha and Eck (2017) David Ha and Douglas Eck. 2017. A neural representation of sketch drawings. arXiv preprint arXiv:1704.03477 (2017).
Hähnlein et al. (2022) Felix Hähnlein, Changjian Li, Niloy J Mitra, and Adrien Bousseau. 2022. CAD2Sketch: Generating Concept Sketches from CAD Sequences. ACM Transactions on Graphics (TOG) 41, 6 (2022), 1–18.
Han et al. (2020) Wenyu Han, Siyuan Xiang, Chenhui Liu, Ruoyu Wang, and Chen Feng. 2020. Spare3d: A dataset for spatial reasoning on three-view line drawings. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 14690–14699.
Heusel et al. (2017) Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, and Sepp Hochreiter. 2017. Gans trained by a two time-scale update rule converge to a local nash equilibrium. Advances in neural information processing systems 30 (2017).
Huang et al. (2024b) Jiancheng Huang, Mingfu Yan, Songyan Chen, Yi Huang, and Shifeng Chen. 2024b. MagicFight: Personalized Martial Arts Combat Video Generation. In ACM Multimedia 2024. https://openreview.net/forum?id=7JhV3Pbfgk
Huang et al. (2024a) Yi Huang, Jiancheng Huang, Yifan Liu, Mingfu Yan, Jiaxi Lv, Jianzhuang Liu, Wei Xiong, He Zhang, Shifeng Chen, and Liangliang Cao. 2024a. Diffusion model-based image editing: A survey. arXiv preprint arXiv:2402.17525 (2024).
Judd et al. (2007) Tilke Judd, Frédo Durand, and Edward Adelson. 2007. Apparent ridges for line drawing. ACM transactions on graphics (TOG) 26, 3 (2007), 19–es.
Khrulkov and Oseledets (2018) Valentin Khrulkov and Ivan Oseledets. 2018. Geometry score: A method for comparing generative adversarial networks. In International conference on machine learning. PMLR, 2621–2629.
Kingma and Welling (2013) Diederik P Kingma and Max Welling. 2013. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114 (2013).
Kirillov et al. (2023) Alexander Kirillov, Eric Mintun, Nikhila Ravi, Hanzi Mao, Chloe Rolland, Laura Gustafson, Tete Xiao, Spencer Whitehead, Alexander C Berg, Wan-Yen Lo, et al. 2023. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision. 4015–4026.
Krizhevsky et al. (2012) Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. 2012. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems 25 (2012).
Kuhn (1955) Harold W Kuhn. 1955. The Hungarian method for the assignment problem. Naval research logistics quarterly 2, 1-2 (1955), 83–97.
Kynkäänniemi et al. (2019) Tuomas Kynkäänniemi, Tero Karras, Samuli Laine, Jaakko Lehtinen, and Timo Aila. 2019. Improved precision and recall metric for assessing generative models. Advances in neural information processing systems 32 (2019).
Lee et al. (2023) Hyundo Lee, Inwoo Hwang, Hyunsung Go, Won-Seok Choi, Kibeom Kim, and Byoung-Tak Zhang. 2023. Learning Geometry-aware Representations by Sketching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 23315–23326.
Li et al. (2020b) Changjian Li, Hao Pan, Adrien Bousseau, and Niloy J. Mitra. 2020b. Sketch2CAD: sequential CAD modeling by sketching in context. ACM Trans. Graph. 39, 6, Article 164 (nov 2020), 14 pages. https://doi.org/10.1145/3414685.3417807
Li et al. (2022) Changjian Li, Hao Pan, Adrien Bousseau, and Niloy J. Mitra. 2022. Free2CAD: parsing freehand drawings into CAD commands. ACM Trans. Graph. 41, 4, Article 93 (jul 2022), 16 pages. https://doi.org/10.1145/3528223.3530133
Li et al. (2020a) SuChang Li, Kan Li, Ilyes Kacher, Yuichiro Taira, Bungo Yanatori, and Imari Sato. 2020a. Artpdgan: Creating artistic pencil drawing with key map using generative adversarial networks. In Computational Science–ICCS 2020: 20th International Conference, Amsterdam, The Netherlands, June 3–5, 2020, Proceedings, Part VII 20. Springer, 285–298.
Lin et al. (2020) Hangyu Lin, Yanwei Fu, Xiangyang Xue, and Yu-Gang Jiang. 2020. Sketch-bert: Learning sketch bidirectional encoder representation from transformers by self-supervised learning of sketch gestalt. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 6758–6767.
Liu et al. (2020a) Difan Liu, Mohamed Nabail, Aaron Hertzmann, and Evangelos Kalogerakis. 2020a. Neural contours: Learning to draw lines from 3d shapes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 5428–5436.
Liu et al. (2020b) Runtao Liu, Qian Yu, and Stella X Yu. 2020b. Unsupervised sketch to photo synthesis. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part III 16. Springer, 36–52.
Liu et al. (2021) Songhua Liu, Tianwei Lin, Dongliang He, Fu Li, Ruifeng Deng, Xin Li, Errui Ding, and Hao Wang. 2021. Paint Transformer: Feed Forward Neural Painting With Stroke Prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV). 6598–6607.
Luhman and Luhman (2020) Troy Luhman and Eric Luhman. 2020. Diffusion models for handwriting generation. arXiv preprint arXiv:2011.06704 (2020).
Ma et al. (2023) Yue Ma, Xiaodong Cun, Yingqing He, Chenyang Qi, Xintao Wang, Ying Shan, Xiu Li, and Qifeng Chen. 2023. MagicStick: Controllable Video Editing via Control Handle Transformations. arXiv preprint arXiv:2312.03047 (2023).
Ma et al. (2024a) Yue Ma, Yingqing He, Xiaodong Cun, Xintao Wang, Siran Chen, Xiu Li, and Qifeng Chen. 2024a. Follow your pose: Pose-guided text-to-video generation using pose-free videos. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 38. 4117–4125.
Ma et al. (2024b) Yue Ma, Yingqing He, Hongfa Wang, Andong Wang, Chenyang Qi, Chengfei Cai, Xiu Li, Zhifeng Li, Heung-Yeung Shum, Wei Liu, et al. 2024b. Follow-Your-Click: Open-domain Regional Image Animation via Short Prompts. arXiv preprint arXiv:2403.08268 (2024).
Ma et al. (2022a) Yue Ma, Yali Wang, Yue Wu, Ziyu Lyu, Siran Chen, Xiu Li, and Yu Qiao. 2022a. Visual knowledge graph for human action reasoning in videos. In Proceedings of the 30th ACM International Conference on Multimedia. 4132–4141.
Ma et al. (2022b) Yue Ma, Tianyu Yang, Yin Shan, and Xiu Li. 2022b. Simvtp: Simple video text pre-training with masked autoencoders. arXiv preprint arXiv:2212.03490 (2022).
Manda et al. (2021) Bharadwaj Manda, Shubham Dhayarkar, Sai Mitheran, VK Viekash, and Ramanathan Muthuganapathy. 2021. ‘CADSketchNet’-An annotated sketch dataset for 3D CAD model retrieval with deep neural networks. Computers & Graphics 99 (2021), 100–113.
Manushree et al. (2021) V Manushree, Sameer Saxena, Parna Chowdhury, Manisimha Varma, Harsh Rathod, Ankita Ghosh, and Sahil Khose. 2021. XCI-Sketch: Extraction of Color Information from Images for Generation of Colored Outlines and Sketches. arXiv preprint arXiv:2108.11554 (2021).
Marr (1977) David Marr. 1977. Analysis of occluding contour. Proceedings of the Royal Society of London. Series B. Biological Sciences 197, 1129 (1977), 441–475.
Nichol and Dhariwal (2021) Alexander Quinn Nichol and Prafulla Dhariwal. 2021. Improved denoising diffusion probabilistic models. In International conference on machine learning. PMLR, 8162–8171.
Ohtake et al. (2004) Yutaka Ohtake, Alexander Belyaev, and Hans-Peter Seidel. 2004. Ridge-valley lines on meshes via implicit surface fitting. In ACM SIGGRAPH 2004 Papers. 609–612.
Para et al. (2021) Wamiq Para, Shariq Bhat, Paul Guerrero, Tom Kelly, Niloy Mitra, Leonidas J Guibas, and Peter Wonka. 2021. SketchGen: Generating Constrained CAD Sketches. In Advances in Neural Information Processing Systems, M. Ranzato, A. Beygelzimer, Y. Dauphin, P.S. Liang, and J. Wortman Vaughan (Eds.), Vol. 34. Curran Associates, Inc., 5077–5088. https://proceedings.neurips.cc/paper_files/paper/2021/file/28891cb4ab421830acc36b1f5fd6c91e-Paper.pdf
Paviot (2018) T Paviot. 2018. pythonocc, 3d cad/cae/plm development framework for the python programming language.
Prewitt et al. (1970) Judith MS Prewitt et al. 1970. Object enhancement and extraction. Picture processing and Psychopictorics 10, 1 (1970), 15–19.
Radford et al. (2021) Alec Radford, Jong Wook Kim, Chris Hallacy, Aditya Ramesh, Gabriel Goh, Sandhini Agarwal, Girish Sastry, Amanda Askell, Pamela Mishkin, Jack Clark, et al. 2021. Learning transferable visual models from natural language supervision. In International conference on machine learning. PMLR, 8748–8763.
Ramesh et al. (2021) Aditya Ramesh, Mikhail Pavlov, Gabriel Goh, Scott Gray, Chelsea Voss, Alec Radford, Mark Chen, and Ilya Sutskever. 2021. Zero-shot text-to-image generation. In International conference on machine learning. Pmlr, 8821–8831.
Ribeiro et al. (2020) Leo Sampaio Ferraz Ribeiro, Tu Bui, John Collomosse, and Moacir Ponti. 2020. Sketchformer: Transformer-Based Representation for Sketched Structure. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR).
Seff et al. (2020) Ari Seff, Yaniv Ovadia, Wenda Zhou, and Ryan P Adams. 2020. Sketchgraphs: A large-scale dataset for modeling relational geometry in computer-aided design. arXiv preprint arXiv:2007.08506 (2020).
Sobel et al. (1968) Irwin Sobel, Gary Feldman, et al. 1968. A 3x3 isotropic gradient operator for image processing. a talk at the Stanford Artificial Project in 1968 (1968), 271–272.
Szegedy et al. (2016) Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jon Shlens, and Zbigniew Wojna. 2016. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE conference on computer vision and pattern recognition. 2818–2826.
Tong et al. (2021) Zhengyan Tong, Xuanhong Chen, Bingbing Ni, and Xiaohang Wang. 2021. Sketch generation with drawing process guided by vector flow and grayscale. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 35. 609–616.
Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. Advances in neural information processing systems 30 (2017).
Vinker et al. (2022) Yael Vinker, Ehsan Pajouheshgar, Jessica Y Bo, Roman Christian Bachmann, Amit Haim Bermano, Daniel Cohen-Or, Amir Zamir, and Ariel Shamir. 2022. Clipasso: Semantically-aware object sketching. ACM Transactions on Graphics (TOG) 41, 4 (2022), 1–11.
Wang et al. (2022) Qiang Wang, Haoge Deng, Yonggang Qi, Da Li, and Yi-Zhe Song. 2022. SketchKnitter: Vectorized Sketch Generation with Diffusion Models. In The Eleventh International Conference on Learning Representations.
Wang et al. (2020) Tianying Wang, Wei Qi Toh, Hao Zhang, Xiuchao Sui, Shaohua Li, Yong Liu, and Wei Jing. 2020. Robocodraw: Robotic avatar drawing with gan-based style transfer and time-efficient path optimization. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 34. 10402–10409.
Willis et al. (2021) Karl DD Willis, Pradeep Kumar Jayaraman, Joseph G Lambourne, Hang Chu, and Yewen Pu. 2021. Engineering sketch generation for computer-aided design. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2105–2114.
Winnemöller et al. (2012) Holger Winnemöller, Jan Eric Kyprianidis, and Sven C Olsen. 2012. XDoG: An eXtended difference-of-Gaussians compendium including advanced image stylization. Computers & Graphics 36, 6 (2012), 740–753.
Xie et al. (2013) Ning Xie, Hirotaka Hachiya, and Masashi Sugiyama. 2013. Artist agent: A reinforcement learning approach to automatic stroke generation in oriental ink painting. IEICE TRANSACTIONS on Information and Systems 96, 5 (2013), 1134–1144.
Xie et al. (2017) Saining Xie, Ross Girshick, Piotr Dollár, Zhuowen Tu, and Kaiming He. 2017. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE conference on computer vision and pattern recognition. 1492–1500.
Ye et al. (2019) Meijuan Ye, Shizhe Zhou, and Hongbo Fu. 2019. DeepShapeSketch : Generating hand drawing sketches from 3D objects. In 2019 International Joint Conference on Neural Networks (IJCNN). 1–8. https://doi.org/10.1109/IJCNN.2019.8851809
Yue Ma (2024) Hongfa Wang Heng Pan Yingqing He Junkun Yuan Ailing Zeng Chengfei Cai Heung-Yeung Shum Wei Liu Qifeng Chen Yue Ma, Hongyu Liu. 2024. Follow-Your-Emoji: Fine-Controllable and Expressive Freestyle Portrait Animation. (2024). arXiv:2406.01900 [cs.CV]
Zaremba et al. (2014) Wojciech Zaremba, Ilya Sutskever, and Oriol Vinyals. 2014. Recurrent neural network regularization. arXiv preprint arXiv:1409.2329 (2014).
Zeng et al. (2019) Long Zeng, Zhi kai Dong, Jia yi Yu, Jun Hong, and Hong yu Wang. 2019. Sketch-based Retrieval and Instantiation of Parametric Parts. Computer-Aided Design 113 (2019), 82–95. https://doi.org/10.1016/j.cad.2019.04.003
Zeng et al. (2012) Long Zeng, Yong-Jin Liu, Sang Hun Lee, and Matthew Ming-Fai Yuen. 2012. Q-Complex: Efficient non-manifold boundary representation with inclusion topology. Computer-Aided Design 44, 11 (2012), 1115–1126. https://doi.org/10.1016/j.cad.2012.06.002
Zhang et al. (2015) Liliang Zhang, Liang Lin, Xian Wu, Shengyong Ding, and Lei Zhang. 2015. End-to-end photo-sketch generation via fully convolutional representation learning. In Proceedings of the 5th ACM on International Conference on Multimedia Retrieval. 627–634.
Zhao et al. (2018) Hengshuang Zhao, Xiaojuan Qi, Xiaoyong Shen, Jianping Shi, and Jiaya Jia. 2018. Icnet for real-time semantic segmentation on high-resolution images. In Proceedings of the European conference on computer vision (ECCV). 405–420.
Zheng et al. (2018) Ningyuan Zheng, Yifan Jiang, and Dingjiang Huang. 2018. Strokenet: A neural painting environment. In International Conference on Learning Representations.

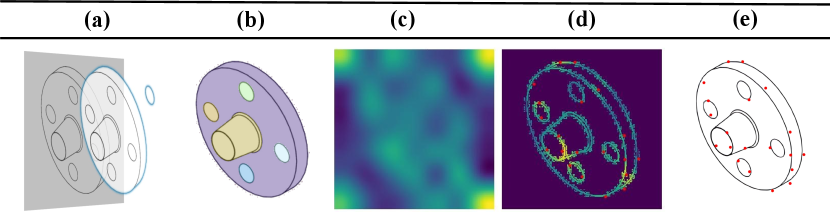
Appendix A Initialization Analysis

In this section, we will meticulously contrast and analyze our Edge-constant initialization with the original CLIPasso (Vinker et al., 2022) initialization method.

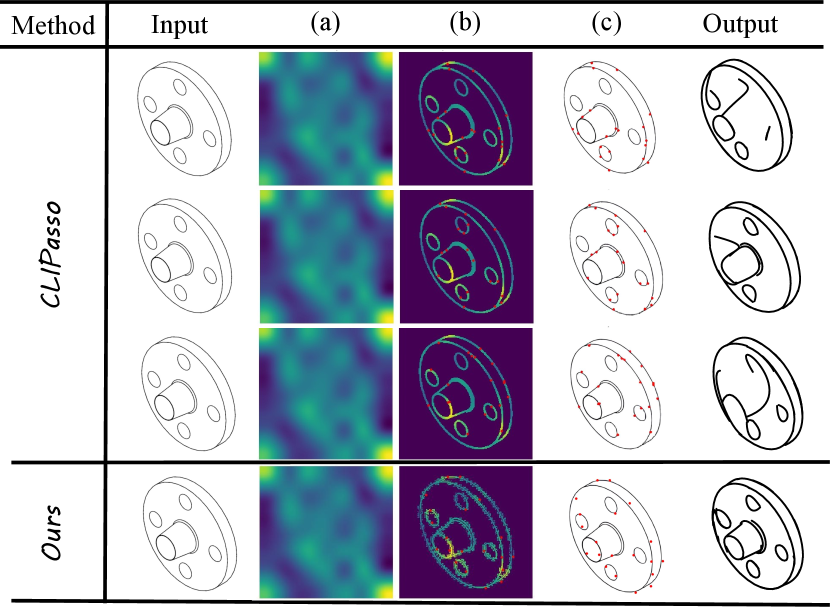
As described in CLIPasso (Vinker et al., 2022), it utilizes the ViT-32/B CLIP (Radford et al., 2021) to obtain the salient regions of a target image. This is achieved by averaging the attention outputs from all attention heads across each self-attention layer, generating a total of 12 attention maps. These maps are further averaged to derive the relevancy map, obtained by examining the attention between the final class embedding and all 49 patches. Subsequently, this relevancy map is combined with the edge map obtained through XDoG (Winnemöller et al., 2012) extraction. The resulting attention map is then utilized to determine the locations for the initial strokes. In the process of determining the initial positions of strokes, CLIPasso(Vinker et al., 2022) utilizes random seeds on the saliency map to sample positions for the first control point of each curve. Following this, it randomly selects the subsequent three control points of each Bezier curve within a small radius (0.05) of the initial point.

Such random initialization methods often result in the initial points of strokes being inadequately distributed around the critical features of mechanical components during sketch generation, leading to the loss of substantial modeling information. Moreover, this approach frequently results in an excessive placement of initial stroke points in certain prominent feature areas, causing confusion in generating sketch strokes and preventing accurate representation of modeling features. To address this issue, we propose the edge-constant initialization to deterministically sample. We utilize SAM (Kirillov et al., 2023) to perform feature segmentation on the input contour sketch. Based on the segmentation results, we predefine four stroke initialization points evenly spaced along the edge of each segmented feature. Subsequently, we dynamically change the initialization points based on the comparison with the manually required number of generated strokes. If the requested number of strokes is less than the total predefined initialization points, we evenly discard points contained within each segmented feature. Conversely, if the requested number of strokes exceeds the total predefined initialization points, we employ a greedy algorithm on the saliency map of the target image to determine additional stroke initialization points in the most salient regions (Lee et al., 2023). This initialization method not only ensures the precise generation of mechanical component features but also optimizes the distribution of generated strokes, resulting in clearer generated sketches.

As shown in Figure 10, we conduct experiments using three sampling strategies of random seeds provided by CLIPasso(Vinker et al., 2022). It is evident that in the first instance, no stroke initialization points are placed at the three through-holes of the input flange contour sketch, resulting in the loss of this important feature in the result. In the second instance, the placement of three stroke initialization points on the upper right through-hole is unnecessary, as it is a simple feature that does not require three strokes to depict. In the third instance, three stroke initialization points are clustered around the edge contour of the flange, while only two initialization points are placed on the structurally complex cylindrical section. These illustrate the irrational distribution of stroke initialization points caused by the random seed sampling method, ultimately leading to unsatisfactory sketch generation results. In contrast, our proposed edge-constant initialization optimizes the placement of stroke initialization points, ensuring their rational distribution on modeling feature edges. It can be observed that sketches generated through our improved method adequately preserve crucial modeling features, with a clear and rational distribution of strokes.

Appendix B Stability Analysis

In this section, we will evaluate the stability of our transformer-based (Ribeiro et al., 2020; Liu et al., 2021; Lee et al., 2023) stroke generator.

In Stage-Two, our improved initialization method has enhanced the guidance sketch generator to produce informative freehand sketches. However, the guidance sketch generator employs an optimizer to create sketches through thousands of optimization iterations during sketch generation, leading to uncertainty in the outcomes. Each step of this optimization-based process is guided by CLIP (Radford et al., 2021) in terms of both semantic and geometric similarities to create strokes. This optimization process is uncontrollable and the optimized result from each step exhibits variability. It results in unstable and uncontrollable quality performance of the generated sketches. In order to consistently generate high-quality sketches, we adopt a transformer-based (Ribeiro et al., 2020; Liu et al., 2021; Lee et al., 2023) generative framework. We extract intermediate sketches from the optimization process of the guidance sketch generator as ideal guides for process sketches from each intermediate layer in the stroke generator. we utilize guidance loss during training to ensure that the stroke generator learns features from corresponding intermediate process guidance sketches. We employ CLIP-based (Radford et al., 2021) perceptual loss to ensure the similarity between the generated freehand sketches and contour sketches in both geometry and semantic information. Through training, all learned features are fixed into determined weights. During the inference phase, our model can rapidly infer freehand sketches based on the trained weights. This generation approach ensures output consistency and achieves satisfactory generation quality.

We design comparative experiments to validate the numerical stability of our generative framework. Using the same inputs, we conduct five rounds of sketch generation experiments separately with only the guidance sketch generator (GSG) and the complete generative framework (trained on the collected mechanical component dataset). As shown in Figure 11, the outcomes produced by the guidance sketch generator (GSG) for mechanical freehand sketches vary each time, and some of them exhibit suboptimal performance. For instance, in the case of the first instance, the distribution of the gear teeth slots varies significantly in each generated result, and due to the instability of the optimization-based generation method, issues arise such as chaotic stroke composition in the second round’s results and erroneous connections between teeth slot strokes and through-hole strokes in the fifth round’s generated sketches. Similar situations are also evident in the second and third instances. For example, in the second instance, the distribution of continuous sections of the flat-head screws differs in each round of the experiment. And results occasionally are accompanied by contour loss such as the loss of the bottom circle of the screw in the second round of experiments, and the loss of connection at the head of the screw in the fourth round. In the third instance, involving a complex motor model, the strokes creating the main body of the motor within the area marked by the red rectangle exhibit significant variations in distribution across each experimental round. Additionally, some results accurately depict small through-holes on the motor surface, while others fail to capture this information. The reason for these issues arises from the uncontrollable nature of the optimization-based generation process. Despite our efforts to accurately position stroke initialization points on features during preprocessing, deviations in geometric and semantic guidance during optimization may result in inadequate representations of certain details in the generated sketches. In contrast, our comprehensive generation framework, after being trained on a large and diverse dataset of mechanical components, fixes learned features into weights. This ensures consistent outputs in each round of testing, and stable representations of modeling features for the components.

Appendix C Implementation Details

In order to tailor our method specifically for freehand sketch generation in engineering freehand sketch modeling, we build a CAD dataset exclusively comprising mechanical components in the STEP format. we invite numerous mechanical modeling researchers to collect mechanical components from the TraceParts (Tra, 2001). They are asked to encompass a diverse array of categories to enhance the inference generalization of our generative model. In the end, we obtain a Raw dataset including nearly 2,000 mechanical components. For the collected raw dataset, we employ hashing techniques for deduplication, ensuring the uniqueness of models in the dataset. Subsequently, we remove models with poor quality, which are excessively simplistic or intricate, as well as exceptionally rare instances. Following this, we classify these models based on the International Classification for Standards (ICS) (ICS, 2015) into 24 main categories, comprising 180 corresponding subcategories. Ultimately, we obtained a clean dataset consisting of 926 models.

We implement the methods of Stage One using Python3 with PythonOCC and PyTorch, where PyTorch supports the viewpoint selector. For Stage Two, PyTorch and DiffVG are used to implement the model, where DiffVG is used for the differentiable rasterizer.

Table 4. Quantitative comparison results by metrics using real human-drawn sketches as standard data.

	Simple				Moderate				Complex
Method	FID↓	GS↓	Prec↑	Rec↑	FID↓	GS↓	Prec↑	Rec↑	FID↓	GS↓	Prec↑	Rec↑
Han et al. (Han et al., 2020)	12.66	9.54	0.48	0.75	13.83	11.44	0.39	0.69	14.68	17.22	0.35	0.68
Manda et al. (Manda et al., 2021)	14.51	9.71	0.47	0.74	15.17	12.73	0.41	0.70	15.43	18.80	0.33	0.66
CLIPasso (Vinker et al., 2022)	12.75	7.59	0.42	0.71	13.67	10.61	0.32	0.67	14.51	13.94	0.29	0.65
LBS (Lee et al., 2023)	12.40	7.53	0.43	0.73	13.19	9.24	0.30	0.65	14.03	12.60	0.28	0.63
Ours	8.35	4.77	0.51	0.83	8.83	5.43	0.46	0.81	9.26	6.57	0.40	0.78

Appendix D Additional Quantitative Evaluation

Metrics Evaluation In section 4.3 of this paper, we employ evaluation metrics for image generation to assess the quality of generated sketches. Given the absence of benchmark datasets specifically for mechanical component freehand sketches within the sketch community, we utilize component outlines processed through PythonOCC (Paviot, 2018), which encapsulate the most comprehensive engineering information, as the standard data. The experiment results demonstrate the superiority of our method over existing freehand sketch generation methods in preserving the modeling features of mechanical components. In this section, we will conduct quantitative metric evaluations on our method and other competitors using real human-drawn sketches of mechanical components collected by ourselves.

We firstly introduce the construction process of the real human-drawn sketch dataset of mechanical component. From our collection of 926 three-dimensional mechanical component dataset, we randomly select 500 components. We invite 58 researchers with sketching expertise in the mechanical modeling domain, requesting them to draw a sketch for each component from a given perspective. We then obtain a test dataset comprising 500 mechanical sketches drawn by human engineers. As shown in the Figure 12, we showcase the collection of real human-drawn sketches. Sketches of components drawn by researchers in the mechanical modeling domain preserve crucial modeling features which are essential for freehand sketch modeling. Correspondingly, certain minor details for modeling may be simplified, or overlooked by the researchers and not drawn. Moreover, it is evident that sketches crafted by humans exhibit a distinctive freehand style.

In this experiment, we utilize real human-drawn sketches of mechanical components as benchmark data, which balances maintaining crucial modeling features with exceptional freehand style well. We employ the same 500 components which are randomly selected during the construction of our real human-drawn sketches dataset as a test dataset for this experiment. Consistent with our previous approach, we generate sketches for components using different strokes based on their complexity, and categorize the generated sketches into three levels according to the number of strokes ( $NoS$ ): Simple ( $16\leq NoS<24$ strokes), Moderate ( $24\leq NoS<32$ strokes), and Complex ( $32\leq NoS<40$ strokes). We continue to evaluate the generated sketches using metrics such as FID, GS, and so on. As shown in Table 4, we compare our method with methods designed for generating engineering sketches as well as methods for producing freehand sketches. It is evident that our generation method achieved the most favorable metric scores across three different levels of complexity, demonstrating the superiority of our approach in generating freehand sketches for mechanical components. In the experimental results, our outcomes obtain lower FID and GS scores and higher Prec and Rec scores. It indicates that our sketches more closely resemble real human-drawn sketches, exhibiting a higher level of consistency in preserving key modeling features and maintaining the freehand style between our results and real ones.

Details for User Study. In the user study conducted in this paper, we invited 47 mechanical modeling researchers to rate the generated mechanical component sketches based on two dimensions: ”information” and ”style.” In this part, we provide detailed explanations of the specific criteria represented by these two dimensions. In the ”information” dimension, we ask the researchers to evaluate the completeness of modeling features contained in the sketches. This means that the higher the number of accurate modeling features retained in the generated sketches, the higher the score obtained. In the ”style” dimension, we ask the researchers to assess the overall hand-drawn style of the sketches. Specifically, they were required to consider whether the generated sketches exhibit a hand-drawn style, whether the distribution of strokes in the generated sketches is reasonable, and whether it is more similar to the distribution structure of strokes drawn by humans.

From the results of the user study, it can be observed that Han et al. (Han et al., 2020) and Manda et al. (Manda et al., 2021) perform better in the ”information” dimension. This is because their sketches are generated by contour extraction from components, nearly retaining all modeling features. However, it is worth emphasizing that, to meet the requirements of improving modeling efficiency and lowering the modeling threshold, sketches used for freehand sketch modeling should mimic human-drawn characteristics as closely as possible that preserving key modeling features while simplifying or disregarding minor ones. Therefore, although Han et al. (Han et al., 2020) and Manda et al. (Manda et al., 2021) retain relatively comprehensive features, they fail to meet the data requirements for freehand sketch modeling and they results lack a hand-drawn style, which fundamentally does not align with the demands of the task. Meanwhile, It can be observed that our generation results outperform in preserving key features of modeling among methods for generating freehand sketches. It demonstrates the effectiveness of the modules designed in our framework to retain crucial features. In terms of ”style” dimension, our sketches perform best because they exhibit a hand-drawn style while maintaining a more reasonable stroke distribution, resembling the stroke distribution habits of human drawings. Considering both dimensions, our method achieved the highest overall scores, indicating that our approach performs better than existing methods in balancing the retention of key component modeling features and mimicking human hand-drawn style.

Appendix E Additional Qualitative Results

Figure 13, Figure 14, and Figure 15 show a large number of excellent freehand sketches of mechanical components generated by our method.