Free Energy Cost to Assemble Superlattices of Polymer-Grafted Nanoparticles

Thermodynamic integration is a standard free energy calculation method which connects the reference state “0” with the state of interest “1” by a reversible path denoted by a parameter, e.g. $\lambda\in[0,1]$ Frenkel and Smit (2002). If the potential energy at the two endpoints are $U_{0}$ and $U_{1}$, then the potential energy for the coupled system at intermediate $\lambda$ can be defined as $U(\lambda)=(1-\lambda)U_{0}+\lambda U_{1}$ and the free energy of interest is calculated by the integral along the path

$$F_{1}=F_{0}+\int_{0}^{1}\left\langle\frac{\partial U(\lambda)}{\partial\lambda}\right\rangle_{\lambda}d\lambda$$

(1)

where $\left\langle\cdots\right\rangle_{\lambda}$ means to take ensemble average in the system interacting with potential energy $U(\lambda)$.

We choose isolated PGNPs as our reference state “0” and consider a reversible thermodynamic path to assemble crystalline superlattices of PGNPs in two steps (Fig. 1). In step I, each spherical PGNP in isolated state is slowly compressed into a polyhedron (usually with a shape of the Wigner-Seitz cell) by gradually increasing the repulsion strength of confining walls. In step II, confined PGNPs are stacked to form the desired superlattice, whose interactions are slowly turned on while wall confinement is being removed. In this work, we do not calculate the reference free energy $F_{0}$ for the hyperthetical crystal formed by uncompressed spherical PGNPs. We also neglect the contribution from collective vibrations of PGNPs on the superlattice, which should be small for highly compressed states. Therefore, the free energy $F$ reported in this work is the cost (per PGNP) to assemble the superlattice from uncompressed spherical PGNPs, neglecting lattice vibration. We break $F$ into two terms corresponding to the two steps (to be explained below)

$$F=F_{V}+F_{S}.$$

(2)

In step I, the starting point is the system of one isolated spherical PGNP with volume $V_{0}$ and potential energy $U_{0}=U_{\rm bond}+U_{\rm nonbond}$, where $U_{\rm bond}$ is the energy of covalent bonds in polymer chains and $U_{\rm nonbond}$ is pairwise-additive non-bonded interactions between monomers or nanoparticles. During compression along the path, the PGNP experices repulsion $W$ from several confining walls adopting the corresponding geometry of the desired superlattice. The positions of these walls define the final volume $V<V_{0}$ of the PGNP after compression. The coupled potential energy at integration parameter $\lambda$ is defined as

$$U_{\rm I}(\lambda)=U_{\rm bond}+U_{\rm nonbond}+\lambda W$$

(3)

with $\lambda$ changing from $0$ to $1$. The free energy cost $F_{V}$ in this step can be roughly associated with volume compression of the PGNP and is calculated by the integral

$\displaystyle F_{V}=\int_{0}^{1}\left\langle W\right\rangle_{\lambda}\,d\lambda.$

(4)

In step II, the fully compressed PGNPs from step I are packed into the desired superlattice. Non-bonded interactions in the system can be decomposed into three parts, $U_{\rm nonbond}=U_{N}+U_{N^{\prime}}+U_{NN^{\prime}}$, where $U_{N}$ is the interaction energy among the $N$ particles of the central PGNP, $U_{N^{\prime}}$ is the interaction energy among the $N^{\prime}$ particles of the surrounding PGNPs (usually just first nearest neighbors), and $U_{NN^{\prime}}$ is interaction energy between particles of the central PGNP and particles of the surrounding PGNPs. In addition to the walls confining the central PGNP (same as in step I), an equal number of extra walls facing outward are needed to confine the surrounding PGNPs. There is no wall between two surrounding PGNPs. If the interaction with all the walls is $W$, then the coupled potential energy is written as

$$U_{\rm II}(\lambda)=U_{\rm bond}+U_{N}+U_{N^{\prime}}+\lambda U_{NN^{\prime}}+(1-\lambda)W$$

(5)

with $\lambda$ changing from $0$ to $1$. In practice, one might need to start from over-compressed PGNPs with smaller volume $V^{\prime}<V$, which leave small gaps between them to avoid initial overlap of polymer chains. After relaxation, these gaps are filled by polymer chains. The contribution of the free energy $F_{S}(<0)$ in step II to the total free energy cost per PGNP $F$ is

$\displaystyle F_{S}=\frac{1}{2}\int_{0}^{1}\left\langle U_{NN^{\prime}}-W\right\rangle_{\lambda}\,d\lambda,$

(6)

which is related to the relaxation of surfaces between PGNPs after walls are removed. The factor $\frac{1}{2}$ is due to the sharing of each surface by two PGNPs.

We use the coarse-grained model of polymer chains and nanoparticles, in which non-bonded interactions between a pair $(i,j)$ of monomers ($m$) and/or nanoparticles ($n$) at a distance $r_{ij}$ apart follow the repulsive shifted Lennard-Jones (LJ) potential, when $r_{ij}<r_{c}+\Delta_{ij}$, $u_{\rm LJ}(r_{ij})=4\epsilon\left[\left(\frac{\sigma}{r_{ij}-\Delta_{ij}}\right)^{12}-\left(\frac{\sigma}{r_{ij}-\Delta_{ij}}\right)^{6}\right],$ where $\epsilon$ is the unit of energy and the monomer size $\sigma$ is the unit of length Bilchak et al. (2017). The choice of $\Delta_{nn}=9\sigma$, $\Delta_{mn}=4.5\sigma$ and $\Delta_{mm}=0$ makes the effective size of bare nanoparticles roughly $10\sigma$. The cutoff distance is set to $r_{c}=1.12\sigma$ so that all pair interactions are purely repulsive. Polymers are first modeled as bead-spring chains connected by finite extensible nonlinear elastic (FENE) bonds, $u_{\rm FENE}(r)=-0.5KR_{0}^{2}\ln[1-(r/R_{0})^{2}]$ $(r<R_{0})$, with force constant $K=30\epsilon/\sigma^{2}$ and bond length $R_{0}=1.5\sigma$ Kremer and Grest (1990). We also consider semiflexible chains with the harmonic bond angle potential $u_{\theta}(\theta)=K_{\theta}(\theta-\theta_{0})^{2}$ added on top of FENE bonds, where $K_{\theta}=300\epsilon\cdot$rad^-2 and $\theta_{0}=109.5^{\circ}$. We graft $N_{c}=200$ polymers by anchoring the first monomer of each chain on the surface of the nanoparticle with a rigid bond. The corresponding surface graft density is $\Sigma=0.637\sigma^{-2}$. Several chain lengths are studied with the number of monomers per chain $N_{p}=20,40,60$.

When PGNPs need to be confined into the desired polyhedral shape, polymers also interact with several repulsive walls around the PGNP through a harmonic potential $u_{w}(r)=80\epsilon(r/\sigma)^{2}$, where $r$ is the penetration depth of a monomer into the wall surface. In a system with $Z$ walls and $N$ monomers, the total wall energy is $W=\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{Z}u_{w}(r_{ij})$. For the BCC, FCC and A15 structures under study, walls are placed at the faces of the corresponding Wigner-Seitz cells, which are truncated octahedron (BCC), rhombic dodecahedron (FCC), tetrakaidecahedron and irregular dodecahedron (A15), respectively. Details of wall positions are described in Supporting Information. In step I, only one PGNP is needed under open boundary conditions. In step II, several surrounding PGNPs (not only nearest neighbors, but also some next nearest neighbors) are needed to enclose the central one. By properly choosing the simulation box under periodic boundary condisions, we use 16, 16 and 64 PGNPs to study BCC, FCC and A15, respectively (Fig 2).

The LAMMPS package is used to run constant volume molecular dynamics simulations at fixed temperature $T=1.0\epsilon/k_{B}$ with a time step $\Delta t=0.005\sigma\sqrt{m/\epsilon}$, where the mass $m$ is set the same for all particles Plimpton (1995). Each system is equilibrated for $\sim 10^{6}$ time steps before ensemble average is taken. To evaluate each thermodynamic integral numerically, $n_{\lambda}=50$-$60$ $\lambda$ points are used within Gauss-Lobatto quadrature Press et al. (1992). Two independent runs are performed for each system, whose numerical discrepancy is an order of magnitude smaller than the free energy difference between different phases studied here. All free energy results are reported in unit of $\epsilon$.

We calculate the free energy cost $F$ to assemble BCC, FCC and A15 superlattices at various Wigner-Seitz (Voronoi) cell volumes $V$ for PGNPs with flexible (FENE bonds) or semiflexible (FENE bonds plus bond angles) grafts. The volume $V$ of the polyhedron in superlattice is compared with the original volume $V_{0}=\frac{4\pi}{3}R_{0}^{3}$ of an isolated spherical PGNP, whose radius $R_{0}$ is estimated as the average of the location of the last monomer on each chain. The typical thermodynamic integration curves in step I and II are shown in Fig. 3. The curve drops rapidly, by orders of magnitude, close to the state without confining walls ($\lambda=0$ in step I and $\lambda=1$ in step II). To capture this fast change, we use $n_{\lambda}=50-60$ $\lambda$ points in each integration. The calculated volume $F_{V}$ and surface $F_{S}$ free energy cost is reported as per PGNP value.

As expected, the volume cost $F_{V}$ increases as $V$ decreases because more work is needed to compress a spherical PGNP into a smaller polyhedron (Fig. 4a). The surface term $F_{S}$ is negative because it corresponds to the free energy gain (entropy increase) after the confined flat interface is relaxed, allowing interpenetration of polymers from two neighboring PGNPs. The overall free energy cost $F=F_{V}+F_{S}$ still increases monotonically with decreasing $V$.

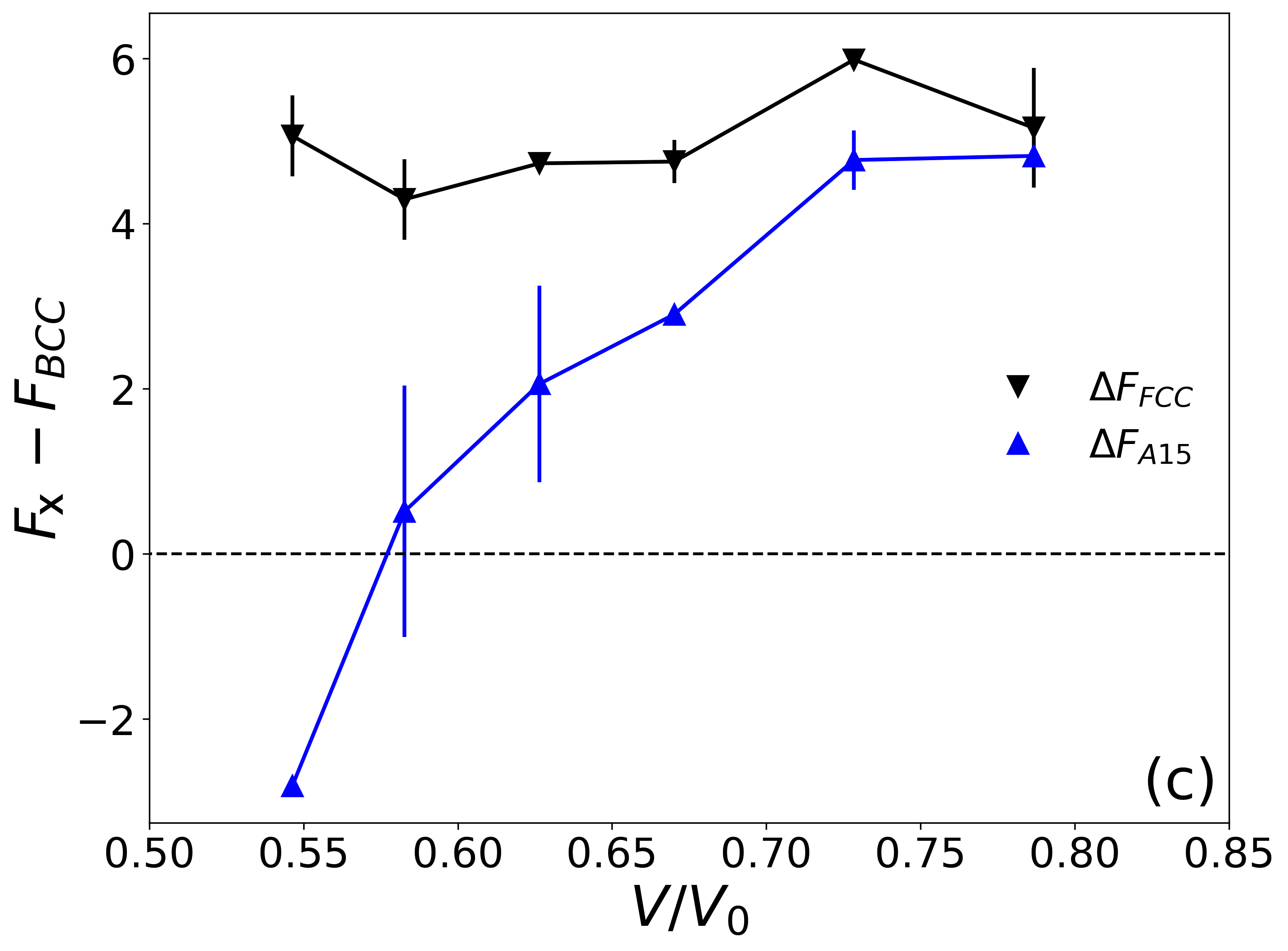
For all the chain lengths $N_{p}=20,40,60$ studied, being flexible or semiflexible, we find that BCC is more stable than FCC structure at large $V$ (Fig. 4b). We can first identify a higher free energy cost $F_{V}$ for confined FCC as shown in Fig. 4b, but the difference $\Delta F_{V}=F_{V}({\rm FCC})-F_{V}({\rm BCC})$ is only $\lesssim 1\%$ of $F_{V}({\rm BCC})$. To compare the total free energy cost $F$, we also need to include the free energy gain $F_{S}(<0)$ from surface relaxation. Since rhombic dodecahedron has $0.58\%$ more surface area than truncated octahedron, $|F_{S}|$ is slightly larger in FCC than BCC. But this surface relaxation is not strong enough to compensate the volume cost $F_{V}$. Combining two effects, the free energy cost $F$ of BCC is lower than that of FCC structure by at most $\sim 1\%$ (see data in Supporting Information). This is in agreement with previous calculations on ligand-capped nanocrystals Zha and Travesset (2018), but in contrast to the theoretical analysis of entropy penalty for chain compression/extension, which estimates that BCC can be $15\%$ more stable than FCC in ligand-capped nanocrystals Goodfellow et al. (2015). In the small $V$ limit, the numerical results of $F$ of FCC is close to or even smaller than that of BCC. But the relative difference, $\frac{F_{\rm FCC}-F_{\rm BCC}}{F_{\rm BCC}}$, is on the order of $0.1\%$, which is near the numerical precison of our thermodynamic integration scheme. Therefore, there is no clear evidence to claim that FCC is more stable than BCC at small volume, although it is possible.

We also examine the stability of A15 systems with short ($N_{p}=20$) flexible chains. Because the unit cell of A15 contains eight particles and 64 PGNPs are used in step II of thermodynamic integration, it is computationally too expensive to study longer chains under current protocol. In Voronoi tessellation of A15 structures, the two types of Frank-Kasper polyhedra, tetrakaidecahedron (Z14) and irregular dodecahedron (Z12), can have different volumes in principle. Previous study on block copolymers found that the free energy of A15 is optimized, when the volumes of Z14 and Z12 are slightly different Reddy et al. (2018). Here we focus on the equal-cell partition as in Weaire-Phelan foam Weaire and Phelan (1994), where the same $V$ for the Z14 and Z12 is assumed. The calculated the free energy $F$ shows that, although being slightly more stable than FCC, A15 is still less stable than BCC structure except at small $V$ (Fig. 4c). Since the surface area $A$ of the Wigner-Seitz polyhedron for a given volume $V$ obeys $A_{\rm FCC}>A_{\rm BCC}>\bar{A}_{\rm A15}$ ($\bar{A}_{\rm A15}$ should be the weighted average of $A_{\rm Z14}$ and $A_{\rm Z12}$ ), this results suggests that the stability of different supperlattices does not simply follow the minimum-area rule as in foams Ziherl and Kamien (2001).

To reveal the underlying mechanisms for superlattice stability, we analyze the spatial distribution of polymer chains around nanoparticle cores. We first calculate monomer density profile $\rho(z)$ along a certain crystallographic direction perpendicular to polyhedral faces. In either BCC or FCC, the inter-particle space is filled with monomers from the two neighboring PGNPs structured in three layers (Fig. 5). Close to the core, monomer density $\rho(z)$ is higher than the bulk density $\bar{\rho}$ and decays from the maximum value corresponding to the high surface grafting density $\Sigma=0.637\sigma^{-2}$. At intermediate distances, there is a “dry layer” with $\rho(z)=\bar{\rho}$ and monomers come from only one PGNP. Further away, coronas from two PGNPs start to overlap, forming an “interpenetration layer” Midya et al. (2020).

By symmetry, each shared polyhedral face bisects the center-to-center line at the location where monomer density from one PGNP equals to half of the total monomer density. This location can also be read from half of the lattice constant $a$ along each crystallographic direction (see Supporting Information for the value of $a$). Due to the interpenetration of chains, the faces of PGNP polyhedra on supperlattice are strongly roughened, and the shape of PGNPs is more smoothened and spherical than a perfect Wigner-Seitz polyhedron, as will be revealed below.

We can quantify the states of grafted polymer chains by studying the distribution of their end-to-end vector ${\bf r}$, which points from the first anchoring monomer to the last monomer on each chain. The radial distribution $P(r)$ for isolated spherical PGNPs, confined PGNPs under wall compression (after step I of thermodynamic integration) and relaxed PGNPs of our interest are shown in Fig. 6a. Here $P(r)dr$ is the probability for the chain end to fall in the spherical shell beween radius $r$ and $r+dr$, regardless of chain orientation. For confined polyhedra (see inset in Fig. 3a), $r$ are more narrowly distributed. FCC has a slightly higher $P(r)$ at $r>13$ and $r<10$, but BCC has more chains with $10<r<13$. This trend qualitatively agrees with the solid angle distribution for perfect truncated octahedron and rhombic dodecahedron Ungar et al. (2003); Goodfellow et al. (2015). In the study of ligand-capped nanocrystals Goodfellow et al. (2015), FCC Wigner-Seitz cell is considered to have a more anisotropic chain length (corona thickness) distribution, and to carry more entropy penalty than BCC when deformed from a hyperthetical sphere of the same volume $V$. Although this argument about the entropy of chain length distribution may explain the higher stability of our confined BCC structure with a relatively regular polyhedron cell, it cannot resolve the stability of different relaxed structures as shown below.

We observe that, after wall confinement is removed, the distributions $P(r)$ of relaxed BCC and FCC are almost indistinguishable (empty symbols in Fig. 6a), which agrees with our expectation that interpenetration of chains blurs the boundary of Wigner-Seitz polyhedra. Because the radial distribution of chain length alone does not even distinguish the shape of the two polyhedra, we need to study the orientational distribution of ${\bf r}=(r,\theta,\phi)$, i.e. $P(\theta)$ of polar angle $\theta$ and $P(\phi)$ of azimuthal angle $\phi$. In Fig. 6b, we plot $P(\theta)$ and $P(\phi)$ for relaxed polyhedra of BCC and FCC. Surprisingly, both distributions have a larger deviation from the spherical case (black dotted lines) in BCC than in FCC. The distribution $P(\phi)$ suggests that chains are more concentrated around the six square faces in truncated octahedron ($\phi=0,\pi/2,\pi,3\pi/2$), which separate the central PGNP from its second nearest neighbors. In these directions of BCC, the lattice constant is $2/\sqrt{3}=1.155$ times of the nearest neighbor distance. In the case of rhombic dodecahedron, chains are slightly more clustered around $\phi=\pi/4,3\pi/4,5\pi/4,7\pi/4$, which correspond to the corner formed by four rhombus faces at a distance $\sqrt{2}=1.414$ times of the nearest neighbor distance.

After obtaining the radial $P(r)$ and angular $P(\theta)$, $P(\phi)$ distribution of the end-to-end vector ${\bf r}=(r,\theta,\phi)$ of grafted chains, we can compute the (Gibbs) entropy $S$ of the overall distribution $P({\bf r})$ for a given (relaxed) Wigner-Seitz polyhedron. If the total distribution of vector ${\bf r}$ can be factored as $P({\bf r})=R(r)\Theta(\theta)\Phi(\phi)$, the corresponding normalization condition should be

$\displaystyle\begin{aligned} 1&=\int d{\bf r}P({\bf r})\\ &=\int_{0}^{\infty}drr^{2}R(r)\int_{0}^{\pi}d\theta\sin\theta\Theta(\theta)\int_{0}^{2\pi}d\phi\Phi(\phi).\end{aligned}$

By comparing with our three normalized distributions, $\int\limits_{0}^{\infty}drP(r)=1$, $\int\limits_{0}^{\pi}d\theta P(\theta)=1$ and $\int\limits_{0}^{2\pi}d\phi P(\phi)$, we can relate $P(r)=r^{2}R(r)$, $P(\theta)=\sin\theta\Theta(\theta)$ and $P(\phi)=\Phi(\phi)$ such that $P({\bf r})=\frac{P(r)}{r^{2}}\frac{P(\theta)}{\sin\theta}P(\phi)$.

The entropy of the distribution $P({\bf r})$ can thus be expanded as

$\displaystyle\begin{aligned} S&=-k_{B}\int d{\bf r}P({\bf r})\ln P({\bf r})\\ &=-k_{B}\int drd\theta d\phi P(r)P(\theta)P(\phi)\ln\left[\frac{P(r)}{r^{2}}\frac{P(\theta)}{\sin\theta}P(\phi)\right]\\ &=S_{r}+S_{\theta}+S_{\phi}\end{aligned}$

(7)

where

$\displaystyle\begin{aligned} S_{r}&=-k_{B}\int_{0}^{\infty}drP(r)\ln\frac{P(r)}{r^{2}}\\ S_{\theta}&=-k_{B}\int_{0}^{\pi}d\theta P(\theta)\ln\frac{P(\theta)}{\sin\theta}\\ S_{\phi}&=-k_{B}\int_{0}^{2\pi}d\phi P(\phi)\ln P(\phi).\end{aligned}$

(8)

For spherically symmetric distributions, $P(\theta)=\frac{1}{2}\sin\theta$ and $P(\phi)=\frac{1}{2\pi}$ (black dotted lines in Fig. 6b), which gives constant entropy terms $S_{\theta}({\rm sphere})=k_{B}\ln 2$ and $S_{\phi}({\rm sphere})=k_{B}\ln(2\pi)$.

We fit the sampled distributions of relaxed BCC and FCC polyhedra with following functions (the trivial phase shift of $\pi/4$ is applied to the $\phi$ angle of FCC before the fitting)

$\displaystyle\begin{aligned} P(r)&=ar^{2}e^{-b(r-c)^{2}}\\ P(\theta)&=\frac{\sin\theta}{2}\left[c_{1}\cos(4\theta)+c_{2}\cos(8\theta)+1\right]\\ P(\phi)&=c_{3}\cos(4\phi)+c_{4}\cos(8\phi)+\frac{1}{2\pi}.\end{aligned}$

(9)

The fitting curves for relaxed BCC and FCC are shown in Fig. 6, from which the entropy of the distribution $P({\bf r})$ is calculated as in Table 1.

It can be seen that the total entropy $S$ and its radial or angular contributions of BCC structure are all lower or close to those of FCC. This disagrees with the previous knowledge that the higher stability of BCC superlattice can be explained by the entropy of chain length alone Goodfellow et al. (2015). It is worth emphasizing that chain interpenetration makes the radial distribution $P(r)$ of chain length almost identical for BCC and FCC polyhedra. We thus argue that the free energy and stability of various superlattices should be dominated by energy and other entropy contributions, for instance, the configuration entropy of individual monomers.

Although designed to calculate the free energy of superlattices of PGNPs, the current method can be straightforwardly modified to compute the potential of mean force (PMF) between a pair of PGNPs. Only one confining wall per PGNP is needed at the bisecting plane of the center-to-center line and only the two interacting PGNPs need to be considered under open boundary conditions in step II of the thermodynamic integration. Previously, the PMF has been estimated from the radial distribution function Striolo and Egorov (2007), interaction energy Verso et al. (2011) and force Meng et al. (2012) between two PGNPs. The similar problem has been studied in the context of polymer brush Milner et al. (1988); Milner (1991) and steric stabilization of colloidal particles Centeno et al. (2014).

We test this idea on a system with chain length $N_{p}=60$ by calculating the PMF $F$ as a function of the center-to-center distance $d$. Obviously, the two PGNPs only start to experience a repulsion when $d<2R_{0}$, where $R_{0}$ is the radius of the isolated spherical PGNP with that chain length. Instead of the combined power law and inverse power law in terms of surface-to-surface distance $h$ (or brush height $h/2$) Milner et al. (1988); Centeno et al. (2014), our results show that the PMF can follow a simpler Hertzian-like repulsion $F\sim(1-\frac{d}{2R_{0}})^{\alpha}$ with a fitting exponent $\alpha=2.6$ Johnson (1987).