Formulations of Hydrodynamic Force in the Transition Stage of the Water Entry of Linear Wedges with Constant and Varying Speeds

In this section, the fully nonlinear potential flow model based the hybrid BEM-FEM approach is presented. The method is mainly based on the studies of Refs. [24, 37], where full details are provided.

Figure 5 shows the grid independence validation of the CFD simulations for the water entry of a wedge with $\beta=30^{\circ}$ in a constant speed, where the slamming coefficient $C_{s}$ and pressure coefficient $C_{p}$ are defined as follows

where $U_{w}$ is the entering speed of the body. Three grids of cell numbers of 50,000, 100,000 and 200,000 are adopted to simulate the impact flow with adaptive time steps. The courant number is set to be 0.95 during the adaptive time steps. The $C_{s}$ of the whole time-history between the three grids match well. The $C_{p}$ distribution and free surface of $h/h_{0}=0.8$ ($h_{0}=l\tan\beta$) are also consistent between the three grids except for some discrepancies at the tip of jet. The grid independence of CFD method is successfully validated. Therefore, the CFD grid with cell number of 100,000 is adopted for further simulations by balancing both the accuracy of spatial resolution and the computational cost.

Figure 6 shows the description of the HBF model in which the fluid boundary is divided into three parts: (1) free surface panels; (2) wall surface panels and (3) jet panels. The free surface and wall surface panels are solved by BEM solver while the jet panels are solved by the FEM solver. The panel distribution is determined by three parameters in Tab. 2: growth factors $\kappa$ of BEM panels and FEM panels, as well as the ratio $r$ between the normal distance between the two side of the jet in proximity of the spray root and the minimun panel size. The $C_{s}$ and $C_{p}$ at the tip of wedge of the three distributions of HBF for the constant speed case in Fig. 7 match well with each other. Here, a normal grid is adopted for most of the HBF calculations in present study.

For the slamming stage of constant speed impact in which the self-similar flow is satisfied, the present CFD and HBF methods are compared with the similarity solution of Dobrovol’skaya[22, 36]. For the varying speed impact of both the slamming and transition stages, the present CFD and HBF methods are compared with the predictions of Bao et al.’s BEM [32] for the freefall motion case. In this case, the impact speed is small and the gravity effect will become significant in the transition stage. In the simulations of Bao et al.’s case [32], the gravity of fluid is included. For the other cases, the gravity of fluid is excluded.

For the slamming stage with $h/h_{0}=0.6$ in the case of the water entry of a wedge with $\beta=30^{\circ}$ in a constant speed, Fig. 8 shows the comparisons of the pressure coefficient $C_{p}$ on the wedge surface and the free surface profiles between the predictions of CFD, HBF and similarity solution [36]. The spray root of the jet remains under the knuckle of the wedge, which means the self-similar flow is still satisfied and thereby the similarity solution can be used for a validation. The good agreement between the present methods and the similarity solution is excellent.

For the transition stage, Fig. 9 shows the comparisons of the force ($a$), pressure distribution ($b$) and free surface ($c$) between the present CFD and HBF for the water entry of a wedge with $\beta=30^{\circ}$ in a constant speed. The CFD results are all consistent with those of HBF, except for the jet tip of free surface. Since the jet tip is of little relevance with the pressure and force acting on the wedge surface, the mutual validations between the present CFD and HBF are properly conducted. Fig. 10 shows the comparisons of the acceleration ($a$), pressure distribution ($b$) and free surface ($c$) between the CFD method, HBF and BEM of Bao et al. [32] for the water entry of wedges of $\beta=30^{\circ}$ in a freefall motion. The CFD and HBF results are in good agreement with those of the BEM of Bao et al. [32], while there are still minor discrepancies of the jet tip of free surface and the pressure distribution near the apex of wedge. These differences are acceptable for the validations of CFD and HBF methods.

It can be concluded that the CFD method and HBF method are consistent with each other and can deal with the slamming and transition stages of the constant and varying speed impacts. In this paper, the CFD method is mainly used to produce the numerical results of constant speed impact, while the HBF method is to used produce those of varying speed impact.

The pressure distributions and free surface of different penetration depths in the transition stage during the water entry of a wedge with $\beta=30^{\circ}$ in a constant speed are shown in Fig. 11. It is clearly observed that the high pressure region located at the spray root rapidly vanishes after the spray root leaves the knuckle of the wedge. In the slamming stage, the high pressure region is formed because the water under the wedge has to accumulate in the spray root and turns into a jet with high speed, as the wetted area of wedge keeps increasing. In the transition stage, the wetted length of the wedge stops increasing and the wall surface of the spray root no longer exists, and thus the high pressure region disappears. Fig. 12 shows the pressure distributions on the wedge surface. With the increasing penetration depth, the pressure on the whole wedge surface decreases and finally approaches the distribution of steady supercavitating flow. It is difficult to figure out the way how the pressure drops from the original distribution of slamming stage. In this paper, we focus on the formulation of the force and expect to find a general expression of slamming and transition stages .

Figure 13 ($a$) shows the slamming coefficient $C_{s0}$ of different deadrise angles varying from $25^{\circ}$ to $45^{\circ}$. The $C_{s0}$ of a single $\beta$ increases linearly to the maximum $C_{\rm max}$ and declines to a steady value $C_{s\infty}$. The $C_{s\infty}$ of different deadrise angles are shown in Fig. 32 in Appendix 7.1, which is calculated by a potential theory [12]. In order to formulate the slamming coefficient $C_{s0}$ in the transition stage, new variables are adopted:

where $h_{2}$ is the penetration depth corresponding to the maximum slamming coefficient $C_{s\rm max}$. The new parameter $\lambda$ is determined by a gradient algorithm enforcing on the following function

where $\sigma_{i}(\lambda)$ is the standard deviation of $C_{s0}^{*}$ between different deadrise angles for the $i^{th}$ node in the range of $h^{*}\in[0,\,\,7]$ and thereby becomes a function of $\lambda$. An uniform distribution with $N$=7001 nodes in the range of $h^{*}\in[0,\,\,7]$ is adopted, and the initial values are chosen as $\lambda=1.4$ and $1.35$. After 35 steps, the gradient algorithm is convergent with $\lambda=1.3075$ ($\Delta\lambda<$1e-6). The $C_{s0}^{*}$ of different deadrise angles with $\lambda=1.3075$ are also shown in Fig. 13 ($b$), and it can be seen that the $C_{s0}^{*}$ of different deadrise angles in the transition stage coincide well with each other.

Owing to the linear increasing slamming coefficient in the slamming stage and the coinciding results in the transition stage, the hydrodynamic force of both the slamming and transition stages of water entry can be formulated as shown in Fig. 14, where the slamming stage is in the range of $[h_{1}^{*},\,\,0]$ and the transition stage is in that of $[0,+\infty]$. The coinciding $C_{s0}^{*}$ of Fig. 13 ($b$) in the transition stage is formulated by a rational function in $h^{*}\in[0,\,\,7]$ based on the mean results of the $C_{s0}^{*}$ of different deadrise angles

Due to the fitting errors, $C_{s0}^{*}$ in Eq. (19) is larger than 1 when $h^{*}\in[0,\,\,0.067]$. In order to deal with the continuity between Eq. (19) and the linear increasing $C_{s0}^{*}$ of slamming stage, $C_{s0}^{*}$ of is approximately as 1 in $h^{*}\in[0,\,\,0.067]$. The linear increasing $C_{s0}^{*}$ appears the following form

By taking the derivative of $C_{s0}^{*}$ with respect to $h^{*}$, the slope of the linear expression of Eq. (20) in $[h_{1}^{*},\,\,0]$ appears to be

where $k_{1}=h_{2}/h_{0}$, $k_{2}=\frac{{\rm d}C_{s0}}{{\rm d}(h/h_{0})}$. $C_{s\max}=k_{1}k_{2}$ according to the definations of $k_{1}$ and $k_{2}$. Fig. 15 shows the $k_{1}$ and $k_{2}$ of various deadrise angles from 15^∘ to 45^∘, which are calculated by the present CFD method. In the Wagner theory, $k_{1}={2}/{\pi}$. $k_{1}$ from CFD results match $2/\pi$ when $\beta\leq 30^{\circ}$. Thus, $k_{1}=2/\pi$ can be adopted for small deadrise angle. $k_{2}$ appears to be equal to $B_{2}\tan\beta$ of the similarity solution [22, 39, 21]. The CFD results of $k_{2}$ are in good agreement with the similarity solution. In this paper, the results of $k_{1}$ and $k_{2}$ for an arbitrarily deadrise angle within the range of $[15^{\circ},\,\,45^{\circ}]$ are given by a least square fitting method (LSF) of a quadratic function ${k_{1}}=0.2027{\beta^{2}}-0.1295\beta+0.655$ and a quadratic function multiplying $\cot\beta$, e.g., ${k_{2}}=\left({1.585{\beta^{2}}-6.856\beta+7.764}\right)\cot\beta$ from the CFD results, and the maximum fitting errors are $0.62\%$ and $1.91\%$ respectively. Therefore

By combining the Eqs. (16) - (17) and (22), it is possible to find the $C_{s0}$ value and then the hydrodynamic force acting on the wedge surface (half model) for the cases in a constant speed is given

In Sec. 4.2, the formulation of slamming stage in the slamming and transition stages is set up by Eqs. (16)-(17) and (22), and the hydrodynamic force is finally calculated by Eq. (23). The formulation is based on the CFD results in a range of deadrise angles from $15^{\circ}$ to $45^{\circ}$. In order to explore its application range of deadrise angles, this section compares the predictions of Eq. (23) and the CFD results in the range of $\beta\in[5^{\circ},70^{\circ}]$.

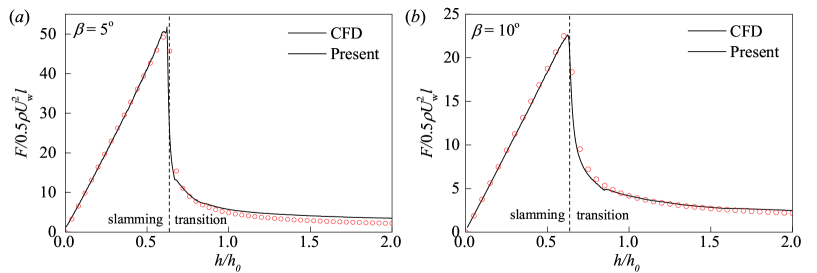
For the comparisons in $\beta\in[15^{\circ},\,\,45^{\circ}]$, Fig. 16 shows the comparisons between the predictions of Eq. (23), the modified Wagner’s model (MWM) [25] and the CFD method for the cases of $\beta=15^{\circ}$, $25^{\circ}$ and $45^{\circ}$. The agreement between the present model and the CFD results is good except that a tiny discrepancy occurs at the maximum $C_{s}$ for the case of $\beta=45^{\circ}$. The WMW can only work in the range of $\beta\in[15^{\circ},\,\,35^{\circ}]$. For the cases of $\beta=15^{\circ}$ and $25^{\circ}$, the accuracy of the present model and MWM is close.

The comparisons in the ranges of small and large deadrise angles are also provided in Figs. 17 and  18. The agreement between the predictions of Eq. (23) and the CFD results is generally good, though with some discrepancies. Eq. (23) slightly underestimates the force at a large penetration depth for the case of $\beta=5^{\circ}$ and overestimates the forces for the cases of large deadrise angles at an early period of the transition stage. But the agreement becomes better as the penetration depth increases. Therefore, it can be concluded that the present formula can provide accurate predictions for the slamming coefficients of various deadrise angles from $5^{\circ}$ to $70^{\circ}$.

Since there exists entrainment of air when the deadrise angle is smaller than $5^{\circ}$ [40, 41], the predictions of force without involvement of the effect of air cushion may be inaccurate. Thus, this paper does not consider the validations of a smaller deadrise angle, and $5^{\circ}\leq\beta\leq 70^{\circ}$ will be a proper range of deadrise angle for most of the engineering applications.

Figure 19 ($a$) shows the $C_{p}$ distributions on the wedge surface in the transition stage of Case 1 (see Tab. 3). For the case of $\beta=30^{\circ}$, the transition stage starts at $h/h_{0}=0.639$ and thus the result of $h/h_{0}=0.502$ is still in the slamming stage while the other are in the transition stage. As can be seen in Fig. 19 ($a$), the $C_{p}$ distributions along the wedge surface decline with the increasing penetration depth. The reasons of the pressure drop includes two different aspects: the vanishing of high pressure region at spray root (see Sec. 3.1) and the deceleration of wedge. In order to distinguish these two kinds of influence, the pressure is split into two parts: (1) the pressure only related to the constant speed impact $p_{0}=0.5\rho U_{w}^{2}C_{p0}$ (see Fig. 12); (2) the pressure changing $\Delta p=p-p_{0}$ caused by the acceleration of wedge, where $p_{0}$ and $p$ are the pressure of the constant and varying speed impacts respectively in a same penetration depth and with a same instantaneous speed. Fig. 19 ($b$) shows the distributions of $\Delta p/\left(0.5\rho a_{w}c\right)$, where the effective wetted length (half length) is $c=\min\left\{{h\cot\beta/{k_{1}},\,\,l}\right\}$. The $\Delta p/\left(0.5\rho a_{w}c\right)$ of different penetration depths show similar distributions and have a small increase along the whole wedge surface with the increasing penetration depth. The result of similarity solution $k_{1}\tan\beta(-2\Phi)$ [36] in the slamming stage is well consistent with the result $h/h_{0}=0.502$ in the slamming stage. It can be concluded that the distribution of $\Delta p/\left(0.5\rho a_{w}c\right)$ remains as $k_{1}\tan\beta(-2\Phi)$ in the slamming stage and then has a small increase in the transition stage. The results become steady as the penetration depth continues to increase. The small increase pressure will also result in the small increase of slamming coefficient, which will be further discussed in Sec. 5.2.

From the studies of slamming stage [36, 21], the pressure changing caused by the acceleration of wedge can be quantified by the dimensionless velocity potential $-2\Phi$. Fig. 20 shows the dimensionless velocity potential $-2\phi/\left(U_{w}c\right)$ (a similar dimensionless variable like $-2\Phi$) on the wedge surface of Case 1 in the transition stage. The $-2\phi/(U_{w}c)$ distribution of $h/h_{0}=0.502$ is identical to $-2\Phi$ of the similarity solution [21] since it still remains in the slamming stage. The other distributions show large differences with $-2\Phi$ of the similarity solution and the $\Delta p/\left(0.5\rho a_{w}c\right)$ distributions in Fig. 19 ($b$). It can be concluded that the pressure changing caused by the acceleration of wedge can not be quantified by the velocity potential in the transition stage as it does in the slamming stage. Although the $\Delta p/\left(0.5\rho a_{w}c\right)$ distributions have a similar distribution and small increase as the penetration depth increases, there is still some challenging problems to formulate the pressure changing caused by the acceleration effect. In this paper, we focus on the formulation of the hydrodynamic force caused by the acceleration effect and hope to find an effective method to formulate the hydrodynamic force caused by the acceleration effect.

Similar to the pressure distribution on the wedge surface, the force can also be divided into two part: (1) the force caused by the constant speed impact $F_{0}=0.5\rho U_{w}^{2}lC_{s0}$, where $C_{s0}$ can be given by Eqs. (16) - (17) and (22); (2) the force caused by the acceleration effect $\Delta F=F-F_{0}$, where $F_{0}$ and $F$ are the forces of constant and varying speed impacts respectively in a same penetration depth and with a same instantaneous speed. Fig. 21 shows the $\Delta F/(0.5\rho c^{2}a_{w})$ of different prescribed speeds (Cases 1,2 and 3 in Tab. 3). All of the cases are decelerating with different decelerations. Case 1 has a constant deceleration, Case 2 has an increasing deceleration and Case 3 has a decreasing deceleration. The $\Delta F/(0.5\rho c^{2}a_{w})$ show good consistence between different cases in the transition stage of $h/h_{0}\in[0.639\,\,1.0]$, though with some numerical fluctuations. Therefore, $C_{a}=\Delta F/(0.5\rho c^{2}a_{w})$ is defined as an added mass coefficient, and independent of $a_{w}$ in $h/h_{0}\in[0.639\,\,1.0]$. It can be concluded that the effects of acceleration on the hydrodynamic force have a fixed pattern in the transition stage as it does in the slamming stage [21]. In the slamming stage, the acceleration effect on the hydrodynamic force is given as $\Delta F=\rho A_{2}a_{w}h^{2}$ from the similarity solution [36], indicating an added mass coefficient $C_{a0}=A_{2}(k_{1}\tan\beta)^{2}$. The $C_{a}$ in the slamming stage can be given as $C_{a0}=1.0459$, and in the transition stage, $C_{a}$ has an averaged result of 1.3297 in $h/h_{0}\in[0.639\,\,1.0]$, which is $\xi=27.13\%$ larger than the result of similarity solution $C_{a0}$. In this paper, a hybrid added mass coefficient is adopted to formulate the acceleration effect corresponding to Eq. (22)

The results of $h^{*}\in[0,\,0.067]$ are given by a linear distribution from $C_{a0}$ to $(1+\xi)C_{a0}$. For the case of $\beta=30^{\circ}$, the approximation of $C_{a}$ in the transition stage is summarized from the HBF results of $h/h_{0}\in[0.639,\,1.0]$, corresponding to $h^{*}\in[0,\,1.1586]$. However, further validations of Eq. (24) by the numerical results in Sec. 5.3 indicates that Eq. (24) can work in a larger range of $h^{*}$ and deadrise angles. Therefore, for the water entry of linear wedges with an acceleration, the hydrodynamic force can be predicted by Eq. (24) together with Eqs. (16) - (17) and (22), and the final expression of the force (half model) has the following form:

where $c=\min\left\{{h\cot\beta/{k_{1}},\,\,l}\right\}$.

In the linear FBC of Tassin et al. [23] based on MLM, the acceleration effect was addressed by the following form of $C_{a}$ of in the slamming and transition stages

As can be seen in Fig. 21, the present model has a different $C_{a}$ from that of Tassin et al. [23].

Figure 22 shows the comparisons of the forces acting on the wedge surface between the present predictions and the HBF results for Case 1, 2 and 3. The results of Eq. (23) only include the effect of constant speed impact while those of Eqs. (25) include the effect of constant speed impact and the acceleration effect. The predictions of Eqs. (25) are in good agreement with the HBF results, while those of Eqs. (23) show much discrepancies with the HBF results. Fig. 23 shows comparisons for Case 4, 5 and 6 of different deadrise angles and different ways of decelerations. The same $C_{a}$ correction of $\xi=27.13\%$ is adopted for the cases of different deadrise angles, and the good agreement is also obtained. It indicates that the $C_{a}$ correction of $\xi=27.13\%$ also works for other deadrise angles.

To explore the application ranges of deadrise angles and of different ways of wedge motions for the present model, Fig. 24 shows the comparisons of the forces acting on the wedge surface between the present predictions and the CFD results for the freefall cases of ($a$) $\beta=5^{\circ}$ and $\beta=70^{\circ}$. The wedges are in freefall motions with masses of $m=1.5\rho l^{2}$. For the small and high deadrise angles, the present model can provide good predictions for the hydrodynamic forces, even for the freefall motions where the acceleration of wedge is unknown before the predictions.

The case in Fig. 10 is also used for a validation for the present model. Fig. 25 shows the comparisons of the predictions of accelerations of wedge with $\beta=30^{\circ}$ between the CFD without gravity of fluid, BEM of Bao et al. [32] with gravity of fluid, theory of Wen et al. [21] without considering the transition stage, Eq. (23) and Eq. (25) during the water entry in freefall motion. The agreement between the CFD result and the present model with acceleration effect, e.g., Eq. (25), is good in both slamming and transition stages, while the theory of approximate solution without considering the transition stage [21] can only address the slamming stage. The present model without acceleration effect, e.g., Eq. (23), also shows large differences compared with the CFD result. The gravity effect has small influence on the hydrodynamic force in the transition stage for the cases of $Fr=1.9587$. For the high speed impact of higher $Fr$, the gravity of fluid can be neglected and the present model will have better predictions.

A comparison of the forces between an experimental test of Zhao et al. [13] and the present model is shown in Fig. 26. The case is a three-dimensional water entry with deadrise angle of $\beta=30^{\circ}$. The half width of wedge is $l=0.25\,\rm m$ and the thickness is $L=1\,\rm m$. The vertical speed of the wedge is given by the experimental result of an optical sensor. The acceleration of wedge is given by the derivative of vertical speed. The present 2D model has large discrepancies compared with the experimental result. As Zhao et al. indicated, the reason is due to the three dimensional (3D) effect and the force should be corrected by a force coefficient $f_{\rm 3D}$ (a function of $c/L$). They used Meyerhoff’s results [42] of $f_{\rm 3D}(0.25)=0.95$, $f_{\rm 3D}(0.4)=0.87$, $f_{\rm 3D}(0.5)=0.8$ from the added masses of thin rectangular plates with a generalization of Wagner theory to formulate the 3D effect. In this paper, a parabolic $f_{\rm 3D}=1-0.80(c/L)^{2}$ is approximately formulated by fitting from the above results. After using the 3D correction, the present model with 3D effect can predict the force of the experimental test.

To sum up, Eq. (25) together with Eqs. (16), (17), Eq. (24) and (22) can be used for both the predictions of hydrodynamic force in slamming and transition stages for the water entry of wedges with different deadrise angles in constant and varying speeds.

For the slamming stage, the traditional added mass methods have the forms of added mass and the hydrodynamic force (half model)

where $c=\gamma h\cot\beta$ for the traditional methods. Tab. 4 shows the correction factor $\gamma$ of the wetted length, the dimensionless coefficient of constant speed impact $C_{\rm const}$ and the added mass coefficient $C_{a}$ of slamming stage for different theories [4, 5, 17, 19, 23]. The Wagner’s new model [5] was proposed to improve the predictions of forces of constant speed impact for different deadrise angles, but the acceleration term remained unchanged. $\gamma_{\rm Mei}$ can be found in Refs.  [19, 21]. $B_{2\rm Mei}$ and $A_{2\rm Mei}$ are calculated by direct pressure and velocity potential integrations of Mei et al.’s model [19]. $C_{\rm Korobkin}$ is from the theoretical results of Korobkin [20]. $B_{2}$ and $A_{2}$ of the present model were calculated from the similarity solution [22], and the results are shown in Ref. [21].

In early researches of Refs. [4, 5, 17, 19, 20] for the slamming stage, the hydrodynamic force of constant speed impact received the most attention and the researchers proposed their models by comparing the results of similarity solution [22, 16] to correct the underestimated results of Von Karman [4] and overestimated results of Wagner’s original model [5], as shown in Fig. 27 ($a$). The models of Mei et al. [19], Tassin et al. [23] and Wagner’s new model [5] have been approximately close to the results of similarity solution, but these models actually violate the framework of added mass methods. Their $C_{\rm const}$ are no longer $2C_{a}\gamma^{2}$, which are different from the models of Von Karman [4], Wagner [5] (original model) and Faltinsen [17]. Although these models [19, 23, 5] brought good predictions for the constant speed impact, they still can not properly model the acceleration effect, as shown in Fig. 27 ($b$). The Faltinsen’s model cannot properly address both the constant speed impact and acceleration effect. The present model formulates the models of constant speed impact and acceleration effect directly from the approximate solution [21] based on the similarity solution of Dobrovol’skaya [22], regardless of the framework of added mass methods and the consistency of $C_{\rm const}$ and $C_{a}$. The validations by numerical results in Ref. [21] and Figs. 22 and 23 have completely verified the present model.

For the transition stage, Tassin et al.’s model [23], the MWM of Wen et al. [25] and the present model can address both the slamming and transition stages, while the models of Ref. [4, 5, 17, 19] can only work in the slamming stage. Wen et al. had greatly improved the predictions of hydrodynamic forces for the constant speed impact in the range of $\beta\in[15^{\circ},\,\,35^{\circ}]$ compared with the linear FBC of Tassin et al. and the improved model of zero pressure condition [18, 23]. The accuracy of present model is close to Wen et al.’s MWM, but with a much larger range of deadrise angle. Besides, the acceleration effect in the transition stage is missing in MWM. Tassin et al.’s model provided the formulation of acceleration effect and the $C_{a}$ is given by Eq. (26). The comparison of $C_{a}$ of $\beta=30^{\circ}$ between the present model and Tassin et al.’s model is shown in Fig. 27 ($b$). In contrast to an increase of $C_{a}$ in the transition stage, the $C_{a}$ of Tassin et al.’s model declines and finally reaches a constant value lower than $C_{a0}$, which is inconsistent with the HBF results in Fig. 27 ($b$).

In general, we rewrite the formula of hydrodynamic force and extend it to the transition stage for the constant and varying speed impacts. Although the present model is more sophisticated, it works better than the traditional added mass methods and the asympotic theories and can work in a larger range of deadrise angle.

The water entry in the infinite penetration depth becomes a steady supercavitating flow with an incoming currency with velocity $v_{0}$. The theory can be extended from the water entry on a plate by the theory of Gurevich [12]. The free surface CD and $\rm C^{\prime}D^{\prime}$ of impact flow is shown in Fig. 28 after the solution is solved. The direction of incoming flow is upward and the stream-function on the streamline passing A is 0. The velocity potential at A is chosen as 0. A parameter plane $\tau$ mapping to the geometry in Fig. 28 is shown in Fig. 29 and thus the complex velocity potential of impact flow can be calculated as

where $\phi_{0}$ is the velocity potential at C and $C^{\prime}$. Another parameter plane $\omega=v_{0}\frac{{\rm d}z}{{\rm d}w}=v_{0}e^{{\rm i}\theta}/v$ ($\rm i$ being the imaginary unit) mapping to the velocity is shown in Fig. 30 and can be formulated by the Schwarz-Christoffel formula as

The complex coordinate can be derived

By considering the distance from A to C, the velocity potential at C and $C^{\prime}$ can be determined

where

Therefore, the $x$ on AC is given as

and the velocity on AC is

The pressure coefficient $C_{p}$ has the form

The $C_{p}$ distributions of different deadrise angles $\beta$ are shown in Fig. 31. The $C_{p}$ is 1 at the stagnation A and 0 at the separation C for a steady supercavitating flow. The free surface profile in Fig. 28 is given by the following $x$ and $y$ expressions

The force acting on the wedges is calculated by integrating the pressure with the $C_{p}$ expression Eq. (36). The slamming coefficient $C_{s\infty}$ of different deadrise angles is shown in Fig. 32. The result of $\beta=0$ is equal to 0.88, which is consistent with that of water entry on a plate derived by Gurevich [12]. The $C_{s\infty}$ decreases with the increasing deadrise angle and reaches 0 at $\beta=90^{\circ}$.