Forming pressure-traps at the snow-line to isolate isotopic reservoirs in the absence of a planet.

Protoplanetary disks are thought to have a vertically stratified structure due to non-ideal MHD effects. The disk’s midplane may have a low turbulence, and low accretion rate, due to ohmic diffusion that prevents the onset of magneto-rotational instability (Turner et al. 2014). This results in a quiet ’dead’ midplane with equivalent $\alpha$ (called $\alpha_{d}$) in the range $10^{-5}$ to $10^{-3}$ depending on local hydrodynamic turbulence (Bai & Stone 2013; Turner et al. 2014; Gressel et al. 2015; Kadam et al. 2019). It is topped by an active layer with high accretion rate, but with a low column-density ($\Sigma_{a}$), in the range 100 to 1000 $kg/m^{2}$ (Turner et al. 2014) and that may have a low level of turbulence (Béthune et al. (2017)) despite of a high accretion rate. In the active layer the effective value of $\alpha$ is designated by $\alpha_{a}$. The very upper layer may be occupied by disk-winds, a region in which ambipolar diffusion is active, that torques the two previous layers and where low-density winds breeze outwards. The transition between the dead and active layers (in terms of column density) may be very sharp (Turner & Sano 2008; Bai & Stone 2013; Turner et al. 2014). In 1D models it is useful to introduce the vertically averaged $\alpha$ :

where $\rho(z)$ and $\alpha(z)$ are the values of the gas density and $\alpha$ at altitude z respectively. As the transition of the active to the dead layer is very sharp, it is possible to use a parameterization of $\left<\alpha\right>$ assuming that the disk is made of two layers: an active layer with constant column density $\Sigma_{a}$ (100 to 1000 $kg/m^{2}$, largely independent of the distance to the star, Turner & Sano (2008); Turner et al. (2014)) and constant $\alpha=\alpha_{a}$, and a dead midplane layer with surface density $\Sigma_{d}=\Sigma-\Sigma_{a}$ and constant $\alpha=\alpha_{d}$ (see Appendix). Thus we get (Terquem 2008; Zhu et al. 2010; Bai & Stone 2013; Charnoz et al. 2019; Kadam et al. 2019):

Following Kadam et al. (2019) we use $\alpha_{a}=10^{-2}$ and $\alpha_{d}=10^{-5}$. In the following, to make the discussion clear, we use a simpler parameterization of $\left<\alpha\right>$ so that $\left<\alpha\right>\propto\Sigma^{-p}$. So it is useful to introduce $p$ the exponent of the power-law locally approximating $\left<\alpha\right>(\Sigma)$, it is :

Inserting Equation 3 into 4 we find that p ranges from 0 to $(\alpha_{a}-\alpha_{d})/\alpha_{a}$. Since $\alpha_{a}>>\alpha_{d}$, p can get very close to 1. $p$ is plotted in Figure 1. For $\Sigma<\Sigma_{a}$, p=0 because $\left<\alpha\right>$ is a constant equal to $\alpha_{a}$. For $\Sigma>\Sigma_{a}$ and $\Sigma<\Sigma_{a}\alpha_{a}/\alpha_{d}$ p decreases from $\sim 1$ to 0. For $\Sigma>\Sigma_{a}\alpha_{a}/\alpha_{d}$ p is almost equal to 0.

For illustrative purpose we start by considering the case of a small sound velocity perturbation, to emphasize the strong effect it has on the disk’s pressure profile. The disk is described through the standard $\alpha$ disk formalism, with gas surface density $\Sigma$ evolution obeying to :

where $\nu$ and $r$ are the local viscosity and distance to the star. Steady states are those solutions for which $\partial\Sigma/\partial t=0$ implying $\nu\Sigma=cst$. Noting that the mass flux $\dot{M}=3\pi\nu\Sigma$, we get at steady state $\Sigma=\frac{\dot{M}}{3\pi\nu}$, which is well known. The effective viscosity is $\nu=\left<\alpha\right>C_{s}^{2}/\Omega$ where $C_{s}$ is the local sound velocity. We assume that $\left<\alpha\right>$ can be written:

where A is a constant and p is a positive real number $\leq 1$. Note that for every-value of $\Sigma$ there is a different value of p.

We replace Equation 6 into the expression of the steady state surface density: $\dot{M}=3\pi\nu\Sigma$. After solving for $\Sigma$ we get the surface density in the midplane at steady state $\Sigma_{ss}$ inside a dead-zone and for a fixed value of p and $\Sigma$:

It is obvious from Equation 7 that $\Sigma_{ss}$ has no steady-state solution for p=1, and for p¡1 we see that a minimum of sound velocity induces a maximum of surface density. Note that in the above equation p is fixed (given by Equation 4). For locally isothermal pressure $P=\Sigma\Omega C_{s}/(2\pi)^{1/2}$, we get for the local pressure at steady state $P_{ss}$:

We now quantify the effect of a sound velocity perturbation ($\delta C_{s}$) on the pressure profile at steady state. Such a sound velocity perturbation may result from a local variation of gas-mean molecular weight because of the release of water vapor at the snow-line. By doing a first order expansion of $P_{ss}$ as a function of $C_{s}$ we get $\delta P_{ss}$ the pressure perturbation at steady state, as a function of the sound velocity perturbation $\delta C_{s}$:

Again we see that the amplitude of the pressure perturbation diverges when $p\rightarrow 1$, and that $\delta P_{ss}$ has a sign opposite to the sound-velocity perturbation. We now determine how strong must be $\delta C_{s}$ to induce a pressure bump by taking the derivative of equation 8 and setting that for a pressure bump $\partial P_{ss}/\partial r\geq 0$. We write $\Omega=Br^{-3/2}$ (with $B$ a constant) and we obtain the condition for a pressure bump to appear by deriving equation 8 with respect to $r$:

with $a=(2-p)/(1-p)$ and $b=(1+p)/(1-p)$ (two positive constants). Thus a pressure bump appears if the local derivative of $C_{s}$ verifies $\partial C_{s}/\partial r\leq-3a/2br$, which is a negative sound velocity perturbation.

Assuming that the disk is radiatively heated by the star, the unperturbed sound velocity profiles behaves like $C_{r}=Dr^{-1/4}$ , with D standing for a positive constant. We compute the amplitude of the sound velocity perturbation $\delta C$, above the unperturbed radiative profile, $C_{r}$, to trigger a pressure bump. We simply write $C_{s}=C_{r}+\delta C$ and introduce it in equation 10. We get the amplitude of the sound velocity perturbation to induce a pressure bump :

for p close-to, but smaller than, 1, we get $-\frac{\partial\delta C}{\partial r}\geq\frac{1}{2}\frac{C_{r}}{r}$. So the possibility to form a pressure bump depends both on the amplitude of the sound perturbation ($\delta C$) and on its width ($\delta r$) by approximating $\frac{\partial\delta C}{\partial r}\simeq\delta C/\delta r$. In the present paper we are interested in sound-velocity perturbations induced by the release of water vapor just inward the snow-line that modify the mean-molecular weight of the gas at constant temperature. As the isothermal sound velocity is $C=(RT/\mu)^{1/2}$ we get $\delta C=-1/2C\delta\mu/\mu$. So Equation 11 is simply rewritten :

$H_{2}O$ has a molecular weight $\mu_{H2O}=18g/mol$ and the average gas of solar composition has $\mu_{g}=2.3g/mol$. The mean molecular weight is $1/\mu=f/\mu_{H2O}+(1-f)/\mu_{g}$ (Schoonenberg & Ormel 2017). Noting $f$ the water mass fraction, we get $\delta\mu/\mu=\delta f\mu(1/\mu_{g}-1/\mu_{H2O})\simeq 0.87\delta f$. So the previous equation is rewritten in term of water mass fraction :

Here $\delta r$ is the radial spatial scale of variation of water vapor content, typically the physical width of the snow-line controlled by the saturating vapor. $\delta r$ is derived in Hyodo et al. (2021a) and $\delta r$ is about $\sim 0.2$ AU (their Equation 54) with the model settings used in Schoonenberg & Ormel (2017). $\delta f$ is the amplitude of variation of the water vapor mass fraction. Before the inflow of water ice coming from beyond the snow-line $f\simeq 0.01$ that is the average water mass fraction in a disk of solar composition. Equation 13 provides a condition for the apparition of a pressure bump in the presence of increasing water-vapor at the snow-lines. It states that a pressure bump will appear if $\delta f\geq 0.28$ for p=0.5 or $\delta f\geq 0.14$ for p=1. To test this criterion, we have done some simple tests with an $\alpha$ disk model solving Equation 5 for gas and computing the viscosity using Equation 6, so that p can be fixed. The initial water mass fraction, $f$, and $\delta r$, are set by hand using a gaussian profile with standard deviation 0.1 au (Hyodo et al. 2021a). When Equation 13 is satisfied, we do see the formation of a pressure bump with this ”toy” model. A pressure maximum appears for $\delta f\simeq 0.2$ in Figure 2. Of course the surface density profiles changes also slightly according to Equation 7. So in for p close to 1, we will keep the criterion for pressure bump formation as $\delta f>0.2$

We have considered above for illustrative purpose, only a small perturbation of the sound velocity, and thus a small amount of water vapor. But it is found that the sound velocity perturbation necessary to induce a bump is, in fact, not so small (since $-\frac{\partial\delta C}{\partial r}\geq\frac{1}{2}\frac{C_{r}}{r}$). So, to continue our demonstration we abandon our first order development and go back to the original equations. We first compute the steady-state surface density by inserting Equation 3 into the steady state flux $\dot{M}=3\pi\nu\Sigma$. As it is common to parameterize the disk’s evolution using the accretion rate, $\dot{M}$, we have computed for different $\dot{M}$ the steady state disk surface density assuming the dead-zone prescription for $\left<\alpha\right>$ (Equation 3) combined with the steady-state relation $\dot{M}=3\pi\nu\Sigma$. After a little algebra one finds the steady state surface density $\Sigma_{ss}$:

where $\dot{M}_{DZ}$ is the critical accretion rate beyond which a region is embedded in dead-zone : $\dot{M}_{DZ}=\Sigma_{a}\alpha_{a}3\pi C_{s}^{2}/\Omega$.

Assuming $\dot{M}>\dot{M}_{DZ}$, the pressure in the Dead Zone at steady state is then :

Then, we simply determine the condition for which $\partial P/\partial r\geq 0$ in the DZ. We get :

with coefficients:

We now try to reformulate the above criterion in terms of water mass fraction enhancement at the snow-line. Since $C_{s}=(RT/\mu)^{1/2}$, then $dC_{s}=1/2C_{s}dT/T-1/2C_{s}d\mu/\mu$. In the region at the snow-line where water vapor is released we assume that $d\mu/\mu>>dT/T$ so $dC_{s}\simeq-1/2d\mu/\mu$ (Hyodo et al. 2021a). Since $\delta\mu/\mu\simeq 0.87\delta f$, the bump formation criterion (Equation 16 is rewritten in terms of water vapor mass fraction ($\delta f$):

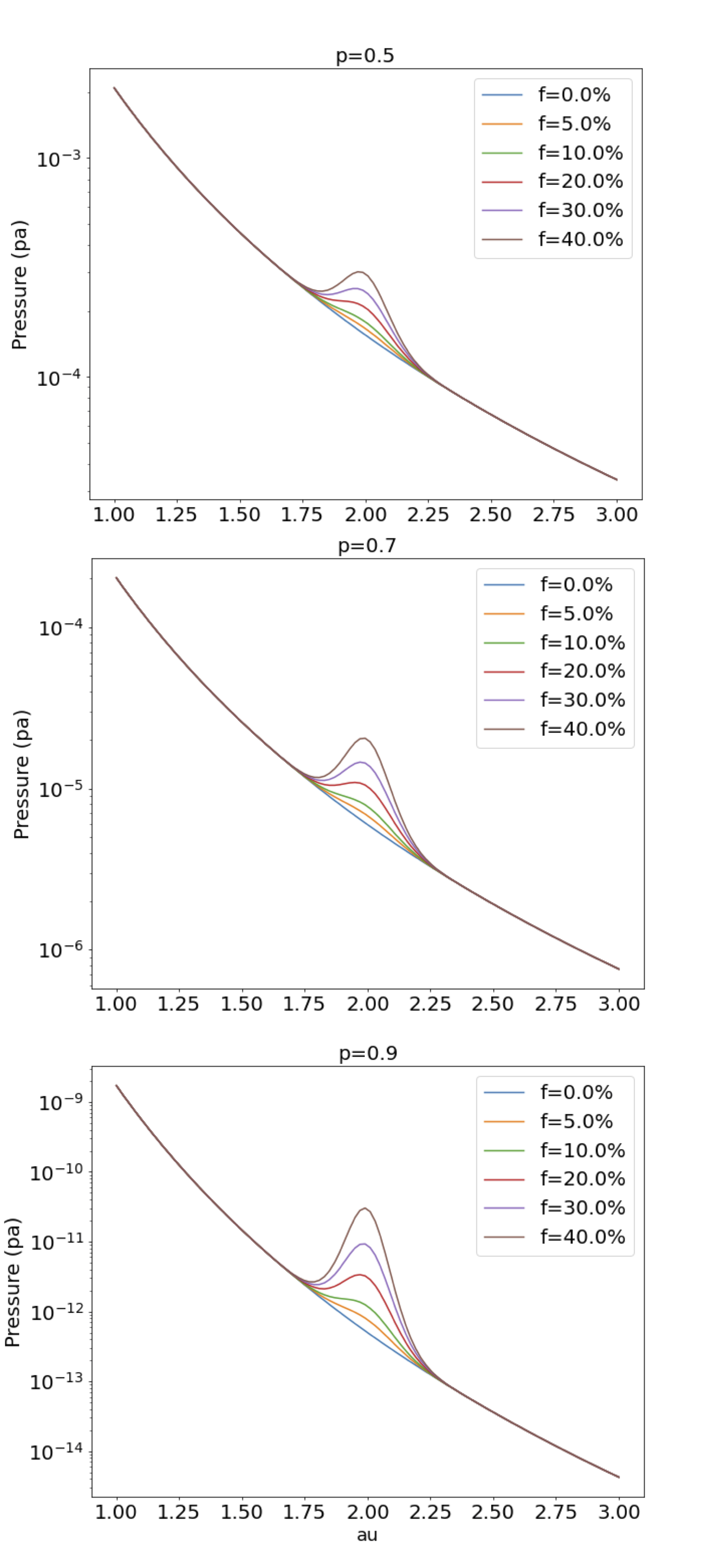
The above equation gives a much better criterion for forming a pressure bump even in the case of strong sound velocity perturbation. The water vapor enhancement necessary for forming a pressure bump, $\delta f$ as a function of $\dot{M}$ is plotted in figure 3 for $\delta r/r\simeq 0.1$. At high surface densities and high accretion rate $\delta f\simeq 0.7$ (equivalent to $A_{2}<<A_{1}$ in Equation 19). A low accretion rate, $\delta f\simeq 0.7$ in agreement with estimates of the previous section. So it is interesting to see that, as the accretion rate decreases, it is increasingly easy for the disk to develop a pressure bump (as $\delta f$ drops from 0.7 to 0.2). Once the disk has lost most of its mass, and once the snow-line is no longer inside the dead-zone it is no longer possible to develop a pressure bump.

For the high accretion rates, relevant to young disks, we will keep, for simplicity purpose, the criterion :

The criterion derived in Equation 12 does not allow to predict the range of pebble and gas flux for which a pressure bump may form inside a dead-zone. Thus, we propose the following order of magnitude estimate : the vaporization region (the region around the snow-line where icy pebbles evaporate) is located at distance $r$ and with width $\delta r$. The water mass contained in this region is $M_{w}$. It is fed by the incoming flux of icy pebbles $F_{i}=2\pi rv_{i}\Sigma_{i}$ with ice surface density $\Sigma_{i}$ and icy pebbles velocity $v_{i}$. Water vapor leaves this region with the same velocity as the gas $v_{g}$ so the water vapor flux leaving the region is $F_{v}=2\pi rv_{g}\Sigma_{w}$. After a transient phase, the surface density of water vapor will reach a steady state, with surface density at steady-state $\Sigma_{w,ss}=\Sigma_{i}v_{i}/v_{g}$. For a pressure bump to appear we must have $\Sigma_{w,ss}/\Sigma>\delta f$. So we get another (equivalent) condition for a pressure bump to form, as a function of gas velocity and ice surface density :

for $\delta r\simeq 0.2$ au (Hyodo et al. 2021a) and $r\simeq 2.0$ au and for $\Sigma_{i}/\Sigma\simeq 0.01$ (as typical values) we get $v_{i}/v_{g}>70$ for a pressure bump to appear. Equivalently Equation 21 can be formulated in terms of pebble/gas flux:

and with the above values we get $F_{i}/F_{g}>0.7$.

In summary, the conditions for pressure bump to appear at the snow-line are :

• •

  The snow-line must be embedded within the dead-zone (and not necessarily close to its edge).

• •

  The ice flux necessary for form a pressure bump depends on the surface density at the snow-line. The higher the surface density (for young disks with high accretion rates), the higher the necessary flux. Conversely, as surface density decreases, as as the accretion rate decreases also, the lower the necessary ice flux to form a pressure bump.

• •

  For high surface density disk, corresponding to high accretion rate ($>10^{-}7M_{\odot}/year$), assuming the $\Sigma_{i}/\Sigma\simeq 0.01$, a pressure bump will form at the snow-line if $v_{i}/v_{g}$ ¿ 70, or equivalently, if $F_{i}/F_{g}>0.7$ for an ice to gas ratio of $1\%$. This corresponds to $p$ close to 0. So a high pebble flux is needed in dense disks to form a pressure bump.

• •

  For low surface density disk ( and accretion rate in the range$\simeq 10^{-}9M_{\odot}/year$), assuming the $\Sigma_{i}/\Sigma\simeq 0.01$, a pressure bump will form at the snow-line if $v_{i}/v_{g}$ ¿ 20, or equivalently, if $F_{i}/F_{g}>0.2$ for an ice to gas ratio of $1\%$. This corresponds to case with $p$ close to 1, so it is easier in low surface density dead-zones to form a pressure bump.

Note that the above calculations assume that the surface density of the disk has reached a steady state (i.e. constant accretion rate everywhere). However, simulations of disks with including Dead Zone (Zhu et al. 2010; Hasegawa & Takeuchi 2015; Charnoz et al. 2019) show that in general, a steady state is never reached, and that the disk suffers episodic phases of high and low accretion rates. So in the next section, we study numerically the formation of a pressure bump, for a disk which is not at steady state.

We have detailed a process by which a pressure bump can form in a stratified protoplanetary disk, including a central layer dead to turbulence, and an actively accreting upper layer with surface density $\Sigma_{a}$. Considering that the vertically averaged $\alpha$ is a decreasing function of surface density ($\left<\alpha\right>\propto\Sigma^{-p})$, we have shown that when a local sound velocity drop appears (due to release of vapor inward the snow-line), a maximum of local pressure appears, with magnitude increasing with $p$. A physical explanation of this process, implying an interplay between the dead and active layer, is provided in Appendix A. This effect is especially efficient when $p$ is close to 1, in other words, that the surface density at the snow-line is less than 10 times the active layer column density (which does not necessarily imply that the snow-line is located close to the outer edge of the dead-zone). Note that for a minimum mass solar nebula profile with $\Sigma(r)=1.7\times 10^{4}(r/1au)^{-1.5}$ we have p¿0.9 in the terrestrial planet region for $\Sigma_{a}>100kg/m^{2}$ (check on Figure 1), that is already a situation very favourable for forming a pressure bump. The outer edge of the dead-zone for the same nebula is located much beyond 10 au (when $\Sigma=\Sigma_{a}$).

The conditions for the pressure-bump to form are summarized below

• •

  (1) A stratified disk with a dead-zone embedding the snow-line.

• •

  (2) An high influx of icy pebbles.

• •

  (3) For the pressure bump to appear, a sufficient condition is that the pebble/gas velocity ratio must be $>$ 60, or in terms of ice/gas mass flux ratio the condition is $F_{i}/F_{g}>0.6$ for a disk with $1\%$ of water by mass.

• •

  For our Solar System $1\%$ is approximately the mass fraction of all condensible material. The water mass fraction for our Solar System may be rather in the range $\sim 0.3\%$ (e.g. Bitsch & Johansen (2016)). In that case $F_{i}/F_{g}>1.8$ is needed. Such a flux is easily reached in a disk with $\Sigma_{a}=100kg/m^{2}$, where Stokes number $>0.03$ is needed. Conversely in a disk with $\Sigma_{a}=1000kg/m^{2}$, a Stokes number $>0.3$ is needed.

• •

  (4) A gas surface density at the snow-line with $\Sigma_{a}<\Sigma<\alpha_{a}/\alpha_{d}\times\Sigma_{a}$ (i.e. a few $10^{3}$ to a few $10^{4}Kg/m^{2}$) to create the pressure bump.

• •

  In the case the disk reaches a steady state accretion rate, the flux of icy particle necessary to maintain a pressure bump depend on accretion rate. It is about $F_{i}/F_{g}>0.2$ for $10^{-9}M_{\oplus}/year<\dot{M}<10^{-8}M_{\oplus}/year$ up to $F_{i}/F_{g}>0.6$ for $10^{-7}M_{\oplus}/year<\dot{M}$. These fluxes must be multiplied by $\sim 3$ if the ice/gas ratio is about $0.3\%$ (rather than $1\%$) like it was probably in our Solar Nebula.

The mechanism described here has the following important properties :

• •

  The formation of a pressure bump just inward the snow-line as long as the icy-pebble flux is maintained and is high-enough.

• •

  The accumulation of ice-free pebbles at the pressure bump, that may result in the formation of water-free planetesimal at the bump location.

• •

  Pebbles accumulating at the pressure bump are inherited from beyond the snow-line due to the inward drift of icy pebbles. But they would not cross the bump, as the bump acts as a dynamical barrier, and because they are progressively incorporated into larger planetesimals.

• •

  In addition to this process, beyond the snow-line, planetesimal formation can still happen at any time, following the processes described in Dr\każkowska & Alibert (2017) (like traffic jam effect or recondensation of water vapor beyond the snow-line).

We emphasize again that this mechanism does not necessarily take place close to the outer edge of the dead-zone. Indeed there is no need for a coincidence between the location of the snow-line and the outer edge of the dead-zone (defined as $\Sigma=\Sigma_{a})$. For example for having p¿0.7 (a condition very favorable for the formation of the bump) the surface density at the snow-line must be larger than $1000\Sigma_{a}$ (Figure 1). For a minimum mass solar nebula, with snow-line around 2 au, the outer edge of the dead-zone would be around ¿10 and ¿100 au for $\Sigma_{a}=1000kg/m^{2}$ and $\Sigma_{a}=100kg/m^{2}$ respectively.

The formation of the pressure bump may lead to a strong enhancement of the dust/gas ratio in the disk midplane, necessary to trigger the streaming-instability, and thus, planetesimal formation. In Figure 5, that is our most realistic disk simulation of the present paper, we see that, at the bump, the ratio of dust to gas surface density increases to about $\Sigma_{d}/\Sigma_{d}\simeq 0.1$. At this place the pebble stokes number is about 0.3 (Charnoz et al. 2019). So we can estimate the dust/gas ratio of volumetric densities in the midplane. Assuming the pebbles are in a vertical steady state where turbulent diffusion acts against sedimentation, the dust scale height $H_{d}\simeq H_{g}\sqrt{\alpha/(\alpha+St)}$ Dr\każkowska & Dullemond (2014), where $\alpha$ is $\alpha_{d}$ here.The ratio of volumetric densities of dust and gas in the midplane is also equal to $\rho_{d}/\rho_{g}=(\Sigma_{d}H_{g})/(\Sigma_{g}H_{d})$. So we get $\rho_{d}/\rho_{g}=(\Sigma_{d}/\Sigma_{g})\sqrt{(\alpha+St)/\alpha}\simeq 17$, much larger that 1. So it is very possible that planetesimal can form in the pressure bump visible in Figure 5. However, we remind the reader that other instabilities may develop, that may or may not act against concentration of dust. Hasegawa & Takeuchi (2015) investigates a viscous instability process using a new parameterization of $\alpha$ depending on the local magnetic field, and is a generalization of the parametrisation of $\alpha$ we use here. They show that at the outer edge of the dead zone, the effective $\alpha$ may become negative, leading to a viscously unstable situation where density maxima can grow without bounds because of negative effective diffusion coefficient. This instability may happen at the outer edge of the dead-zone, when the surface density becomes comparable to $\Sigma_{a}$. So the pressure bump formation process may take place in addition to the instability described in Hasegawa & Takeuchi (2015). However, we do emphasize here that whereas the instability process of Hasegawa & Takeuchi (2015) happens at the outer edge of the dead-zone, the pressure bump formation process we describe here occurs well inside the dead-zone, at the snow-line.Large scale hydrodynamical instabilities are also known to develop, like the Rosby Wave instability, in the presence of a large viscosity gradient (that may occur at the outer edge of the dead-zone) or in the presence of a strong pressure or density bump (as in our case) (Regály et al. 2012; Mohanty et al. 2013). This may imply that a large scale vortex may potentially form at the pressure bump (a physics which is not captured in our simple 1D model) which could potentially concentrate pebbles, and may lead to big planetesimals formation. In conclusion, the evolution of dust in such a bump, that could be subject to different kind of hydrodynamical instabilities should be investigated with 3D simulations in the future.

The mechanism for forming a pressure bump detailed here may potentially work at every condensation fronts, provided the flux of heavy evaporating species is strong enough and that an evaporating front is embedded in the dead-zone. Observations of the TW-Hydra disk potentially reveals efficient trapping of CO or $N_{2}$ dust ¿10 au at their evaporation front (Bosman & Banzatti 2019; McClure et al. 2019). However the present paper only focuses on water evaporation. The viability of such a process at the CO or $N_{2}$ condensation fronts must be quantified in a future study.

We wish to acknowledge the financial support of the Region Île-de-France through the DIM-ACAV + project: “HOC -Origine de l’eau et du carbone dans le Système Solaire”, the french ”Programme National de Planetologie” (PNP), the program ANR-15-CE31-0004-1 (ANR CRADLE), the IdEx Université de Paris ANR-18-IDEX-0001, and program ANR-20-CE49-0006 (ANR DISKBUILD). R.H. was supported by JSPS Kakenhi JP17J01269 and 18K13600. R.H. also acknowledges JAXA’s International Top Young program. We warmly thank S. Ida, T. Guillot and R. Brasser for useful comments. We also thank our anonymous reviewer for a thoughtful review that helped us to largely improve the quality of the paper.