Formation of nonlinear waves in decelerated centrifuges of noncircular cross-section

Nonstationary flows with a free boundary have been an important part of the classical hydrodynamics, mainly due to the inexhaustible interest to waves on the sea surface and on other bodies of water. Gravity water waves are excitations caused by the presence of the uniform gravity field and propagating in the two horizontal directions. The amount of published scientific articles on this subject is indeed huge. Essentially, in most theoretical models the approximation of an ideal incompressible fluid is employed, together with the potentiality condition for the velocity field. Cartesian coordinates are quite natural in description of small deviations from the equilibrium plane, so below we will conventionally call such waves “Cartesian waves”.

In contrast to “Cartesian” waves, surface waves in partially filled, rapidly rotating containers — centrifuges — have been studied so far in a considerably less extent (see, e.g., Phillips ; IKC2004 ; IKP2005 , and references therein). It should be said that in a fast rotating coordinate system, the efficient gravity field is created by the centrifugal force in the radial direction from the rotation axis, and this field is dominating over the usual gravitational acceleration $g$. Therefore, the angular coordinate plays here the role analogous to the role of one of the horizontal coordinates for “Cartesian” waves, whereas the radial coordinate is analogous to the vertical coordinate in the uniform gravity field. Besides that, a very essential influence on the dynamics of surface waves in centrifuges is caused by the Coriolis force. The problem is especially difficult when the shape of the container cross-section is different from circular, and when the rotation occurs with an angular acceleration. The fluid dynamics in such systems is interesting both for the fundamental science and for possible technological applications, and therefore it is deserving of serious attention. In this work, we consider decelerated centrifuges with cross-sections as shown in Fig.1, thus making a new step in theoretical investigation of nonlinear water waves.

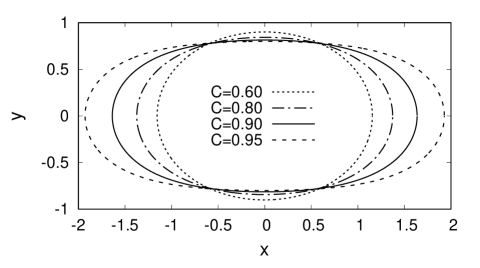
Let us start with simplifying approximations. If the container of a typical transverse size $L$ is rotating for a long time with a constant angular velocity $\Omega$ around some horizontal axis, then (under condition $g/(L\Omega^{2})\ll 1$) an almost rigid-body regime of rotation arises, and all the dissipative vortex structures practically disappear. After that, an applied external action, for example linear acceleration of the container axis or its rotational acceleration (in the case of noncircular shape), leads to deformation and subsequent nontrivial dynamics of the free internal surface. It is important that with sufficiently large values of $\Omega$, inertia is dominating over dissipation for some initial time period, until large gradients have been formed near the free surface, or until boundary-layer separation has occurred near possible wall irregularities. On this initial stage, the ideal-fluid approximation is quite admissible, and it is able to provide a rich information about wave dynamics in centrifuges.

The second simplification is to consider the problem in the class of planar flows. The two-dimensionality makes possible application of time-dependent conformal mappings (of the flow domain) and the mathematical apparatus of the corresponding analytical functions Ovs1 ; Ovs2 . This approach allows one to reduce the spatial dimensionality of the dynamical system to 1D (the evolutional system of equations contains only one independent spatial variable being a parameter along the free boundary). The equations themselves can be written in an exact form suitable for numerical simulations using fast Fourier transform routines Z1 ; Z2 ; Z3 ; D1 . At present, equations of motion of the free surface in conformal variables have been a working tool for many researchers (see Refs. Z4 ; Z5 ; Z6 ; Z7 ; ChoiC1999 ; LHChoi2004 ; Sh2006 ; Sh2008 ; Sh2010 ; ZSh2010 ; ZSh2012 ; ChS2005 ; Ch2009 ; Sl2009 ; Choi2009 ; LDK2013 ; ZK2014 ; L2016 ; TB2016 ; T2016 ; BP2016 ; LDS2017 ; DLZ2019 ; DDLZ2019 ; D2019 ; GDVW2019 ; FMN2019 ; KDG2019 , and many references therein). Mainly, waves over infinitely deep water are simulated, but the method was also generalized to the case of a curved static bottom, by introducing a composition of two conformal mappings R1 . The second, auxiliary mapping is realized by some given analytical function, and it corresponds to the bed profile. Waves over a time-dependent bottom were then considered in Ref. R2 , and shear flows with a free boundary over variable depth were modeled for the first time by the composite conformal mapping method in R3 . High efficiency and practical convenience of this method were confirmed in solution of some meaningful physical problems R4 ; R5 ; R6 ; R7 ; R8 . Finally, for uniformly swirled flows in centrifuges, conformal variables were introduced and approved in the recent work R2020 .

In contrast to typical “Cartesian” waves propagating over initially static body of fluid, for consideration of planar flows in centrifuges, instead of the potentiality condition, it is more natural to put the condition of constant vorticity (in the laboratory frame of reference). Therefore in a uniformly rotating coordinate system the velocity field is purely potential: ${\bf V}=(V^{(x)},V^{(y)})=(\varphi_{x},\varphi_{y})=(\theta_{y},-\theta_{x})$, where the subscripts denote partial derivatives, function $\varphi(x,y,t)$ is the velocity potential, and $\theta(x,y,t)$ is the corresponding harmonically conjugate stream function. It is very important that $\varphi(x,y,t)$ obeys the generalized Bernoulli equation R2020 ,

where $\tilde{P}$ is the pressure divided by (constant) fluid density. The effective vertical gravity field $g(t)$ depends on time if the rotation axis experiences vertical accelerations. Besides the potential of centrifugal force, the term $2\Omega\theta$ is present here, which is due to the Coriolis force. Equation (1), taken on the free internal boundary, determines the wave dynamics in centrifuge (together with two kinematic conditions, on the free boundary and on the container wall). When expressed in terms of the conformal variables, the equations serve as the basis for a highly accurate numerical method, described in detail in work R2020 . It is very essential that employment of composite conformal mappings allows one to deal easily with centrifuges of noncircular shape, if the wall profile is given parametrically as an image of the unit circle under some conformal mapping of its interior, i.e., $X+iY=F(e^{i\zeta})$, $0\leq\zeta\leq 2\pi$, with an analytical function $F(W)$.

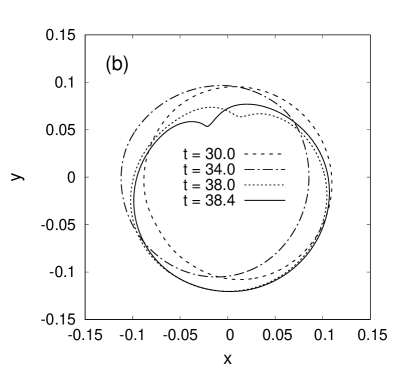
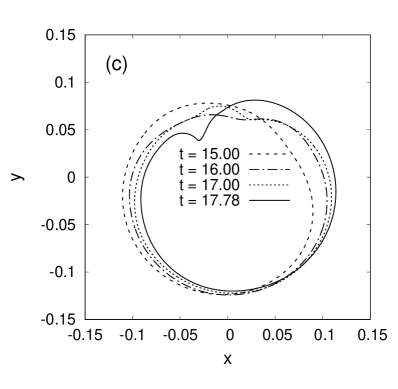
In this work, the method is applied to simulate strongly nonlinear processes taking place in centrifuges with elongated shape of the cross-section under their angular deceleration, when (non-dimensionalized by $\Omega$) angular velocity varies with time according to the linear law $\omega(t)=1-\alpha t$. Such a statement of the problem seems rather natural. For the centrifuge cross-section shape (at the time moment $t=0$), the following function was chosen,

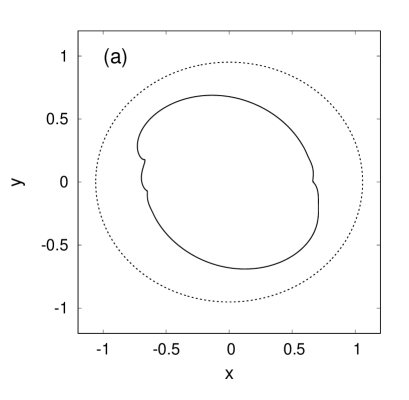
with parameter $0<C<1$. All the lengths are non-dimensionalized here to $L$. As $C\to 0$, we have the unit circle here, whereas in the limit $C\to 1$ the domain elongates to the horizontal stripe of width $\pi/2$. In Fig.1, examples of cross-sections for several intermediate values of $C$ are presented. At an arbitrary time moment, expression (2) is multiplied by $\exp(i\int_{0}^{t}\omega(t)dt)$. It is clear in advance that in the coordinate system attached to the container of such elongated shape, under deceleration of its rotation, a shear component of the flow appears, which interacts with the free boundary and tends to deform it. A shear flow around the free cavity is accompanied by formation of surface waves. It is quite obvious that investigation of nonlinear fluid dynamics in such geometry is impossible by the present-day-existing analytical methods. Meanwhile, the numerical method copes with the problem easily, keeping a high accuracy typically exceeding 8-10 decimal places.

In the performed numerical experiments, initial shape of the free boundary was given parametrically as $x(u)+iy(u)=F(s_{0}e^{iu})$, with some parameter $s_{0}$. Under condition $s_{0}C\lesssim 0.4$, it was close to the circle of radius $s_{0}$. The initial velocity potential was equal to zero.

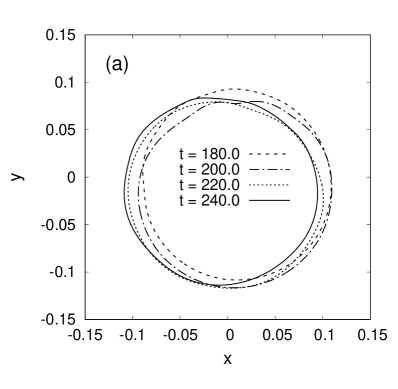
It should be said that in the coordinate system attached to the container, the vertical gravity field plays the role of a time-dependent driving force capable to excite waves. Therefore it was also taken into account, and its non-dimensionalized to $L\Omega^{2}$ value was chosen as $g=0.02$ in the main series of our numerical simulations. Separately it was checked that under uniform rotation (when $\alpha=0$), even an essentially larger value as $g=0.06$ does not lead to formation of nonlinear waves for a rather long time period, at least for values $s_{0}\sim 0.4$ that are not too large and not too small. In general, for each $s_{0}$ there exists a characteristic value $g_{*}(s_{0})$, near which the time of nonlinear wave formation changes abruptly. The function $g_{*}(s_{0})$ turns out to be increasing. For example, with $s_{0}=0.1$ (smaller cavity size), the transient regime takes place just near $g=0.02$, as it follows from Fig.2 where profiles of the free boundary at different time moments are shown for three numerical experiments (the rotation occurs anti-clockwise). It is seen that at $g>0.02$ the nonlinear wave rises just after a few revolutions of the centrifuge, whereas at $g=0.018$ big waves are still absent after dozens of revolutions. Since at small $s_{0}$ the free surface is in the deep-water regime, the relevant parameter is the ratio $g/s_{0}$. From here we obtain a rough empirical estimate $g_{*}\approx 0.2s_{0}$. Such a tendency is explained by weakening of the stabilizing effect of centrifugal acceleration at smaller distances from the rotation axis.

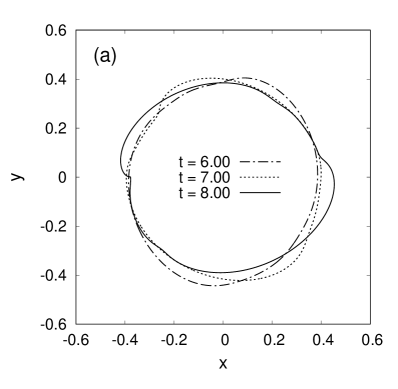
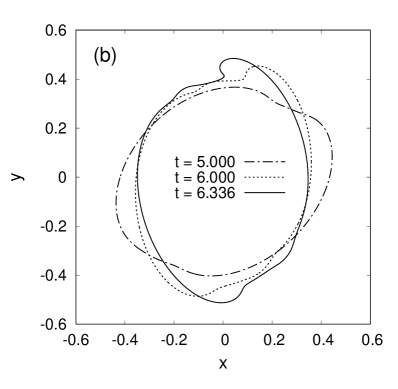
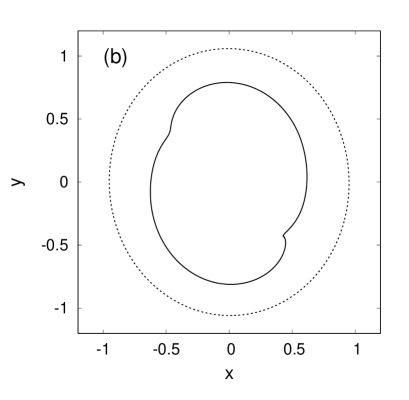
Finally, let us pass to the main results for decelerated centrifuges. The simulations have shown that arising shear flow leads the shape of free boundary away from being circular and “skews” it, and after that several strongly nonlinear waves with steep and sharp crests appear in the system. Examples of such behavior are presented in Fig.3 for $C=0.9$, $s_{0}=0.4$. We emphasize that, in contrast to Fig.2 where the waves appeared always in the upper sector of the free cavity due to the action of gravity force, here we clearly observe the tendency to wave emergence in two diametrically opposite directions, which fact is related to the corresponding symmetry of the centrifuge cross-section. The gravity force however slightly breaks the wave symmetry. It is also seen that overturning of the wave crests occurs against the direction of centrifuge rotation at small values of the angular deceleration $\alpha$, whereas with increase of this parameter the crests overturn already in the rotation direction. The reason for this is not clarified yet.

Qualitatively similar results were obtained also for somewhat smaller cavity sizes, down to $s_{0}\approx 0.15$, but a characteristic value $\alpha_{*}$, at which the overturning direction is changed, slightly decreases there (from $\alpha_{*}\approx 0.06$ at $s_{0}=0.4$ to $\alpha_{*}\approx 0.04$ at $s_{0}=0.15$). Besides that, at smaller $s_{0}$ the diametrical asymmetry increases.

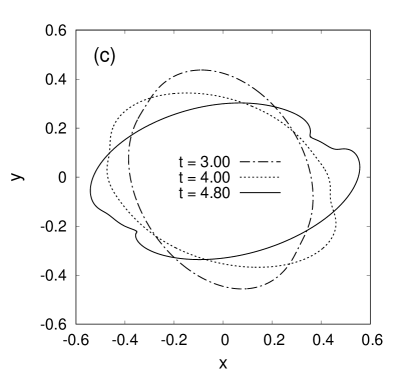
With the purpose of comparison, simulations for a less filled ($s_{0}=0.7$) and not so deformed ($C=0.4$) centrifuge were also carried out. Of course, with such geometrical parameters, one cannot already speak about a shear flow around the cavity, but rather about immediate wave interaction with an azimuthally nonuniform bottom profile, on the general background of accelerated angular stream. Nonlinear waves with sharp crests appear here as well. The corresponding examples are given in Fig.4.

It is clear that with the formation of a sharp crest, the stage of applicability of the ideal fluid approximation comes to the end. Correspondingly, next stages require completely different approaches. Likely, the further evolution in real conditions includes appearance of “white caps” and three-dimensional turbulent domains. The number of involved degrees of freedom rapidly increases by orders of magnitude (depending upon Reynolds number), and it can make subsequent modeling quite problematic, sometimes even practically unavailable. That circumstance, however, cannot devaluate the importance of investigation of the first, inviscid stage.

To conclude, in this work an initial stage of the dynamics of free fluid surface in decelerated centrifuges with noncircular shapes has been accurately modeled for the first time. The perfect fluid approximation, together with conformal mappings, allowed us to observe evolution of nonlinear waves up to the breaking of their crests. As one of the practical conclusions, we can say that in the deep-water regime the main dissipative structures in a nonuniformly rotating centrifuge will first appear most probably near the free surface, rather than near a smooth wall.

As in every profound problem, here new results generate many new questions too. The subsequent work on the problem can be aimed, in particular, on the search of new interesting numerical solutions in different parametric domains, and on the achievement of qualitative understanding of the basic properties of observed nonlinear wave structures.