FoMo: A Foundation Model for Mobile Traffic Forecasting with Diffusion Model

Haoye Chai Tsinghua UniversityChina , Shiyuan Zhang Tsinghua UniversityChina , Xiaoqian QI Tsinghua UniversityChina and Yong Li Tsinghua UniversityChina

Abstract.

Mobile traffic forecasting allows operators to anticipate network dynamics and performance in advance, offering substantial potential for enhancing service quality and improving user experience. However, existing models are often task-oriented and are trained with tailored data, which limits their effectiveness in diverse mobile network tasks of Base Station (BS) deployment, resource allocation, energy optimization, etc., and hinders generalization across different urban environments. Foundation models have made remarkable strides across various domains of NLP and CV due to their multi-tasking adaption and zero/few-shot learning capabilities. In this paper, we propose an innovative Foundation model for Mobile traffic forecasting (FoMo), aiming to handle diverse forecasting tasks of short/long-term predictions and distribution generation across multiple cities to support network planning and optimization. FoMo combines diffusion models and transformers, where various spatio-temporal masks are proposed to enable FoMo to learn intrinsic features of different tasks, and a contrastive learning strategy is developed to capture the correlations between mobile traffic and urban contexts, thereby improving its transfer learning capability. Extensive experiments on 9 real-world datasets demonstrate that FoMo outperforms current models concerning diverse forecasting tasks and zero/few-shot learning, showcasing a strong universality. We further deploy the FoMo on the JiuTian optimization platform of China Mobile, where we use the predicted mobile data to formulate network planning and optimization applications, including BS deployment, resource block scheduling, and BS sleep control.

Mobile traffic forecasting; foundation model; diffusion model; spatio-temporal prediction

1. Introduction

In recent years, foundation models (Brown, 2020; Touvron et al., 2023; Radford et al., 2021) have made substantial strides in natural language processing and computer vision. These models are reshaping the AI ecosystem by harnessing their powerful data processing, generalization, and zero/few-shot learning capabilities. An increasing number of specialized domains have developed foundational models tailored to their specific data and contextual demands, including healthcare, medicine, urban navigation, intelligent manufacturing, and beyond (Yuan et al., 2024b; Yeh et al., 2023; Kang, 2024; Bozic et al., 2024). Mobile networks and computing encompass massive amounts of mobile traffic, user, and geographical data, providing natural data support for foundation models. However, such dedicated foundation models for mobile network domains have yet to be established. We hence aim to construct a foundation model for mobile traffic forecasting, which can handle diverse features of large-scale mobile data while retaining the generalization needed across multiple cities and scenarios (Wu et al., 2021b; Chai et al., 2024a; Yin et al., 2022).

Constructing such a foundation model of mobile traffic forecasting is vital for mobile networks (Feng et al., 2024; Wu et al., 2021a; Zhou et al., 2023). On the one hand, mobile traffic forecasting offers great potential for network planning and optimization. It enables operators to anticipate traffic dynamics, facilitating proactive perceptions of resource utilization and service quality, and allowing for the preemptive development of optimization strategies. On the other hand, mobile networks encompass a variety of optimization tasks, including radio resource scheduling (Miao et al., 2012; Lohani et al., 2016), Base Station (BS) deployment (Dong et al., 2020; Fahim and Gadallah, 2023), and antenna configuration (Mei and Zhang, 2023; Lin et al., 2022), etc. These tasks involve diverse objectives like throughput, coverage, and energy efficiency, which impose distinct requirements on traffic forecasting. For example, radio resource scheduling prioritizes short-term traffic dynamics to improve user experience (Chen et al., 2020b; Ghandri et al., 2024), whereas BS deployment focuses on long-term traffic patterns within a region to match network demands (Zhao et al., 2021; Wang et al., 2021). Regarding the differentiated forecasting needs of optimization tasks, current methods typically employ one-to-one approaches: designing customized models by leveraging task-specific data (Yang et al., 2019; Hu et al., 2023; Zhou et al., 2023; Li et al., 2024), and focus on one single application scenario, making it challenging to generalize the models across different cities and tasks.

On the contrary, foundation models possess large-scale learnable parameters with powerful feature representation and generalization capabilities, enabling them to learn universal features from vast amounts of mobile traffic data (Liang et al., 2024; Chaccour et al., 2024). Moreover, it is endowed with robust few/zero-shot abilities to be applied across different cities and scenarios (Cai et al., 2023; Rahman et al., 2018). By constructing foundation models for traffic forecasting, it becomes possible to achieve precise traffic predictions for various scenarios and cities via one unified model, thereby efficiently addressing the diverse tasks involved in mobile networks.

However, designing the foundation model remains a significant challenge. Although numerous notable works have emerged in the area of mobile traffic forecasting (Gong et al., 2023; Kang et al., 2024; Pandey et al., 2024; Kavehmadavani et al., 2024; Xu et al., 2021; Zhang et al., 2023), the majority of these models are typically tailored to specific tasks that fall short of the universality expected from foundation models. Specifically, current mobile traffic forecasting models face three key limitations:

i) Limited generalization. Mobile traffic data is inherently shaped by the spatio-temporal dynamics of population distribution and communication demands. Due to variations in geographic environments, lifestyle habits, and urban layouts across different cities, mobile traffic can differ significantly (Yin et al., 2020; Xu et al., 2017). With relatively small parameters, current models struggle to capture the diverse spatio-temporal patterns inherent in large-scale data across multiple cities. Additionally, it is challenging to encapsulate the complex correlations between contextual factors and mobile traffic, resulting in poor transferability in multi-city scenarios.

ii) Constrained adaptability to multiple scenarios. Mobile traffic forecasting is extensively applied across varying optimization scenarios. However, current models are often designed with specialized modules tailored to specific tasks. For instance, in short-term forecasting, models usually focus on capturing traffic fluctuations that employ autoregressive or event-driven methods. In contrast, long-term predictions emphasize the regular patterns of traffic and typically utilize time series decomposition techniques. These dedicated models increase design complexity and raise deployment costs when applied to diverse scenarios.

iii) Lack of universal representation of mobile traffic. Unlike standardized formats in language and vision domains, mobile traffic data is inherently heterogeneous of various collection granularity and scope. For example, Measure Report (MR) data primarily collects millisecond-level user traffic, while Performance Management (PM) data gathers cell-level traffic statistics over 15-minute intervals (Naboulsi et al., 2016; Wang et al., 2017b), leading to the absence of a unified representation akin to that found in natural language. Consequently, it is challenging to directly apply pre-trained models from the natural language/visual domains to mobile traffic data. Although some efforts have been made to reprogram mobile traffic data into a natural language format (Gruver et al., 2023; Jin et al., 2024), this approach heavily relies on the quality of manually crafted prompts, making it difficult to capture a universal representation of mobile traffic.

To tackle the challenges, we propose a Foundation model for Mobile traffic forecasting (FoMo), which aims to learn universal features of mobile traffic data and to handle multitasks in mobile networks across multiple cities, thereby establishing a one-for-all forecasting model. First, inspired by Sora (Brooks et al., 2024), FoMo adopts the transformer-based diffusion model as the backbone instead of the U-Net structure, to help the model understand the diverse features of massive mobile data. Furthermore, We propose a contrastive diffusion algorithm and modify the variational lower bound of the training objective by analyzing the cross-entropy between mobile traffic and contextual features, enabling the model to better integrate environmental information, thereby enhancing generalization capabilities and addressing the first research challenge. Second, we adopt a mask-based and self-supervised training paradigm (He et al., 2022; Wei et al., 2023), where we categorize traffic forecasting in mobile networks into three tasks: short-term prediction, long-term prediction, and generation. We design the corresponding masking strategies to enable the model to learn data features for various tasks and adapt to multiple tasks, thus addressing the second research challenge. Finally, we develop a mobile tokenization scheme to represent mobile traffic. The token standardizes mobile traffic data collected from various periods and diverse urban regions into unified units. The model leverages these tokens to learn the underlying patterns of large-scale mobile traffic data, enabling more accurate forecasting.

$\bullet$ To the best of our knowledge, it is the first foundation model designed for mobile traffic forecasting. The proposed model enables various forecasting tasks in mobile networks across different urban environments under a unified framework, assisting network operators in achieving highly efficient network planning and optimization.

$\bullet$ We develop our foundation model using a masked diffusion approach with spatio-temporal masking strategies tailored for diverse forecasting tasks, including short/long-term predictions and distribution generation. To strengthen the correlation between contextual features and mobile traffic, we further propose a context-aware contrastive learning fine-tuning strategy, which can enhance forecasting and transfer learning capabilities.

$\bullet$ We conduct extensive experiments with 4G and 5G mobile traffic data from 9 real-world datasets. The experimental results validate FoMo’s superior transferability, multi-task capabilities, and robust few/zero-shot performance in unseen scenarios. We further experiment with the scaling properties of our model, preliminarily uncovering the scaling law of the mobile traffic foundation model concerning data size, model scale, and model performance.

2. Preliminaries and Problem Formulation

2.1. Diffusion model and training object

Denoising Diffusion Probabilistic Model (DDPM). The underlying idea of DDPM is to use two Markov chains to characterize the transition from original data to noise data (Mukhopadhyay et al., 2023). The forward chain gradually adds Gaussian noise $\epsilon\sim N(0,1)$ to the original data that can be expressed as $q(x_{k}|x_{k-1})=N(\sqrt{1-\beta_{k}}x_{k-1},\beta_{k}\textbf{I})$ , $\{\beta_{k}\in(0,1),k\in(1,K)\}$ is a set of scheduled noise weight. Based on the forward transition probability, the generated noised data in step k can be calculated by $x_{k}=\sqrt{\hat{\alpha}_{k}}x_{0}+(1-\hat{\alpha}_{k})\epsilon.$ The reversed chain utilizes a well-trained network $p_{\theta}$ to recurrently denoise $x_{K}$ for recovering original data $x_{0}$ , which can be expressed as $p_{\theta}(x_{k-1}|x_{k})=N(\mu_{\theta}(x^{k},k),\sigma_{\theta}(x_{k},k)\textbf{I})$ .

Training objective. It is essentially to maximize the log-likelihood function of the denoising network $p_{\theta}$ for the initial data $x_{0}$ , i.e., $L(\theta)=\mathbb{E}_{x_{0}\sim q(x_{0})}\{-logp_{\theta}(x_{0})\}$ . Subsequently, this function is optimized using the Variational Lower Bound (VLB), which can be expressed as:

(1)			$\displaystyle-logp_{\theta}(x_{0})\leq-logp_{\theta}(x_{0})+D_{KL}(q_{(}x_{1:T}\|x_{0})\|\|p_{\theta}(x_{1:T}\|x_{0}))$
(1)			$\displaystyle\quad\quad=\mathbb{E}_{q_{(}x_{1:T}\|x_{0})}\{log\frac{q_{(}x_{1:T}\|x_{0})}{p_{\theta}(x_{0:T}\|x_{0}))}\}.$

Taking the expectation on both sides of the above equation and applying Fubini’s theorem (Yang et al., 2023b), we can derive:

(2)			$\displaystyle\mathbb{E}_{q(x_{0})}\{-logp_{\theta}(x_{0})\}\leq\mathbb{E}_{q(x_{0})}\bigg{\{}\mathbb{E}_{q_{(}x_{1:T}\|x_{0})}\{log\frac{q_{(}x_{1:T}\|x_{0})}{p_{\theta}(x_{0:T}\|x_{0}))}\}\bigg{\}}$
(2)			$\displaystyle\quad\quad=\mathbb{E}_{q_{(}x_{0:T})}\{log\frac{q_{(}x_{1:T}\|x_{0})}{p_{\theta}(x_{0:T}\|x_{0}))}\}\triangleq L_{vb}(\theta).$

We can minimize the upper bound of $L(\theta)$ by minimizing $L_{vb}$ , thereby maximizing the log-likelihood function of $p_{\theta}$ . Ho et al. (Ho et al., 2020) proved that $L_{vb}(\theta)$ can be further parameterized by $\mu_{\theta}(x_{k},k)=\alpha_{k}^{-0.5}[x_{k}-\beta_{k}(1-\hat{\alpha}_{k})^{-0.5}\epsilon_{\theta}(x_{k},k)]$ , and $\sigma_{\theta}$ can be parameterized as $\sigma_{\theta}(x_{k},k)=\sqrt{(1-\hat{\alpha}_{k-1})/(1-\hat{\alpha}_{k})\beta_{k}}$ . The network $p_{\theta}$ can then be optimized by the following objective:

(3)

\underset{\theta}{min}L_{vb}(\theta)\approx\underset{\theta}{min}\mathbb{E}_{x_{0}\sim q(x_{0}),\epsilon\sim N(0,I)}[||\epsilon-\epsilon_{\theta}(x_{k},k)||_{2}^{2}].

2.2. Problem formulation

Mobile Traffic refers to the volume of data transmitted over wireless channels between mobile devices and BSs within a period of time. In this paper, we primarily focus on the aggregated downlink mobile traffic generated by all mobile devices within the coverage area of BSs. We consider a discrete-time scenario $T=\{1,2,...t\}$ with equal time intervals. For a single BS, the traffic variation over time $T$ can be represented as $\{b_{t}\}_{t=1:T}$ , where $b_{t}$ denotes the aggregated traffic within the coverage area of BS at time $t$ . To characterize the mobile traffic features across an urban region $\mathcal{G}$ , we define the geographical length and width of that region as $H$ and $V$ , respectively. The mobile traffic of region $\mathcal{G}$ can then be defined as the sum of the aggregate traffic of all BSs located at $\mathcal{G}$ : $\mathcal{S}_{t=1:T}=\sum_{b}\{b_{t}\}_{t=1:T}$ . Based on the definition above, the mobile traffic forecasting problem can be viewed as predicting dynamics in future traffic $\mathcal{S}_{t=T:T_{0}}$ , based on historical traffic information $\mathcal{S}_{t=1:T}$ and complex factors that influence network usage $C_{\mathcal{G}}$ , such as user behavior and geographical contexts, which can be expressed as:

Probelm Definition: Given arbitrary urban region $\mathcal{G}$ with geographical length and width $H\times V$ . The goal is to use a model $\mathcal{F}$ to predict the mobile traffic sequence $\mathcal{S}_{t=T:T_{0}}$ for the next $T_{0}$ time steps, conditioning on historical mobile traffic $\mathcal{S}_{t=1:T}$ and urban contextual factors $C$ , i.e., $\mathcal{F}(\mathcal{S}_{t=T:T_{0}}|\mathcal{S}_{t=1:T},C_{\mathcal{G}})$ .

There are two key requirements for achieving the above problem in large-scale urban environments. First, the model must be capable of processing massive traffic data across diverse urban spatiotemporal environments. Second, the model must flexibly handle various types of forecasting tasks in mobile networks. We identify 3 primary tasks:

$\bullet$ Short-term prediction task uses long historical data to predict mobile traffic dynamics over a short future period, $i.e.,$ $\{\mathcal{S}_{t=1:T},C_{\mathcal{G}}\}\rightarrow\mathcal{S}_{t=T:T_{0}}$ , where $T\geq(T_{0}-T)$ . It mainly focuses on the fluctuations with less periodicity of traffic. Based on the forecasts, operators can understand upcoming network demands and make strategies for wireless resource and access control to improve user experience in real time.

$\bullet$ Long-term prediction task estimates future traffic patterns based on limited historical data, $i.e.,$ $\{\mathcal{S}_{t=1:T},C_{\mathcal{G}}\}\rightarrow\mathcal{S}_{t=T:T_{0}}$ , where $T\leq(T_{0}-T)$ . It primarily explores inherent patterns and periodical features within the traffic. This forecasting enables operators to assess and analyze network performance from a global perspective, thereby facilitating the formulation of network optimization planning strategies, such as cell dormancy and network capacity expansion.

$\bullet$ Generation task focuses on identifying underlying network demand within a specific area without referring to historical data, $i.e.,$ $\{C_{\mathcal{G}}\}\rightarrow\mathcal{S}_{t=1:T_{0}}$ . Traffic generation helps operators assess potential communication demands in new regions lacking historical data, allowing them to develop planning strategies such as BS deployment, network segmentation, and capacity planning, etc.

However, building such a foundation model is not straightforward. Specifically, three key challenges arise: i). How can we generalize the large-scale traffic data across multiple cities and accurately model their rich spatiotemporal features? ii). What strategies can be employed for the training process, ensuring that the model is capable of handling the diverse forecasting tasks? iii). How to effectively integrate user dynamics and contextual features with mobile traffic?

3. Design of FoMo

3.1. Framework overview

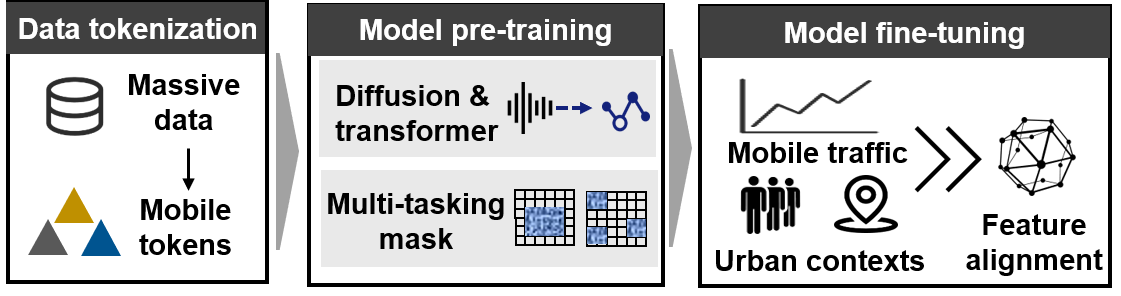
Refer to caption — Figure 1. The flowchart of the FoMo framework

To tackle the challenges, we propose the FoMo framework that incorporates three stages: data tokenization, model pre-training, and model fine-tuning, as illustrated in Figure 1.

i). Data tokenization. The stage reshapes mobile traffic data from various spatial ranges and time spans across multiple cities into a unified mobile token for model training and capturing the diverse features in mobile traffic.

ii). Masked diffusion-based pre-training. The stage enables the model to fully grasp the fundamental spatio-temporal features of mobile traffic across various forecasting tasks, where we design a masked diffusion model as the backbone, enabling the multitasking learning process.

iii). Urban context-aware fine-tuning. We design a contrastive learning algorithm that integrates external factors closely associated with mobile traffic, including network user dynamics and urban POI distributions.

3.2. Mobile traffic data tokenization

We draw inspiration from NLP tokenization (Dosovitskiy et al., 2021), where we decompose heterogeneous traffic data, with varying sampling intervals and diverse spatial ranges, into basic units. Embedding layers are then used to extract the intricate features of these tokens and learn their dependencies. Specifically, we define the minimum granularity of mobile tokens in space and time as $h_{0}$ , $v_{0}$ , and $t_{0}$ , respectively. For traffic data $S$ of length $T$ within an urban region $H\times V$ , the tokenization process breaks down $S$ into multiple small mobile tokens $X$ , which can be expressed as

(4)

S\in\mathbb{R}^{H\times V\times T}\rightarrow X\in\mathbb{R}^{(H^{\prime}\times V^{\prime}\times T^{\prime})\times(h_{0}\times v_{0}\times t_{0})},

where $H^{\prime}=H/h_{0}$ , $V^{\prime}=V/v_{0}$ , and $T^{\prime}=T/t_{0}$ , the $(h_{0},t_{0},v_{0})$ of X represents the mobile token. Subsequently, we use an embedding layer $E_{x}(X)$ ( $e.g.,$ pooling layer, convolutional layer, or fully connected layer) to map the mobile token with hidden features $C$ , $i.e.,$ $E_{x}(X)\in\mathbb{R}^{(H^{\prime}\times V^{\prime}\times T^{\prime})\times C}$ .

3.3. Masked diffusion-based pre-training

Pre-training primarily serves to enhance the foundation model’s understanding of various forecasting tasks and to capture the spatio-temporal correlations inherent in massive mobile data. We propose a masked diffusion model with self-supervised training (Zhao et al., 2024; He et al., 2022), where specific masks are tailored for the three forecasting tasks, as shown in Figure 2.

3.3.1. Multitasking mask

We develop 4 distinct masks $m\in\mathbb{R}^{H^{\prime}\times V^{\prime}\times T^{\prime}}$ : short-term masking, long-term masking, generative masking, and random masking. The first three schemes align with specific forecasting tasks, while random masking aims to further explore spatio-temporal correlations within mobile traffic, and enhance its generalization capability.

$\bullet$ Short/Long-masking masking. The schemes mask the time dimension $T^{\prime}$ at a specific spatial location $(h,v)$ , primarily to reconstruct the mobile traffic within the period $T^{\prime}-t_{0}$ , where $t_{0}\in T^{\prime}$ . Depending on the ratio of $t_{0}$ to $T^{\prime}$ , the schemes correspond to short-term and long-term predictions, respectively, and can be expressed as:

(5)

m_{h,v,t}=\{0,\ t_{0}<t\leq T^{\prime}|\ 1,\ 0<t\leq t_{0}\},\ \ h\in H^{\prime},v\in V^{\prime}.

$\bullet$ Generation masking. This type of mask fully obscures the temporal dimension of adjacent spatial regions $(h_{i\sim j},v_{i\sim j})$ , enabling the model to generate complete temporal mobile traffic within the regions, where $i\sim j$ represents multiple consecutive adjacent mobile tokens. Unlike prediction masks that depend on prior historical temporal information, this mask requires capturing the spatio-temporal dependencies between the target spatial region and its surrounding regions to generate underlying distributions, which yields:

(6)

m_{h_{x},v_{x}}=\{0,\ i<x\leq j|\ 1,\ else\}

$\bullet$ Random masking. The scheme masks mobile traffic across both spatial and temporal dimensions, which aims to capture diverse correlations of mobile tokens, aiding the model in understanding the complex features of mobile data. Denote $\mathcal{R}(H^{\prime},V^{\prime},T^{\prime})$ as randomly choosing items from $H^{\prime}$ , $V^{\prime}$ , and $T^{\prime}$ , the masking scheme follows:

(7)

m_{h,v,t}=\{0,\ \mathcal{R}(H^{\prime},V^{\prime},T^{\prime})|\ 1,\ else\}.

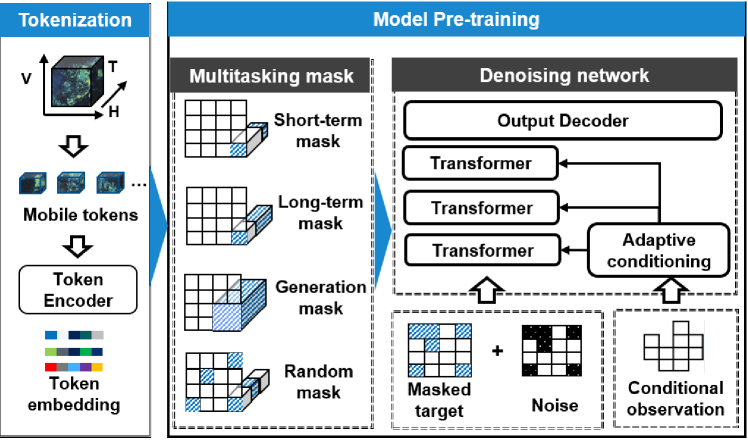
3.3.2. Self-supervised masked diffusion model

This part reconstructs the masked mobile token $E_{x}(X)$ that includes the following three important processes.

$\bullet$ Forward noising process. After completing the multi-task masking process, the original mobile token $E_{x}(X)$ is divided into two parts: the masked portion $e$ requiring to be reconstructed, and the unmasked observation $o$ :

(8)

e=E_{x}(X)\odot m,\quad o=E_{x}(X)\odot(1-m),

where $m$ corresponds to the four mask strategies, and $\odot$ represents element-wise products. Subsequently, $o$ is input as conditions into the denoising network, while $e$ adds noise according to the forward process, which is given by

(9)

e_{k}=\sqrt{\hat{\alpha}_{k}}e+(1-\hat{\alpha}_{k})\epsilon,\ \ \epsilon\sim N(0,1).

Afterward, $e_{k}$ is fed into the transformer-based denoising network for further feature extraction.

$\bullet$ Adaptive conditioning mechanism. To fully capture the dependencies between conditions and network traffic latent features, we employ an adaptive layernorm method (Peebles and Xie, 2023). The method reshapes the scale and shift parameters of the layernorm of transformers by referring to the given conditions, which is proven to offer better effectiveness and computational efficiency (Perez et al., 2018). It can be formulated as follows:

(10)

\displaystyle\alpha,\beta,\gamma=\mathcal{F}_{\theta}(o),\quad e_{k}\leftarrow e_{k}+\alpha\mathcal{A}_{\theta}(\beta e_{k}+\gamma),

where $\mathcal{F}_{\theta}$ and $\mathcal{A}_{\theta}$ denote linear layer and attention layer. $\alpha,\beta,\gamma$ are residual, scale, and shift parameters, respectively.

$\bullet$ Masked loss function. The denoising network aims to fit the posterior distribution of the diffusion process to predict the mean noise, ultimately reconstructing the final network traffic through an output decoder. Our objective thus emphasizes the reconstruction accuracy of the masked portion, which can be given as indicated in (9):

(11)

L_{\theta}=\underset{\theta}{min}\mathbb{E}_{e\sim q(e)}\bigg{\{}||\epsilon-\epsilon_{\theta}(e_{k},k|o)||^{2}\odot m\bigg{\}}.

3.4. Urban context-aware fine-tuning

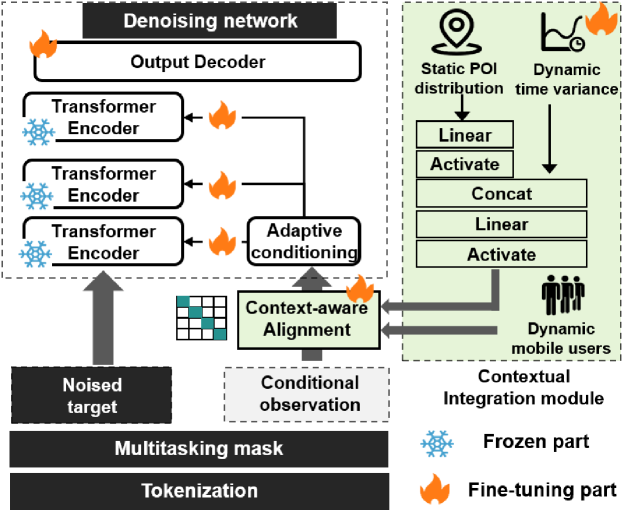
Mobile traffic is not only a spatio-temporal sequence but also influenced by urban contexts. Extensive literature has demonstrated that incorporating contextual features can enhance traffic prediction performance (Wang et al., 2023; Yu et al., 2021; Xu et al., 2022). Therefore, we propose a fine-tuning scheme, where two modules are encapsulated into the pre-trained model:

$\bullet$ Contextual integration: The module introduces mobile users and POI distributions, which aims to integrate human dynamics with the static features of urban environments.

$\bullet$ Context-aware alignment: The module employs a contrastive learning approach to align mobile traffic with contextual features.

3.4.1. Contextual integration

Mobile user refers to the number of users accessing the network. Similar to mobile traffic, it is inherently a spatio-temporal sequence that is denoted as $U\in\mathbb{R}^{H\times V\times T}$ . We apply the same processing method as traffic tokens where we perform tokenization on mobile users as $c^{u}\in\mathbb{R}^{(H^{\prime}\times V^{\prime}\times T^{\prime})\times(h_{0}\times v_{0}\times t_{0})}$ , allowing this data to be directly input into the network for training.

Urban POIs reflect the static distribution of urban layout that can be denoted as $P\in\mathbb{R}^{H\times V}$ . We cannot directly utilize spatio-temporal tokenization methods. Hence, we design a dynamic POI transformation scheme. Although the distribution of POIs is static, the impact of different categories of POIs on human behavior varies across different times, leading to corresponding variations in mobile traffic. For example, restaurant-type POIs typically show higher traffic during lunchtime and evening. We first extract the intrinsic static features of POI distribution, which can be written as:

(12)

h^{s}_{p}=\sigma(W^{s}\cdot P+B^{s}),

where $\sigma$ is the Sigmoid activation function, $W^{s}$ and $B^{s}$ are the weight and bias parameters of a linear layer. Inspired by (Wang et al., 2017a), we introduce temporal projection $\tau(t)$ related to timestamp (we use an MLP network). Then, the indicators and static features of POIs $h^{s}_{p}$ are concatenated as $h^{(0)}=h^{s}_{p}\oplus\tau(t)$ , where $\oplus$ denotes vector concatenation. We utilize an MLP network to fuse both the time embeddings and POI features:

(13)

h^{(l+1)}=\sigma(W^{l}\cdot h^{(l)}+B^{l}),\ \ \ l\in[0,L),

where $h^{(l)}$ is the hidden feature of the $l$ -th layer of MLP, $W^{l}$ and $B^{l}$ is the weight and bias parameters in each layer. In this way, we can obtain spatio-temporal dynamic representations as $h_{p}^{d}=h^{(L)}\in\mathbb{R}^{H\times V\times T}$ . The final features of POI can be calculated via the same tokenization method as $c^{p}\in\mathbb{R}^{(H^{\prime}\times V^{\prime}\times T^{\prime})\times(h_{0}\times v_{0}\times t_{0})}$ . The ultimate contextual feature tokens can be denoted as $y=c^{u}+c^{p}$ .

3.4.2. Context-aware alignment

Contextual features can be viewed as another modality of data that contains much information related to mobile traffic. We propose a contrastive learning algorithm (He et al., 2020; Chen et al., 2020a) to establish bridges between mobile traffic and contextual features.

$\bullet$ Contrastive sample construction. We define positive samples as mobile traffic tokens and contextual feature tokens within the same spatio-temporal block, denoted as $(e,y)$ ; while negative samples are defined as the two types of tokens from different spatio-temporal blocks, denoted $(e^{\prime},y)$ .

$\bullet$ Contrastive goal. Our goal is to maximize the mutual information between the traffic feature $e$ and contextual feature $y$ . According to previous research (van den Oord et al., 2019), a density ratio can be utilized while preserving the mutual information as $I(e,y)\propto\frac{p(e|c)}{p(e)}$ , and the maximization problem is equivalent to minimizing the InfoNCE loss that yields:

(14)

L=\underset{e\in\mathbb{B}}{\mathbb{E}}-log\frac{I(e,y)}{I(e,y)+\sum_{e^{\prime}}I(e^{\prime},y)}\leq log(N)-I(e,y),

where $\mathbb{B}$ denotes the entire batch of samples.

$\bullet$ Contrastive learning with diffusion paradigm. For diffusion models, the objective is to fit the posterior distribution through a neural network $p_{\theta}(x_{k-1}|x_{k})$ that maximizes the likelihood of $p_{\theta}(x_{0})$ . We clarify that the objective is fundamentally equivalent to that of InfoNCE in contrastive learning. We use $p_{\theta}$ to represent the probability in the mutual information as $I(e,y)=p_{\theta}(e_{0:K}|y)/p_{\theta}(e_{0:K})$ . In this way, the origin InfoNCE loss can be rewritten as:

(15)			$\displaystyle L=\underset{e\in\mathbb{B}}{\mathbb{E}}-log\frac{p_{\theta}(e_{0:K}\|y)/p_{\theta}(e_{0:K})}{p_{\theta}(e_{0:K}\|y)/p_{\theta}(e_{0:K})+\sum_{e^{\prime}}p_{\theta}(e^{\prime}_{0:K}\|y)/p_{\theta}(e^{\prime}_{0:K})}$
(15)			$\displaystyle\ \ \ =\underset{e\in\mathbb{B}}{\mathbb{E}}log\{1+\frac{p_{\theta}(e_{0:K})}{p_{\theta}(e_{0:K}\|y)}\cdot N\mathbb{E}_{e^{\prime}}\frac{p_{\theta}(e^{\prime}_{0:K}\|y)}{p_{\theta}(e^{\prime}_{0:K})}\},$

where $e^{\prime}$ denotes all negative samples. Referencing the parameterization $p_{\theta}(x_{k-1}|x_{k})=\sum_{x_{0}\in q}q(x_{k-1|x_{k},x_{0}})p_{\theta}(x_{0}|x_{k})$ in (Zhu et al., 2023; Austin et al., 2021), the above loss can be further formulated as:

(16)			$\displaystyle L\approx\underset{\mathbb{B}}{\mathbb{E}}\bigg{\{}\mathbb{E}_{q}\{-log\frac{p_{\theta}(e_{0:K}\|y)}{q(e_{1:K}\|e_{0})}\}-logN\mathbb{E}_{e^{\prime}}\mathbb{E}_{q}\{-log\frac{p_{\theta}(e^{\prime}_{0:K}\|y)}{q(e^{\prime}_{1:K}\|e^{\prime}_{0})}\}\bigg{\}}$
			$\displaystyle\ \ =L^{e}_{vb}-logN\sum\nolimits_{e^{\prime}}L^{e^{\prime}}_{vb}$
			$\displaystyle\ \ \doteq\mathbb{E}\bigg{\{}(\\|\epsilon-\epsilon_{\theta}(e,k\|y)\\|^{2}-\lambda\sum\nolimits_{e^{\prime}}\\|\epsilon-\epsilon_{\theta}(e^{\prime},k\|y)\\|^{2})\odot m\bigg{\}},$

where symbol $\doteq$ denotes the loss function we used during the model training process and $\lambda$ is a scaling parameter proportional to $logN$ . Building on the above analysis, we can guide FoMo’s fine-tuning strategy:

By optimizing the Mean Squared Error (MSE) of positive and negative samples, we can achieve alignment between mobile traffic and contextual information features.

$\bullet$ Partially frozen fine-tuning. During the fine-tuning process, we froze the main parameters of the pre-trained model, including the attention layer, linear layer, and MLP network, to preserve the model’s ability to learn general spatio-temporal features of mobile traffic. We primarily update the parameters in the adaptive layernorm, contextual integration module, and output decoder layer. By partially updating these components, the time and computational cost of the fine-tuning process can be reduced (Shen et al., 2021; Ye et al., 2023).

4. Evaluation

We perform evaluations on nine real-world datasets to discuss the universality of the FoMo with 13 baselines. The experiments need to address the following three questions.

•

RQ1: How does it perform in multi-task forecasting across multiple datasets?
•

RQ2: How does the model perform in zero-shot and few-shot learning tasks?
•

RQ3: How does the proposed model perform in terms of scalability?

4.1. Evaluation settings

4.1.1. Datasets

Mobile traffic data. We collect mobile traffic data from 7 cities of varying scales in China, which encompass downlink traffic including both 4G and 5G data. The time granularity of the data ranges from 15 minutes to 1 hour. Additionally, we utilized mobile traffic data from 2 other cities in China and Germany to validate FoMo’s zero/few-shot capabilities, where the Germany dataset is generated using the traffic prediction method described in (Xu et al., 2021).

Table 1. Description of datasets

Dataset	Usage	Data	Mobile	Mobile	Time
Dataset	Usage	description	traffic	users	granularity
Beijing		5G data, October, 2021, 4000+ BSs	$\checkmark$	$\checkmark$	30 min
Shanghai		4G data, August, 2014, 5000+ BSs	$\checkmark$	$\checkmark$	30 min
Nanjing	Model training	5G data, February to March, 2021, 6000+ BSs	$\checkmark$	$\checkmark$	15 min
Nanjing-4G		4G data, February to March, 2021, 6000+ BSs	$\checkmark$	$\checkmark$	15 min
Nanchang		5G data, July, 2023, 5000+ BSs	$\checkmark$	$\checkmark$	30 min
Nanchang-4G		4G data, July, 2023, 7000+ BSs	$\checkmark$	$\checkmark$	30 min
Shandong		5G data, February, 2024, 1000+ BSs	$\checkmark$	$\checkmark$	1 hour
Hangzhou	Zero/Few	5G data, July, 2023, 1000+ BSs	$\checkmark$	$\checkmark$	1 hour
Munica	shot tests	4G generated data, 2022	$\checkmark$	—	1 hour
POI	Shopping, Enterprise, Restaurant, Local Living, Transportation,
	Public Health, Automobile, Physical facilities, Accomodation, Finance,
	Government organs, Education, Business, Public facilities, scenic spot.

Urban Contextual data. We collect mobile user data in conjunction with mobile traffic data in each dataset. We crawl POI data from each city through public map services, including 15 categories related to living, entertainment, and other aspects. We summarize the collected data in Table 1.

Table 2. Performance of short-term prediction task. Bold numbers denote the best results and

\underline{underline}

numbers denote the second-best results. The proposed FoMo has the best prediction performance across 7 datasets.

Model	Beijing		Shanghai		Nanjing		Nanjing-4G		Nanchang		Nanchang-4G		Shandong
	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE
HA	0.1199	0.0697	0.1151	0.0576	0.0788	0.0353	0.0830	0.0371	0.0589	0.0266	0.0702	0.0339	0.1739	0.0578
ARIMA	0.2212	0.1333	0.1609	0.0819	0.1353	0.0622	0.1443	0.0668	0.1532	0.0666	0.1740	0.0789	0.1366	0.0531
SpectraGAN	0.2675	0.1228	0.2086	0.1226	0.2412	0.1186	0.2152	0.1151	0.2974	0.1467	0.1892	0.0935	0.2492	0.0814
keGAN	0.3307	0.2994	0.3456	0.2174	0.3586	0.3318	0.3579	0.3297	0.3123	0.1913	0.2521	0.2206	0.2662	0.2616
Adaptive	0.2779	0.2138	0.3007	0.2164	0.2606	0.1906	0.2219	0.1469	0.2305	0.1709	0.2572	0.1919	0.2688	0.1937
CSDI	0.1752	0.1015	0.2060	0.1141	0.1722	0.0929	0.2299	0.1251	0.1797	0.0929	0.1587	0.0758	0.2131	0.0976
KG-Diff	0.1214	0.0984	0.1423	0.1001	0.1222	0.0891	0.1344	0.1013	0.1346	0.0887	0.1501	0.0802	0.1361	0.0768
Time-LLM	0.1511	0.1115	0.1388	0.0964	0.2351	0.1817	0.1754	0.1309	0.2039	0.1474	0.1770	0.1242	0.1571	0.0846
Tempo	0.1206	0.0873	0.0747	0.0455	0.0805	0.0625	0.0652	0.0498	0.0830	0.0638	0.0749	0.0550	0.0969	0.0763
patchTST	0.1107	0.0686	0.1288	0.0872	0.0935	0.0616	0.0960	0.0631	0.1182	0.0635	0.1162	0.0638	0.1089	0.0703
TimeGPT	0.0598	0.0422	0.0866	0.0457	0.0646	0.0397	0.0657	0.0388	0.0502	0.0281	$\underline{0.0576}$	$\underline{0.0299}$	0.1219	$\underline{0.0358}$
Lagllama	0.0501	0.0349	0.0853	$\underline{0.0441}$	$\underline{0.0529}$	$\underline{0.0302}$	$\underline{0.0530}$	$\underline{0.0286}$	0.0505	0.0271	0.0625	0.0322	0.1272	0.0371
UniST	$\underline{0.0332}$	$\underline{0.0252}$	$\underline{0.0658}$	0.0448	0.0623	0.0442	0.0608	0.0409	$\underline{0.0433}$	$\underline{0.0246}$	0.0852	0.0525	$\underline{0.0766}$	0.0489
FoMo (our)	0.0284	0.0135	0.0588	0.0349	0.0442	0.0247	0.0439	0.0143	0.0360	0.0178	0.0408	0.0221	0.0609	0.0343

4.1.2. Baselines

We select a total of 13 baselines across 4 major types.

$\bullet$ Statistical models. Historical moving average method (HA) and ARIMA method that integrate autoregressive with acreage moxing (Xu et al., 2023).

$\bullet$ Natural language-based model. Time-LLM (Jin et al., 2024) describes time series features using natural language and uses these descriptions as prompts into a natural language pre-trained model (LLAMA-7B) for forecasting. Tempo (Cao et al., 2024) designs temporal prompts with trend and seasonal features for pre-trained models (GPT-2) to predict time series.

$\bullet$ Spatio-temporal-based models. They primarily forecast mobile traffic as spatio-temporal series via autoregression, decomposition, and spatial convolution. TimeGPT (Garza and Mergenthaler-Canseco, 2023) replaces the Feedforward layer in the transformer with a CNN network and is trained on vast spatio-temporal data. Laglla- ma (Rasul et al., 2024) uses a set of lag indices to capture different periodic correlations in the time series. PatchTST (Nie et al., 2023) decomposes time series into multiple segments and uses transformers for feature extraction. UniST (Yuan et al., 2024a) segments spatio-temporal data and fine-tunes the model using features like geographical proximity and temporal correlations.

$\bullet$ Dedicated models for mobile traffic forecasting. In addition to the general spatio-temporal forecasting models, we select 5 models dedicated to mobile networks. SpectraGAN (Xu et al., 2021) converts mobile traffic generation into an image generation problem and utilizes a CNN-based GAN network for traffic forecasting. KEGAN (Hui et al., 2023) is a hierarchical GAN that utilizes a self-constructed Urban Knowledge Graph (UKG) to explicitly incorporate urban features during the forecasting process. ADAPTIVE (Zhang et al., 2023) leverages the UKG and a BS aligning scheme to transfer mobile traffic knowledge from one city to another. CSDI (Tashiro et al., 2021) is a conditional diffusion model that uses a masking method for mobile traffic forecasting. KG-Diff (Chai et al., 2024b) inputs both the seasonal part of mobile traffic and the UKG into a diffusion model, aiding the model in understanding the spatio-temporal dynamics.

4.1.3. Metrics

We choose 3 metrics to investigate the performance of the algorithms. MAE evaluates the similarity of generated values $S$ and real values $\hat{S}$ , which can be expressed as $e=Avg(|S-\hat{S}|)$ . RMSE measures the average magnitude of the errors between predicted values and actual observed values, which can be expressed as $e=\sqrt{Avg(|S-\hat{S}|^{2})}$ . Jensen–Shannon divergence (JSD) is a commonly used metric to measure the similarity between two distributions.

4.2. Multitask forecasting (RQ1)

Table 3. Performance of Long-term prediction task. Bold numbers denote the best results and

\underline{underline}

numbers denote the second-best results. The proposed FoMo has the best prediction performance across 7 datasets.

Model	Beijing		Shanghai		Nanjing		Nanjing-4G		Nanchang		Nanchang-4G		Shandong
	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE	RMSE	MAE
HA	0.2945	0.1887	0.2214	0.1180	0.1808	0.0877	0.1914	0.0941	0.2011	0.0948	0.2285	0.1116	0.1331	0.0409
ARIMA	0.2023	0.1237	0.1560	0.0811	0.1269	0.0592	0.1340	0.0634	0.1533	0.0709	0.1751	0.0848	0.1224	0.0380
SpectraGAN	0.3880	0.3005	0.1962	0.1234	0.3621	0.2717	0.3212	0.2160	0.2432	0.1787	0.2352	0.1260	0.2438	0.0809
keGAN	0.3041	0.3716	0.2695	0.1837	0.2525	0.1809	0.2623	0.1917	0.2241	0.1770	0.2132	0.1837	0.1742	0.1315
Adaptive	0.2885	0.2234	0.3019	0.2197	0.2631	0.1876	0.2619	0.1907	0.1959	0.1419	0.2436	0.1752	0.1605	0.1144
CSDI	0.3822	0.2836	0.2880	0.1856	0.4164	0.3034	0.3492	0.2520	0.3879	0.2913	0.3452	0.2347	0.2973	0.1705
KG-Diff	0.3051	0.2041	0.1556	0.1347	0.2311	0.1505	0.1975	0.1511	0.2211	0.1942	0.2123	0.1897	0.1543	0.1237
Time-LLM	0.1472	0.1099	0.1765	0.1124	0.2463	0.1843	0.2239	0.1602	0.2261	0.1751	0.2199	0.1621	0.1789	0.0868
Tempo	0.3514	0.2559	0.1518	0.0787	0.2896	0.1892	0.2780	0.1793	0.2380	0.1347	0.2365	0.1306	0.1020	0.0275
patchTST	0.1512	0.1331	0.1627	0.0817	0.1521	0.1236	0.1644	0.0999	0.1430	0.0905	0.1789	0.1060	0.0985	0.0676
TimeGPT	0.3422	0.2433	$\underline{0.1110}$	$\underline{0.0766}$	0.2272	0.1391	0.2116	0.1345	0.1994	0.1001	0.1953	0.0919	0.0887	$\underline{0.0253}$
Lagllama	0.2318	0.1879	0.1453	0.08742	$\underline{0.0960}$	$\underline{0.0683}$	$\underline{0.1115}$	$\underline{0.0959}$	$\underline{0.1091}$	$\underline{0.0788}$	0.1684	0.0889	0.1076	0.0439
UniST	$\underline{0.1426}$	$\underline{0.1014}$	0.1264	0.0803	0.1831	0.0845	0.1268	0.0869	0.1387	0.0835	$\underline{0.1445}$	$\underline{0.0763}$	$\underline{0.0622}$	0.0337
FoMo (our)	0.1035	0.0696	0.0983	0.0679	0.0818	0.0532	0.0849	0.0570	0.0853	0.0576	0.1206	0.0563	0.0518	0.0197

In our experiments, the temporal length is 64. For short-term prediction, the model forecasts 16 future points using the previous 48. For long-term prediction, the model forecasts 48 future points using the previous 16. For data generation, the model predicts all 64 points based on the current timestamp.

4.2.1. Short-term prediction

The results of the short-term forecasting task are presented in Table 2. Since sufficient historical data is available for reference, most baselines, leveraging their temporal feature extraction modules, effectively predict short-term changes. Our proposed FoMo outperforms the best baseline across multiple datasets, where FoMo can improve the RMSE metric by up to 29.1% (Shandong dataset) and the MAE metric by up to 50% (Nanjing-4G dataset), which exhibits stronger generalization capabilities compared to other models. Through the adaptive layernorm module, the diffusion model iteratively integrates contextual features and leverages the transformer to capture long-term dependencies between mobile traffic and the environment. We believe this correlation can transfer across different cities, improving the model’s generalization capability.

4.2.2. Long-term prediction

The long-term forecasting results are also shown in Table 3. For this task, the lack of sufficient historical observations often leads to performance degradation in some baselines. However, FoMo consistently achieves the best performance, it achieves a maximum improvement of 31.4% in RMSE (Beijing dataset) and a maximum enhancement of 40.6% in MAE (Nanjing-4G dataset), which showcasing its adaptability to various tasks.

4.2.3. Mobile traffic generation

Table 4. Performance of generation task. Bold numbers denote the best results and

\underline{underline}

numbers denote the second-best results. The proposed FoMo has the best generation performance across 7 datasets.

Model	Beijing		Shanghai		Nanjing		Nanjing-4G		Nanchang		Nanchang-4G		Shandong
	JSD	MAE	JSD	MAE	JSD	MAE	JSD	MAE	JSD	MAE	JSD	MAE	JSD	MAE
SpectraGAN	0.3621	0.1584	0.3788	0.1284	0.3477	0.2888	0.3352	0.2494	$\underline{0.2285}$	$\underline{0.1288}$	0.3482	0.1762	0.3364	0.1794
keGAN	0.3435	0.2297	0.4909	0.2183	0.3071	0.1801	0.4862	0.1865	0.4032	0.1988	0.4792	0.2493	0.4007	0.2387
Adaptive	0.3044	0.2143	0.2751	0.1848	0.3040	0.1536	0.2587	0.2304	0.2730	0.2251	0.3201	0.1681	0.2806	0.1889
CSDI	0.3385	0.1431	$\underline{0.2331}$	$\underline{0.1025}$	0.4044	0.1844	0.3875	0.2516	0.3416	0.2163	0.2895	0.1734	0.2666	0.2170
KG-Diff	$\underline{0.2397}$	$\underline{0.1299}$	0.2504	01245	$\underline{0.2223}$	$\underline{0.1214}$	$\underline{0.2323}$	$\underline{0.1514}$	0.2683	0.1356	$\underline{0.2744}$	$\underline{0.1363}$	$\underline{0.2041}$	$\underline{0.1101}$
FoMo (our)	0.2013	0.0894	0.2259	0.1002	0.1971	0.0948	0.2164	0.0938	0.2226	0.1043	0.2494	0.1159	0.1558	0.0993

As shown in Table 4, the absence of historical observation of the generation task prevents some existing baselines from completing the task. Nevertheless, the FoMo still achieved strong generative results. It can achieve up to a 23.7% improvement in the JSD metric (Shandong dataset), and a maximum enhancement of 38.1% in MAE (Nanjing-4G dataset). This is due to the contextual feature fusion module used during fine-tuning, which captures the correlation between contextual and mobile traffic features through contrastive learning. This allows the model to infer potential traffic distribution based on environmental changes, even without historical data.

4.2.4. Visualization

To intuitively demonstrate our model’s universality for different tasks, we select two datasets as examples (Beijing and Nanchang) and plot the forecasting results in Figure LABEL:visual_res. From left to right, it represents the tasks of short-term prediction $\rightarrow$ long-term prediction $\rightarrow$ traffic generation. The blue-shaded area indicates the model’s predicted results, while the unshaded area represents historical observations. FoMo generates mobile traffic closely aligned with real values across all tasks, accurately predicting periodic trends and capturing fast dynamics, which shows that our FoMo model achieves forecasting across multiple cities and tasks, highlighting its generalization capability.

4.3. Zero/Few shot learning (RQ2)

To evaluate FoMo’s zero/ few-shot learning capabilities, we select two datasets that FoMo has not encountered during training: Hangzhou (China) and Munich (Germany). We choose 4 baselines that perform well in previous multitask forecasting: KG-Diff, TimeGPT, Lagllama, and UniST. The results are shown in Figure LABEL:zero_few1, where 5% few-shot and 10% few-shot represent the model training with a small amount of data (5% and 10%, respectively). It shows that FoMo exhibits good zero-shot performance, especially in the Munich dataset, where FoMo’s zero-shot performance even surpasses that of KG-Diff after small-scale training. After training with a small amount of data, all models show varying degrees of improvement. FoMo still demonstrates the best performance, indicating that FoMo can utilize the pre-trained model to quickly capture general features within unseen mobile data. We also visualize the performance in zero/few-shot scenarios, as shown in Figure LABEL:zero_few2. We select a long-term forecasting task, with the results for zero-shot $\rightarrow$ 5% few-shot $\rightarrow$ 10% few-shot from left to right in the figure. It can be observed that FoMo can learn the general distribution characteristics of mobile traffic in the zero-shot phase, and after training with a small sample, the model realizes accurate traffic forecasting.

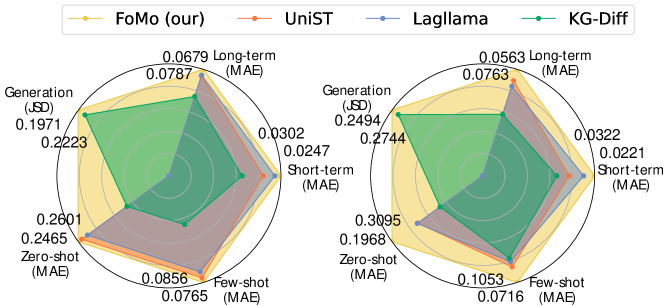
We comprehensively summarize and compare the FoMo algorithm, UniST, Lagllama, and KG-Diff, as shown in Figure 5. In the figure, we highlight the performance of our model as well as the performance of the second-best model. FoMo consistently delivers the best performance across various tasks and multiple cities. For example, in few-shot tasks, FoMo achieves performance improvements of 10.6% and 32.1% in different cities, demonstrating the model’s universality.

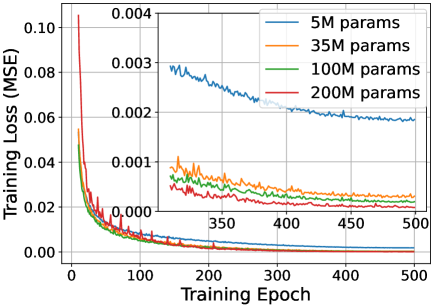
4.4. Scaling performance of FoMo (RQ3)

Scaling performance reflects the relationship between model parameters, data size, and overall performance. Understanding the scaling performance of foundation models provides valuable guidance for parameter selection during model deployment, which optimizes computational and storage overheads for the entire system. We provide 5 different model settings based on various transformer layers and hidden features: FoMo with 5M parameters (5M params), 35M FoMo (35M params), 100M FoMo (100M params), 150M FoMo (150M params), and 200M FoMo (200M params).

We first examine the scaling performance between model parameters and training loss in Figure 6, where the loss is calculated via MSE (Equation 16). The results indicate that as the model size increases, the denoising network’s capability improves, leading to enhanced learning capability of mobile traffic features. For smaller models, increasing the number of parameters significantly boosts learning capacity (as seen from 5M parameters $\rightarrow$ 35M parameters in the figure). In contrast, for larger models, a marginal diminishing becomes apparent (as depicted of 100M parameters $\rightarrow$ 200M parameters). To explore these observations, we examine the relationship between model size and performance across tasks, as shown in Figure LABEL:scale2(a). The results align with Figure 6: smaller models improve rapidly with more parameters, while larger models show minimal gains due to diminishing returns. We attribute this to parameter redundancy in larger models relative to fixed training data, leading to overfitting and limiting performance improvements. To validate the model’s scaling performance, we assess how it performs with varying dataset sizes, as shown in Figure LABEL:scale2(b). The results indicate that with small datasets, models with excessive parameters may suffer performance degradation, consistent with earlier findings. However, as data volume increases, larger models utilize their extensive parameters to improve performance. In contrast, smaller models struggle to capture diverse features, leading to a performance decline.

Discussion. From these observations, we preliminarily identify a scaling law for FoMo: For mobile traffic forecasting, merely increasing model parameters doesn’t guarantee better performance. The model size should be chosen based on the amount of collected data. This insight leads us to further investigate the quantitative relationship between model scale and factors like urban size, population, and temporal granularity to optimize performance.

Table 5. Performance of ablation study.

\Delta

represents the degradation after removing certain modules.

Model	Beijing		Shanghai		Nanchang
	Prediction	Generation	Prediction	Generation	Prediction	Generation
	(RMSE)	(JSD)	(RMSE)	(JSD)	(RMSE)	(JSD)
FoMo (our)	0.1035	0.2213	0.0983	0.2202	0.0360	0.2226
FoMo-user	0.1230	0.2294	0.1295	0.2264	0.0421	0.2260
$\Delta$	-23.82%	-21.77%	-47.75%	-24.31%	-19.81%	-34.69%
FoMo-POI	0.1758	0.2464	0.1507	0.2363	0.0636	0.2301
$\Delta$	-88.38%	-67.47%	-80.36%	-63.13%	-89.61%	-76.53%
Pre-train	0.1853	0.2585	0.1635	0.2457	0.0668	0.2324

4.5. Ablation study

We conduct ablation experiments on FoMO, as shown in Table 5, with FoMo-user and FoMo-POI representing the incorporation of mobile users and POI distributions, respectively, during the fine-tuning process. It can be observed that adding these two contextual features at the fine-tuning stage enhances model performance to varying degrees. Moreover, the performance degradation of FoMo-POI is more significant, indicating that mobile users better reflect the dynamic characteristics of mobile traffic and are more critical for mobile traffic forecasting compared to POI distribution.

5. Deployment Applications

To validate FoMo’s prediction effectiveness, we deploy the model on the Jiutian platform, an AI platform developed by China Mobile, featuring functions like scenario construction, network simulation, optimization strategy formulation, and performance evaluation, as shown in Figure 8. The Jiutian platform offers full-element network simulation capabilities, enabling efficient simulation of interactions between communication systems and user behavior. It also supports operators in developing customized algorithms and applications, deploying them into production environments, and performing product validation and testing with real network data. The platform has now been fully deployed within China Mobile, supporting network development across 31 provinces in China.

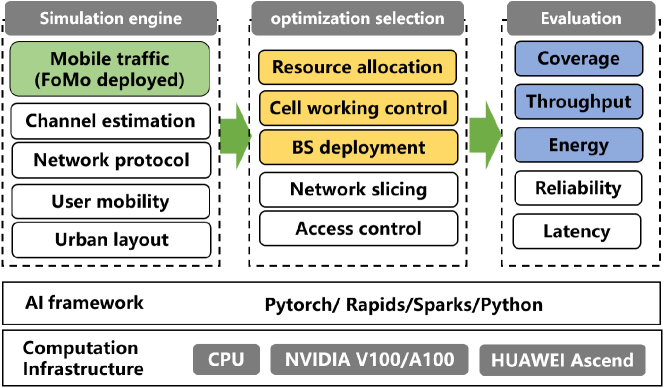
Deployment. We select predefined urban layout and human mobility data. FoMo is deployed in the mobile traffic module, with its predictions feeding into the optimization selection module. We focus on 3 optimization scenarios (highlighted in yellow in the figure) and evaluate the performance via network coverage, throughput, and energy consumption. The training of FoMo is conducted on 4 NVIDIA A100 GPUs (80GB each) using PyTorch 2.0.1. Table 6 summarizes the model’s parameters and training/inference time per sample.

Table 6. Model deployment efficiency on JiuTian.

Model	Layers	Hidden	Parameter	Training	Inference
Model	Layers	feature	scale	time	time
KG-Diff	12	128	4.1M	0.12 min	0.029 min
UniST	12	512	28.2M	0.19 min	0.009 min
Lagllama	8	144	9.9M	0.21 min	0.011min
FoMo	12	128	4.9M	0.24 min	0.043 min
	16	256	34.1M	0.32 min	0.054 min
	20	768	217.7M	0.82 min	0.162 min

Optimization. Mobile traffic is predicted in three ways: using historical data, predicted by Lagllama, and FoMo. The optimization module then applies the same decision-making algorithms (e.g., reinforcement learning or genetic algorithms) by referring to the three predicted data to generate 3 optimization strategies (i.e., Hist-based, Lag-based, and FoMo-based), which are then evaluated in the platform via real-world mobile traffic and human mobility.

5.1. Energy efficient BS sleep mode control

We consider the C-RAN scenario, where the BS achieves cell coverage by activating different numbers of RRUs (202, 2023). The strategy for BS sleep modes involves controlling the RRU operational status (activated or sleep) based on the network load. We model the problem from the perspectives of service quality, depreciation cost, and energy consumption. We set $N$ BSs, each of which has $M$ cells to serve at time $t$ . Define the traffic load that a single RRU can serve as $c_{0}$ , then for BS $n$ , its Quality of Service (QoS) equals $Q(n)=\sum_{t}\sum_{m}max(L_{m,t}-x_{m,t}c_{0},0)/L_{m,t}$ , where $L_{t,m}$ is the actual cell load and $x_{m,t}$ is the activated RRUs. Moreover, frequent switching of RRUs can lead to a reduction in the lifespan of BSs, and the depreciation yields $W(n)=\sum_{t}\sum_{m}|x_{m,t}-x_{m,t-1}|$ . BS energy consumption equals $E(n)=\sum_{t}\sum_{m}\mathcal{P}[min(L_{m,t},x_{m,t}c_{0})]$ that is determined by the load at the RRU (Zhang et al., 2017), where $\mathcal{P}[L]=\alpha L+\beta(L/c_{0})$ is the energy consumption function. Therefore, the optimization objective yields:

(17)

min\sum\nolimits_{n}Y(x^{(n)}_{m,t}|L^{(n)}_{m,t})=Q(n)+W(n)+E(n).

For the BS sleeping strategy, frequently adjusting RRUs over a short period is impractical. A more reasonable approach is to assess network dynamics over a longer period and develop a long-term adjustment strategy. Therefore, we leverage FoMo’s long-term prediction capability to estimate $L_{m,t}$ via the long-term prediction mask in (5). The optimization results are shown in Figure LABEL:app(a), it can be seen that the FoMo-based strategy closely matches the real data-based strategy across different metrics, with a 21.9% improvement in QoS and a 40.7% reduction in BS depreciation better than the other two. While energy consumption lags behind the comparison strategies, our algorithm aligns with that of the Real-based strategy, indicating that FoMo accurately predicts mobile traffic and effectively meets real user demands.

5.2. Traffic-aware resource allocation

We consider cellular networks involving a single cloud server and $N$ cells, where the server allocates $K$ PRBs to each cell (Wang et al., 2024; Zafar et al., 2022). We aim to optimize the average delay of each cell by allocating a limited number of PRBs across multiple time slots. We assume that the average channel quality $h_{t}$ of each cell remains constant at time slot $t$ and varies independently between different slots. The average rate in cell $n$ can be expressed as $r_{n}(t)=B\sum\nolimits_{k}\rho_{k,n}(t)log_{2}[1+p_{n}(t)h_{n}(t)/\sigma^{2}]$ , where $B$ is the PRB bandwidth and $p_{n}(t)$ is the transmission power. $\rho_{k,n}(t)$ is a binary variable indicating PRB allocation ( $\rho_{k,n}(t)=1$ represents PRB $k$ is allocated to cell $n$ , and vice versa). Based on the PRB selection, the end-to-end delay is expressed as $d_{n}(t)=U_{n}(t)/r_{n}(t)$ , where $U_{n}(t)$ is the overall transmission tasks. When there are too many transmission tasks for a cell, it might not be possible to complete all transmissions within a single time slot, leading to data backlog. Therefore, the backlog data at time $t+1$ for the cell can be expressed as $U_{n}(t+1)=max\{U_{n}(t)+P_{n}(t)-r_{n}(t),0\}$ , where $P_{n}(t)$ represents the newly arriving transmission data. Our ultimate goal is to minimize the accumulated backlog data and end-to-end delay for the cells, which yields:

(18)

\displaystyle min\sum\nolimits_{t}\sum\nolimits_{n}U_{n}(t+1)+d_{n}(t),

where $P_{n}(t)$ is provided by the FoMo. Compared to the BS sleep modes control, the PRB allocation primarily focuses on the user experience over a relatively short period. Therefore, we use the short-term prediction mask in (5) to generate network traffic for the near future. As shown in Figure LABEL:app(b), our FoMo-based strategy significantly reduces system latency and overall data backlog by 16.4% and 3.5%, respectively. This is because FoMo can more accurately characterize the cells’ future transmission tasks, allowing us to make decisions based on the predicted data that are closer to reality, and improve the system performance.

5.3. Coverage-oriented BS deployment

BS deployment requires an accurate assessment of the potential network demand (Dong et al., 2020). However, there is often insufficient historical traffic data in new regions, making it hard to make reasonable deployment strategies. In this case, FoMo can use information such as population and POIs in new regions to generate potential distributions of mobile traffic, thereby guiding BS deployment. Specifically, we select a target region and divide it into a 16×16 grid of square areas. FoMo employs the generation mask in (6) to generate mobile traffic. We input the number of residents and the POI distributions into FoMo, guiding it to infer the mobile traffic in the masked portions. We calculate the cumulative traffic for each area over one day (24 hours), and the BS deployment strategy is proportional to the traffic density of each area.

To validate the effectiveness, we assess the average coverage ratio across the entire region, defined as (user quantities served by BS) / (the total population of that region), with changes in regional population obtained via the population dynamics interface of the Jiutian platform. We implement two comparison schemes: the Resident population-based scheme and the POI-based scheme, as shown in Figure LABEL:app(c). It can be observed that during the night, when most people rest in residential areas, the Resident population-based scheme achieves better coverage. In contrast, during the day, when people predominantly gather around POIs, the POI-based strategy performs better. Although our Traffic generation-based scheme does not significantly outperform the other two strategies, it effectively makes a trade-off regarding dynamic human dynamics and regional functions.

6. Related Work

Mobile traffic forecasting. It can be broadly categorized into two types: prediction and generation. Mobile traffic prediction involves estimating future values using historical traffic data, while generation learns the underlying distribution of mobile traffic data relying on external contextual information and samples new data from this distribution. Early forecasting used statistical approaches or simulation techniques (Bothe et al., 2019; De Biasio et al., 2019), but these methods typically struggled to capture complex traffic patterns. With the rise of machine learning, many studies used AI for mobile traffic forecasting. For mobile traffic prediction, LSTM models have been used to capture long-term dependencies in traffic patterns (Dalgkitsis et al., 2018; Zhu et al., 2020; Wang et al., 2022). Some studies further incorporated spatial attributes into traffic prediction, with Li et al (Li et al., 2023) combining transformer and GCN to capture spatio-temporal correlations. Wu et al (Wu et al., 2022) combined GAN with GCN to capture spatial correlations across multiple cities. The MVSTGN model (Yao et al., 2023) divided urban spaces into multi-attribute graphs to capture mobile traffic features in low-dimensional space. For mobile traffic generation, early work used GANs to capture the overall distribution of mobile traffic (Ring et al., 2019; Lin et al., 2020). SpectraGAN (Xu et al., 2021) viewed cities as images, extracting POI and land use information via CNNs and incorporating it into traffic generation. Sun et al (Sun et al., 2022) added user usage features to a GAN network, improving the accuracy of traffic generation. Hui et al (Hui et al., 2023) built a city knowledge graph incorporating extensive semantic features into traffic generation models. KGDiff (Chai et al., 2024b) used a diffusion model to generate controlled traffic while considering traffic periodicity and spatial features.

Foundation models. The models typically have a large scale of parameters and deep layers. They have been proven to exhibit powerful multitasking, zero/few-shot learning, and some reasoning abilities. Inspired by this, foundational models in various vertical domains have been developed. Yang et al (Yang et al., 2023a) and Hao et al proposed foundation models in financial and biomedical domains, respectively, aim to achieve various specialized tasks like investment, quantification, and gene expression. Zhang et al (Zhang et al., 2024) proposed utilizing an urban foundation model to address various applications, including urban navigation, urban Q&A, and urban planning. Notably, many foundation models for spatio-temporal forecasting have been proposed. Leveraging existing Large Language Models(LLMs), TEMPO (Cao et al., 2024) and Time-LLM (Jin et al., 2024) introduces a prompt mechanism in the pre-trained LLM for long-term forecasting by aligning features between mobile traffic and natural language tokens with a reprogramming approach. Some methods do not rely on existing language models but reconstruct spatio-temporal foundation models using transformer architectures. STEP (Shao et al., 2022) employed a pre-training model and graph neural networks to capture spatio-temporal features. LagLLama (Rasul et al., 2024) used lag indices to annotate multi-dimensional periodic features such as monthly, daily, and hourly periods. TimeGPT (Garza and Mergenthaler-Canseco, 2023) replaced the Feedforward layer in the transformer with a CNN to enhance temporal correlations. UniST (Yuan et al., 2024a) achieved spatio-temporal prediction in urban contexts by employing a memory network.

While existing models offer advantages in forecasting mobile traffic, they are often designed for specific tasks like short-term prediction or generation. In real-world deployments, network optimization involves multiple forecasting tasks across cities, requiring frequent model switching and complex adaptations, which increases deployment costs. Foundation models are well-suited for multi-task adaptation and transfer in wireless networks. A promising approach is to develop a foundation model for mobile traffic forecasting. However, no such foundation model has emerged. The main challenge lies in mastering various forecasting tasks while integrating contextual features such as human dynamics and geographical traits. This integration is essential for building a robust model that captures the intrinsic correlations between the environment, users, and traffic.

7. Conclusion

In this paper, we propose FoMo, a foundation model with diffusion models for mobile traffic forecasting. To the best of our knowledge, it is the first foundation model in mobile networks. By capturing the temporal, spatial, human dynamics, and geographical features related to mobile traffic, FoMo exhibits robust multi-task adaptability and zero/few-shot learning capability for diverse tasks across multiple cities, which exhibits good universality. Moreover, we identify the scaling properties of FoMo by examining the model performance with diverse parameter scales and data sizes. We deploy FoMo on the Jiutian platform, where it is used to optimize various aspects of network coverage, throughput, and energy consumption based on its accurate traffic forecasts. FoMo offers valuable insights for integrating multi-dimensional data from users, mobile networking and computing, services, and traffic in mobile networks, further advancing the development of large models in the telecommunications field.

References

(1)
202 (2023) 2023. Artificial intelligence for reducing the carbon emissions of 5G networks in China. Nature Sustainability 6 (2023), 1522–1523. https://api.semanticscholar.org/CorpusID:260979998
Austin et al. (2021) Jacob Austin, Daniel D. Johnson, Jonathan Ho, Daniel Tarlow, and Rianne van den Berg. 2021. Structured Denoising Diffusion Models in Discrete State-Spaces. In Advances in Neural Information Processing Systems, M. Ranzato, A. Beygelzimer, Y. Dauphin, P.S. Liang, and J. Wortman Vaughan (Eds.), Vol. 34. Curran Associates, Inc., 17981–17993. https://proceedings.neurips.cc/paper_files/paper/2021/file/958c530554f78bcd8e97125b70e6973d-Paper.pdf
Bothe et al. (2019) Shruti Bothe, Haneya Naeem Qureshi, and Ali Imran. 2019. Which Statistical Distribution Best Characterizes Modern Cellular Traffic and What Factors Could Predict Its Spatiotemporal Variability? IEEE Communications Letters 23, 5 (2019), 810–813. https://doi.org/10.1109/LCOMM.2019.2908370
Bozic et al. (2024) Vukasin Bozic, Abdelaziz Djelouah, Yang Zhang, Radu Timofte, Markus Gross, and Christopher Schroers. 2024. Versatile Vision Foundation Model for Image and Video Colorization. In ACM SIGGRAPH 2024 Conference Papers (Denver, CO, USA) (SIGGRAPH ’24). Association for Computing Machinery, New York, NY, USA, Article 94, 11 pages. https://doi.org/10.1145/3641519.3657509
Brooks et al. (2024) Tim Brooks, Bill Peebles, Connor Holmes, Will DePue, Yufei Guo, Li Jing, David Schnurr, Joe Taylor, Troy Luhman, Eric Luhman, Clarence Ng, Ricky Wang, and Aditya Ramesh. 2024. Video generation models as world simulators. (2024). https://openai.com/research/video-generation-models-as-world-simulators
Brown (2020) Tom B Brown. 2020. Language models are few-shot learners. arXiv preprint arXiv:2005.14165 (2020).
Cai et al. (2023) Dongqi Cai, Shangguang Wang, Yaozong Wu, Felix Xiaozhu Lin, and Mengwei Xu. 2023. Federated Few-Shot Learning for Mobile NLP. In Proceedings of the 29th Annual International Conference on Mobile Computing and Networking (Madrid, Spain) (ACM MobiCom ’23). Association for Computing Machinery, New York, NY, USA, Article 63, 17 pages. https://doi.org/10.1145/3570361.3613277
Cao et al. (2024) Defu Cao, Furong Jia, Sercan O Arik, Tomas Pfister, Yixiang Zheng, Wen Ye, and Yan Liu. 2024. TEMPO: Prompt-based Generative Pre-trained Transformer for Time Series Forecasting. arXiv:2310.04948 [cs.LG] https://arxiv.org/abs/2310.04948
Cardoso and Vieira (2019) Alisson Assis Cardoso and Flávio Henrique Teles Vieira. 2019. Generation of Synthetic Network Traffic Series Using a Transformed Autoregressive Model Based Adaptive Algorithm. IEEE Latin America Transactions 17, 08 (2019), 1268–1275. https://doi.org/10.1109/TLA.2019.8932335
Chaccour et al. (2024) Christina Chaccour, Walid Saad, Mérouane Debbah, Zhu Han, and H. Vincent Poor. 2024. Less Data, More Knowledge: Building Next Generation Semantic Communication Networks. IEEE Communications Surveys & Tutorials (2024), 1–1. https://doi.org/10.1109/COMST.2024.3412852
Chai et al. (2024a) Haoye Chai, Tao Jiang, and Li Yu. 2024a. Diffusion Model-based Mobile Traffic Generation with Open Data for Network Planning and Optimization. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (Barcelona, Spain) (KDD ’24). Association for Computing Machinery, New York, NY, USA, 4828–4838. https://doi.org/10.1145/3637528.3671544
Chai et al. (2024b) Haoye Chai, Tong Li, Fenyu Jiang, Shiyuan Zhang, and Yong Li. 2024b. Knowledge Guided Conditional Diffusion Model for Controllable Mobile Traffic Generation. In Companion Proceedings of the ACM Web Conference 2024 (Singapore, Singapore) (WWW ’24). Association for Computing Machinery, New York, NY, USA, 851–854. https://doi.org/10.1145/3589335.3651530
Chen et al. (2020b) Min Chen, Yiming Miao, Hamid Gharavi, Long Hu, and Iztok Humar. 2020b. Intelligent Traffic Adaptive Resource Allocation for Edge Computing-Based 5G Networks. IEEE Transactions on Cognitive Communications and Networking 6, 2 (2020), 499–508. https://doi.org/10.1109/TCCN.2019.2953061
Chen et al. (2020a) Ting Chen, Simon Kornblith, Mohammad Norouzi, and Geoffrey Hinton. 2020a. A Simple Framework for Contrastive Learning of Visual Representations. In Proceedings of the 37th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 119), Hal Daumé III and Aarti Singh (Eds.). PMLR, 1597–1607. https://proceedings.mlr.press/v119/chen20j.html
Dalgkitsis et al. (2018) Anestis Dalgkitsis, Malamati Louta, and George T. Karetsos. 2018. Traffic forecasting in cellular networks using the LSTM RNN. In Proceedings of the 22nd Pan-Hellenic Conference on Informatics (Athens, Greece) (PCI ’18). Association for Computing Machinery, New York, NY, USA, 28–33. https://doi.org/10.1145/3291533.3291540
De Biasio et al. (2019) Alvise De Biasio, Federico Chiariotti, Michele Polese, Andrea Zanella, and Michele Zorzi. 2019. A QUIC Implementation for Ns-3.
Dong et al. (2020) Miaomiao Dong, Taejoon Kim, Jingjin Wu, and Eric Wing-Ming Wong. 2020. Millimeter-Wave Base Station Deployment Using the Scenario Sampling Approach. IEEE Transactions on Vehicular Technology 69, 11 (2020), 14013–14018. https://doi.org/10.1109/TVT.2020.3026216
Dosovitskiy et al. (2021) Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, Jakob Uszkoreit, and Neil Houlsby. 2021. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv:2010.11929 [cs.CV] https://arxiv.org/abs/2010.11929
Fahim and Gadallah (2023) Ahmed Fahim and Yasser Gadallah. 2023. An Optimized LTE-Based Technique for Drone Base Station Dynamic 3D Placement and Resource Allocation in Delay-Sensitive M2M Networks. IEEE Transactions on Mobile Computing 22, 2 (2023), 732–743. https://doi.org/10.1109/TMC.2021.3089329
Feng et al. (2024) Zhiying Feng, Qiong Wu, and Xu Chen. 2024. Communication-efficient Multi-service Mobile Traffic Prediction by Leveraging Cross-service Correlations. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (Barcelona, Spain) (KDD ’24). Association for Computing Machinery, New York, NY, USA, 794–805. https://doi.org/10.1145/3637528.3671730
Garza and Mergenthaler-Canseco (2023) Azul Garza and Max Mergenthaler-Canseco. 2023. TimeGPT-1. arXiv:2310.03589 [cs.LG]
Ghandri et al. (2024) Abdennaceur Ghandri, Houssem Eddine Nouri, and Maher Ben Jemaa. 2024. Deep Learning for VBR Traffic Prediction-Based Proactive MBSFN Resource Allocation Approach. IEEE Transactions on Network and Service Management 21, 1 (2024), 463–476. https://doi.org/10.1109/TNSM.2023.3311876
Gong et al. (2023) Jiahui Gong, Yu Liu, Tong Li, Haoye Chai, Xing Wang, Junlan Feng, Chao Deng, Depeng Jin, and Yong Li. 2023. Empowering Spatial Knowledge Graph for Mobile Traffic Prediction. In Proceedings of the 31st ACM International Conference on Advances in Geographic Information Systems (Hamburg, Germany) (SIGSPATIAL ’23). Association for Computing Machinery, New York, NY, USA, Article 24, 11 pages. https://doi.org/10.1145/3589132.3625569
Gruver et al. (2023) Nate Gruver, Marc Finzi, Shikai Qiu, and Andrew G Wilson. 2023. Large Language Models Are Zero-Shot Time Series Forecasters. In Advances in Neural Information Processing Systems, A. Oh, T. Naumann, A. Globerson, K. Saenko, M. Hardt, and S. Levine (Eds.), Vol. 36. Curran Associates, Inc., 19622–19635. https://proceedings.neurips.cc/paper_files/paper/2023/file/3eb7ca52e8207697361b2c0fb3926511-Paper-Conference.pdf
Hao et al. (2024) Minsheng Hao, Jing Gong, Xin Zeng, Chiming Liu, Yucheng Guo, Xingyi Cheng, Taifeng Wang, Jianzhu Ma, Xuegong Zhang, and Le Song. 2024. Large-scale foundation model on single-cell transcriptomics. Nature methods 21, 8 (August 2024), 1481—1491. https://doi.org/10.1038/s41592-024-02305-7
He et al. (2022) Kaiming He, Xinlei Chen, Saining Xie, Yanghao Li, Piotr Dollár, and Ross Girshick. 2022. Masked Autoencoders Are Scalable Vision Learners. In 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 15979–15988. https://doi.org/10.1109/CVPR52688.2022.01553
He et al. (2020) Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, and Ross Girshick. 2020. Momentum Contrast for Unsupervised Visual Representation Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR).
Ho et al. (2020) Jonathan Ho, Ajay Jain, and Pieter Abbeel. 2020. Denoising diffusion probabilistic models. In Proceedings of the 34th International Conference on Neural Information Processing Systems (Vancouver, BC, Canada) (NIPS ’20). Curran Associates Inc., Red Hook, NY, USA, Article 574, 12 pages.
Hu et al. (2023) Yahui Hu, Yujiang Zhou, Junping Song, Luyang Xu, and Xu Zhou. 2023. Citywide Mobile Traffic Forecasting Using Spatial-Temporal Downsampling Transformer Neural Networks. IEEE Transactions on Network and Service Management 20, 1 (2023), 152–165. https://doi.org/10.1109/TNSM.2022.3214483
Hui et al. (2023) Shuodi Hui, Huandong Wang, Tong Li, Xinghao Yang, Xing Wang, Junlan Feng, Lin Zhu, Chao Deng, Pan Hui, Depeng Jin, and Yong Li. 2023. Large-scale Urban Cellular Traffic Generation via Knowledge-Enhanced GANs with Multi-Periodic Patterns. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (Long Beach, CA, USA) (KDD ’23). Association for Computing Machinery, New York, NY, USA, 4195–4206. https://doi.org/10.1145/3580305.3599853
Jin et al. (2024) Ming Jin, Shiyu Wang, Lintao Ma, Zhixuan Chu, James Y. Zhang, Xiaoming Shi, Pin-Yu Chen, Yuxuan Liang, Yuan-Fang Li, Shirui Pan, and Qingsong Wen. 2024. Time-LLM: Time Series Forecasting by Reprogramming Large Language Models. arXiv:2310.01728 [cs.LG] https://arxiv.org/abs/2310.01728
Kang (2024) Inwon Kang. 2024. Advancing Web Science through Foundation Model for Tabular Data. In Companion Publication of the 16th ACM Web Science Conference (Stuttgart, Germany) (Websci Companion ’24). Association for Computing Machinery, New York, NY, USA, 32–36. https://doi.org/10.1145/3630744.3658614
Kang et al. (2024) Migyeong Kang, Juho Jung, Minhan Cho, Daejin Choi, Eunil Park, Sangheon Pack, and Jinyoung Han. 2024. Poster: ISOML: Inter-Service Online Meta-Learning for Newly Emerging Network Traffic Prediction. In Proceedings of the 22nd Annual International Conference on Mobile Systems, Applications and Services (Minato-ku, Tokyo, Japan) (MOBISYS ’24). Association for Computing Machinery, New York, NY, USA, 718–719. https://doi.org/10.1145/3643832.3661437
Kavehmadavani et al. (2024) Fatemeh Kavehmadavani, Van-Dinh Nguyen, Thang X. Vu, and Symeon Chatzinotas. 2024. Empowering Traffic Steering in 6G Open RAN with Deep Reinforcement Learning. IEEE Transactions on Wireless Communications (2024), 1–1. https://doi.org/10.1109/TWC.2024.3396273
Li et al. (2023) He Li, Duo Jin, Xuejiao Li, Jianbin Huang, Xiaoke Ma, Jiangtao Cui, Deshuang Huang, Shaojie Qiao, and Jaesoo Yoo. 2023. DMGF-Net: An Efficient Dynamic Multi-Graph Fusion Network for Traffic Prediction. ACM Trans. Knowl. Discov. Data 17, 7, Article 97 (apr 2023), 19 pages. https://doi.org/10.1145/3586164
Li et al. (2024) Tong Li, Shuodi Hui, Shiyuan Zhang, Huandong Wang, Yuheng Zhang, Pan Hui, Depeng Jin, and Yong Li. 2024. Mobile User Traffic Generation Via Multi-Scale Hierarchical GAN. ACM Trans. Knowl. Discov. Data 18, 8, Article 189 (jul 2024), 19 pages. https://doi.org/10.1145/3664655
Liang et al. (2024) Yuxuan Liang, Haomin Wen, Yuqi Nie, Yushan Jiang, Ming Jin, Dongjin Song, Shirui Pan, and Qingsong Wen. 2024. Foundation Models for Time Series Analysis: A Tutorial and Survey. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (Barcelona, Spain) (KDD ’24). Association for Computing Machinery, New York, NY, USA, 6555–6565. https://doi.org/10.1145/3637528.3671451
Lin et al. (2022) Sheng-Hong Lin, Youyun Xu, Lei Wang, and Jin-Yuan Wang. 2022. Coverage Analysis and Chance-Constrained Optimization for HSR Communications With Carrier Aggregation. IEEE Transactions on Intelligent Transportation Systems 23, 9 (2022), 15107–15120. https://doi.org/10.1109/TITS.2021.3137030
Lin et al. (2020) Zinan Lin, Alankar Jain, Chen Wang, Giulia Fanti, and Vyas Sekar. 2020. Using GANs for Sharing Networked Time Series Data: Challenges, Initial Promise, and Open Questions. In Proceedings of the ACM Internet Measurement Conference (Virtual Event, USA) (IMC ’20). Association for Computing Machinery, New York, NY, USA, 464–483. https://doi.org/10.1145/3419394.3423643
Lohani et al. (2016) Sudha Lohani, Roya Arab Loodaricheh, Ekram Hossain, and Vijay K. Bhargava. 2016. On Multiuser Resource Allocation in Relay-Based Wireless-Powered Uplink Cellular Networks. IEEE Transactions on Wireless Communications 15, 3 (2016), 1851–1865. https://doi.org/10.1109/TWC.2015.2496943
Lu et al. (2024) Qinghua Lu, Liming Zhu, Xiwei Xu, Yue Liu, Zhenchang Xing, and Jon Whittle. 2024. A Taxonomy of Foundation Model based Systems through the Lens of Software Architecture. In Proceedings of the IEEE/ACM 3rd International Conference on AI Engineering - Software Engineering for AI (Lisbon, Portugal) (CAIN ’24). Association for Computing Machinery, New York, NY, USA, 1–6. https://doi.org/10.1145/3644815.3644956
Mei and Zhang (2023) Weidong Mei and Rui Zhang. 2023. Joint Base Station and IRS Deployment for Enhancing Network Coverage: A Graph-Based Modeling and Optimization Approach. IEEE Transactions on Wireless Communications 22, 11 (2023), 8200–8213. https://doi.org/10.1109/TWC.2023.3260805
Miao et al. (2012) Jie Miao, Zheng Hu, Kun Yang, Canru Wang, and Hui Tian. 2012. Joint Power and Bandwidth Allocation Algorithm with QoS Support in Heterogeneous Wireless Networks. IEEE Communications Letters 16, 4 (2012), 479–481. https://doi.org/10.1109/LCOMM.2012.030512.112304
Mukhopadhyay et al. (2023) Soumik Mukhopadhyay, M. Gwilliam, Vatsal Agarwal, Namitha Padmanabhan, Archana Ashok Swaminathan, Srinidhi Hegde, Tianyi Zhou, and Abhinav Shrivastava. 2023. Diffusion Models Beat GANs on Image Classification. ArXiv abs/2307.08702 (2023). https://api.semanticscholar.org/CorpusID:259937835
Naboulsi et al. (2016) Diala Naboulsi, Marco Fiore, Stephane Ribot, and Razvan Stanica. 2016. Large-Scale Mobile Traffic Analysis: A Survey. IEEE Communications Surveys & Tutorials 18, 1 (2016), 124–161. https://doi.org/10.1109/COMST.2015.2491361
Nichol and Dhariwal (2021) Alexander Quinn Nichol and Prafulla Dhariwal. 2021. Improved Denoising Diffusion Probabilistic Models. In Proceedings of the 38th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 139), Marina Meila and Tong Zhang (Eds.). PMLR, 8162–8171. https://proceedings.mlr.press/v139/nichol21a.html
Nie et al. (2023) Yuqi Nie, Nam H. Nguyen, Phanwadee Sinthong, and Jayant Kalagnanam. 2023. A Time Series is Worth 64 Words: Long-term Forecasting with Transformers. arXiv:2211.14730 [cs.LG] https://arxiv.org/abs/2211.14730
Pandey et al. (2024) Chandrasen Pandey, Vaibhav Tiwari, Joel J. P. C. Rodrigues, and Diptendu Sinha Roy. 2024. 5GT-GAN-NET: Internet Traffic Data Forecasting With Supervised Loss Based Synthetic Data Over 5 G. IEEE Transactions on Mobile Computing (2024), 1–12. https://doi.org/10.1109/TMC.2024.3364655
Peebles and Xie (2023) William Peebles and Saining Xie. 2023. Scalable Diffusion Models with Transformers. In 2023 IEEE/CVF International Conference on Computer Vision (ICCV). 4172–4182. https://doi.org/10.1109/ICCV51070.2023.00387
Perez et al. (2018) Ethan Perez, Florian Strub, Harm de Vries, Vincent Dumoulin, and Aaron Courville. 2018. FiLM: visual reasoning with a general conditioning layer. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence and Thirtieth Innovative Applications of Artificial Intelligence Conference and Eighth AAAI Symposium on Educational Advances in Artificial Intelligence (New Orleans, Louisiana, USA) (AAAI’18/IAAI’18/EAAI’18). AAAI Press, Article 483, 10 pages.
Radford et al. (2021) Alec Radford, Jong Wook Kim, Chris Hallacy, Aditya Ramesh, Gabriel Goh, Sandhini Agarwal, Girish Sastry, Amanda Askell, Pamela Mishkin, Jack Clark, et al. 2021. Learning transferable visual models from natural language supervision. In International conference on machine learning. PMLR, 8748–8763.
Rago et al. (2020) Arcangela Rago, Giuseppe Piro, Gennaro Boggia, and Paolo Dini. 2020. Multi-Task Learning at the Mobile Edge: An Effective Way to Combine Traffic Classification and Prediction. IEEE Transactions on Vehicular Technology 69, 9 (2020), 10362–10374. https://doi.org/10.1109/TVT.2020.3005724
Rahman et al. (2018) Shafin Rahman, Salman Khan, and Fatih Porikli. 2018. A Unified Approach for Conventional Zero-Shot, Generalized Zero-Shot, and Few-Shot Learning. IEEE Transactions on Image Processing 27, 11 (2018), 5652–5667. https://doi.org/10.1109/TIP.2018.2861573
Ramesh et al. (2021) Aditya Ramesh, Mikhail Pavlov, Gabriel Goh, Scott Gray, Chelsea Voss, Alec Radford, Mark Chen, and Ilya Sutskever. 2021. Zero-Shot Text-to-Image Generation. In Proceedings of the 38th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 139), Marina Meila and Tong Zhang (Eds.). PMLR, 8821–8831. https://proceedings.mlr.press/v139/ramesh21a.html
Rasul et al. (2024) Kashif Rasul, Arjun Ashok, Andrew Robert Williams, Hena Ghonia, Rishika Bhagwatkar, Arian Khorasani, Mohammad Javad Darvishi Bayazi, George Adamopoulos, Roland Riachi, Nadhir Hassen, Marin Biloš, Sahil Garg, Anderson Schneider, Nicolas Chapados, Alexandre Drouin, Valentina Zantedeschi, Yuriy Nevmyvaka, and Irina Rish. 2024. Lag-Llama: Towards Foundation Models for Probabilistic Time Series Forecasting. arXiv:2310.08278 [cs.LG] https://arxiv.org/abs/2310.08278
Ring et al. (2019) Markus Ring, Daniel Schlör, Dieter Landes, and Andreas Hotho. 2019. Flow-based network traffic generation using generative adversarial networks. Computers & Security 82 (2019), 156–172.
Shao et al. (2022) Zezhi Shao, Zhao Zhang, Fei Wang, and Yongjun Xu. 2022. Pre-training Enhanced Spatial-temporal Graph Neural Network for Multivariate Time Series Forecasting. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (Washington DC, USA) (KDD ’22). Association for Computing Machinery, New York, NY, USA, 1567–1577. https://doi.org/10.1145/3534678.3539396
Shen et al. (2021) Zhiqiang Shen, Zechun Liu, Jie Qin, Marios Savvides, and Kwang-Ting Cheng. 2021. Partial Is Better Than All: Revisiting Fine-tuning Strategy for Few-shot Learning. In Thirty-Fifth AAAI Conference on Artificial Intelligence, AAAI 2021, Thirty-Third Conference on Innovative Applications of Artificial Intelligence, IAAI 2021, The Eleventh Symposium on Educational Advances in Artificial Intelligence, EAAI 2021, Virtual Event, February 2-9, 2021. AAAI Press, 9594–9602. https://doi.org/10.1609/AAAI.V35I11.17155
Sun et al. (2022) Chuanhao Sun, Kai Xu, Marco Fiore, Mahesh K. Marina, Yue Wang, and Cezary Ziemlicki. 2022. AppShot: A Conditional Deep Generative Model for Synthesizing Service-Level Mobile Traffic Snapshots at City Scale. IEEE Transactions on Network and Service Management 19, 4 (2022), 4136–4150. https://doi.org/10.1109/TNSM.2022.3199458
Tashiro et al. (2021) Yusuke Tashiro, Jiaming Song, Yang Song, and Stefano Ermon. 2021. CSDI: Conditional Score-based Diffusion Models for Probabilistic Time Series Imputation. In Advances in Neural Information Processing Systems, M. Ranzato, A. Beygelzimer, Y. Dauphin, P.S. Liang, and J. Wortman Vaughan (Eds.), Vol. 34. Curran Associates, Inc., 24804–24816. https://proceedings.neurips.cc/paper_files/paper/2021/file/cfe8504bda37b575c70ee1a8276f3486-Paper.pdf
Tekgul et al. (2024) Ezgi Tekgul, Thomas Novlan, Salam Akoum, and Jeffrey G. Andrews. 2024. Joint Uplink–Downlink Capacity and Coverage Optimization via Site-Specific Learning of Antenna Settings. IEEE Transactions on Wireless Communications 23, 5 (2024), 4032–4048. https://doi.org/10.1109/TWC.2023.3313916
Touvron et al. (2023) Hugo Touvron, Thibaut Lavril, Gautier Izacard, Xavier Martinet, Marie-Anne Lachaux, Timothée Lacroix, Baptiste Rozière, Naman Goyal, Eric Hambro, Faisal Azhar, et al. 2023. Llama: Open and efficient foundation language models. arXiv preprint arXiv:2302.13971 (2023).
van den Oord et al. (2019) Aaron van den Oord, Yazhe Li, and Oriol Vinyals. 2019. Representation Learning with Contrastive Predictive Coding. arXiv:1807.03748 [cs.LG] https://arxiv.org/abs/1807.03748
Wang et al. (2023) En Wang, Weiting Liu, Wenbin Liu, Yongjian Yang, Bo Yang, and Jie Wu. 2023. Spatiotemporal Urban Inference and Prediction in Sparse Mobile CrowdSensing: A Graph Neural Network Approach. IEEE Transactions on Mobile Computing 22, 11 (2023), 6784–6799. https://doi.org/10.1109/TMC.2022.3195706
Wang et al. (2024) Heng Wang, Yixuan Bai, and Xin Xie. 2024. Deep Reinforcement Learning Based Resource Allocation in Delay-Tolerance-Aware 5G Industrial IoT Systems. IEEE Transactions on Communications 72, 1 (2024), 209–221. https://doi.org/10.1109/TCOMM.2023.3322736
Wang et al. (2017a) Ruoxi Wang, Bin Fu, Gang Fu, and Mingliang Wang. 2017a. Deep & Cross Network for Ad Click Predictions. In Proceedings of the ADKDD’17 (Halifax, NS, Canada) (ADKDD’17). Association for Computing Machinery, New York, NY, USA, Article 12, 7 pages. https://doi.org/10.1145/3124749.3124754
Wang et al. (2022) Xiaojie Wang, Laisen Nie, Zhaolong Ning, Lei Guo, Guoyin Wang, Xinbo Gao, and Neeraj Kumar. 2022. Deep Learning-Based Network Traffic Prediction for Secure Backbone Networks in Internet of Vehicles. ACM Trans. Internet Technol. 22, 4, Article 87 (nov 2022), 20 pages. https://doi.org/10.1145/3433548
Wang et al. (2021) Zi Wang, Jia Hu, Geyong Min, Zhiwei Zhao, and Jin Wang. 2021. Data-Augmentation-Based Cellular Traffic Prediction in Edge-Computing-Enabled Smart City. IEEE Transactions on Industrial Informatics 17, 6 (2021), 4179–4187. https://doi.org/10.1109/TII.2020.3009159
Wang et al. (2017b) Zhen Wang, Guofu Wei, Yaling Zhan, and Yanhuan Sun. 2017b. Big Data in Telecommunication Operators: Data, Platform and Practices. Journal of Communications and Information Networks 2, 3 (2017), 78–91. https://doi.org/10.1007/s41650-017-0010-1
Wei et al. (2023) Chen Wei, Karttikeya Mangalam, Po-Yao Huang, Yanghao Li, Haoqi Fan, Hu Xu, Huiyu Wang, Cihang Xie, Alan Yuille, and Christoph Feichtenhofer. 2023. Diffusion Models as Masked Autoencoders. In 2023 IEEE/CVF International Conference on Computer Vision (ICCV). 16238–16248. https://doi.org/10.1109/ICCV51070.2023.01492
Wu et al. (2021a) Qiong Wu, Xu Chen, Zhi Zhou, Liang Chen, and Junshan Zhang. 2021a. Deep Reinforcement Learning With Spatio-Temporal Traffic Forecasting for Data-Driven Base Station Sleep Control. IEEE/ACM Trans. Netw. 29, 2 (apr 2021), 935–948. https://doi.org/10.1109/TNET.2021.3053771
Wu et al. (2021b) Qiong Wu, Kaiwen He, Xu Chen, Shuai Yu, and Junshan Zhang. 2021b. Deep Transfer Learning Across Cities for Mobile Traffic Prediction. IEEE/ACM Trans. Netw. 30, 3 (dec 2021), 1255–1267. https://doi.org/10.1109/TNET.2021.3136707
Wu et al. (2022) Qiong Wu, Kaiwen He, Xu Chen, Shuai Yu, and Junshan Zhang. 2022. Deep Transfer Learning Across Cities for Mobile Traffic Prediction. IEEE/ACM Transactions on Networking 30, 3 (2022), 1255–1267. https://doi.org/10.1109/TNET.2021.3136707
Xu et al. (2017) Fengli Xu, Yong Li, Huandong Wang, Pengyu Zhang, and Depeng Jin. 2017. Understanding Mobile Traffic Patterns of Large Scale Cellular Towers in Urban Environment. IEEE/ACM Trans. Netw. 25, 2 (apr 2017), 1147–1161. https://doi.org/10.1109/TNET.2016.2623950
Xu et al. (2022) Kai Xu, Rajkarn Singh, Hakan Bilen, Marco Fiore, Mahesh K. Marina, and Yue Wang. 2022. CartaGenie: Context-Driven Synthesis of City-Scale Mobile Network Traffic Snapshots. In 2022 IEEE International Conference on Pervasive Computing and Communications (PerCom). 119–129. https://doi.org/10.1109/PerCom53586.2022.9762395
Xu et al. (2021) Kai Xu, Rajkarn Singh, Marco Fiore, Mahesh K. Marina, Hakan Bilen, Muhammad Usama, Howard Benn, and Cezary Ziemlicki. 2021. SpectraGAN: spectrum based generation of city scale spatiotemporal mobile network traffic data. In Proceedings of the 17th International Conference on Emerging Networking EXperiments and Technologies (Virtual Event, Germany) (CoNEXT ’21). Association for Computing Machinery, New York, NY, USA, 243–258. https://doi.org/10.1145/3485983.3494844
Xu et al. (2023) Xiongxiao Xu, Xin Wang, Elkin Cruz-Camacho, Christopher D. Carothers, Kevin A. Brown, Robert B. Ross, Zhiling Lan, and Kai Shu. 2023. Machine Learning for Interconnect Network Traffic Forecasting: Investigation and Exploitation. In Proceedings of the 2023 ACM SIGSIM Conference on Principles of Advanced Discrete Simulation (Orlando, FL, USA) (SIGSIM-PADS ’23). Association for Computing Machinery, New York, NY, USA, 133–137. https://doi.org/10.1145/3573900.3591123
Yang et al. (2023a) Hongyang Yang, Xiao-Yang Liu, and Christina Dan Wang. 2023a. FinGPT: Open-Source Financial Large Language Models. FinLLM Symposium at IJCAI 2023 (2023).
Yang et al. (2023b) Ling Yang, Zhilong Zhang, Yang Song, Shenda Hong, Runsheng Xu, Yue Zhao, Wentao Zhang, Bin Cui, and Ming-Hsuan Yang. 2023b. Diffusion Models: A Comprehensive Survey of Methods and Applications. ACM Comput. Surv. 56, 4, Article 105 (nov 2023), 39 pages. https://doi.org/10.1145/3626235
Yang et al. (2019) Shun-Ren Yang, Yu-Ju Su, Yao-Yuan Chang, and Hui-Nien Hung. 2019. Short-Term Traffic Prediction for Edge Computing-Enhanced Autonomous and Connected Cars. IEEE Transactions on Vehicular Technology 68, 4 (2019), 3140–3153. https://doi.org/10.1109/TVT.2019.2899125
Yao et al. (2023) Yang Yao, Bo Gu, Zhou Su, and Mohsen Guizani. 2023. MVSTGN: A Multi-View Spatial-Temporal Graph Network for Cellular Traffic Prediction. IEEE Transactions on Mobile Computing 22, 5 (2023), 2837–2849. https://doi.org/10.1109/TMC.2021.3129796
Ye et al. (2023) Peng Ye, Yongqi Huang, Chongjun Tu, Minglei Li, Tao Chen, Tong He, and Wanli Ouyang. 2023. Partial Fine-Tuning: A Successor to Full Fine-Tuning for Vision Transformers. arXiv:2312.15681 [cs.CV] https://arxiv.org/abs/2312.15681
Yeh et al. (2023) Chin-Chia Michael Yeh, Xin Dai, Huiyuan Chen, Yan Zheng, Yujie Fan, Audrey Der, Vivian Lai, Zhongfang Zhuang, Junpeng Wang, Liang Wang, and Wei Zhang. 2023. Toward a Foundation Model for Time Series Data. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management (Birmingham, United Kingdom) (CIKM ’23). Association for Computing Machinery, New York, NY, USA, 4400–4404. https://doi.org/10.1145/3583780.3615155
Yin et al. (2020) Jieli Yin, Yali Fan, Tong Xia, Yong Li, Xiang Chen, Zhi Zhou, and Xu Chen. 2020. Mobile App Usage Patterns Aware Smart Data Pricing. IEEE Journal on Selected Areas in Communications 38, 4 (2020), 645–654. https://doi.org/10.1109/JSAC.2020.2971896
Yin et al. (2022) Yucheng Yin, Zinan Lin, Minhao Jin, Giulia Fanti, and Vyas Sekar. 2022. Practical GAN-based synthetic IP header trace generation using NetShare. In Proceedings of the ACM SIGCOMM 2022 Conference (Amsterdam, Netherlands) (SIGCOMM ’22). Association for Computing Machinery, New York, NY, USA, 458–472. https://doi.org/10.1145/3544216.3544251
Yu et al. (2021) Lixing Yu, Ming Li, Wenqiang Jin, Yifan Guo, Qianlong Wang, Feng Yan, and Pan Li. 2021. STEP: A Spatio-Temporal Fine-Granular User Traffic Prediction System for Cellular Networks. IEEE Transactions on Mobile Computing 20, 12 (2021), 3453–3466. https://doi.org/10.1109/TMC.2020.3001225
Yuan et al. (2024b) Jinliang Yuan, Chen Yang, Dongqi Cai, Shihe Wang, Xin Yuan, Zeling Zhang, Xiang Li, Dingge Zhang, Hanzi Mei, Xianqing Jia, Shangguang Wang, and Mengwei Xu. 2024b. Mobile Foundation Model as Firmware. In Proceedings of the 30th Annual International Conference on Mobile Computing and Networking (Washington D.C., DC, USA) (ACM MobiCom ’24). Association for Computing Machinery, New York, NY, USA, 279–295. https://doi.org/10.1145/3636534.3649361
Yuan et al. (2024a) Yuan Yuan, Jingtao Ding, Jie Feng, Depeng Jin, and Yong Li. 2024a. UniST: A Prompt-Empowered Universal Model for Urban Spatio-Temporal Prediction. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (Barcelona, Spain) (KDD ’24). Association for Computing Machinery, New York, NY, USA, 4095–4106. https://doi.org/10.1145/3637528.3671662
Zafar et al. (2022) Saniya Zafar, Sobia Jangsher, and Arafat Al-Dweik. 2022. Resource Allocation Using Deep Learning in Mobile Small Cell Networks. IEEE Transactions on Green Communications and Networking 6, 3 (2022), 1903–1915. https://doi.org/10.1109/TGCN.2022.3146487
Zhang et al. (2019) Mingyang Zhang, Haohao Fu, Yong Li, and Sheng Chen. 2019. Understanding Urban Dynamics From Massive Mobile Traffic Data. IEEE Transactions on Big Data 5, 2 (2019), 266–278. https://doi.org/10.1109/TBDATA.2017.2778721
Zhang et al. (2023) Shiyuan Zhang, Tong Li, Shuodi Hui, Guangyu Li, Yanping Liang, Li Yu, Depeng Jin, and Yong Li. 2023. Deep Transfer Learning for City-scale Cellular Traffic Generation through Urban Knowledge Graph. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (Long Beach, CA, USA) (KDD ’23). Association for Computing Machinery, New York, NY, USA, 4842–4851. https://doi.org/10.1145/3580305.3599801
Zhang et al. (2017) Sheng Zhang, Shenglin Zhao, Mingxuan Yuan, Jia Zeng, Jianguo Yao, Michael R. Lyu, and Irwin King. 2017. Traffic Prediction Based Power Saving in Cellular Networks: A Machine Learning Method. In Proceedings of the 25th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (Redondo Beach, CA, USA) (SIGSPATIAL ’17). Association for Computing Machinery, New York, NY, USA, Article 29, 10 pages. https://doi.org/10.1145/3139958.3140053
Zhang et al. (2024) Weijiao Zhang, Jindong Han, Zhao Xu, Hang Ni, Hao Liu, and Hui Xiong. 2024. Towards Urban General Intelligence: A Review and Outlook of Urban Foundation Models. ArXiv abs/2402.01749 (2024). https://api.semanticscholar.org/CorpusID:267412420
Zhang et al. (2021) Yue Zhang, Lin Dai, and Eric W. M. Wong. 2021. Optimal BS Deployment and User Association for 5G Millimeter Wave Communication Networks. IEEE Transactions on Wireless Communications 20, 5 (2021), 2776–2791. https://doi.org/10.1109/TWC.2020.3044288
Zhao et al. (2024) Ruijie Zhao, Mingwei Zhan, Xianwen Deng, Fangqi Li, Yanhao Wang, Yijun Wang, Guan Gui, and Zhi Xue. 2024. A Novel Self-Supervised Framework Based on Masked Autoencoder for Traffic Classification. IEEE/ACM Trans. Netw. 32, 3 (jan 2024), 2012–2025. https://doi.org/10.1109/TNET.2023.3335253
Zhao et al. (2021) Zhongliang Zhao, Lucas Pacheco, Hugo Santos, Minghui Liu, Antonio Di Maio, Denis Rosário, Eduardo Cerqueira, Torsten Braun, and Xianbin Cao. 2021. Predictive UAV Base Station Deployment and Service Offloading With Distributed Edge Learning. IEEE Transactions on Network and Service Management 18, 4 (2021), 3955–3972. https://doi.org/10.1109/TNSM.2021.3123216
Zhou et al. (2023) Shenghan Zhou, Chaofan Wei, Chaofei Song, Xing Pan, Wenbing Chang, and Linchao Yang. 2023. Short-Term Traffic Flow Prediction of the Smart City Using 5G Internet of Vehicles Based on Edge Computing. IEEE Transactions on Intelligent Transportation Systems 24, 2 (2023), 2229–2238. https://doi.org/10.1109/TITS.2022.3147845
Zhu et al. (2020) Feiyue Zhu, Lixiang Liu, and Teng Lin. 2020. An LSTM-Based Traffic Prediction Algorithm with Attention Mechanism for Satellite Network. In Proceedings of the 2020 3rd International Conference on Artificial Intelligence and Pattern Recognition (Xiamen, China) (AIPR ’20). Association for Computing Machinery, New York, NY, USA, 205–209. https://doi.org/10.1145/3430199.3430208
Zhu et al. (2023) Ye Zhu, Yu Wu, Kyle Olszewski, Jian Ren, Sergey Tulyakov, and Yan Yan. 2023. Discrete Contrastive Diffusion for Cross-Modal Music and Image Generation. In International Conference on Learning Representations (ICLR).