Floquet topological phase of nondriven $p$-wave nonequilibrium excitonic insulators

A quantum system with nontrivial bulk topological properties admits localized single-particle states at the system edges Read and Green (2000); Hasan and Kane (2010); Qi and Zhang (2011). Existence of well-defined quasi-particles is of course a prerequisite for the bulk–edge correspondence to have physical relevance. In fact, most topological invariants are constructed from a quasi-particle hamiltonian which is treated either as “non-interacting”, i.e., independent of the charge distribution, or at a “mean-field” level. Mean-field hamiltonians introduce an appealing twist in the topological characterization since, at fixed external potentials, they depend on the (self-consistent) charge distribution of the stationary state. Thus, in principle, a quantum system can change its topological properties upon a transition from an excited state to another. Furthermore, the possibility of self-sustained, i.e., not driven by external fields, oscillatory solutions extends the class of topological invariants to the Floquet realm Rechtsman et al. (2013); Cayssol et al. (2013); Kitagawa et al. (2010); Rudner et al. (2013).

Non-equilibrium (NEQ) excitonic insulators (EI) are excited states of band-insulator (BI) mean-field hamiltonians giving rise to a self-sustained oscillating order parameter, i.e., the excitonic condensate (EC) Östreich and Schönhammer (1993); Triola et al. (2017); Pertsova and Balatsky (2018); Hanai et al. (2016, 2017, 2018); Becker et al. (2019); Yamaguchi et al. (2012, 2013); Hannewald et al. (2000); Perfetto et al. (2019). In this Letter we show that a p-wave NEQ-EI undergoes a topological transition with increasing the EC density, leading to the formation of Floquet Majorana edge modes Jiang et al. (2011). We further demonstrate that the Floquet topological p-wave NEQ-EI can be built up in real time by laser pulses of finite duration provided that $p$-excitons exist and are optically active. As the initial BI ground-state has vanishing EC density and trivial topology the system experiences a dynamical phase transition (from BI to non-topological NEQ-EI) followed by a topological one. The density of topological defects predicted by the Kibble-Zurek mechanism Kibble (1976); Zurek (1985) for external drivings of finite duration Sengupta et al. (2008); Mondal et al. (2008); Bermudez et al. (2009, 2010); Lee et al. (2015); Defenu et al. (2019) can indeed be made sufficiently small to preserve the topological character of the final state. Unique spectral signatures for experimental ARPES investigations are also discussed. In particular, at the topological transition point the spectrum becomes gapless and the p-wave NEQ-EI turns into a Dirac semimetal.

Nonvanishing topological invariants Read and Green (2000); Qi and Zhang (2011) and existence of Majorana edge modes Kitaev (2001) in quantum matter with a p-wave symmetry–broken ground state have been recently reported for superconductors Volovik (1999); Ivanov (2001); Kallin and Berlinsky (2016); Sato and Ando (2017), superfluids of ultracold atomic gases Gurarie and Radzihovsky (2007), insulators Hasan and Kane (2010) and excitonic insulators Pikulin and Hyart (2014); Wang et al. (2019). In nonequilibrium and nondriven conditions, however, a nontrivial topology has so far been found only in the mean-field Floquet hamiltonian of a p-wave superfluid Foster et al. (2014).

The simplest description of a NEQ-EI is provided by a spinless one-dimensional hamiltonian with a single valence and conduction bands separated by a direct gap of magnitude $\epsilon_{g}$ Perfetto et al. (2019):

$$\hat{H}=\sum_{\alpha j}(-)^{\alpha}[V\hat{\psi}^{{\dagger}}_{\alpha j}\hat{\psi}_{\alpha j+1}-(2V+\epsilon_{g}/2)\hat{n}_{\alpha j}]+\sum_{ij}U_{ij}\hat{n}_{vi}\hat{n}_{cj},$$

(1)

where $\hat{\psi}_{vj}$ ($\hat{\psi}_{cj}$) annihilates a valence (conduction) electron in the $j$-th cell, $\hat{n}_{\alpha j}\equiv\hat{\psi}^{{\dagger}}_{\alpha j}\hat{\psi}_{\alpha j}$ and $(-)^{\alpha}=1,-1$ for $\alpha=v,c$ (the hopping integral $V$ is chosen positive). The hamiltonian is invariant under the “local” gauge symmetry $\hat{\psi}_{\alpha j}\to e^{i\theta_{\alpha}}\hat{\psi}_{\alpha j}$ associated to the commutation relation $[\hat{H},\hat{N}_{\alpha}]=0$, with $\hat{N}_{\alpha}=\sum_{j}\hat{n}_{\alpha j}$. For large enough $U_{ij}$ the ground state is a BI with a filled (empty) valence (conduction) band. Charge neutral excited states with $N_{c}=1$ can be calculated by solving the Bethe-Salpeter equation (BSE). For short-range interactions, e.g., $U_{ij}=\delta_{ij}U$, the BSE admits only one discrete solution corresponding to an s-wave (even) exciton Perfetto et al. (2019). A Rydberg-like series, and hence p-wave (odd) excitons, appears with long-range interactions such as the soft-Coulomb one: $U_{ij}=U/\sqrt{|i-j|^{2}+1}$. Henceforth we express all energies in units of $\epsilon_{g}$ and choose $U=2V=1$. Then, the BSE admits multiple excitonic solutions, the two lowest having energy $\epsilon_{\mathrm{x}}^{s}=0.40$ (s-wave) and $\epsilon_{\mathrm{x}}^{p}=0.82$ (p-wave) above the valence band maximum. Charge-neutral excited states with a finite density in the conduction band will be treated in the mean-field approximation.

The lowest-energy excited state of $\hat{H}$ with a finite density of conduction electrons and valence holes equals the ground state of the NEQ gran-canonical Hamiltonian $\hat{H}_{\rm NEQ-GC}\equiv\hat{H}-\mu_{v}\hat{N}_{v}-\mu_{c}\hat{N}_{c}$, where $\mu_{\alpha}$ is the chemical potential for electrons in band $\alpha$. Charge neutrality is guaranteed by $\mu_{v}=-\mu_{c}=-\delta\mu/2$ since $\hat{H}$ is particle-hole symmetric (the BI ground state is recovered for $\delta\mu=0$). Exploiting the translational invariance, the mean-field equations for $\hat{H}_{\rm NEQ-GC}$ can be written as foo

$$\left(\begin{array}[]{cc}-\epsilon_{k}+\delta\mu/2&\Delta_{k}\\ \Delta_{k}&\epsilon_{k}-\delta\mu/2\end{array}\right)\left(\begin{array}[]{c}\varphi^{\xi}_{vk}\\ \varphi^{\xi}_{ck}\end{array}\right)=\xi e_{k}\left(\begin{array}[]{c}\varphi^{\xi}_{vk}\\ \varphi^{\xi}_{ck}\end{array}\right),$$

(2)

where $\epsilon_{k}=[2V(1-\cos(k))+\epsilon_{g}/2]$, $k\in(-\pi,\pi)$ is the quasimomentum, $\xi=\pm$ labels the two eigensolutions and $\Delta_{k}=-\sum_{q}\tilde{U}_{k-q}b_{q}$ is the excitonic order parameter, $\tilde{U}_{k}$ being the Fourier transform of $U_{ij}$ and $b_{q}\equiv\varphi^{-}_{cq}\varphi^{-\ast}_{vq}$ the EC density. Only states of the minus branch are occupied since $e_{k}=\sqrt{(\varepsilon_{k}-\delta\mu/2)^{2}+\Delta_{k}^{2}}\geq 0$. Equation (2) has to be solved self-consistently and $\Delta_{k}\neq 0$ implies a symmetry-broken NEQ-EI state. The system remains a BI ($\Delta_{k}=0$) for $\delta\mu<\epsilon_{\mathrm{x}}^{s}$, as it should be Yamaguchi et al. (2012); Perfetto et al. (2019). A unique solution $\Delta_{k}=\Delta_{-k}$ (even in $k$) exists for $\epsilon_{\mathrm{x}}^{s}<\delta\mu<\epsilon_{\mathrm{x}}^{p}$ ($s$-wave NEQ-EI). For $\delta\mu>\epsilon_{\mathrm{x}}^{p}$ we can find a solution $\Delta_{k}=\Delta^{s}_{k}+\Delta^{p}_{k}$ with $\Delta^{s}_{k}$ ($\Delta^{p}_{k}$) even (odd) in $k$ for any fixed angle $\theta={\rm arctan}(\Delta^{s}_{\pi}/\Delta^{p}_{\pi})\in(0,2\pi)$. The $p$-wave NEQ-EI state is realized when $\theta=0$ and hence $\Delta_{k}=-\Delta_{-k}$. Below we show that this state can be generated by suitable laser pulses provided that the $p$-wave ($s$-wave) exciton is bright (dark).

Independently of the symmetry the NEQ-EI state evolves according to the time-dependent mean-field equations $i\frac{d}{dt}\varphi^{\xi}_{k}(t)=h^{\rm MF}_{k}(t)\varphi^{\xi}_{k}(t)$ where

$$h^{\mathrm{MF}}_{k}(t)=\left(\begin{array}[]{cc}-\epsilon_{k}&\Delta_{k}(t)\\ \Delta^{\ast}_{k}(t)&\epsilon_{k}\end{array}\right)$$

(3)

is the physical mean-field Hamiltonian. The excitonic order parameter $\Delta_{k}(t)=\sum_{q}\tilde{U}_{k-q}\varphi^{-}_{cq}(t)\varphi^{-\ast}_{vq}(t)$ acquires a dependence on time through the wavefunctions. In Ref. Perfetto et al. (2019) we have shown that this dependence is monochromatic and given by

$$\Delta_{k}(t)=\Delta_{k}e^{i\delta\mu t}.$$

(4)

Thus, the mean-field hamiltonian supports self-sustained Josephson-like oscillations driven by the broken gauge symmetry. We then construct the Floquet hamiltonian $h^{\mathrm{Floq}}_{k}$ from $\mathcal{T}e^{-i\int_{0}^{T}dt\,h^{\mathrm{MF}}_{k}(t)}=e^{-ih^{\mathrm{Floq}}_{k}T}$, where $\mathcal{T}$ is the time-ordered operator and $T=2\pi/\delta\mu$, and look for nonvanishing Floquet topological invariants. Since $h^{\mathrm{MF}}_{k}(t)$ is a $2\times 2$ monochromatic and hermitian matrix the Floquet hamiltonian can easily be calculated Perfetto and Stefanucci (2015)

$$h^{\mathrm{Floq}}_{k}=\left(\begin{array}[]{cc}-\epsilon_{k}&\Delta_{k}\\ \Delta_{k}&\epsilon_{k}-\delta\mu\end{array}\right)=-\frac{\delta\mu}{2}\mathds{1}+e_{k}\,\vec{n}(k)\cdot\vec{\sigma}$$

(5)

where $\sigma_{x,y,z}$ are the Pauli matrices and $\vec{n}(k)=\{n_{x}(k),n_{y}(k),n_{z}(k)\}=\{\Delta_{k}/e_{k},0,(\delta\mu/2-\epsilon_{k})/e_{k}\}$. Interestingly, $h^{\mathrm{Floq}}_{k}$ coincides with the NEQ gran-canonical mean-field hamiltonian in Eq. (2) up to a constant diagonal shift. The winding number Niu et al. (2012); Tong et al. (2013); Thakurathi et al. (2013)

$$W=\frac{1}{2\pi}\int_{-\pi}^{\pi}d\Theta_{k}\quad,\quad\Theta_{k}=\arctan\frac{n_{z}(k)}{n_{x}(k)}.$$

(6)

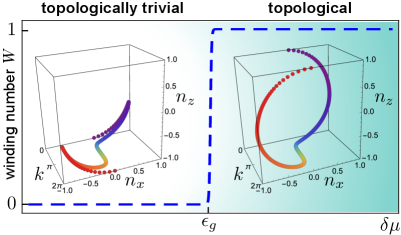
measures the number of windings of the unit vector $\vec{d_{k}}=\{n_{x}(k),n_{z}(k)\}$ as $k$ crosses the first Brillouin zone. $W$ is a positive or negative integer in the topological phase and it is otherwise zero. It is immediate to realize that $W=0$ for any even $\Delta_{k}$. If, instead, $\Delta_{k}$ is an odd function then $W=\pm 1$ provided that $\delta\mu>\epsilon_{g}$, see Fig. 1. Thus a topological transition occurs in a p-wave NEQ-EI as $\delta\mu$, and hence the average EC density $b=\frac{1}{\mathcal{N}}\sum_{q}b_{q}$ (with $\mathcal{N}$ the number of cells), exceeds a critical value. In Fig. 1 we also show the path of $\vec{d}_{k}$ resulting from the self-consistent solution of Eq. (2). The difference in chemical potentials is $\delta\mu=0.96$ (left panel) and $\delta\mu=1.04$ (right panel).

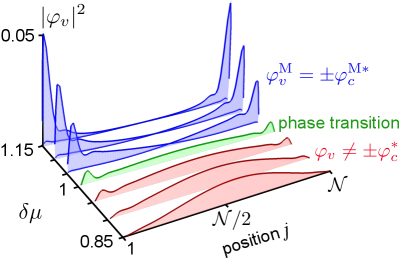
According to the bulk-edge correspondence, a number $|W|$ of topologically protected Floquet Majorana modes should form at each open boundary Tong et al. (2013). As the the Floquet hamiltonian in Eq. (5) coincides with the mean-field NEQ gran-canonical hamiltonian in Eq. (2) we consider $\hat{H}_{\rm NEQ-GC}$ on an open wire of $\mbox{$\mathcal{N}$}=100$ cells and solve the mean-field equations in the site basis. The spectrum is symmetric around zero energy with positive and negative eigenvalues $e^{+}_{\lambda}=-e^{-}_{\lambda}\geq 0$. For $\delta\mu<\epsilon_{g}$ the maximum energy $e_{\rm max}={\rm max}_{\lambda}\{e^{-}_{\lambda}\}$ is strictly negative and the eigenfunctions $\varphi^{\pm}_{\rm max}$ of energies $\pm e_{\rm max}$ are delocalized along the wire. In Fig. 2 we plot the valence probability $|\varphi^{+}_{{\rm max},vj}|^{2}$ versus site $j$ (the conduction probability $|\varphi^{-}_{{\rm max},cj}|^{2}$ is identical). A sharp transition occurs for $\delta\mu>\epsilon_{g}$ since the spectrum is almost the same as for $\delta\mu<\epsilon_{g}$ except for two degenerate eigenvalues appearing at zero energy. The corresponding eigenfunctions can be chosen to satisfy $\varphi^{\rm M}_{vj}=\pm\varphi_{cj}^{\rm M\ast}$, i.e., they are Majorana modes, and their valence components are plot in Fig. 2. The Majorana modes are correctly localized at the system boundaries and the degree of localization increases as $\delta\mu$ moves deeper inside the topological phase.

The topological transition in a (bulk) p-wave NEQ-EI leave unique fingerprints on the ARPES spectrum The spectral function $A_{k}(\omega)$ is the sum of a removal ($<$) and addition ($>$) contribution, $A_{k}(\omega)=A^{<}_{k}(\omega)+A^{>}_{k}(\omega)$ with

$\displaystyle A^{\gtrless}_{k}(\omega)$

$\displaystyle=|\varphi^{\pm}_{vk}|^{2}\delta(\omega\mp e_{k}+\frac{\delta\mu}{2})+|\varphi^{\pm}_{ck}|^{2}\delta(\omega\mp e_{k}-\frac{\delta\mu}{2}).$

(7)

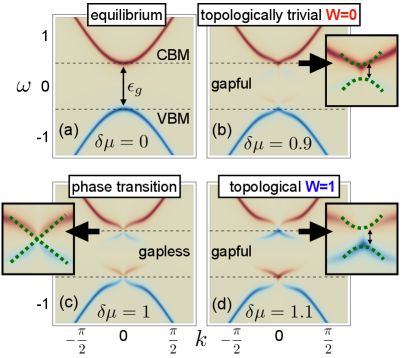
In Fig. 3 we show how $A_{k}(\omega)$ changes from the equilibrium (panel a) to the symmetry-broken (panel b) and topological phase (panels c-d). As $\delta\mu$ overcomes $\epsilon_{\mathrm{x}}^{p}=0.82$ the system becomes a nontopological NEQ-EI and an excitonic structure appears inside the gap (panel b) Perfetto et al. (2016, 2019). For $\delta\mu=0.9<\epsilon_{g}$ the conduction density is $n_{c}=\frac{1}{\mathcal{N}}\sum_{k}|\varphi^{-}_{ck}|^{2}=0.03$ and the averaged order parameter $\Delta\equiv\frac{2}{\mathcal{N}}\sum_{0<k<\pi}\Delta_{k}=0.04$ (with $\mathcal{N}$ the number of cells). The removal (blue) component of the excitonic structure is separated from the bottom of the conduction band (red) by a small gap, consistently with the insulating character of the state (see inset of Fig. 3 b). In contrast with the s-wave NEQ-EI Perfetto et al. (2019, 2020), however, the excitonic structure has a vanishing spectral weight around the $\Gamma$-point since $n_{ck}=|\varphi^{-}_{ck}|^{2}$ vanishes at $k=0$ in the nontopological phase (see also the dashed line in Fig. 4 d). At the topological critical point ($\delta\mu=\epsilon_{g}$) we find $n_{c}=0.07$ and $\Delta=0.06$ (both larger than for $\delta\mu=0.9$). Despite $\Delta\neq 0$ the gap closes (see inset of Fig. 3 c) and the dispersion of the excitonic structure around the $\Gamma$-point becomes, see Eq. (7), $E_{k}=\frac{\delta\mu}{2}-e_{k}\approx\frac{\delta\mu}{2}-\gamma|k|$ where we have approximated $\Delta_{k}\approx\gamma k$ (see also the dashed line in Fig. 4 c and Fig. 5 c). Thus, the system becomes a Dirac semimetal. The transition point is also characterized by a discontinuity in $n_{ck=0}$ which varies abruptly from 0 ($\delta\mu<\epsilon_{g}$) to 1 ($\delta\mu>\epsilon_{g}$). In the topological phase $\delta\mu=1.1>\epsilon_{g}$ both $n_{c}=0.11$ and $\Delta=0.08$ increase and the gap re-opens, see Fig. 3 d. Noteworthy, the spectral weight of the excitonic structurelorentzians is now largest at the $\Gamma$-point due to the aforementioned discontinuity in $n_{ck=0}$.

The remaining issue to be addressed is whether and how the topological p-wave NEQ-EI state can be prepared. We answer affirmatively provided that the p-exciton is much brighter than the s-exciton. We consider the system initially in the BI ground state and drive it out of equilibrium by a laser pulse

$$\hat{H}_{\rm laser}(t)=E(t)\sum_{k}D_{k}(\hat{\psi}^{{\dagger}}_{ck}\hat{\psi}_{vk}+\hat{\psi}^{{\dagger}}_{vk}\hat{\psi}_{ck}),$$

(8)

where $D_{k}$ is the valence-conduction dipole moment. The electric field $E(t)$ is a pulse of finite duration $T_{P}$ centered around frequency $\omega_{P}$:

$$E(t)=\theta(1-|1-2t/T_{P}|)E_{P}\sin^{2}(\frac{\pi t}{T_{P}})\sin(\omega_{P}t).$$

(9)

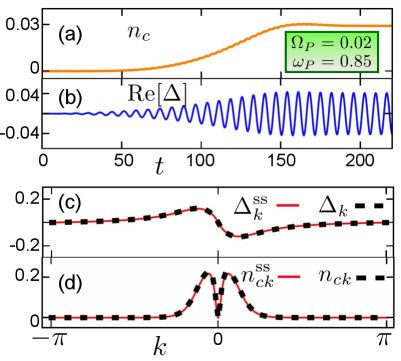
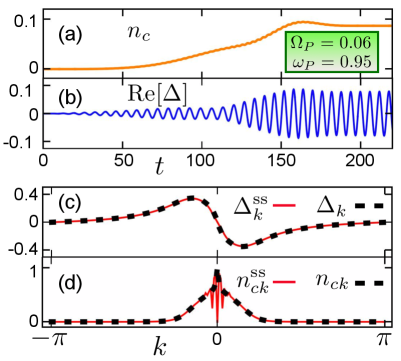
To enhance absorption by the $p$-exciton we take $D_{k}$ odd in $k$. First we generate the p-wave NEQ-EI in the nontopological phase by tuning the Rabi frequency $\Omega_{P}\equiv E_{P}D$ and the central frequency $\omega_{P}$ in the range $(\epsilon_{\mathrm{x}}^{p},\epsilon_{g})$. In Fig. 4 we show the outcome of a real-time mean-field simulation performed with the CHEERS code Perfetto and Stefanucci (2018) using $D_{k}=D\sin(k)$ and optimal laser parameters $T_{P}=200$, $\Omega_{P}=0.02$ and $\omega_{P}=0.85$ (times in units of $1/\epsilon_{g}$). At the end of the pulse the system has steady-state occupations $n^{\rm ss}_{ck}$ giving a density $n_{c}=0.03$ (panel a) and an averaged order parameter oscillating in time as $\Delta(t)=\Delta^{\rm ss}e^{i\delta\mu^{\rm ss}t}$ with steady-state amplitude $\Delta^{\rm ss}=0.02$ and $\delta\mu^{\rm ss}=0.907$ (panel b). This oscillatory behavior is actually found for each $k$, i.e. $\Delta_{k}(t)=\Delta^{\mathrm{ss}}_{k}e^{i\delta\mu^{\rm ss}t}$ (not shown). We mention that the self-sustained oscillations (persistent at the mean-field level) survive for long time when numerically exact propagation schemes are used Murakami et al. (2019). In Fig. 4 c-d we compare $\Delta_{k}$ and $n_{ck}$ obtained from the self-consistent solution of Eq. (2) at $\delta\mu=\delta\mu^{\rm ss}<\epsilon_{g}$ against $\Delta^{\rm ss}_{k}$ and $n^{\rm ss}_{ck}$ obtained from the real-time simulation. The agreement is remarkably good, thereby proving that a dynamical phase transition from a BI to a nontopological p-wave NEQ-EI can be induced by properly choosing the laser pulse.

Less obvious is the possibility of driving the BI toward a topological p-wave NEQ-EI. The BI ground state has $W=0$ and hence the system should experience a dynamical topological transition featuring a gap closure at the quantum critical point. According to the Kibble-Zurek mechanism Kibble (1976); Zurek (1985) this introduces a diverging time-scale preventing the realization of the topological target state with an external field of finite duration $T_{P}$ Perfetto (2013); Sacramento (2014). In fact, topological defects are produced around the $\Gamma$-point (gap-closure point) for any $T_{P}<\infty$ Sengupta et al. (2008); Mondal et al. (2008); Bermudez et al. (2009, 2010); Lee et al. (2015); Defenu et al. (2019). One can easily show that for odd dipoles $D_{k}$ the density $n_{ck=0}(t)=0$ at every time (in the topological phase $n_{ck=0}=1$). In Fig. 5 we show the results of a mean-field real-time simulation for a laser pulse with $T_{P}=200$, $\Omega_{P}=0.06$ and $\omega_{P}=0.95$. As expected, the conduction density (panel a) and the amplitude of the averaged order parameter (panel b) are larger than in the previous case, see Fig. 4. Of more importance is that they both attain a steady-state value after the pulse ($t>T_{P}$) and that (with high numerical accuracy) the entire order parameter oscillates monochromatically as $\Delta_{k}(t)=\Delta^{\mathrm{ss}}_{k}e^{i\delta\mu^{\rm ss}t}$ with $\delta\mu^{\rm ss}=1.04>\epsilon_{g}$. As Fig. 5 c shows, $\Delta^{\mathrm{ss}}_{k}$ is indistinguishable from the self-consistent $\Delta_{k}$ of Eq. (2) at $\delta\mu=\delta\mu^{\rm ss}$. We conclude that for $t>T_{P}$ the mean-field hamiltonian has the same form as Eqs. (3,4); hence the corresponding Floquet hamiltonian has winding number $W=1$. Although the two hamiltonians are identical the time-dependent state differs from the self-consistent one. This is shown in Fig. 5 d where a difference between $n_{ck}^{\rm ss}$ and the self-consistent $n_{ck}$ is clearly visible around $k=0$. Such topological defect, however, does not destroy the topological phase since the Floquet hamiltonian depends only on $\Delta_{k}$.

To summarize, we have shown the existence of a Floquet topological phase in nondriven nonequilibrium matter and how to steer a nontopological BI toward this phase with laser pulses of finite duration. The nontrivial topology emerges exclusively from the electron-hole Coulomb attraction and it leaves unique fingerprints in the ARPES spectra. Our discussion is based on a paradigmatic 1D model, but the results are general and can easily be extended to 2D systems. In this case the $p_{x}+ip_{y}$ symmetry of the EC order parameter can be exploited to generate a nonvanishing Chern number $\frac{1}{4\pi}\int d^{2}k\,\vec{n}\cdot(\partial_{k_{x}}\vec{n}\times\partial_{k_{y}}\vec{n})$ that, again, counts the Majorana edge modes. Materials with optically bright $p$-excitons for realizing the topological p-wave NEQ-EI phase may include semiconducting nanotubes Maultzsch et al. (2005); Verdenhalven and Malić (2013), biased graphene bilayers Park and Louie (2010), and low-dimensional compounds with strong spin-orbit coupling Garate and Franz (2011). An s-wave NEQ-EI phase has been recently observed in bulk GaAs Murotani et al. (2019): the way to light-induced topological phases of NEQ-EI has therefore been opened.

Akcknowledgements We acknowledge useful discussions with Andrea Marini and Davide Sangalli. We also acknowledge funding from MIUR PRIN Grant No.20173B72NB and from INFN17-Nemesys project.