FLNeRF: 3D Facial Landmarks Estimation in Neural Radiance Fields

Hao Zhang

{}^{*}{}^{1}

Tianyuan Dai

{}^{*}{}^{1}

Yu-Wing Tai¹ Chi-Keung Tang¹
¹The Hong Kong University of Science and Technology
{hzhangcc, tdaiaa}@connect.ust.hk, [email protected], [email protected]

Abstract

This paper presents the first significant work on directly predicting 3D face landmarks on neural radiance fields (NeRFs). Our 3D coarse-to-fine Face Landmarks NeRF (FLNeRF) model efficiently samples from a given face NeRF with individual facial features for accurate landmarks detection. Expression augmentation is applied to facial features in a fine scale to simulate large emotions range including exaggerated facial expressions (e.g., cheek blowing, wide opening mouth, eye blinking) for training FLNeRF. Qualitative and quantitative comparison with related state-of-the-art 3D facial landmark estimation methods demonstrate the efficacy of FLNeRF, which contributes to downstream tasks such as high-quality face editing and swapping with direct control using our NeRF landmarks. Code and data will be available. Github link: https://github.com/ZHANG1023/FLNeRF.

Figure 1: Accurate 3D landmarks on face NeRF. FLNeRF directly operates on dynamic NeRF, so that an animator can easily edit, control, and even transfer emotion from another face NeRF. With precise landmarks on facial features (eye brows, nostrils, mouth), exaggerated facial expressions with wide grinning, mouth wide open, cheek blowing can be readily achieved.

1 Introduction

Facial landmarks prediction is an important computer vision task. Early models including Active Shape Models (ASM) [1, 15, 14] and Active Appearance Models (AAM) [13, 60] localize 2D landmarks on 2D images. However, 2D landmarks do not work well under large variance of pose and illumination. Moreover, applying 2D landmark prediction individually to multiple images capturing the same 3D face does not guarantee consistency. Even for single-image scenarios, some 3D face information (e.g. depth) is often estimated where 3D facial landmarks can be directly predicted. Thus, 3D landmarks estimation methods have been developed, which are applied in various modern downstream tasks, e.g., face recognition [63, 62, 45], face synthesis [91], face alignment [81], augmented reality [3, 90, 17], and face reenactment [33, 26]. Note that the input are still often 2D image(s) although 3D representations such as mesh, voxel, and point cloud are available, where controlled illumination, special sensors or synchronized cameras are required during data acquisition [43, 54, 2]. The demanding acquisition of such explicit and discrete 3D representation has hindered development of models for predicting 3D face landmarks from a 3D face representation, until the emergence of Neural Radiance Field (NeRF). NeRF is a game-changing approach to 3D scene representation model for novel view synthesis, which represents a static 3D scene by a compact fully-connected neural network [43]. The network, directly trained on 2D images, is optimized to approximate a continuous scene representation function which maps 3D scene coordinates and 2D view directions to view-dependent color and density values. The implicit 5D continuous scene representation allows NeRF to represent more complex and subtle real-world scenes, overcoming reliance of explicit 3D data, where custom capture, sensor noise, large memory footprint, and discrete representations are long-standing issues. Further studies [32, 67, 68, 30, 77, 59, 83, 39, 92, 56, 38, 72, 44, 23, 58, 88, 28, 12] have been done to improve the performance, efficiency and generalization of NeRF, with its variants quickly and widely adopted in dynamic scene reconstruction [52, 82, 37, 55, 18], novel scene composition [51, 89, 48, 25, 41, 85, 46, 35], articulated 3D shape reconstruction [86, 61, 78, 93, 31, 94, 84, 11, 49, 53], and various computer vision tasks, including face NeRFs [21, 5, 50, 69, 16, 29], the focus of this paper.

This paper presents FLNeRF, which is to our knowledge the first work to accurately estimate 3D face landmarks directly on NeRFs. FLNeRF contributes a coarse-to-fine framework to predict 3D face landmarks directly on NeRFs, where keypoints are identified from the entire face region (coarse), followed by detailed keypoints on facial features such as eyebrows, cheekbones, and lips (fine). To encompass non-neutral, expressive and exaggerated expressions e.g. half-open mouth, closed eyes, and even smiling fish face, we apply effective expression augmentation and consequently, our augmented data consists of 110 expressions, including subtle as well as exaggerated expressions. This expressive facial data set will be made available. We demonstrate application of FLNeRF, by simply replacing the shape and expressions codes in [99] with our facial landmarks, to show how direct control using landmarks can achieve comparable or better results on face editing and swapping. In summary, our main contributions are:

•

We propose FLNeRF, a coarse-to-fine 3D face landmark predictor on NeRFs, as the first significant model for 3D face landmark estimation directly on NeRF without any intermediate representations. The 110-expression augmented dataset will be made available.
•

We demonstrate applications of accurate 3D landmarks produced by FLNeRF on multiple high-quality downstreamon tasks, such as face editing and face swapping (Figure 1).

2 Related Work

2D Face Landmarks Prediction ASM [1, 15, 14] and AAM [13, 60] are classic methods in 2D face landmarks prediction. Today CNN-based methods have become mainstream, consisting of heatmap regression models and coordinate regression models. Heatmap models [80, 96, 70, 75] generate probability maps for each landmark location. However, face landmarks are not independent sparse points. Heatmap methods are prone to occlusion and appearance variations due to lack of face structural information. In contrast to heatmap regression models, directly learning landmarks coordinates could encompass weak structural knowledge [73, 36]. Most coordinate regression methods [71, 74, 42, 97, 66] progressively migrate predictions toward ground truth landmarks on 2D image.

Refer to caption — Figure 2: FLNeRF pipeline of our 3D facial landmarks detection. We choose 4 representative regions, i.e., eyes, mouth, and the whole face to detect facial landmarks. In each region, 4 channel volumes are sampled from the NeRF. Together with the 3D position encoding, feature volumes are encoded as an 1D vector by 3D VolResNet or VGG backbone. Four separate 1D vectors received from the 4 coarse-to-fine scales (i.e., the whole face, left and right eyes including eyebrows, and mouth are concatenated and decoded to bilinear parameters and pose (given by the transform matrix) using MLPs.

3D Face Model and 3D Face Landmarks Prediction 3D Morphable Model (3DMM) [6] is among the earliest methods in representing 3D face which is usually used as an intermediate to guide learning of face models. However, it also restricts flexibility of face models due to its strong 3D prior and biased training data. To represent faces with wider range of expressions and preserve identity information, [76] proposed bilinear model, which parameterizes face models in identity and expression dimensions. Facescape [95] builds bilinear models from topologically uniformed models, through which 3D landmarks can be extracted, achieving better representation quality especially for identity preservation and wide range of expressions.

3D models in face-related tasks are more preferable than 2D ones for representation power and robustness against pose and illumination changes. Before NeRFs, traditional 3D representation methods include voxel, mesh, and point cloud. However, building 3D models using these methods requires controlled illumination, explicit 3D images, special sensors or synchronized cameras [43, 54, 2]. Due to the demanding requirements for data acquisition, state-of-the-art 3D face landmarks prediction methods focus on localizing 3D landmarks on a single 2D image [98, 79, 8, 19, 24, 34, 87]. [79, 24, 98, 87] regress parameters of 3DMM, after which 3D landmarks could be extracted. [8, 19, 34] regress the coordinates of dense vertices or other 3D representations. These methods suffer from large memory footprint and long inference time, since they usually adopt heavy networks such as hourglass [47].

State-of-the-art 3D face landmarks localization methods have suboptimal accuracy and limited expression range and pose variations due to the 2D input. Although representations like voxels and meshes can be constructed, an expressive face contains important subtle features which can easily get lost in such discrete representations. While low-resolution processing leads to severe information loss, high-resolution processing induces large memory footprint and long training and rendering time. Thus, a continuous, compact, and relatively easy-to-obtain 3D representation is preferred as input to 3D landmarks localization models for more direct and accurate estimation.

Face NeRFs Since NeRF represents 3D face continuously as solid (i.e., unlike point cloud crust surface), encoding 3D information in a compact set of weights (e.g., a 512 $\times$ 512 $\times$ 512 voxel versus a 256 $\times$ 256 $\times$ 9 network), and only requires multiview RGB images with camera poses, applying NeRF on face-related tasks has recently attracted research efforts. [21] combines a scene representation network with a low-dimensional morphable model, while [5] utilizes a deformation field and uses 3DMM as a deformation prior. In [50], a NeRF-style volume renderer is used to generate high fidelity face images. In face editing and synthesis, training NeRF generators [69, 16, 29] reveals promising prospects for the inherently continuous 3D representation of the volume space, with drastic reduction of demanding memory and computational requirements of voxel-based methods. MoFaNeRF [99] encodes appearance, shape, and expression and directly synthesizes photo-realistic face. Continuous face morphing can be achieved by interpolating the three codes. We modify MoFaNeRF to support high-quality face editing and face swapping to demonstrate the advantages of direct control using 3D landmarks. [22, 57, 64, 9] reconstruct face NeRFs from a single image. We will show our FLNeRF can be generalized to estimate 3D face landmarks on 2D in-the-wild images, using face NeRFs reconstructed by EG3D Inversion [9].

Table 1: Quantitative comparison of FLNeRF and representative methods in terms of average Wing loss. All values are multiplied by 10.

Method	Input	Average Wing Loss of All Expressions				Average Wing Loss of Exaggerated Expression
		Whole Face	Mouth	Eyes	Nose	Whole Face	Mouth	Eyes	Nose
[27]	Multi-View Images	2.91 $\pm$ 0.17	2.27 $\pm$ 0.32	1.55 $\pm$ 0.15	2.90 $\pm$ 0.23	2.88 $\pm$ 0.23	2.34 $\pm$ 0.30	1.52 $\pm$ 0.14	2.59 $\pm$ 0.34
[8]	A Front-View Image	2.78 $\pm$ 0.20	1.48 $\pm$ 0.32	2.57 $\pm$ 0.33	2.12 $\pm$ 0.37	2.71 $\pm$ 0.09	1.72 $\pm$ 0.07	2.13 $\pm$ 0.28	1.96 $\pm$ 0.42
	A 45°Side-View Image	2.66 $\pm$ 0.18	1.95 $\pm$ 0.27	1.71 $\pm$ 0.26	2.31 $\pm$ 0.20	2.65 $\pm$ 0.13	2.17 $\pm$ 0.22	1.44 $\pm$ 0.11	2.22 $\pm$ 0.09
	A 90°Side-View Image	Malfunction: Unable to Detect Faces
[98]	A Front-View Image	2.85 $\pm$ 0.34	2.39 $\pm$ 0.59	1.45 $\pm$ 0.25	2.53 $\pm$ 0.32	3.30 $\pm$ 0.21	3.43 $\pm$ 0.26	1.36 $\pm$ 0.15	2.37 $\pm$ 0.33
	A 45°Side-View Image	2.99 $\pm$ 1.04	2.39 $\pm$ 0.79	1.82 $\pm$ 1.30	2.69 $\pm$ 0.43	3.37 $\pm$ 0.26	3.01 $\pm$ 0.26	1.83 $\pm$ 0.27	2.61 $\pm$ 0.20
	A 90°Side-View Image	Malfunction: Unable to Detect Faces
[19]	A Front-View Image	2.75 $\pm$ 0.27	2.18 $\pm$ 0.35	2.00 $\pm$ 0.33	2.31 $\pm$ 0.25	3.14 $\pm$ 0.21	2.66 $\pm$ 0.22	2.29 $\pm$ 0.18	2.00 $\pm$ 0.17
	A 45°Side-View Image	2.75 $\pm$ 0.27	2.15 $\pm$ 0.33	1.94 $\pm$ 0.30	2.40 $\pm$ 0.33	3.16 $\pm$ 0.17	2.54 $\pm$ 0.04	2.54 $\pm$ 0.21	2.10 $\pm$ 0.20
	A 90°Side-View Image	2.96 $\pm$ 0.45	1.90 $\pm$ 0.48	2.55 $\pm$ 0.64	2.82 $\pm$ 0.39	3.73 $\pm$ 0.57	3.16 $\pm$ 0.88	3.24 $\pm$ 0.50	2.50 $\pm$ 0.23
[79]	A Front-View Image	2.87 $\pm$ 0.17	2.54 $\pm$ 0.37	1.42 $\pm$ 0.22	2.63 $\pm$ 0.30	3.15 $\pm$ 0.11	3.24 $\pm$ 0.23	1.26 $\pm$ 0.07	2.27 $\pm$ 0.24
	A 45°Side-View Image	2.95 $\pm$ 0.20	2.71 $\pm$ 0.40	1.46 $\pm$ 0.22	2.51 $\pm$ 0.33	3.31 $\pm$ 0.14	3.35 $\pm$ 0.20	1.51 $\pm$ 0.11	2.23 $\pm$ 0.21
	A 90°Side-View Image	3.53 $\pm$ 0.46	2.75 $\pm$ 0.50	2.40 $\pm$ 0.64	2.93 $\pm$ 0.31	4.29 $\pm$ 0.50	3.97 $\pm$ 0.89	2.72 $\pm$ 0.49	3.00 $\pm$ 0.38
Ours	Single Face NeRF	0.72 $\pm$ 0.17	0.85 $\pm$ 0.37	0.62 $\pm$ 0.16	0.55 $\pm$ 0.20	0.67 $\pm$ 0.13	0.78 $\pm$ 0.20	0.61 $\pm$ 0.11	0.57 $\pm$ 0.22

3 3D Face NeRF Landmarks Detection

Figure 2 shows the pipeline of FLNeRF which is a multi-scale coarse-to-fine 3D face landmarks predictor on NeRF.

Our coarse model takes a face NeRF as input and produces rough parameter estimates of the bilinear model, location, and orientation (Sec. 3.1) of the input face by performing 3D convolution of the sampled face NeRF with position encoding. Unlike SynergyNet [79] which crops faces in 2D images, our coarse model can localize the pertinent 3D head in the NeRF space. Based on the estimated coarse landmarks, our fine model resamples from four regions: whole face, the left and right eyes including eyebrows, and mouth. In our coarse-to-fine implementation, the resolution of the sampled 3D volumes (coarse and fine) is $64^{3}$ .

The resampled volumes are then used to estimate more accurate bilinear model parameters with position encoding in Sec. 3.1. After describing how to benefit from the underlying continuous NeRF representation in sampling in Sec. 3.2, we will explain our coarse model in Sec. 3.3 and fine model in Sec. 3.4. Since there are only 20 discrete expressions in FaceScape [95] with fixed head location and orientation, more diverse expressions and head poses are not covered in the dataset. To alleviate this limitation, we apply data augmentation to enrich our dataset to 110 expressions with different head poses per person, allowing our model to accurately locate and predict landmarks for faces with more complex expressions. We will describe our coarse data augmentation and fine expressions augmentation in Sec. 4.

3.1 Bilinear Model

We utilize the bilinear model to approximate face geometry. FaceScape builds the bilinear model from generated blendshapes in the space of 26317 vertices $\times$ 52 expressions $\times$ 938 identities. Tucker decomposition is used to decompose the large rank-3 tensor into a small core tensor $C_{r}\in\mathbb{R}^{26317\times 52\times 50}$ and two low dimensional components $\textbf{w}_{exp}\in\mathbb{R}^{52}$ , $\textbf{w}_{id}\in\mathbb{R}^{50}$ for expression and identity. Here, we only focus on the 68 landmarks subspace $C_{r}^{\prime}\in\mathbb{R}^{68\cdot 3\times 52\times 50}$ . The 68 3D landmarks $V_{f}\in\mathbb{R}^{3\times 68}$ can be generated by Eq. 1:

V_{f}=C_{r}^{\prime}\times\textbf{w}_{id}\times\textbf{w}_{exp}

(1)

To align $V_{f}$ with an input face NeRF, a transform matrix $P\in\mathbb{R}^{3\times 4}$ is predicted. New aligned landmarks can be written as:

V_{a}=P\begin{bmatrix}V_{f}\\ 1\end{bmatrix}.

(2)

3.2 NeRF Sampling

NeRF is a continuous representation underlying a 3D scene. So far, most feature extractors are applied in discrete spaces such as voxel, mesh and point cloud, which inevitably induces information loss. In order to maximize the benefit of the continuous representation, we adopt a coarse-to-fine sampling strategy. Specifically, given a NeRF containing a human head, uniform coarse sampling will first be performed in the whole region of the NeRF with respect to the radiance and density channels to generate feature volumes (RGB is used to represent radiance). To make the radiance sampled on the face surface more accurate, we assume the viewing direction is looking at the frontal face when we sample the NeRF. We only utilize the radiance and density queried at given points of the NeRF, thus our model is applicable to most NeRF representations. To discard noisy samples, voxels with density smaller than a threshold (set to 20 by experiments) will be set to 0 in all channels (RGB and density), and voxel with density larger than the threshold will have the value one in density channel with RGB channels remaining the same. In the fine sampling, given the predicted coarse landmarks, orientation and translation of the head, the sampling regions of the whole face, eyes, and mouth are cubic boxes centered at the mean points of the landmarks belonging to corresponding regions with a suitable size proportional to the scale of the head. These cubic sampling boxes are aligned to the same rotation of the head. The same noise discarding strategy is used here.

3.3 Coarse Model

Inspired by CoordConv [40], to enhance ability of 3D CNNs to represent spatial information, we add position encoding channels to each feature volume. Instead of directly using the Cartesian coordinates, a higher dimensional vector encoded from $x,y,z$ normalized to [0,1] are used as position encoding. The mapping function from $x,y,z$ to higher dimensional space is modified from that in [43] which includes the original Cartesian coordinates:

\small\begin{split}\gamma(p)=(p,\sin(2^{0}\pi p),\cos(2^{0}\pi p),...,\sin(2^{L-1}\pi p),\cos(2^{L-1}\pi p)).\end{split}

(3)

We set $L=4$ , and $\gamma(\cdot)$ is applied to individual coordinates.

We adopt the VoxResNet [10] and 3D convolution version of VGG [65] as our backbone to encode the pertinent feature volumes into a 1D long vector. Three seperate fully-connected layers are used as decoder to predict the transform matrix and bilinear model parameters. The transform matrix contains the head location and orientation. The loss we used is the Wing loss [20]:

\mathit{wing}(x)=\begin{cases}\omega\ln(1+|x^{\prime}-x|/\epsilon)&\mbox{if $|x^{\prime}-x|<\omega$}\\ |x^{\prime}-x|-C&\mbox{otherwise}\end{cases}

(4)

where we set $\omega=10$ and $\epsilon=2$ . The $x^{\prime}$ $\in\mathbb{R}^{204\times 1}$ is the predicted landmarks. The $x$ $\in\mathbb{R}^{204\times 1}$ is reshaped from ground truth landmarks $\in\mathbb{R}^{68\times 3}$ .

3.4 Fine Model

With the location, orientation, and coarse landmarks of the face given by the coarse model, a bounding box aligned with the head can be determined. Usually, the eyes and mouth have more expressive details. The bounding box of the eyes and mouth can also be determined, according to the coarse landmarks. Due to the low sampling resolution used in the coarse model and inaccuracy of coarse model predictions, bounding boxes are made slightly larger to include all necessary facial features and their proximate regions. The same sampling method and position encoding as the coarse model is performed on these bounding boxes. Similar to the coarse model, VoxResNet and the 3D convolution version of VGG are used as the backbone to encode these four feature volumes into four 1D long vectors. These 1D long vectors containing expressive information on eyes, mouth, and the whole face are concatenated to predict the bilinear model parameters and a transform matrix, which are used to compute fine 3D landmarks. The loss function is the same as that in the coarse model.

3.5 Evaluation and Comparison

For more examples, training and testing details, please refer to the supplementary material.

Accuracy. Fig. 3 shows qualitative results of our 3D landmark detection from NeRFs over a wide range of expressions. For quantitative evaluation and comparison with state-of-the-art methods, we randomly choose 5 identities as our test dataset. For the scale of prediction, we divide ground truth coordinates of 3D landmarks in Facescape [95] by 100, and transform all predicted landmarks to the same coordinate system and scale of the divided ground truth. Tab. 1 shows quantitative comparison of our FLNeRF with state-of-the-art 3D face landmarks prediction methods [98, 79, 8, 19] on all expressions (20 unaugmented expressions) and the exaggerated expression (unaugmented mouth stretching expression). The last row of Tab. 2 shows performance of FLNeRF on all 110 expressions. Fig. 4 shows qualitative comparison. For each method, we show prediction results on a single image captured from 3 different view directions, i.e., front view, 45°lateral view, and 90°lateral view. Fig. 4 shows prediction results on front view, while results on lateral views could be found on our supplementary material. FLNeRF outperforms SOTA methods significantly. Since current methods perform prediction on a single image without adequate 3D information, their depth estimation is highly inaccurate. Performance of current methods also deteriorates under lateral view directions, where [98, 8] cannot work on 90°lateral-view image.

Why 3D NeRF landmarks? To show that our 3D input data, i.e., NeRF, trained on multi-view 2D images, can benefit 3D face landmarks prediction, where our FLNeRF exploits NeRF well, we use a state-of-the-art 2D landmark localization method [27] to predict 2D landmarks on 10 images captured from different view directions of the same identity. Then we perform triangulation of estimated 2D landmarks to calculate 3D coordinates of landmarks. As Tab. 1 and Fig. 4 shows, even given multiple images, 2D localization followed by triangulation is still inaccurate. This shows that predicting 3D landmarks directly from NeRF, a continuous, compact, and relatively easy-to-obtain 3D representation, is more preferred.

Work for in-the-wild Single Images? To show FLNeRF is robust under various scenes and generalizable to in-the-wild faces, we perform 3D face landmarks localization on face NeRFs reconstructed from a single in-the-wild face image using EG3D Inversion [9], which incorporates face localization and background removal, thus allowing FLNeRF to predict 3D landmarks on NeRFs containing only a face (and sparse noise). Fig. 5 shows that despite suboptimal reconstruction quality, FLNeRF can still accurately localize most feature points on the reconstructed face NeRF.

4 Augmentation and Ablation

4.1 Data Augmentation For Coarse Model

FaceScape consists of forward-looking faces situated at the origin. Taking into account NeRF implementations with different scales or coordinate systems, to boost generality and support 3D landmarks prediction on a wide variety of input NeRF containing a head, we augment the data set with various face locations, orientations and scales. We perform data augmentation during sampling these NeRFs into feature volumes $\mathbb{R}^{4\times N\times N\times N}$ and assume the meaningful region of NeRF is within $[-1,1]^{3}$ , which can be easily normalized as such otherwise. Each sampled point $S\in[-1,1]^{3}$ will be transformed by a matrix $\tau[\mathbf{R}t]$ to a new position, where $\mathbf{R}\in SO(3)$ , $\tau\in[2,3]$ and $t\in\mathbb{[}-1,1]^{3}$ . New augmented feature volumes are generated by sampling NeRF at new sampling positions. This operation is equivalent to scale, translate and rotate the head in the feature volumes. Although the sampled points may lie outside the captured NeRF, their densities are usually less than the threshold. Even some exceed the threshold, they are random noise points in feature volumes that can be discarded by FLNeRF easily.

4.2 Expression Augmentation For Fine Model

Fig. 6 illustrates our data augmentation to include more expressive facial features for training. First, we rig 20 expressions to 52 blendshapes based on FACS [4]. Then, we linearly interpolate these 52 blendshapes to 110 expressions. A total of 110 expression volumes from FaceScape [95] are sampled non-uniformly from the given 20 expression NeRFs using 3D thin plate spline (3D TPS) [7]. Note that the variation of 20 discrete expressions in the FaceScape [95] is insufficient for training a 3D landmarks detector on NeRF to cover a wide range of facial expressions. Given the original $N$ 3D landmarks $\mathbf{L}\in\mathbb{R}^{N\times 3}$ and the target $N$ 3D landmarks $\mathbf{L}^{\prime}\in\mathbb{R}^{N\times 3}$ , we can construct $f(\mathbf{x})$ to warp $\mathbf{x}\in\mathbb{R}^{3}$ to $\mathbf{x}^{\prime}\in\mathbb{R}^{3}$ . Let $[\mathbf{l}_{1},\mathbf{l}_{2},\cdot\cdot\cdot,\mathbf{l}_{N-1},\mathbf{l}_{N}]^{\intercal}=\mathbf{L}$ and $[\mathbf{l}^{\prime}_{1},\mathbf{l}^{\prime}_{2},\cdot\cdot\cdot,\mathbf{l}^{\prime}_{N-1},\mathbf{l}^{\prime}_{N}]^{\intercal}=\mathbf{L}^{\prime}$ : $\mathbf{x}^{\prime}=f(\mathbf{x})=\mathbf{A}_{0}+\mathbf{A}_{1}\mathbf{x}+\displaystyle\sum\limits_{i=1}^{N}\mathbf{\omega_{i}}U(\lVert\ \mathbf{l}_{i}-\mathbf{x}\rVert),$ where $\mathbf{A}_{0}=\begin{bmatrix}a_{x}\\ a_{y}\\ a_{z}\end{bmatrix},\mathbf{A}_{1}=\begin{bmatrix}a_{xx}&a_{xy}&a_{xz}\\ a_{yx}&a_{yy}&a_{yz}\\ a_{zx}&a_{zy}&a_{zz}\end{bmatrix},\mathbf{\omega}_{i}=\begin{bmatrix}\omega_{ix}\\ \omega_{iy}\\ \omega_{iz}\end{bmatrix}$ . $\mathbf{A}_{0}+\mathbf{A}_{1}\vec{x}$ is the best linear transformation mapping $\mathbf{L}$ to $\mathbf{L^{\prime}}$ . $U(\lVert\mathbf{x}_{i}-\mathbf{x}\rVert)$ measures the distance from $\mathbf{x}$ to control points $\mathbf{L}$ . We use $U(r)=r^{2}\log(r)$ as the radial basis kernel and $\lVert\cdot\rVert$ denotes $L_{2}$ norm. These coefficients $\mathbf{A}_{0}$ , $\mathbf{A}_{1}$ and $\mathbf{\omega}_{i}$ can be found by solving a linear system (supplemental material). In summary, a warped feature volume can be sampled non-uniformly from a NeRF by 3D TPS warp specified by the original and target landmarks. For each person in the FaceScape data set, a total of 110 expressions are available for training.

4.3 Ablation Study

We conduct ablation on: (a) remove fine model, (b) remove expression augmentation, (c) use only two sampling scales, i.e., the first two rows in Fig. 2, (d) our full model.

Tab. 2 tabulates the ablation results, while Tab. 3 tabulates the ablation results replacing bilinear model with 3DMM to show the advantage of bilinear model, where both of them use VoxResNet as backbone. Although the average Wing loss of (b) is not significantly larger than (d) in Tab. 2, (b) produces large loss values (nearly 1.9) on mouth-stretching expressions. Ablation results using VGG as backbone can be found in our supplementary material.

Table 2: Since train/test data for coarse model only contains 20 basic expressions, we calculate the average Wing loss on these expressions for (a). For (b), (c) and (d), whole face losses are calculated on the test data set with 110 different expressions. Mouth and Eyes losses measure the corresponding landmarks’ accuracy based on Wing loss. The last column shows results on basic mouth stretching expression and 10 augmented exaggerated expressions by method described in Sec. 4.2. All values are multiplied by 10.

	Average Wing Loss of All Expressions			Exaggerated
	Whole Face	Mouth	Eyes	Expressions
(a)	2.50 $\pm$ 1.19	-	-	-
(b)	0.74 $\pm$ 0.23	0.88 $\pm$ 0.50	0.60 $\pm$ 0.12	0.76 $\pm$ 0.34
(c)	1.38 $\pm$ 0.34	1.61 $\pm$ 0.53	1.25 $\pm$ 0.31	1.35 $\pm$ 0.31
(d)	0.64 $\pm$ 0.21	0.74 $\pm$ 0.44	0.57 $\pm$ 0.13	0.54 $\pm$ 0.10

Table 3: Ablation study replacing bilinear model with 3DMM. All values are multiplied by 10.

	Average Wing Loss of All Expressions			Exaggerated
	Whole Face	Mouth	Eyes	Expressions
(a)	2.55 $\pm$ 0.94	-	-	-
(b)	1.19 $\pm$ 0.31	1.25 $\pm$ 0.65	1.09 $\pm$ 0.19	1.70 $\pm$ 0.51
(c)	0.94 $\pm$ 0.17	0.96 $\pm$ 0.17	0.88 $\pm$ 0.07	0.91 $\pm$ 0.07
(d)	0.92 $\pm$ 0.21	0.94 $\pm$ 0.46	0.83 $\pm$ 0.09	0.90 $\pm$ 0.16

5 Applications

There has been no representative work on 3D facial NeRF landmarks detection that enables NeRF landmark-based applications, such as face swapping and expression editing, while producing realistic 3D results on par with ours. In this section, we will show how the landmarks estimated by FLNeRF can directly benefit MoFaNeRF [99].

While MoFaNeRF generates SOTA results, we believe the range of expressive emotions is limited by its shape and expression code. 3D NeRF facial landmarks on the other hand provides explicit controls on facial expressions including fine and subtle details from exaggerated facial emotions. To directly benefit MoFaNeRF, we simply replace their shape and expression code with our 3D face landmarks location, which allows us to directly control NeRF’s facial features and thus produce impressive results on morphable faces, face swapping and face editing, alleviating the two limitations of MoFaNeRF (supplemental material).

5.1 Face Swapping

We can swap the expressions of two identities by swapping their 3D landmarks. Two identities ${\cal I}_{1}$ and ${\cal I}_{2}$ may have different ways to perform the same expression. Feeding ${\cal I}_{2}$ ’s landmarks on a given facial expression with ${\cal I}_{1}$ ’s texture map to our modified MoFaNeRF enables ${\cal I}_{1}$ to perform the corresponding expression in ${\cal I}_{2}$ ’s way, the essence of face swapping. We show our modified MoFaNeRF can perform face swapping in Fig. 7, where the man takes on the woman’s landmarks to produce the corresponding expression faithful to the woman’s, and vice versa.

By connecting the modified MoFaNeRF at the end of our FLNeRF, so as to perform downstream face swapping task after obtaining accurate prediction of 3D face landmarks, Fig. 1 shows that given two face NeRFs and their respective face landmarks, we can swap their expressions by simply swapping their face landmarks on NeRF. In detail, given the landmarks and textures of ${\cal I}_{1}$ and ${\cal I}_{2}$ , we obtain their respective face NeRFs by our modified MoFaNeRF, where we apply FLNeRF to predict landmarks on these input two face NeRFs. The predicted landmarks of ${\cal I}_{1}$ are fed to the modified MoFaNeRF with ${\cal I}_{2}$ ’s texture map, while predicted landmarks of ${\cal I}_{2}$ are fed to the modified MoFaNeRF with ${\cal I}_{1}$ ’s texture map. In doing so, our modified MoFaNeRF can synthesize swapped face images from any view direction.

5.2 Face Editing

We can produce an identity’s face with any expression given the corresponding landmarks and texture. Fig. 8 shows that our model can morph face by directly manipulating landmarks, where images on each row are rendered from NeRFs synthesized by linearly interpolating between the two corresponding NeRFs with landmarks of the leftmost expression and landmarks of the rightmost expression. Fig. 8 clearly demonstrates that our model can produce complex expressions even not included in our dataset. For example, middle images in the fifth row demonstrate our model’s ability to represent a face with simultaneous chin raising and eye closing. Fig. 8 also shows that we can independently control eyes, eyebrows, mouth, and even some subtle facial muscles, with better disentanglement ability over MoFaNeRF [99] using shape and expression code.

We connect our modified MoFaNeRF at the end of FLNeRF, so as to perform downstream face editing after obtaining accurate prediction of 3D face landmarks. Fig. 9 shows that we can transfer one person’s expression to another. In detail, we first obtain a face NeRF with the desired expression by feeding the corresponding landmarks into the modified MoFaNeRF. Then we apply our FLNeRF on the generated face NeRF to obtain accurate landmarks prediction. Finally, we use the predicted landmarks as input to the modified MoFaNeRF, together with texture map of another person, so that we obtain face NeRF of another person with our desired expression. Refer to the supplemental video where face images are rendered from many viewpoints.

5.3 Ablation Study

We perform ablation on: (a) original MoFaNeRF, (b) using three codes: texture, shape and landmarks; (c) our modified model which uses two codes: texture and landmarks. We render 300 images of the first 15 identities in our dataset [95] for evaluation, where one image is synthesized for every expression and every identity with random view direction. Following [99], we use PSNR, SSIM and LPIPS criteria to assess objective, structural, and perceptual similarity, respectively. Tab. 4 tabulates the quantitative statistics on the corresponding coarse models.

Table 4: Quantitative evaluation of on our application model. (a) is original MoFaNeRF, (b) is our 3-code (texture, shape, landmark) MoFaNeRF model, (c) is our 2-code (texture, landmark) MoFaNeRF model. With our landmarks which effectively encode 3D shape, the original shape code in MoFaNeRf can be eliminated while outperforming (a) and (b). Values of SSIM and LPIPS are multiplied by 10.

	PSNR(dB) $\uparrow$	SSIM $\uparrow$	LPIPS $\downarrow$	$\#$ params
(a)	24.85 $\pm$ 1.91	8.53 $\pm$ 0.35	1.72 $\pm$ 0.32	29,100,936
(b)	21.71 $\pm$ 1.46	7.28 $\pm$ 0.50	3.50 $\pm$ 0.42	29,584,776
(c)	25.47 $\pm$ 1.68	8.60 $\pm$ 0.32	1.66 $\pm$ 0.28	29,456,776

From the testing statistics, our model outperforms (a) and (b). Interestingly, comparing (b) and (c), adding shape code as input substantially decreases performance, indicating the shape code does have redundant information with 3D landmarks. For a given identity with different expressions, the shape code remains the same while landmarks vary which confuses the network in (b). Comparing (a) with (c), 3D landmarks location alone outperform combination of shape and learnable expression code.

6 Concluding Remarks

We propose the first 3D coarse-to-fine face landmarks detector (FLNeRF) with multi-scale sampling that directly predicts accurate 3D landmarks on NeRF. Our FLNeRF is trained on augmented dataset with 110 discrete expressions generated by local and non-linear NeRF warp, which enables FLNeRF to give accurate landmarks prediction on a large number of complex expressions. We perform extensive quantitative and qualitative comparison, and demonstrate 3D landmark-based face swapping and editing applications. We hope FLNeRF will enable future works on more accurate and general 3D face landmarks detection on NeRF.

References

[1] Locating facial features with an extended active shape model. In David A. Forsyth, Philip H. S. Torr, and Andrew Zisserman, editors, European Conference on Computer Vision (ECCV), 2008.
[2] 2nd 3d face alignment in the wild challenge, 2019.
[3] Augmented faces introduction, 2022.
[4] Mohammed Alkawaz, Ahmad Hoirul Basori, Dzulkifli Mohamad, and Tanzila Saba. Blend shape interpolation and facs for realistic avatar. 3D Research, 6:1–10, 01 2015.
[5] ShahRukh Athar, Zexiang Xu, Kalyan Sunkavalli, Eli Shechtman, and Zhixin Shu. Rignerf: Fully controllable neural 3d portraits. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[6] Volker Blanz and Thomas Vetter. A morphable model for the synthesis of 3d faces. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH, pages 187–194, 1999.
[7] F.L. Bookstein. Principal warps: thin-plate splines and the decomposition of deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11(6):567–585, 1989.
[8] Adrian Bulat and Georgios Tzimiropoulos. How far are we from solving the 2d & 3d face alignment problem? (and a dataset of 230,000 3d facial landmarks). In International Conference on Computer Vision, 2017.
[9] Eric R. Chan, Connor Z. Lin, Matthew A. Chan, Koki Nagano, Boxiao Pan, Shalini De Mello, Orazio Gallo, Leonidas Guibas, Jonathan Tremblay, Sameh Khamis, Tero Karras, and Gordon Wetzstein. Efficient geometry-aware 3D generative adversarial networks. In CVPR, 2022.
[10] Hao Chen, Qi Dou, Lequan Yu, and Pheng-Ann Heng. Voxresnet: Deep voxelwise residual networks for volumetric brain segmentation. arXiv preprint arXiv:1608.05895, 2016.
[11] Hsiao-yu Chen, Edith Tretschk, Tuur Stuyck, Petr Kadlecek, Ladislav Kavan, Etienne Vouga, and Christoph Lassner. Virtual elastic objects. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 15827–15837, June 2022.
[12] Forrester Cole, Kyle Genova, Avneesh Sud, Daniel Vlasic, and Zhoutong Zhang. Differentiable surface rendering via non-differentiable sampling. In IEEE/CVF International Conference on Computer Vision (ICCV), 2021.
[13] Timothy F. Cootes, Gareth J. Edwards, and Christopher J. Taylor. Active appearance models. In Hans Burkhardt and Bernd Neumann, editors, European Conference on Computer Vision (ECCV), pages 484–498, 1998.
[14] Timothy F. Cootes and Christopher J. Taylor. Active shape models - ’smart snakes’. In David C. Hogg and Roger Boyle, editors, British Machine Vision Conference(BMVC), 1992.
[15] Timothy F. Cootes, Christopher J. Taylor, David H. Cooper, and Jim Graham. Active shape models-their training and application. Comput. Vis. Image Underst., 61(1):38–59, 1995.
[16] Yu Deng, Jiaolong Yang, Jianfeng Xiang, and Xin Tong. Gram: Generative radiance manifolds for 3d-aware image generation. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[17] Joey deVilla. Augmented reality in android with google’s face api, 2017.
[18] Yilun Du, Yinan Zhang, Hong-Xing Yu, Joshua B. Tenenbaum, and Jiajun Wu. Neural radiance flow for 4d view synthesis and video processing. In IEEE/CVF International Conference on Computer Vision (ICCV), 2021.
[19] Yao Feng, Haiwen Feng, Michael J. Black, and Timo Bolkart. Learning an animatable detailed 3D face model from in-the-wild images. volume 40, 2021.
[20] Zhen-Hua Feng, Josef Kittler, Muhammad Awais, Patrik Huber, and Xiao-Jun Wu. Wing loss for robust facial landmark localisation with convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), June 2018.
[21] Guy Gafni, Justus Thies, Michael Zollhöfer, and Matthias Nießner. Dynamic neural radiance fields for monocular 4d facial avatar reconstruction. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 8649–8658, June 2021.
[22] Chen Gao, Yichang Shih, Wei-Sheng Lai, Chia-Kai Liang, and Jia-Bin Huang. Portrait neural radiance fields from a single image. arXiv preprint arXiv:2012.05903, 2020.
[23] Stephan J. Garbin, Marek Kowalski, Matthew Johnson, Jamie Shotton, and Julien Valentin. Fastnerf: High-fidelity neural rendering at 200fps. In IEEE/CVF International Conference on Computer Vision (ICCV), 2021.
[24] Jianzhu Guo, Xiangyu Zhu, Yang Yang, Fan Yang, Zhen Lei, and Stan Z. Li. Towards fast, accurate and stable 3d dense face alignment. In Andrea Vedaldi, Horst Bischof, Thomas Brox, and Jan-Michael Frahm, editors, European Conference on Computer Vision (ECCV), pages 152–168, 2020.
[25] Michelle Guo, Alireza Fathi, Jiajun Wu, and Thomas Funkhouser. Object-centric neural scene rendering. arXiv preprint arXiv:2012.08503, 2020.
[26] Hanxiang Hao, Sriram Baireddy, Amy R. Reibman, and Edward J. Delp. Far-gan for one-shot face reenactment. CoRR, abs/2005.06402, 2020.
[27] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In CVPR, 2016.
[28] Peter Hedman, Pratul P. Srinivasan, Ben Mildenhall, Jonathan T. Barron, and Paul Debevec. Baking neural radiance fields for real-time view synthesis. In IEEE/CVF International Conference on Computer Vision (ICCV), 2021.
[29] Yang Hong, Bo Peng, Haiyao Xiao, Ligang Liu, and Juyong Zhang. Headnerf: A real-time nerf-based parametric head model. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[30] Tao Hu, Shu Liu, Yilun Chen, Tiancheng Shen, and Jiaya Jia. Efficientnerf: Efficient neural radiance fields. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[31] Yuheng Jiang, Suyi Jiang, Guoxing Sun, Zhuo Su, Kaiwen Guo, Minye Wu, Jingyi Yu, and Lan Xu. Neuralfusion: Neural volumetric rendering under human-object interactions. arXiv preprint arXiv:2202.12825, 2022.
[32] M. M. Johari, Y. Lepoittevin, and F. Fleuret. Geonerf: Generalizing nerf with geometry priors. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[33] Ivan Kosarevych, Marian Petruk, Markian Kostiv, Orest Kupyn, Mykola Maksymenko, and Volodymyr Budzan. Actgan: Flexible and efficient one-shot face reenactment. In 2020 8th International Workshop on Biometrics and Forensics (IWBF), pages 1–6, 2020.
[34] Abhinav Kumar, Tim K. Marks, Wenxuan Mou, Ye Wang, Michael J. Jones, Anoop Cherian, Toshiaki Koike-Akino, Xiaoming Liu, and Chen Feng. Luvli face alignment: Estimating landmarks’ location, uncertainty, and visibility likelihood. CoRR, abs/2004.02980, 2020.
[35] Abhijit Kundu, Kyle Genova, Xiaoqi Yin, Alireza Fathi, Caroline Pantofaru, Leonidas Guibas, Andrea Tagliasacchi, Frank Dellaert, and Thomas Funkhouser. Panoptic Neural Fields: A Semantic Object-Aware Neural Scene Representation. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[36] Weijian Li, Yuhang Lu, Kang Zheng, Haofu Liao, Chihung Lin, Jiebo Luo, Chi-Tung Cheng, Jing Xiao, Le Lu, Chang-Fu Kuo, and Shun Miao. Structured landmark detection via topology-adapting deep graph learning. In European Conference on Computer Vision (ECCV), pages 266–283, 2020.
[37] Zhengqi Li, Simon Niklaus, Noah Snavely, and Oliver Wang. Neural scene flow fields for space-time view synthesis of dynamic scenes. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020.
[38] David B. Lindell, Julien N.P. Martel, and Gordon Wetzstein. Autoint: Automatic integration for fast neural volume rendering. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2021.
[39] Lingjie Liu, Jiatao Gu, Kyaw Zaw Lin, Tat-Seng Chua, and Christian Theobalt. Neural sparse voxel fields. In Advances in Neural Information Processing Systems (NeurIPS), 2020.
[40] Rosanne Liu, Joel Lehman, Piero Molino, Felipe Petroski Such, Eric Frank, Alex Sergeev, and Jason Yosinski. An intriguing failing of convolutional neural networks and the coordconv solution. In Advances in Neural Information Processing Systems (NeurIPS), 2018.
[41] Steven Liu, Xiuming Zhang, Zhoutong Zhang, Richard Zhang, Jun-Yan Zhu, and Bryan Russell. Editing conditional radiance fields. In IEEE/CVF International Conference on Computer Vision (ICCV), 2021.
[42] Jiang-Jing Lv, Xiaohu Shao, Junliang Xing, Cheng Cheng, and Xi Zhou. A deep regression architecture with two-stage re-initialization for high performance facial landmark detection. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 3691–3700, 2017.
[43] Ben Mildenhall, Pratul P. Srinivasan, Matthew Tancik, Jonathan T. Barron, Ravi Ramamoorthi, and Ren Ng. Nerf: Representing scenes as neural radiance fields for view synthesis. In European Conference on Computer Vision (ECCV), 2020.
[44] Ben Mildenhall, Pratul P. Srinivasan, Matthew Tancik, Jonathan T. Barron, Ravi Ramamoorthi, and Ren Ng. Nerf: Representing scenes as neural radiance fields for view synthesis. In European Conference on Computer Vision (ECCV), 2020.
[45] Shokoufeh Mousavi, Mostafa Charmi, and Hossein Hassanpoor. A distinctive landmark-based face recognition system for identical twins by extracting novel weighted features. Computers & Electrical Engineering, 94:107326, 2021.
[46] Norman Müller, Andrea Simonelli, Lorenzo Porzi, Samuel Rota Bulò, Matthias Nießner, and Peter Kontschieder. Autorf: Learning 3d object radiance fields from single view observations. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[47] Alejandro Newell, Kaiyu Yang, and Jia Deng. Stacked hourglass networks for human pose estimation. CoRR, abs/1603.06937, 2016.
[48] Michael Niemeyer and Andreas Geiger. Giraffe: Representing scenes as compositional generative neural feature fields. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020.
[49] Atsuhiro Noguchi, Xiao Sun, Stephen Lin, and Tatsuya Harada. Neural articulated radiance field. In IEEE/CVF International Conference on Computer Vision (ICCV), 2021.
[50] Roy Or-El, Xuan Luo, Mengyi Shan, Eli Shechtman, Jeong Joon Park, and Ira Kemelmacher-Shlizerman. StyleSDF: High-Resolution 3D-Consistent Image and Geometry Generation. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 13503–13513, June 2022.
[51] Julian Ost, Fahim Mannan, Nils Thuerey, Julian Knodt, and Felix Heide. Neural scene graphs for dynamic scenes. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020.
[52] Keunhong Park, Utkarsh Sinha, Jonathan T. Barron, Sofien Bouaziz, Dan B Goldman, Steven M. Seitz, and Ricardo Martin-Brualla. Nerfies: Deformable neural radiance fields. IEEE/CVF International Conference on Computer Vision (ICCV), 2021.
[53] Sida Peng, Junting Dong, Qianqian Wang, Shangzhan Zhang, Qing Shuai, Xiaowei Zhou, and Hujun Bao. Animatable neural radiance fields for modeling dynamic human bodies. In IEEE/CVF International Conference on Computer Vision (ICCV), 2021.
[54] Rohith Krishnan Pillai, László A. Jeni, Huiyuan Yang, Zheng Zhang, Lijun Yin, and Jeffrey F. Cohn. The 2nd 3d face alignment in the wild challenge (3dfaw-video): Dense reconstruction from video. 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), pages 3082–3089, 2019.
[55] Albert Pumarola, Enric Corona, Gerard Pons-Moll, and Francesc Moreno-Noguer. D-nerf: Neural radiance fields for dynamic scenes. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020.
[56] Daniel Rebain, Wei Jiang, Soroosh Yazdani, Ke Li, Kwang Moo Yi, and Andrea Tagliasacchi. Derf: Decomposed radiance fields. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020.
[57] Daniel Rebain, Mark Matthews, Kwang Moo Yi, Dmitry Lagun, and Andrea Tagliasacchi. Lolnerf: Learn from one look, 2022.
[58] Christian Reiser, Songyou Peng, Yiyi Liao, and Andreas Geiger. Kilonerf: Speeding up neural radiance fields with thousands of tiny mlps. In IEEE/CVF International Conference on Computer Vision (ICCV), 2021.
[59] Sara Fridovich-Keil and Alex Yu, Matthew Tancik, Qinhong Chen, Benjamin Recht, and Angjoo Kanazawa. Plenoxels: Radiance fields without neural networks. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[60] Patrick Sauer, Timothy F. Cootes, and Christopher J. Taylor. Accurate regression procedures for active appearance models. In Jesse Hoey, Stephen J. McKenna, and Emanuele Trucco, editors, British Machine Vision Conference, BMVC 2011, Dundee, UK, August 29 - September 2, 2011. Proceedings, pages 1–11. BMVA Press, 2011.
[61] Ruizhi Shao, Hongwen Zhang, He Zhang, Mingjia Chen, Yanpei Cao, Tao Yu, and Yebin Liu. Doublefield: Bridging the neural surface and radiance fields for high-fidelity human reconstruction and rendering. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[62] Ziaaddin Sharifisoraki, Marzieh Amini, and Sreeraman Rajan. A novel face recognition using specific values from deep neural network-based landmarks. In 2023 IEEE International Conference on Consumer Electronics (ICCE), pages 1–6, 2023.
[63] Sahil Sharma and Vijay Kumar. 3d landmark-based face restoration for recognition using variational autoencoder and triplet loss. IET Biom., 10(1):87–98, 2021.
[64] Zifan Shi, Yinghao Xu, Yujun Shen, Deli Zhao, Qifeng Chen, and Dit-Yan Yeung. Improving 3d-aware image synthesis with a geometry-aware discriminator. In NeurIPS, 2022.
[65] Karen Simonyan and Andrew Zisserman. Very deep convolutional networks for large-scale image recognition. In Yoshua Bengio and Yann LeCun, editors, 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings, 2015.
[66] Jinzhan Su, Zhe Wang, Chunyuan Liao, and Haibin Ling. Efficient and accurate face alignment by global regression and cascaded local refinement. In IEEE Conference on Computer Vision and Pattern Recognition Workshops, CVPR Workshops 2019, Long Beach, CA, USA, June 16-20, 2019, pages 267–276. Computer Vision Foundation / IEEE, 2019.
[67] Mohammed Suhail, Carlos Esteves, Leonid Sigal, and Ameesh Makadia. Light field neural rendering. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[68] Cheng Sun, Min Sun, and Hwann-Tzong Chen. Direct voxel grid optimization: Super-fast convergence for radiance fields reconstruction. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[69] Jingxiang Sun, Xuan Wang, Yong Zhang, Xiaoyu Li, Qi Zhang, Yebin Liu, and Jue Wang. Fenerf: Face editing in neural radiance fields. arXiv preprint arXiv:2111.15490, 2021.
[70] Ke Sun, Bin Xiao, Dong Liu, and Jingdong Wang. Deep high-resolution representation learning for human pose estimation. CoRR, abs/1902.09212, 2019.
[71] Yi Sun, Xiaogang Wang, and Xiaoou Tang. Deep convolutional network cascade for facial point detection. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 3476–3483. IEEE Computer Society, 2013.
[72] Matthew Tancik, Ben Mildenhall, Terrance Wang, Divi Schmidt, Pratul P. Srinivasan, Jonathan T. Barron, and Ren Ng. Learned initializations for optimizing coordinate-based neural representations. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020.
[73] George Trigeorgis, Patrick Snape, Mihalis A. Nicolaou, Epameinondas Antonakos, and Stefanos Zafeiriou. Mnemonic descent method: A recurrent process applied for end-to-end face alignment. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 4177–4187, 2016.
[74] George Trigeorgis, Patrick Snape, Mihalis A. Nicolaou, Epameinondas Antonakos, and Stefanos Zafeiriou. Mnemonic descent method: A recurrent process applied for end-to-end face alignment. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 4177–4187. IEEE Computer Society, 2016.
[75] Roberto Valle, José Miguel Buenaposada, Antonio Valdés, and Luis Baumela. A deeply-initialized coarse-to-fine ensemble of regression trees for face alignment. In European Conference on Computer Vision (ECCV), 2018.
[76] Daniel Vlasic, Matthew Brand, Hanspeter Pfister, and Jovan Popovic. Face transfer with multilinear models. In John W. Finnegan and Dave Shreiner, editors, International Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 2006, Boston, Massachusetts, USA, July 30 - August 3, 2006, Courses, page 24. ACM, 2006.
[77] Liao Wang, Jiakai Zhang, Xinhang Liu, Fuqiang Zhao, Yanshun Zhang, Yingliang Zhang, Minye Wu, Jingyi Yu, and Lan Xu. Fourier plenoctrees for dynamic radiance field rendering in real-time. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 13524–13534, June 2022.
[78] Chung-Yi Weng, Brian Curless, Pratul P. Srinivasan, Jonathan T. Barron, and Ira Kemelmacher-Shlizerman. HumanNeRF: Free-viewpoint rendering of moving people from monocular video. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 16210–16220, June 2022.
[79] Cho-Ying Wu, Qiangeng Xu, and Ulrich Neumann. Synergy between 3dmm and 3d landmarks for accurate 3d facial geometry. In 3DV, 2021.
[80] Wayne Wu, Chen Qian, Shuo Yang, Quan Wang, Yici Cai, and Qiang Zhou. Look at boundary: A boundary-aware face alignment algorithm. CoRR, abs/1805.10483, 2018.
[81] Jiahao Xia, Weiwei Qu, Wenjian Huang, Jianguo Zhang, Xi Wang, and Min Xu. Sparse local patch transformer for robust face alignment and landmarks inherent relation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 4052–4061, June 2022.
[82] Wenqi Xian, Jia-Bin Huang, Johannes Kopf, and Changil Kim. Space-time neural irradiance fields for free-viewpoint video. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020.
[83] Qiangeng Xu, Zexiang Xu, Julien Philip, Sai Bi, Zhixin Shu, Kalyan Sunkavalli, and Ulrich Neumann. Point-nerf: Point-based neural radiance fields. arXiv preprint arXiv:2201.08845, 2022.
[84] Tianhan Xu, Yasuhiro Fujita, and Eiichi Matsumoto. Surface-aligned neural radiance fields for controllable 3d human synthesis. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[85] Bangbang Yang, Yinda Zhang, Yinghao Xu, Yijin Li, Han Zhou, Hujun Bao, Guofeng Zhang, and Zhaopeng Cui. Learning object-compositional neural radiance field for editable scene rendering. In IEEE/CVF International Conference on Computer Vision (ICCV), October 2021.
[86] Gengshan Yang, Minh Vo, Neverova Natalia, Deva Ramanan, Vedaldi Andrea, and Joo Hanbyul. Banmo: Building animatable 3d neural models from many casual videos. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022.
[87] Hongwei Yi, Chen Li, Qiong Cao, Xiaoyong Shen, Sheng Li, Guoping Wang, and Yu-Wing Tai. Mmface: A multi-metric regression network for unconstrained face reconstruction. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, June 16-20, 2019, pages 7663–7672. Computer Vision Foundation / IEEE, 2019.
[88] Alex Yu, Ruilong Li, Matthew Tancik, Hao Li, Ren Ng, and Angjoo Kanazawa. PlenOctrees for real-time rendering of neural radiance fields. In IEEE/CVF International Conference on Computer Vision (ICCV), 2021.
[89] Wentao Yuan, Zhaoyang Lv, Tanner Schmidt, and Steven Lovegrove. Star: Self-supervised tracking and reconstruction of rigid objects in motion with neural rendering. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 13144–13152, 2021.
[90] HiuKim Yuen. Augmented reality in android with google’s face api, 2022.
[91] Egor Zakharov, Aliaksandra Shysheya, Egor Burkov, and Victor Lempitsky. Few-shot adversarial learning of realistic neural talking head models. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), October 2019.
[92] Kai Zhang, Gernot Riegler, Noah Snavely, and Vladlen Koltun. Nerf++: Analyzing and improving neural radiance fields. arXiv:2010.07492, 2020.
[93] Fuqiang Zhao, Wei Yang, Jiakai Zhang, Pei Lin, Yingliang Zhang, Jingyi Yu, and Lan Xu. Humannerf: Efficiently generated human radiance field from sparse inputs. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 7743–7753, June 2022.
[94] Zerong Zheng, Han Huang, Tao Yu, Hongwen Zhang, Yandong Guo, and Yebin Liu. Structured local radiance fields for human avatar modeling. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), June 2022.
[95] Hao Zhu, Haotian Yang, Longwei Guo, Yidi Zhang, Yanru Wang, Mingkai Huang, Qiu Shen, Ruigang Yang, and Xun Cao. Facescape: 3d facial dataset and benchmark for single-view 3d face reconstruction. arXiv preprint arXiv:2111.01082, 2021.
[96] Meilu Zhu, Daming Shi, Mingjie Zheng, and Muhammad Sadiq. Robust facial landmark detection via occlusion-adaptive deep networks. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 3481–3491, 2019.
[97] Shizhan Zhu, Cheng Li, Chen Change Loy, and Xiaoou Tang. Face alignment by coarse-to-fine shape searching. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 4998–5006. IEEE Computer Society, 2015.
[98] Xiangyu Zhu, Xiaoming Liu, Zhen Lei, and Stan Z. Li. Face alignment in full pose range: A 3d total solution. IEEE Transactions on Pattern Analysis and Machine Intelligence, 41(1):78–92, jan 2019.
[99] Yiyu Zhuang, Hao Zhu, Xusen Sun, and Xun Cao. Mofanerf: Morphable facial neural radiance field. In European Conference on Computer Vision (ECCV), 2022.

Please watch the supplementary video for dynamic 3D face visualization.

Appendix A TPS

The coefficients $\mathbf{A}_{0}$ , $\mathbf{A}_{1}$ and $\mathbf{\omega}_{i}$ mentioned in Section 4.2 can be found by solving the following linear system. Let $\mathbf{W}=[\mathbf{\omega}_{1},\cdot\cdot\cdot,\mathbf{\omega}_{N}]$ and $\mathbf{Y}=[{\mathbf{L}^{\prime}}^{\intercal}\hskip 5.69054pt\mathbf{0}\hskip 5.69054pt\mathbf{0}\hskip 5.69054pt\mathbf{0}\hskip 5.69054pt\mathbf{0}]^{\intercal}$ :

\mathbf{K}=\begin{bmatrix}0&U(\lVert\mathbf{l}_{1}\!-\!\mathbf{l}_{2}\rVert)&\cdot\cdot\cdot&U(\lVert\mathbf{l}_{1}\!-\!\mathbf{l}_{N}\rVert)\\ U(\lVert\mathbf{l}_{2}\!-\!\mathbf{l_{1}}\rVert)&0&\cdot\cdot\cdot&U(\lVert\mathbf{l}_{2}\!-\!\mathbf{l}_{N}\rVert)\\ \cdot\cdot\cdot&\cdot\cdot\cdot&\cdot\cdot\cdot&\cdot\cdot\cdot\\ U(\lVert\mathbf{l}_{N}\!-\!\mathbf{l}_{1}\rVert)&U(\lVert\mathbf{l}_{N}\!-\!\mathbf{l}_{2}\rVert)&\cdot\cdot\cdot&0\end{bmatrix}_{N\times N}

(5)

\mathbf{P}=\begin{bmatrix}\mathbf{1}&\mathbf{l}_{1}^{\intercal}\\ \mathbf{1}&\mathbf{l}_{2}^{\intercal}\\ \cdot\cdot\cdot&\cdot\cdot\cdot\\ \mathbf{1}&\mathbf{l}_{n}^{\intercal}\end{bmatrix}_{N\times 4}

(6)

\mathbf{M}=\begin{bmatrix}\mathbf{K}&\mathbf{P}\\ \mathbf{P}^{\intercal}&\mathbf{0}\end{bmatrix}_{(N+4)\times(N+4)}

(7)

(\mathbf{W}\rvert\mathbf{A}_{1}\hskip 5.69054pt\mathbf{A}_{0})^{\intercal}=\mathbf{M}^{-1}\mathbf{Y}

(8)

Appendix B Training Details

We train the coarse and fine models one after the other. First, the coarse model is trained on the augmented data set as described in Section 4.1. Then, the well-trained coarse model predicts the transform matrix and coarse landmarks which locate the 4 sampling positions for the fine model. Together with the expression augmentation Section 4.2, the training data set for fine model is generated.

To balance training speed and sampling fidelity, the resolution of NeRF sampling box in the coarse and fine models are respectively $64\times 64\times 64$ . We select 100 identities from FaceScape dataset to perform data augmentation for coarse and fine models. Furthermore, 5 extra identities are randomly chosen for testing with data augmentation.

When training the coarse and fine model, we set learning rate to 0.001 and batch size 32. The learning rate will finally decay to 8e-6. We train our coarse model for 100 epochs and fine model for 50 epochs. We train our FLNeRF on 4x GTX 1080 GPUs. Training coarse model takes around 8 hours and fine model takes around 12 hours.

Appendix C More Ablation Studies of FLNeRF

Tab. 5 and Tab. 6 tabulate ablation study results of our FLNeRF using VGG as backbone, while Table 2 and Table 3 in Section 4.3 in our main paper show statistics with VoxResNet as the backbone. We still conduct ablation on: (a) remove fine model, (b) remove expression augmentation, (c) use only two sampling scales, i.e., the first two rows in Figure 2 in the main paper, (d) our full model.

We follow the same test strategy as Section 4.3 to conduct this experiment. Similar to the results obtained by VoxResNet backbone, FLNeRF achieves the best among all ablation studies using VGG backbone.

Table 5: Since train/test data for coarse model only contains 20 basic expressions, we calculate the average Wing loss on these expressions for (a). For (b), (c) and (d), whole face losses are calculated on the test data set with 110 different expressions. Mouth and Eyes losses measure the corresponding landmarks’ accuracy based on Wing loss. The last column shows results on basic mouth stretching expression and 10 augmented exaggerated expressions. All values are multiplied by 10.

	Average Wing Loss of All Expressions			Exaggerated
	Whole Face	Mouth	Eyes	Expressions
(a)	3.65 $\pm$ 1.26	-	-	-
(b)	0.78 $\pm$ 0.26	0.88 $\pm$ 0.54	0.63 $\pm$ 0.12	0.87 $\pm$ 0.43
(c)	0.69 $\pm$ 0.24	0.86 $\pm$ 0.46	0.55 $\pm$ 0.12	0.60 $\pm$ 0.15
(d)	0.63 $\pm$ 0.20	0.77 $\pm$ 0.43	0.55 $\pm$ 0.13	0.53 $\pm$ 0.12

Table 6: Ablation study replacing bilinear model with 3DMM. All values are multiplied by 10.

	Average Wing Loss of All Expressions			Exaggerated
	Whole Face	Mouth	Eyes	Expressions
(a)	2.49 $\pm$ 0.91	-	-	-
(b)	0.94 $\pm$ 0.22	0.97 $\pm$ 0.52	0.86 $\pm$ 0.090	1.27 $\pm$ 0.44
(c)	0.90 $\pm$ 0.069	0.88 $\pm$ 0.37	0.88 $\pm$ 0.048	0.86 $\pm$ 0.048
(d)	0.86 $\pm$ 0.084	0.87 $\pm$ 0.39	0.85 $\pm$ 0.062	0.84 $\pm$ 0.076

Appendix D Application Model Architecture

Our modified MoFaNeRF model architecture is shown in Fig. 10, where we remove shape code, expression code, and ISM in the original MoFaNeRF model. This is because by [99]’s design, expression code is learnable, while shape code remains the same among all expressions of the same identity. However, face shape including location of mouth and eyebrows may also change during expression changes (e.g., brow raises, brow lowers, mouth twists to left or right, mouth stretches, jaw moves to left or right, etc). The combination of a static shape code with a learnable expression code may thus conflict with each other.

Instead, we directly concatenate 3D face landmarks to the encoded space position. The concatenated vector is fed into the density decoder. By doing so, our model takes in 3D space location, view direction, texture code, and 3D face landmarks as inputs to generate a face NeRF. Given texture map, we can render a face image with any given expression from any view points by manipulating the face landmarks. We believe that the original MoFaNeRF [99] attempts to extract deep information from each expression that is independent from the shape code, where such information mainly comes from 3D landmarks. That is why our application model outperforms MoFaNeRF a bit in terms of objective, structural, and perceptual similarity as validated in Table 4 in our main paper. Figure 6 in our main paper presents the qualitative results, showing that we can independently control movements of mouth, nose, eyes, and eyebrows by directly manipulating landmarks owing to our better disentanglement than [99] in their shape and expression codes.

Since our FLNeRF, which is trained on expanded data set with 110 expressions adopting the same training configurations as [99], can produce accurate 3D face landmark locations, and that our modified MoFaNeRF operates on landmarks directly, we can perform downstream tasks employing our face landmarks prediction on NeRF, i.e., face editing and face swapping.

Appendix E More Visualization Results

E.1 Qualitative Comparison

We have shown qualitative comparison of our FLNeRF with state-of-the-art 3D face landmarks detection methods by Figure 4 in our main paper, where the input image to single-image 3D landmarks prediction methods [8, 98, 19, 79] is from frontal view. Here Fig. 11 shows qualitative comparison where the input image to [8, 98, 19, 79] is from 45°lateral view. And Fig. 11 shows qualitative comparison where the input image to [19, 79] is from 90°lateral view, where [8, 98] malfunction. We can see clearly from Table 1 and Figure 4 in our main paper, together with Fig. 11 and Fig. 12, that state-of-the-art methods perform highly inaccurate depth estimation of 3D landmarks and are not robust against large variations of view directions, while our FLNeRF could learn accurate depth and structural information from face NeRFs.

E.2 3D landmarks Detection On NeRF

As extension of Figure 3 in our main paper, Fig. 13 shows more visualization results of accurate 3D landmarks prediction of our FLNeRF on face NeRFs. Observing the two figures, we can see how robust our FLNeRF is, that it predicts accurate 3D face landmarks for both males and females, people with various skin colors, faces under different illuminations, and even faces with glasses and beard.

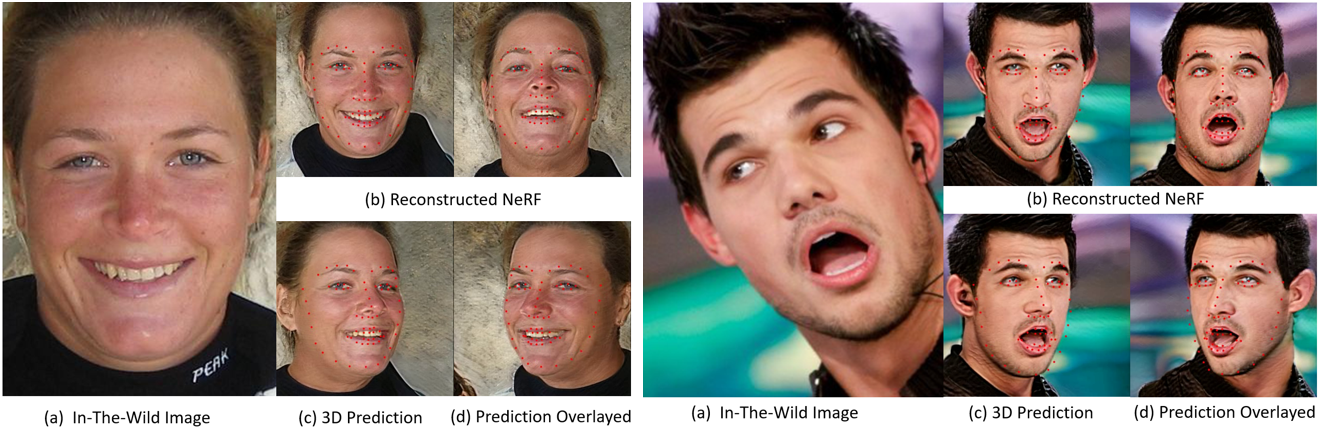
E.3 Generalization On In-The-Wild Single Images

As stated in Section 3.5 in our main paper, our FLNeRF could be generalized to localize 3D face landmarks on face NeRFs reconstructed from a single in-the-wild face image leveraging EG3D Inversion [9]. Fig. 14 shows more qualitative results as supplement to Figure 5 in our main paper. Since in-the-wild images vary from view directions, illumination, races, genders, make-up, and many complex and subtle factors, the accurate generalization results illustrate the power of our FLNeRF.

E.4 Video

By capitalizing our accurate 3D face landmarks, our modified MoFaNeRF could perform various downstream tasks, like face swapping and face editing introduced in section 4 in our main paper. Here we produce a video for more direct visualization. The video contains five parts:

1.

Accurate 3D face landmarks detection on NeRF. Each row shows the visualization of the accurate 3D facial landmarks detection on the same identity from 3 different camera poses. The landmarks overlapped on the face NeRF are the estimated facial landmarks.
2.

Generalization on in-the-wild single images. This part gives an intuitive illustration of how our FLNeRF could be generalized to detect accurate 3D landmarks on face NeRFs reconstructed from a single in-the-wild image as described in Section 3.5 in our main paper. In the video, we first show four in-the-wild images. Then we show reconstructed face NeRFs using EG3D inversion [9]. Finally, we show overlayed 3D face landmarks predicted by our FLNeRF.
3.

Face editing by directly manipulating 3D face landmarks. The two columns show the results obtained by manipulating 3D face landmarks on two different identities using our modified MoFaNeRF. The results are coherent in expression transitions and consistent in different view directions. The landmarks overlapped on the face NeRF are the target landmarks.
4.

3D face reenactment on NeRF. For 3D face reenactment, we use FLNeRF to predict 3D face landmarks, given any face NeRF. The left face in the video is driver face NeRF with estimated landmarks overlaid. The predicted landmarks are fed together with the same person’s texture map to our modified MoFaNeRF, which then produce the right face in the video.
5.

3D expression transfer on NeRF. For 3D expression transfer, we use FLNeRF to predict 3D face landmarks on ${\cal I}_{1}$ ’s face NeRF. The left face in the video is driver face NeRF ( ${\cal I}_{1}$ ’s face NeRF) with estimated landmarks overlaid. The predicted landmarks are fed together with ${\cal I}_{2}$ ’s’s texture map to our modified MoFaNeRF, which then produce the right face in the video ( ${\cal I}_{2}$ ’s face NeRF).

This video demonstrates that our FLNeRF could produce accurate 3D face landmarks on NeRF. By leveraging EG3D Inversion [9], our FLNeRF could be well generalized to localize accurate 3D face landmarks on face NeRFs reconstructed from in-the-wild single images. Furthermore, with the help of our modified MoFaNeRF, FLNeRF could directly operate on dynamic NeRF, so an animator can easily edit, control, and even transfer emotion from another face NeRF.

Appendix F Ethics Discussion

Images we use for training, testing and visualization in this paper are from FaceScape [95], an open-source dataset for research purpose. Our technology has the potential to cheat face recognition system. Therefore, it should not be abused for illegal purposes.