Flexible Two-point Selection Approach for Characteristic Function-based Parameter Estimation of Stable Laws

Stable distribution, also known as $\alpha$-stable distribution, or Lévy’s stable distribution, was first introduced by Paul Lévy (1937) PaulLevy1937 , which is a family of parametric distribution with tails that are expressed as power-functions. In the far tails the PDF can be written as SamoTaqqu1994a ,

$\displaystyle f(x;\alpha,\beta,\gamma,\delta)\simeq\begin{cases}c_{\alpha}\gamma^{\alpha}\alpha\,(1+\beta)\,|x|^{-(1+\alpha)}\;\;\mbox{for}\;\;(x\rightarrow+\infty)\\ c_{\alpha}\gamma^{\alpha}\alpha\,(1-\beta)\,|x|^{-(1+\alpha)}\;\;\mbox{for}\;\;(x\rightarrow-\infty),\end{cases}$

and the cumulative distribution function (CDF) written as,

$\displaystyle\begin{cases}P(X>x)\simeq c_{\alpha}\gamma^{\alpha}(1+\beta)\,|x|^{-\alpha}\;\;\mbox{for}\;\;(x\rightarrow+\infty)\\ P(X<x)\simeq c_{\alpha}\gamma^{\alpha}(1-\beta)\,|x|^{-\alpha}\;\;\mbox{for}\;\;(x\rightarrow-\infty),\end{cases}$

where $c_{\alpha}$ is a constant value $[\sin(\pi\alpha/2)\Gamma(\alpha)]/\pi$. Stable distribution is represented by four parameters; the tail index parameter $\alpha\in(0,2]$ representing the fatness of the tail, the skewness parameter $\beta\in[-1,1]$, the scaling parameter $\gamma>0$, and the location parameter $\delta\in\mathbb{R}$. Especially the parameters $\alpha$ and $\beta$ determine the shape of distribution, including various forms of widely-known distributions such as the Gaussian and Cauchy distribution. Smaller value of $\alpha$ indicates fatter tails and hence it is well known that the variance diverges for ${0<\alpha<2}$, and also the mean cannot be defined for ${0<\alpha\leq 1}$. Note that if $\beta=0$, the distribution is symmetric, if $\beta>0$, right-tailed, and if $\beta<0$, left-tailed.

The definition of stable distribution is that the linear combination of independent random variables that follow a stable distribution with tail index $\alpha$ invariably becomes again a stable distribution with the same tail index $\alpha$. More particularly, when variables $X_{1},X_{2}$ are i.i.d. copies of a random variable $X$ and ${a,b}$ are positive constant numbers, $X$ is said to be stable and follows a stable distribution if there is a positive constant number $c$ and a real number $d\in\mathbb{R}$ that satisfies

$\displaystyle aX_{1}+bX_{2}\overset{\mathrm{d}}{=}cX+d,$

also known for stability property. When a variable $X$ follows a stable distribution, the notation $X\overset{\mathrm{d}}{=}S(\alpha,\beta,\gamma,\delta)$ is often used, where ${\overset{\mathrm{d}}{=}}$ denotes equality in distribution SamoTaqqu1994 . Variable $X$ can be standardized according to the following property:

$\displaystyle\frac{X-\delta}{\gamma}\overset{\mathrm{d}}{=}S(\alpha,\beta,0,1).$

(1)

Another important property of stable distribution is the GCLT, which implies that the only possible limit distributions for sums of i.i.d random variables is a family of stable distribution. When $\alpha=2$, that is, when i.i.d. random variables have finite variance, the limit distribution then becomes a Gaussian according to the well-known classical Central Limit Theorem (CLT).

The PDF of stable distribution cannot be written in a closed form except for some cases; Cauchy distribution (${\alpha=1,\,\beta=0}$), Lévy distribution (${\alpha=1/2,\,\beta=1}$), and Gaussian distribution (${\alpha=2}$). Alternatively, the features are expressed by the characteristic function (CF), ${\varphi(k)}$, which is the Fourier transform of the PDF. By taking the inverse Fourier transform of the CF, the PDF can be obtained as

$\displaystyle f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathrm{e}^{-ikx}\varphi(k)dk.$

When variable $X$ follows a stable distribution with ${S(\alpha,\beta,\gamma,\delta)}$, the CF is shown as

	$\displaystyle\varphi(k)$	$\displaystyle=\exp\left\{i\delta k-\gamma^{\alpha}|k|^{\alpha}\left(1-i\beta\operatorname{sgn}(k)\omega(k,\alpha)\right)\right\},$
	$\displaystyle\omega(k,\alpha)$	$\displaystyle=\begin{cases}\tan(\frac{\pi\alpha}{2})&\alpha\neq 1\\ -\frac{2}{\pi}\log|k|&\alpha=1,\end{cases}$		(2)

which corresponds to the one-parameterization form of $S(\alpha,\beta,\gamma,\delta;1)$ in Nolan (2003) Nolan2018 . This is the most popular parameterization among many other forms of the stable distribution owing to the simplicity of the form. Figure 1 shows the standardized stable distributions with the one-parameterization form for different parameters of $\alpha$ and $\beta$, as an example.

One-parameterization is preferred when one is interested in the basic properties of the distribution, but the CF takes a discontinuous form at $\alpha=1$. Nolan suggests the use of the zero-parameterization form $S(\alpha,\beta,\gamma,\delta_{0};0)$ with different $\omega(k,\alpha)$ shown as

$\displaystyle\omega(k,\alpha)$

$\displaystyle=\begin{cases}-\left(|\gamma k|^{1-\alpha}-1\right)\tan(\frac{\pi\alpha}{2})&\alpha\neq 1\\ -\frac{2}{\pi}\log|\gamma k|&\alpha=1,\end{cases}$

(3)

giving a more complex form, but provides a continuous form. The only difference between the parameterization is the location parameter, which they are related by

	$\displaystyle\delta_{0}=\left\{\begin{array}[]{ll}{\delta+\beta\gamma\tan\frac{\pi\alpha}{2}}&{\alpha\neq 1}\\ {\delta+\beta\frac{2}{\pi}\gamma\log\gamma}&{\alpha=1}\end{array},\right.$		(6)
	$\displaystyle\delta=\left\{\begin{array}[]{ll}{\delta_{0}-\beta\gamma\tan\frac{\pi\alpha}{2}}&{\alpha\neq 1}\\ {\delta_{0}-\beta\frac{2}{\pi}\gamma\log\gamma}&{\alpha=1}\end{array}.\right.$		(9)

In this paper, we employ the simple one-parameterization, as we are interested in estimating the four parameters through the CF, and many existing estimation methods comply with that form. However, since this CF does not have a continuous form at $\alpha=1$, arguments with different parameterizations may be more appropriate for discussing distributions when we already know that $\alpha$ is 1, for instance, the case of Cauchy distribution ($\alpha=1,\beta=0$).

McCulloch (1986) proposes the use of five sample quantiles $x_{0.05},x_{0.25},x_{0.5},x_{0.75}$, and $x_{0.95}$ as an informative measure for estimating the four parameters of stable laws, known as the quantile method (QM) McCulloch1986 . He improves the former method of Fama & Roll (1971) by eliminating bias in estimates and relaxing estimation restrictions FamaRoll1971 . The idea is to calculate the functions $\phi_{i}(\alpha,\beta)\>(i=1,2,3,4)$, where the relationships between the function values and the parameters are already studied and known beforehand. The method first sets out to estimate $\alpha$ and $\beta$ by using the functions $\phi_{1}(\alpha,\beta)$ and $\phi_{2}(\alpha,\beta)$ independent of both $\gamma$ and $\delta$ defined as

	$\displaystyle\phi_{1}(\alpha,\beta)$	$\displaystyle=\frac{x_{0.95}-x_{0.05}}{x_{0.75}-x_{0.25}}$		(10)
	$\displaystyle\phi_{2}(\alpha,\beta)$	$\displaystyle=\frac{\left(x_{0.95}-x_{0.5}\right)-\left(x_{0.5}-x_{0.05}\right)}{x_{0.95}-x_{0.05}}.$		(11)

Equation (10) refers to the measure of fat-tail behaviors with the focus on estimating $\alpha$, and equation (11) is a measure of skewness effects with the focus on estimating $\beta$. With empirical values of sample quantiles and employing linear interpolation with tabular look-ups, the estimates $\hat{\alpha},\hat{\beta}$ are inversely obtained. To avoid $\hat{\alpha}$ being larger than 2, outside the parameter range, $\hat{\phi}_{1}=\frac{\left(\hat{x}_{0.95}-\hat{x}_{0.5}\right)-\left(\hat{x}_{0.5}-\hat{x}_{0.05}\right)}{\hat{x}_{0.95}-\hat{x}_{0.05}}$ can be no larger than the upper range 2.439, which corresponds to the case of $\alpha=2$ (note that $\beta$ is not identified in this case).

Next, the scale and location parameter $\gamma$ and $\delta$ can be estimated using the functions defined as

	$\displaystyle\phi_{3}(\alpha,\beta)$	$\displaystyle=\frac{x_{0.75}-x_{0.25}}{\gamma}$		(12)
	$\displaystyle\phi_{4}(\alpha,\beta)$	$\displaystyle=\frac{\mu-x_{0.5}}{\gamma}+\beta\tan\left(\frac{\pi\alpha}{2}\right).$		(13)

The function $\phi_{3}(\alpha,\beta)$ indicates the standardized form of sample sizes for the middle part of distribution. Since it does not depend on $\gamma$ nor $\delta$, the value can be informed by tabular look-ups based on $\alpha$ and $\beta$, which the relations are studied and known beforehand. After calculating $\hat{\gamma}=\frac{\hat{x}_{0.75}-\hat{x}_{0.25}}{\hat{\phi}_{3}(\hat{\alpha},\,\hat{\beta})}$ in equation (12), the location parameter $\delta$ can be estimated from equation (13) using the values $\hat{\phi}_{4}(\hat{\alpha},\hat{\beta})$ and $\hat{\gamma}$. The relations of the parameter values and the function value $\phi_{4}(\alpha,\beta)$ are again, studied and known beforehand. In the case of $\alpha=1$, $\phi_{4}(\alpha,\beta)$ diverges and we cannot obtain the estimates for $\delta$. McCulloch therefore suggests a complicated approach to overcome the discontinuity of the stable CF. The method improves other issues and provides accurate estimates, however, it has parameter restrictions and can be applied only when $\alpha\geq 0.6$.

The CF-based method relies on the use of a consistent estimator of the CF $\varphi(k)$ for any fixed $k$. The advantage of this method essentially lies in the fact that the stable CF can be expressed explicitly, making discussions straightforward compared to methods based on other distribution forms. Under the assumption that given data $X_{n}\,(n=1,2,\ldots,N)$ are ergodic ArnoldAvez , the CF is obtained empirically by the following equation,

$\displaystyle\hat{\varphi}\left(k\right)=\frac{1}{N}\sum_{n=1}^{N}\mathrm{e}^{ikX_{n}}.$

(14)

There are several approaches for estimating parameters of stable laws that take advantage of the explicit form of CF. Koutrouvelis (1980) Koutrouvelis1980 proposed a regression-type approach, which employs the iteration of two regression runs. Moreover, the regression of the method requires different values of initial points $k$ depending on initial estimates of the parameters and sample sizes. The number of points necessary for the regression also varies over initial conditions. Although the accuracy of $\beta$ is unsatisfactory in some cases, the method generally shows accurate estimates of $\alpha$, and hence it is often suggested as a practical method for empirical analysis Wang2015 ; Kateregga2017 . However, some studies compare the method to McCulloch’s quantile method and report that the regression-type method does not significantly improve the classical quantile method Akgiray1989 ; Rene2011 , especially for $\alpha$ smaller than 1. Other studies simplified the method by eliminating the iteration process and fixing the initial points to some extent, but still leaves behind the issues of estimating when $\alpha$ is small Kogon1998 ; Borak2005 . We do not consider the regression-type approach in this paper as the method generally relies on iteration and the estimates cannot be written analytically.

Another approach is based on the method of moment Press1972 , which was later remodeled and simplified with the use of two given points of the CF Krutto2016 ; Bibalan2017 ; Krutto2018 . Starting off with the CF with the points $k_{0}$ and $k_{1}$, taking the absolute value cancels out the effect of parameters $\beta$ and $\delta$, and we obtain

$\displaystyle\begin{cases}|\varphi(k_{0};\alpha,\beta,\gamma,\delta)|=\exp(-\gamma^{\alpha}|k_{0}|^{\alpha})\\ |\varphi(k_{1};\alpha,\beta,\gamma,\delta)|=\exp(-\gamma^{\alpha}|k_{1}|^{\alpha}).\end{cases}$

(15)

Taking the cumulant function, which is the natural logarithm of the CF, leads to the same discussion neutralizing the effect of parameters $\beta$ and $\delta$. The equation $\ln\varphi=\ln|\varphi|+j(\arg\varphi+2n\pi)$ implies that the real part of the cumulant function corresponds to the natural logarithm of the absolute value of CF, shown as

$\displaystyle\begin{cases}\Re\left\{\ln\varphi(k_{0};\alpha,\beta,\gamma,\delta)\right\}=\ln|\varphi(k_{0};\alpha,\beta,\gamma,\delta)|=-\gamma^{\alpha}|k_{0}|^{\alpha}\\ \Re\left\{\ln\varphi(k_{0};\alpha,\beta,\gamma,\delta)\right\}=\ln|\varphi(k_{1};\alpha,\beta,\gamma,\delta)|=-\gamma^{\alpha}|k_{1}|^{\alpha},\end{cases}$

(16)

for any value of $k$. We consider only the positive values for convenience, since the CF is a symmetric function. By solving the above equations simultaneously, parameters $\alpha$ and $\gamma$ can be estimated shown as

		$\displaystyle\hat{\alpha}=\frac{\ln\left(-\Re\left\{\ln\hat{\varphi}\left(k_{0}\right)\right\}\right)-\ln\left(-\Re\left\{\ln\hat{\varphi}\left(k_{1}\right)\right\}\right)}{\ln k_{0}-\ln k_{1}},$		(17)
		$\displaystyle\hat{\gamma}=$
		$\displaystyle\exp\left\{\frac{\ln k_{0}\ln\left(-\Re\left\{\ln\hat{\varphi}\left(k_{1}\right)\right\}\right)-\ln k_{1}\ln\left(-\Re\left\{\ln\hat{\varphi}\left(k_{0}\right)\right\}\right)}{\ln\left(-\Re\left\{\ln\hat{\varphi}\left(k_{0}\right)\right\}\right)-\ln\left(-\Re\left\{\ln\hat{\varphi}\left(k_{1}\right)\right\}\right)}\right\}.$		(18)

Since the one-parameterization form in equation (II.2) is discontinuous at $\alpha=1$, the estimation of the remaining parameters $\beta$ and $\delta$ is divided into two cases. When $\alpha\neq 1$, the cumulant function of stable distributions with the points $k_{0},k_{1}>0$ are

$\displaystyle\begin{cases}\vspace{0.5em}\ln\varphi(k_{0};\alpha,\beta,\gamma,\delta)=-\gamma^{\alpha}{k_{0}}^{\alpha}+i\left[\delta k_{0}+\gamma^{\alpha}{k_{0}}^{\alpha}\beta\tan\left(\frac{\pi\alpha}{2}\right)\right]\\ \ln\varphi(k_{1};\alpha,\beta,\gamma,\delta)=-\gamma^{\alpha}{k_{1}}^{\alpha}+i\left[\delta k_{1}+\gamma^{\alpha}{k_{1}}^{\alpha}\beta\tan\left(\frac{\pi\alpha}{2}\right)\right].\end{cases}$

(19)

As we need the information of the parameters $\beta$ and $\delta$, we take the imaginary part. Then the parameters $\beta$ and $\delta$ are estimated by solving the above equations simultaneously and using the estimates $\hat{\alpha}$ and $\hat{\gamma}$:

	$\displaystyle\hat{\beta}$	$\displaystyle=\frac{k_{1}\Im\left\{\ln\hat{\varphi}(k_{0})\right\}-k_{0}\Im\left\{\ln\hat{\varphi}(k_{1})\right\}}{\hat{\gamma}^{\hat{\alpha}}\tan\left(\frac{\pi\hat{\alpha}}{2}\right)({k_{0}}^{\hat{\alpha}}k_{1}-{k_{1}}^{\hat{\alpha}}k_{0})}$		(20)
	$\displaystyle\hat{\delta}$	$\displaystyle=\frac{{k_{1}}^{\hat{\alpha}}\Im\left\{\ln\hat{\varphi}(k_{0})\right\}-{k_{0}}^{\hat{\alpha}}\Im\left\{\ln\hat{\varphi}(k_{1})\right\}}{k_{0}{k_{1}}^{\hat{\alpha}}-k_{1}{k_{0}}^{\hat{\alpha}}}.$		(21)

In the case of $\alpha=1$, the CF takes a discontinuous form and the cumulant functions are written as

$\displaystyle\begin{cases}\vspace{0.5em}\ln\varphi(k_{0};1,\beta,\gamma,\delta)=-\gamma{k_{0}}+i\left[\delta k_{0}-\beta\frac{2}{\pi}\ln k_{0}\right]\\ \ln\varphi(k_{1};1,\beta,\gamma,\delta)=-\gamma{k_{1}}+i\left[\delta k_{1}-\beta\frac{2}{\pi}\ln k_{1}\right].\end{cases}$

(22)

Then the parameters are estimated by solving the above equations simultaneously as well:

	$\displaystyle\hat{\beta}$	$\displaystyle=\frac{\pi}{2}\frac{k_{1}\Im\left\{\ln\hat{\varphi}(k_{0})\right\}-k_{0}\Im\left\{\ln\hat{\varphi}(k_{1})\right\}}{\hat{\gamma}k_{0}k_{1}\left(\ln k_{1}-\ln k_{0}\right)}$		(23)
	$\displaystyle\hat{\delta}$	$\displaystyle=\frac{{k_{1}}\Im\left\{\ln\hat{\varphi}(k_{0})\right\}\ln k_{1}-{k_{0}}\Im\left\{\ln\hat{\varphi}(k_{1})\right\}\ln k_{0}}{k_{0}k_{1}\left(\ln k_{1}-\ln k_{0}\right)}.$		(24)

For simplicity, we express the estimates as a function of given points $k_{0}$ and $k_{1}$ as follows:

	$\displaystyle\hat{\alpha}$	$\displaystyle=F_{\alpha}(k_{0},k_{1})$		(25)
	$\displaystyle\hat{\gamma}$	$\displaystyle=F_{\gamma}(k_{0},k_{1})$		(26)
	$\displaystyle\hat{\beta}$	$\displaystyle=F_{\beta}(k_{0},k_{1},\hat{\alpha},\hat{\gamma})$		(27)
	$\displaystyle\hat{\delta}$	$\displaystyle=F_{\delta}(k_{0},k_{1},\hat{\alpha}),$		(28)

where $\hat{\beta}$ and $\hat{\delta}$ additionally needs the information of the estimates $\hat{\alpha}$ and $\hat{\gamma}$. Sometimes, the estimates can possibly outrange the parameter spaces $\alpha\in(0,2],\,\beta\in[-1,1]$, and $\gamma>0$, especially when the true parameters are close to the borders. In such cases, the parameters are set to the closet border, except for $\alpha$ and $\gamma$, the estimates are set no lower than 0.01. Applications with other parameterizations use slightly different forms of CF, but the stable parameters are estimated essentially by the same procedure as explained above. For the zero-parameterization, which is another common parameterization form, the CF is replaced to its corresponding form shown in equations (3) and (6) for equations (15) and  (19) (or (22)). For parameterization with a different definition of the scaling parameter written as $c\,(=\gamma^{\alpha})$ Nikias1995 ; Bibalan2017 ; Liu2018 , Bibalan et al. (2017) Bibalan2017 presents an alternative procedure for the estimation. They first directly obtain the scaling parameter $c$ from taking the absolute value of the empirical CF, or the real part of the cumulant function as

$\displaystyle\hat{c}=-\ln|\hat{\varphi}(1)|=-\Re\left\{\ln\hat{\varphi}(1)\right\}.$

(29)

Next $\alpha$ is estimated as shown in equation (17). Then, the scale parameter in our criterion, $\hat{\gamma}$, is obtained as,

$\displaystyle\hat{\gamma}=\exp\left(\frac{\ln\hat{c}}{\hat{\alpha}}\right).$

(30)

The remaining parameters $\beta$ and $\delta$ are then estimated straightforwardly as similar to the case of the one-parameterization form. By replacing $\hat{\gamma}^{\hat{\alpha}}$ to $\hat{c}$ in equations (20) and (21) (or equations (23) and (24)), and using the points $k_{0}$ and $k_{1}$ give the estimates.

Two positive points of the CF, $k_{0}$ and $k_{1}(k_{0}\neq k_{1})$, are ought to be selected to identify all four parameter estimates. As mentioned before in this paper, the absolute value of the CF in equation (15) is independent of the skew and location parameters for any $k$, and provides information of $\alpha$ and $\gamma$. When $k=1/\gamma$ is satisfied, the absolute value of the CF takes a constant value

$\displaystyle\left|\varphi\left(1/\gamma\right)\right|=\mathrm{e}^{-1}.$

(31)

The advantage of setting $k=1/\gamma$ as one of the candidate points is to reduce any estimation bias influenced by certain parameter values since we expect to get a constant estimate which is independent of all four parameters. When $\gamma\gg 1$, however, empirically obtained values can cause significant estimation errors for the scale parameter in equation (31) Krutto2018 ; Paulson1975 . Therefore, we first consider a temporary estimate of the scaling parameter, $\tilde{\gamma}$, just in case the data exhibits scale far from the standardized form ($\gamma=1$).

Take the natural logarithm of equation (31). The temporary estimate can be obtained by approximately solving the equation that numerically satisfies

$\displaystyle\ln\left|\hat{\varphi}\left(1/\tilde{\gamma}\right)\right|\simeq-1,$

(32)

using a simple one-dimensional search function Brent2013 , or any other optimization procedure. Our rough estimate $\tilde{\gamma}$ is then used for standardizing, or pre-standardizing, the candidate points. Specifically, point $k_{1}$ is set to $1/\tilde{\gamma}$, where $\ln|\varphi(k_{1})|$ empirically takes $-1$.

As explained above, pre-standardization is preferred especially when we suspect that datasets have too large or small scales. Whenever a new set of points is required for the parameter estimation process, we conduct pre-standardization. Point $k_{1}$ is replaced to $1/\check{\gamma}$, where $\check{\gamma}$ is the latest scaling parameter estimate available at that time.

For the argument of selecting point $k_{0}>0$, which is perhaps the most important proposal in our study. We focus on the absolute value of the CF. Bibalan et al. (2017) proposed to calculate the distance between two absolute values of CFs with different index parameters $\alpha$, the Gaussian case ($\alpha=2$) and the Cauchy case ($\alpha=1$) Bibalan2017 . They set $k_{0}>0$ to the point which corresponds to the maximum distance and the other point to $k_{1}=1$. Although the absolute CF changes depending on the index parameter $\alpha$, their approach considers a fixed distance and essentially chooses an identical point for any value of $\alpha\in(1,2]$. In addition, the distance they consider does not account for the case of $\alpha\in(0,1]$.

Our approach is an extension of Bibalan et al. (2017), and provides a more generalized technique of selecting the points. We deal with the problem that the distance between two absolute values of CFs can vary depending on the parameters. The basic idea is to find the point where the absolute CF, $|\varphi(k;\alpha)|$, presents the maximum sensitivity with respect to $\alpha$. In other words, we discuss the point where the distance between the absolute CF of index parameter $\alpha$, $|\varphi(k;\alpha,\beta,\gamma,\delta)|$, and the absolute CF of $\alpha+\Delta\alpha$, $|\varphi(k;\alpha+\Delta\alpha,\beta,\gamma,\delta)|$, shows the largest distance. Such a point is considered as $k_{0}$ in our study.

To make our discussion more simple, we consider the absolute CF as a function of variable $\eta$:

$\displaystyle|\varphi(k;\alpha,\beta,\gamma,\delta)|=\exp(-\eta^{\alpha}),$

where $\eta=\gamma k\;(k>0)$ is a newly introduced variable which depends on $\gamma$ and $k$. The distance can be expressed as $\left|\exp(-\eta^{\alpha+\Delta\alpha})-\exp(-\eta^{\alpha})\right|$. The candidate point for $\eta_{0}=\gamma k_{0}$, where the maximum distance is achieved, can be calculated by

$\displaystyle\frac{d}{d\eta}\left|\exp(-\eta^{\alpha+\Delta\alpha})-\exp(-\eta^{\alpha})\right|=0,\;\eta>0.$

(33)

Solving this equation for $\eta>0$ yields two solutions, $\eta\in(0,1/\gamma)$ and $\eta\in(1/\gamma,\infty)$. For both points, the absolute value of CF shows the largest ratio of change in a local sense. The smaller point $\eta\in(0,1/\gamma)$ is employed, because the distance at the smaller point tends to have larger values than that at the larger point $\eta\in(1/\gamma,\infty)$, which enables us to estimate $\alpha$ and $\gamma$ in a more desirable and informative manner. Another reason is that smaller $|k|$ is preferred rather than larger $|k|$. As $|k|\rightarrow 0$, the asymptotic variance of the empirical cumulant function decreases Krutto2018 . With empirical CF obtained by i.i.d. distributed datasets, the relation

$\displaystyle E\left[\left|\varphi_{N}(k)\right|^{2}\right]=|\varphi(k)|^{2}+\frac{1}{N}\left(1-|\varphi(k)|^{2}\right),$

(34)

holds Kakinaka2020 , which implies that as $k$ becomes larger, the empirical absolute CF $|\varphi_{N}(k)|$ is likely to be subject to sample errors. Thus, the smaller $\eta=\gamma k$ should be considered in this study.

The above discussion implies that $k$ should be set close to zero (but not at zero because then the CF takes a constant value and no information of the parameters will be provided). But at the same time, the employed smaller point is standapart from zero to some extent, so that the empirical CF will be more or less exposed by sample errors. Therefore, the choice of points derived from equation (33) is unsatisfactory, and hence the distance $\left|\exp(-\eta^{\alpha+\Delta\alpha})-\exp(-\eta^{\alpha})\right|$ should be modified. To reduce the effect of sample errors, we introduce a weight function $w(\eta)$ that decreases monotonically as $\eta$ becomes larger (note that the introduced variable $\eta=\gamma k$ has a linear relationship with $k$).

Using the weight function $w(\eta)$, we now introduce a weighted distance $\left|\exp(-\eta^{\alpha+\Delta\alpha})-\exp(-\eta^{\alpha})\right|w(\eta)$ for $\eta>0$. For convenience, we employ $w(\eta)=\exp{(-\tau|\eta|)}$, where $\tau>0$, since the CF exhibits an exponential form. This choice leads to the association of the weighted distance with a statistical measure used for goodness-of-fit tests, developed by Matsui and Takemura (2008) Matsui2008 . They propose the following test statistic based on empirical CFs,

	$\displaystyle D_{N,\kappa}$	$\displaystyle:=N\int_{-\infty}^{\infty}\left|\hat{\varphi}(t)-\exp{(-|t|^{\alpha})}\right|^{2}h(t)dt,$
	$\displaystyle h(t)$	$\displaystyle=\exp{(-\kappa|t|)},\;\;\kappa>0,$		(35)

where $h(t)$ is a monotonically decreasing weight function. $D_{N,\kappa}$ denotes the weighted $L^{2}$-distance between the empirical CF and the symmetric standardized stable CF $\varphi(t;\alpha,0,1,0)$. This weighted $L^{2}$-distance can be associated with the weighted distance we are considering now.

Taking the absolute value of a CF yields again a standardized form of a CF with $\beta=0$ and $\delta=0$:

$\displaystyle\exp(-\eta^{\alpha})=|\varphi(k;\alpha,\beta,\gamma,\delta)|=\varphi(\eta;\alpha,0,1,0).$

Thus, the absolute values of CF with index parameter $\alpha$ and $\alpha+\Delta\alpha$ are equivalent to the symmetric standardized stable CFs, $\varphi(\eta;\alpha,0,1,0)$ and $\varphi(\eta;\alpha+\Delta\alpha,0,1,0)$, respectively. The weighted $L^{2}$-distance between these CFs essentially coincides $D_{N,\kappa}$, when the weight function satisfies

$\displaystyle w(\eta)=\sqrt{h(\eta)},$

for $\eta>0$. In this case, the difference between the CFs can be evaluated more accurately with the background of a meaningful measurement. Following Matsui and Takemura (2008), the asymptotic distribution of $D_{N,\kappa}$ is numerically evaluated and the critical values of the test statistics are approximately obtained Matsui2008 . Through computational simulation, they provide evidence that the test is most powerful when $\kappa=5.0$ ($h(\eta)=\exp(-5|\eta|)$), especially for heavy tailed distributions. Thus, our choice of the weight function is $w(\eta)=\exp(-2.5|\eta|)$, since $\tau=\kappa/2$. Other weight functions such as $w(\eta)=\exp{(-|\eta|)}$ and $w(\eta)=\exp{(-\eta^{2})}$ Paulson1975 ; Heathcote1977 can be employed, but lacks a conclusive evidence for the use of these alternatives.

With the weight function, the candidate points $\eta>0$ are calculated by solving the following equation:

		$\displaystyle g(\alpha,\eta)$
		$\displaystyle=\frac{d}{d\eta}\left\{\left(\exp(-\eta^{\alpha+\Delta\alpha})-\exp(-\eta^{\alpha})\right)\cdot\exp(-\tau\eta)\right\}=0,$		(36)

where $\tau=2.5$. Then we have

	$\displaystyle g(\alpha,\eta)$	$\displaystyle=(\alpha\eta^{\alpha-1}+\tau)\exp(-\eta^{\alpha}-\tau\eta)$
		$\displaystyle-\left((\alpha+\Delta\alpha)\eta^{\alpha+\Delta\alpha-1}+\tau\right)\exp(-\eta^{\alpha+\Delta\alpha}-\tau\eta).$		(37)

For convenience, $\Delta\alpha$ is set to $0.01$ for all cases in this study. Equation $g(\alpha,\eta)=0$ indicates the relationship between the index parameter $\alpha$ and point $\eta$ that exhibits the maximum rate of a change, or the maximum sensitivity, of the absolute CF with respect to $\alpha$.

There could exist some relationship between $\alpha$ and $\eta$ since they are interrelated due to $g(\alpha,\eta)=0$. When some estimate $\hat{\alpha}$ is given, the corresponding point is obtained by computing $\eta$ that satisfies $g(\hat{\alpha},\eta)=0$, and vice versa (the corresponding parameter $\alpha$ of a given point $\hat{\eta}$ can be calculated by computing the equation $g(\alpha,\hat{\eta})=0$). As we have discussed previously in this subsection, we focus on the point closer (smaller) to zero out of the two candidates of the calculated points from equation (36). Figure 2 ascertains whether our approach of equation (36) correctly estimates the parameters of stable distribution. The model clearly characterizes the distinctive relationship between $\alpha$ and $\eta$, which are empirically verified via simulation using synthetic data generated from random stable variables Weron1996 . This indicates that our selection of points is valid for identifying desired points in the estimation process.

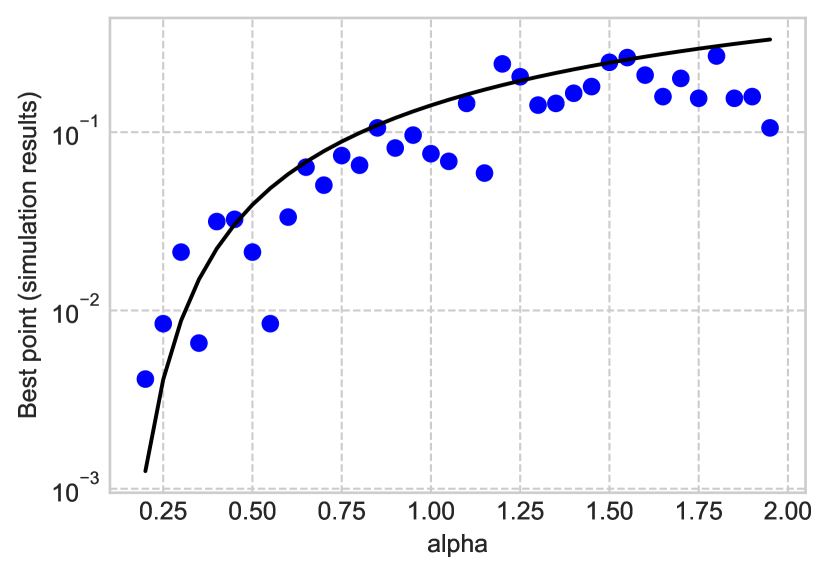
In practice, $\alpha$ is unknown. Hence the selection of point $\eta_{0}=\gamma k_{0}$ is undecidable, so that the parameters for the stable law cannot be estimated directly. To cope with this problem, we first aim to get a rough estimate of $\alpha$ calculated by using the temporary scale estimate $\tilde{\gamma}$. The rough estimate is considered poor as the estimation method, but it plays a role in starting off the estimation process with reasonable initial values. The accuracy of both points ($\eta_{0}=\gamma k_{0}$ and $\eta_{1}=\gamma k_{1}$) and the parameters ($\alpha,\beta,\gamma,\delta$) can be improved by alternating searches of $\alpha$ and $\eta$ from our relation model $g(\alpha,\gamma)=0$ several times to get sophisticated estimates. With estimates $\eta_{0}$ and $\eta_{1}$, the four parameters are ultimately calculated.

Here we present our proposed algorithm for the estimation of all four parameters of stable laws by utilizing the relationship between $\alpha$ and $\eta$. Regarding the fact that empirically obtained estimates occur substantial errors induced by $\gamma\gg 1$, we conduct a pre-standardization with $k$ replaced to $\eta=\gamma k$. Using the expressions of the estimates in equations (25) (26) (27) (28), our algorithm is written as follows:

1. Step 1:

   Compute a temporary estimate $\tilde{\gamma}_{\mathrm{temp}}$ from sample data $X_{n}\,(n=1,2,\ldots,N)$ that satisfies the equation,

   $\displaystyle\left.\ln\left|\frac{1}{N}\sum_{n=1}^{N}e^{iX_{n}/\gamma}\right|\,\right|_{\gamma=\tilde{\gamma}_{\mathrm{temp}}}=-1.$

2. Step 2:

   Set

   $\displaystyle\begin{cases}\tilde{k}_{0}=\xi/\tilde{\gamma}_{\mathrm{temp}}\\ \tilde{k}_{1}=1/\tilde{\gamma}_{\mathrm{temp}},\end{cases}$

   where $\xi$ is any initial value of $\xi\in(0,1)$.

3. Step 3:

   Make a rough estimate of $\alpha$ and $\gamma$ from

   	$\displaystyle\tilde{\alpha}$	$\displaystyle=F_{\alpha}(\tilde{k}_{0},\tilde{k}_{1})$
   	$\displaystyle\tilde{\gamma}$	$\displaystyle=F_{\gamma}(\tilde{k}_{0},\tilde{k}_{1}),$

   respectively, where $F_{\alpha}(\cdot,\cdot)$ and $F_{\gamma}(\cdot,\cdot)$ are given in equations (25) and (26).

4. Step 4:

   Compute $\tilde{\eta}$ that satisfies $\left.g(\tilde{\alpha},\eta)\right|_{\eta=\tilde{\eta}}=0$, where $g(\cdot,\cdot)$ is given in equation (IV.2).

5. Step 5:

   Recalculate the points associated with $\tilde{\eta}$,

   $\displaystyle\begin{cases}\tilde{k}_{0}=\tilde{\eta}/\tilde{\gamma}\\ \tilde{k}_{1}=1/\tilde{\gamma},\end{cases}$

6. Step 6:

   Estimate $\alpha$ and $\gamma$ as

   	$\displaystyle\hat{\alpha}$	$\displaystyle=F_{\alpha}(\tilde{k}_{0},\tilde{k}_{1})$
   	$\displaystyle\hat{\gamma}$	$\displaystyle=F_{\gamma}(\tilde{k}_{0},\tilde{k}_{1}),$

7. Step 7:

   Compute $\tilde{\eta}$ that satisfies $\left.g(\hat{\alpha},\eta)\right|_{\eta=\hat{\eta}}=0.$

8. Step 8:

   Recalculate the points associated with $\hat{\eta}$,

   $\displaystyle\begin{cases}\hat{k}_{0}=\hat{\eta}/\hat{\gamma}\\ \hat{k}_{1}=1/\hat{\gamma},\end{cases}$

9. Step 9:

   Finally, we estimate the parameters $\alpha$ and $\gamma$ as

   	$\displaystyle\hat{\alpha}$	$\displaystyle=F_{\alpha}(\hat{k}_{0},\hat{k}_{1})$
   	$\displaystyle\hat{\gamma}$	$\displaystyle=F_{\gamma}(\hat{k}_{0},\hat{k}_{1}),$

10. Step 10:

    Estimate the parameters $\beta$ and $\delta$ from the functions $F_{\beta}(\cdot,\cdot,\cdot,\cdot)$ and $F_{\delta}(\cdot,\cdot,\cdot)$ given in equations (27) and (28), as

    	$\displaystyle\hat{\beta}$	$\displaystyle=F_{\beta}(\hat{k}_{0},\hat{k}_{1},\hat{\alpha},\hat{\gamma})$
    	$\displaystyle\hat{\delta}$	$\displaystyle=F_{\delta}(\hat{k}_{0},\hat{k}_{1},\hat{\alpha}),$

    which leads to the estimates of all four parameters of stable laws.

The performance of the estimated parameters are examined by the MSE criterion:

$\displaystyle\mathrm{MSE}(\theta)=\frac{1}{L}\sum_{l=1}^{L}\left(\theta-\hat{\theta}_{l}\right),$

where $\theta$ and $L=500$ is the parameter of stable laws and the number of times the simulation is implemented, respectively. We calculate the MSE of all four parameters and evaluate each parameter individually.

Table 1 shows the simulation results of the MSE associated with the estimate bias for each parameter. We consider the cases of parameters with $\alpha=0.5,1.5,1.8$ and $\beta=0,0.5$, all with a standardized form of $\gamma=1$ and $\delta=0$. Our proposed approach generally provides the most accurate estimation with the smallest MSE. Especially for the index parameter $\alpha$ and $\delta$, our approach significantly improves the accuracy of the estimates. Note that for the QM, the method has parameter restrictions of $\alpha\geq 0.6$ and hence the cases with $\alpha$ smaller than 0.6 can not be implemented. More detailed simulation results for different cases of parameters are shown in Figures 5, 6, 7 in Appendix A. In particular, we show the cases of $S(\alpha,-0.1,1,0),S(0.8,\beta,1,0)$ and $S(1.6,\beta,1,0)$, with parameter values varying within the parameter ranges. The results imply that for whatever parameter combination, our method generally outperforms the others with the highest accuracy. Although we find that other methods sometimes show higher accuracy on either the parameter $\alpha$ or $\delta$ in cases of $0.6\leq\alpha\leq 1.2$ in $S(\alpha,-0.1,1,0)$ in Figure 5 and $-0.3\leq\beta\leq 0.3$ for $S(0.8,\beta,1,0)$ in Figure 6, our method appears to be powerful for estimating all four stable parameters.

Next, we examine the performance of estimating stable laws from a different perspective; evaluation of the entire distribution. We use the KS distance expressed as

$\displaystyle D=\max_{x}|P(x)-\hat{P}(x)|,$

which represents the maximum distance between two distributions in terms of the CDF. Here $P(x)$ and $\hat{P}(x)$ denotes the empirically obtained CDF, and the theoretical estimated CDF, respectively. The standard density and distribution functions of stable distributions are numerically derived approximately by implementing the Fourier integral formulas Zolotarev1986 ; Nolan1997 , which are available in package libstable that provides good approximation values Roy2017 . KS distance is one of the most major standards for numerical assessments when discussing stable laws. We set aside any issues related to numerical approximations of stable distributions, so that we can focus on the performance between the methods. The root mean square (RMS) of the KS distance is used for the numerical assessment to make the small differences of the comparison results more apparent.

Figure 3 shows the simulation results of the KS distance for several cases of stable distributions; $S(\alpha,0.1,1,0)$, $S(1.7,\beta,1,0)$, $S(1.3,0.2,\gamma,0)$, and $S(0.7,-0.4,1,\delta)$. The RMS of the KS distance is calculated for each case with various values of parameters ranging within parameter ranges. We find in Figure 3 (c) that the estimation for the scaling parameter $\gamma\neq 1$ poses significant estimation errors. This is caused by the effect of sample errors induced by the scaling parameter $\gamma$ far from the standardized form, as shown in equation (31). On the other hand, our proposed method achieves the smallest value of KS distances for all cases of parameter combinations. This proves that we are also successful in improving the estimation of the entire stable distribution.

Needless to say, the accuracy of the estimation method strongly depends on the number of samples. Larger sample sizes give more information of the dataset whereas smaller sample sizes have only little information making it challenging to detect the true values. We examine the effect of sample size by comparing the performance among the estimation methods. Figure 4 displays the MSE of each parameter of stable distribution as the sample size $N$ changes from 300 to 10000. The study is examined for the case of $S(1.4,0.2,1,0)$. The MSE simulated by means of our method decreases with the order $\mathcal{O}(1/N)$ while the MSE simulated by means of other representative methods also exhibited similar behaviors of order. Our proposed approach offers the best performance except for the location parameter $\delta$, where the QM method sometimes give more accurate estimates for large datasets.