Flat-band localization in Creutz superradiance lattices

Flat bands are characterized by the zero bandwidth over the whole Brillouin zone. Owing to the destructive interference between the hopping pathways [sutherland1986localization, , bergman2008band, ], the group velocity of excitations vanishes, and hence the diffusion in flat bands is inhibited. The resulting compact localized eigenstates (CLSs) [flach2014detangling, , leykam2018artificial, ] have been experimentally realized in photonics vicencio2015 , mukherjee2015a , mukherjee2015b , mukherjee2017 , mukherjee2018 , kremer2020 , xia2016 , xia2018 , ma2020 and polariton-exciton condensates baboux2016 , harder2020 . Immune to environmental noises, localized states in flat bands are promising candidates for realizing quantum networks rontgen2019 and diffraction-free photonics vicencio2013 , rojas2017 , yu2020 . Flat bands are also of fundamental interest in many-body physics because of their high degeneracy. The density of states is divergent such that even weak interactions lead to strong correlations and exotic topological phases bergholtz2013 , junemann2017exploring , spanton2018 , chen2020 .

Many-body interactions can be engineered to realize correlated topological phases in atoms bloch2008 , li2020 . However, in previous realizations of the flat bands in optical lattices, the underlying lattices jo2011 , taie2015 are gapless and topologically trivial. A feasible model that integrates both band flatness and topology is the two-leg ladder in a uniform magnetic field with cross-linked couplings, i.e., the Creutz lattice Creutz1999End , hugel2014 (see Fig.  1(a)). Despite theoretical proposals in photonic waveguides mukherjee2018 and ultracold atoms [junemann2017exploring, ], flat bands in the Creutz lattice have never been experimentally realized kang2018 , alaeian2019 , kang2020 .

Here we report the synthesis of a Creutz ladder with tunable tight-binding parameters in the form of a momentum-space lattice, i.e., the superradiance lattice [WangPRL2015, , Chen2018, ], in room-temperature cesium atoms. The bipartite ladder consists of timed Dicke states with different momenta [ScullyPRL2006, ]. We find that the corresponding energy band structure exhibits a flat band and a dispersive band, which are distinguished by localized and delocalized excitations, respectively. In the experiment, we excite one site in the ladder with a weak probe field and measure the optical response of the adjacent site. The hopping strengths and the Aharonov-Bohm (AB) phases in the lattice are carefully tuned, which enables us to excite a particular band and control the flat-band localization. We observe that the optical response is significantly suppressed when the flat band is selectively excited. By controlling the AB phases, we reveal the relation between the flat-band localization and gauge fields khomeriki2016 . Our work demonstrates a versatile platform for flat bands of atoms with multiple tunable parameters, which holds promising applications in exploring correlated topological phases.

We first introduce the experimental scheme implemented in the hyperfine levels of the ¹³³Cs D1 line in a bichromatic standing-wave-coupled configuration, as shown in Fig.  1(a). Two standing waves couple

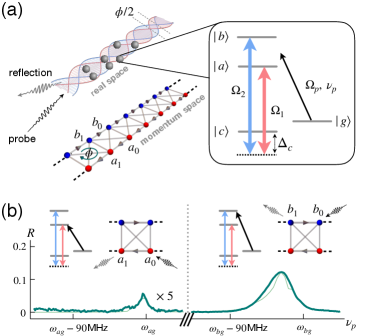
two excited states $\left|a\right\rangle\equiv\left|6^{2}P_{1/2},F=3\right\rangle$ and $\left|b\right\rangle\equiv\left|6^{2}P_{1/2},F=4\right\rangle$ to the same metastable state $\left|c\right\rangle\equiv\left|6^{2}S_{1/2},F=3\right\rangle$. The frequency of the $j$th standing-wave coupling field $\nu_{j}$ fulfills the two-photon resonance condition $\Delta_{c}=\nu_{1}-\omega_{ac}=\nu_{2}-\omega_{bc}$, where $\omega_{ij}$ being the atomic transition frequency between $\left|i\right\rangle$ and $\left|j\right\rangle$. The envelopes of the Rabi frequency amplitude of the two standing waves are $2\Omega_{1}\cos(k_{c}x-\phi/4)$ and $2\Omega_{2}\cos(k_{c}x+\phi/4)$, where $k_{c}$ is the $x$ component of the wave vectors and $\phi/2$ is the phase difference between the envelopes. The wave-vector difference between the two standing waves is negligible in the length of the atomic vapor cell. We use a weak travelling field with the wave vector $k_{p}$ to probe the standing-wave-coupled atomic vapor and measure the backward reflection. The frequency of the probe field $\nu_{p}$ is scanned to couple the ground state $\left|g\right\rangle\equiv\left|6^{2}S_{1/2},F=4\right\rangle$ to either the state $\left|a\right\rangle$ or $\left|b\right\rangle$. Featured signals can be observed when the probe field is near resonant with each atomic transition. A typical spectrum is shown in Fig.  1(b).

In order to show that our experiment constructs a Creutz ladder and reveal the connection between the reflection signal and the excitation transport in the ladder, we write the Hamiltonian $H=H_{s}+H_{p}$ in momentum space supp , with $H_{s}$ and $H_{p}$ being the parts of the Hamiltonian corresponding to the couplings of standing waves and the probe field, respectively. Here, we set $\hbar=1$ and $H_{s}$ reads

which gives a tight-binding superradiance lattice composed of the collective atomic excitation operators $d_{j}^{\dagger}=\sqrt{1/N}\sum_{m}\left|d_{m}\right\rangle\left\langle g_{m}\right|\exp[i(k_{p}-2jk_{c})x_{m}]$ ($d=a,b$) [WangPRL2015, ], where $m$ labels the $m$th atom at the position $x_{m}$, $j$ is an integer, and $N$ is the total number of atoms. $t_{1}=-\Omega_{1}^{2}/\Delta_{c}$ and $t_{2}=-\Omega_{2}^{2}/\Delta_{c}$ are the hopping amplitudes along $a$-leg and $b$-leg, respectively. Here, we can adiabatically eliminate the state $\left|c\right\rangle$, since $\Delta_{c}$ is much larger than all relevant Rabi frequencies $(\Delta_{c}\gg\Omega_{j})$. The two hoppings acquire a phase $\phi/2$ in opposite directions. The loop transition along a plaquette accumulates an AB phase $\phi$, such that the lattice is effectively in a uniform magnetic field. $t_{3}=-\Omega_{1}\Omega_{2}/\Delta_{c}$ and $2t_{3}\cos\phi/2$ are the hopping strengths along the diagonals and the rungs of each plaquette in the ladder. The on-site energies of the $a$-leg and $b$-leg sites are $2t_{1}$ and 2$t_{2}$, respectively.

The probe field coupling Hamiltonian is $H_{p}=\sqrt{N}\Omega_{p}e^{-i\Delta_{p}^{\prime}t}a_{0}^{\dagger}+\sqrt{N}\Omega_{p}^{\prime}e^{-i\Delta_{p}t}b_{0}^{\dagger}+h.c.$, where $\Omega_{p}$ ($\Omega_{p}^{\prime}$) and $\Delta_{p}=\nu_{p}-\omega_{bg}$ ($\Delta_{p}^{\prime}=\nu_{p}-\omega_{ag}$) are the Rabi frequency and the frequency detuning of the coupling between the probe field and the atomic transition between $\left|a\right\rangle$ ($\left|b\right\rangle$) and $\left|g\right\rangle$. Hence, $H_{p}$ shows that the excitation is prepared by the probe field to the site $a_{0}$ or $b_{0}$ in the ladder. When we probe the site $a_{0}$ ($b_{0}$), the phase-matching condition $k_{p}-2k_{c}\approx-k_{p}$ is only satisfied for the excitation on the site $a_{1}$ ($b_{1}$), which results in a superradiant backward emission collected by a photodetector. The spectrum in the left (right) of Fig.  1(b) characterizes the excitation transport from $a_{0}$ to $a_{1}$ ($b_{0}$ to $b_{1}$) in the ladder of Eq.  (1). In the experiment, the probe field is weak $(\Omega_{p}\ll t_{i})$ such that only a small fraction of the atoms are excited. In this condition, $a_{j}$, $b_{j}$ are approximately bosonic annihilation operators [WangPRL2015, ].

The Creutz ladder in Eq.  (1) constructed in momentum space is tunable in the experiment. We diagonalize $H_{s}$ in real space supp and the band structures are shown in Fig.  2. We define $\eta\equiv t_{2}/t_{1}$ as the relative hopping strength along the two legs. One can see that all three band structures with different $\eta$ are composed of a flat band and a dispersive band. In general, the dynamics of the excitation is governed by both bands and cannot be distinguished. Probing only one band by controlling the excitation energy jacqmin2014 , drost2017 , slot2017 is inapplicable since the band gap closes when $\phi$ approaches zero supp .

Nevertheless, the tunability of the hopping strengths enables us to determine which band to excite by controlling the state component of the bands. In the experiment, we tune $\eta$, which is proportional to $P_{2}/P_{1}$, where $P_{1}$ and $P_{2}$ are the powers of the two standing waves.

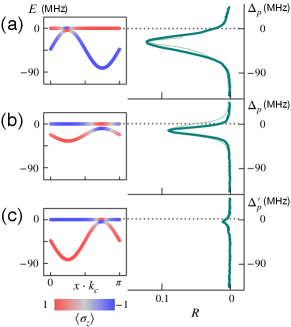
An interesting correlation can be noticed between the parameter $\eta$ and the band components, where the color represents the polarization $\left\langle\sigma_{z}\right\rangle\equiv\left\langle\left|a\right\rangle\left\langle a\right|-\left|b\right\rangle\left\langle b\right|\right\rangle$ of the eigenstates. In particular, $\left\langle\sigma_{z}\right\rangle=+1$ or $-1$ means the band fully locates on the $a$- or $b$-leg. In Fig.  2(a), one can see that $\langle\sigma_{z}\rangle\approx-1$ for almost the whole dispersive band, meaning that the dispersive band supports a large excitation component on the $b$-leg for $\eta\gg 1$ (we take $\eta=20.7$ according to the experimental parameters). Therefore, the $b_{0}\rightarrow b_{1}$ transport dynamics is governed by the dispersive band. On the other hand, for $\eta\ll 1$ ($\eta=1/20.7$ as shown in 2(c)), $\langle\sigma_{z}\rangle\approx-1$ for almost the entire flat band, so the $b_{0}\rightarrow b_{1}$ transport dynamics is governed by the flat band.

This band selection is manifested in the bandwidth, the central frequency, and the magnitude of the reflection spectrum in Fig.  2. In the experiment, we change $\eta$ and keep $t_{3}\propto\sqrt{P_{1}P_{2}}$ a constant. In Fig.  2(a) for $\eta\gg 1$, the reflection spectrum of the dispersive band has a larger bandwidth and a lower central frequency. As a comparison, in Fig.  2(c) for $\eta\ll 1$, the reflection spectrum due to the flat band has a much narrower bandwidth and the peak locates near the predicted frequency of the flat band. The localization in the flat band is demonstrated by the decrease of the reflection peak when we decrease $\eta$, during which the reflection is more contributed by the flat band.

As a side note, in obtaining Fig.  2(c), we use the symmetry that lattice Hamiltonian $H_{s}$ is invariant when we exchange the sublattices $a$ and $b$, inverse $\eta$, and flip the flux $\phi$ supp . In the experiment, the $b_{0}\rightarrow b_{1}$ transport dynamics with $\phi$ and $\eta>1$ is characterized by the reflection spectrum near resonant with level $\left|b\right\rangle$ (labelled with $R_{\eta}(\phi)$), while the one with $-\phi$ and $(1/\eta)<1$ is effectively obtained from the $\left|a\right\rangle$-side reflection spectrum (labelled with $R_{1/\eta}(-\phi)$).

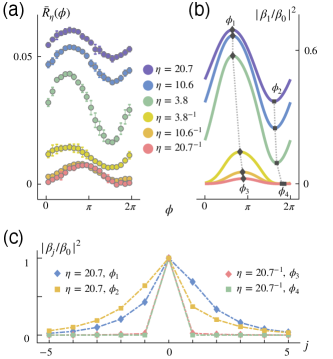
The reflection spectrum is mostly contributed by the slowly moving atoms that have Doppler shifts smaller than the lattice bandwidth cai2019 . We take the average of reflectivity over the bands, i.e., $\bar{R}=\int Rd\nu_{p}/\int d\nu_{p}$, to investigate the localization and its dependence on $\phi$. In Fig.  3(a), the flat-band localization is demonstrated by the suppression of $\bar{R}$ when $\eta$ decreases. Furthermore, we notice that the $\phi$-dependence of $\bar{R}$ changes with $\eta$ (see the $\phi$ calibration in supp ). The sinusoidal curve of averaged reflectivity $\bar{R}_{\eta}(\phi)$ is shifted from top to bottom in Fig.  3(a).

The $\phi$-dependent shift shows the distinct responses to the gauge fields of the two bands. We consider two ideal cases to explain the physics. If the excitation is completely prepared in the dispersive band, the transport dynamics is determined by the flux-dependent unidirectional chiral edge current atala2014 , mancini2015 , stuhl2015 , livi2016 , anisimovas2016 , an2017 , cai2019 , dutt2020 of the dispersive band. The unidirectional chiral current breaks the symmetry between the transition from $b_{0}$ to $b_{1}$ and the one from $b_{0}$ to $b_{-1}$. When the magnetic flux $\phi\in(0,\pi)$, the chiral current enhances the probability in the site $b_{1}$, and hence the reflectivity increases (vice versa). On the other hand, flat-band response to the gauge field can be understood by the CLSs $\left|F_{j}\right\rangle$ [flach2014detangling, ]. When $\phi=2n\pi$ ($n$ is an integer), $\left|F_{j}\right\rangle\propto(\eta a_{j}^{\dagger}-b_{j}^{\dagger})\left|G\right\rangle$ is localized within the $j$th unit cell. Therefore, only $\left|F_{0}\right\rangle$ is excited when we probe the site $b_{0}$, leading to the maximum localization. Otherwise, $\left|F_{j}\right\rangle\propto(\eta a_{j+1}^{\dagger}-e^{i\phi/2}b_{j+1}^{\dagger}+\eta e^{i\phi/2}a_{j}^{\dagger}-b_{j}^{\dagger})\left|G\right\rangle$ is localized within two unit cells. Probing site $b_{0}$ leads to a coherent superposition between $\left|F_{0}\right\rangle$ and $\left|F_{-1}\right\rangle$, and hence results in a finite overlap with $b_{\pm 1}$, which is similar to the “breathing motions” in Refs. mukherjee2018 , kremer2020 .

The two responses can be further investigated by the steady state of the collective excited states of atoms, where the wave function $\left|\psi_{s}\right\rangle\approx[1+\sum_{j}(\alpha_{j}a_{j}^{\dagger}+\beta_{j}b_{j}^{\dagger})]\left|G\right\rangle$ $(\alpha_{j},\beta_{j}\ll 1)$ in the weak excitation approximation. In the steady state, we obtain the probability amplitude $\beta_{j}=\sqrt{N}\Omega_{p}\left\langle G\right|b_{j}(\Delta_{p}+i\hat{\gamma}-H_{s})^{-1}b_{0}^{\dagger}\left|G\right\rangle$ [ozawa2014anomalous, ], where $\hat{\gamma}=\sum_{j}(\gamma_{a}a_{j}^{\dagger}a_{j}+\gamma_{b}b_{j}^{\dagger}b_{j})$ and $\gamma_{a}$ ($\gamma_{b}$) is the decoherence rate between the excited state $\left|a\right\rangle$ ($\left|b\right\rangle$) and $\left|g\right\rangle$. Especially, we plot $\left|\beta_{1}/\beta_{0}\right|^{2}$, i.e., the normalized probability on the site $b_{1}$ in Fig.  3(b). Since the reflectivity is approximately proportional to $\left|\beta_{1}/\beta_{0}\right|^{2}$ [Wang2015, ], both features of the $\bar{R}$ in Fig.  3(a) are demonstrated, including the magnitude suppression and the $\phi$-dependence. We also plot four typical probability amplitude distributions along the $b$-leg in Fig.  3(c) with $\eta\gg 1$ and $\eta\ll 1$. For $\eta=20.7$, the distributions of $|\beta_{j}|^{2}$ with $\phi_{1}=0.64\pi$ and $\phi_{2}=1.62\pi$ are almost symmetric to each other with respect to the $0$th site, implying flux-dependent unidirectional chiral edge current of the dispersive band. However, the distributions with $\phi_{3}=0.9\pi$ and $\phi_{4}=1.86\pi$ are symmetrically localized at $b_{0}$ with different localization lengths. $\left|\beta_{1}/\beta_{0}\right|^{2}$ for $\eta=1/20.7$ is minimized at $\phi_{4}$, which means that the eigenstates are maximally localized when the synthetic gauge field almost vanishes. We notice that $\phi_{4}$ is slightly different from $2n\pi$, which comes from the suppressed but finite contribution from the dispersive band.

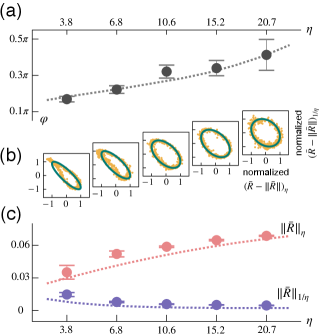
In Fig.  4(b), the different $\phi$-dependences of the dispersive and flat bands are illustrated with Lissajous curves. The spatial phase difference between the envelopes of the two standing waves is slowly tuned to cover all values of $\phi$. We obtain the data sets {$\bar{R}_{\eta}(\phi),\bar{R}_{1/\eta}(-\phi)$} and fit them with ellipses to reconstruct the Lissajous curves. The shape of the ellipse elucidates the phase differences between the two underlying functions. For example, a Lissajous curve composed of two parametric equations with argument $u$, e.g., $x=\sin(u)$ and $y=\sin(-u+\varphi)$, is a line (circle) when $\varphi=0$ ($\pi/2$). In Fig.  4(a), $\varphi$ obtained by fitting the Lissajous curve approaches $\pi/2$ when $\eta$ increases, indicating the different types of the excitations on the flat and dispersive bands. In Fig.  4(c), we notice that $\|\bar{R}\|_{\eta}$ increases with $\eta$ monotonically, where $\|.\|$ indicates the mean value of the averaged reflectivity $\bar{R}$ over all $\phi$. The numerical simulation agrees with the data.

In conclusion, we experimentally realize Creatz ladders with tunable gauge fields, where the flat band can be selectively excited and the interplay between the flatband localization and the AB phases was investigated. We study the flat-band localization in an open system, where the steady state balanced by pumping, driving, and dissipation exhibits the dynamics in the corresponding closed system [ozawa2014anomalous, ]. We also need to emphasize that our scheme is substantially different from the incoherently pumped polariton-exciton condenstates baboux2016 , harder2020 , masumoto2012 , klembt2017 , whittaker2018 , where coherence is not accessible between multiple CLSs. It is interesting to notice that both bands of the Creutz ladder are topologically non-trivial kremer2020 , kang2020 provided that $\phi\neq 2n\pi$ supp . It is a step towards the simulation of the strong correlated quantum phases, including the fractional Chern insulators bergholtz2013 , disorder-free many-body localization kuno2020 , and unusual ferromagnetism tasaki1992 . An interaction term between the sites in momentum space can be introduced by weakly coupling the excited atomic level to a Rydberg state li2020 or by $s$-wave interactions an2018 , xie2020 . With a negative $\Delta_{c}$, the flat band has the lowest energy and can be used to study the many-body ground states of ultracold atoms li2020 , supp .

We acknowledge the support from the National Natural Science Foundation of China (Grants No. 11934011, No. 11874322, No. 91736209 and No. U1330203), the National Key Research and Development Program of China (Grants No. 2019YFA0308100 and No. 2018YFA0307200), and the Fundamental Research Funds for the Central Universities.

^∗These authors contributed equally to this work.

^†[email protected]

^††junxiang$\_$[email protected]