First Use of a Polarized 3He Neutron Spin Filter on the Back-n White Neutron Source of CSNS
Polarized eV neutrons can address interesting scientific questions in nuclear physics, particle physics, and astrophysics/cosmology. We present the first experiment to polarize the neutrons on the Back-n beamline at the Chinese Spallation Neutron Source (CSNS) using an in-situ NSF using spin-exchange optical pumping (SEOP) of 3He. A 3He polarization of 68%±0.7% for this in-situ NSF was measured through neutron transmission method at Back-n.This is high enough to enable new experiments on the Back-n beamline.
Polarized neutron, Polarized nuclei, CSNS, White neutron, Fundamental physics research, Parity Violation
PACS number(s): 24.80.+y, 67.30.ep, 29.27.Hj , 24.70.+s , 32.10.Dk
1 Introduction
The discovery of parity violation in the decay of polarized 60Co in the late 1950s shocked physicists and motivated a reexamination of the validity of discrete symmetries in physics which remains a vital research frontier. Soon after the discovery of parity violation, in 1964, indirect time reversal symmetry violation was discovered in the 2 decay of the meson[1] which was later accommodated into the CKM matrix. As shown by A. Sakharov[2] in 1967, CP-violation was demonstrated to be an essential criterion required to produce the matter-antimatter asymmetry in the early stage of the universe in Big Bang theory. However the CP violation seen in decay was several orders of magnitude smaller than the size needed to explain the lack of anti-matter we see in today’s universe. Thus, new sources of CP/T violation are required to explain the currently observed baryon asymmetry of the universe within the Big Bang theory.
Starting in the 80s, scientists started the construction of the theory and the experimental search for parity violation in p-wave resonances in heavy nuclei. Very large P-odd effects were discovered in 81Br, 111Cd, 117Sn, 139La and 238U at Dubna [3] and at KEK. In the 90s, the TRIPLE collaboration performed a very broad survey of parity violation in heavy nuclei at LANSCE. They scanned through many nuclei with a neutron beam with energies of 1 eV to several keV, polarized using a polarized proton spin filter at their p-wave resonances. They discovered more than 75 P-odd asymmetries in p-wave resonances and were able to perform a statistical analysis of the distribution of results to show that the observed effects were consistent with the expected size of the nucleon-nucleon weak interaction[18]. The ongoing work of the Neutron Optics Party and Time Reversal EXperiment (NOPTREX) collaboration builds upon the previous work at Dubna, KEK, and LANSCE to continue the search for PV in p-wave resonances and to perform TRIV searches. The Chinese NOPTREX collaboration at China Spallation Neutron Source (CSNS) aims to utilize the special properties of the Back-n white neutron source[20] and 3He neutron polarizer[25] to perform PV and TRIV experiments in China.
Parity Violation (PV) and Time Reversal Invariance Violation (TRIV) can be probed using polarized neutrons in the p-wave resonances of nuclei. More detailed discussions on such new physics search exists[4, 5]. Both PV and TRIV can be amplified in p-wave resonances by very large factors of compared to their size in NN interactions[3, 6, 7]. The amplification occurs through the mixing of p-wave resonances (neutron orbital angular momentum: l=1) and s-wave resonances (l=0) through a parity-odd matrix element. This resonance amplification mechanism makes the compound nucleus a very sensitive system to probe fundamental interactions and is complementary to neutron or nuclear EDM searches[8, 9, 10, 11] which also search for TRIV.
For a neutron of spin , momentum incident on a target nucleus of spin , we can construct an expression for the forward scattering amplitude as the following[4]:
| (1) | ||||
| (2) |
Notice each term reacts differently under parity and/or time-reversal. is P-even/T-even and spin-independent, is P-even/T-even but spin-dependent (leading to the so-called “pseudomagnetic precession ”), is P-odd/T-even the parity violating time-reversal conserving term, is P-odd/T-odd parity and time-reversal violating term and is P-even/T-odd parity conserving time-violating term. A more detailed discussion of the formalism shown above exists [16, 17].
The different symmetries of each term access different physics and require different experimental setups to observe. As we can see from Eqn.1, all the terms excluding the most trivial one have a neutron helicity () dependence which makes a neutron polarizer a critical and essential tool to probe such terms especially and that may lead to a beyond standard model discovery. From thermal to epithermal neutron energies, the SEOP in-situ 3He polarizer is the optimum choice for neutron polarization due to its high neutron polarization efficiency, low cost and convenience in installation relative to a proton polarizer that usually requires a high-power liquid helium cryostat to operate.
The optical theorem of quantum scattering theory relates the imaginary part of the forward scattering amplitude to the total cross-section.
| (3) |
The forward scattering amplitude describes how initial state and final state are connected by the parity violating and parity and time reversal violating weak interaction potentials:
| (4) |
Weak mixing matrix elements and are obtained by acting s- and p- wave resonance wave functions and on and :
| (5) |
The connection between terms and in the approximation where the ixing with the p-wave amplitude is dominated by one nearby s-wave amplitude is then illustrated by the following[16]:
| (6) |
for which is an amplification term and , are the weak mixing matrix elements. and are the difference of and total cross-section by varying neutron helicity going into target nuclei which is directly proportional to the size of observed asymmetries. Term and are both amplified at p-wave resonances by the mixing of s- and p-wave resonances for to times. Although through different channel, the same mixing mechanism lets us connect the size of effect of these two types of asymmetries. By measuring and , we can estimate the size of for a particular p-wave resonance of a nuclei. Due to the statistical model of atomic nuclei, these quantities of interest along with resonance parameters are unique for each individual resonance. Hence, each p-wave resonance of interest should have their size of PV asymmetry and amplification term measured in order to come up with a list of hierarchy for the future TRIV measurement.
A helicty dependent resonance cross-section is defined as the following:
| (7) |
is the helicity dependent resonance cross-section for which is defined as neutron polarization along its direction of travel and as the opposite, is the p-wave resonance cross-section of a nuclear target, is the polarization of the neutron beam and is the parity-odd longitudinal analyzing power which is an intrinsic property of a p-wave resonance.
Longitudinal asymmetry can be measured by transmission of neutrons with opposite helicities through a target defined in the following equation:
| (8) |
where is the helicity dependent neutron transmission yield for which and are defined as neutron polarization aligned and anti-aligned with its momentum vector. for is the detector yield when the p-wave cross section , the number density of the nuclear target in nuclei/cm2. can be rewritten as[18]:
| (9) | ||||
| (10) |
Any non-p-wave resonances or p-waves without an asymmetry will exhibit a near zero behavior on the calculations while the actual effect of interest should reveal itself with an value that stands out from the in nearby neutron energies.
In this paper we describe the first operation of a polarized 3He Neutron Spin Filter (NSF) on the Back-n beamline at the CSNS. The polarized neutron beam created by this device on the Back-n beamline can enable many new types of experimental investigations on the different spectrometers and detector systems installed at this facility. We begin by reviewing the operation principles of polarized 3He NSF and present the transmission measurements that demonstrate the effective operation of the polarized 3He NSF on the Back-n beamline. We then describe the spectrometer systems on the Back-n beamline which we expect to be most well-suited to take advantage of this new polarized beam capability. Finally we describe one example of such a scientific application in the conclusion and discussion section: the search for parity violation in polarized neutron interactions in p-wave neutron-nucleus resonance reactions.
2 Polarized 3He as a NSF
Polarized 3He NSF is a widely used instrument for neutron polarization. 3He NSF is very useful for material science and neutron scattering research due to its high efficiency in polarizing Angstrom-wavelength neutrons. The less well known application of 3He NSF is to polarize neutrons to probe fundamental nucleon nucleon (NN) interactions in the compound nucleus[12, 13, 14]. An off-situ 3He NSF may have a high 3He polarization (8̃5%) to start with[15], the advantage of an in-situ system lies in it’s ability to constantly pump a 3He cell that is in the beam, maintaining a stable polarization for an experiment and is free from cell change.
3He neutron transmission formalism
For unpolarized 3He gas, the neutron transmission is given by the following equation:
| (11) | ||||
| (12) |
is neutron transmission through an empty glass cell with no 3He gas. is the neutron opacity factor. is linearly proportional to the number density of 3He gas, [29] is the total cross section of unpolarized 3He in barn, and the length of 3He gas neutrons have to travel through. For 3He gas, can be expressed into a more convenient form: for which is the pressure of 3He at 20°C in bar, in cm, and is the neutron wavelength in Å. Polarized 3He neutron transmission is given by:
| (13) | ||||
| (14) |
for which is the 3He polarization and let’s define the neutron transmission yield .
The ratio between polarized 3He neutron transmission and unpolarized 3He neutron transmission is then:
| (15) |
Polarization of neutrons through a spin filter is,
| (16) |
We can use the figure of merit ,
| (17) |
to evaluate the analyzing power of certain spin filter system. Using Eqn.15, through the ratio of and , we can obtain the absolute 3He polarization of our in-situ NSF system and the resulting neutron transmission and polarization .

3He polarizer developed at CSNS CSNS neutron polarization device development started in 2019. Since then, a spin-exchange optical pumping (SEOP)-platform[25], a 3He glass cell workshop[26] and further development in 3He polarization instrument techniques[28] were conducted at CSNS. Currently, the group manages to produce a ~8 cm long by 5 cm standard cylindrical 3He GE180 glass cell capable of holding 3.1 bar gas pressure at room temperature which can withstand 200 °C temperature. The previous in-situ system achieves a 74% 3He polarization as measured on BL-20 of CSNS[27]. The typical 3He polarization fluctuation is for the in-situ system we developed at CSNS.
3He transmission experimental results In this experiment, we applied a new-designed in-situ 3He NSF system developed at the CSNS on the Back-n White Neutron Source (WNS). This is the first time that an in-situ 3He SEOP NSF system has been applied to the only WNS in China. From Fig: 2 we can see where the 3He NSF and NTOX detector were placed. The 3He system was placed at a flight path of 55 m from the spallation target at ES#1. NTOX installed at ES#2 down stream of ES#1 at 77.1 m flight path to measure neutron transmission through the 3He NSF. A cell with 2.53 bar pressure, 7.2 cm gas length was used in the in-situ 3He SEOP system shown in Fig:1 [27]. The in-situ 3He NSF system was deployed on the Back-n beam at location ES#1 and the NTOX detector for the neutron flux measurement was located at ES#2. The flight path distance of 77.1m from the spallation target was calibrated using a pre-established method[21].

Our neutron transmission experiment of the 3He in-situ NSF system performed on Back-n beamline took 75 h of data, consisting of a polarized run of 57 h and an unpolarized run of 18 h. The 3He cell was pre-pumped before the experiment for in order to reach maximum polarization. The polarized 3He neutron transmission was measured first, with continuous pumping during the measurement to maintain the high 3He polarization. Second, depolarizing procedure was performed through period off-resonance Adiabatic Fast Passage (AFP) operation. Finally, the neutron transmission for the fully unpolarized in-situ 3He NSF was measured.
A 1.7 mm thick BN (boron nitride) filter was applied upstream in the beamline to extend the neutron energy cutoff to below 19 meV, much lower than the 0̃.3 eV cutoff energy than is normal on the Back-n beam, which usually employs a Cd+Ag+Co filter configuration. Frame overlap was observed for neutron energies lower than 19.4 meV, so data lower than this energy was ignored in our analysis. This was the first experiment of Back-n with such a filter configuration. Normalization of the neutron transmission data was performed using the number of protons injected to the spallation target.

The result shown in Fig:3 is the plot of ratio of polarized 3He transmission data and unpolarized 3He transmission data fitted using Eqn.15. All the data are normalized with the number of protons injected to the spallation target as discussed in the previous section. The error bar on is purely from fitting and does not include any systematic error. The larger error bars in at longer wavelengths in Fig:3 comes from the significant decrease in neutron flux near the cutoff. The neutron flux of Back-n beamline from 0.3 to 0.9 Å (10-1 - 100 eV) is about 10 to 102 lower than higher neutron energy regions [30].
3He system on Parity Violation measurement
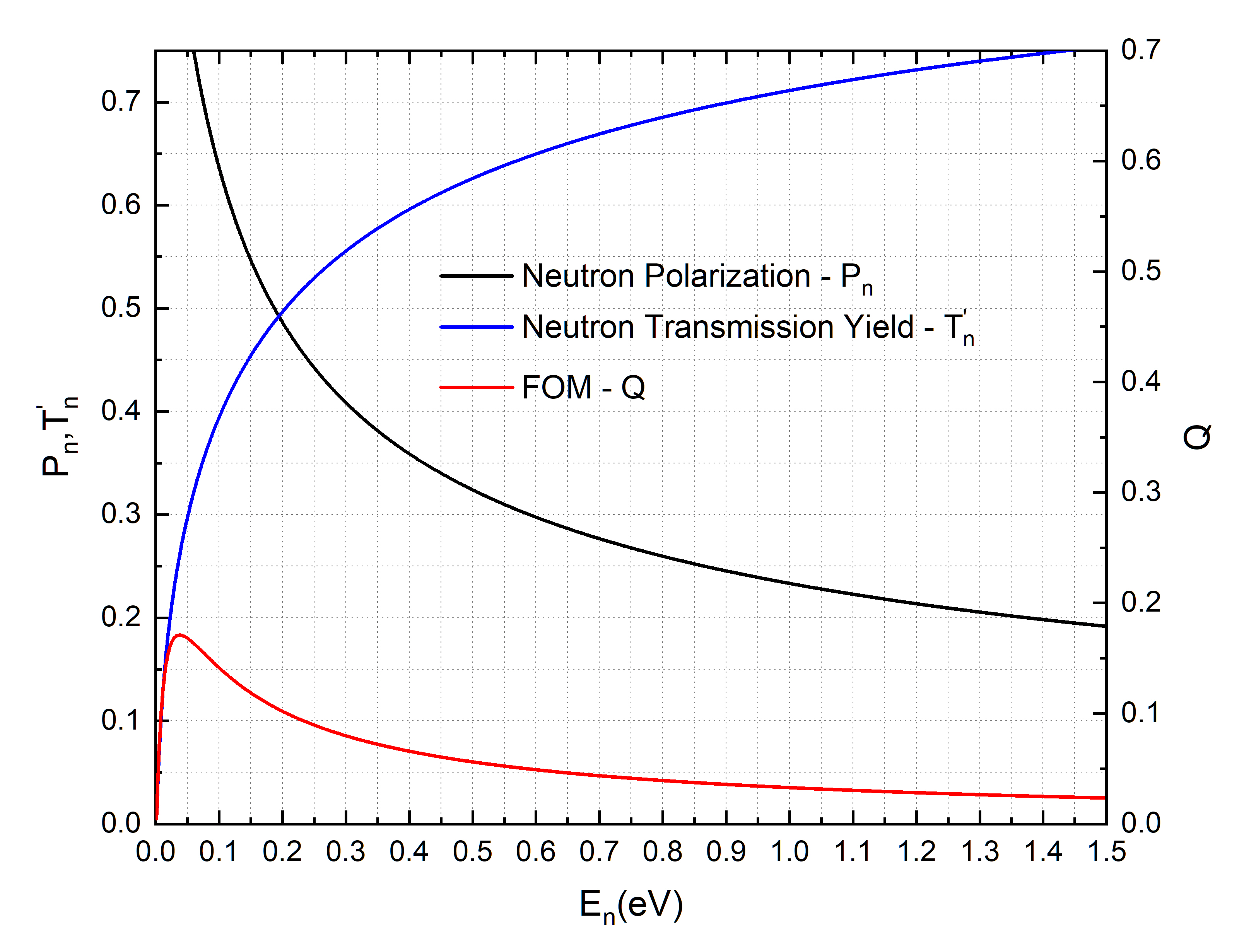
Fig. 4 shows the theoretical performance of a polarized 3He cell of p=2.53 bar, l=7.2 cm and = 68% in the measured in-situ NSF system. Figure of merit Q peaks at 0.038 eV indicates this NSF balances polarization and transmission near this energy.
The effect of neutron polarization fluctuation on the relative error of is:
| (18) |
using the approximated form of from Eqn.9 we get:
| (19) |
using Eqn. 16 we can get the effect of on the relative error of :
| (20) |
If we do an first order approximation on Eqn.16 of just like what we did to to . At thermal to epithermal energy, the contribution of neutron energy uncertainty is significantly suppressed so is treated as a constant here. We then get:
| (21) |
Combining equations above, we get the estimate of the effect of 3He polarization fluctuation on
| (22) | ||||
| (23) |
Eventually, we can estimate the rough size of relative error from 3He polarization fluctuation contributing to the relative error of . Using the in-situ NSF system we discussed before for which: bar, cm, and , for a natLa of 2cm thickness nuclei/cm2, barns, [12], and eV, we get the contribution to be . Hence, such fluctuation in 3He polarization will not be the major source of error in asymmetry measurements.
A commonly used resonance in the measurement of PV as a check to a PV experimental setup is the 0.734 eV p-wave resonance of 139La since it has the largest measured parity violation asymmetry ( 10%) at epithermal neutron region. From Fig. 4 we can see at 0.734 eV there 2̃9% of neutron polarization P. Previous NOPTREX experiments at J-PARC on BL-04[15] used an off-situ 3He cell that provides 2̃7% neutron polarization at 0.734eV when at maximum polarization. This current in-situ polarizer developed at CSNS is capable to carrying out PV measurements for near 1eV p-wave resonances. At 10 eV, only 8% neutron polarization remains. We can still measure to a desired statistical accuracy but with the expense of greatly increase the required beam time. We can see from Eqn.16 we can improve neutron polarization as either the neutron polarization or the opacity factor increases. The simplest solution is to increase by increasing neutron travel through polarized 3He gas which can be achieved through stacking two or more in-situ systems in the beamline.
3 Back-n Beamline Properties and Instrumentation

The CSNS Back-n WNS is an unique beamline due to its wide energy range of incident neutrons, from thermal to 300 MeV, and its long flight path: approximately 54 meters to ES #1 and 77 meters to ES #2. It also features a high neutron flux of when operating at 125 kW power with a 25 Hz double bunch pulse [20]. The NOPTREX collaboration consider the Back-n beamline most suitable for Parity and Time violating asymmetry measurements due to its high flux, long flight path, low beam divergence and spacious ES#1 and ES#2 which opens up many possible experimental setups.
Neutron total cross-sectional spectrometer (NTOX)

The NTOX detector[21] shown in Fig.6 is basically a multilayer fast fission chamber for fission cross-section or neutron total cross-section measurement usually setup at the ES#2 location.
GTAF-II (n,) spectrometer

The Gamma Total Absorption Facility - II (GTAF-II) shown in Fig.7 is a 4 BaF2 (n,) spectrometer located at location ES#2 of Back-n. It consists of 42 detector elements of which 40 are BaF2 scintillation detectors capable of covering near 90% of 4 solid angle[22]. The near unity detection efficiency combined with the high intensity of WNS can perform efficient searches for neutron parity violation in p-wave resonances. Its high precision in neutron energy measurement and the capability of measuring the gamma angular distribution is invaluable in probing T-violating terms in spin-angular correlations between incoming neutrons and outgoing gamma-rays. The combination of a polarized eV neutron beam and a BaF2 gamma calorimeter on an intense spallation neutron source like the CSNS is unique in the world and will enable new physics measurements.
4 Conclusion
An in-situ SEOP 3He neutron polarizer was successfully operated on the Back-n beamline and 3He neutron transmission under different conditions was measured. The 3He NSF achieved a maximum polarization. This successful demonstration opens up various different types of future possible experiments probing fundamental symmetries at the Back-n WNS.
5 Discussion
In this section, we present a possilbe future experiment on the Back-n beamline PV and TRIV experimental setups which only need the addition of a 3He NSF of the type that we have just described. A description of the extensive range of possibilities for combining a WNS with a neutron polarizer warrants a separate article.
P-odd/T-even() experiment

In Fig. 8 is the setup which can probe the P-odd/T-even parity violating time reversal conserving term. By changing the direction of polarization of the 3He NSF, T+/- or R+/- can be measured and an asymmetry acquired as specified in Eqn:8. The two methods differ mainly in the means of detection from an instrumental point of view. At Back-n, the existing spectrometers that are most adequate for the requirements of both PV experiment methods are NTOX and GTAF shown in Fig.6 and Fig.7 respectively.
6 Acknowledgement
W.M.S. and M.Z. acknowledge support from the US National Science Foundation (NSF) grant PHY-2209481 and the Indiana University Center for Spacetime Symmetries. The work was supported by National Natural Science Foundation of China funded projects (12205326). This work was also supported by the National Key Research and Development Program of China (Grant No. 2020YFA0406000, No. 2020YFA0406004 and 2023YFA1606602). The 3He spin filter implemented in the experiment was developed within the Guangdong Provincial Key Laboratory of Extreme Conditions: 2023B1212010002 and the Dongguan Introduction Program of Leading Innovative and Entrepreneurial Talents (No. 20191122).
References
- [1] J. H. Christenson, J. W. Cronin, V. L. Fitch, and R. Turlay Phys. Rev. Lett. 13, 138(1964).
- [2] A. D. Sakharov, “Violation of CP Invariance, C Asymmetry, and Baryon Asymmetry of the Universe”, Pisma Zh. Eksp. Teor. Fiz. 5, 32 (1967).
- [3] V.P. Alfimenkov et al., Nucl.Phys.A 398 (1983) 93-106.
- [4] J. David Bowman and Vladimir Gudkov, ”Search for time reversal invariance violation in neutron transmission”, Phys. Rev. C 90, 065503 (2014)
- [5] William Michael Snow, Chris Haddock and Ben Heacock, ”Searches for Exotic Interactions Using Neutrons”, Symmetry 2022, 14, 10.
- [6] V. E. Bunakov and V. P. Gudkov, Nucl. Phys. A 401, 93 (1983) .
- [7] V. P. Gudkov, Phys. Rep. 212, 77 (1992).
- [8] M. Pospelov and A. Ritz, “Electric dipole moments as probes of new physics”, Ann. Phys. 318, 119 (2005).
- [9] J. Engel, M. J. Ramsey-Musolf, U. van Kolck, “Electric Dipole Moments of Nucleons, Nuclei, and Atoms: The Standard Model and Beyond”, Prog. Part. Nucl. Phys. 71, 21 (2013).
- [10] C. Abel et al., Phys. Rev. Lett. 124, 081803 (2020)
- [11] T. A. Zheng, Y. A. Yang, S.-Z. Wang, J. T. Singh, Z.-X. Xiong, T. Xia, and Z.-T. Lu, Phys. Rev. Lett. 129, 083001 (2022)
- [12] K. P. Coulter et al., Nuclear Instruments and Methods in Physics Research A 288 (1990) 463-466
- [13] Yamamoto T. et al., EPJ Web Conf., 219 (2019), p. 09002
- [14] Yamamoto T. et al., Phys. Rev. C, 101 (2020), p. 064624
- [15] Okudaira T et al., 2020 Nucl. Instrum. Methods A 977 164301
- [16] V. Gudkov and H. M. Shimizu, “Nuclear spin dependence of time reversal invariance violating effects in neutron scattering”, Phys. Rev. C 97, 065502 (2018).
- [17] V. Gudkov and H. M. Shimizu, Phys. Rev. C 102, 015503 (2020).
- [18] G.E. Mitchell, J.D. Bowman, S.I. Penttila , E.I. Sharapov, Parity violation in compound nuclei: experimental methods and recent results, Physics Reports 354 (2001) 157–241
- [19] M. T. Gericke et al., Upper bounds on parity-violating γ -ray asymmetries in compound nuclei from polarized cold neutron capture, Phys. Rev. C 74, 065503 (2006).
- [20] Jing-Yu Tang, et al., Back-n white neutron source at CSNS and its applications, Nuclear Science and Techniques, 32 (2021) 11
- [21] Liu, XY., Yang, YW., Liu, R. et al. Measurement of the neutron total cross section of carbon at the Back-n white neutron beam of CSNS. NUCL SCI TECH 30, 139 (2019).
- [22] Zhang Qi-Wei et al., Acta Phys. Sin. Vol. 70, No. 22 (2021) 222801
- [23] M. Batz, S. Baeßler, W. Heil, E., W. Otten, D. Rudersdorf, J., Schmiedeskamp, Y. Sobolev, and M. Wolf, 3He Spin Filter for Neutrons, J. Res. Natl. Inst. Stand. Technol. 110, 293-298 (2005)
- [24] G.L. Jones, T.R. Gentile, A.K. Thompson, Z. Chowdhuri, M.S. Dewey, W.M. Snow, and F.E. Wietfeldt, Test of 3He-based neutron polarizers at NIST, Nuclear Instruments and Methods in Physics Research A 440 (2000) 772-776
- [25] Chuyi Huang et al 2021 Chinese Phys. Lett. 38 092801
- [26] Zecong Qin et al 2021 Chinese Phys. Lett. 38 052801
- [27] Zhang, J., Huang, C., Qin, Z. et al. In-situ optical pumping for polarizing 3He neutron spin filters at the China Spallation Neutron Source. Sci. China Phys. Mech. Astron. 65, 241011 (2022).
- [28] Long Tian et al 2023 J. Phys.: Conf. Ser. 2481 012008
- [29] W. Heil, J. Dreyer, D. Hofmann, H. Humblot, E.Lelievre-Berna, andF. Tasset, Phys. B-Condens. Matter 267-268, 328 (1999).
- [30] Yonghao Chen, et al., Neutron energy spectrum measurement of the Back-n white neutron source at CSNS, Eur. Phys. J. A (2019) 55: 115