First principles theory for the magnetic and charge instabilities in AV3Sb5 systems
Abstract
Vanadium-based materials AV3Sb5 (A=K, Rb, Cs) with layered kagome lattice structures have drawn great attention recently due to the discoveries of topologically nontrivial band structures, charge density wave states, giant anomalous Hall effect, as well as unusual superconducting phase at low temperatures. In this work, we theoretically study the magnetic and charge instabilities for this class of materials based on first principles calculations. We develop a method to calculate the generalized susceptibility tensor defined in the sublattice-orbital-spin space, with the effects of Coulomb interactions treated by generalized random phase approximation (RPA). The RPA susceptibility calculations indicate that there are three leading ferromagnetic instability modes at point, which are further verified by unrestricted self-consistent Hartree-Fock calculations including both the on-site and inter-site Coulomb interactions. The inclusion of inter-site interactions tend to suppress the spin ferromagnetism due to charge transfer from the V to Sb sites, leading to weak spin magnetic moments per V atom with small intrinsic anomalous Hall conductivity. Current loops can be generated in such weak spin ferromagnetic states as a result of spin-orbit coupling effects, giving rise to orbital magnetic fluxes. The electronic structures in the ferromagnetic states are significantly reconstructed which have nearly compensated electron and hole carriers from two bands. On the other hand, we do not find any diverging instability mode at point driven by electron-electron Coulomb interactions. First principles phonon calculations indicate that there are unstable phonon modes which tend to drive the system into an inverse star-of-David structure. Our results indicate that there may be separate phase transitions in the magnetic and charge channels in the system.
pacs:
Quantum materials with layered kagome structures are of great interest due to the frustrated lattice geometry, which can give rise to interesting non-interacting band structures with both flat bands and Dirac cones Bergman et al. (2008). The nontrivial Berry phase associated with the Dirac fermions and the vanishing kinetic energy of the flat bands make the kagome lattice system an ideal platform to study the interplay between band topology and strong electron-electron (-) correlations, which can lead to various exotic quantum states Tang et al. (2011); Kiesel et al. (2013a); Wang et al. (2013); Kiesel and Thomale (2012); Yu and Li (2012); Yin et al. (2018); Ye et al. (2018); Liu et al. (2018); Yin et al. (2020); Ko et al. (2009); Balents (2010); Kiesel et al. (2013b). Recently, vanadium-based layered kagome materials AV3Sb5 (A=K, Rb, Cs) have been successfully synthesized Ortiz et al. (2019); Yang et al. (2020), which exhibit various intriguing properties including charge density wave states Jiang et al. (2021a); Li et al. (2021a); Yu et al. (2021a); Liang et al. (2021); Zhao et al. (2021a); Li et al. (2021b); Wang et al. (2021a); Ortiz et al. (2021a); Nakayama et al. (2021); Li et al. (2021c); Kang et al. (2021); Xiang et al. (2021); Wang et al. (2021b); Liu et al. (2021); Cho et al. (2021); Zhou et al. (2021); Xie et al. (2021); Wulferding et al. (2021); Wang et al. (2021c); Song et al. (2021), the signature of time-reversal symmetry breaking Yang et al. (2020); Mielke III et al. (2021); Yu et al. (2021b); Wu et al. (2021a), as well as unusual superconductivity Ortiz et al. (2021b); Yin et al. (2021a); Ortiz et al. (2020); Chen et al. (2021a); Zhang et al. (2021); Chen et al. (2021b); Li et al. (2021d); Zhao et al. (2021b); Gupta et al. (2021); Xu et al. (2021); Yu et al. (2021c); Lou et al. (2021); Ni et al. (2021); Song et al. (2021); Chen et al. (2021c); Yin et al. (2021b).
These experimental observations have boosted intensive theoretical interest Park et al. (2021); Wu et al. (2021b); Denner et al. (2021); Miao et al. (2021); Lin and Nandkishore (2021); Feng et al. (2021a); Consiglio et al. (2021); Ye et al. (2021); Tan et al. (2021); Gu et al. (2021); Wang et al. (2021d); Jiang et al. (2021b); Feng et al. (2021b). First principles calculations reveal that the band structures of AV3Sb5 are topologically nontrivial with nonzero indices and Dirac-like linear dispersions, and there are multiple van Hove singularties near the Fermi level Ortiz et al. (2020). Theoretical studies on the interaction-driven Fermi-surface instabilities based on simplified model Hamiltonians predict the presence of “chiral flux modes” and various other instability channels, which provide a unified picture for the formation of charge density wave and time-reversal breaking states Wu et al. (2021b); Feng et al. (2021a); Gu et al. (2021).
However, recent phonon calculations indicate the presence of unstable phonon modes in the system, which provides another possible scenario for the emergence of CDW phase Tan et al. (2021); Wang et al. (2021d); Cho et al. (2021); Ye et al. (2021). There are also a lot of sublattice, orbital, and spin degrees of freedom in each primitive cell, and interactions can lead to incredibly complicated symmetry-breaking states in the charge-orbit-spin space. In order to unambiguously identify the leading Fermi-surface instability modes and shed light on the nature of the charge and magnetic properties in this system, we calculate the generalized two-particle susceptibility tensor defined the sublattice-orbital-spin space based on realistic 60-band Wannier tight-binding models generated from first principles calculations, including the effects of Coulomb interactions as treated by random phase approximation Ren et al. (2012); Korshunov (2014). Taking the leading eigenmodes of the generalized susceptibility tensor as an initial ansatz, we further perform un-restricted self consistent Hartree Fock calculations for both primitive cell and inverse-star-of-David (ISD) structures of AV3Sb5 (A=K, Rb, Cs) system, including both on-site Kanamori-type interactions and inter-site density-density interactions, with nonlocal exchange effects being treated exactly. Through these calculations, we find that the ground-state manifold of the system consists of three nearly degenerate spin ferromagnetic states. The inclusion of inter-site Coulomb interactions tend to suppress the spin ferromagnetism, leading to weak spin magnetic moments per V atom. Charge current loops (with current amplitudes nA) can be generated in such weak spin ferromagnetic states as a result of spin-orbit coupling effects, giving rise to orbital magnetic fluxes threaded through the kagome plane. We further study the phonon properties of the AV3Sb5 (A=K, Rb, Cs) system, and find unstable phonon modes that can give rise to the ISD crystal structure, which implies a phonon-driven mechanism for the CDW phase. Our results indicate that there are separate magnetic and charge instabilities in the system, and that there may be additional magnetic phase transition within the ISD CDW phase.
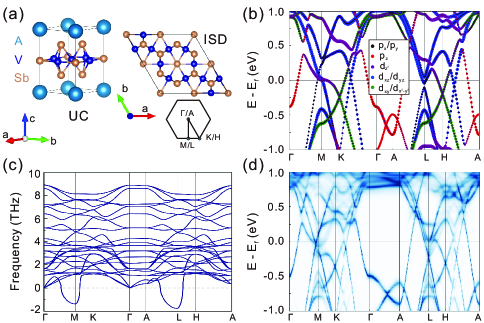
Preliminaries —
The AV3Sb5 (A=K, Rb, Cs) system crystallizes in a layered kagome lattice structure as shown in Fig. 1(a). In each primitive cell there are three V sublattices forming kagome plane, within which one Sb atom is intercalated into each primitive cell. There are two layers of Sb atoms forming honeycomb lattices above and below the vanadium kagome planes, forming V-Sb hexahedra frameworks. The alkali metal are further intercalated between the V-Sb layers, donating electrons and making this system highly metallic. In Fig. 1(b) we show the band structure of RbV3Sb5 projected onto V orbitals and Sb orbitals in the pristine lattice structure which are calculated by first principles density functional theory (DFT). Clearly there are Dirac-like dispersions near and points contributed by V orbitals, van Hove singularities near point contributed by both V and Sb orbitals, as well as electron pockets centered at which are mostly contributed by Sb orbitals. Such complicated Fermi surfaces and orbital characters make it difficult to realistically describe the electronic structure of this system using a simplified lattice model with few orbitals. In Fig. 1(c) we present the phonon dispersions calculated by DFT, where we see two unstable phonon modes at the and points, consistent with previous reports. A linear combination of the unstable modes at the three equivalent points result in an inverse-star-of-David structure with supercell as shown in the right panel of Fig. 1(a). The band structures of the system are strongly re-constructed in the ISD lattice structure as clearly shown by the spectral function unfolded to the original primitive Brillouin zone (Fig. 1(d)), and new van Hove singularities emerge as a result of the lattice deformation Cho et al. (2021).
Fermi surface instabilities —
The presence of van Hove singularities both in the pristine and in the ISD structures indicate that the non-interacting Fermi surfaces may be unstable to Coulomb interactions. In order to study the interaction effects on the complicated Fermi surfaces with diverse orbital characters as shown in Fig. 1(b), we construct a realistic tight-binding model in the Wannier-function basis using the Wannier90 code package Mostofi et al. (2008). To be specific, the Bloch functions generated from DFT calculations are projected onto 60 spinor Wannier functions (for each pristine primitive cell) including all the V 3 orbitals and Sb orbitals, from which we obtain the following Wannier tight-binding model denoted by :
| (1) |
where the sets of indices , , denote, in turn, all the V and Sb atomic sites, orbitals and spin degrees of freedom, and denotes the real-space hopping amplitude including spin-orbit coupling effects . and are the electron creation and annihilation operators. The Wannier interpolated band structures can exactly reproduce those obtained from DFT calculations within an energy window extending from 2 eV below to 2 eV above the Fermi energy. We include the on-site multi-orbital Coulomb interactions of the Kanamori type for the V 3 orbitals Kanamori (1963),
| (2) |
where and are the intra-orbital and inter-orbital direct Coulomb interactions. and denote the Hunds’ coupling and pair hoppings respectively, and is the density operator. We set eV and eV throughout this paper, and we let and such that Eq. (2) has full rotational invariance Georges et al. (2013). We further consider the density-density inter-site interactions between the neighboring V-Sb sites and V-V sites, the interaction amplitudes are denoted by and respectively,
where “” means a summation over all the first-neighbor V-Sb sites (including both intralayer ones and interlayer ones), and the symbol “” means summing over all the in-plane nearest neighbor V-V sites. In this work and are treated as two free parameters which vary from 0 to 1 eV. The full Hamiltonian is then .
As discussed above, the system has a quite complicated primitive cell with multiple sublattice, orbital, and spin degrees of freedom. For the 60-band tight-binding model, there are 3600 independent matrix elements of the density operator (consider as sublattice sites within the same primitive cell), each of which can be considered as an “order parameter” that break certain symmetries of the system and bring about Fermi surface instability. The actual ground state may be characterized by a complicated linear combination of the density matrix elements, which is difficult to guess a priori due to such complexity. Therefore, in order to find the leading Fermi-surface instability mode, we propose to calculate the interaction-renormalized generalized susceptibility tensor defined in the sublattice-orbital-spin space, the tensor element of which is denoted as , with being a composite index referring to all the sublattice, orbital, and spin degrees of freedom (so do , and ). Suppose there is a weak static field with wavevector that is only coupled with some given element of the density operator (denoted as ) is applied to the system, a change of density matrix element would be induced by the field, i.e., . One can further consider a field that is only coupled to (or “parallel” to) the th eigenmode of the susceptibility tensor, i.e., , then the system would respond to such a field along the eigenvector direction via
| (3) |
where and are the eigenvalues and eigenvectors of the susceptibility tensor . If any of the eigenmodes has a diverging eigenvalue , it means that the system would develop a spontaneous order parameter characterized by the diverging eigenmode upon the application of an infinitesimal field, and would enter a spontaneous symmetry-breaking state through a second order phase transition. Note that similar idea has been used in the studies of surface-state instabilities of nodal-line semietals Liu and Balents (2017) and octupolar instabilities of RuCl3 etc. Qiu et al. (2021); Uehara et al. (2015)
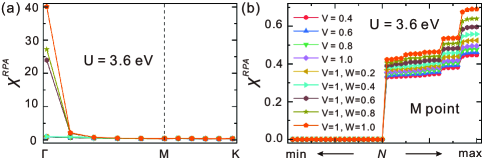
Following the above argument, we calculate the generalized susceptibility tensor for the AV3Sb5 (A=K, Rb, Cs) system based on the Wannierized tight-binding Hamiltonian given by Eqs. (1)-(LABEL:eq:intersite), and the effects of the on-site and inter-site Coulomb interactions are treated by random phase approximation (RPA), the details of which are presented in Supplementary Information sup . For clarity’s sake, in main text we only present the results for RbV3Sb5, and the results of the other two compounds are given in Supplementary Information sup . In Fig. 2(a) we present the 10 eigenmodes with maximal eigenvalues (of the RPA susceptibility) as a function of the wavevector , with on-site interaction only and the inter-site interactions being temporarily turned off. We see that there are three diverging modes only at point. These diverging modes at point turn out to be three spin magnetic modes. The inclusion of inter-site interactions does not change the diverging nature of the three spin ferromagnetic modes.On the other hand, since the system undergoes a CDW transition forming an ISD structure around 100 K, it is worthwhile to study the microscopic origin of such CDW transition. In such a context, we also carefully study the eigenmodes of the RPA susceptibility tensor at the three points, and find that there are no notable unstable modes. We further include V-Sb and V-V inter-site interactions, and find that the eigenvalues of the susceptibility tensor at points only increase by small amounts due to the inclusion of intersite interactions, as clearly shown in Fig. 2(b), where the different markers represent data sets for different choices of and values. Therefore, the CDW phase is likely driven by phonon instability and electron-phonon couplings instead of - interactions.
Hartree-Fock calculations —
In order to verify the conclusions obtained from the susceptibility calculations, we further perform un-restricted self-consistent Hartree-Fock (HF) calculations including both the on-site Kanamori interaction (Eq. (2)) and the inter-site interactions (Eq. (LABEL:eq:intersite)), with the nonlocal exchangee effects being treated exactly. We first perform HF calculations for the pristine primitive cell, and we take the three leading instability modes at point (Fig. 2(a)) as initial anstza for the density matrices in the HF calculations. The HF ground states turn out to be three spin ferromagnetic states with the magnetizations primarily pointing along the crystalline , , and directions with slight cantings, which are denoted as FMx, FMy, and FMz states respectively. With on-site interactions only (eV, eV, ), the spin magnetization is as large as per V atom. Real-space current loops are generated in the ferromagnetic states as a result of spin-orbit coupling, which are shown in the three panels of Fig. 3(a) for the FMy, FMz, and FMx phases. The red (double) arrows indicate interlayer V-Sb currents, while the black arrows indicate V-V in-plane currents. The maximal current amplitudes nA, generating an orbital moment , e.g., for the hexagonal current loop in the middle panel of Fig. 3(a). The filling dependence of the calculated anomalous Hall conductivity (AHC) in the FMz state is shown in Fig. 3(b), where we see a peak of S/cm when the Fermi energy is assumed to be eV above the physical Fermi energy; otherwise is quite small S/cm. The HF band structures (with on-site interactions only) are shown in Fig. 3(c).
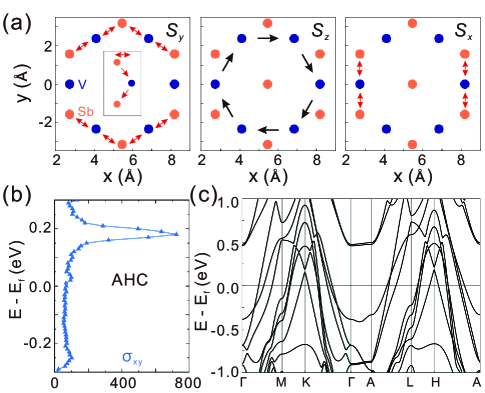
The results presented in Fig. 3 are generated for the case with on-site interactions only. The inclusion of inter-site interactions, e.g., with eV and , would significantly suppress the spin ferromagnetism, resulting in a spin moment per V atom, and the corresponding AHC is two orders of magnitudes smaller S/cm. This can be interpreted from the charge transfer induced by the inter-site Sb-V Coulomb interactions. Once the inter-site interaction is taken into account, charges tend to transfer from the V to the Sb sites to minimize the Hartree energy, resulting in a charge occupation per V atom for eV, which is reduced by a factor of 6 compared with the case when . As a result, the spin magnetization driven by the strong on-site Coulomb interactions of the V sites is also significantly diminished. Moreover, the energies differences of the three FM states are incredibly close to each other meV, which imply strong magnetic fluctuations in real space. Therefore, the giant anomalous Hall effect observed in experiments Yang et al. (2020) likely arises from skew scatterings due to strong real-space magnetic fluctuations Ishizuka and Nagaosa (2021). The detailed results for the HF calculations including inter-site interactions with pristine primitive cell are presented in Supplementary Information sup .
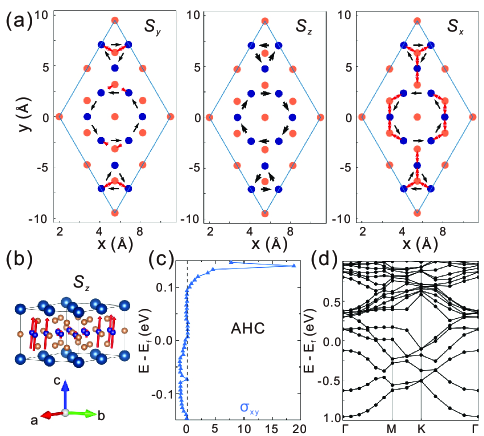
We have also performed un-restricted self-consistent HF calculations for the ISD lattice structure with a realistic tight-binding model including 240 Wannier orbitals, including both the on-site and inter-site interactions as given by Eqs. (1)-(LABEL:eq:intersite), and the non-local exchange effects are treated exactly. We take the three spin ferromagnetic modes at point and four leading modes at point (obtained from RPA susceptibility calculations) as our initial ansatz for the HF calculations. The ground states, again, involve three nearly degenerate spin ferromagnetic states with their magnetizations pointing along the crystalline , , and directions respectively, with the energy difference meV. Similar to the case of pristine primitive cell, the magnetizations in the ISD structure are on the order of if only on-site interactions are included, and can be suppressed by one order of magnitude due to the inclusion of inter-site interactions. Interestingly, in the ISD structure, the magnetization distribution is inhomogeneous within the ISD primitive cell: the spin magnetizations are mostly concentrated at the six V atoms forming two contracted kagome triangles, and the other six V atoms forming a hexagon have nearly vanishing spin magnetizations, as schematically shown in Fig. 4(b) for the FMz phase.
As in the case of the pristine cell, current loops are generated in the FM states as a result of spin-orbit coupling. The current-loop patterns in the three FM states are shown in Fig. 4(a) for the FMy, FMz, and FMx states respectively. For example, for the FMz state, there are three current loops: two of them are counter-clockwise circulating around the two kagome triangles, and the other one is clockwise circulating around the hexagon. With the intersite interaction eV, the current amplitudes are very small nA, which can generate a small orbital moment for each current loop. We have further calculated the anomalous Hall conductivities of the three FM states in the ISD structure. The inclusion of V-Sb inter-site Coulomb interactions significantly suppress ferromagnetism and anomalous Hall effect (AHE), and the calculated AHC in the FMz state S/cm as shown in Fig. 4(c). Again, this indicates an incredibly small intrinsic contribution to AHE, and the giant AHC measured in experiments Yang et al. (2020) are likely due to skew scatterings from the strong magnetic fluctuations in real-space by virtue of the near degeneracy of the three ferromagnetic states Ishizuka and Nagaosa (2021). In Fig. 4(d), we have shown the calculated HF band structures of the ISD structure (plotted in the supercell Brillouin zone) with intersite interaction V=1.0 eV, from which we see a strong renormalization effects on the electronic structures due to the inclusion of nonlocal interactions. Notably, the Fermi surfaces are mostly contributed by two bands with nearly compensated electron-type and hole-type carriers due to the onset of magnetism, which is consistent with the Hall-effect measurements below K Yang et al. (2020). Our results indicate that there may be two transitions in the AV3Sb5 (A=K, Rb, Cs) system, the first one is the phonon-driven CDW transition, and the other is the magnetic transition (likely with lower ) marked by the emergence of giant anomalous Hall effect and the reconstruction of Fermi surfaces due to the onset of weak spin ferromagnetism.
Summary —
To summarize, in this work we have comprehensively studied the magnetic and charge instabilities of the AV3Sb5 system based on first principles tight-binding models including effects of both on-site and inter-site Coulomb interactions. Results from both RPA susceptibility calculations and un-restricted Hartree-Fock calculations indicate that the leading Fermi-surface instabilities driven by - interactions are three nearly degenerate spin ferromagnetic modes regardless whether the system is in the pristine structure or ISD structure. The competition between the nearly degenerate ferromagnetic states can lead to strong real-space magnetic fluctuations, which may be responsible for the giant anomalous Hall effect observed in experiments. Current loops can be generated in the weak spin ferromagnetic states as a result of spin-orbit coupling effects, giving rise to spin-dependent orbital magnetic fluxes. The electronic structures in the ferromagnetic states are significantly reconstructed which have nearly compensated electron and hole carriers from two bands, which may explain the recent transport data at low temperatures. On the other hand, we do not find any diverging instability mode at point driven by electron-electron Coulomb interactions. The unstable phonon modes at and points indicate that the CDW state in the system is likely driven by phonon instability and electron-phonon couplings. Our results imply separate magnetic and charge instabilities in the AV3Sb5 (A=K, Rb, Cs) system, and the system may undergo an additional magnetic phase transition marked by the onset of anomalous Hall effect and reconstruction of Fermi surfaces at a critical temperature lower than the CDW transition temperature. Our work sheds light on the puzzling magnetic and charge properties of the V-based kagome metal systems, and will provide useful guidelines for future studies.
Acknowledgements.
Acknowledgements. —
We thank Yueshen Wu, Jun Li, Kun Jiang, and Zheng Han for valuable discussions. This work is supported by the National Science Foundation of China (grant no. 12174257), the National Key R & D program of China (grant no. 2020YFA0309601), and the start-up grant of ShanghaiTech University.
References
- Bergman et al. (2008) D. L. Bergman, C. Wu, and L. Balents, Phys. Rev. B 78, 125104 (2008).
- Tang et al. (2011) E. Tang, J.-W. Mei, and X.-G. Wen, Phys. Rev. Lett. 106, 236802 (2011).
- Kiesel et al. (2013a) M. L. Kiesel, C. Platt, and R. Thomale, Phys. Rev. Lett. 110, 126405 (2013a).
- Wang et al. (2013) W.-S. Wang, Z.-Z. Li, Y.-Y. Xiang, and Q.-H. Wang, Phys. Rev. B 87, 115135 (2013).
- Kiesel and Thomale (2012) M. L. Kiesel and R. Thomale, Phys. Rev. B 86, 121105 (2012).
- Yu and Li (2012) S.-L. Yu and J.-X. Li, Phys. Rev. B 85, 144402 (2012).
- Yin et al. (2018) J.-X. Yin, S. S. Zhang, H. Li, K. Jiang, G. Chang, B. Zhang, B. Lian, C. Xiang, I. Belopolski, H. Zheng, et al., Nature 562, 91 (2018).
- Ye et al. (2018) L. Ye, M. Kang, J. Liu, F. Von Cube, C. R. Wicker, T. Suzuki, C. Jozwiak, A. Bostwick, E. Rotenberg, D. C. Bell, et al., Nature 555, 638 (2018).
- Liu et al. (2018) E. Liu, Y. Sun, N. Kumar, L. Muechler, A. Sun, L. Jiao, S.-Y. Yang, D. Liu, A. Liang, Q. Xu, et al., Nature physics 14, 1125 (2018).
- Yin et al. (2020) J.-X. Yin, W. Ma, T. A. Cochran, X. Xu, S. S. Zhang, H.-J. Tien, N. Shumiya, G. Cheng, K. Jiang, B. Lian, et al., Nature 583, 533 (2020).
- Ko et al. (2009) W.-H. Ko, P. A. Lee, and X.-G. Wen, Physical Review B 79, 214502 (2009).
- Balents (2010) L. Balents, Nature 464, 199 (2010).
- Kiesel et al. (2013b) M. L. Kiesel, C. Platt, and R. Thomale, Physical review letters 110, 126405 (2013b).
- Ortiz et al. (2019) B. R. Ortiz, L. C. Gomes, J. R. Morey, M. Winiarski, M. Bordelon, J. S. Mangum, I. W. Oswald, J. A. Rodriguez-Rivera, J. R. Neilson, S. D. Wilson, et al., Physical Review Materials 3, 094407 (2019).
- Yang et al. (2020) S.-Y. Yang, Y. Wang, B. R. Ortiz, D. Liu, J. Gayles, E. Derunova, R. Gonzalez-Hernandez, L. vSmejkal, Y. Chen, S. S. Parkin, et al., Science advances 6, eabb6003 (2020).
- Jiang et al. (2021a) Y.-X. Jiang, J.-X. Yin, M. M. Denner, N. Shumiya, B. R. Ortiz, G. Xu, Z. Guguchia, J. He, M. S. Hossain, X. Liu, et al., Nature Materials pp. 1–5 (2021a).
- Li et al. (2021a) H. Li, S. Wan, H. Li, Q. Li, Q. Gu, H. Yang, Y. Li, Z. Wang, Y. Yao, and H.-H. Wen, arXiv preprint arXiv:2107.11326 (2021a).
- Yu et al. (2021a) F. H. Yu, T. Wu, Z. Y. Wang, B. Lei, W. Z. Zhuo, J. J. Ying, and X. H. Chen, Phys. Rev. B 104, L041103 (2021a).
- Liang et al. (2021) Z. Liang, X. Hou, F. Zhang, W. Ma, P. Wu, Z. Zhang, F. Yu, J.-J. Ying, K. Jiang, L. Shan, et al., Physical Review X 11, 031026 (2021).
- Zhao et al. (2021a) H. Zhao, H. Li, B. R. Ortiz, S. M. Teicher, T. Park, M. Ye, Z. Wang, L. Balents, S. D. Wilson, and I. Zeljkovic, Nature 599, 216 (2021a).
- Li et al. (2021b) H. Li, Y.-X. Jiang, J. Yin, S. Yoon, A. R. Lupini, C. Nelson, A. Said, Y. Yang, H. Lei, B. Yan, et al., arXiv e-prints pp. arXiv–2109 (2021b).
- Wang et al. (2021a) Z. Wang, Y.-X. Jiang, J.-X. Yin, Y. Li, G.-Y. Wang, H.-L. Huang, S. Shao, J. Liu, P. Zhu, N. Shumiya, et al., Physical Review B 104, 075148 (2021a).
- Ortiz et al. (2021a) B. R. Ortiz, S. M. Teicher, L. Kautzsch, P. M. Sarte, N. Ratcliff, J. Harter, J. P. Ruff, R. Seshadri, and S. D. Wilson, Physical Review X 11, 041030 (2021a).
- Nakayama et al. (2021) K. Nakayama, Y. Li, T. Kato, M. Liu, Z. Wang, T. Takahashi, Y. Yao, and T. Sato, Physical Review B 104, L161112 (2021).
- Li et al. (2021c) H. Li, H. Zhao, B. R. Ortiz, T. Park, M. Ye, L. Balents, Z. Wang, S. D. Wilson, and I. Zeljkovic, arXiv preprint arXiv:2104.08209 (2021c).
- Kang et al. (2021) M. Kang, S. Fang, J.-K. Kim, B. R. Ortiz, J. Yoo, B.-G. Park, S. D. Wilson, J.-H. Park, and R. Comin, arXiv preprint arXiv:2105.01689 (2021).
- Xiang et al. (2021) Y. Xiang, Q. Li, Y. Li, W. Xie, H. Yang, Z. Wang, Y. Yao, and H.-H. Wen, arXiv e-prints pp. arXiv–2104 (2021).
- Wang et al. (2021b) Z. Wang, S. Ma, Y. Zhang, H. Yang, Z. Zhao, Y. Ou, Y. Zhu, S. Ni, Z. Lu, H. Chen, et al., arXiv preprint arXiv:2104.05556 (2021b).
- Liu et al. (2021) Z. Liu, N. Zhao, Q. Yin, C. Gong, Z. Tu, M. Li, W. Song, Z. Liu, D. Shen, Y. Huang, et al., arXiv preprint arXiv:2104.01125 (2021).
- Cho et al. (2021) S. Cho, H. Ma, W. Xia, Y. Yang, Z. Liu, Z. Huang, Z. Jiang, X. Lu, J. Liu, Z. Liu, et al., Phys. Rev. Lett. 127, 236401 (2021).
- Zhou et al. (2021) X. Zhou, Y. Li, X. Fan, J. Hao, Y. Dai, Z. Wang, Y. Yao, and H.-H. Wen, Phys. Rev. B 104, L041101 (2021).
- Xie et al. (2021) Y. Xie, Y. Li, P. Bourges, A. Ivanov, Z. Ye, J.-X. Yin, M. Z. Hasan, A. Luo, Y. Yao, Z. Wang, et al., arXiv preprint arXiv:2111.00654 (2021).
- Wulferding et al. (2021) D. Wulferding, S. Lee, Y. Choi, Q. Yin, Z. Tu, C. Gong, H. Lei, and K.-Y. Choi, arXiv preprint arXiv:2108.11690 (2021).
- Wang et al. (2021c) Z. X. Wang, Q. Wu, Q. W. Yin, C. S. Gong, Z. J. Tu, T. Lin, Q. M. Liu, L. Y. Shi, S. J. Zhang, D. Wu, et al., Phys. Rev. B 104, 165110 (2021c).
- Song et al. (2021) B. Q. Song, X. M. Kong, W. Xia, Q. W. Yin, C. P. Tu, C. C. Zhao, D. Z. Dai, K. Meng, Z. C. Tao, Z. J. Tu, et al., arXiv e-prints arXiv:2105.09248 (2021).
- Mielke III et al. (2021) C. Mielke III, D. Das, J.-X. Yin, H. Liu, R. Gupta, C. Wang, Y.-X. Jiang, M. Medarde, X. Wu, H. Lei, et al., arXiv preprint arXiv:2106.13443 (2021).
- Yu et al. (2021b) L. Yu, C. Wang, Y. Zhang, M. Sander, S. Ni, Z. Lu, S. Ma, Z. Wang, Z. Zhao, H. Chen, et al., arXiv preprint arXiv:2107.10714 (2021b).
- Wu et al. (2021a) Q. Wu, Z. Wang, Q. Liu, R. Li, S. Xu, Q. Yin, C. Gong, Z. Tu, H. Lei, T. Dong, et al., arXiv preprint arXiv:2110.11306 (2021a).
- Ortiz et al. (2021b) B. R. Ortiz, P. M. Sarte, E. M. Kenney, M. J. Graf, S. M. Teicher, R. Seshadri, and S. D. Wilson, Physical Review Materials 5, 034801 (2021b).
- Yin et al. (2021a) Q. Yin, Z. Tu, C. Gong, Y. Fu, S. Yan, and H. Lei, Chinese Physics Letters 38, 037403 (2021a).
- Ortiz et al. (2020) B. R. Ortiz, S. M. Teicher, Y. Hu, J. L. Zuo, P. M. Sarte, E. C. Schueller, A. M. Abeykoon, M. J. Krogstad, S. Rosenkranz, R. Osborn, et al., Physical Review Letters 125, 247002 (2020).
- Chen et al. (2021a) K. Chen, N. Wang, Q. Yin, Y. Gu, K. Jiang, Z. Tu, C. Gong, Y. Uwatoko, J. Sun, H. Lei, et al., Physical Review Letters 126, 247001 (2021a).
- Zhang et al. (2021) Z. Zhang, Z. Chen, Y. Zhou, Y. Yuan, S. Wang, J. Wang, H. Yang, C. An, L. Zhang, X. Zhu, et al., Physical Review B 103, 224513 (2021).
- Chen et al. (2021b) X. Chen, X. Zhan, X. Wang, J. Deng, X.-B. Liu, X. Chen, J.-G. Guo, and X. Chen, Chinese Physics Letters 38, 057402 (2021b).
- Li et al. (2021d) H. Li, T. T. Zhang, T. Yilmaz, Y. Y. Pai, C. E. Marvinney, A. Said, Q. W. Yin, C. S. Gong, Z. J. Tu, E. Vescovo, et al., Phys. Rev. X 11, 031050 (2021d).
- Zhao et al. (2021b) C. Zhao, L. Wang, W. Xia, Q. Yin, J. Ni, Y. Huang, C. Tu, Z. Tao, Z. Tu, C. Gong, et al., arXiv preprint arXiv:2102.08356 (2021b).
- Gupta et al. (2021) R. Gupta, D. Das, C. H. Mielke III, Z. Guguchia, T. Shiroka, C. Baines, M. Bartkowiak, H. Luetkens, R. Khasanov, Q. Yin, et al., arXiv preprint arXiv:2108.01574 (2021).
- Xu et al. (2021) H.-S. Xu, Y.-J. Yan, R. Yin, W. Xia, S. Fang, Z. Chen, Y. Li, W. Yang, Y. Guo, and D.-L. Feng, Phys. Rev. Lett. 127, 187004 (2021).
- Yu et al. (2021c) F. Yu, D. Ma, W. Zhuo, S. Liu, X. Wen, B. Lei, J. Ying, and X. Chen, Nature communications 12, 1 (2021c).
- Lou et al. (2021) R. Lou, A. Fedorov, Q. Yin, A. Kuibarov, Z. Tu, C. Gong, E. F. Schwier, B. Büchner, H. Lei, and S. Borisenko, arXiv preprint arXiv:2106.06497 (2021).
- Ni et al. (2021) S. Ni, S. Ma, Y. Zhang, J. Yuan, H. Yang, Z. Lu, N. Wang, J. Sun, Z. Zhao, D. Li, et al., Chinese Physics Letters 38, 057403 (2021).
- Chen et al. (2021c) H. Chen, H. Yang, B. Hu, Z. Zhao, J. Yuan, Y. Xing, G. Qian, Z. Huang, G. Li, Y. Ye, et al., arXiv preprint arXiv:2103.09188 (2021c).
- Yin et al. (2021b) L. Yin, D. Zhang, C. Chen, G. Ye, F. Yu, B. R. Ortiz, S. Luo, W. Duan, H. Su, J. Ying, et al., Physical Review B 104, 174507 (2021b).
- Park et al. (2021) T. Park, M. Ye, and L. Balents, Phys. Rev. B 104, 035142 (2021).
- Wu et al. (2021b) X. Wu, T. Schwemmer, T. Müller, A. Consiglio, G. Sangiovanni, D. Di Sante, Y. Iqbal, W. Hanke, A. P. Schnyder, M. M. Denner, et al., Physical review letters 127, 177001 (2021b).
- Denner et al. (2021) M. M. Denner, R. Thomale, and T. Neupert, arXiv preprint arXiv:2103.14045 (2021).
- Miao et al. (2021) H. Miao, H. Li, W. Meier, A. Huon, H. Lee, A. Said, H. Lei, B. Ortiz, S. Wilson, J. Yin, et al., Physical Review B 104, 195132 (2021).
- Lin and Nandkishore (2021) Y.-P. Lin and R. M. Nandkishore, arXiv preprint arXiv:2104.02725 (2021).
- Feng et al. (2021a) X. Feng, K. Jiang, Z. Wang, and J. Hu, Science Bulletin (2021a).
- Consiglio et al. (2021) A. Consiglio, T. Schwemmer, X. Wu, W. Hanke, T. Neupert, R. Thomale, G. Sangiovanni, and D. Di Sante, arXiv preprint arXiv:2111.09342 (2021).
- Ye et al. (2021) Z. Ye, A. Luo, J.-X. Yin, M. Z. Hasan, and G. Xu, arXiv preprint arXiv:2111.07314 (2021).
- Tan et al. (2021) H. Tan, Y. Liu, Z. Wang, and B. Yan, Phys. Rev. Lett. 127, 046401 (2021).
- Gu et al. (2021) Y. Gu, Y. Zhang, X. Feng, K. Jiang, and J. Hu, arXiv preprint arXiv:2108.04703 (2021).
- Wang et al. (2021d) C. Wang, S. Liu, H. Jeon, and J.-H. Cho, arXiv preprint arXiv:2109.01921 (2021d).
- Jiang et al. (2021b) K. Jiang, T. Wu, J.-X. Yin, Z. Wang, M. Z. Hasan, S. D. Wilson, X. Chen, and J. Hu (2021b), eprint 2109.10809.
- Feng et al. (2021b) X. Feng, Y. Zhang, K. Jiang, and J. Hu, Phys. Rev. B 104, 165136 (2021b).
- Ren et al. (2012) X. Ren, P. Rinke, C. Joas, and M. Scheffler, Journal of Materials Science 47, 7447 (2012).
- Korshunov (2014) M. M. Korshunov, Uspekhi Fizicheskikh Nauk 184, 882 (2014).
- Mostofi et al. (2008) A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt, and N. Marzari, Computer physics communications 178, 685 (2008).
- Kanamori (1963) J. Kanamori, Progress of Theoretical Physics 30, 275 (1963), ISSN 0033-068X.
- Georges et al. (2013) A. Georges, L. d. Medici, and J. Mravlje, Annu. Rev. Condens. Matter Phys. 4, 137 (2013).
- Liu and Balents (2017) J. Liu and L. Balents, Phys. Rev. B 95, 075426 (2017).
- Qiu et al. (2021) W.-X. Qiu, J.-Y. Zou, A.-Y. Luo, Z.-H. Cui, Z.-D. Song, J.-H. Gao, Y.-L. Wang, and G. Xu, Phys. Rev. Lett. 127, 147202 (2021).
- Uehara et al. (2015) A. Uehara, H. Shinaoka, and Y. Motome, Phys. Rev. B 92, 195150 (2015).
- (75) See Supplemental Information for: (a) the details for the first principles calculations, (b) formalism and more results for the RPA susceptibility calculations, (c) formalism and more results for the Hartree-Fock calculations, (d) details about the calculations for the inter-site currents, and (e) more results about anomalous Hall conductivities.
- Ishizuka and Nagaosa (2021) H. Ishizuka and N. Nagaosa, Phys. Rev. B 103, 235148 (2021).