First-principles study of carrier mobility in MX (M=Sn, Pb; X=P, As) monolayers

The top and side views of Fig. 1(a) and (b) exhibit the crystalline structure of the MX (M=Sn, Pb; X=P, As) monolayers, which belong to the P3m1 space group. In these figures, red atoms stand for Sn and Pb, and blue atoms for P and As. As shown by the example of SnP, two Sn atoms live in the outermost layer of P atoms, forming bonds with nearby P atoms. According to the z-direction, this arrangement is Sn-P-P-Sn. The structural optimization led to the determination of the lattice constants of 3.96 Å, 3.39 Å, 4.20 Å, and 4.37 Å for SnP, SnAs, PbP, and PbAs, respectively. As illustrated in Fig. 1(c), molecular dynamics simulations were conducted to evaluate the thermal stability of MX. The findings verify that MX retains an independent and stable monolayer structure at room temperature. Furthermore, Fig. 3 displays the phonon dispersion relations, which demonstrate the dynamic stability of MX in the absence of imaginary frequencies.

As depicted in Fig. 2, SnP, SnAs, and PbAs are recognized as indirect band gap semiconductors. They are distinguished by their valence band maximum (VBM) located at the $\Gamma$ point and their CBM at the M point with band gaps reported at 0.38 eV, 0.24 eV, and 0.39 eV, respectively. On the other hand, PbP is a direct band gap semiconductor that has a band gap of 0.55 eV. Its VBM and CBM are both situated at the $\Gamma$ points. One notable finding across these materials is that the conduction band has a secondary energy minimum. For example, SnP exhibits this secondary minimum at the K’ valley, which is located 66 meV above the M valley and on the line connecting the K and $\Gamma$ points. Similarly, the secondary minimum of SnAs is located 40 meV above the M valley at the K valley (directly at the K point). The secondary minimum of PbP’s conduction band is merely 0.1 meV higher in the M valley than in the $\Gamma$ valley.FLastly, the secondary minimum of PbAs at the $\Gamma$ valley is located 10 meV above the M valley. Considering the close spacing between the two energy minima and the large impact of interval scattering on carrier transport, this feature is particularly crucial for our discussion. Atomic orbital contributions were investigated by a projected energy band analysis to corroborate the band gap properties of the MX monolayer. As indicated in Fig. 2, the p_x/p_y orbitals of Sn atoms as well as the p_x/p_y and p_z orbitals of P atoms contribute mostly to electronic states close to the Fermi energy level in SnP. Moreover, the p_x/p_y and p_z orbitals of Sn (Pb) atoms and P (As) atoms are the main contributors to the electronic states at the Fermi energy level in SnAs, PbP, and PbAs.

As shown in Fig. 3, it is essential to understand the phonon dispersion, phonon linewidth, and the $\alpha$${}^{2}_{tr}$F($\omega$) transport spectral function for comprehending the electron transport properties. As the atomic mass of X (P, As) increases, the phonon dispersion curves indicate a decrease in phonon frequencies, particularly for optical phonons. This variation is critical for determining the function of atomic mass in phonon behavior. The degree of electron-phonon coupling is illustrated by the phonon linewidth, which is overlaid on the phonon dispersion diagram. With a distribution that is in line with the $\alpha$${}^{2}_{tr}$F($\omega$) transport spectral function, it highlights key phonon modes that have a major impact on electron-phonon interactions. Specifically, the ZO₁, LO₂, and ZO₃ phonon modes close to the $\Gamma$ point become important in promoting electron-phonon coupling and causing a substantial amount of intravalley scattering. The LO₂ optical phonon mode is remarkable due to its dominant influence on electron-phonon coupling among them. Supplementary Fig. S2 displayed the vibrational patterns of optical phonon modes at the $\Gamma$ point. The ZO₁ and ZO₃ modes include out-of-plane atomic vibrations. As indicated by the peak of the $\alpha$${}^{2}_{tr}$F($\omega$) function, the electron-phonon coupling that controls carrier scattering is primarily induced by the in-plane LO₂ mode. The analysis extends beyond the $\Gamma$ point in the case of PbAs, demonstrating the ZO₁, LO₂, and ZO₃ modes at the $\Gamma$ point as well as the important role played by the ZO₁ and ZO₃ modes at the M point in electron-phonon coupling. This is especially significant to PbAs because of the small energy gap between the CBM and the $\Gamma$ valley. Furthermore, it combines with phonon activity around the M point, enabling significant intervalley scattering from the M valley to the $\Gamma$ valley in the electronic structure.

As the inverse of the carrier lifetime, we first analyzed the total scattering rate of the MX compounds. Fig. 4 illustrates that the scattering rate of MX at 100 K is substantially lower than at 300 K and increases with rising temperature regimes. In addition, an upward trend in the overall scattering rate is correlated with the atomic mass of X, revealing that optical phonon energy increases as X’s atomic mass grows. Stronger electron-phonon coupling results from this heightened energy, which raises the scattering rate.

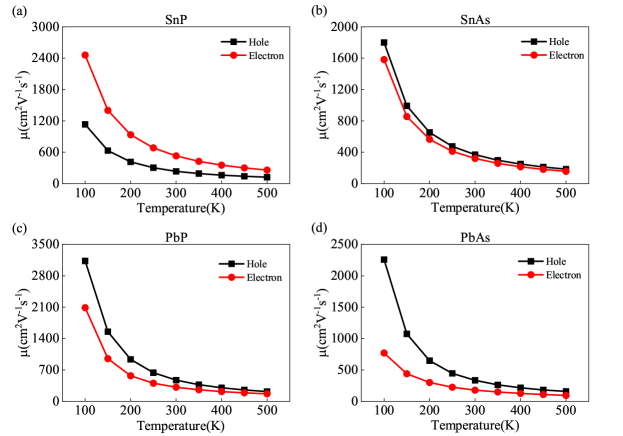
At a fixed carrier concentration of n_2D=$1\times 10^{13}$cm^-2, the temperature-dependent changes in electron and hole carrier mobilities for MX compounds are demonstrated in Fig. 5. In particular, SnP has an electron mobility of 528.6 cm${}^{2}V^{-1}s^{-1}$ and hole mobility of 234.9 cm${}^{2}V^{-1}s^{-1}$ at 300 K. The electron and hole mobilities for SnAs are 319.4 and 368.2 cm${}^{2}V^{-1}s^{-1}$, respectively. PbP exhibits electron mobility of 312.2 cm${}^{2}V^{-1}s^{-1}$ and hole mobility of 472.8 cm${}^{2}V^{-1}s^{-1}$. In contrast, PbAs record electron mobility of 178.1 cm${}^{2}V^{-1}s^{-1}$ and hole mobility of 332.5 cm${}^{2}V^{-1}s^{-1}$. As the temperature rises, the data in Fig. 5 clearly show that carrier mobility within MX compounds decreases. This trend may be attributed to increased scattering events, which in turn lower carrier mobility. As described in Table S1 of the supplementary material, the effective masses of electron carriers (m${}^{*}_{e}$) and hole carriers (m${}^{*}_{h}$) were obtained from the band structure analysis. Among the compounds studied, SnP is noteworthy as an exception because its electron-effective mass is lower than that of hole carriers. On the other hand, the electron-effective mass is greater than the hole carriers for the other three materials. Since carrier effective mass and carrier mobility are inversely related [39, 40], this implies that hole mobility surpasses electron mobility in all materials studied except SnP.

Previous research has revealed the impact of strain engineering on carrier mobility [41]. SnP has the greatest electron mobility of all the MX monolayers. Consequently, we performed carrier mobility estimates for SnP at biaxial elongation of 2%, 4%, and 6%. The phonon dispersion and molecular dynamics at these elongations are presented in Figs. S4 and S5 in the supplementary files, which validate that SnP is stable at all three levels of stretching. The electronic energy band structure of SnP during biaxial stretching is displayed in Fig. 6(a). The VBM and CBM stay at the $\Gamma$ and M points, respectively, at 2% and 4% stretching, which correspond to the unstretched state. It is notable that the band gap expands from 0.383 eV to 0.632 eV to 0.845 eV as the strain increases. However, significant shifts take place at 6% biaxial stretch. 0.784 eV is the band gap caused by the VBM moving from point $\Gamma$ to point M and the CBM shifting from point M to point $\Gamma$. Besides, we found that the interpolation of the second energy minimum of the conduction band with the CBM falls for biaxial stretching of 2% and 4%, but increases for 6%.

As demonstrated in Fig. 6 (b), we investigated the changes in electron carrier mobility under biaxial tensile strain. Interestingly, electron mobility drops at the same level of biaxial stretching as temperature rises. However, electron carrier mobility declines at the same temperature under 2% and 4% biaxial stretching, but boots to 2,511.9 cm${}^{2}V^{-1}s^{-1}$ at 6% biaxial stretching. Two primary factors are responsible for this trend. First, as explained in Table S2 in the supplementary material, the effective carrier mass of electrons increases progressively with 2% and 4% biaxial stretching but reduces to 0.22 m₀ at 6% stretching because of changes in the CBM. Second, the difference between the second energy minimum and CBM in the conduction band diminishes at 2% and 4% biaxial stretching, which amplifies intervalley scattering. On the other hand, this difference rises at 6% biaxial stretching, which results in reduced intervalley scattering, lowered electron-phonon coupling strength, and greater carrier mobility.