First-principles investigation of Nd(Fe,M)₁₂ (M = K–Br) and Nd(Fe,Cr,Co,Ni,Ge,As)₁₂: Possible enhancers of Curie temperature for NdFe₁₂ magnetic compounds

Taro Fukazawa [email protected] CD-FMat, National Institute of Advanced Industrial Science and Technology, Tsukuba, Ibaraki 305-8568, Japan Hisazumi Akai The Institute for Solid State Physics, The University of Tokyo, Kashiwa, Chiba 277-8581, Japan ESICMM, National Institute for Materials Science, Tsukuba, Ibaraki 305-0047, Japan Yosuke Harashima CD-FMat, National Institute of Advanced Industrial Science and Technology, Tsukuba, Ibaraki 305-8568, Japan ESICMM, National Institute for Materials Science, Tsukuba, Ibaraki 305-0047, Japan Center for Computational Sciences, University of Tsukuba, Tsukuba, Ibaraki 305-8577, Japan Takashi Miyake CD-FMat, National Institute of Advanced Industrial Science and Technology, Tsukuba, Ibaraki 305-8568, Japan ESICMM, National Institute for Materials Science, Tsukuba, Ibaraki 305-0047, Japan

Abstract

We investigate the effects of various dopants ( $M$ = K–Br) on the Curie temperature of the magnetic compound NdFe₁₂ through first-principles calculations. Analysis by the Korringa–Kohn–Rostoker method with the coherent potential approximation reveals that doping the Fe sites with optimal concentrations of Ge and As is a promising strategy for increasing the Curie temperature. To search over a wider space, we also perform Bayesian optimization. Out of over 180,000 candidate compositions, co-doped systems with Co, Ge, and As are found to have the highest Curie temperatures.

TBD

pacs:

TBD

^†^†preprint: Ver.0.4.4

I Introduction

Rare-earth–iron compounds are used in the highest-performance permanent magnets currently available. The magnetic compound Nd₂Fe₁₄B is especially well known as the main phase of neodymium magnets, which are the strongest magnets used industrially. In such magnets, rare-earth elements are the main source of the magnetic anisotropy and iron is the main source of the magnetic moment.

Compounds with the ThMn₁₂ structure are considered promising because they can accommodate a larger amount of Fe than Nd₂Fe₁₄B. Hirayama et al. synthesized films of NdFe₁₂ and reported that the nitrogenated film exhibited larger magnetization and higher Curie temperature than Nd₂Fe₁₄B.Hirayama15 ; Hirayama15b However, NdFe₁₂(N) is not thermodynamically stable.

Doping of $R$ Fe₁₂ has been investigated as a method for stabilizing the structure as a bulk material and enhancing the magnetic properties. Optimization of the material properties by changing the composition of the system is one of the central issues in the field.

Titanium energetically stabilizes the structure, and an Fe-rich magnetic compound with a ThMn₁₂-type structure was first found as a Ti-doped system.Ohashi87 ; Ohashi88 However, Ti also greatly reduces the magnetization of the system owing to its antiferromagnetic coupling to the host Fe.Harashima16 Cobalt is a typical enhancer of finite-temperature magnetism. With respect to ThMn₁₂ compounds, Hirayama et al. reported the synthesis of Co-doped Sm(Fe,Co)₁₂ films that displayed excellent magnetic properties at room temperature and a higher Curie temperature than the pristine system.Hirayama17 First-principles calculations have suggested that Co not only improves the magnetic properties but also contributes to the stability of the ThMn₁₂ structure.Harashima16 We also discussed the enhancement of the Curie temperature, $T_{\mathrm{C}}$ , and demonstrated that Cr is a better enhancer of this parameter than Co in $R$ Fe₁₂ ( $R$ =Y, Nd, Sm) when the dopant concentration is low.Fukazawa18 Using V, which is adjacent to Cr in the periodic table, Schönhöbel et al. synthesized SmFe ${}_{11}V$ and reported that its Curie temperature was 635 K,Schoenhoebel19 which is significantly higher than the value of 555 K for SmFe₁₂.Hirayama17

These works motivated us to explore a wider composition space for $T_{\mathrm{C}}$ -enhancing dopants. We have recently developed a Bayesian optimization framework for such exploration and demonstrated that it can greatly reduce the number of first-principles calculations required to identify the optimal system from a large candidate set.Fukazawa19c However, we considered only a few dopant elements in our previous study. In this paper, we examine a series of dopants, namely, $M$ = K, Ca, Sc, Ti, V, Cr, Mn, Co, Ni, Cu, Zn, Ga, Ge, As, Se, and Br, as potential enhancers of the Curie temperature through first-principles calculations and also consider co-doping with some of these elements.

In Section II, we describe the details of the calculations. As the first step, we performed first-principles calculations of NdFe ${}_{12-\delta}M_{\delta}$ for all of the dopants in the dilute limit of $M$ $(\delta\ll 1)$ . In Section III.1, we discuss how the dopants affect the Curie temperature. On the basis of the results, we selected six dopants (V, Cr, Co, Ni, Ge, and As) with the potential to enhance the Curie temperature, and we examine how a single dopant changes the Curie temperature at a finite concentration in Section III.2. We also consider the effects of Ge and As as dopants on the Curie temperature in terms of hybridization between the Fe 3d and $M$ 4p orbitals.

In Section III.3, we consider the case of multiple dopants and report on their advantages over a single dopant. In the case of co-doping, the number of possible combinations becomes very large. To deal with this difficulty, we applied the Bayesian optimization framework that we proposed previously.Fukazawa19c We demonstrate that co-doping with Co, Ge, and As has an advantage over doping with Co alone. Finally, we present our conclusions in Section IV.

II Methods

We performed first-principles electronic structure calculations based on density functional theory.Hohenberg64 ; Kohn65 We used the Korringa–Kohn–RostokerKorringa47 ; Kohn54 (KKR) Green’s function method to solve the Kohn–Sham equations and the local density approximation for the exchange–correlation functional. Although the spin–orbit coupling was not explicitly included in the energy functional, the electronic configuration of the f electrons at the Nd site was assumed to obey Hund’s rule. The f electrons were treated with the open-core approximation and the self-interaction correctionPerdew81 was applied to the f states. The randomness due to the occupation of dopants was treated within the coherent potential approximation (CPA).Soven67 ; Soven70 ; Shiba71

We assumed that NdFe₁₂ possesses the crystal structure of ThMn₁₂ [space group: I4/mmm (#139)] (Fig. 1),

Refer to caption — Figure 1: Structure of a ThMn₁₂-type crystal and its Wyckoff positions.

and we adopted the lattice constant of NdFe₁₂ previously obtained Harashima15g for undoped and doped systems.

The Curie temperature was calculated from a classical Heisenberg model whose parameters were determined using Liechtenstein’s method Liechtenstein87 within the mean-field approximation. Although this method overestimates the Curie temperature, the relative changes among Fe-rich magnetic compounds are adequately described.Fukazawa19b Readers are referred to Ref. Fukazawa18, for the details of the calculations.

We considered the doping of the Fe(8f), Fe(8i), and Fe(8j) sites in NdFe₁₂. The magnetic moment of the dopant $M$ was assumed to be parallel or antiparallel to the total magnetic moment of the system. Thus, we performed calculations with the initial magnetic moment of the dopant set parallel and antiparallel and carefully checked for the existence of metastable states. The results for NdFe ${}_{12-\delta}M_{\delta}$ at an infinitesimal concentration (i.e., the dilute limit: $\delta\ll 1$ ) were obtained by fitting the data for $\delta$ = 0, 0.04, 0.08, 0.12, and 0.16 with polynomial curves. The derivatives of the physical quantities are calculated from the results.

To consider the case of co-doping with multiple elements, we used a Bayesian framework for composition optimization to identify the optimal system from a large search space. The search framework was previously described in Ref. Fukazawa19c, . For the Bayesian optimization, we used the COMBO package, which can accommodate a large number of candidates.Ueno16 ; COMBO The choice of system to explore next was conducted by Thompson sampling after the initial 20 systems had been chosen at random. The dimensionality of the random feature maps was set to 2000.

III Results and Discussion

III.1 NdFe ${}_{12-\delta}M_{\delta}\ (\delta\ll 1)$

In this subsection, we present the results for NdFe ${}_{12-\delta}M_{\delta}$ in the dilute limit of $M$ ( $\delta\ll 1$ ). Figure 2 shows the derivative of $T_{\mathrm{C}}$ with respect to concentration, $\left.\frac{dT_{\mathrm{C}}}{d\delta}\right|_{\delta=0}$ .

In a previous paper,Fukazawa18 we demonstrated the potential of Cr in enhancing the Curie temperature of $R$ Fe₁₂ ( $R$ =Y, Nd, Sm) more efficiently than Co for low dopant concentrations. The curve of the derivative shown in the figure exhibits a peak at $M$ =Cr. We also see that there are significant increases for both $M$ =K and $M$ =Ge–Br.

To analyze the origin of the enhancement, we performed direct–indirect decomposition (DID), which we previously proposed.Fukazawa18 The Curie temperature can be calculated from the intersite couplings $J_{ij}$ and concentration $\delta$ within the mean-field approximation. Because $J_{ij}$ is also a function of $\delta$ , we see that the change of $T_{\mathrm{C}}$ with respect to concentration can be expressed as

\left.\frac{dT_{\mathrm{C}}[\{J_{ij}(\delta)\},\delta]}{d\delta}\right|_{\delta=0}=\left.\frac{\partial T_{\mathrm{C}}}{\partial\delta}\right|_{\{J_{ij}(0)\}}+\sum_{ij}\left.\frac{\partial T_{\mathrm{C}}}{\partial J_{ij}}\frac{dJ_{ij}}{d\delta}\right|_{\delta=0}.

(1)

The first and second terms are referred to as the direct and indirect parts, respectively.

Figure 3 shows the direct contribution to the derivative of $T_{\mathrm{C}}$ , which originates from the difference in the magnetic couplings between the replacing Fe– $M$ couplings and the replaced Fe–Fe couplings.

The direct contribution is largely positive for $M$ = Co, Cr, and V, whereas it is negative for most of the remaining cases.

Figure 4 shows the indirect contribution obtained from the DID, which originates from the enhancement of the magnetic Fe–Fe couplings due to the introduction of $M$ .

It is noteworthy that the significant enhancement observed for $M$ =K and Ge–Br in Fig. 2 can be attributed solely to the indirect contribution. We discuss the atomic-scale origin of this enhancement in terms of hybridization between the Fe 3d and $M$ 4p orbitals in the next subsection.

To roughly estimate the Curie temperature for finite dopant concentrations, we constructed a quadratic model of $T_{\mathrm{C}}$ as a function of the concentration through estimation of the first and second derivatives by data fitting:

T_{\mathrm{C}}(\delta)=T_{\mathrm{C}}(0)+\frac{dT_{\mathrm{C}}}{d\delta}(0)\,\delta+\frac{1}{2}\frac{d^{2}T_{\mathrm{C}}}{d\delta^{2}}(0)\,\delta^{2}.

(2)

This model is valid for low dopant concentrations. Figure 5 presents the highest values of $T_{\mathrm{C}}$ for Nd(Fe_12-δM_δ) in the range of $0\leq\delta\leq 1$ as a function of $M$ . The numbers below each data point indicate the concentrations that afforded the highest values of $T_{\mathrm{C}}$ .

From the figure, we can expect a large enhancement of the Curie temperature by doping with $M$ = V, Cr, Co, Ni, Ge, or As alone.

III.2 Finite amount of $M$

In this subsection, we investigate the Curie temperature of Nd(Fe_12-xM_x) for a finite concentration $x$ (we let $x$ denote the concentration to indicate that it is finite). First, we consider the results for $M$ = V, Cr, Co, Ni, Ge, and As (which we selected on the basis of Fig. 5) to examine the validity of the rough estimation described above. To obtain the data, we performed calculations for finite concentrations of $x=0,0.25,...,2$ .

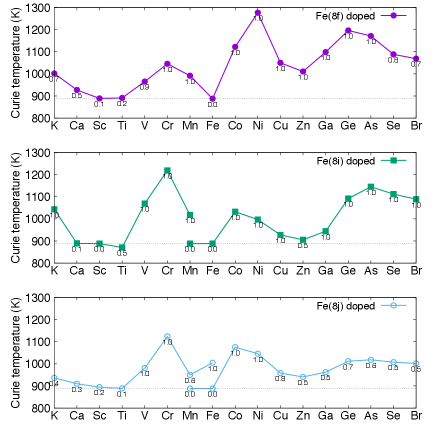
Figure 6 shows the calculated values of the Curie temperature.

It follows from this figure that the maximum $T_{\mathrm{C}}$ was overestimated by the results shown in Fig. 5; however, the relative changes among the dopants are described well. For V and Cr, $T_{\mathrm{C}}$ begins to decrease around $x=1$ . In the case of Co, the maximum $T_{\mathrm{C}}$ occurs outside the range of the figure. Ni is less favorable for maintaining $T_{\mathrm{C}}$ . Ge and As display similar curves, where the maximum values of $T_{\mathrm{C}}$ occur at a higher concentration than those observed for V and Cr.

As we have previously reported,Fukazawa18 Cr is a better enhancer of $T_{\mathrm{C}}$ than Co for low dopant concentrations. This is attributable to the strong antiferromagnetic Fe–Cr coupling, which leads to the direct contribution shown in Fig. 3. Vanadium plays a similar role owing to the strong Fe–V coupling, although it is less effective than Cr. In the case of Cr or V doping, the second-order effects of $x$ decrease the Curie temperature and cause the curve to first increase and then decrease.

For $M$ =Co or Ni, the dopants largely reinforce the magnetic Fe–Fe couplings,Fukazawa18 which is the indirect contribution. The second-order effects are weak because the moment of $M$ is parallel to the host and the $M$ – $M$ coupling is ferromagnetic. Therefore, Co and Ni can serve as enhancers of $T_{\mathrm{C}}$ over a wider range of concentrations.

In the cases of $M$ =Ge and As, the enhancement of the Curie temperature can be ascribed to the indirect contribution as shown in Fig. 4. This effect can be explained in terms of hybridization between the Fe 3d and $M$ 4p states. It is also noteworthy that the maxima for $M$ =Ge and As occur at higher concentrations than for V and Cr and lower concentrations than for Co and Ni because Ge and As are non-magnetic dopants.

To examine the chemical trends, we performed calculations for 8f-doped Nd(Fe ${}_{11}M$ ) with $M$ =Ge, As, Se, and Br (atomic numbers 32–35). Figure 7 shows the partial densities of states (DOSs).

In the case of $M$ =Ge, we can see from the DOS for the $M$ p orbitals that a large part of the antibonding states remains unoccupied. This situation is comparable to cobaltization, in which the DOS of Fe is deformed to become similar to that of Co by hybridization with unoccupied states at a neighboring site.Kanamori90 ; Ogura11 ; Harashima15e This is considered to reinforce the magnetism by strengthening the magnetic coupling between the Co-like Fe and the surrounding Fe.

Upon increasing the atomic number of the dopant from $M$ =Ge, the potential becomes deeper and more majority-spin channels are occupied (Fig. 7), while the minority-spin channels remain unoccupied. This enhances the local moment of the Fe sites (Fig. 8) and makes the spin-rotational perturbation considered in Liechtenstein’s formula larger, which increases the estimated values of the intersite magnetic couplings and the Curie temperature.

However, the cobaltization is simultaneously weakened by the partial occupation of the antibonding states, which decreases the Curie temperature. The crossover of these two effects is responsible for the peak in $T_{\mathrm{C}}$ for $M$ =As observed in Fig. 9, although the local moments of Fe monotonically increase with increasing atomic number (Fig. 8).

III.3 Systems with multiple dopants

Finally, we consider the co-doping of NdFe₁₂ to enhance the Curie temperature. It should be readily apparent that the investigation of all possible combinations of $M$ =K–Br would be impractical. We avoided this problem by screening the dopants on the basis of the results shown in Fig. 5; we hereinafter consider doping with Co, Ni, Ge, and As for the 8f site, Cr and Co for the 8i site, and Cr, Co, and Ni for the 8j site.

We also focus on the regime of low dopant concentrations because Fe-rich compounds are favorable in terms of magnetization, and several of the dopants were expected to afford $T_{\mathrm{C}}$ maxima at low concentrations in the range of $x\leq 2$ (Fig. 6). We prepared two lists of candidates, lists (A) and (B), with different upper limits of dopant concentration. In list (A), the amount of each dopant per formula was varied from $0$ to $1$ in intervals of $0.1$ with the constraint that the total amount of dopants was $x\leq 1$ . In list (B), the amount of each dopant was varied from $0$ to $2$ in intervals of $0.2$ with the constraint of $x\leq 2$ . Each list consisted of 92,378 systems and up to nine site–dopant combinations per system. The total number of unique items is 182754 (2002 duplicates).

Even with this screening, considerable time and resources would be required to perform first-principles calculations for all of the candidates. To overcome this problem, we applied our efficient framework for optimization of the chemical composition based on Bayesian optimization.Fukazawa19c With this framework, it is possible to identify high-performance materials from a candidate list with a small number of data acquisition processes by alternately performing data acquisition and stochastic modeling.

Figure 10 shows the obtained Curie temperature versus the number of data acquisition steps. In these plots, the score ( $T_{\mathrm{C}}$ ) at each step and cumulative best score are shown for lists (A) and (B). In both cases, the best system observed during the run was found within the first 60 steps. After this point, the score oscillated between lower values, indicating that there remained few or no better systems.

The ten best identified systems are shown in Table 1 for list (A) and Table 2 for list (B).

Table 1: Ten best systems found in the optimization using list (A).

Formula	$T_{\mathrm{C}}$ (K)	$\mu_{0}M$ (T)
NdFe₁₁As	1119	1.58
NdFe₁₁As_0.9Ge_0.1	1117	1.58
NdFe₁₁As_0.8Ge_0.2	1114	1.58
NdFe₁₁As_0.9Co(8j)_0.1	1112	1.60
NdFe₁₁As_0.8Co(8f)_0.2	1111	1.61
NdFe₁₁As_0.7Ge_0.3	1111	1.58
NdFe₁₁As_0.7Ge_0.2Co(8f)_0.1	1109	1.60
NdFe₁₁As_0.7Ge_0.1Co(8f)_0.2	1108	1.61
NdFe₁₁As_0.8Ge_0.1Co(8i)_0.1	1108	1.59
NdFe₁₁As_0.6Ge_0.4	1108	1.58
NdFe₁₂	881	1.73

Table 2: Ten best systems found in the optimization using list (B).

Formula	$T_{\mathrm{C}}$ (K)	$\mu_{0}M$ (T)
NdFe₁₀Co(8f)_1.8As_0.2	1201	1.72
NdFe₁₀Co(8f)_1.6As_0.4	1200	1.69
NdFe₁₀Co(8f)_1.8Ge_0.2	1199	1.71
NdFe₁₀Co(8f)_1.4As_0.6	1198	1.65
NdFe₁₀Co(8f)_1.2As_0.8	1198	1.62
NdFe₁₀Co(8f)_2.0	1198	1.76
NdFe₁₀Co(8f)_1.6Ge_0.2As_0.2	1197	1.68
NdFe₁₀Co(8f)As	1197	1.59
NdFe₁₀Co(8f)_1.6Ge_0.4	1195	1.68
NdFe₁₀Co(8f)_0.8Ge_1.2	1195	1.56
NdFe₁₂	881	1.73

All of the top ten systems contain the maximal amount of dopants, namely, $x=1$ for list (A) and $x=2$ for list (B). For list (A), doping with As and Ge give high scores than doping with Co. For list (B), which could accommodate more dopant atoms, doping with Co was more advantageous. However, the system with the highest Curie temperature was obtained by co-doping with As and Co. From comparison of NdFe₁₀Co(8f)_1.8As_0.2 and NdFe₁₀Co(8f)₂, the direct and indirect contributions of As to the enhancement of $T_{\mathrm{C}}$ can be estimated as $-22$ and $+24$ K, respectively. Arsenic enhances the magnetic couplings between surrounding transition metals, and this effect is evidently slightly larger than that of the loss of the Co–Fe and Co–Co couplings resulting from the substitution. It is also noteworthy that substitution with Ge and As can reduce the amount of Co, which is an expensive element, without sacrificing the Curie temperature.

IV Conclusion

In this paper, we have discussed the effects of various dopants (K–Br) on the magnetism of NdFe₁₂. We first investigated doping with a single dopant at an infinitesimal concentration, then extended the analysis to finite concentrations of selected dopants. We have demonstrated the potential of As and Ge in enhancing the Curie temperature and discussed the origin of this enhancement in terms of the interaction between the Fe 3d and $M$ 4p electrons. These results were used to screen the dopants prior to further optimization using a wider search space that allowed for simultaneous doping. We found that co-doping with As, Ge, and Co has the potential to enhance the Curie temperature more efficiently than doping with Co alone. The results also indicate that doping with As and Ge can reduce the amount of Co, which is a scarce element, without reducing the Curie temperature.

Acknowledgment

This work was supported by a project (JPNP20019) commissioned by the New Energy and Industrial Technology Development Organization (NEDO), the Elements Strategy Initiative Center for Magnetic Materials (ESICMM, Grant Number JPMXP0112101004), and the “Program for Promoting Researches on the Supercomputer Fugaku” (DPMSD) by MEXT. The calculations were conducted in part using the facilities of the Supercomputer Center at the Institute for Solid State Physics, University of Tokyo, the supercomputer of the Academic Center for Computing and Media Studies (ACCMS), Kyoto University, and the supercomputer Fugaku provided by the RIKEN Center for Computational Science through the HPCI System Research Project (Project ID: hp200125, hp210179).

Appendix A Magnetic moment

A.1 NdFe ${}_{12-\delta}M_{\delta}\ (\delta\ll 1)$

In this subsection, we present results for the magnetic moments in NdFe ${}_{12-\delta}M_{\delta}\ (\delta\ll 1)$ . In Fig. 11, the local magnetic moments of $M$ at the 8f, 8i, and 8j sites are shown. Parallel and antiparallel solutions coexist only in the cases of Fe(8i) doping with $M$ = Mn and Fe(8j) doping with $M$ = Fe and Mn. Irrespective of the choice of doping site, the stable solution was antiparallel for $M$ = Mn and parallel for $M$ = Fe.

It has been discussed in the context of magnetic impurity problems that metastable states are more likely to exist when the host has a small magnetic moment.Akai90 The host is identical in our calculations, but the existence of a metastable state depends on the doping site. The calculated local moments of Fe in NdFe₁₂ were 1.70 $\mu_{B}$ at the 8f site, 2.41 $\mu_{B}$ at the 8i site, and 2.38 $\mu_{B}$ at the 8j site. Therefore, the Fe moments surrounding the 8f site were larger than those surrounding the other sites. This leads to the non-existence of the metastable state in the range of our calculations for 8f doping.

Let us next consider the rate of change of the magnetization $m$ with respect to the concentration. Figure 12 shows the derivative of the magnetization, $\left.\frac{dm}{d\delta}\right|_{\delta=0}$ , as a function of the dopant $M$ .

The magnetic moment decreases upon doping. In the case of the elements to the left of the plot (K–Fe), this is because the local moment of $M$ is antiparallel to the host. In the case of those to the right of the plot (Mn–Br), this is because the local moment of the replacing element is smaller than that of the replaced Fe, which we call the direct contribution in DID analysis. However, this decrease is suppressed for $M$ =Ge–Br, even though the local moment of $M$ is almost zero. This indicates that these elements have an indirect effect on the magnetic moment which is proportional to the first order of the concentration and counteracts the direct effect.

A.2 Finite amount of $M$

Figure 13 shows the results for the magnetization of NdFe ${}_{12-x}M_{x}\ (0\leq x\leq 2)$ .

In the cases of $M$ =V and Cr, the magnetic moment of $M$ is antiparallel to the host magnetization, and the total magnetization sharply decreases as the concentration of $M$ increases. In the cases of $M$ =Co and Ni, the magnetic moment of $M$ is parallel to the host, and the total magnetization is retained at higher concentrations. Because Ge and As are nonmagnetic, the decrease in the total magnetization is moderate compared with the cases of $M$ =Ge and As.

References

(1) Y. Hirayama, Y. Takahashi, S. Hirosawa, K. Hono, NdFe ${}_{1}2$ N_x hard-magnetic compound with high magnetization and anisotropy field, Scripta Materialia 95 (2015) 70–72.
URL http://www.sciencedirect.com/science/article/pii/S1359646214004163
(2) Y. Hirayama, T. Miyake, K. Hono, Rare-earth lean hard magnet compound ndfe12n, JOM 67 (6) (2015) 1344–1349.
(3) K. Ohashi, T. Yokoyama, R. Osugi, Y. Tawara, The magnetic and structural properties of R-Ti-Fe ternary compounds, IEEE transactions on magnetics 23 (5) (1987) 3101–3103.
(4) K. Ohashi, Y. Tawara, R. Osugi, J. Sakurai, Y. Komura, Identification of the intermetallic compound consisting of sm, ti, fe, Journal of the Less Common Metals 139 (2) (1988) L1–L5.
URL http://www.sciencedirect.com/science/article/pii/0022508888900203
(5) Y. Harashima, K. Terakura, H. Kino, S. Ishibashi, T. Miyake, First-principles study on stability and magnetism of NdFe₁₁ $M$ and NdFe₁₁ $M$ N for M= Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, arXiv preprint arXiv:1609.07227 (2016).
(6) Y. Hirayama, Y. K. Takahashi, S. Hirosawa, K. Hono, Intrinsic hard magnetic properties of Sm(Fe_1-xCo_x)₁₂ compound with the ThMn₁₂ structure, Scripta Materialia 138 (2017) 62–65.
(7) T. Fukazawa, H. Akai, Y. Harashima, T. Miyake, First-principles study of intersite magnetic couplings and Curie temperature in RFe_12-xCr_x (R = Y, Nd, Sm), Journal of Physical Society of Japan 87 (4) (2018) 044706.
(8) A. Schönhöbel, R. Madugundo, O. Y. Vekilova, O. Eriksson, H. C. Herper, J. Barandiarán, G. Hadjipanayis, Intrinsic magnetic properties of smfe12- xvx alloys with reduced v-concentration, Journal of Alloys and Compounds 786 (2019) 969–974.
(9) T. Fukazawa, Y. Harashima, Z. Hou, T. Miyake, Bayesian optimization of chemical composition: A comprehensive framework and its application to $R$ Fe₁₂-type magnet compounds, Physical Review Materials 3 (5) (2019) 053807.
(10) P. Hohenberg, W. Kohn, Inhomogeneous electron gas, Physical Review 136 (3B) (1964) B864.
(11) W. Kohn, L. J. Sham, Self-consistent equations including exchange and correlation effects, Physical Review 140 (4A) (1965) A1133.
(12) J. Korringa, On the calculation of the energy of a bloch wave in a metal, Physica 13 (6-7) (1947) 392–400.
(13) W. Kohn, N. Rostoker, Solution of the schrödinger equation in periodic lattices with an application to metallic lithium, Phys. Rev. 94 (1954) 1111–1120. doi:10.1103/PhysRev.94.1111.
URL http://link.aps.org/doi/10.1103/PhysRev.94.1111
(14) J. P. Perdew, A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B 23 (1981) 5048–5079. doi:10.1103/PhysRevB.23.5048.
URL http://link.aps.org/doi/10.1103/PhysRevB.23.5048
(15) P. Soven, Coherent-potential model of substitutional disordered alloys, Physical Review 156 (3) (1967) 809.
(16) P. Soven, Application of the coherent potential approximation to a system of muffin-tin potentials, Physical Review B 2 (12) (1970) 4715.
(17) H. Shiba, A reformulation of the coherent potential approximation and its applications, Progress of Theoretical Physics 46 (1) (1971) 77–94.
(18) Y. Harashima, K. Terakura, H. Kino, S. Ishibashi, T. Miyake, First-principles study of structural and magnetic properties of r (fe, ti) 12 and r (fe, ti) 12n (r= nd, sm, y), in: Proceedings of Computational Science Workshop 2014 (CSW2014), Vol. 5 of JPS Conference Proceedings, 2015, p. 1021.
URL http://journals.jps.jp/doi/abs/10.7566/JPSCP.5.011021
(19) A. I. Liechtenstein, M. Katsnelson, V. Antropov, V. Gubanov, Local spin density functional approach to the theory of exchange interactions in ferromagnetic metals and alloys, Journal of Magnetism and Magnetic Materials 67 (1) (1987) 65–74.
(20) T. Fukazawa, H. Akai, Y. Harashima, T. Miyake, Curie temperature of Sm₂Fe₁₇ and Nd₂Fe₁₄B: a first-principles study, IEEE Transaction on Magnetics (in press).
URL https://ieeexplore.ieee.org/document/8653984
(21) T. Ueno, T. D. Rhone, Z. Hou, T. Mizoguchi, K. Tsuda, COMBO: An efficient Bayesian optimization library for materials science, Materials discovery 4 (2016) 18–21.
(22) COMmon Bayesian Optimization Library (COMBO), https://github.com/tsudalab/combo.
URL https://github.com/tsudalab/combo
(23) J. Kanamori, Interplay between electronic structure and correlation through the sd mixing in transition metal systems, Progress of Theoretical Physics Supplement 101 (1990) 1–10.
(24) M. Ogura, H. Akai, J. Kanamori, Enhancement of Magnetism of Fe by Cr and V, Journal of the Physical Society of Japan 80 (10) (2011) 104711.
(25) Y. Harashima, K. Terakura, H. Kino, S. Ishibashi, T. Miyake, Nitrogen as the best interstitial dopant among $X$ =B, C, N, O, and F for strong permanent magnet ${\mathrm{NdFe}}_{11}\mathrm{Ti}X$ : First-principles study, Phys. Rev. B 92 (2015) 184426. doi:10.1103/PhysRevB.92.184426.
URL http://link.aps.org/doi/10.1103/PhysRevB.92.184426
(26) H. Akai, M. Akai, S. Blügel, B. Drittler, H. Ebert, K. Terakura, R. Zeller, P. Dederichs, Theory of hyperfine interactions in metals, Progress of Theoretical Physics Supplement 101 (1990) 11–77.
URL http://ptps.oxfordjournals.org/content/101/11.short

First-principles investigation of Nd(Fe,M)12 (M = K–Br) and Nd(Fe,Cr,Co,Ni,Ge,As)12: Possible enhancers of Curie temperature for NdFe12 magnetic compounds