Finite elements for divdiv-conforming symmetric tensors in three dimensions
Abstract.
Two types of finite element spaces on a tetrahedron are constructed for divdiv conforming symmetric tensors in three dimensions. The key tools of the construction are the decomposition of polynomial tensor spaces and the characterization of the trace operators. First, the divdiv Hilbert complex and its corresponding polynomial complexes are presented. Several decompositions of polynomial vector and tensors spaces are derived from the polynomial complexes. Then, traces for div-div operator are characterized through a Green’s identity. Besides the normal-normal component, another trace involving combination of first order derivatives of the tensor is continuous across the face. Due to the smoothness of polynomials, the symmetric tensor element is also continuous at vertices, and on the plane orthogonal to each edge. Third, a finite element for sym curl-conforming trace-free tensors is constructed following the same approach. Finally, a finite element divdiv complex, as well as the bubble functions complex, in three dimensions are established.
2010 Mathematics Subject Classification:
65N30; 65N12; 65N22;1. Introduction
In this paper, we shall construct finite elements for space
which consists of symmetric tensors such that with the inner applied row-wisely to resulting a column vector for which the outer operator is applied. -conforming finite elements can be applied to discretize the linearized Einstein-Bianchi system [21, Section 4.11] and the mixed formulation of the biharmonic equation [19].
The construction in three dimensions is much harder than that in two dimensions. The essential difficulty arises from the underline divdiv Hilbert complex
where , and are standard Sobolev spaces, and is the space of traceless tensor such that with the row-wise operator. In the divdiv complex in three dimensions, the Sobolev space before consists of tensor functions rather than vector functions in two dimensions. By comparison, the divdiv Hilbert complex in two dimensions is
Finite element spaces for are relatively mature. Then the design of divdiv conforming finite elements in two dimensions is relatively easy; see [6] and also Section § 5.3.
We start our construction from the two polynomial complexes
| (1) |
|
and reveal several decompositions of polynomial vector and tensors spaces from (1). We then present a Green’s identity
and give a characterization of two traces for
see Section § 4.3 for detailed definition of the negative Sobolev space for traces.
Based on the decomposition of polynomial tensors and the characterization of traces, we are able to construct two types of -conforming finite element spaces on a tetrahedron. Here we present the BDM-type (full polynomial) space below. Let be a tetrahedron and let be a positive integer. The shape function space is simply . The set of edges of is denoted by , the set of faces by , and the set of vertices by . For each edge, we chose two normal vectors and . The degrees of freedom (d.o.f) are given by
| (2) | ||||
| (3) | ||||
| (4) | ||||
| (5) | ||||
| (6) | ||||
| (7) | ||||
| (8) |
where is an arbitrary but fixed face. The last degrees of freedom (8) will be regarded as interior degrees of freedom to the tetrahedron . Namely when a face is chosen in different elements, the degrees of freedom (8) are double-valued when defining the global finite element space. The RT-type (incomplete polynomial) space can be obtained by further reducing the index of degree of freedoms by except the moment with . To the best of our knowledge, these are the first -conforming finite elements for symmetric tensors in three dimensions. We notice in the recent work [17], a new family of divdiv-conforming finite elements are introduced for triangular and tetrahedral grids in a more unified way. The constructed finite element spaces there are in , which are smoother than ours.
To help the understanding of our construction, we sketch a decomposition of a finite element space associated to a generic differential operator in Fig. 1, where is the adjoint of .
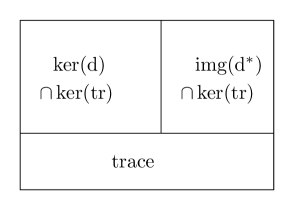
The boundary degree of freedoms (4)-(5) are obviously motivated by the Green’s formulae and the characterization of the trace of . The extra continuity (2)-(3) is to ensure the cancellation of the edge term when adding element-wise Green’s identity over a mesh. All together (2)-(5) will determine the trace on the boundary of a tetrahedron.
The interior moments of is to determine the image , which is isomorphism to – the upper right block in Fig. 1. Together with , the volume moments can determine the polynomial of degree only up to . We then use the vanished trace and the symmetry of the tensor to figure out the rest d.o.f. The degrees of freedom (7)-(8) will determine – the upper left block in Fig. 1.
For the symmetric tensor space, it seems odd to have degrees of freedom not symmetric, as a face is singled out. In view of Fig. 1 and the exactness of the polynomial divdiv complex (1), a symmetric set of d.o.f. is replacing (7)-(8) by
| (9) |
where is the so-called bubble function space and will be characterized precisely in Section § 5.2. Although (9) is more symmetric, it is indeed not simpler than (7)-(8) in implementation as the formulation of is much more complicated than polynomials on a face.
With the help of the -conforming finite elements for symmetric tensors and two traces and of space , we construct -conforming finite elements for trace-free tensors with as the space of shape functions with . The degrees of freedom are
| (10) | ||||
| (11) | ||||
| (12) | ||||
| (13) | ||||
| (14) | ||||
| (15) | ||||
| (16) | ||||
| (17) |
Combining previous finite elements for tensors and the vectorial Hermite element in three dimensions, we arrive at a finite element divdiv complex in three dimensions, and the associated finite element bubble divdiv complex. Recently a finite element divdiv complex in three dimensions involving the -conforming finite elements for symmetric tensors constructed in this paper is devised in [16]. The -conforming finite elements for trace-free tensors and -conforming finite elements for vectors employed in [16] are smoother than ours. Two dimensional finite element divdiv complexes can be found in [4, 6, 17].
The rest of this paper is organized as follows. We present some operations for vectors and tensors in Section 2. Two polynomial complexes related to the divdiv complex, and direct sum decompositions of polynomial spaces are shown in Section 3. We derive the Green’s identity and characterize the trace of on polyhedrons in Section 4, and then construct the conforming finite elements for in three dimensions in Section 5. In Section 6 we construct conforming finite elements for . With previous devised finite elements for tensors, we form a finite element divdiv complex in three dimensions in Section 7.
2. Matrix and Vector Operations
In this section, we shall survey operations for vectors and tensors. In particular, we shall distinguish operators applied to columns and rows of a matrix.
2.1. Matrix-vector products
The matrix-vector product can be interpreted as the inner product of with the row vectors of . We thus define the dot operator Similarly we can define the row-wise cross product from the right . Here rigorously speaking when a column vector is treat as a row vector, notation should be used. In most places, however, we will sacrifice this precision for the ease of notation. When the vector is on the left of the matrix, the operation is defined column-wise. For example, . For dot products, we will still mainly use the conventional notation, e.g. . But for the cross products, we emphasize again the cross product of a vector from the left is column-wise and from the right is row-wise. The transpose rule still works, i.e. . Here again, we mix the usage of column vector and row vector .
The ordering of performing the row and column products does not matter which leads to the associative rule of the triple products
Similar rules hold for and and thus parentheses can be safely skipped when no differentiation is involved.
For two column vectors , the tensor product is a matrix which is also known as the dyadic product with more clean notation (one ⊺ is skipped). The row-wise product and column-wise product with another vector will be applied to the neighboring vector
| (18) | |||
| (19) |
2.2. Differentiation
We treat Hamilton operator as a column vector. For a vector function , , and are standard differential operations. Define , which can be understood as the dyadic product of Hamilton operator and column vector .
Apply these matrix-vector operations to the Hamilton operator , we get column-wise differentiation and row-wise differentiation Conventionally, the differentiation is applied to the function after the symbol. So a more conventional notation is
By moving the differential operator to the right, the notation is simplified and the transpose rule for matrix-vector products can be formally used. Again the right most column vector is treated as a row vector to make the notation cleaner.
In the literature, differential operators are usually applied row-wisely to tensors. To distinguish with notation, we define operators in letters as
Then the double divergence operator can be written as
Again as the column and row operations are independent, the ordering of operations is not important and parentheses is skipped.
2.3. Matrix decompositions
Denote the space of all matrices by , all symmetric matrices by , all skew-symmetric matrices by , and all trace-free matrices by . For any matrix , we can decompose it into symmetric and skew-symmetric parts as
We can also decompose it into a direct sum of a trace free matrix and a diagonal matrix as
| (20) |
Define operator for a matrix
We define an isomorphism of and the space of skew-symmetric matrices as follows: for a vector
Obviously is a bijection. We define by .
2.4. Projections to a plane
Given a plane with normal vector , for a vector , we have the orthogonal decomposition
The vector is also on the plane and is a rotation of by counter-clockwise with respect to . We treat Hamilton operator as a column vector and define
For a scalar function ,
are the surface gradient of and surface , respectively. For a vector function , is the surface divergence
By the cyclic invariance of the mix product and the fact is constant, the surface rot operator is
which is the normal component of . The tangential trace of is
| (25) |
By definition,
| (26) |
Note that the three dimensional operator restricted to a two dimensional plane results in two operators: maps a scalar to a vector, which is a rotation of , and maps a vector to a scalar which can be thought as a rotated version of . The surface differentiations satisfy the property and and when is simply connected, and .
Differentiation for two dimensional tensors can be defined similarly.
3. Divdiv Complex and Polynomial Complexes
In this section, we shall consider the divdiv complex and establish two related polynomial complexes. We assume is a bounded and Lipschitz domain, which is topologically trivial in the sense that it is homeomorphic to a ball. Without loss of generality, we also assume .
Recall that a Hilbert complex is a sequence of Hilbert spaces connected by a sequence of linear operators satisfying the property: the composition of two consecutive operators is vanished. A Hilbert complex is exact means the range of each map is the kernel of the succeeding map. As is topologically trivial, the following de Rham Complex of is exact
| (27) |
We will abbreviate a Hilbert complex as a complex.
3.1. The complex
The complex in three dimensions reads as [1, 19]
| (28) |
|
where is the space of shape funcions of the lowest order Raviart-Thomas element [22]. For completeness, we prove the exactness of the complex (28) following [19].
Theorem 3.1.
Assume is a bounded and topologically trivial Lipschitz domain in . Then (28) is an exact Hilbert complex.
Proof.
We verify the composition of consecutive operators is vanished from the left to the right. Take a function , then and . For any , it holds from (23) that
By the density argument, we get . For any ,
Again by the density argument, . Thus (28) is a complex.
We then verify the exactness of (28) from the right to the left.
1. .
Recursively applying the exactness of de Rham complex (27), we can prove without the symmetry requirement, where the space .
Any skew-symmetric can be written as for . Assume , it follows from (22) that
| (29) |
Since for any smooth skew-symmetric tensor field , we obtain
2. , i.e. if and , then there exists a , s.t. .
Since , by the exactness of the de Rham complex and identity (22), there exists such that
Namely . Again by the exactness of the de Rham complex, there exists such that
By the symmetry of , we have
From (23) we get
which indicates with .
3. , i.e. if and , then there exists a , s.t. .
Since and , we have from (21) that
Then by (22),
Thus there exists satsifying , which together with (23) implies
Namely . Hence there exists such that . Noting that is trace-free, we achieve
4. , i.e. if and , then .
Notice that
| (30) |
Apply on both sides of (30) and use (23) to get
Hence is a constant, which combined with (30) implies that is a linear function. Assume with and , then (30) becomes , i.e. is diagonal and consequently .
Thus the complex (28) is exact. ∎
3.2. A polynomial divdiv complex
Given a bounded domain and a non-negative integer , let stand for the set of all polynomials in with the total degree no more than , and with being or denote the tensor or vector version. Recall that , and . For a linear operator defined on a finite dimensional linear space , we have the relation
| (31) |
which can be used to count provided the space is identified and vice verse.
The polynomial de Rham complex is
| (32) |
As is topologically trivial, complex (32) is also exact, i.e., the range of each map is the kernel of the succeeding map.
Lemma 3.2.
The polynomial complex
| (33) |
|
is exact.
Proof.
1. . By the exactness of the complex (28),
2. , i.e. if and , then there exists a , s.t. .
By , there exists satisfying , i.e. . Then we get from (23) that
which implies . Hence . And thus . As a result .
3. . Recursively applying the exactness of de Rham complex (32), we can prove . Then from (29) we have that
4. .
Obviously . As is surjective by step 3, using (31), we have
| (34) |
Thank to results in steps 1 and 2, we can count the dimension of
| (35) |
We conclude that as the dimensions matches, cf. (34) and (35).
Therefore the complex (33) is exact. ∎
3.3. A Koszul complex
The Koszul complex corresponding to the de Rham complex (32) is
| (36) |
where the operators are appended to the right of the polynomial, i.e. , , or . The following complex is a generalization of the Koszul complex (36) to the divdiv complex (33), where operator is defined as
and other operators are appended to the right of the polynomial, i.e., , , or . The Koszul operator can be constructed based on Poincaré operators constructed in [8], but others are simpler.
Lemma 3.3.
The following polynomial sequence
| (37) |
|
is an exact Hilbert complex.
Proof.
To verify (37) is a complex, we use the product rule (18)-(19):
To verify for , we use the formulae
| (38) |
and therefore evaluating at is zero.
We then verify the exactness from right-to-left.
1. .
It is straightforward to verify
| (39) |
Namely is a projector. Consequently, the operator is surjective as .
2. , i.e. if and , then there exists a , s.t. .
Since , by the fundamental theorem of calculus,
Using the decomposition (20), we conclude that there exist and such that . Again by (38), we have
which indicates . As , we conclude . Again using the fundamental theorem of calculus to conclude that there exists such that . Taking , we get
3. , i.e. if and , then there exists a , s.t. .
Thanks to , there exists such that . By the symmetry of , it follows
which indicates . Then there exists satisfying . Hence .
4. .
Therefore the complex (37) is exact. ∎
3.4. Decomposition of polynomial tensors
Those two complexes (33) and (37) can be combined into one double direction complex
|
|
Unlike the Koszul complex for vectors functions, we do not have the identity property applied to homogenous polynomials. Fortunately decomposition of polynomial spaces using Koszul and differential operators still holds.
Let be the space of homogeneous polynomials of degree . Then by Euler’s formula
| (41) |
Due to (41), we have
| (42) | ||||
| (43) |
for any positive number .
Lemma 3.4.
We have the decomposition
| (44) |
Proof.
Finally we present a decomposition of space . Let
Their dimensions are
| (46) |
The calculation of is easy and is detailed in (35).
Lemma 3.5.
We have
-
(i)
for any
-
(ii)
is a bijection.
-
(iii)
Proof.
Since and , we get
| (47) |
Hence property (i) follows from (41). Property (ii) is obtained by writing . Now we prove property (iii). First the dimension of space in the left hand side is the summation of the dimension of the two spaces in the right hand side in (iii). Assume satisfies , which means
Thus from (47) and (43) and consequently property (iii) holds. ∎
For the simplification of the degree of freedoms, we need another decomposition of the symmetric tensor polynomial space, which can be derived from the polynomial Hessian complex
| (48) |
|
where A proof of the exactness of (48) is similar to that of Lemma 3.3 and can be found in [5]. Based on (48), we have the following decomposition of symmetric polynomial tensors.
Lemma 3.6.
It holds
| (49) |
Proof.
Obviously the space on the right is contained in the space on the left. We then count the dimensions of spaces on both sides:
| (50) |
Then by direct calculation,
We only need to prove that the sum is direct.
Similarly for a two dimensional domain , we have the following divdiv polynomial complex and its Koszul complex
| (51) |
where , is the rotation of . A two dimensional Hessian polynomial complex and its Koszul complex are
| (52) |
where Verification of the exactness of these two complexes and corresponding space decompositions can be found in [6].
4. Green’s Identities and Traces
We first present a Green’s identity based on which we can characterize two traces of on polyhedrons and give a sufficient continuity condition for a piecewise smooth function to be in .
4.1. Notation
Let be a regular family of polyhedral meshes of . Our finite element spaces are constructed for tetrahedrons but some results, e.g., traces and Green’s formulae etc, hold for general polyhedrons. For each element , denote by the unit outward normal vector to , which will be abbreviated as for simplicity. Let , , , , and be the union of all faces, interior faces, all edges, interior edges, vertices and interior vertices of the partition , respectively. For any , fix a unit normal vector and two unit tangent vectors and , which will be abbreviated as and without causing any confusions. For any , fix a unit tangent vector and two unit normal vectors and , which will be abbreviated as and without causing any confusions. For being a polyhedron, denote by , and the set of all faces, edges and vertices of , respectively. For any , let be the set of all edges of . And for each , denote by the unit vector being parallel to and outward normal to . Furthermore, set
4.2. Green’s identities
We first derive a Green’s identity for smooth functions on polyhedrons.
Lemma 4.1 (Green’s identity in 3D).
Let be a polyhedron, and let and . Then we have
| (53) |
Proof.
We start from the standard integration by parts
We then decompose and apply the Stokes theorem to get
Now we rewrite the term
Thus the Green’s identity (53) follows by merging all terms. ∎
When the domain is smooth in the sense that is an empty set, the term disappears. When is continuous on edge , this term will define a jump of the tensor.
A similar Green’s identity in two dimensions is included here for later usage. To avoid confusion with three dimensional version, is used to emphasize it is a normal vector of edge of a polygon and differential operators with subscript are used.
Lemma 4.2 (Green’s identity in 2D).
Let be a polygon, and let and . Then we have
where
Here the trace is called the effective transverse shear force respectively for being a moment and is the normal bending moment in the context of elastic mechanics [11].
4.3. Traces and continuity across the boundary
The Green’s identity (53) motives the definition of two trace operators for function :
We first recall the trace of the space on the boundary of polyhedron (cf. [12, Lemma 3.2] and [23, 20]). Let be the closure of with respect to the norm , which includes all functions in whose continuation to the whole boundary by zero belongs to . Define trace spaces
with norm
and
with norm
Let for , and for .
Lemma 4.3 (Lemma 3.2 in [12]).
For any , it holds
Conversely, for any and , there exists some such that
The hidden constants depend only the shape of the domain .
Notice that the term in the Green’s identity (53) is not covered by Lemma 4.3. Indeed, the full characterization of the trace of is defined by , which cannot be equivalently decoupled [12, Lemma 3.2]. It is possible, however, to face-wisely localize the trace if imposing additional smoothness.
We then present a sufficient continuity condition for piecewise smooth functions to be in .
Lemma 4.4 (cf. Proposition 3.6 in [12]).
Let such that
-
(i)
for each polyhedron ;
-
(ii)
is single-valued for each ;
-
(iii)
is single-valued for each ;
-
(iv)
is single-valued for each , ,
then .
Proof.
For any , we get from the Green’s identity (53) that
Since the terms in (ii)-(iv) are single-valued and each interior face is repeated twice in the summation with opposite orientation, it follows
Thus we have by the definition of derivatives of the distribution, and for each . ∎
For any piecewise smooth , the single-valued term in (iv) in Lemma 4.4 implies that there is some compatible condition for at each vertex . Indeed, for any and with being a vertex of , let and , where and are the unit tangential vectors of two edges of sharing . Then by (iv) we have
|
|
where is the jump across . Hence this suggests the tensor value at vertex as the degree of freedom when defining the finite element.
Continuity of is a sufficient but not necessary condition for functions in . Sufficient and necessary conditions are presented in [12, Proposition 3.6].
5. Didiv Conforming Finite Elements
In this section we construct conforming finite element space for and prove the unisolvence.
5.1. Finite element spaces for symmetric tensors
Let be a tetrahedron. Take the space of shape functions
with and . Recall that
By Lemma 3.5, we have
The most interesting cases are and , which correspond to RT (incomplete polynomial) and BDM (complete polynomial) -conforming elements for the vector functions, respectively.
For each edge, we chose two normal vectors and . The degrees of freedom are given by
| (54) | ||||
| (55) | ||||
| (56) | ||||
| (57) | ||||
| (58) | ||||
| (59) | ||||
| (60) |
where is an arbitrary but fixed face. The degrees of freedom (60) will be regarded as interior degrees of freedom to the tetrahedron , that is the degrees of freedom (60) will be double-valued if is selected in different elements.
Before we prove the unisolvence, we give characterization of the space of shape functions restricted to edges and faces, and derive some consequence of vanishing degree of freedoms.
Lemma 5.1.
For any , we have
for each edge , each face and .
Proof.
Take any with . Since is constant on each edge of and is constant on each face of ,
and
Thus we conclude the results from the requirement . ∎
Proof.
With previous preparations, we prove the unisolvence as follows. For any satisfying , we have as no contribution from . By (64) the volume moments can only determine the polynomial of degree up to .
We then use the vanished trace. Similarly as the RT and BDM elements [2], the vanishing normal-normal trace (62) implies the normal-normal part of is zero. To determine the normal-tangential terms, further degrees of freedoms are needed.
Unlike the traditional approach by transforming back to the reference element, we will chose an intrinsic coordinate. For ease of presentation, denote the four faces in by , which is opposite to the th vertex of , and by the outward unit normal vector of for . Let be the unit tangential vector of the edge from vertex to vertex ; see Fig. 2. The set of three vectors forms a basis of although they may not be orthogonal in general. Consequently forms a basis of the second order tensor and for .
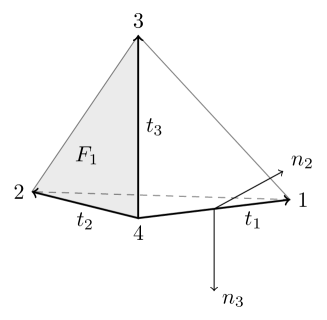
Let be the th barycentric coordinate with respect to the tetrahedron for . Then and for some .
Proof.
We first count the number of the degrees of freedom (54)-(60). Calculation of d.o.f. (59) can be found in (50). The number of d.o.f. (54)-(60) is
which is same as cf. (46).
Take any and suppose all the degrees of freedom (54)-(60) vanish. We are going to prove the function . Using the local coordinate sketched in Fig. 2, we can expand as
As is symmetric, . By (62), it follows
Thus there exists satisfying for . Taking in (64) will produce
| (65) |
Namely the diagonal of is zero. So far, in the chosen coordinate, has no simple formulation and will be used later on.
On the other hand, from (61) we have . As in cf. (65), it follows . Therefore (63) becomes
Hence there exists such that , where is the cubic bubble function on face . Together with (60) and the fact , we get . Thus . Then there exists such that , combined with (64) yields . That is the first row of is zero, i.e. .
By the symmetry, now . Multiplying by from both sides and restricting to , we have
The denominator is non-zero as are non tangential vectors of face . Again there exists satisfying . Taking in (64) gives . We thus have proved and consequently the unisolvence. ∎
5.2. Polynomial bubble function spaces and the bubble complex
Let
Together with vanishing (58), we can conclude that . In view of Fig. 1 and Lemma 5.2, the last two set of d.o.f. (59)-(60) can be replaced by
Next we give characterization of .
By the exactness of divdiv complex, if and , it is possible that for some . We will give an explicit characterization of , show , and consequently get a set of computable and symmetric d.o.f..
We begin with a characterization of the trace of functions in .
Lemma 5.4 (Green’s identity).
Let be a polyhedron, and let and . Then we have
Proof.
As is symmetric,
On each face, we expand the boundary term
Then we use the fact is symmetric to arrive the desired identity. ∎
Based on the Green’s identity, we introduce the following trace operators for space
-
(1)
,
-
(2)
,
-
(3)
.
Both and are symmetric tensors on each face and is a vector function. Obviously if and only if as is just a rotation of . Using the trace operators, polynomial bubble function space can be defined as
We shall give an explicit characterization of .
Lemma 5.5.
Let . It holds
| (66) |
Proof.
It is straightforward to verify (66) on the reference tetrahedron for which and two normal vectors of the face containing is and . To avoid complicated transformation of trace operators, we provide a proof using an intrinsic basis of on .
Take any edge with the tangential vector . Let and be the unit outward normal vectors of two faces sharing edge . Set for . By direction computation, we get on edge for that
Both and form the same normal vector space of edge , then the last identity implies
Then it is sufficient to prove the eight trace-free tensors
| (67) |
are linear independent. Assume there exist , such that
Multiplying the last equation by from the right and left respectively, we obtain
Hence , which yields
Multiplying the last equation by from the right, it follows
As a result , and then . ∎
We write as and use the barycentric coordinate representation of a polynomial. That is a polynomial has a unique representation in terms of
| (68) |
Lemma 5.5 implies that must contain a face bubble where are three vertices of . Otherwise, if , then is not zero on the edge .
We consider the subspace and identify its intersection with . Due to the face bubble , the polynomial is zero on the other faces. So we only need to consider the trace on face . Without loss of generality, we can chose the coordinate s.t. . Chose the canonical basis of associated to this coordinate. Then by direct calculation to find out consists of
Switch to an intrinsic basis, we obtain the following explicit characterization of .
Lemma 5.6.
For each face , we chose two unit tangent vectors s.t. forms an orthonormal basis of . Then
| (69) |
where the three bubble functions are:
Proof.
We only give a generating set of the bubble function space as the constant matrices are not linear independent. Next we find out a basis from this generating set.
Lemma 5.7.
Let be three vertices of face and . Define and . Then
| (70) |
and consequently
Proof.
The constant matrices are not linear independent as . Among them, forms a basis of which can be proved as verifying the linear independence of (67) in Lemma 5.5 or see [15].
For each , with , we can group into either or depending on if the polynomial is zero or not, respectively. That is, for one fixed face :
The sum is direct in view of the barycentric representation (68) of a polynomial. Then coupled with , we get the basis (70) of the bubble function space.
The dimension of is
as required. ∎
We then verify by verifying all boundary d.o.f. are vanished.
Lemma 5.8.
Let . Assume edge is shared by faces and . It holds .
Proof.
For the ease of notation, let . Suppose with . By , we get
Since , we can see that . Thus for ,
Next consider . When , the face bubble has a factor , which implies . Thus
When , the face bubble has a factor . By the fact that forms an orthonormal basis of ,
which implies
As a result,
Similarly holds. Hence .
Therefore . ∎
Next we show the two traces is in and in .
Lemma 5.9.
When with , we can express the trace in terms of the differential operators on surface of
| (71) | ||||
| (72) | ||||
Proof.
Note that is an equivalent formulation of the second trace of . Combining Lemmas 5.8 and 5.9 gives the following result.
Lemma 5.10.
It holds
| (73) |
Proof.
Indeed the in (73) can be changed to “=”. This will be clean after we present a bubble complex.
Lemma 5.11.
For each , it holds
| (74) |
where is a subspace of being orthogonal to with respect to the -inner product . Consequently
| (75) |
Proof.
Define
Now we are in the position to present the so-called bubble complex.
Theorem 5.12.
The bubble function spaces for the divdiv complex
| (76) |
|
form an exact Hilbert complex.
Proof.
Take any with . We have on each face ,
| (77) |
and
| (78) |
Hence . Thanks to Lemma 5.10 and (74), we conclude that (76) is a complex.
We then verify the exactness from the left to the right.
1. , i.e. if and , then there exists a , s.t. .
Firstly, by the exactness of the polynomial divdiv complex (33), there exists such that . As , we can further impose constraint for each . By (77), we get . Hence , which indicates for each vertex . By (78), we obtain , i.e. . This combined with for each vertex means , and then for each . Thus .
2. .
Therefore complex (76) is exact. ∎
As a result of complex (76), we can replace the degrees of freedom (59)-(60) by
| (80) |
The dimension of (80) is counted in (79), which also matches the sum of (59)-(60).
We summarize the unisolvence below.
5.3. Two dimensional divdiv conforming finite elements
Recently we have constructed divdiv conforming finite elements in two dimensions in [6]. Here we briefly review the results and compare to the three dimensional case.
Let be a triangle. Take the space of shape functions
| (81) |
with and and
Here the polynomial space for is the vector space not a tensor space, which simplifies the construction significantly.
The degrees of freedom are given by
| (82) | ||||
| (83) | ||||
| (84) | ||||
| (85) | ||||
| (86) |
Here to avoid confusion with three dimensional version, we use to emphasize it is a normal vector of edge vector .
The unisolvence is again better understood with the help of Fig. 1. By the vanishing degrees of freedom (82)-(84), the trace is vanished. Then together with the vanishing (85), . The rest is to identify the intersection of the bubble space and the kernel of . Define
It turns out the space is much simpler in two dimensions.
The key is the following formulae on the trace .
Lemma 5.14.
When , we have
| (87) |
Proof.
Lemma 5.15.
The following bubble complex:
is exact.
Proof.
The fact is surjective can be proved similarly to Lemma 5.11.
For , from the complex (51), we can find s.t. . We will prove .
Since , we can further impose constraint for each . The fact implies
Hence . This also means for each .
By Lemma 5.14, since
and , we acquire
That is on each edge . Noting that for each , we get and consequently , i.e.,
∎
We now prove the unisolvence as follows.
Proof.
We first count the number of the degrees of freedom (82)-(85) and the dimension of the space, i.e., . Both of them are
Then suppose all the degrees of freedom (82)-(85) applied to vanish. We are going to prove the function .
By the vanishing degrees of freedom (82)-(84), the two traces are vanished. Together with (85), the Green’s identity implies . Then
We then use the fact is bijection, cf. the complex (52), to find s.t. . Finally we finish the unisolvence proof by choosing in (86). The fact
will imply and consequently . ∎
As finite element spaces for are relatively mature and the bubble function space of , the design of divdiv conforming finite elements in two dimensions is relatively easy. By rotation, we can also get finite elements for the strain space ; see [6, Section 3.4].
6. Finite Elements for Sym Curl-Conforming Trace-Free Tensors
In this section we construct conforming finite element spaces for .
6.1. A finite element space
Let be a tetrahedron. For each edge , we have a direction vector and then chose two orthonormal vectors and being orthogonal to such that and . Take the space of shape functions as . The degrees of freedom are given by
| (88) | ||||
| (89) | ||||
| (90) | ||||
| (91) | ||||
| (92) | ||||
| (93) | ||||
| (94) | ||||
| (95) |
The degree of freedom (89), (90), and (95) are motivated by (54), (55), and (80), respectively, as . Recall that and , cf. Lemma 5.9. Let be the norm vector of sitting on the face . For elements on face , the normal trace becomes
which motivates d.o.f. (91). Together with d.o.f. (94), can be determined. For the element, the normal-normal trace becomes
| (96) |
which can be also determined by (91). Notice that for each edge , there are two inside one tetrahedron. In (91), the two normal vectors are chosen independent of elements and (91) can determine the projection of vector to the plane orthogonal to edge including .
The other trace of a element will be determined by (90) and (92), which is less obvious. The following lemma is borrowed from [16, Lemma 9 and Remark 8].
Lemma 6.1.
Proof.
On the plane orthogonal to , the vectors and form an orthonormal basis. We expand in this coordinate, with for . Then Then in this coordinate
Thus we acquire (97) from the fact .
The trace depends on . For one edge in a tetrahedron , there are two such traces. Lemma 6.1 shows that these two traces are linear dependent and only one d.o.f. (92) is needed.
Proof.
We are in the position to prove the unisolvence.
6.2. Lagrange-type Degree of freedoms
The d.o.f. is designed to form a finite element divdiv complex. If the exactness of the sequence is not the concern, we can construct simpler degree of freedoms. Below is the Lagrange-type -conforming finite elements for trace-free tensors. Take the space of shape functions as . The degrees of freedom are given by
| (99) | ||||
| (100) | ||||
| (101) | ||||
| (102) | ||||
| (103) |
It is straightforward to verify the unisolvence of (99)-(103) due to the characterization of trace operators and bubble functions.
7. A Finite Element Divdiv Complex in Three Dimensions
In this section, we collect finite element spaces defined before to form a finite element div-div complex. We assume is a triangulation of a topological trivial domain .
7.1. A finite element divdiv complex
We start from the vectorial Hermite element space in three dimensions [9]
The local degrees of freedom for are
| (109) | ||||
| (110) | ||||
| (111) | ||||
| (112) |
The unisolvence for is trivial. And
Let
then
Clearly Lemma 6.2 ensures . Let
then
It follows from the proof of Lemma 5.2 ensures . Let
be the discontinuous polynomial space. Obviously
Lemma 7.1.
It holds
Proof.
Apparently . Then we focus on .
Take any . By the fact [10], there exists such that
Let be determined by
for all d.o.f. from (54) to (60). Note that for functions in , the integrals on edge and pointwise value are well-defined. Since , it follows from the Green’s identity (53) that
Hence . Applying (74), there exists such that for each , and
Therefore , where , as required. ∎
Theorem 7.2.
Assume is a bounded and topologically trivial Lipschitz domain in . The finite element divdiv complex
| (113) |
is exact.
Proof.
For any sufficient vector function and , we have from that
Hence by (77)-(78) it is easy to see that . It holds from Lemma 6.2 and the degrees of freedom (89)-(90) that
| (114) |
We then verify the exactness.
1. . By the exactness of the complex (28),
2. , i.e. if and , then there exists a , s.t. .
Since , by the divdiv complex (28), there exists such that . Due to (91), we obtain for each edge and . Hence is well-defined for each vertex . Take satisfying , where goes through all the degrees of freedom (109)-(112). Then it follows from the integration by parts that
This indicates .
3. . This is Lemma 7.1.
4. .
We verify the identity by dimension count. By Lemma 7.1,
| (115) |
As a result of step 2,
Applying the Euler’s formula , we get from (115) that . Then the result follows from (114).
Therefore the finite element divdiv complex (113) is exact. ∎
For the completeness, we present a two dimensional finite element divdiv complex but restricted to one element. A global version of (116) as well as a commutative diagram involving quasi-interpolation operators from Sobolev spaces to finite element spaces can be found in [6].
Lemma 7.3.
For any triangle , the polynomial complex
| (116) |
is exact.
Acknowledgement.
The authors appreciate the anonymous reviewers for valuable suggestions and careful comments, which significantly improved the readability of an early version of the paper. The authors also want to thank Prof. Jun Hu, Dr. Yizhou Liang in Peking University, and Dr. Rui Ma in University of Duisburg-Essen for showing us the proof of the key Lemma 6.1 for constructing -conforming element.
References
- [1] D. N. Arnold and K. Hu. Complexes from complexes. arXiv preprint arXiv:2005.12437, 2020.
- [2] D. Boffi, F. Brezzi, and M. Fortin. Mixed finite element methods and applications. Springer, Heidelberg, 2013.
- [3] S. C. Brenner and L. R. Scott. The mathematical theory of finite element methods. Springer, New York, third edition, 2008.
- [4] L. Chen, J. Hu, and X. Huang. Multigrid methods for Hellan–Herrmann–Johnson mixed method of Kirchhoff plate bending problems. J. Sci. Comput., 76(2):673–696, 2018.
- [5] L. Chen and X. Huang. Discrete Hessian complexes in three dimensions. arXiv preprint arXiv:2012.10914, 2020.
- [6] L. Chen and X. Huang. Finite elements for divdiv-conforming symmetric tensors. arXiv preprint arXiv:2005.01271, 2020.
- [7] L. Chen and X. Huang. A finite element elasticity complex in three dimensions. Submitted, 2021.
- [8] S. H. Christiansen, K. Hu, and E. Sande. Poincaré path integrals for elasticity. J. Math. Pures Appl., 135:83–102, 2020.
- [9] P. G. Ciarlet. The finite element method for elliptic problems. North-Holland Publishing Co., Amsterdam, 1978.
- [10] M. Costabel and A. McIntosh. On Bogovskiĭ and regularized Poincaré integral operators for de Rham complexes on Lipschitz domains. Math. Z., 265(2):297–320, 2010.
- [11] K. Feng and Z.-C. Shi. Mathematical theory of elastic structures. Springer-Verlag, Berlin, 1996.
- [12] T. Führer, N. Heuer, and A. Niemi. An ultraweak formulation of the Kirchhoff–Love plate bending model and DPG approximation. Math. Comp., 88(318):1587–1619, 2019.
- [13] K. Hellan. Analysis of elastic plates in flexure by a simplified finite element method. Acta Polytechnica Scandinavia, Civil Engineering Series, 46, 1967.
- [14] L. R. Herrmann. Finite element bending analysis for plates. Journal of the Engineering Mechanics Division, 93(EM5):49–83, 1967.
- [15] J. Hu and Y. Liang. Conforming discrete Gradgrad-complexes in three dimensions. arXiv preprint arXiv:2008.00497, 2020.
- [16] J. Hu, Y. Liang, and R. Ma. Conforming finite element divdiv complexes and the application for the linearized Einstein-Bianchi system. arXiv preprint arXiv:2103.00088, 2021.
- [17] J. Hu, R. Ma, and M. Zhang. A family of mixed finite elements for the biharmonic equations on triangular and tetrahedral grids. arXiv preprint arXiv:2010.02638, 2020.
- [18] C. Johnson. On the convergence of a mixed finite-element method for plate bending problems. Numer. Math., 21:43–62, 1973.
- [19] D. Pauly and W. Zulehner. The divdiv-complex and applications to biharmonic equations. Applicable Analysis, 99(9):1579–1630, 2020.
- [20] A. S. Pechstein and J. Schöberl. An analysis of the TDNNS method using natural norms. Numer. Math., 139(1):93–120, 2018.
- [21] V. Quenneville-Belair. A new approach to finite element simulations of general relativity. PhD thesis, University of Minnesota, 2015.
- [22] P.-A. Raviart and J. M. Thomas. A mixed finite element method for 2nd order elliptic problems. In Mathematical aspects of finite element methods (Proc. Conf., Consiglio Naz. delle Ricerche (C.N.R.), Rome, 1975), pages 292–315. Lecture Notes in Math., Vol. 606. Springer, Berlin, 1977.
- [23] A. Sinwel. A new family of mixed finite elements for elasticity. PhD thesis, Johannes Kepler University Linz, 2009.