Finding the Reflection Point: Unpadding Images to Remove Data Augmentation Artifacts in Large Open Source Image Datasets for Machine Learning
Abstract
In this paper, we address a novel image restoration problem relevant to machine learning dataset curation: the detection and removal of noisy mirrored padding artifacts. While data augmentation techniques like padding are necessary for standardizing image dimensions, they can introduce artifacts that degrade model evaluation when datasets are repurposed across domains. We propose a systematic algorithm to precisely delineate the reflection boundary through a minimum mean squared error approach with thresholding and remove reflective padding. Our method effectively identifies the transition between authentic content and its mirrored counterpart, even in the presence of compression or interpolation noise. We demonstrate our algorithm’s efficacy on the SHEL5k dataset, showing significant performance improvements in zero-shot object detection tasks using OWLv2, with average precision increasing from 0.47 to 0.61 for hard hat detection and from 0.68 to 0.73 for person detection. By addressing annotation inconsistencies and distorted objects in padded regions, our approach enhances dataset integrity, enabling more reliable model evaluation across computer vision tasks.
1 Introduction
Data augmentation is a fundamental task in data preprocessing and training for deep learning tasks. However, when repurposing data between learning tasks or domains, images altered by task-specific augmentations are not always desired. Therefore, to recover the raw data when only an altered form is available, image restoration becomes a necessary computer vision subtask. Here, we introduce a novel and niche problem in image restoration, which can be introduced through errors in dataset curation during machine learning: the detection and removal of noisy mirrored regions. In mass image data collection or curation, especially when images may come from different cameras or feature cropped regions of interest of varying sizes, image dimensions may be inconsistent. However, many deep learning architectures require images of fixed input size. This is often remedied by resizing or padding; it is the padding case that we handle in this research.
As an alternative to padding at training time, machine learning practitioners may choose to pad their dataset prior to training as a precomputation step, which is also helpful in reducing repeated computations during multiple epochs of training or isolating features of interest for learning. Examples of such public dataset artifacts are shown in Figure 1. However, if this padded dataset is saved and publicized instead of the original images, the artifacts it contains can lead to problems in evaluation, especially when the data used is transferred to other tasks. With large and redundant data volumes, the padding may be fine for training, but during evaluation, the presence of padding – particularly symmetric or reflective padding – can simultaneously create realistic objects or patterns that should be recognized but are left out of annotation, and unrealistic objects or patterns that should not be recognized and actually distort the meaning of the original object. In both cases, for symmetrically-padded images, using annotations centered on object detection of the original objects will lead to misleading performance evaluation. A solution we propose in this research is image unpadding, where the padding on an image can be removed to restore an original image.









In cases of true zero-padding, the problem is trivial. When it comes to symmetric padding, further trivial methods, such as iterating through columns of pixels and identifying a consecutive repeating section in reverse, are only feasible when the image is saved without compression or resizing, as these processes can introduce interpolation noise. The presence of noise on either or both sides of a reflection makes detecting the boundary of an artificially-mirrored region non-trivial. Reflection removal requires a precise delineation of the mirrored boundary to separate authentic scene content from its redundant and often non-naturalistic counterpart.
In this research, we propose a systematic approach to identify the reflection boundary, accurately localize the mirrored region, and remove redundant, inaccurate, or non-naturalistic information. We then demonstrate the effectiveness of this unpadding on inference and evaluation of a zero-shot object detection task.
2 Related Research
The necessity of image restoration, specifically unpadding mirrored regions, arises from the advent of image augmentation due to the necessity in variability and quantity of data with deep learning. To our knowledge, we are the first to address this issue and include further motivation in this section.
Having large volumes of high-quality data is paramount to the training of neural networks; for most tasks, the best-performing models are those that train on the greatest volume of data [29, 8, 17, 27]. In current tasks, this volume has increased to “internet-scale” amounts of images, which can be thought of (in some regard) as a ‘dataset augmentation’ by grabbing as much data as possible, even if from different sources, enabling transfer learning, foundation model learning, and more. This is a parallel path to standard data augmentation, where a dataset itself is used as the basis for generating different variations or augmentations on image samples. For example, a survey by Khalifa et al. [16] describes the benefits that data augmentation contributes to deep-learning models. They note that image augmentation overcomes data scarcity, with fields such as medical imaging lacking sufficient labeled data [3]. Additionally, compared to collecting and labeling new data, augmentation provides a cost-effective alternative by transforming existing data into new samples. Augmentation techniques help reduce overfitting and ensure models achieve higher accuracy during testing by diversifying training samples [28] and allowing for model generalizability [31, 23]. Finally, augmentation allows for more control over dataset characteristics, helping to balance class distributions and improve performance on imbalanced datasets [20].
Due to these advantages of both data and dataset augmentation, their usage is becoming prevalent. However, when altered datasets such as those exemplified in Figure 1 are released without the original naturalistic data, it is difficult for future researchers to repurpose and apply the dataset for their own training, evaluation, or dataset augmentation. Aligned with these concerns, these augmentation or padding artifacts can be detrimental to neural network training and validation [6], especially as augmented data does not accurately represent real-world data, further emphasizing the necessity of naturalistic original data.
3 Algorithm for Image Unpadding
Our algorithm for detecting the padded, mirrored area in an image is described in this section. We will explain the algorithm for just one side of the image (in this case, top), but we note that the algorithm should be applied to all four sides of the image.
We first create a variable for the dividing line, which iterates from the top to the middle of the image. At each position of the dividing line, we crop from the top of the image to the line as well as a section of the image with the same area as the crop right below the dividing line. We then mirror the first cropped image over the x-axis and obtain the mean squared error (MSE), calculated as
of these two cropped image segments. The line where the minimum MSE is located is then estimated to be the line between the padded area and the raw image, as the two cropped regions are most similar.
However, it is also noted that the given images do not always have mirrored padding. To detect these instances and ensure that we do not necessarily crop parts of the raw image, we determine a threshold for the MSE, where if the MSE is greater than the threshold, the obtained dividing line is disregarded. This is based on the assumption that images without reflected padding should have a higher MSE since the content of the cropped images across the dividing line is not identical.
When iterating the dividing line, we initially set it at some offset value from the boundary. This is since the portion of the image near the boundary sometimes has little to no difference in pixel values due to being part of the ground or sky. To clearly distinguish between unaltered images and padded images, the dividing-line offset ensures that MSE calculations focus on image regions where variability begins to appear. Without an offset, the minimum MSEs from unaltered images and padded images can be very low and overlapping in range due to cropping small sections of the image with low variability. By creating a clearer differentiation in the MSEs, we can better choose an MSE-threshold for unaltered and padded images. In the case of zero-padding, starting at the border would result in an extremely low MSE since the sections within the padding are identical. Therefore, it is necessary to start sufficiently positioned within the padding to increase the MSE. A pseudocode version of our algorithm is provided in Algorithm 1.
3.1 Threshold Selection Algorithm
We describe and compare various methods to obtain a threshold by labeling a small training set of images randomly selected from the dataset, which may or may not contain padding. The first method is iteration through threshold values and counting the number of dividing lines that are correctly estimated (within a pixel of tolerance). From this, an estimate of precision and recall can be formed for each threshold value, and the optimal threshold parameter for differentiating MSEs can be selected. As with most hyperparameter tuning, this result can be refined by repeating this process with smaller iteration step sizes around the previously obtained threshold.
The second method we employ is a variant of Otsu’s thresholding method [26], using MSEs of a training set rather than image intensity values. This involves taking the MSEs, normalizing them to a scale of [0, 255], and finding the Otsu’s threshold of the normalized MSEs. Otsu’s method selects the threshold that maximizes the between-class variance:
where is the threshold value, and are the class probabilities, and and are the class means. This gives the threshold to divide the lower and upper portions of the MSEs, which corresponds to the padded and unpadded images.
4 Experimental Evaluation
4.1 Dataset
To apply this reflected padding detection algorithm, we use an image dataset in a construction setting, namely the SHEL5k [25]. This dataset has 5,000 images with mirrored padding of either the top and bottom or the left and right of each image, as shown in Figure 1. This is likely created by the creators of the dataset through image augmentation to resize the images.

4.2 Threshold Selection
To calculate the MSE threshold for the dividing line of the padding, we first sample 400 training images from the 5,000 images of the SHEL5k dataset [25], selecting 200 with padding and 200 without for training balance. We compute and store the minimal MSEs of each image according to the unpadding algorithm presented in Section 3.
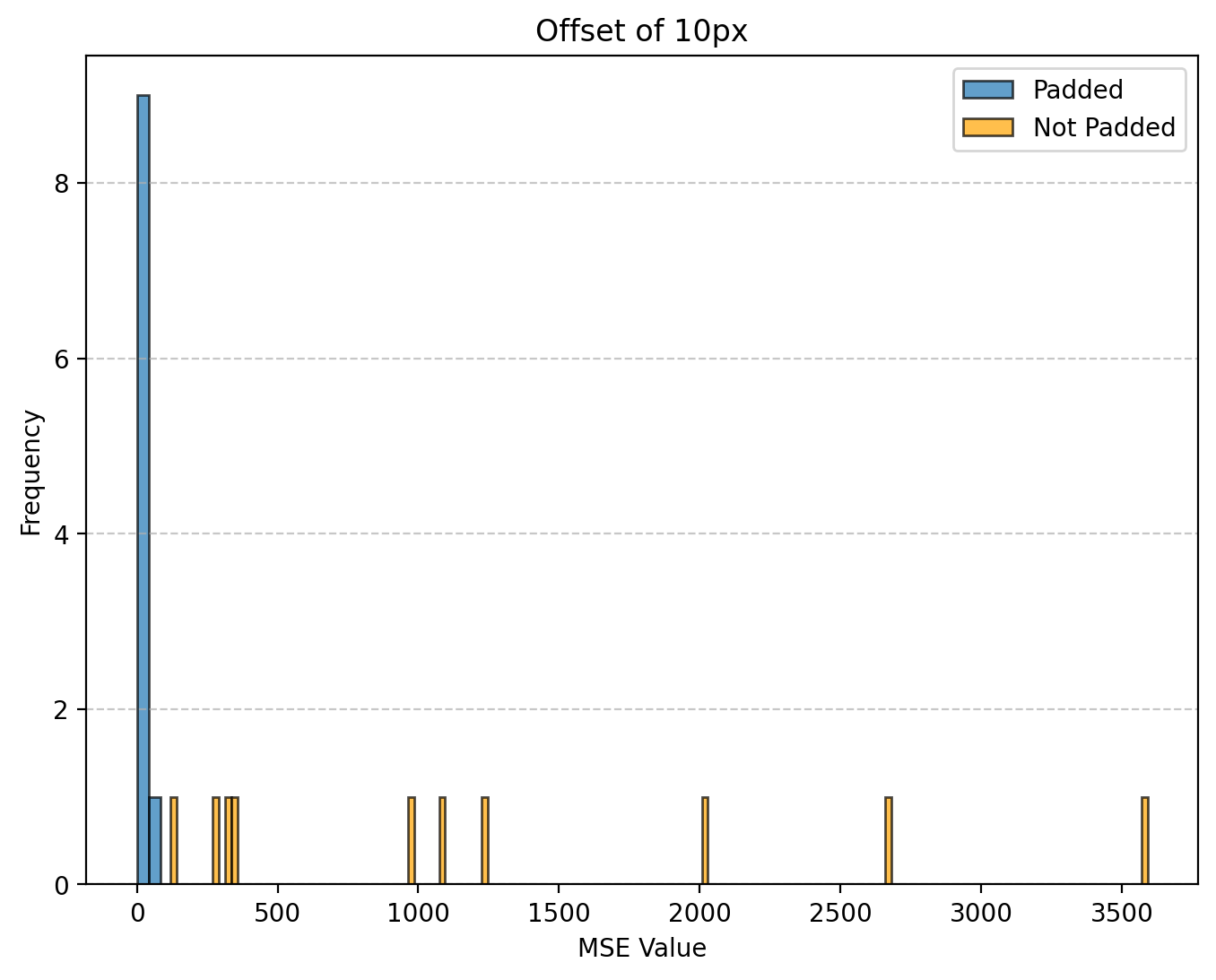
We use a parameter of the 10th pixel as the dividing line offset for the threshold estimates. A sample of MSEs from 10 images of unpadded and padded images is shown in Figure 3 to illustrate the impact of this starting point hyperparameter.
For the first iterative threshold method described in Section 3.1, we set the MSE-threshold to 70 and iterate it by 5 until 180. We calculate the precision and recall at each threshold value using the training sample. The start and end points of the threshold iteration were chosen based on where the precision or recall started to fall off. The threshold with the highest precision and recall is chosen as the optimal threshold. The second method takes the minimum MSEs from all images in the dataset and applies Otsu’s method to estimate an optimal threshold. We evaluated this threshold with the precision and recall on the training sample.

From the first method, we found that the best MSE-threshold is 110. The resulting precision-recall curve from the first method is shown in Figure 4

For the second method, the MSE-threshold given by Otsu’s method is 1408. This discrepancy in thresholds is discussed later in the Discussion section. The precision and recall of both methods are provided in Table 1.
4.3 Threshold Evaluation
Utilizing the best obtained MSE-threshold of 110, we apply the complete unpadding algorithm to the SHEL5k dataset, cropping the images and annotations accordingly to create a new dataset. We note the removed padding of the image in Figure 5 as a qualitative example.


We test for an improved model performance, specifically foundation vision language model performance in the task of zero-shot object detection [21, 1, 13, 14, 9, 34] to benchmark this method without having variability in the training.
The model we utilize is OWLv2 [21], and we use the cascaded detection strategy described by Choi and Greer [4], specifically detecting hard hats inside of the bounding boxes of persons to automatically associate the two classes. For the prompts, we use ‘person,’ ‘helmet,’ and ‘hard hat.’
The model’s performance in detecting hard hats and persons on both the original and unpadded datasets is provided in Table 2, evaluated by average precision. The comparison in precision-recall curves is presented in Figure 6. There was a clear increase in performance after unpadding the data, as the removal of padding artifacts reduced misinterpretations of distorted persons by OWLv2.
| Method | Precision | Recall |
|---|---|---|
| Threshold Value Iteration | 0.9886 | 0.9355 |
| Otsu’s Thresholding Method | 0.9915 | 0.6463 |
| Dataset | Hard Hat (AP) | Person (AP) |
|---|---|---|
| Original | 0.4672 | 0.6767 |
| Unpadded | 0.6115 | 0.7348 |


5 Discussion
The threshold estimation method utilizing Otsu’s method is observed to have lower accuracy compared to iteratively testing the threshold as demonstrated in Table 1. This behavior is due to the MSEs and Otsu thresholds of the unpadded and padded images not having clear peaks and not being strongly separable. As shown in Figure 3, the MSEs of the unpadded images are dispersed, disallowing Otsu’s method to find a clear point for the threshold. Therefore, manually testing the threshold based on observed patterns in the MSEs would be more accurate. This causes the large discrepancy of the thresholds from the first and second methods.
Our threshold evaluation showed improved performance after removing padding, as it reduced ambiguities that could mislead the model. Additionally, the original dataset’s annotations for the mirrored padding were inconsistent, as often the entire person was not presented in the padding. This contributed to the model’s false negatives, contributing to an inaccurate representation of OWLv2’s performance. Figure 7 demonstrates both the missing ground truth annotations of the padded area as well as OWLv2’s imprecise detections in the symmetrically padded region. By removing the padding, our approach eliminates these ambiguous regions of missing annotations and distorted objects, leading to more accurate detections.

6 Concluding Remarks
In this research, we proposed an algorithm to remove noisy artificially padded mirrored areas from images, utilizing a minimization of the MSE with potential borders of the original image. Our method has achieved robust performance, effectively identifying the transition between mirrored and non-mirrored regions. This led to a significant increase in performance on the task of zero-shot detection as we allow for more precise and reliable predictions and evaluations, with an increase from 0.47 to 0.61 in OWLv2’s average precision for hard hat detection and 0.68 to 0.73 in person detection.
Beyond artifact removal, ensuring that data augmentation techniques produce realistic transformations is an alternative solution to this reflective padding issue. Khalifa et al. [16] demonstrate this possibility as they describe that recent advances in augmentation now include complex strategies such as adversarial training, neural style transfer, and synthetic data generation rather than simple geometric transformations. By leveraging neural networks, they look to avoid augmentations that inaccurately represent real-world scenarios.
In light of recent trends in massive dataset augmentation by amalgamation of multi-source datasets to solve foundational learning tasks, we propose that the theme of finding unified visual qualities will be applicable in further use cases. For example, combined surveillance-related datasets may have combinations of both fisheye [10, 30] and non-fisheye lenses [18, 24], and detecting and correcting for these distortions is important for learning to detect visual patterns [32, 22]. The ability to recognize and correct for fundamentally disagreeing patterns between datasets will be important to rectify by restoring images before network training.
As large-scale machine learning continues to stay prevalent, ensuring high-quality, naturalistic data remains essential for enhancing generalization and real-world applicability across diverse applications.
References
- Bansal et al. [2018] Ankan Bansal, Karan Sikka, Gaurav Sharma, Rama Chellappa, and Ajay Divakaran. Zero-shot object detection. In Proceedings of the European conference on computer vision (ECCV), pages 384–400, 2018.
- China [2022] Northeastern University China. Hard hat workers dataset. https://universe.roboflow.com/joseph-nelson/hard-hat-workers, 2022. visited on 2024-06-24.
- Chlap et al. [2021] Phillip Chlap, Hang Min, Nym Vandenberg, Jason Dowling, Lois Holloway, and Annette Haworth. A review of medical image data augmentation techniques for deep learning applications. Journal of Medical Imaging and Radiation Oncology, 65(5):545–563, 2021.
- Choi and Greer [2024] Lucas Choi and Ross Greer. Evaluating cascaded methods of vision-language models for zero-shot detection and association of hardhats for increased construction safety, 2024.
- Das [2025] Subhajeet Das. Iq-oth/nccd lung cancer dataset (augmented), 2025.
- Elgendi et al. [2021] Mohamed Elgendi, Muhammad Umer Nasir, Qunfeng Tang, David Smith, John-Paul Grenier, Catherine Batte, Bradley Spieler, William Donald Leslie, Carlo Menon, Richard Ribbon Fletcher, et al. The effectiveness of image augmentation in deep learning networks for detecting covid-19: A geometric transformation perspective. Frontiers in Medicine, 8:629134, 2021.
- Fernández [2025] Miguel Fernández. Markov transition field images of heart beats, 2025.
- Geirhos et al. [2022] Robert Geirhos, Kantharaju Narayanappa, Benjamin Mitzkus, Tizian Thieringer, Matthias Bethge, Felix A Wichmann, and Wieland Brendel. The bittersweet lesson: data-rich models narrow the behavioural gap to human vision. Journal of Vision, 22(14):3273–3273, 2022.
- Ghita et al. [2024] Ahmed Ghita, Bjørk Antoniussen, Walter Zimmer, Ross Greer, Christian Creß, Andreas Møgelmose, Mohan M Trivedi, and Alois C Knoll. Activeanno3d-an active learning framework for multi-modal 3d object detection. In 2024 IEEE Intelligent Vehicles Symposium (IV), pages 1699–1706. IEEE, 2024.
- Gochoo et al. [2023] Munkhjargal Gochoo, Munkh-Erdene Otgonbold, Erkhembayar Ganbold, Jun-Wei Hsieh, Ming-Ching Chang, Ping-Yang Chen, Byambaa Dorj, Hamad Al Jassmi, Ganzorig Batnasan, Fady Alnajjar, et al. Fisheye8k: A benchmark and dataset for fisheye camera object detection. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 5305–5313, 2023.
- Gohil and Gurjar [2025] Ronak Gohil and Amit Gurjar. License plate dataset, 2025.
- Greer et al. [2024] Ross Greer, Akshay Gopalkrishnan, Maitrayee Keskar, and Mohan M Trivedi. Patterns of vehicle lights: Addressing complexities of camera-based vehicle light datasets and metrics. Pattern Recognition Letters, 178:209–215, 2024.
- Greer et al. [2025] Ross Greer, Bjørk Antoniussen, Andreas Møgelmose, and Mohan Trivedi. Language-driven active learning for diverse open-set 3d object detection. In Proceedings of the Winter Conference on Applications of Computer Vision, pages 980–988, 2025.
- Huang et al. [2024] Rui Huang, Henry Zheng, Yan Wang, Zhuofan Xia, Marco Pavone, and Gao Huang. Training an open-vocabulary monocular 3d detection model without 3d data. Advances in Neural Information Processing Systems, 37:72145–72169, 2024.
- Keskar et al. [2025] Maitrayee Keskar, Ross Greer, Akshay Gopalkrishnan, Nachiket Deo, and Mohan Trivedi. Lights as points: Learning to look at vehicle substructures with anchor-free object detection. Robotics and Automation Letters, 2025.
- Khalifa et al. [2022] Nour Eldeen Khalifa, Mohamed Loey, and Seyedali Mirjalili. A comprehensive survey of recent trends in deep learning for digital images augmentation. Artificial Intelligence Review, 55(3):2351–2377, 2022.
- [17] Tobit Klug and Reinhard Heckel. Scaling laws for deep learning based image reconstruction. In The Eleventh International Conference on Learning Representations.
- Li et al. [2018] Dangwei Li, Zhang Zhang, Xiaotang Chen, and Kaiqi Huang. A richly annotated pedestrian dataset for person retrieval in real surveillance scenarios. IEEE transactions on image processing, 28(4):1575–1590, 2018.
- Mark et al. [1982] RG Mark, PS Schluter, G Moody, P Devlin, and D Chernoff. An annotated ecg database for evaluating arrhythmia detectors. In IEEE Transactions on Biomedical Engineering, pages 600–600. IEEE-INST ELECTRICAL ELECTRONICS ENGINEERS INC 345 E 47TH ST, NEW YORK, NY …, 1982.
- Mikołajczyk and Grochowski [2018] Agnieszka Mikołajczyk and Michał Grochowski. Data augmentation for improving deep learning in image classification problem. In 2018 international interdisciplinary PhD workshop (IIPhDW), pages 117–122. IEEE, 2018.
- Minderer et al. [2024] Matthias Minderer, Alexey Gritsenko, and Neil Houlsby. Scaling open-vocabulary object detection. Advances in Neural Information Processing Systems, 36, 2024.
- Morris and Trivedi [2008] Brendan Tran Morris and Mohan Manubhai Trivedi. A survey of vision-based trajectory learning and analysis for surveillance. IEEE transactions on circuits and systems for video technology, 18(8):1114–1127, 2008.
- Nagaraju et al. [2022] Mamillapally Nagaraju, Priyanka Chawla, and Neeraj Kumar. Performance improvement of deep learning models using image augmentation techniques. Multimedia Tools and Applications, 81(7):9177–9200, 2022.
- Oh et al. [2011] Sangmin Oh, Anthony Hoogs, Amitha Perera, Naresh Cuntoor, Chia-Chih Chen, Jong Taek Lee, Saurajit Mukherjee, Jake K Aggarwal, Hyungtae Lee, Larry Davis, et al. A large-scale benchmark dataset for event recognition in surveillance video. In CVPR 2011, pages 3153–3160. IEEE, 2011.
- Otgonbold et al. [2022] Munkh-Erdene Otgonbold, Munkhjargal Gochoo, Fady Alnajjar, Luqman Ali, Tan-Hsu Tan, Jun-Wei Hsieh, and Ping-Yang Chen. Shel5k: An extended dataset and benchmarking for safety helmet detection. Sensors, 22(6):2315, 2022.
- Otsu et al. [1975] Nobuyuki Otsu et al. A threshold selection method from gray-level histograms. Automatica, 11(285-296):23–27, 1975.
- Schulz et al. [2020] Marc-Andre Schulz, BT Thomas Yeo, Joshua T Vogelstein, Janaina Mourao-Miranada, Jakob N Kather, Konrad Kording, Blake Richards, and Danilo Bzdok. Different scaling of linear models and deep learning in ukbiobank brain images versus machine-learning datasets. Nature communications, 11(1):4238, 2020.
- Shorten and Khoshgoftaar [2019] Connor Shorten and Taghi M Khoshgoftaar. A survey on image data augmentation for deep learning. Journal of big data, 6(1):1–48, 2019.
- Sun et al. [2017] Chen Sun, Abhinav Shrivastava, Saurabh Singh, and Abhinav Gupta. Revisiting unreasonable effectiveness of data in deep learning era. In Proceedings of the IEEE international conference on computer vision, pages 843–852, 2017.
- Tezcan et al. [2022] Ozan Tezcan, Zhihao Duan, Mertcan Cokbas, Prakash Ishwar, and Janusz Konrad. Wepdtof: A dataset and benchmark algorithms for in-the-wild people detection and tracking from overhead fisheye cameras. In Proceedings of the IEEE/CVF winter conference on applications of computer vision, pages 503–512, 2022.
- Xu et al. [2023] Mingle Xu, Sook Yoon, Alvaro Fuentes, and Dong Sun Park. A comprehensive survey of image augmentation techniques for deep learning. Pattern Recognition, 137:109347, 2023.
- Yang et al. [2023] Lu Yang, Liulei Li, Xueshi Xin, Yifan Sun, Qing Song, and Wenguan Wang. Large-scale person detection and localization using overhead fisheye cameras. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 19961–19971, 2023.
- Zhang [2025] Edward Zhang. Face mask detection, 2025.
- Zhao et al. [2022] Shiyu Zhao, Zhixing Zhang, Samuel Schulter, Long Zhao, BG Vijay Kumar, Anastasis Stathopoulos, Manmohan Chandraker, and Dimitris N Metaxas. Exploiting unlabeled data with vision and language models for object detection. In European conference on computer vision, pages 159–175. Springer, 2022.