SupportingInfo

Thermal and photochemical hydrogen and proton transfer reactions are among the most ubiquitous in chemistry and biology.[1, 2, 3] Directly following hydrogen and proton dynamics with time-resolved experimental methods is complicated by their fast time scales down to the few femtosecond regime. Moreover, typical time-resolved spectroscopic techniques exhibit only indirect sensitivity to these dynamics, due to the preferential interaction of the light with the electrons rather than the nuclei. Direct sensitivity to the motion of the nuclei can in principle be achieved with novel time-resolved imaging methods, such as ultrafast X-ray[4, 5, 6] and electron diffraction.[7, 8, 9, 10, 11]

X-rays exclusively scatter off the electron density of a molecule (Thomson scattering).[12] The information about relative positions of atoms in a molecule from X-ray diffraction largely originates from inner-shell electrons with strong localization and, thus, high density at the positions of the nuclei. Since hydrogens do not posses inner-shell electrons, the sensitivity of X-ray diffraction to hydrogens and hydrogen motion is extremely limited. In contrast, electrons scatter off the Coulomb potential of a molecule (Rutherford scattering), which contains contributions from both electrons and nuclei.[13] Therefore, the relative cross-section of hydrogen with respect to carbon is more than an order of magnitude higher for electron compared to X-ray diffraction.[14] The observation of hydrogen motion has recently been demonstrated in an investigation of the energy dissipation from the O-H stretching mode of bulk water using megaelectronvolt ultrafast electron diffraction (MeV-UED).[11, 15, 16] Here, we demonstrate that MeV-UED can resolve the femtosecond excited-state hydrogen dynamics in dilute gas phase ammonia, photoexcited at $\sim$200 nm.

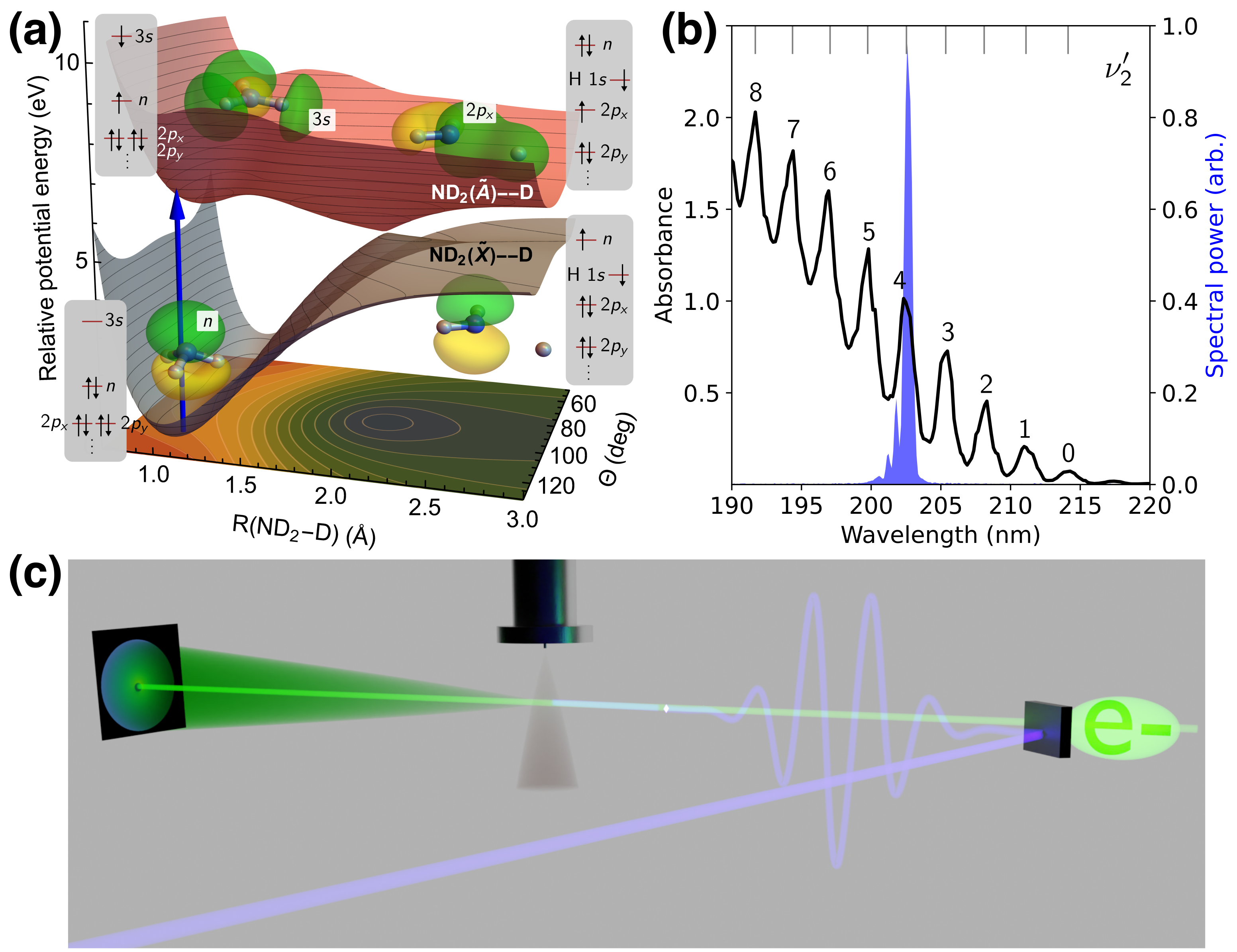
The photodissociation of ammonia is a benchmark case for multi-channel nonadiabatic photochemical dynamics and, therefore, has been the subject of many previous experimental steady-state[17, 18, 19, 20, 21, 22] and time-resolved studies,[23, 24, 25] as well as theoretical investigations.[26, 27] Ammonia (C_3v symmetry) exhibits a double minimum in its electronic ground state connected by an umbrella-type inversion motion (see potential energy surfaces, PESs, in Fig. 1a). Photoexcitation around 200 nm populates the $2^{1}A$ state, which is dominated by a single-electron excitation from the nitrogen lone pair ($n$) orbital to a $3s$ Rydberg orbital (see visualizations in Fig. 1a) and, therefore, exhibits Rydberg character. The $2^{1}A$ state has a minimum at a planar geometry of D_3h symmetry. The large geometric difference between the ground state and $2^{1}A$ state results in a strong vibrational progression in its absorption spectrum (see Fig. 1b). Although \chH2N-H dissociation is impeded by a barrier, the hydrogen atom can cross the barrier (potentially aided by tunnelling) leading to $<$100 fs lifetimes in the D_3h minimum for all but the lowest two out-of-plane bending vibrational states. Isotopic substitution with deuterium significantly increases the lifetimes in the D_3h minimum for a number of out-of-plane vibrational levels,[17] making it easier to resolve the dynamics in time. Hence, we employ fully deuterated ammonia and excite the 4th excited state vibrational level at 202.5 nm (see Fig. 1b). Deuteration only affects the timescales here, and is not expected to have any effect on the diffraction signal intensity. Thus, our findings on the sensitivity of MeV-UED for deuterated ammonia are fully transferable to experimental signatures of proton dynamics in other systems.

The dissociation barrier results from the presence of an avoided crossing between the excited Rydberg state and a higher-lying $n\sigma^{*}$ state with \chD2N-D antibonding character.[28] Thus, the excited state gradually changes its electronic character from $n3s$ to $n\sigma^{*}$ along the \chD2N-D dissociation coordinate. After passing the dissociation barrier, the wavepacket proceeds along the \chD2N-D coordinate towards adiabatic and nonadiabatic photodissociation channels, yielding \chND2($\tilde{X}$)+\chD and \chND2($\tilde{A}$)+\chD (see Fig. 1).

The sensitivity of electron scattering to the electronic structure of molecules has long been established and benchmarked, among other molecules, with the help of ammonia.[29, 30, 31] Elastic scattering processes are sensitive to the electron density in a molecule. In contrast, inelastic scattering is sensitive to electron correlation.[32] We have recently demonstrated that inelastic scattering can be employed to follow electronic structure changes during photochemical dynamics.[8] Such changes in electron correlation can originate from population transfer between excited states of different electronic character through conical intersections[8] or due to more gradual excited-state character changes like the change $n3s$ to $n\sigma^{*}$ when crossing the excited-state barrier of ammonia. The strongest contributions from inelastic scattering appear at momentum transfer values $<$2 $\mathrm{\AA^{-1}}$ whereas difference diffraction signatures of nuclear geometry changes can typically be measured up to 10 $\mathrm{\AA^{-1}}$.[9] Thus, complementary information from electronic- and nuclear-structure changes can be detected in a well-separable fashion in the experimental diffraction patterns. In the present study, we observe, in addition to signatures of the structural N-D dissociation, clear signatures of the electronic excitation and electronic character change from $n3s$ to $n\sigma^{*}$.

The experiment was performed at the MeV-UED facility at SLAC National Accelerator Laboratory.[33] Fig. 1c shows a schematic of the experimental setup. A 202.5 nm pump pulse was spatially and temporally overlapped with an electron pulse of 4.2 MeV kinetic energy in a pulsed jet of \chND3. Diffracted electrons were detected with a combination of a phosphor screen and a camera. The simulations were performed using ab initio multiple spawning[34] (AIMS) in combination with ab initio elastic and inelastic electron scattering simulations.[8] A detailed description of both the experimental and theoretical methods can be found in Sec. S1 of the supplemental material.

Our AIMS simulations are based on the PESs and nonadiabatic couplings reported by Yarkony et al.[35, 27] and provide a picture consistent with previous numerically exact quantum dynamics.[27] In particular, following photoexcitation and progress along the \chD2N-D dissociation coordinate (Sec. S2 and Fig. S3), the majority of the population undergoes nonadiabatic photodissociation ($\sim$66 %) with a smaller portion ($\sim$24 %) proceeding along the adiabatic channel (Fig. S4). A small fraction ($<10$ %) remains trapped (after 0.84 ps) on the excited state by the predissociation barrier and hence retains Rydberg character (Fig. S5).

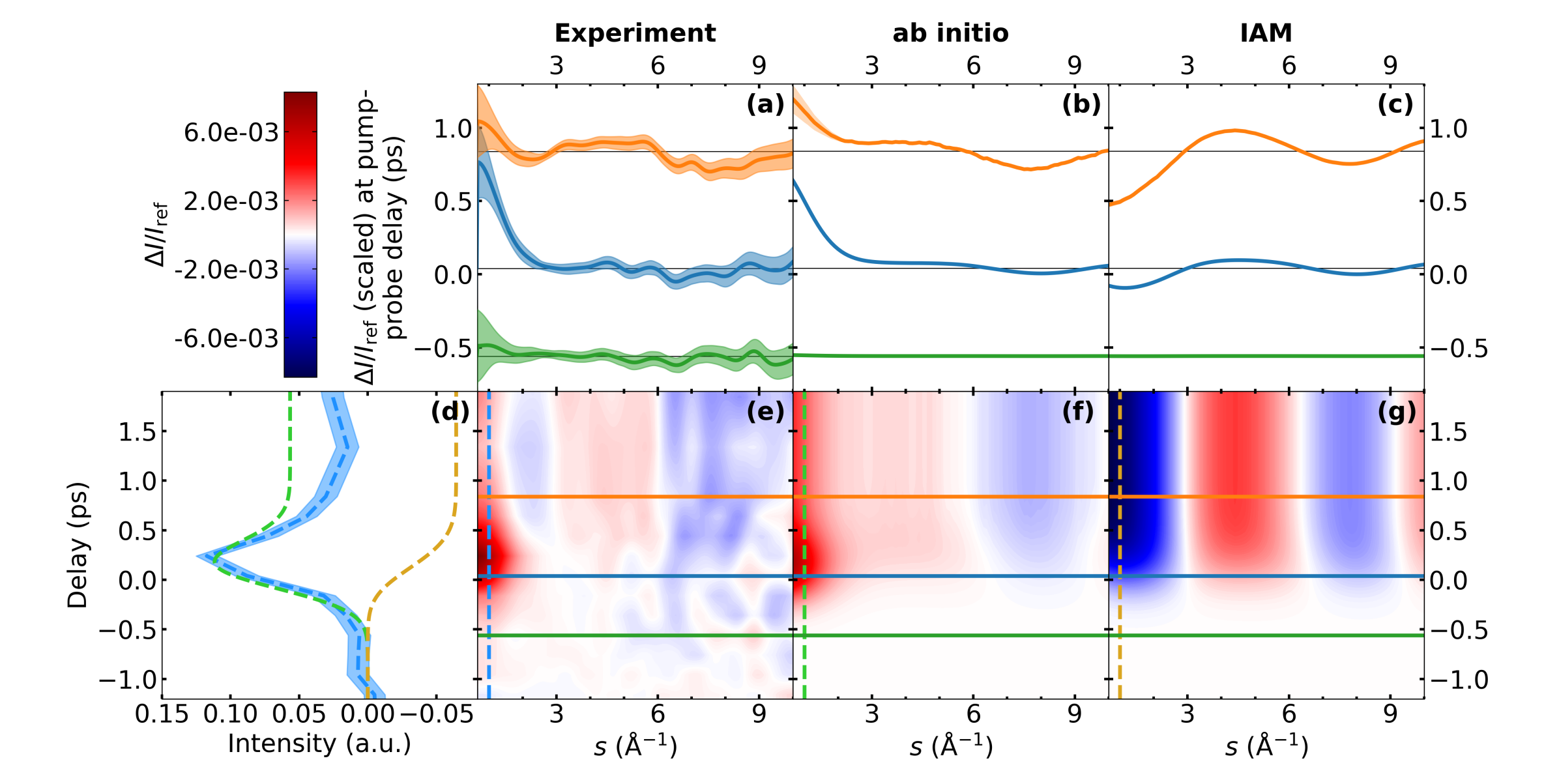
In Fig. 2e, we present the results of our MeV-UED experiment as a false-color plot in the form of the difference between the time-dependent diffraction and the static diffraction of \chND3 normalized by the static diffraction ($\Delta I/I_{\text{ref}}(s,t)$). Additionally, Fig. 2a shows $\Delta I/I_{\text{ref}}(s)$ at the three different delay times ($t=$ -0.56 ps, 0.04 ps, and 0.84 ps), which are marked by the color-coded horizontal lines in Fig. 2e. These delay times are chosen to include one delay clearly before time zero as a reference for the noise level of the experimental signals, the closest experimental delay to time zero, and one delay where the dissociation reaction is expected to be finished. The $s$-integrated $\Delta I/I_{\text{ref}}(0.67\ \mathrm{\AA}^{-1}<s<1\ \mathrm{\AA}^{-1},t)$ (dashed blue vertical line in Fig. 2e) is shown in Fig. 2d, blue. At time zero, a strong positive feature turns on in the $s<2$ $\mathrm{\AA}^{-1}$ regime and decays within the instrument response function (500-fs full width at half maximum, FWHM) to a weaker, delay-independent level (Fig. 2d). Simultaneously, substantially weaker features appear: specifically, a broad positive signature between 3 and 6 $\mathrm{\AA}^{-1}$ and a broad negative signature at $s>6$ $\mathrm{\AA}^{-1}$ that stay constant over the whole remaining time delay window.

The experimental results in Fig. 2e are compared with the simulated scattering signals computed based on AIMS dynamics of photoexcited \chND3 (see Secs. S1 D and S2). We use two different approaches to simulate the electron diffraction observable from the simulated wavepacket. First, using ab initio scattering where the $\Delta I/I_{\text{ref}}(s,t)$ signatures are computed by scattering off the Coulomb potential from the nuclei and the electronic wavefunction as evaluated in our wavepacket simulations (Figs. 2b/f). This scattering simulation includes both elastic and inelastic scattering contributions. Analogous to the experimental data, the time-dependence of the integrated difference diffraction $0.67\ \mathrm{\AA}^{-1}<s<1\ \mathrm{\AA}^{-1}$ is plotted in Fig. 2d (dashed green line). Second, we also provide $\Delta I/I_{\text{ref}}(s,t)$ signatures based on the independent atom model (IAM, Figs. 2c/g) that neglect both inelastic scattering and changes in electron density around individual atoms due to chemical bonding or electron density redistribution (e.g., following electronic excitation). The time-dependence of the integrated signal at low $s$-values is plotted in Fig. 2d (dashed brown line).

To understand the time-dependent signatures in Fig. 2, we begin by considering the respective signatures at late delays (Fig. 2a-c, orange). The signature from the IAM scattering simulation in Fig. 2c exclusively originates from changes in the nuclear geometry (interatomic distances) due to the atomic superposition approximation inherent to IAM. Since it is a $\Delta I/I_{\text{ref}}(s,t)$ signature, it results from the difference of signatures from the atomic distances in and between the dissociation products at a delay time of 0.84 ps and signatures from the distances in the \chND3 reactant geometry. Due to the relatively large atomic form factor of nitrogen, it is dominated by the difference of N-D distance signatures from the evolving photoexcited population and from the reactant geometry (see Sec. S3 for details). Moreover, the presence of the predissociation barrier leads to a blurring of the diffraction signatures from the photoexcited population. This effect is further increased by the limited time resolution of the experiment (modeled in the IAM simulations in Fig. 2 by convolution with a Gaussian in time, see Sec. S1 D). The signature at late delays in the IAM simulation (Fig. 2c) is, therefore, dominated by the loss of one N-D bond distance (see Sec. S3).

A qualitatively similar, but weaker, signal is found both in the experimental and ab initio scattering signatures for $s>3$ $\mathrm{\AA}^{-1}$ (Figs. 2a and b). A decomposition of the ab initio scattering signature into elastic and inelastic scattering contributions (Figs. 3 and S6) shows that it is exclusively due to elastic scattering. Due to the incoherent nature of inelastic scattering, we do not expect any direct signatures from changes in the molecular geometry.[8] Thus, the absence of the signature at $s>3$ $\mathrm{\AA}^{-1}$ in the inelastic scattering supports the assignment of this signature as the loss of one N-D bond, analogous to the IAM scattering signature. The relative weakness of the signatures with respect to the IAM simulation is a direct result of the deviation of the actual electron distribution in \chND3 from a superposition of atomic densities assumed in IAM.

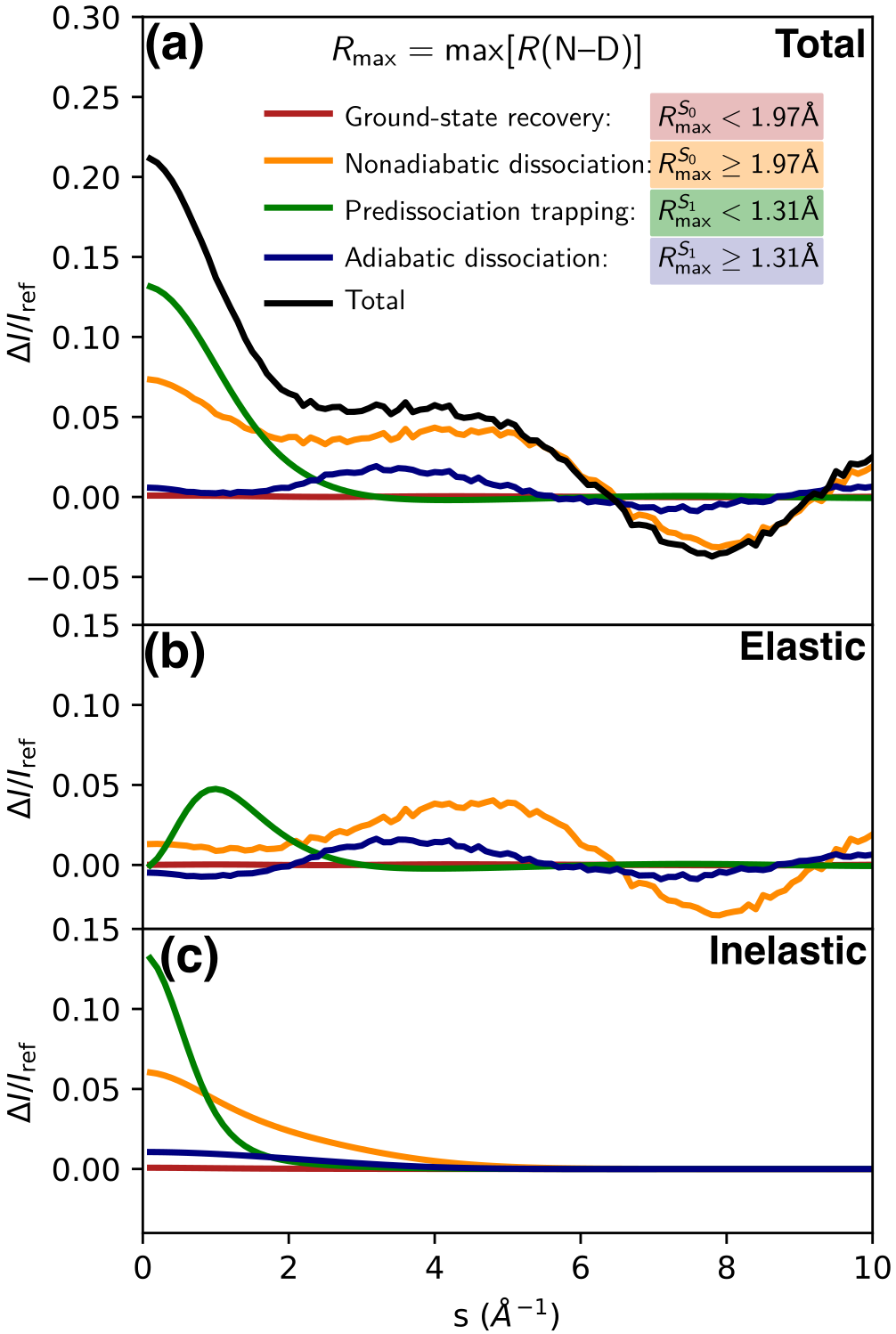
Considering next the low-$s$ ($s<3$ $\mathrm{\AA}^{-1}$) region at late delays (orange plots), the ab initio scattering and experimental signals deviate qualitatively from the IAM. Both show a strong positive signature for $s<1$ $\mathrm{\AA}^{-1}$ whereas the IAM simulations exhibit a negative signature. Decomposition of the ab initio scattering simulations (Figs. 3 and S6) show that its main contribution below 1 $\mathrm{\AA}^{-1}$ originates from the small fraction ($<10$ %, Fig. S4) of population that is trapped on the excited state due to the predissociation barrier. As shown in Fig. S5, this is mainly due to the Rydberg character of the excited state rather than geometric changes from the difference between ground- state and excited-state potentials in the Franck–Condon region.

It should be noted that both elastic and inelastic scattering contribute to the low-$s$ signature (see Figs. 3 and S6). Both contributions can be directly connected to the Rydberg character of the excited state. First, the strength of the elastic scattering contribution originates from the significant change in electron density distribution induced by the Rydberg excitation: one electron, i.e., 10 % of the overall electron density, is redistributed from a fairly localized lone pair orbital to a strongly delocalized Rydberg orbital. Second, the excitation from the electronic ground state (strongly correlated motion of the two electrons occupying the $n$ orbital) to a $n3s$ Rydberg state (weak correlation between remaining electron in the $n$ orbital and the electron in the $3s$ Rydberg orbital) can be expected to yield a significant change in the inelastic scattering signature.

Weaker contributions to the $s<1$ $\mathrm{\AA}^{-1}$ signal arise from the large population ($\sim$66%) in the nonadiabatic dissociation channel, mainly from inelastic scattering contributions (see Fig. 3). The less populated adiabatic dissociation channel ($\sim$24%) shows negligible contributions in this region. The disagreement between experimental and ab initio scattering simulation between $1<s<2$ $\mathrm{\AA}^{-1}$ can be explained by a baseline offset in the experimental data in this region in combination with a slight overestimation of the inelastic scattering intensities in the ab initio simulations.

Summing up our theoretical analysis at long time delays, we can distinguish two regions in the $\Delta I/I_{\text{ref}}(s,t)$ signal: (i) the $<1\ \mathrm{\AA}^{-1}$ region which is almost exclusively sensitive to the electronic character of the excited electronic state, and (ii) the $>3\ \mathrm{\AA}^{-1}$ region which is exclusive sensitivity to nuclear structural changes, i.e. the loss of an N-D bond upon photodissociation.

We can interpret the time-zero signal (blue curves in Fig. 2a-c) along the same $s$-regions. Experimental and ab initio scattering signals are dominated by a stronger signature at $s<1$ $\mathrm{\AA}^{-1}$ than at later delay times. The region at $s>3$ $\mathrm{\AA}^{-1}$ shows the same (albeit weaker) signatures as at later delay times. The strong signature at $s<1$ $\mathrm{\AA}^{-1}$ is easily explained by the fact that initially all of the excited-state population is residing behind the predissociation barrier, where the electronic state exhibits Rydberg character. Accordingly, the decay of the signal at $s<1$ $\mathrm{\AA}^{-1}$ after time zero is related to the depopulation of the quasi-bound Franck–Condon region due to the associated change in electronic character (see also Fig. S5). Since IAM is insensitive to the electronic state, this feature is entirely missing in the IAM scattering signal. The weak dissociation signatures at $s>3$ $\mathrm{\AA}^{-1}$ are the result of a temporal smearing of the onset of the dissociation signatures due to the limited temporal resolution (see Fig. S6 for the raw, i.e., without temporal convolution, theoretical difference scattering signals).

In conclusion, we observed signatures from both deuterium structural dynamics and electronic structure changes during the photodissociation of \chND3 in well-separated momentum transfer ranges of ultrafast electron diffraction. Our results mark a powerful demonstration of the ability of MeV-UED to follow nonadiabatic proton and hydrogen photochemistry. Alternative and emerging methods with similar or higher sensitivity to hydrogens and their dynamics are laser-induced electron diffraction[36, 37, 38, 39] and Coulomb explosion imaging.[40, 41] The sensitivity of these techniques to hydrogen has been established for static structures.[40, 39] Time-resolved studies of hydrogen motion with Coulomb explosion imaging have been recently demonstrated in a seminal study on the roaming reaction in formaldehyde.[42] Structural dynamics studies with laser-induced electron diffraction have so far been limited to dynamics of the ionic states populated during its self-diffraction process with photoelectrons.[39] However, both methods lack the complementary electronic structure information which MeV-UED is able to deliver as a well-separable observable. Our results lack so far in temporal resolution (500 fs FWHM), a crucial parameter for the investigation of reaction dynamics involving hydrogens and protons. However, structural dynamics of more strongly scattering second row elements can already be investigated at the existing MeV-UED facility using lower electron pulse charges, which result in a 3-fold improved time resolution (150 fs FWHM).[9] The signal levels required for the observation of proton dynamics at this higher temporal resolution can be achieved, e.g., by an increase of the repetition rate. An increase of the repetition rate by several orders of magnitude has already been achieved with the electron injector guns for next-generation X-ray free electron lasers and, thus, does not pose a fundamental obstacle.