Favorable phase transitions induced by spinful electron-electron interactions in two-dimensional semimetal with a quadratic band crossing point
Abstract
We study the effects of marginally spinful electron-electron interactions on the low-energy instabilities and favorable phase transitions in a two-dimensional (2D) spin- semimetal that owns a quadratic band crossing point (QBCP) parabolically touched by the upper and lower bands. In the framework of a renormalization group procedure, all sorts of interactions are treated on the equal footing to derive the coupled energy-dependent evolutions of all interaction couplings that govern the low-energy properties. Deciphering the essential physical information of such flows, we at first find that the tendencies of interaction parameters fall into three categories including Limit case, Special case, and General case based on the initial conditions. In addition, the 2D QBCP system is attracted to several distinct kinds of fixed points (FPs) in the interaction-parameter space, namely /, / /, and with the subscripts characterizing the features of FPs for the Limit, Special, and General cases, respectively. Furthermore, as approaching these FPs, we demonstrate that the spinful fermion-fermion interactions can induce a number of favorable instabilities accompanied by certain phase transitions. Specifically, the quantum anomalous Hall (QAH), quantum spin Hall (QSH), and nematic (Nem.) site(bond) states are dominant for , , and , respectively. Rather, QSH becomes anisotropic nearby with one component leading and the others subleading. Besides, Nem.site(bond), chiral superconductivity, and nematic-spin-nematic (NSN.) site(bond) are subleading candidates around these FPs. Our findings provide valuable insights for further research into the 2D QBCP and similar systems.
pacs:
73.43.Nq, 71.55.Jv, 71.10.-w, 11.30.QcI Introduction
The study of semimetal materials is one of the hottest research fields in contemporary condensed matter physics Lee2005Nature ; Neto2009RMP ; Fu2007PRL ; Roy2009PRB ; Moore2010Nature ; Hasan2010RMP ; Qi2011RMP ; Sheng2012book ; Bernevig2013book ; Herbut2018Science . Last two decades have witnessed a phenomenally rapid development on these materials Lee2005Nature ; Neto2009RMP ; Fu2007PRL ; Roy2009PRB ; Moore2010Nature ; Hasan2010RMP ; Qi2011RMP ; Sheng2012book ; Bernevig2013book ; Herbut2018Science ; Armitage2018RMP ; Roy2018RRX , which typically include the Dirac semimetals Wang2012PRB ; Young2012PRL ; Steinberg2014PRL ; Liu2014NM ; Liu2014Science ; Xiong2015Science and Weyl semimetals Neto2009RMP ; Burkov2011PRL ; Yang2011PRB ; Wan2011PRB ; Huang2015PRX ; Xu2015Science ; Xu2015NP ; Lv2015NP ; Weng2015PRX . Such materials are equipped with well-known discrete Dirac points, around which gapless quasiparticles are excited with linear energy dispersions along two or three directions Lee2005Nature ; Neto2009RMP ; Fu2007PRL ; Roy2009PRB ; Moore2010Nature ; Hasan2010RMP ; Qi2011RMP ; Sheng2012book ; Bernevig2013book ; Korshunov2014PRB ; Hung2016PRB ; Nandkishore2013PRB ; Potirniche2014PRB ; Nandkishore2017PRB ; Sarma2016PRB ; Herbut2018Science . Recently, there has been a gradual shift of interest from linear-dispersion toward quadratic-dispersion semimetal-like materials Chong2008PRB ; Fradkin2008PRB ; Fradkin2009PRL ; Cvetkovic2012PRB ; Vafek2014PRB ; Herbut2012PRB ; Mandal2019CMP ; Zhu2016PRL ; Vafek2010PRB ; Yang2010PRB ; Wang2017PRB ; Wang2020-arxiv ; Roy2020-arxiv ; Janssen2020PRB ; Shah2011.00249 ; Nandkishore2017PRB ; Luttinger1956PR ; Murakami2004PRB ; Janssen2015PRB ; Boettcher2016PRB ; Janssen2017PRB ; Boettcher2017PRB ; Mandal2018PRB ; Lin2018PRB ; Savary2014PRX ; Savary2017PRB ; Vojta1810.07695 ; Lai2014arXiv ; Goswami2017PRB ; Szabo2018arXiv ; Foster2019PRB ; Wang1911.09654 ; Wang2303.10163 . In particular, significant attention has been focused on the two-dimensional (2D) electronic system with the upper and lower bands parabolically touching at certain quadratic band crossing point (QBCP) Chong2008PRB ; Fradkin2008PRB ; Fradkin2009PRL ; Cvetkovic2012PRB ; Vafek2014PRB ; Herbut2012PRB ; Mandal2019CMP ; Zhu2016PRL ; Vafek2010PRB ; Yang2010PRB ; Wang2017PRB ; Wang2020-arxiv ; Roy2020-arxiv ; Janssen2020PRB ; Shah2011.00249 . These QBCPs can be established by distinct kinds of models consisting of the kagomé lattice Huse2003PRB ; Fradkin2009PRL ; Janssen2020PRB , checkerboard lattice Fradkin2008PRB ; Vafek2014PRB , collinear spin density wave state Chern2012PRL , and Lieb lattice Tsai2015NJP . Besides, recent studies using the large-scale density-matrix renormalization group have demonstrated a series of essential properties of the QBCP systems Schollwock2005RMP ; Stoudenmire2012ARCMP ; Hubig2015PRB ; Sarma2016PRB ; He2017PRX ; Chatterjee2022PRB ; Nishimoto2010PRL ; Zeng2018npj ; Zhu2016PRL .
In marked contrast to their 2D Dirac/Weyl counterparts, in which the density of state (DOS) vanishes at Dirac points, the 2D QBCP materials possess a finite DOS exactly at their reduced Fermi surfaces (i.e., QBCP) Fradkin2009PRL ; Vafek2014PRB . This unique feature together with the gapless quasiparticles (QPs) from discrete QBCPs plays an essential role in activating a plethora of critical behavior in the low-energy regime Fradkin2009PRL ; Vafek2010PRB ; Yang2010PRB ; Vafek2014PRB ; Venderbos2016PRB ; Wu2016PRL ; Zhu2016PRL ; Wang2017PRB . It is of remarkable significance to highlight that the 2D QBCP systems are unstable under the electron-electron interactions, giving rise to the possibility of weak-coupling interaction-driven phase transitions Fradkin2009PRL ; Venderbos2016PRB ; Wu2016PRL ; Vafek2014PRB ; Vafek2010PRB ; Yang2010PRB ; Wang2020-arxiv . As delivered recently Fradkin2009PRL ; Vafek2014PRB ; Vafek2010PRB ; Yang2010PRB , one can expect the development of the quantum anomalous Hall (QAH) with breaking time-reversal symmetry and quantum spin Hall (QSH) protected by time-reversal symmetry states in the presence of electron-electron repulsions in the checkerboard lattice Fradkin2009PRL ; Vafek2014PRB or two-valley bilayer graphene with QBCPs Vafek2010PRB ; Yang2010PRB .
However, the spinful effects can play a critical role in modifying the low-energy behavior as well. The authors in Refs. Vafek2010PRB ; Cvetkovic2012PRB carefully investigated the spinful effects on the honeycomb lattice and showed several interesting results. In addition, an investigation of such effects on the instability was examined for a checkerboard lattice Fradkin2009PRL ; Vafek2014PRB , which principally considered the contributions from spin up and down are equivalent and hence employed the two-component spinor to describe the low-energy excitations. Motivated by these works and given the important role of spinful effects, we will explicitly take into account the spinful ingredients by adopting a four-component spinor to establish the low-energy theory as presented in Sec. II. This expansion can involve more kinds of electron-electron interactions and enable us to capture all the potential instabilities induced by the spinful degrees of freedom. In consequence, this implies that it is inadequate to capture all the potential instabilities generated by the electron-electron interactions without considering the spinful effects. Therefore, it is possible that other phase transitions from 2D QBCP semimetals to certain fascinating states, aside from QAH and QSH states, may occur once the spinful contributions are taken into account. Unambiguously clarifying this issue would be particularly helpful to improve our understandings on the low-energy properties of 2D QBCP and analogous materials.
To this goal, we explicitly consider all the marginal spinful electron-electron interactions in this work. This involves sixteen different types, which are distinguished by the coupling vertexes (matrices) shown in Sec. II, compared to only four spinless sorts of interactions in earlier studies Vafek2014PRB ; Wang2017PRB . In order to unbiasedly treat all these kinds of interactions and their intimate interplay, it is suitable to adopt the momentum-shell renormalization-group (RG) approach Shankar1994RMP ; Wilson1975RMP ; Polchinski9210046 , which is a powerful tool to unravel the energy-dependent hierarchical properties in the presence of various types of physical ingredients. Performing the RG analysis yields a set of coupled energy-dependent evolutions of all fermion-fermion interaction parameters, from which the several interesting results are obtained in the low-energy regime.
At first, we realize the electron-electron interactions are closely coupled to exhibit various energy-dependent tendencies, which are broken down into three categories including the Limit case, Special case, and General case as designated in Sec. IV. With variations of the initial values of interaction parameters and sign of structure parameter, the 2D QBCP systems flow towards several distinct sorts of fixed points in the low-energy regime. In the Limit and Special cases, the system can be driven to the fixed points / and / /, respectively. The General case, in addition to and , also harbors the (all these fixed points will be designated and explained in Sec. IV).
Additionally, accessing the fixed points is always accompanied by certain instabilities that result in breaking some symmetries Cvetkovic2012PRB ; Vafek2014PRB ; Wang2017PRB ; Maiti2010PRB ; Altland2006Book ; Vojta2003RPP ; Halboth2000RPL ; Halboth2000RPB ; Eberlein2014PRB ; Chubukov2012ARCMP ; Nandkishore2012NP ; Chubukov2016PRX ; Roy2018RRX ; Wang2020NPB . This motives us to examine and carefully select the favorable phase transitions from the candidate states shown in Table 1 nearby these distinct kinds of fixed points. Detailed analysis reveals that the spinful fermion-fermion interactions can induce a number of leading and subleading instabilities as collected in Table 2. Notably, the QAH, QSH, and Nem.site(bond) states are dominant nearby , , and , respectively. Instead, around , QSH becomes anisotropic, with one component being the leading instability and the others being subleading. Besides, Nem.site(bond), Chiral SC-I, and NSN.site(bond) are subleading candidates for these fixed points. It is worth highlighting that the spinful fermion-fermion interactions, compared to the spinless case Vafek2014PRB ; Wang2017PRB , generate more fixed points and induce more favorable phase transitions, and henceforth play an essential role in reshaping the low-energy properties of 2D QBCP materials.
The rest of this paper is organized as follows. In Sec. II, we introduce the microscopic model and construct the effective theory and then carry out the RG analysis in Sec. III to derive the coupled RG equations of all spinful interaction parameters. In Sec. IV, we present the tendencies of interaction parameters and all potential sorts of fixed points in the interaction-parameter space that dictate the low-energy behavior of 2D QBCP materials. Sec. V is followed to address the leading and subleading instabilities around all these fixed points that are induced by the spinful fermion-fermion interactions. At last, we exhibit a brief summary of the basic results in Sec. VI.
II Microscopic model and effective action
The microscopic noninteracting model for a 2D QBCP semimetal with spin one-half electrons on a checkerboard lattice in the low-energy regime can be expressed by the following Hamiltonian Fradkin2008PRB ; Fradkin2009PRL ; Vafek2014PRB ,
| (1) |
where serves as the momentum cutoff that is associated with the lattice constant and the Hamiltonian density takes the form of
| (2) |
with , and being the microscopic structure parameters. Hereby, characterizes the low-energy quasi-particles excitations coming from two energy bands, which is a four-component spinor and designated as with and denoting two sublattices in the checkerboard lattice Fradkin2008PRB ; Fradkin2009PRL . In addition, the matrix is introduced by , where and are Pauli matrices and identity matrix, which act on the lattice space and spin space, respectively.
After diagonalizing the free Hamiltonian density (2), we are left with the parabolical energy eigenvalues Fradkin2008PRB ; Fradkin2009PRL ; Vafek2014PRB
| (3) |
where the related coefficients are defined as
with specifying the direction of momentum. There exist one upward and one downward dispersing band at , which touch parabolically at and are invariant under point group and time-reversal symmetry Fradkin2008PRB ; Fradkin2009PRL ; Vafek2014PRB .
Without loss of generality, we will consider in the remainder a particle-hole and rotational symmetric QBCP semimetal, which requires and . To proceed, the interacting part which includes all the marginal short-range electron-electron interactions can be introduced as follows Fradkin2009PRL ; Vafek2014PRB ; Vafek2010PRB ; Yang2010PRB ; Wang2020-arxiv
| (4) | |||||
where the with , which are positive and represent the repulsive interactions between electrons, are adopted to measure the coupling strengths that are related to the interactions distinguished by the matrices . Given that the fermionic couplings are marginal at the tree level due to the unique features of the 2D QBCP semimetals and become relevant at the one-loop level, it is worth highlighting that the fermion-fermion interactions are much more important than the other interactions and play an essential role in determining the low-energy properties of 2D QBCP materials. Accordingly, we obtain our effective action by taking into account both the free part (1) and the interacting part (4) as follows
| (5) | |||||
The free electron propagator can be extracted from the noninteracting terms and written as
| (6) |
With these in hand, we are in a suitable position to make the RG analysis.
III Renormalization group analysis
To proceed, we within this section perform the RG analysis to construct the coupled energy-dependent flows of all spinful electron-electron couplings, which contain the low-energy behaviors of 2D QBCP materials. Following the spirit of RG framework Shankar1994RMP ; Wilson1975RMP ; Polchinski9210046 , we separate the fermionic fields into the fast and slow modes within the momentum shell and , respectively. Hereby, we utilize to characterize the energy scale and a variable parameter with to serve as a running energy scale Vafek2014PRB ; Altland2006Book ; Cvetkovic2012PRB ; Wang2011PRB ; Wang2013PRB ; Wang2017PRB ; Huh2008PRB ; Kim2008PRB ; Maiti2010PRB ; She2010PRB ; She2015PRB ; Cvetkovic2012PRB ; Vafek2014PRB ; Roy2016PRB . On the basis of these, the noninteracting parts of the effective field action (5) consequently can be selected as a free fixed point. Keeping such fixed point invariant under RG transformations gives rise to the RG rescaling transformations of fields and momenta as follows Vafek2014PRB ; Wang2011PRB ; Wang2013PRB ; Wang2017PRB ; Huh2008PRB ; Wang2020-arxiv ,
| (7) | |||||
| (8) | |||||
| (9) | |||||
| (10) |
Here, the parameter is so-called anomalous dimension of fermionic spinor which is equivalent to zero owing to the marginal fermion-fermion interactions for 2D QBCP systems Vafek2014PRB .
In order to include the higher-level contributions, we endeavor to carry out the analytical calculations of one-loop electron-electron corrections to interaction parameters as depicted in Fig. 11 of Appendix A. For convenience, the cutoff which is linked to the lattice constant can be adopted to measure the momenta and energy with rescaling and Vafek2014PRB ; Wang2011PRB ; Huh2008PRB ; She2010PRB . Subsequently, we obtain the one-loop corrections in Appendix A after paralleling the tedious but straightforward evaluations Vafek2014PRB ; Wang2017PRB ; Wang2018JPCM ; Wang2019JPCM ; Wang2020-arxiv . At current stage, we are able to derive the coupled RG flow equations by combining the RG scalings (7)-(10) and the one-loop corrections in Appendix A Wang2011PRB ; Wang2013PRB ; Wang2017PRB ; Huh2008PRB ; Kim2008PRB ; Maiti2010PRB ; She2010PRB ; She2015PRB ; Cvetkovic2012PRB ; Vafek2014PRB ; Roy2016PRB , which take the form of
| (11) | |||||
| (12) | |||||
| (13) | |||||
| (14) | |||||
| (15) | |||||
| (16) | |||||
| (17) | |||||
| (18) | |||||
| (19) | |||||
| (20) | |||||
| (21) | |||||
| (22) | |||||
| (23) | |||||
| (24) | |||||
| (25) | |||||
| (26) | |||||





These RG equations are closely coupled and ferociously compete with each other, which give rise to the energy-dependent interaction parameters and govern the physical behavior in the low-energy regime Shankar1994RMP ; Altland2006Book . In order to unveil the underlying physical information of 2D QBCP system, we are going to investigate the potential fixed points of such interaction parameters in the following Sec. IV, and defer the study of accompanying instabilities and phase transitions induced by fermionic interactions to Sec. V, respectively.
IV Potential fixed points


As aforementioned, the low-energy fate of 2D QBCP system is dictated by the coupled RG equations (11)-(26), which capture the interplay among all electron-electron interactions. In this section, we examine the behavior of the interaction parameters as the energy scales decrease, aiming to reveal their tendencies and identify potential fixed points at the lowest-energy regime. After carrying out the numerical analysis of RG equations (11)-(26), we figure out that the energy-dependent interaction parameters exhibit a series of interesting evolutions and are attracted to distinct kinds of fixed points that are of close dependence upon the initial conditions. As the symmetries of the free Hamiltonian do not impose strict constraints on the independence of fermion-fermion interactions, the initial values of fermion-fermion interactions can be taken independently. To simplify our analysis, we cluster the starting conditions into three distinct cases: (i) Limit case in which all 16 interaction parameters are assigned the same value at the beginning, (ii) Special case for which only parts of interaction parameters share certain initial value, and (iii) General case where all 16 interaction parameters are independent and hence randomly take their own starting values. Hereby, it is necessary to highlight that such three distinct cases are denominated only based on the initial conditions of fermion-fermion interactions. As the parameter in our model (1) is an energy-independent constant to the one-loop level, the QBCP semimetal owns both the particle-hole and rotational symmetry for all these three cases unless certain instabilities are induced at the lowest-energy limit. In the following, we are going to consider these three cases one by one.
IV.1 Limit case
For the sake of simplicity, we consider the Limit case at first. In this scenario, we assume that all interaction couplings have the same value at the start. Based on our numerical analysis of the RG evolutions, we have identified the basic tendencies of the interaction parameters as shown in Fig. 1.
Learning from Fig. 1, we notice that several interaction parameters flow towards divergence at the low-energy regime owing to the intimate competition among them. In order to seek the potential fixed points, we are suggested to rescale the parameters by an unsign-changed parameter Vafek2010PRB ; Vafek2014PRB ; Chubukov2016PRX . On the basis of this spirit, we bring out and then measure all interactions with , namely designating the transformation . For convenience, we from now on regard as the rescaled interaction parameters (unless stated otherwise). In addition to the interaction parameters, the structure parameter in our model (5) also appears in the coupled RG flows and can alter the RG equations based on its sign.




Under this circumstance, we perform the numerical analysis and present the primary results for evolutions of rescaled parameters in Fig. 2 for both a positive and negative starting value of parameter (For completeness, we have varied the initial parameters from to and found that the qualitative behavior of the parameters are similar). One can find that the basic evolutions of parameters in the Limit case are insusceptible to the initial interaction values, but instead heavily hinge upon the sign of parameter . In other words, there exist two distinct kinds of fixed points in the Limit case, which are distinguished by the sign of . For the sake of simplicity, we hereafter introduce the notation to denominate and distinguish the potential fixed points, where the subscript is an integer to denote the order of the fixed points, and capture the sign of . In this sense, we can refer to the fixed point in Fig. 2(a) as and Fig. 2(b) as , respectively. Specifically, they appropriately take the form of
| (27) |
and
| (28) |
where the element corresponds to the interaction parameter .
IV.2 Special case
Next, we move to study the Special case. Upon closer inspection of Fig. 1, one can notice that several interaction couplings are overlapped and all interaction parameters cluster into six new classes, namely Class-1 (), Class-2 (, , ), Class-3 (, ), Class-4 (, , , , ), Class-5 (), and Class-6 (, , ), respectively.
Due to the complexity of real materials, parts interaction parameters may be deviated from the same initial condition that is required in the Limit case. To account for this, let us go beyond the Limit case and consider a little more complicate case (i.e., Special case), in which the interaction parameters within the same class still share the a starting value but instead initial values of different classes can be independently tuned.



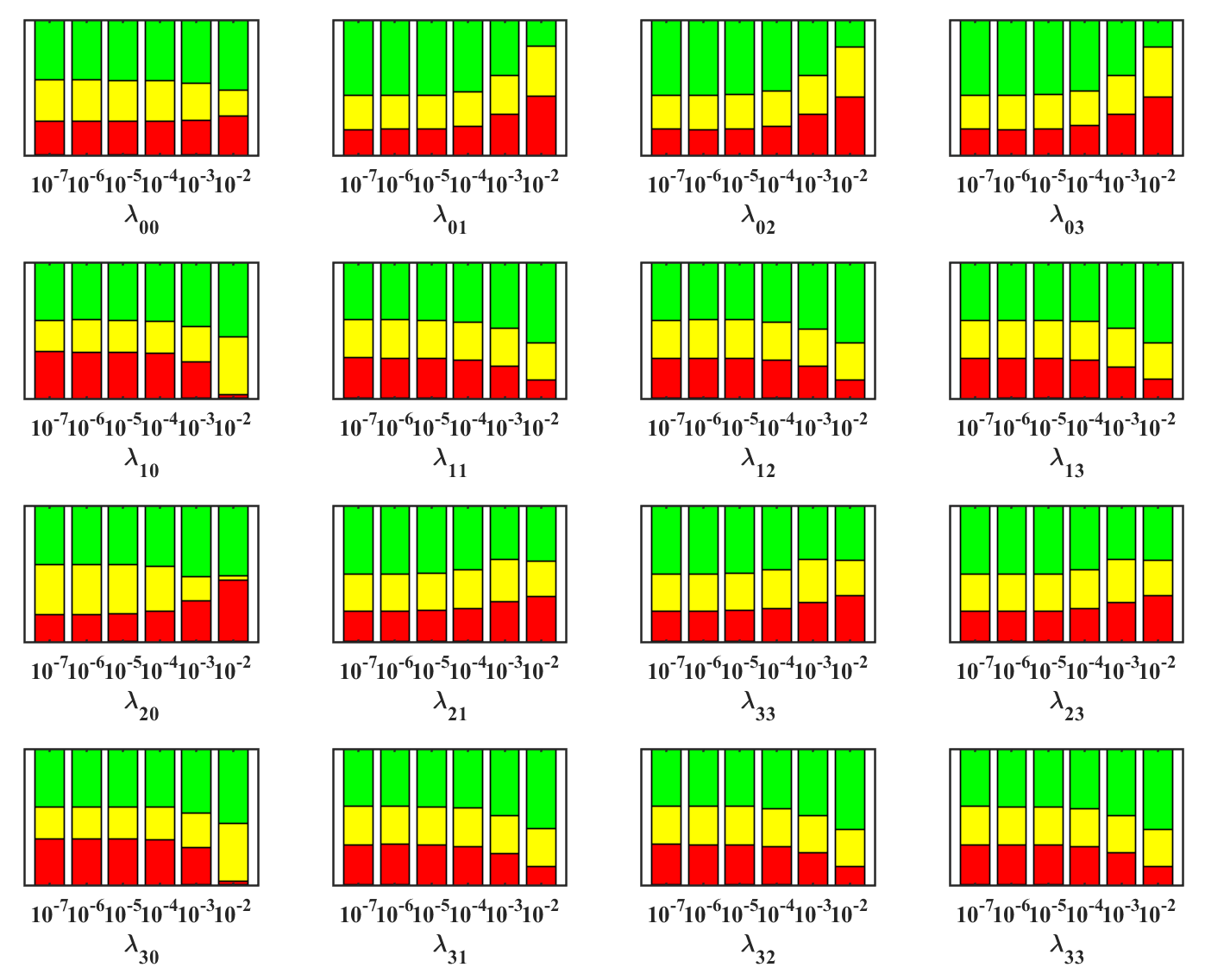

After paralleling analogous numerical analysis in Limit case, we find that several new fixed points can be generated. As to , in addition to the obtained in the Limit case shown in Fig 2(a), fixed points and are induced as presented in Fig. 3, which are appropriately expressed as
with running from to , which can also be compactly expressed as
With respect to , three more fixed points are found to be closely related to their counterparts, including , and .
On the basis of above analysis, one can realize that the interplay among distinct types of interactions coaxes the system to flow towards certain fixed points. As both the structure parameter and the interaction couplings are involved in the coupled RG equations, their interplay and competition determine the structure of fixed points. With respect to the Limit case shown in Fig. 2, the sign of parameter plays a more significant role in pinning down the fixed points than the concrete initial values of interaction parameters.


In sharp contrast, regarding the Special case, six classes of interaction parameters can be adjusted independently at the starting point, which in tandem with the sign of gives rise to more interesting consequences.
At first, we fix the initial values of five classes and vary the starting value of the sixth class to study the influence on the fixed points as displayed in Fig. 4 where the proportion of each type of fixed point can exhibit the average distribution of fixed points. In the case of shown in Fig. 4(a), it manifestly indicates that the increase of is profitable to flowing towards , and particularly, plays a critical role and also hinders the onset of . In comparison, the parameters , , and with in Fig. 4(b) dominate over other parameters. It is unambiguous that the increase of and are very helpful to the development of and , respectively. Besides, tuning up the is of particular help to .
In addition, we tune the starting values of three parameters simultaneously while keeping the other three fixed to further examine the stabilities of fixed points. For instance, with selecting from six classes, Fig. 5 presents the competition among different fixed points with variance of the sign of parameter and magnitudes of three parameters.
On one hand, one can notice that overall structures of fixed points for differ significantly from those for . In consequence, this implies that the sign of has an important contribution to the fixed points. On the other hand, once the sign of is selected, it can also be clearly found that the initial values of the parameters play a significant role in determining which fixed point the system flows towards. As shown in Fig. 5(a) with , the increase of and is helpful to the onset of and , but instead once all three parameters are small enough. The basic structure of Fig. 5(b) is close in resemblance to that of Fig. 5(a). Particularly, when the parameters are restricted to , there exists a ferocious competition among various fixed points and hence the dominant FP, to a large extent, is sensitive to initial interaction strengths. As to , although it bears similarities to Fig. 5(a), Fig. 5(c) shows that tuning up and are instructive to the generation of and , but rather decreasing them to . In sharp contrast to Fig. 5(b), Fig. 5(d) exhibits that the system is either attracted by or , indicating the sign of parameter plays a more crucial role.



IV.3 General case
Furthermore, let us go beyond above two simplified cases and consider the General case in which the initial values of all 16 interaction parameters can be independently assigned. After carrying the similar analysis in Sec. IV.1 and Sec. IV.2, we find several interesting results in the low-energy regime.
At first, we realize that the intimate competition among all interactions melt the garnered in the Limit and Special cases. In other words, are only present in certain special situations which demand the system to satisfy strict constrictions. As a result, the related physics accompanied by such fixed point would be baldly sabotaged. Additionally, it is of particular importance to highlight that another three fixed points can be induced by the close interaction competition with the suitable initial conditions, namely , , and with corresponding to and , respectively. Concretely, they appropriately take the form of
| (29) | |||
| (30) | |||
| (31) |
for as displayed in Fig. 6, and their counterparts share the same structures but own the opposite values. What is more, the effects of initial parameters and sign of on the potential fixed points of the system are examined and presented in Fig. 7. One can clearly read that the vanishes due to strong interplay of interactions, and the other kinds of fixed points compete strongly for both and as varying the initial values of interaction parameters. The case displays a fierce competition between distinct fixed points. In comparison, some interaction parameters play a more important role than others in reshaping the fixed points for . Particularly, is helpful to , while , , and prefer to drive the system to .
| P-H charge channel | P-H spin channel | P-P channel | |||
| charge instability | FM | chiral SC-I | |||
| Nem.(bond) | NSN(bond) | chiral SC-II | |||
| QAH | QSH | s-wave SC | |||
| Nem.(site) | NSN(site) | triplet SC | |||
Before going further, we make brief comments on the underlying fixed points. Compared to the spinless case Vafek2014PRB ; Wang2017PRB , the close interplay of spinful interactions gives rise to more systematical results including all potential fixed points and their complicated competition in the low-energy regime. Besides, three new fixed points including , , and can be developed by the intimate interplay of spinful electron-electron interactions. Armed with these in hand, we can expect potential instabilities around distinct kinds of fixed points, which we are going to deliver in the forthcoming section V.




V Instabilities and phase transitions
Through a systematical analysis of the coupled RG equations (11)-(26) in Sec. IV, we present that the 2D QBCP system is attracted by a series of fixed points (i.e., ) for all three distinct cases due to the electron-electron interactions, which are primarily dependent upon the initial conditions. Particularly, parts of the electron-electron couplings go towards divergence as approaching these fixed points shown in Fig. 1. In principle, such divergences are of close association with certain instabilities and well-trodden signals for symmetry breakings Cvetkovic2012PRB ; Vafek2014PRB ; Wang2017PRB ; Maiti2010PRB ; Altland2006Book ; Vojta2003RPP ; Halboth2000RPL ; Halboth2000RPB ; Eberlein2014PRB ; Chubukov2012ARCMP ; Nandkishore2012NP ; Chubukov2016PRX ; Roy2018RRX ; Wang2020NPB . Accordingly, an important question naturally arises which instabilities and phase transitions with certain symmetry breakings are dominant and preferable around these fixed points. Clarifying this inquiry would be of particular help to improve our understandings on the low-energy properties of 2D QBCP materials.
V.1 Source terms and susceptibilities
In order to examine the behaviors nearby the fixed points, we adopt the following source terms consisting of fermionic bilinears to characterize the potential candidates of instabilities Vafek2010PRB ; Vafek2014PRB ; Roy2018RRX ; Roy2009.05055
| (32) | |||||
Here, the matrix with and acting on space and spin serve as the fermion bilinears for the candidates of symmetry breakings for our system as explicitly collected in Table. 1 Vafek2010PRB ; Vafek2014PRB . In addition, correspond to the strength of related fermion-source terms for the particle-hole and particle-particle channels, respectively.
To proceed, the susceptibilities that are linked to the instabilities can be expressed as follows Vafek2010PRB ; Vafek2014PRB
| (33) |
where specifies the free energy density. In order to identify the very dominant instabilities, we need to obtain the energy-dependent susceptibilities as accessing the fixed points. To this end, we add the source terms (32) into our effective action (5) and then derive the related RG equations of by paralleling the analysis in Sec. III, which are provided in Appendix B for the details.
At current stage, as approaching certain fixed point, the energy-dependent susceptibilities can be obtained via combining the RG evolutions of both fermionic couplings (11)-(26) and source terms (51)-(72) and the relationship in Eq. (33). To proceed, we are able to select the dominant instabilities from the candidates in Table. 1 in that the ground state can be characterized by the susceptibility with the strongest divergence Cvetkovic2012PRB ; Vafek2014PRB ; Wang2017PRB ; Maiti2010PRB ; Altland2006Book ; Vojta2003RPP ; Halboth2000RPL ; Halboth2000RPB ; Eberlein2014PRB ; Chubukov2012ARCMP ; Nandkishore2012NP ; Chubukov2016PRX ; Roy2018RRX ; Nandkishore2008.05485 . Before going further, it is of particular importance to emphasize that all the phases listed in Table. 1 are the potential candidates for an instability induced by some fixed point, and accordingly, not all of them happen simultaneously, but instead only one of them would win the competition and become the leading instability. The corresponding results for three distinct cases will be addressed one by one in the following.
V.2 Leading and subleading instabilities
V.2.1 Limit case
At first, we consider the Limit case. As shown in Sec. IV.1, there exist two types of fixed points, namely for and for , respectively.
Fig. 8 presents the energy-dependent susceptibilities as the system approaches such two fixed points. We can clearly read from Fig. 8 that the leading instability corresponds to the QAH phase around but instead the isotropic QSH phase (with the contributions from directions being degenerate) in the vicinity of . Besides, it is also of particular importance to comment on the subleading instabilities, which are currently subordinate to the leading ones but may compete with the leading ones and dominate over them under certain adjusted conditions. Clearly, the subleading phases for Limit case are the Nem.site(bond) and chiral SC-I for accessing and , respectively.
V.2.2 Special case
Subsequently, we move to the Special case which owns three distinct sorts of fixed points including , and .
With respect to , paralleling the analysis in Sec. V.2.1, we notice that the leading instabilities around , and , are occupied by the QAH, the isotropic (, , and are equivalent), and Nem.(site)/Nem.(bond) (these two phases are degenerate), respectively.
In addition, as mentioned in Sec. IV, each fixed point governs a regime in the interaction-parameter space. In this sense, we need to examine the stability of leading phase for certain fixed point with variation of the initial conditions. Fig. 9(a) displays the proportion of leading phases around three fixed points with tuning the initial values of interaction parameters ranging from to . This implies that the leading phases of such three fixed points are adequately stable.
In comparison, the subleading phases around these three fixed points displayed in Fig. 9(b) are much more susceptible to the starting conditions. We can find that there are multiple candidates for subleading phases nearby and chiral SC-II/s-wave SC and Nem.(site)/Nem.(bond) take a slight advantage. As to , it is similar to , but for the chiral SC-I dominates the subleading phase.
For completeness, we provide several comments on the situation. In analogous to their counterparts, the leading phases are robust enough. Fig. 9(c) suggests that the basic results for / are similar to those of /, while the Nem.site(bond) state around wins the competition among other phases in case and become the manifestly subleading phases.
| L case |
|
— | — | — | — | — | |||||||||||||
| S case |
|
|
|
— | — | — | |||||||||||||
| G case |
|
— |
|
|
|
|
|||||||||||||
| L case | — |
|
— | — | — | — | |||||||||||||
| S case |
|
|
|
— | — | — | |||||||||||||
| G case |
|
— |
|
|
|
|
|||||||||||||
V.2.3 General case
At last, let us put our focus on the General case. In this circumstance, it shows in Sec. IV.3 that both and can be reached as well, but are replaced by three new fixed points including , and .
Considering , we carry out the analogous analysis in Sec. V.2.2 and then figure out that the most preferable states that the system flows towards around and are still the QAH and Nem.(site)/Nem.(bond), respectively. However, in sharp contrast, the leading instability accompanied by corresponds to the , in which the susceptibility becomes anisotropic and the direction component dominates over the other two directions. Similarly, and occupy the most favorable phases in the vicinity of and , respectively. It is therefore of remark significance to point out that the rotation symmetry of spin space is broken by the spinful electron-electron interactions. As a result, the are no longer degenerate but instead split and become anisotropic. Again, we investigate the stabilities of leading phases and present Fig. 10(a) to show that these leading phases are stable under the variation of initial conditions.
In addition, we briefly give several comments on the subleading phases around these fixed points. Comparing with the Special case where several subleading instabilities are observed around and , Fig. 10(b) indicates that only Nem.(site) and Nem.(bond) compete for the subleading phases in General case. However, a number of phases including the other two components of as well as chiral SC-I have an opportunity to be the subleading instabilities nearby , , and .
As to the situation, Fig. 10(c) shows that the leading phases for , , , and are analogous to their case. But rather for , there are additional candidates including Nem.site(bond) and NSN.site(bond) that compete for the leading phases. Besides, we notice from Fig. 10(d) that the other two QSH components dominate over the chiral SC-I and have a bigger chance to be the subleading phases around , , and . Different from the case, there exist more phases can be the candidates for the subleading states for and .
To recapitulate, Table 2 summarizes our basic conclusions for the leading and subleading instabilities around all the potential fixed points induced by spinful electron-electron interactions.
V.3 Brief discussions
Before closing this section, we would like to address several comments on the basic results. On one hand, the inclusion of spinful electron-electron interactions, as compared to the spinless case Vafek2014PRB ; Wang2017PRB , can be capable of generating more fixed points including and as presented in Sec. IV, which dictate the low-energy fate of the 2D QBCP system. On the other hand, as approaching these fixed points, we find that a series of instabilities can be induced by the spinful electron-electron interactions as catalogued in Table 2. As to the leading phases, in addition to the QAH and isotropic QSH Vafek2014PRB , the 2D QBCP system can undergo a phase transition to either an anisotropic QSH or a Nem.site(bond) state. Besides, a plethora of candidate instabilities exhibited in Table 2 endeavor to run for the subleading phases, which can compete with the leading ones and may become dominant instabilities under certain modified conditions. To wrap up, the spinful electron-electron interactions play an essential role in inducing the underlying instabilities and reshaping the low-energy behavior of 2D QBCP materials.
Subsequently, let us address several underlying explanations for these new behavior. Fixing a certain model, taking into account more or less physical ingredients is of particular importance to reveal the low-energy behavior. In Ref. Fradkin2009PRL , the authors considered the spin effects but worked at the mean-field level without including the quantum fluctuations, which typically provide basic contributions. Although Ref. Vafek2014PRB considered spin effects, the authors used a spinor to describe the quasiparticle, implying that the contributions from spin-up and spin-down are treated equally in low-energy properties. Consequently, the spinful effects and their interplay with electron-electron interactions cannot be fully included. Working in the space implies that the spinful effects may only be partially taken into account. In sharp contrast, we explicitly employ a -component spinor to characterize the low-energy excitations and work in the space. This approach necessitates dealing with 16 components of interaction couplings compared to 4 couplings in previous works Fradkin2009PRL ; Vafek2014PRB . Accordingly, our renormalization group (RG) equations incorporate one-loop corrections beyond the mean-field level, fully capturing the spinful ingredients to provide more accurate physical information.
VI Summary
In summary, our study presents a systematical investigation of the interplay of sixteen types of marginal spinful electron-electron interactions and the low-energy instabilities of 2D QBCP semimetals by virtue of the RG approach Shankar1994RMP ; Wilson1975RMP ; Polchinski9210046 . After considering all one-loop corrections, we establish the energy-dependent RG evolutions of all interaction parameters, which are closely coupled and dictate the low-energy physics of 2D QBCP system. A detailed numerical analysis addresses a series of interesting behaviors induced by these interactions that exhibit significant differences compared to those of the spinless situation.
To begin with, we find that the 2D QBCP systems are attracted by several distinct kinds of fixed points in the interaction-parameter space. In particular, they are heavily dependent upon the initial conditions, including the value of interaction parameters and structure parameter . These fall into three categories consisting of Limit case, Special case, and General case as demonstrated in Sec. IV. Specifically, there exist the fixed points and in the Limit case, but instead , , and in the Special case. In contrast, the General case gives rise to , , and . Besides, the stabilities of fixed points are also provided in Figs. 4-6 with the variation of parts of interaction parameters. In principle, certain instabilities with certain symmetry breakings that are accompanied by phase transitions can be expected as approaching these fixed points. Subsequently, we bring out the source terms composed of the fermionic bilinears to capture the potential instabilities Vafek2010PRB ; Vafek2014PRB ; Roy2018RRX ; Roy2009.05055 . After evaluating the susceptibilities of all candidate states by combining the source terms and RG equations of interaction parameters, we find that the spinful fermion-fermion interactions can induce sorts of favorable instabilities in the vicinity of these fixed points as summarized in Table 2. In the vicinity of , , and , it clearly indicates that the QAH, QSH, and Nem.site(bond) states are dominant, and correspondingly, Nem.site(bond), Chiral SC-I, and NSN.site(bond) are the most probable candidates to run for the subleading phases, respectively. In comparison, QSH becomes anisotropic nearby the , around which only one component of QSH plays a leading role but the other two components only own the chance to compete for the subleading instabilities with Chiral SC-I. To be brief, the spinful fermion-fermion interactions are of particular importance to pinpoint the low-energy behavior of 2D QBCP materials. Compared to the spinless case Vafek2014PRB ; Wang2017PRB , the spinful fermion-fermion interactions and their intimate competitions bring a series of new critical behavior in the low-energy regime, including more fixed points and more favorable phase transitions which are collected in Table 2. We wish these findings would be instructive to improve our understandings of 2D QBCP semimetals and helpful to study the analogous materials.
ACKNOWLEDGEMENTS
We thank Wen-Hao Bian for the helpful discussions. J.W. was partially supported by the National Natural Science Foundation of China under Grant No. 11504360.
Appendix A One-loop corrections to the electron-electron couplings
On the basis of our effective field action (5), the one-loop diagrams that contribute to the electron-electron couplings are exhibited in Fig. 11. After performing the long but standard calculations Cvetkovic2012PRB ; Vafek2014PRB ; Wang2017PRB , we are left with the following one-loop corrections to electron-electron interaction parameters
| (34) | |||||
| (35) | |||||
| (36) | |||||
| (37) | |||||
| (38) | |||||
| (39) | |||||
| (40) | |||||
| (41) | |||||
| (42) | |||||
| (43) | |||||
| (44) | |||||
| (45) | |||||
| (46) | |||||
| (47) | |||||
| (48) | |||||
| (49) | |||||
with where are defined as
| (50) | |||||


Appendix B One-loop flows of source terms
According to the effective field action (5) and the source terms (32), the electron-electron interactions can contribute to the source terms as illustrated in Fig. 12 for the one-loop level Cvetkovic2012PRB ; Vafek2014PRB ; Wang2017PRB . After carrying out the analogous calculations in Appendix A in tandem with the RG scalings in Sec. III, we obtain the energy-dependent evolutions of source terms as follows (to be convenient and consistent with notations in Table 1, we hereby add the scripts PH and PP to denote the particle-hole and particle-particle channels with and corresponding to the charge and spin cases, respectively)
| (51) | |||||
| (52) | |||||
| (53) | |||||
| (54) | |||||
| (55) | |||||
| (56) | |||||
| (57) |
and
| (58) | |||||
| (59) | |||||
| (60) | |||||
| (61) | |||||
| (62) | |||||
| (63) | |||||
| (64) | |||||
| (65) | |||||
| (66) | |||||
| (67) | |||||
| (68) | |||||
| (69) | |||||
| (70) | |||||
| (71) | |||||
| (72) | |||||
References
- (1) K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos, and A. A. Firsov, Nature 438, 197 (2005).
- (2) A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, Rev. Mod. Phys. 81, 109 (2009).
- (3) L. Fu, C. L. Kane, and E. J. Mele, Phys. Rev. Lett. 98, 106803 (2007).
- (4) R. Roy, Phys. Rev. B 79, 195322 (2009).
- (5) J. E. Moore, Nature 464, 194 (2010).
- (6) M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82, 3045 (2010).
- (7) X. L. Qi and S. C. Zhang, Rev. Mod. Phys. 83, 1057 (2011).
- (8) S. Q. Sheng, 2012 Dirac Equation in Condensed Matter (Berlin: Springer).
- (9) B. A. Bernevig and T. L. Hughes, 2013 Topological Insulators and Topological Superconductors (Princeton, NJ: Princeton University Press).
- (10) H. K. Tang, J. N. Leaw, J. N. B. Rodrigues, I. F. Herbut, P. Sengupta, F. F. Assaad, S. Adam, Science 361, 570 (2018).
- (11) N. P. Armitage, E. J. Mele, and Ashvin Vishwanath, Rev. Mod. Phys. 90, 015001 (2018).
- (12) B. Roy and M. S. Foster, Phys. Rev. X 8, 011049 (2018).
- (13) Z. J. Wang, Y. Sun, X. Q. Chen, C. Franchini, G. Xu, H. M. Weng, X. Dai, and Z. Fang, Phys. Rev. B 85, 195320 (2012).
- (14) S. M. Young, S. Zaheer, J. C. Y. Teo, C. L. Kane, E. J. Mele, and A. M. Rappe, Phys. Rev. Lett. 108, 140405 (2012).
- (15) J. A. Steinberg, S. M. Young, S. Zaheer, C. L. Kane, E. J. Mele, and A. M. Rappe, Phys. Rev. Lett. 112, 036403 (2014).
- (16) Z. K. Liu, J. Jiang, B. Zhou, Z. J. Wang, Y. Zhang, H. M. Weng, D. Prabhakaran, S. K. Mo, H. Peng, P. Dudin, T. Kim, M. Hoesch, Z. Fang, X. Dai, Z. X. Shen, D. L. Feng, Z. Hussain, and Y. L. Chen, Nat. Mater. 13, 677 (2014).
- (17) Z. K. Liu, B. Zhou, Y. Zhang, Z. J. Wang, H. M. Weng, D. Prabhakaran, S. K. Mo, Z. X. Shen, Z. Fang, X. Dai, Z. Hussain, and Y. L. Chen, Science 343, 864 (2014).
- (18) J. Xiong, S. K. Kushwaha, T. Liang, J. W. Krizan, M. Hirschberger, W. Wang, R. J. Cava, and N. P. Ong, Science 350, 413 (2015).
- (19) A. A. Burkov and L. Balents, Phys. Rev. Lett. 107, 127205 (2011).
- (20) K. Y. Yang, Y. M. Lu, and Y. Ran, Phys. Rev. B 84, 075129 (2011).
- (21) X. G. Wan, A. M. Turner, A. Vishwanath, and S. Y. Savrasov, Phys. Rev. B 83, 205101 (2011).
- (22) X. C. Huang, L. X. Zhao, Y. J. Long, P. P. Wang, D. Chen, Z. H. Yang, H. Liang, M. Q. Xue, H. M. Weng, Z. Fang, X. Dai, and G. F. Chen, Phys. Rev. X 5, 031023 (2015).
- (23) S. Y. Xu, I. Belopolski, N. Alidoust, M. Neupane, G. Bian, C. L. Zhang, R. Sankar, G. Q. Chang, Z. J. Yuan, C. C. Lee, S. M. Huang, H. Zheng, J. Ma, D. S. Sanchez, B. K. Wang, A. Bansil, F. C. Chou, P. P. Shibayev, H. Lin, S. Jia, and M. Z. Hasan, Science 349, 613 (2015).
- (24) S. Y. Xu, N. Alidoust, I. Belopolski, Z. J. Yuan, G. Bian, T. R. Chang, H. Zheng, V. N. Strocov, D. S. Sanchez, G. Q. Chang, C. L. Zhang, D. X. Mou, Y. Wu, L. Huang, C. C. Lee, S. M. Huang, B. K. Wang, A. Bansil, H. T. Jeng, T. Neupert, A. Kaminski, H. Lin, S. Jia, and M. Z. Hasan, Nat. Phys. 11, 748 (2015).
- (25) B. Q. Lv, N. Xu, H. M. Weng, J. Z. Ma, P. Richard, X. C. Huang, L. X. Zhao, G. F. Chen, C. E. Matt, F. Bisti, V. N. Strocov, J. Mesot, Z. Fang, X. Dai, T. Qian, M. Shi, and H. Ding, Nat. Phys. 11, 724 (2015).
- (26) H. Weng, C. Fang, Z. Fang, B. A. Bernevig, and X. Dai, Phys. Rev. X 5, 011029 (2015).
- (27) M. M. Korshunov, D. V. Efremov, A. A. Golubov and O. V. Dolgov, Phys. Rev. B 90, 134517 (2014).
- (28) H. H. Hung, A. Barr, E. Prodan and G. A. Fiete, Phys. Rev. B 94, 235132 (2016).
- (29) R. Nandkishore, J. Maciejko, D. A. Huse, and S. L. Sondhi, Phys. Rev. B 87, 174511 (2013).
- (30) I. D. Potirniche, J. Maciejko, R. Nandkishore, and S. L. Sondhi, Phys. Rev. B 90, 094516 (2014).
- (31) R. M. Nandkishore and S. A. Parameswaran, Phys. Rev. B 95, 205106 ( 2017).
- (32) B. Roy and S. Das Sarma, Phys. Rev. B 94, 115137 (2016).
- (33) I. F. Herbut, Phys. Rev. B 85, 085304 (2012).
- (34) W. Zhu, S. S. Gong, T. S. Zeng, L. Fu, and D. N. Sheng, Phys. Rev. Lett. 117, 096402 (2016).
- (35) J. Wang, C. Ortix, J. van den Brink, and D. V. Efremov, Phys. Rev. B 96, 201104(R) (2017).
- (36) Y. M. Dong, Y. H. Zhai, D. X. Zheng, and J. Wang, Phys. Rev. B 102, 134204 (2020).
- (37) B. Roy, arxiv: 2004.13043 (2020).
- (38) I. Mandal and S. Gemsheim, Condens. Matter Phys. 22, 13701 (2019).
- (39) S. Ray , M. Vojta, and L. Janssen, Phys. Rev. B 102, 081112(R) (2020).
- (40) J. Shah and S. Mukerjee, arxiv: 2011.00249 (2020).
- (41) I. Mandal and R. M. Nandkishore, Phys. Rev. B 97, 125121 (2018).
- (42) Y. P. Lin and R. M. Nandkishore, Phys. Rev. B 97, 134521 (2018).
- (43) J. M. Luttinger, Phys. Rev. 102, 1030 (1956).
- (44) S. Murakami, N. Nagaosa, and S. C. Zhang, Phys. Rev. B 69, 235206 (2004).
- (45) L. Janssen and I. F. Herbut, Phys. Rev. B 92, 045117 (2015).
- (46) I. Boettcher and I. F. Herbut, Phys. Rev. B 93, 205138 (2016).
- (47) L. Janssen and I. F. Herbut, Phys. Rev. B 95, 075101 (2017).
- (48) I. Boettcher and I. F. Herbut, Phys. Rev. B 95, 075149 (2017).
- (49) L. Savary, E. G. Moon, and L. Balents, Phys. Rev. X 4, 041027 (2014).
- (50) L. Savary, J. Ruhman, J. W. F. Venderbos, L. Fu, and P. A. Lee, Phys. Rev. B 96, 214514 (2017).
- (51) H. H. Lai, B. Roy, and P. Goswami, arXiv: 1409.8675 (2014).
- (52) P. Goswami, B. Roy, and S. Das Sarma, Phys. Rev. B 95, 085120 (2017).
- (53) A. L. Szabo, R. Moessner, and B. Roy, arXiv:1811.12415 (2018).
- (54) B. Roy, Sayed Ali Akbar Ghorashi, M. S. Foster, and A. H. Nevidomskyy, Phys. Rev. B 99, 054505 (2019).
- (55) S. Ray, M. Vojta, and L. Janssen, Phys. Rev. B 98, 245128 (2018).
- (56) J. R. Wang, W. Li, and C. J. Zhang, Phys. Rev. B 102, 085132 (2020).
- (57) Y. D. Chong, X. G. Wen, and M. Soljai, Phys. Rev. B 77, 235125 (2008).
- (58) K. Sun and E. Fradkin, Phys. Rev. B 78, 245122 (2008).
- (59) K. Sun, H. Yao, E. Fradkin, and S. A. Kivelson, Phys. Rev. Lett. 103, 046811 (2009).
- (60) O. Vafek, Phys. Rev. B 82, 205106 (2010).
- (61) O. Vafek and K. Yang, Phys. Rev. B 81, 041401(R) (2010).
- (62) V. Cvetkovi, R. E. Throckmorton, and O. Vafek, Phys. Rev. B 86, 075467 (2012).
- (63) J. M. Murray and O. Vafek, Phys. Rev. B 89, 201110(R) (2014).
- (64) J. Wang and I. Mandal, arXiv: 2303.10163 (2023).
- (65) Y. Xiao, V. Pelletier, P. M. Chaikin, and D. A. Huse, Phys. Rev. B 67, 104505 (2003).
- (66) G. W. Chern and C. D. Batista, Phys. Rev. Lett. 109, 156801 (2012).
- (67) W. F. Tsai, C. Fang, H. Yao, and J. Hu, New J. Phys. 17, 055016 (2015).
- (68) U. Schollwöck, Rev. Mod. Phys. 77 , 259-315 (2005).
- (69) E. M. Stoudenmire and S. R. White, Annu. Rev. Condens. Matter Phys. 3 , 111-128 (2012).
- (70) C. Hubig, I. P. McCulloch, U. Schollwöck and F. A. Wolf, Phys. Rev. B. 91 , 155115 (2015).
- (71) B. Roy and S. Das Sarma, Phys. Rev. B 94, 115137 (2016).
- (72) Y.-C. He, M. P. Zaletel, M. Oshikawa and F. Pollmann, Phys. Rev. X. 7 , 031020 (2017).
- (73) S. Chatterjee, M. Ippoliti and M. P. Zaletel, Phys. Rev. B. 106 , 035421 (2022).
- (74) S. Nishimoto, M. Nakamura, A. ÓBrien and P. Fulde, Phys. Rev. L 104, 196401 (2010).
- (75) T.-S. Zeng, W. Zhu and D. Sheng, npj Quant Mater 3, 49 (2018).
- (76) W. Zhu, S.-S. Gong, T.-S. Zeng, L. Fu and D. Sheng, Phys. Rev. L 117, 096402 (2016).
- (77) J. W. F. Venderbos, M. Manzardo, D. V. Efremov, J. van den Brink and C. Ortix, Phys. Rev. B 93, 045428 (2016).
- (78) H. Q. Wu, Y. Y. He, C. Fang, Z. Y. Meng, and Z. Y. Lu, Phys. Rev. Lett. 117, 066403 (2016).
- (79) K. G. Wilson, Rev. Mod. Phys. 47, 773 (1975).
- (80) J. Polchinski, arXiv: hep-th/9210046 (1992).
- (81) R. Shankar, Rev. Mod. Phys. 66, 129 (1994).
- (82) S. Maiti and A.V. Chubukov, Phys. Rev. B. 82, 214515 (2010).
- (83) A. Altland and B. Simons, Condensed Matter Field Theory (Cambridge University Press, Cambridge, 2006).
- (84) M. Vojta, Rep. Prog. Phys. 66, 2069 (2003).
- (85) C. J. Halboth and W. Metzner, Phys. Rev. Lett. 85, 5162 (2000).
- (86) C. J. Halboth and W. Metzner, Phys. Rev. B 61, 7364 (2000).
- (87) J. Wang, A. Eberlein, and W. Metzner, Phys. Rev. B 89, 121116(R) (2014).
- (88) A. V. Chubukov, Annu. Rev. Condens. Matter Phys. 3, 57 (2012).
- (89) A. V. Chubukov, M. Khodas, and R. M. Fernandes, Phys. Rev. X 6, 041045 (2016).
- (90) R. Nandkishore, L. S. Levitov, and A. V. Chubukov, Nat. Phys. 8, 158 (2012).
- (91) J. Wang, Nuclear Physics B 961, 115230 (2020).
- (92) I. F. Herbut, V. Juricic, and B. Roy, Phys. Rev. B 79, 085116 (2009).
- (93) J. Wang, G. Z. Liu, and H. Kleinert, Phys. Rev. B 83, 214503 (2011).
- (94) J. Wang, Phys. Rev. B. 87, 054511 (2013).
- (95) Y. Huh and S. Sachdev, Phys. Rev. B 78, 064512 (2008).
- (96) E. A. Kim, M. J. Lawler, P. Oreto, S. Sachdev, E. Fradkin, and S. A. Kivelson, Phys. Rev. B. 77, 184514 (2008).
- (97) J. H. She, J. Zaanen, A. R. Bishop, and A. V. Balatsky, Phys. Rev. B 82, 165128 (2010).
- (98) J. H. She, M. J. Lawler, and E. A. Kim, Phys. Rev. B. 92, 035112 (2015).
- (99) B. Roy, P. Goswami, and J. D. Sau, Phys. Rev. B. 94, 041101 (2016).
- (100) J. Wang, J. Phys.: Condens. Matter. 30, 125401 (2018).
- (101) Y. M. Dong, D. X. Zheng, and J. Wang, J. Phys.: Condens. Matter. 31, 275601 (2019).
- (102) A. L. Szabó and B. Roy, arXiv: 2009.05055 (2020).
- (103) Y. P. Lin and R. M. Nandkishore, arXiv: 2008.05485 (2020).