Fate of Fermi-arc States in Gapped Weyl Semimetals under Long-ranged Interactions

Our model Hamiltonian under periodic boundary conditions is given by

Here $\bm{\sigma}$ is the vector of three Pauli matrices denoting a (pseudo-)spin-$1/2$ operator, $c^{\dagger}_{\mathbf{k}\alpha}$ represents the creation operator for electrons of (pseudo-)spin $\alpha=\;\uparrow$ or $\downarrow$, and $n_{\mathbf{k}\alpha}=c^{\dagger}_{\mathbf{k}\alpha}c_{\mathbf{k}\alpha}$. The first part $H_{0}$ describes a noninteracting two-band model of a WSM. To be specific, we take $\mathbf{h}(\mathbf{k})=(M-\cos k_{x}-\cos k_{y}-\cos k_{z},\;\sin k_{x},\;\sin k_{y})$ with $1<M<3$ not (a). In such a case, only a single pair of Weyl nodes appears at momenta $\mathbf{k}=(0,\,0,\,\pm k_{\mathrm{Weyl}})$ with $k_{\mathrm{Weyl}}=\arccos(M-2)$. The second term $H_{U}$ gives a Hubbard-like interaction but being local in momentum space, rather than in real space.

Because different momentum states are decoupled, the bulk properties of this interacting model can be derived exactly through diagonalizing the Hamiltonian in the number representation for each momentum $\mathbf{k}$. The four eigenstates for each $\mathbf{k}$ are $\{|0\rangle,\;b_{\mathbf{k}-}^{\dagger}|0\rangle,\;b_{\mathbf{k}+}^{\dagger}|0\rangle,\;b_{\mathbf{k}-}^{\dagger}b_{\mathbf{k}+}^{\dagger}|0\rangle\}$ with the corresponding eigenvalues $\{U/2,\;-h(\mathbf{k}),\;h(\mathbf{k}),\;U/2\}$. Here $b^{\dagger}_{\mathbf{k}+}$ and $b^{\dagger}_{\mathbf{k}-}$ denote the eigenmodes of the noninteracting Hamiltonian $H_{0}$, $|0\rangle$ is the vacuum state, and $h(\mathbf{k})=|\mathbf{h}(\mathbf{k})|$. Therefore, the many-body ground state for positive $U$ at zero temperature and half-filling becomes the state with a completely-filled lower band, $|\Psi_{0}\rangle=\prod_{\mathbf{k}}b_{\mathbf{k}-}^{\dagger}|0\rangle$. The single-particle/hole excitations, $b_{\mathbf{k}+}^{\dagger}|\Psi_{0}\rangle$ and $b_{\mathbf{k}-}|\Psi_{0}\rangle$, have nonzero excitation energies $\Delta E_{1p/1h}=h(\mathbf{k})+U/2$ even at the Weyl nodes such that $h(\mathbf{k})=0$. The system thus behaves as a Mott insulator with a full gap. However, we note that the excitation energies of the bosonic charge-neutral particle-hole excitations, $b_{\mathbf{k}+}^{\dagger}b_{\mathbf{k}-}|\Psi_{0}\rangle$, keep their noninteracting values $\Delta E_{\mathrm{ph}}=2h(\mathbf{k})$, which become zero at the Weyl nodes. That is, while the single-particle/hole excitations are always gapful, this interacting WSM retains its gapless Weyl nodes from the viewpoint of particle-hole excitations.

In order to construct the Fermi arc surface states, we need to consider a finite-slab geometry with open boundaries. To this end, we first transform Eq. (1) into its real-space form and then impose the open boundary conditions. Here we take a finite size of $L$ sites in the $x$ direction. By employing Fourier transform in the $x$ direction, $\tilde{c}_{j\mathbf{k}_{\bot}\alpha}=(1/\sqrt{L})\sum_{k_{x}}e^{ik_{x}j}c_{\mathbf{k}\alpha}\,$, the Hamiltonian for a given transverse momentum $\mathbf{k}_{\bot}\equiv(k_{y},\,k_{z})$ reduces to a 1D tight-binding form, where $j=1,\dots,L$ labels the sites in the $x$ direction. After imposing the the open boundary conditions by dropping off the boundary hopping terms, the resulting 1D model with two open ends becomes

with

and

Here the labels of the transverse momentum $\mathbf{k}_{\bot}$ in the fermion operators is suppressed for simplification and $\tilde{n}_{i\alpha}=\tilde{c}_{i\alpha}^{\dagger}\tilde{c}_{i\alpha}$. The two parameters in Eq. (II.2) are given by $t_{\mathbf{k}_{\bot}}=M-\cos k_{y}-\cos k_{z}$ and $h_{\mathbf{k}_{\bot}}=\sin k_{y}$. We note that the non-interacting part $\mathcal{H}_{0}(\mathbf{k}_{\bot})$ is equivalent to the Su-Schrieffer-Heeger model Su et al. (1979) with an alternating on-site potential. The first term of $\mathcal{H}_{U}(\mathbf{k}_{\bot})$ describes the correlated hopping for up and down (pseudo-)spins with the same distances $d$ but in opposite directions. The second term in Eq. (II.2) comes from the zero-distance $d=0$ hopping, which reduces to the density-density interactions between different spin components.

While the model in Eq. (1) under periodic boundary conditions can be solved analytically, the corresponding one under open boundary conditions cannot. In this paper, numerically exact diagonalization is employed to search possible edge states at zero energy for the corresponding 1D models in Eq. (4). The collection of such zero-energy edge states constitutes the surface Fermi arcs of our interacting WSM.

To show the existence of the single-particle edge states lying between two bulk bands, the quasi-particle and the quasi-hole energies, defined by $\epsilon_{+}\equiv\mathcal{E}_{0}(N=L+1)-\mathcal{E}_{0}(N=L)$ and $\epsilon_{-}\equiv\mathcal{E}_{0}(N=L)-\mathcal{E}_{0}(N=L-1)$, are calculated. Here $\mathcal{E}_{0}(N)$ denotes the ground energy of the 1D model in Eq. (4) with $N$ electrons. The appearance of the in-gap edge states can be recognized when $\epsilon_{+}$ and $\epsilon_{-}$ deviate from their bulk values,

for the present case of $M=2$.

Before presenting our numerical results, some symmetry properties of our 1D lattice model $\mathcal{H}(\mathbf{k}_{\bot})$ in Eq. (4) are discussed in order. First, $\mathcal{H}(\mathbf{k}_{\bot})$ is invariant under the parity transformation $\mathcal{P}$: $\tilde{c}_{i\alpha}\rightarrow\tilde{c}_{L-i+1,-\alpha}$ in combination with $k_{y}\rightarrow-k_{y}$. The energy spectrum will thus be symmetric with respect to the $k_{y}=0$ axis. Second, $\mathcal{H}(\mathbf{k}_{\bot})$ is invariant under the operation combining the parity transformation $\mathcal{P}$ with the particle-hole transformation: $\tilde{c}^{\dagger}_{i\uparrow}\leftrightarrow\tilde{c}_{i\uparrow}$ and $\tilde{c}^{\dagger}_{i\downarrow}\leftrightarrow-\tilde{c}_{i\downarrow}$. Therefore, the quasi-particle and the quasi-hole excitation energies, $\epsilon_{+}$ and $|\epsilon_{-}|$, above the ground-state energy will be the same. That is, the energy spectrum will become symmetric with respect to $\epsilon=0$.

In Fig. 1, $\epsilon_{+}$ and $\epsilon_{-}$ as functions of $k_{y}$ for $k_{z}=\pi/4$ and $3\pi/4$ are displayed for the case of $U=2$. For comparison, the results for the noninteracting ($U=0$) case are shown as well. It is clear that our findings do respect the symmetries mentioned above. The $U=0$ results can be derived analytically. When $|k_{z}|<k_{\mathrm{Weyl}}$, the effective 2D system at a fixed $k_{z}$ acts as a Chern insulator with a Chern number $C=1$ and thus supports a pair of chiral edge modes. The edge modes emerge around $k_{y}=0$ with the dispersions $\epsilon=\pm\sin{k_{y}}$. On the other hand, when $k_{\mathrm{Weyl}}<|k_{z}|<\pi$, the effective 2D system behaves as a $C=0$ trivial insulator, in which there exists no edge state and the quasi-particle/quasi-hole energies must equal to their bulk values. As seen from Fig. 1, our numerical data for the $U=0$ case fairly reproduce the analytic predictions.

After turning on the interaction $U$, the conclusions are qualitatively unchanged. The calculated quasi-particle/quasi-hole energies for $k_{z}=3\pi/4>k_{\mathrm{Weyl}}$ agree well with their bulk values $\epsilon^{\mathrm{bulk}}_{\pm}$ and thus no edge state appears. Interestingly, when $k_{z}=\pi/4<k_{\mathrm{Weyl}}$, the edge modes around $k_{y}=0$ are not destroyed by interactions. Nevertheless, the correlation effect makes the slopes of their dispersions around $k_{y}=0$ being steeper. This is consistent with the enhanced bulk gap due to electronic correlations. We note that the calculated single-particle gap $\Delta_{1}$ defined by the minimal value of the energy difference $\epsilon_{+}-\epsilon_{-}$ can have a tiny nonzero value due to finite-size effects. As shown below (Fig. 3), this value approaches zero in the thermodynamic limit, and then the zero-energy edge modes indeed show up in the spectrum. Therefore, our findings clearly demonstrate the robustness of zero-energy single-particle edge modes against the long-ranged interaction $U$.

To further identify the in-gap states around $k_{y}=0$ for $k_{z}=\pi/4$ as edge modes, we need to show that the densities of these quasi-particle/quasi-hole states do distribute near the edges only. The density profile of one electron added is defined as $\delta n_{i}^{+}=\langle\tilde{n}_{i}\rangle_{N=L+1}-\langle\tilde{n}_{i}\rangle_{N=L}$ and that of an extra hole is $\delta n_{i}^{-}=\langle\tilde{n}_{i}\rangle_{N=L}-\langle\tilde{n}_{i}\rangle_{N=L-1}$. Here $\tilde{n}_{i}=\sum_{\alpha}\tilde{c}_{i\alpha}^{\dagger}\tilde{c}_{i\alpha}$ is the total electron number operator on site $i$ and $\langle\tilde{n}_{i}\rangle_{N}$ denotes its expectation value with respect to the ground state with $N$ electrons. The values of $\delta n_{i}^{+}$ and $\delta n_{i}^{-}$ describe how an added particle or hole distributes itself in the system.

Our findings of $\delta n_{i}^{+}$ and $\delta n_{i}^{-}$ at $U=2$ for the states with a typical value of $k_{y}$ around $k_{y}=0$ are shown in Fig. 2 for both the cases of $k_{z}=\pi/4$ and $3\pi/4$. Again, the data for the $U=0$ case are displayed as well for comparison. When $k_{z}=3\pi/4>k_{\mathrm{Weyl}}$, no matter whether the interaction $U$ is present or not, the extra particle/hole always distributes itself in the center of the lattice system. It shows that these quasi-particle/quasi-hole states indeed describe the bulk states, in support of the energy perspective discussed above. For $k_{z}=\frac{\pi}{4}<k_{\mathrm{Weyl}}$, we find that the added particle/hole locates on one or the other edge even in the presence of the long-ranged interaction $U$. Moreover, the density profiles for the $U=2$ case modify little as compared to the noninteracting case. Therefore, the in-gap states for $k_{z}=\pi/4$ do behave as edge modes and they are stable against electronic correlations.

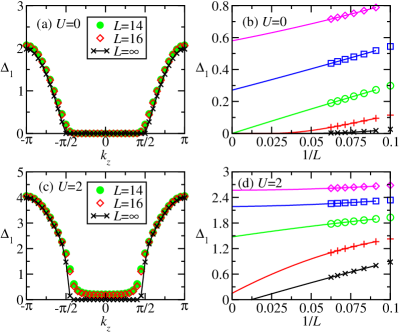
The Fermi arc is constituted by the collection or locus of the zero-energy edge states. In the noninteracting limit, this line segment ends at the projection of the bulk Weyl nodes onto the surface Brillouin zone. It has been shown in Fig. 1 that, for a specific $k_{z}=\pi/4$, the zero-energy edge modes, indicated by vanishing single-particle gap $\Delta_{1}$, persist upon the interaction effect. We now extend such discussions to other $k_{z}$’s and determine the whole Fermi arc for the present interacting model.

In Fig. 3, the single-particle gaps $\Delta_{1}$ for all $k_{z}$’s within the Brillouin zone are displayed for the case of $U=2$. For comparison, the results for the noninteracting ($U=0$) case are shown as well. As illustrated in Fig. 1, the possible zero-energy modes always occur at $k_{y}=0$. We thus fix $k_{y}=0$ in our calculations of $\Delta_{1}$. Besides, $M=2$ is assumed such that $k_{\mathrm{Weyl}}=\pi/2$. The $U=0$ results can be derived analytically. When $|k_{z}|<\pi/2$, $\Delta_{1}=0$ because of the appearance of a pair of degenerate chiral edge mode at $k_{y}=0$ [cf. Fig. 1(a)]. On the other hand, when $\pi/2<|k_{z}|\leq\pi$, there exists no edge mode and the quasi-particle/quasi-hole energies agree well with their bulk values $\epsilon^{\mathrm{bulk}}_{\pm}$ such that $\Delta_{1}=2\left[\epsilon^{\mathrm{bulk}}_{+}\right]_{k_{y}=0}$, which reduces to $\Delta_{1}=2|\cos{k_{z}}|$ for the present case of $M=2$. That is, the Fermi arc at $U=0$ extends from $k_{z}=-\pi/2$ to $\pi/2$. As seen from Fig. 3, our data agree with the analytic predictions, while visible deviation due to finite-size effects is observed around $k_{z}=\pm\pi/2$. Nevertheless, after extrapolating to the thermodynamic limit with $L\rightarrow\infty$, the agreement becomes excellent.

When the long-ranged interaction $U$ is turned on, for $\pi/2<|k_{z}|\leq\pi$, the calculated $\Delta_{1}$ again agrees well with the analytic prediction $\Delta_{1}=2\left[\epsilon^{\mathrm{bulk}}_{+}\right]_{k_{y}=0}=2|\cos{k_{z}}|+U$. However, for $|k_{z}|\leq\pi/2$, enhanced finite-size effects are observed in our calculations not (b). While $\Delta_{1}$ is found to be always nonzero up to our maximum size $L=16$, its extrapolated values for $|k_{z}|\leq 0.4\pi$ does reduce to zero. We note that the edge states are expected to be more and more delocalized when $k_{z}$ approaches the Weyl nodes at $k_{z}=\pm\pi/2$. Therefore, severe finite-size effects exist around the Weyl nodes and calculations for much larger sizes are necessary to reduce such effects. Nevertheless, our findings strongly suggest that the Fermi arcs for nonzero $U$ have the same extent as those in the noninteracting case. We thus conclude that, except the renormalized dispersions, the single-particle Fermi arcs receive no modification by the long-ranged interaction.

It appears that our conclusion disagrees with that obtained in Ref. Meng and Budich (2019), where a gap opening in the single-particle Fermi-arc states is observed for a slightly different model. Actually, after a necessary correction to their model Hamiltonian, gapless single-particle Fermi arcs will be recovered. That is, the same conclusion can be reached even when other long-ranged interactions different from the present model are taken. Instead of Eq. (II.2), the authors in Ref. Meng and Budich (2019) consider the following interaction term to simplify their calculations,

Because this long-ranged density-density interaction depends only on the total particle number $\tilde{N}=\sum_{i=1}^{L}(\tilde{n}_{i\uparrow}+\tilde{n}_{i\downarrow})$, it is clear that both the quasi-particle and the quasi-hole energies, $\epsilon_{+}$ and $\epsilon_{-}$, will be pushed away from the Fermi level by $U(k_{z})/2$ for those $k_{z}$’s with nonzero $U(k_{z})$’s. This gives a gap opening of $U(k_{z})$ for the noninteracting Fermi-arc states. However, the form in Eq. (7) is improper physically. For many-body states with a fixed particle density $\tilde{N}/L=1\pm\delta\rho$, where $\delta\rho$ denotes the density deviation from half-filling, this interaction term gives a contribution in energy density, $U(k_{z})(\delta\rho)^{2}L/2$, which becomes infinite in the thermodynamic limit, $L\rightarrow\infty$. In order to keep the energy density being an intensive quantity, a factor $1/L$ needs to be added in Eq. (7), i.e., $\widetilde{\mathcal{H}}_{U}\rightarrow\widetilde{\mathcal{H}}_{U}/L$. The single-particle gap thus becomes $U(k_{z})/L$, which vanishes in the thermodynamic limit. Therefore, the corrected results are actually in agreement with ours.

While the Weyl nodes are gapped out by the long-ranged interactions, the Hall conductance (and thus the Chern number) for each 2D momentum sector between the nodes remains its quantized value Morimoto and Nagaosa (2016). According to the theory of quantum Hall edge states Wen (1991); Renn (1995); Yoshioka , there must exist chiral edge modes on the boundaries of these 2D sectors. Notice that, instead of quasiparticle excitations, those edge modes are the capillary waves, whose dynamics is described by a 1D chiral boson theory. That is, the Fermi arc states implied by nonzero Chern number are constituted by the collective edge excitations, rather than the single-particle ones. Since the topological Chern number of the bulk system is not affected by the long-ranged interactions, the collective Fermi arcs of particle-hole nature are expected to maintain their noninteracting structures.

To verify this conclusion, we evaluate the particle-hole excitation energies $\Delta\mathcal{E}_{\mathrm{ph}}=\mathcal{E}_{1}-\mathcal{E}_{0}$ for the cases of nonzero $U$’s. Here $\mathcal{E}_{0}$ ($\mathcal{E}_{1}$) denotes the energy of the ground state (first-excited state) for the 1D model in Eq. (4) at half-filling. Because the particle number is fixed, the excited states should represent the particle-hole excitations. The appearance of the edge modes can be recognized once $\Delta\mathcal{E}_{\mathrm{ph}}$ deviates the corresponding bulk value. From the discussions at the end of Sec. II.1, the lowest excitation energy of the bulk particle-hole excitation at zero momentum transfer for a given set of $k_{y}$ and $k_{z}$ can be obtained by

for the present case of $M=2$. This expression is valid no matter whether $U$ is zero or not. We note that, different from the cases of $\epsilon^{\mathrm{bulk}}_{\pm}$, the bulk value of the particle-hole excitation energy $\Delta E_{\mathrm{ph}}^{\mathrm{bulk}}$ can approach zero at the Weyl nodes with $k_{y}=0$ and $k_{z}=\pm\pi/2$, even when $U$ is nonzero.

Our results of $\Delta\mathcal{E}_{\mathrm{ph}}$ as functions of $k_{y}$ for $k_{z}=\pi/4$ and $3\pi/4$ are shown in Figs. 4 (a) and (b) for the $U=2$ case. Because of the symmetry in the energy spectrum mentioned in the last subsection, only the data for $0\leq k_{y}<\pi$ are plotted. As illustrated in Fig. 4 (a), we find that the edge modes do appear around $k_{y}=0$ for $k_{z}<k_{\mathrm{Weyl}}$ even in the presence of long-ranged interactions. Notably, the calculated energies of bulk excitations for either $k_{z}<k_{\mathrm{Weyl}}$ or $k_{z}>k_{\mathrm{Weyl}}$ experience considerable finite-size effects. Nevertheless, their values agree well with the analytic predictions after extrapolating to the thermodynamic limit.

To show the in-gap excited states around $k_{y}=0$ for $k_{z}=\pi/4$ being the edge modes, their density profiles $\delta n_{i}=\langle\tilde{n}_{i}\rangle_{1}-\langle\tilde{n}_{i}\rangle_{0}$ are calculated as well. Here $\langle\cdots\rangle_{0}$ and $\langle\cdots\rangle_{1}$ denote the expectation values with respect to the ground state and the first-excited state at half-filling, respectively. Our result at $U=2$ for the state with $k_{z}=\pi/4$ and a typical value of $k_{y}$ around $k_{y}=0$ is displayed in Fig. 4 (c). For comparison, the counterpart for the case of $k_{z}=3\pi/4$ is plotted in Fig. 4 (d). As illustrated in the figure, the in-gap states around $k_{y}=0$ for $k_{z}=\pi/4$ do behave as edge states, in agreement with the energy perspective. Besides, the disturbed density shows a nonlocal charge transfer from one end to the other. That is, this particle-hole excitation implies the quantized charge pumping via the twisted boundary condition in the $y$ direction with a twist angle $\phi=2\pi$. Such a charge pumping process is expected, since the 2D sector at $k_{z}=\pi/4$ behaves as a quantum Hall system with quantized Hall conductance.

Finally, we determine the extent of the collective Fermi arcs constituted by the collection of the zero-energy edge states of particle-hole excitations. Similar to the discussions in Fig. 3, this can be achieved by evaluating the particle-hole gap $\Delta_{\mathrm{ph}}$ defined by the minimal value of $\Delta\mathcal{E}_{\mathrm{ph}}$. Therefore, the locus of the states with $\Delta_{\mathrm{ph}}=0$ in the surface Brillouin zone gives the collective Fermi arc. As observed in Figs. 4 (a) and (b), the states with the smallest $\Delta\mathcal{E}_{\mathrm{ph}}$ always occur at $k_{y}=0$. We thus fix $k_{y}=0$ in our calculations of $\Delta_{\mathrm{ph}}$ not (c). Here $k_{\mathrm{Weyl}}=\pi/2$ because $M=2$ is assumed. Our findings of $\Delta_{\mathrm{ph}}$ as functions of $k_{z}$ for the case of $U=2$ are displayed in Fig. 4 (e). Because $\Delta_{\mathrm{ph}}=\Delta_{1}$ for $U=0$, the results of $\Delta_{\mathrm{ph}}$ for the noninteracting case can directly refer to Fig. 3 (a). We find that the zero-energy edge states of particle-hole excitations appear when $k_{z}$ lies between two Weyl nodes even in the presence of long-ranged interactions. As compared to the single-particle counterparts in Fig. 3 (c), the particle-hole gaps within $|k_{z}|<\pi/2$ are found to receive less finite-size effects not (b). As mentioned before, the occurrence of such collective zero-energy edge states is actually guaranteed by the nonzero Hall conductances. Our findings provide a numerical support on this bulk-boundary correspondence in terms of collective excitations.