Fast neutrino flavor conversion, ejecta properties, and nucleosynthesis in newly-formed hypermassive remnants of neutron-star mergers

We consider models of binary NS mergers simulated by a three-dimensional relativistic smoothed particle hydrodynamics code that adopts conformal flatness conditions [46]. The code has recently been coupled to an approximate neutrino transport scheme called “improved-leakage-equilibration-absorption scheme (ILEAS),” which is implemented on a three-dimensional (3D) Cartesian coordinate grid ($x,y,z$) with the axis perpendicular to the merging plane chosen as $z-$axis. ILEAS serves as an efficient transport method for multidimensional simulations; when compared to two-moment neutrino transport results for protoneutron stars and post-merger tori, it captures well neutrino energy losses from the densest regions of the system as well as neutrino absorption in the free-streaming regime [23, 44].

Our fiducial models discussed in this section are from Ref. [23] and simulate the mergers of two non-rotating NSs with mass 1.35 $M_{\odot}$ each, with the EoS of DD2 [47, 48] and SFHo [49]. In addition, we consider in later sections cases of unequal mass binaries consisting of two NSs with 1.25 $M_{\odot}$ and 1.45 $M_{\odot}$ each, based on the same numerical scheme of Refs. [23, 44]. We note here that we have taken all simulation data averaged over the azimuthal angle. This is a fairly good assumption as the merger remnant quickly reaches an approximately axi-symmetric state after $\sim 2-3$ ms.

Figure 1 shows the evolution of the energy luminosity of different neutrino species and their average energy during the first 10 ms after the merger of two NSs for our symmetric mergers ¹¹1More precisely, the time is measured with respect to the first minimum of the lapse function (see Ref. [23]).. During this time, the central object is a hypermassive NS supported by differential rotation. The energy luminosity of $\bar{\nu}_{e}$ ($L_{\bar{\nu}_{e}}\simeq 10^{53}$ erg s^-1) is a factor of 2 or 3 larger than the one of $\nu_{e}$ throughout the whole 10 ms, leading to continuous protonization of the remnant. The energy luminosities of the heavy-lepton neutrino flavors, denoted by $\nu_{x}$ (with $\nu_{x}$ being representative of one species of heavy-lepton neutrinos), are $\sim 5\times 10^{52}$ erg s^-1 per species. The averaged energies estimated by the leakage approximation show a clear hierarchy of $\langle E_{\nu_{e}}\rangle<\langle E_{\bar{\nu}_{e}}\rangle<\langle E_{\nu_{x}}\rangle$, reflecting the ordering of the temperature at decoupling; neutrinos that decouple in the innermost region of the remnant have higher average energy (see below and Fig. 2). When comparing the energy luminosity evolution of the models with DD2 and SFHo EoS, one sees that the latter produces higher luminosities in all flavors. This is related to the fact that the SFHo EoS is softer than the DD2 EoS, which results in a NS with smaller radius. Consequently, a more violent collision during the merging leads to higher temperatures, and correspondingly higher neutrino emission rates, when the SFHo EoS was adopted. This gives rise to a faster protonization of the remnant.

Comparing Fig. 1 to Fig. 2 of Ref. [34], where the latter displays the neutrino emission properties for a BH remnant, one can see that the neutrino emission properties of the electron-flavor neutrinos are comparable in the two scenarios. However, the non-electron-flavor neutrinos are more abundant in the models investigated in this work and have average energies higher than the electron-flavor neutrinos. In addition, the neutrino energy luminosities in the case with the BH accretion disk quickly decrease after $\simeq 20$ ms (see Fig. 2 of Ref. [34]). Although we only focus on the first 10 ms after the coalescence, the neutrino energy luminosity reaches a plateau in the models where a hypermassive NS forms.

The first three rows in Fig. 2 and Fig. 3 show the baryon density, temperature, and electron fraction profiles in the half $x-z$ plane for $x>0$ at 2.5, 5, 7.5, and 10 ms post merger for the models with DD2 and SFHO EoS, respectively. Also shown are the locations of the $\nu_{e}$, $\bar{\nu}_{e}$, and $\nu_{x}$ emission surfaces. The emission surface for a given neutrino species $\nu_{\alpha}$ ($\nu_{e}$, $\bar{\nu}_{e}$, or $\nu_{x}$) is defined by a surface where the energy-averaged optical depth is $\tau_{\nu_{\alpha}}=2/3$ (see Sec. II.2 for details). One can see from the density profiles that the remnant consists of a rotating deformed hypermassive NS surrounded by an accretion disk. The central object retains its initial low $Y_{e}\lesssim 0.1$ (see the third rows) and it is surrounded by a dense and neutron-rich disk, which is opaque to neutrinos for an extended radius out to $\sim 40-60$ km. Both $\nu_{e}$ and $\bar{\nu}_{e}$ decouple at locations where the matter density is approximately between $10^{11}-10^{12}$ g cm^-3 and the temperature is $\sim 5$ MeV. The $\bar{\nu}_{e}$ emission surfaces generally sit inside the ones of $\nu_{e}$ during this period, independently of the adopted EoS.

The size of the neutrino emission surfaces slightly expands as the remnant evolves, due to the settling of the post-merger object and the redistribution of matter with high angular momentum toward the equatorial plane, where the disk formation process proceeds. Moreover, as the remnant keeps protonizing, $Y_{e}$ inside the neutrino surfaces gradually increases with time. The thick disk of the remnant in the model with the softer SFHo EoS protonizes faster as discussed above, and thus has higher $Y_{e}$ inside the disk when compared to the profiles with DD2 EoS. Note that in the polar region close to the $z$-axis, a high $Y_{e}\gtrsim 0.4$ funnel forms at later times, as both the differences between the $\nu_{e}$ and $\bar{\nu}_{e}$ luminosities and average energies become smaller.

In the bottom panels of both Fig. 2 and Fig. 3, we show the ratio of the difference of the number densities of $\bar{\nu}_{e}$ and $\nu_{e}$ to the sum of the $\bar{\nu}_{e}$ and $\nu_{e}$ densities, i.e., $(n_{\bar{\nu}_{e}}-n_{\nu_{e}})/(n_{\bar{\nu}_{e}}+n_{\bar{\nu}_{e}})$. Once again, as the remnant is protonizing and emitting more $\bar{\nu}_{e}$ than $\nu_{e}$, nearly any location above the $\nu_{e}$ surface in both models has this ratio larger than zero during the entire first 10 ms. The only exception is represented by the small patches in the polar region at 7.5 and 10 ms for the model with DD2 EoS. These patches are a consequence of the neutronization that takes place locally around the poles of the high-density core of the merger remnant in the DD2 case. Because the stiff EoS prevents the merger core from further contraction, the polar regions cool quickly, and the density just inside the neutrinospheres increases by gravitational settling, forcing the neutrinospheres to move inward to smaller radii. This explains the more pronounced polar trough of the neutrinospheres in the DD2 model compared to the SFHo merger. Striving for a new beta-equilibrium state, now at lower temperature, the plasma begins to neutronize again, radiating more electron neutrinos than antineutrinos in both polar directions. This leads to the excess of $\nu_{e}$ relative to $\bar{\nu}_{e}$ outside the neutrinospheres, visible as the two blue patches in the two bottom right panels of Fig. 2. Correspondingly, $\nu_{e}$ captures dominate $\bar{\nu}_{e}$ captures in this region and the polar outflow becomes more and more proton-rich (red regions of $Y_{e}>0.5$ around the $z$-axis in the right panels of the third row of Fig. 2). The same trends are visible in the SFHo simulation (Fig. 3), though less extreme and less rapidly evolving than in the DD2 run.

The inner regions of the merger remnant are dense enough to trap neutrinos. This allows us to define a neutrino emission surface for each species $\nu_{\alpha}$ above which $\nu_{\alpha}$ can approximately free-stream. As we will use the properties of $\nu_{e}$ and $\bar{\nu}_{e}$ on their respective surfaces to construct their angular distributions outside the $\nu_{e}$ surface in Sec. III, we discuss below the time evolution and the dependence on the adopted EoS of the neutrino densities on their emission surfaces.

For any point $\bm{x}$ inside the simulation domain, the optical depth along a specific path $\gamma$ to another point $\bm{y}$ that a neutrino with an energy $E$ traverses is given by

where $\bm{x}^{\prime}$ is a point, $ds$ is the differential segment along $\gamma$, and $\lambda_{\nu_{\alpha}}(E,\bm{x}^{\prime}(s))$ is the corresponding mean-free-path at $\bm{x}^{\prime}$. For each species $\alpha$, we determine the position of the neutrino decoupling surface in the same way as in Ref. [23], i.e. for every point $\bm{x}$, the minimum of the spectral-averaged $\langle\tau_{\nu_{\alpha}}(\bm{x},i)\rangle$ is computed along the six different directions ($i\in(\pm x,\pm y,\pm z)$) through the edge of the simulation domain. The neutrino decoupling surface is then defined by the location corresponding to $\langle\tau_{\nu_{\alpha}}(\bm{x},i)\rangle=2/3$ in the six directions. The emission surfaces computed in this way for $\nu_{e}$, $\bar{\nu}_{e}$, and $\nu_{x}$ are the ones shown in Figs. 2 and 3.

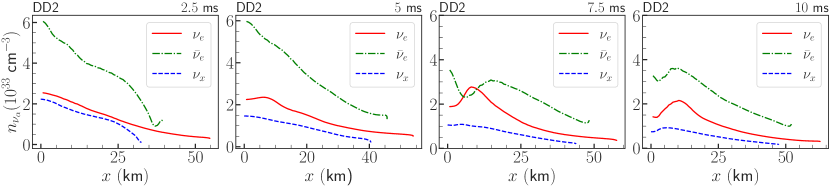
Figure 4 shows the number densities of $\nu_{e}$, $\bar{\nu}_{e}$, and $\nu_{x}$ at their respective emission surfaces as functions of $x$ for different snapshots. Note that the $\nu_{e}$ and $\bar{\nu}_{e}$ number densities are computed by using Fermi-Dirac distribution functions with temperature and chemical potential extracted at each location on the neutrino surfaces, consistently with Ref. [23]. For $\nu_{x}$, we rescale the number density according to the procedure described in Appendix A to account for the trapping effect between the energy-surfaces and the emission surfaces, which is known to considerably reduce the $\nu_{x}$ luminosity when compared to the analogous values directly estimated through the local emission (see, e.g., [50]). The top panels show the neutrino density corresponding to the DD2 EoS, while the bottom panels display the same quantities for the SFHo EoS. As discussed in Sec. II.1, the softer SFHo EoS leads to a generally higher temperature in the merger remnant; as a consequence, the $\bar{\nu}_{e}$ luminosity (Fig. 1) and number density on the emission surface are higher than the one obtained in the model with DD2 EoS. Both $n_{\nu_{e}}$ and $n_{\bar{\nu}_{e}}$ are larger in a region close to the pole where the temperature is higher (see Figs. 2 and 3). Of relevance to the occurrence of fast flavor conversions is the fact that the $\bar{\nu}_{e}$ emission is a factor of 2–3 larger than the one of $\nu_{e}$ across the whole emission surface; it remains quite stable throughout the simulated evolution until 10 ms after the plunge. The only exception is the snapshot at 7.5 ms for the model with DD2 EoS, which shows a dip in the $\bar{\nu}_{e}$ number density around $x\simeq 10$ km. This is because the enhanced deleptonization above the poles of the high-density core (described in Sec. II.1) leads to a short, transient excess of $\nu_{e}$ over $\bar{\nu}_{e}$ near the neutrinospheres in the northern hemisphere (see Fig. 2). The effect is somewhat pathological and unusual, also because it is considerably less strongly developed in the southern hemisphere. Notably, comparing Fig. 4 with the bottom panel of Fig. 1 of Ref. [34], one can see that the neutrino-antineutrino asymmetry is more pronounced in the present models than in the BH remnant case.

We adopt the density matrix formalism to describe the statistical properties of the neutrino dense gas incorporating flavor mixing [51]. For a given density matrix $\varrho(\bm{p},\bm{x},t)$, its diagonal elements in the flavor basis, $\varrho_{\alpha\alpha}$, record the phase-space distributions $f_{\nu_{\alpha}}$ of a given neutrino flavor $\nu_{\alpha}$ at the space-time location $(t,\bm{x})$ and with momentum $\bm{p}$. The off-diagonal terms $\varrho_{\alpha\beta}$ carry the information about the neutrino mixing (neutrino flavor correlations). In the absence of any mixing, i.e., all neutrinos are in their flavor eigenstates, the off-diagonal elements vanish.

Neglecting general-relativistic effects and collisions of neutrinos with matter, the space-time evolution of the density matrix $\varrho(\bm{p},\bm{x},t)$ is governed by a Liouville equation

where $\Omega$ is the Hamiltonian that accounts for the flavor oscillations of neutrinos. On the left hand side of Eq. (2), the first term takes care of the explicit time dependence of $\varrho$ and the second term takes into account the neutrino propagation with velocity $\bm{v_{p}}\simeq{\bm{p}}/|\bm{p}|$ for ultrarelativistic neutrinos. The Hamiltonian matrix $\Omega$ on the right hand side can be decomposed as

where the first term $\Omega_{\text{vac}}$ takes into account flavor conversions in vacuum. In a simplified two-flavor scenario, $\Omega_{\text{vac}}=\text{diag}(\omega_{\rm v}/2,-\omega_{\rm v}/2)$ in the mass basis with $\omega_{\rm v}=(m_{2}^{2}-m_{1}^{2})/2E$ being the vacuum oscillation frequency of the neutrinos with energy $E$.

The second term on the right hand side of Eq. (3) embodies the effects of neutrino coherent forward scattering with electrons and nucleons. In the flavor basis, this term can be expressed as

where $n_{e}$ is the net electron number density. The last term in Eq. (3) is the effective Hamiltonian due to the $\nu$–$\nu$ interaction. For a neutrino traveling with momentum $\bm{p}$, $\Omega_{\nu\nu}$ is given by

where $\bar{\varrho}$ is the corresponding density matrix for antineutrinos. The presence of $(1-\bm{v_{p}\cdot v_{q}})$ in Eq. (5) leads to multi-angle effects, i.e., neutrinos propagating in different directions experience different $\Omega_{\nu\nu}$. The equation of motion for antineutrinos can be obtained in a similar fashion, by replacing $\omega_{\rm v}$ by $-\omega_{\rm v}$ in $\Omega_{\rm vac}$.

We focus on a simplified system that deals with two neutrino flavors. Under this assumption, both the density matrix $\varrho$ and the Hamiltonian $\Omega$ are $2\times 2$ Hermitian matrices and hence can be expanded in terms of the identity matrix and three Pauli matrices. Thus, we write $\varrho=[(f_{\nu_{e}}+f_{\nu_{x}})+(f_{\nu_{e}}-f_{\nu_{x}})\xi]/2$ for neutrinos and $\bar{\varrho}=-[(f_{\bar{\nu}_{e}}+f_{\bar{\nu}_{x}})+(f_{\bar{\nu}_{e}}-f_{\bar{\nu}_{x}})\xi^{*}]/2$ for antineutrinos. The entity $\xi$ is a matrix defined as

where $-1\leq s\leq 1$ and $|s|^{2}+|S|^{2}$ =1. In the absence of any flavor correlation $S=0$. Furthermore, as in previous work that studied the fast neutrino flavor conversion, we omit the vacuum oscillation term in the following discussion as $\omega_{\rm v}$ marginally affects the linear regime [52, 53, 54]. With these assumptions and introducing the metric tensor $\eta^{\mu\nu}=\text{diag}(1,~{}-1,~{}-1,~{}-1)$ and for any contra-variant vector $A^{\mu}$, $A_{\mu}=\eta_{\mu\nu}A^{\nu}$, we can recast the Hamiltonian defined in Eq. (3) into the following form

where $\bm{v}=(\sin\theta\cos\phi,~{}\sin\theta\sin\phi,~{}\cos\theta)$ with velocity $v^{\mu}=(1,\bm{v})$, $d\bm{\Gamma}=\sin\theta d\theta d\phi$ and $\lambda^{\mu}=\sqrt{2}G_{\text{F}}n_{e}(1,\bm{v}_{\text{m}})$ with $\bm{v}_{\text{m}}$ being the vector of the fluid velocity of the background matter. Since the rate of pairwise conversion is much faster than any other inverse time scale involved in the problem, we treat the background matter as stationary and homogeneous: $\lambda_{\mu}v^{\mu}=\lambda_{0}$.

The quantity $g(\bm{v})$ is related to the angular distribution of the neutrino ELN angular distribution

where $\bm{\Phi}_{\nu_{\alpha}}=dn_{\nu_{\alpha}}/d\bm{\Gamma}$. To study the growth of $S$ in the linear regime, we treat the flavor correlation $S$ as a perturbation and neglect all terms of $O(S^{2})$ or higher. Taking $S(t,\bm{x})=Q(\omega,\bm{k})e^{-i(\omega t-\bm{k}\cdot\bm{x})}$, the EoM becomes

In the above Eq. (9) we have introduced the four vector $\bar{\lambda}^{\mu}=(\omega-\lambda_{0}-\epsilon_{0},\bm{k}-\bm{\epsilon})$, $\epsilon_{0}\equiv\int d\bm{\Gamma}g(\bm{v})$ and $\bm{\epsilon}\equiv\int d\bm{\Gamma}\bm{v}g(\bm{v})$. Inspecting Eq. (9), one can make the ansatz $Q(\omega,\bm{k})=v_{\mu}a^{\mu}/v_{\mu}\bar{\lambda}^{\mu}$, with $a^{\mu}$ being the coefficients of eigenfunction solutions. Thus, Eq. (9) becomes

where we have used the definition

The EoM defined in Eq. (10) holds for any $v^{\mu}$. Thus, we have the condition $\Pi^{\mu\nu}a_{\nu}=0$. Eigenfunctions of the latter have non-trivial solution only if $\Pi^{\mu\nu}$ satisfies the condition

Equation (12) is the DR in flavor space. The solutions of the DR have been classified into several types [39, 41]. If $\omega$ is real for real values of $\bm{k}$, a perturbation in $S$ only propagates without growing or damping, i.e., it stays in the linear regime, meaning that no significant flavor conversion occurs. On the other hand, an imaginary solution of $\omega$ with $\text{Im}(\omega)>0$ corresponds to exponentially growing modes. In other words, the flavor correlation $|S|$ grows exponentially with time, leading to significant flavor conversion. Rigorous studies have been carried out to understand the characteristics of the above DR with respect to the ELN angular distribution of neutrinos [38, 39, 41]. It was shown that in the presence of a crossing in the ELN distribution, the DR will yield complex $\omega$ solutions for real $\bm{k}$, leading to temporal instabilities. In the following, we examine the ELN distributions above the merger remnants and the corresponding flavor instabilities.

To construct the ELN distribution above the merger remnant, we follow a method similar to the one adopted in Ref. [34]. First, we assume that both $\nu_{e}$ and $\bar{\nu}_{e}$ freely propagate outside their respective emission surfaces defined in Sec. II.2. Second, we approximate their forward-peaked angular distributions at each point on the emission surfaces as

where $\theta_{n}$ is the angle with respect to the normal direction of the location on the emission surface. Ignoring the minor effect of GR bending, we can then ray-trace the neutrino intensities from the emission surfaces to obtain their angular distributions at any location above the surfaces.

Figures 5 and 6 show the obtained ELN distributions as a function of the local angular variables $\theta$ (angle with respect to the $z$-axis) and $\phi$ (angle with respect to the $x$-axis on the $x$-$y$ plane) at selected locations above the $\nu_{e}$ surface at 2.5, 5, 7.5 and 10 ms after the coalescence, for the $1.35+1.35$ $M_{\odot}$ merger models with DD2 and SFHo EoS, respectively. Here we only show the sign of the ELN distribution to highlight the crossing. The blue shade represents the region where the net ELN is positive while the red region corresponds to negative ELN. The top panel shows the ELN distribution at a representative point on the $z$ axis and the middle and bottom panels show the ELN distributions at near-center and outer regions above the $\nu_{e}$ surface. Note here that Figs. 5 and 6 only show the ELN distribution for $\phi/\pi\geq 0$ as the distributions for axi-symmetric emission surfaces possess reflection symmetry, $\Phi_{\nu_{e},\bar{\nu}_{e}}(\cos\theta,\phi)=\Phi_{\nu_{e},\bar{\nu}_{e}}(\cos\theta,-\phi)$.

The angular coverage of the $\nu_{e}$ and $\bar{\nu}_{e}$ fluxes at a point ($x,z$) is determined by the geometry of the $\nu_{e}$ and $\bar{\nu}_{e}$ emission surfaces. On the other hand, the ELN angular distribution is determined by the combination of the emission surface geometries and their respective emission properties, including the relative strength of $\nu_{e}$ and $\bar{\nu}_{e}$ and the angular dependence of the emission. For example, the ELN angular distribution at any point on the $z$ axis above the emission surface is independent of $\phi$, reflecting the (assumed) rotational symmetry of the merger remnants about the $z$ axis. As we move away from the $z$ axis, the ELN distribution becomes dependent on $\phi$ (second and third panels). For both EoS, the angular coverage in $\theta$ slightly increases with time for a given $(x,z)$, caused by the expansion of the emission surfaces. This is different from what was found in Ref. [34] where the central remnant is a BH for which the size of the $\nu_{e}/\bar{\nu}_{e}$ emitting torus surfaces shrinks with time. As $\bar{\nu}_{e}$ are more abundant than $\nu_{e}$ in most parts of the emission region during the first 10 ms (see Fig. 4), the overall shapes of the ELN crossings are qualitatively similar. The only exception is represented by the snapshot at 7.5 ms for the case with DD2 EoS, for which the inner region above the merger remnant shows a double ELN crossing structure, see the left and middle panels in the third row. This is related to the dip of the $\bar{\nu}_{e}$ density on the $\bar{\nu}_{e}$ surface at $\sim 10$ km discussed in Sec. II.2. Also, the ELN angular distribution in Fig. 6 is more extended toward $\theta=0$ compared to Fig. 5, resulting from slightly larger radii of the neutrino emission surfaces in the SFHo model. For the simulations adopting $1.25+1.45$ $M_{\odot}$ binaries, we have similarly checked the ELN distributions during the same time snapshots for both EoS. Unsurprisingly, ELN crossings appear at all times as those shown here.

After obtaining the ELN distributions above the neutrino emitting surface, we numerically solve the DR [Eq. (12)] starting from the outer neutrino surface to inspect whether solutions containing non-zero $\rm{Im}(\omega)$ for a given $\bm{k}$ can be found²²2Note that the positive and negative $\rm{Im}(\omega)$ solutions always appear together.. As the ELN distributions above the merger remnants with axial-symmetry have a reflection symmetry with respect to $\phi\rightarrow-\phi$, one can obtain two different solutions that correspond to the reflection symmetry-preserving and symmetry-breaking cases [33].

We show the obtained $|\text{Im}(\omega)|$ as a function of $k_{z}$, taking $k_{x}=k_{y}=0$, at different times for a location at $(x,z)=(10,25)$ km above the emitting surfaces in Fig. 7 and the solutions for different locations corresponding to the ELN crossing shown in Fig. 8 at 5 ms. The top (bottom) panels are for cases with DD2 (SFHo) EoS while the left (right) panels show the symmetry-preserving (symmetry-breaking) solutions.

Flavor instabilities with growth rate of $\mathcal{O}(1)$ cm^-1 exist at all locations at all times for a large range of $k_{z}$. The symmetry preserving solution of the DR has two branches while the symmetry breaking solution has only one branch, similar to what was found in Ref. [33]. Comparing the results for the models with DD2 and SHFo EoS, the growth rate of the flavor instability is generally larger in the latter, as the neutrino emission is stronger with the SHFo EoS. The shape of the solutions is rather stable over time for the case with SFHo EoS. On the other hand, the model with DD2 EoS shows a somewhat stronger time-dependence. In particular, the range of $k_{z}$ that leads to non-zero $|{\rm Im}(\omega)|$ as well as the value of $|{\rm Im}(\omega)|$ both decrease at the snapshot of 7.5 ms, when the double crossing shape of the ELN appears (see Fig. 5).

By comparing the solutions at different locations for the $t=5$ ms snapshot, Fig. 8 shows that $|{\rm Im}(\omega)|$ is larger closer to the $z$-axis for both the symmetry-preserving and symmetry-breaking solutions. This, again, is caused by the fact that $\Phi_{\nu_{e}}$ and $\Phi_{\bar{\nu}_{e}}$ are largest in this region (see Fig. 4).

As shown in Figs. 7 and 8, the symmetry-breaking solutions at all times and all locations contain non-zero $|\text{Im}(\omega)|$ for the mode $\bm{k}=0$. We further show in Fig. 9 the contour plot of $|\text{Im}(\omega)|$ above the neutrino surface for this mode. The plots in this figure clearly show that growth rates of the instability of $\sim{\cal O}(1)$ cm^-1 exist everywhere above the remnant at all times. The region closer to the $z$-axis just above the emission surface has the maximal growth rates. Moving away from the surface, the neutrino flux is suppressed by the geometric effects and the magnitude of the instability decreases in all cases. For the sake of comparison with the existing literature, we find $|\rm{Im}(\omega)/\mu|\sim\mathcal{O}(10^{-2})$ for all cases examined here; this value of the growth rate is similar albeit a bit smaller than the ones reported in Refs. [34, 55]. The growth rates $|\rm{Im}(\omega)/\mu|$ are generally larger toward the middle region above the $\nu_{e}$ surface, in agreement with the findings of Ref. [33, 34]. This is due to the relative strength of the positive vs. negative ELN strength, in the proximity of crossings between the $\nu_{e}$ and $\bar{\nu}_{e}$ angular distributions [56]. For a system that is more dominated by $\nu_{e}$ or $\bar{\nu}_{e}$, i.e., where the positive ELN distribution dominates the negative parts or the other way around, one expects that the value of $|\rm{Im}(\omega)/\mu|$ is smaller than in a more balanced system with similar positive and negative parts of the ELN distribution (see e.g., Ref. [41]). Looking at the ELN crossing pattern shown in Figs. 5 and 6, the locations above the middle part of the remnant have large angular area of $g(\bm{v})>0$ due to the larger separation of the $\nu_{e}$ and $\bar{\nu}_{e}$ surfaces (see Fig. 2 and 3). This, in turn, enhances the corresponding values of $|\rm{Im}(\omega)/\mu|$ relative to the ones in the inner region closer to the $z$-axis.

Likewise, when comparing the values of $|\rm{Im}(\omega)/\mu|$ to the ones shown in Ref. [34], the more dominant $\bar{\nu}_{e}$ emission relative to $\nu_{e}$ here, together with the smaller separation of their emission surfaces, results in smaller values of $|\rm{Im}(\omega)/\mu|$.

On the other hand, while Ref. [34] showed that the region where the flavor instability exists shrinks on a time scale of $\sim\mathcal{O}(10)$ ms as the BH-disk remnant evolves, the instability region found here remains stable within the examined 10 ms of post-merger evolution. This can have important consequences for the growth of the instabilities and seems to favor the eventual development of flavor conversions in the non-linear regime. The effect of advection hindering the growth of the flavor instabilities for systems with non-sustained and fluctuating unstable conditions shown by Ref. [56] may therefore not happen above the merger remnant, as shown in Ref. [55]. In the case of the models with unequal mass binaries, due to the similar ELN crossing features, we find unstable regions above the merger remnant disk and growth rates very similar to the symmetric models (results not shown here).

We here focus on the diagnostics of flavor instabilities, but do not distinguish whether they belong to the convective or absolute type (see Refs. [57, 41]). This would require solving the full dispersion relation for the complete $(\omega,\mathbf{k})$ space.

The dynamical ejecta masses extracted at 10 ms post-merger for the $1.35+1.35$ $M_{\odot}$ merger simulations are $\sim 2.0\times 10^{-3}$ $M_{\odot}$ and $3.3\times 10^{-3}$ $M_{\odot}$ with the DD2 and SFHo EoS, represented by 783 and 1263 tracer particles, respectively. For the $1.25+1.45$ $M_{\odot}$ merger cases, the dynamical ejecta masses are $\sim 3.2\times 10^{-3}$ $M_{\odot}$ (DD2) and $8.7\times 10^{-3}$ $M_{\odot}$ (SFHo), represented by 1290 and 4398 tracer particles. In computing the evolution of $Y_{e}$ for a given tracer particle, we first post-process the neutrino emission data from Ref. [23] to calculate the absorption rates of $\nu_{e}$ and $\bar{\nu}_{e}$ on neutrons and protons, $\lambda^{0}_{\nu_{e}}$ and $\lambda^{0}_{\bar{\nu}_{e}}$ (the superscript $0$ here denotes the case where any neutrino flavor conversion is omitted), as detailed in Appendices A and B. These rates are then combined with the nuclear reaction network used in Refs. [58, 59] to compute the nucleosynthesis yields in the merger ejecta. For each tracer particle, we begin the network calculation either at a location where $T=50$ GK or just outside the disk with height of 25 km and radius of 55 km to make sure that it is outside the $\nu_{e}$ emission surface. The initial nuclear abundances are calculated by using the nuclear statistical equilibrium (NSE) condition. For $T>10$ GK, we only compute the weak reaction rates to track the $Y_{e}$ evolution while assuming NSE at each moment to obtain the abundances. When $T\leq 10$ GK, we instead follow the full evolution of all nuclear species and include the feedback due to the nuclear energy release on the ejecta temperature following Ref. [60].

In Fig. 10, we show the distributions of the ejecta mass for the $1.35+1.35$ $M_{\odot}$ models as a function of the time when the ejecta reach the radius $r=100$ km at $t(r=100~{}\rm{km})$ in panel (a), the angle $\theta_{\rm ej}$ (relative to the $z$-axis) when they leave the simulation domain in panel (b), and the radial velocity $v_{r}$ at $r=100$ km in panel (c). We also show, in panel (d), the distributions of $Y_{e}$ for the ejecta at $r=100$ km, in the absence of flavor mixing. Additionally, panels (e) and (g) [(f) and (h)] show the distributions of each tracer particle in the plane spanned by $t(r=100~{}\rm{km})$ [$v_{r}(r=100)~{}\rm{km}$] and $\theta_{\rm ej}$ with the corresponding $Y_{e}$ at 100 km labeled in color for the DD2 and SHFo EoS, respectively. These plots show that, independently of the adopted EoS, most of the material is ejected within the first $\sim 2$ ms with lower $Y_{e}\lesssim 0.3$, within $\sim 45^{\circ}$ away from the mid-plane. The ejecta launched in the second episode [$t(r=100~{}\rm{km})\simeq 3-4$ ms] are similarly distributed closer to the equatorial plane and have $Y_{e}\simeq 0.4$. After that, neutrino irradiation continues to power the mass ejection along the polar direction with $Y_{e}$ reaching $\sim 0.5$. In terms of the ejecta kinematics, because of the weak interactions, it is clear that $Y_{e}$ can be raised up to $0.3-0.4$ mostly for the material expanding more slowly with $v_{r}/c\sim 0.1-0.2$ at $r=100$ km, even around the equatorial plane, and reach $\sim 0.5$ closer to the polar direction.

The main differences between the DD2 and the SFHo EoS results are the following. First, for the simulation with SHFo EoS, the amount of ejecta is larger, particularly during the first ejection episode [see panel (a)], than that with the DD2 EoS; this is a direct consequence of the more violent collision of the two NSs in the case with softer EoS (SHFo), as discussed in Ref. [46]. Second, the amount of high-velocity ejecta with $v_{r}/c\gtrsim 0.5$ for the SFHo case is also higher for the same reason [see panels (c) and (f)]. Third, the $Y_{e}$ distribution [panel (d)] for both models shows that $Y_{e}(r=100~{}\mathrm{km})$ is slightly larger for the DD2 EoS model than for the SFHo EoS one. This reflects the higher $\bar{\nu}_{e}$ luminosity obtained in the SHFo EoS model (see Fig. 1) leading to larger $\bar{\nu}_{e}$ absorption rates on protons; hence, $Y_{e}$ is raised less for the bulk of the ejecta. The high $Y_{e}$ tail extends to values $\gtrsim 0.5$ in the DD2 EoS model, while it remains $\lesssim 0.5$ in the SFHo EoS model [see panels (c) and (e)]. Interestingly, it is noticeable that the high velocity components in the SFHo model have more high-$Y_{e}$ ejecta than in the DD2 model [see panel (f)], different from the main bulk of the ejecta. This is because these ejecta are mainly driven during the early post-merger phase. During this early phase, positron capture is responsible for raising $Y_{e}$ in the ejecta, rather than neutrino absorption. Thus, in the model with SFHo EoS, the higher post-merger temperature of the remnant due to the more violent merger leads to relatively higher $Y_{e}$ material in the early fast ejecta.

We show in Fig. 11 the same quantities as in Fig. 10, but for the models with $1.25+1.45$ $M_{\odot}$ mass binaries. Qualitatively, the features are similar to the ones described above, but they are quantitatively different. For instance, the division between different episodes of mass ejection is less clear, in particular for the SHFo EoS model [see panel (a)]. On average, most of the ejecta have higher velocities, peaked at $\sim 0.25c$ [see panel (c), (f) and (h)]. Moreover, a larger fraction of the ejecta has lower $Y_{e}\lesssim 0.2$, despite the fact that similarly wide distributions of $0.01\lesssim Y_{e}\lesssim 0.5$ are obtained.

Figure 12 shows the resulting abundance distributions for the ejecta of the symmetric and asymmetric merger models with the DD2 and SFHo EoS, in comparison to the re-scaled solar $r$ abundance pattern [61]. Due to the wide-spread $Y_{e}$ distribution ranging from $0.02-0.5$ in all models, all three $r$-process peaks at $A\simeq 90$, $130$, and $195$ are in relatively good agreement with the solar abundance pattern. The difference of the high $Y_{e}$ component discussed above only results in abundance variations at $A\simeq 50-80$. In particular, we compute the amount of strontium present at the time of a day, which is of relevance to the potential identification in the spectral analysis of the GW170817 kilonova [11]. The total amount of strontium is $\simeq 8.9\times 10^{-5}$ $M_{\odot}$ and $\simeq 3.9\times 10^{-5}$ $M_{\odot}$ for the DD2 and SFHo EoS models with equal mass binaries. For the asymmetric merger models, the corresponding amount of strontium is $\simeq 2.66\times 10^{-4}$ $M_{\odot}$ and $3.25\times 10^{-4}$ $M_{\odot}$, respectively. These results are consistent with the findings of Ref. [11].

References [62, 60, 22, 63] found that some merger ejecta have low $Y_{e}$ and fast expansion time scale to allow for a neutron-rich freeze-out during the $r$-process nucleosynthesis. A potentially thin layer of “neutron-skin” at the outskirts of the ejecta may possibly power an early-time UV emission at $\sim$ hours post-merger due to the radioactive heating of neutron decay [62, 7]. We find that the amount of free neutrons at the end of the $r$-process, for equal-mass binaries, is $\simeq 6.2\times 10^{-6}$ $M_{\odot}$ and $6.6\times 10^{-6}$ $M_{\odot}$ with the DD2 and SFHo EoS, respectively. These numbers are roughly a factor of 10 smaller than what was found in Ref. [60], which analyzed simulation trajectories without including the weak interactions. The reduction of the amount of free neutrons at the end of the $r$-process is related to the high post-merger temperature effect raising $Y_{e}$ even for the early fast ejecta. For the unequal mass binaries, the corresponding amount of free neutrons is $\simeq 9.2\times 10^{-6}$ $M_{\odot}$ and $3.1\times 10^{-6}$ $M_{\odot}$ for the DD2 EoS model and for the SFHo model. A future (non)identification of this component may shed light on the role of weak interactions in the post-merger environments.

Following previous work [34, 64], we assume that fast flavor conversions lead to conditions close to flavor equipartition for neutrinos and antineutrinos. The assumption of flavor equilibration is an extreme ansatz, especially in the light of the findings of Ref. [55], which, however, relied on a simplified model of a relic merger disk. Moreover, this simple assumption does not preserve the total electron neutrino lepton number, which is a strictly conserved quantity in the case of pairwise flavor conversions. Nevertheless, our extreme assumption for the flavor ratio is useful to explore the largest possible impact that flavor conversions might have on the nucleosynthesis of the heavy elements. The corresponding neutrino absorption rates can be approximated by

where $\lambda_{\nu_{x}}$ and $\lambda_{\bar{\nu}_{x}}$ are the neutrino absorption rates on free nucleons assuming that all $\nu_{x}$ and $\bar{\nu}_{x}$ are converted to $\nu_{e}$ and $\bar{\nu}_{e}$, as detailed in Appendices A and B. We then perform the same nucleosynthesis calculations as in Sec. IV.1 for all tracer particles in all the merger models by replacing $\lambda^{0}_{\nu_{e}}$ and $\lambda^{0}_{\bar{\nu}_{e}}$ by $\lambda^{\rm osc}_{\nu_{e}}$ and $\lambda^{\rm osc}_{\bar{\nu}_{e}}$. Below, we only focus on the findings for the models with equal mass and different EoS because the results obtained in the unequal mass binaries are qualitatively the same, independent of the EoS.

We show in Fig. 13 the comparison of the ratio of $\lambda_{\nu_{e}}/\lambda_{\bar{\nu}_{e}}$ evaluated at $r=100$ km for all tracer particles for the cases with and without flavor equipartition. The corresponding values of $\lambda_{\bar{\nu}_{e}}$ are also shown. These figures highlight that the neutrino absorption rates are orders of magnitudes larger in the polar region than close to the equator. For the case without neutrino flavor equipartition, nearly all tracer particles have $\lambda^{0}_{\nu_{e}}/\lambda^{0}_{\bar{\nu}_{e}}\lesssim 1$, reflecting the stronger $\bar{\nu}_{e}$ flux emitted from its surface. With flavor equipartition, the nearly equal contribution of the converted $\nu_{x}$ and $\bar{\nu}_{x}$ significantly changes the ratio $\lambda^{\rm osc}_{\nu_{e}}/\lambda^{\rm osc}_{\bar{\nu}_{e}}$ for both EoS. For the case with DD2 EoS, most of the trajectories with $\theta_{\rm ej}\lesssim 60^{\circ}$ or $\theta_{\rm ej}\gtrsim 120^{\circ}$ have $\lambda^{\rm osc}_{\nu_{e}}/\lambda^{\rm osc}_{\bar{\nu}_{e}}\gtrsim 1$. On the other hand, the values of $\lambda^{\rm osc}_{\nu_{e}}/\lambda^{\rm osc}_{\bar{\nu}_{e}}$ scatter around 1 for the model with SFHo EoS.

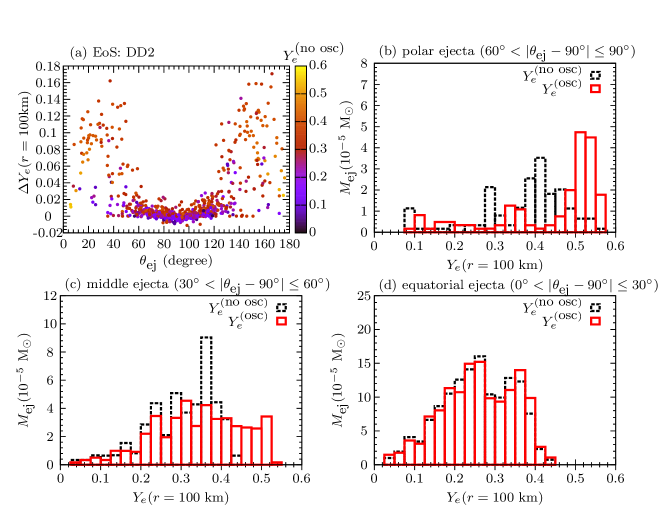
The large change in $\lambda_{\nu_{e}}/\lambda_{\bar{\nu}_{e}}$ strongly affects the $Y_{e}$ distribution of the ejecta. Figures 14(a) and 15(a) show $\Delta Y_{e}\equiv Y_{e}^{({\rm osc})}-Y_{e}^{({\rm no~{}osc})}$ calculated at $r=100$ km for each tracer particles as a function of the corresponding $\theta_{\rm ej}$, where $Y_{e}^{({\rm osc})}$ and $Y_{e}^{({\rm no~{}osc})}$ are the $Y_{e}$ values with and without flavor equipartition. These results show that the flavor equipartition can significantly increase $Y_{e}$ of the ejecta up to $\sim 0.15$ for $\theta_{\rm ej}<60^{\circ}$ or $\theta_{\rm ej}>120^{\circ}$ closer to the polar directions. In particular, the increase of $Y_{e}$ due to flavor equipartition for these ejecta is more pronounced with $Y_{e}^{\rm(no~{}osc)}\simeq 0.3-0.4$. For the ejecta with $Y_{e}^{\rm(no~{}osc)}\lesssim 0.2$ or $Y_{e}^{\rm(no~{}osc)}\simeq 0.5$, $Y_{e}$ is less affected. This is because the ejecta with $Y_{e}^{\rm(no~{}osc)}\lesssim 0.2$ expand too fast for neutrino absorption to raise $Y_{e}$ either with or without flavor conversion. On the other hand, for the ejecta with $Y_{e}^{\rm(no~{}osc)}\simeq 0.5$, $\lambda_{\nu_{e}}/\lambda_{\bar{\nu}_{e}}\simeq 1$ even without flavor conversions. As for the tracer particles with $60^{\circ}\leq\theta_{\rm ej}\leq 120^{\circ}$ closer to the disk mid-plane, $Y_{e}$ is barely influenced by flavor equipartition because of the low neutrino absorption rates (see Fig. 13).

Figures 14(b)-(d) and 15(b)-(d) further show the comparison of the $Y_{e}$ distribution for the cases with and without flavor conversion, for the ejecta classified into three groups according to $\theta_{\rm ej}$: the polar ejecta with $60^{\circ}<|\theta_{\rm ej}-90^{\circ}|\leq 90^{\circ}$, the middle ejecta with $30^{\circ}<|\theta_{\rm ej}-90^{\circ}|\leq 60^{\circ}$, and the equatorial ejecta with $0^{\circ}\leq|\theta_{\rm ej}-90^{\circ}|\leq 30^{\circ}$. Flavor equipartition influences the $Y_{e}$ distribution of the polar ejecta by shifting the peak from $\sim 0.4$ to $\sim 0.55$ (0.5) for the DD2 (SFHo) model. The larger (smaller) shift of the $Y_{e}$ peak in the DD2 (SFHo) model is related to the larger (smaller) values of $\lambda^{\rm osc}_{\nu_{e}}/\lambda^{\rm osc}_{\bar{\nu}_{e}}$ shown in Fig. 13. For the middle ejecta, a fraction of ejecta originally with $0.3\lesssim Y^{(\rm no~{}osc)}_{e}\lesssim 0.4$ has $Y_{e}^{\rm(osc)}\simeq 0.4-0.5$ when flavor equipartition is reached, while the distribution with $Y_{e}\lesssim 0.3$ is barely altered. As for the equatorial ejecta, the corresponding $Y_{e}$ distribution is only affected negligibly, as expected.

The impact of flavor equipartition in the neutrino-driven ejecta studied in Ref. [34] is to lower $Y_{e}$ (see Fig. 11 therein), while $Y_{e}$ increases in the models investigated in this work, as discussed above. The main difference is that flavor equipartition leads to a larger reduction of $\lambda_{\nu_{e}}$ and $\lambda_{\bar{\nu}_{e}}$ in the BH–torus case, due to the vanishingly small $\nu_{x}$ fluxes. Moreover, a significant part of the ejecta in the BH–torus case is ejected on timescales of several tens of milliseconds during which the neutrino luminosities decrease substantially (see Figs. 2 and 8 in Ref. [34]); this leads to much smaller neutrino absorption rates even without assuming neutrino flavor equipartition. As a consequence, since the ejecta start out as neutron-rich material, a largely reduced $Y_{e}$ for the neutrino-driven outflow was found in the BH–torus model of Ref. [34].

We show in Fig. 16 the impact of flavor equipartition on the abundance distribution for the polar ejecta ($60^{\circ}\leq|\theta_{\rm ej}-90^{\circ}|\leq 90^{\circ}$) for the $1.35+1.35$ $M_{\odot}$ model with both EoSs. Since flavor equipartition mainly shifts the distribution of high $Y_{e}\gtrsim 0.3$ material, noticeable changes appear regarding the iron peak and the first peak elements. In particular, the amount of produced $A=56$ nuclei is enhanced by a factor of $\sim 6(27)$ for the DD2(SFHo) EoS model. The amount of lanthanides in the polar ejecta, relevant to the kilonova color, is affected negligibly for the DD2 model and reduced by $\sim$ a factor of 2 for the SHFo model. Since the polar ejecta contribute up to $\sim 10\%$ to the total ejecta mass considered here, the overall modifications induced by flavor equipartition on the total abundance yields are relatively small. For instance, the change of the produced amount of strontium at the time of a day and the amount of free neutrons at the end of the $r$-process is at the level of $\sim 10\%$.