Fast and Scalable Semi-Supervised Learning for Multi-View Subspace Clustering

Subspace clustering assumes that the data points are drawn from a union of multiple low-dimensional subspaces, with each group corresponding to one subspace. This clustering paradigm finds applications in diverse domains, including motion segmentation [22], face clustering [23], and image processing [24]. Within subspace clustering, self-representative subspace clustering achieves state-of-the-art performance by representing each data point as a linear combination of other data points within the same subspace. Such a representation is not unique, and sparse subspace clustering (SSC) [22] pursues a sparse representation by solving the following problem

where $\mathbf{Z}$ is a $n\times n$ self-representative matrix for $n$ data points $\mathbf{X}=[\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{n}]$, and $|\mathbf{Z}_{ij}|$ reflects the affinity between data point $\mathbf{x}_{i}$ and data point $\mathbf{x}_{j}$. Then the affinity matrix is induced by $\mathbf{Z}$ as $\frac{1}{2}\left(|\mathbf{Z}|+\left|\mathbf{Z}\right|^{\top}\right)$, which is further used for spectral clustering (SC) [25] to obtain the final clustering results.

In this paper, we represent each data point using selected landmarks to facilitate linear computational and space complexity relative to the data size $n$.

Owing to the prevalence of extensive real-world datasets with diverse features, numerous semi-supervised learning approaches have been developed specifically for multi-view data [26, 27, 28, 29, 30, 31, 32, 33]. The multiple graphs learning framework (AMGL) in [34] automatically learned the optimal weights for view-specific graphs. Additionally, the work [29] presented a multi-view learning with adaptive neighbors (MLAN) framework, concurrently performing label propagation and graph structure learning. [31] proposed a semi-supervised multi-view clustering method (GPSNMF) that constructs an affinity graph to preserve geometric information. An anti-block-diagonal indicator matrix was introduced in [32] to enforce the block-diagonal structure of the shared affinity matrix. [35] introduced a constrained tensor representation learning model to utilize prior weakly supervision for multi-view semi-supervised subspace clustering task. The work [33] proposed a novel semi-supervised multi-view clustering approach (CONMF) based on orthogonal non-negative matrix factorization. Despite their success in semi-supervised learning, these methods typically entail affinity matrix construction and exhibit at least $\mathcal{O}(n^{2})$ computational complexity, where $n$ denotes the data size. Notably, a semi-supervised learning approach based on adaptive regression (MVAR) was introduced in [30], offering linear scalability with $n$ and quadratic scalability with feature dimension.

This paper introduces FSSMSC, a fast and scalable semi-supervised multi-view learning method to address the prevalent high computational complexity in existing approaches. FSSMSC exhibits linear computational and space complexity relative to data size and feature dimension.

For multi-view data, let $V$ denote the number of views, and $\mathbf{X}^{(v)}\in\mathbb{R}^{d_{v}\times n}$ represent the data matrix for $n$ data points $\mathbf{x}_{1},\mathbf{x}_{2},\ldots,\mathbf{x}_{n}$ in the $v$-th view, where $d_{v}$ and $n$ stand for the dimension of the $v$-th view and the data size, respectively. We perform $k$-means clustering on the concatenated features of all views to establish consistent landmarks across all views. The resulting clustering centers are then partitioned into distinct views, denoted as $\mathbf{U}^{(v)}\in\mathbb{R}^{d_{v}\times m}$, $v=1,\dots,V$. Assuming the first $n_{\ell}$ data points are provided with labels, while the remaining data points remain unlabeled. The label assigned to $\mathbf{x}_{i}$ is denoted as $\ell_{i}\in\{1,\ldots,k\}$, $i=1,\ldots,n_{\ell}$, where $k$ is the number of data categories. We formulate a more flexible form of supervisory information for the $n_{\ell}$ labeled data points, i.e., pairwise constraints $\mathcal{M}=\{(i,j)|\ell_{i}=\ell_{j}\}$ and $\mathcal{C}=\{(i,j)|\ell_{i}\neq\ell_{j}\}$, where $\mathcal{M}$ and $\mathcal{C}$ denote the sets of data pairs subject to must-link and cannot-link constraints, respectively.

Scalable semi-supervised learning methods like [19, 20, 21] compute the soft label vectors for $n$ data points by a linear combination of the soft label vectors of $m$ chosen landmarks (anchors), where $m$ is notably smaller than $n$. Similarly, we compute low-dimensional representations $\mathbf{F}\in\mathbb{R}^{k\times n}$ for $n$ data points through a linear combination of low-dimensional representations $\mathbf{A}\in\mathbb{R}^{k\times m}$ of $m$ landmarks

where $\mathbf{f}_{i}$ is the $i$-th column of $\mathbf{F}$, $\mathbf{a}_{j}$ is the $j$-th column of $\mathbf{A}$. Here, $k$ signifies the dimension of the low-dimensional space, consistently set as the number of data categories throughout this paper. Additionally, $\mathbf{Z}=(\mathbf{Z}_{ji})\in\mathbb{R}^{m\times n}$ is a consensus anchor graph capturing the relationships (similarities) between $n$ data points and $m$ selected landmarks.

However, these previous methods in [19, 20, 21] treat anchor graph learning and the learning of landmarks’ soft label vectors as disjoint sub-problems. In contrast, we formulate a unified optimization model facilitating concurrent advancement in both the anchor graph $\mathbf{Z}$ and the low-dimensional representations $\mathbf{A}$ of the landmarks. Specifically, the proposed unified optimization model of the anchor graph $\mathbf{Z}$ and low-dimensional representations $\mathbf{A}$ is based on the following observations.

Firstly, each entry $\mathbf{Z}_{ji}$ within the anchor graph $\mathbf{Z}$ should capture the affinity between the $i$-th data point and the $j$-th landmark. To fulfill this requirement, we extend the optimization model in (1) to a landmark-based multi-view clustering scenario. As discussed in Section 2.1, the optimization model (1) proposed in [22] represents each data point as a sparse linear combination of other data points within the same subspace, and induces the affinity matrix using these linear combination coefficients. Denote $\mathbf{X}^{(v)}=[\mathbf{x}^{(v)}_{1},\dots,\mathbf{x}^{(v)}_{n}]$, where $\mathbf{x}^{(v)}_{i}$ represents the feature vector of the $i$-th data point $\mathbf{x}_{i}$ in the $v$-th view. In this paper, we depict each $\mathbf{x}_{i}^{(v)}$ as a linear combination of the landmarks $\mathbf{U}^{(v)}$ and assume that the combination coefficients are shared across views. Therefore, we explore the relationship among views by assuming that the anchor graph $\mathbf{Z}$ is shared across views to capture their consensus. Furthermore, we enforce coefficient sparsity by utilizing the $\ell_{1}$-norm on $\mathbf{Z}$, leading to the following optimization problem:

where we impose non-negativity constraints on the elements in $\mathbf{Z}$. The parameter $\lambda_{Z}>0$ governs the sparsity level in $\mathbf{Z}$.

Secondly, the low-dimensional representations for the $n$ data points, denoted as $\mathbf{F=AZ}$ following (2), need to conform to the provided pairwise constraints. Specifically, data points with must-link (cannot-link) constraints should exhibit similar (distinct) low-dimensional representations. To fulfill this requirement, we encode the pairwise constraints into two matrices, $\mathbf{M}=(m_{ij})\in\mathbb{R}^{n_{\ell}\times n_{\ell}}$ and $\mathbf{C}=(c_{ij})\in\mathbb{R}^{n_{\ell}\times n_{\ell}}$, with elements defined as:

where $n_{m}$ ($n_{c}$) is the total number of must-link (cannot-link) constraints in $\mathcal{M}$ ($\mathcal{C}$). The matrix $\mathbf{M}$ represents prior pairwise similarity constraints among data points. The element $m_{ij}$ functions as a reward factor, with a positive value indicating a constraint that data points $i$ and $j$ should be grouped into the same cluster. In contrast, the matrix $\mathbf{C}$ denotes prior pairwise dissimilarity constraints. The element $c_{ij}$ acts as a penalty factor, where positive values suggest that data points $i$ and $j$ should be assigned to different clusters. To balance the influence of must-link and cannot-link constraints, we normalize the non-zero entries in $\mathbf{M}$ and $\mathbf{C}$ by $n_{m}$ and $n_{c}$, respectively. Subsequently, we utilize $m_{ij}$ and $c_{ij}$ to measure intra-class and inter-class distances for labeled data points, respectively, in the low-dimensional space. Specifically, we ensure that data pairs in $\mathcal{M}$ share similar low-dimensional representations through the minimization of

where $\mathbf{Z}_{\ell}$ is the first $n_{\ell}$ columns of $\mathbf{Z}$ and $\mathbf{z}_{i}$ is any $i$-th column of $\mathbf{Z}$, $\mathbf{L}_{\mathbf{M}}=\mathbf{D_{M}}-\mathbf{M}$, where $\mathbf{D_{M}}$ is a diagonal degree matrix with the $i$-diagonal element being $\sum_{j=1}^{n_{\ell}}m_{ij}$. Similarly, we ensure that data pairs in $\mathcal{C}$ exhibit distinct low-dimensional representations through the maximization of

where $\mathbf{L}_{\mathbf{C}}=\mathbf{D_{C}}-\mathbf{C}$ and $\mathbf{D_{C}}$ is a diagonal degree matrix with the $i$-diagonal element being $\sum_{j=1}^{n_{\ell}}c_{ij}$.

Thirdly, the representations $\mathbf{A}$ of landmarks should exhibit smoothness on the graph structure of landmarks, signifying that landmarks with higher similarity ought to possess spatially close representations. This objective is commonly achieved through the application of manifold smoothing regularization. Specifically, for a symmetric similarity matrix $\mathbf{W}\in\mathbb{R}^{m\times m}$ of $m$ chosen landmarks, the manifold smoothing regularization is given by

where $\mathbf{D}$ is the diagonal degree matrix with $\mathbf{D}_{ii}=\sum_{j=1}^{m}\mathbf{W}_{ij}$. Minimizing this objective ensures that landmarks $i$ and $j$ with high similarity value $\mathbf{W}_{ij}$ have their scaled low-dimensional representations $\mathbf{a}_{i}$ and $\mathbf{a}_{j}$ close to each other.

Given that $\mathbf{Z}_{ij}\geq 0$ signifies the similarity between landmark $i$ and data point $j$, we define the graph structure $\mathbf{W}$ for landmarks as $\mathbf{W}=\mathbf{Z}\mathbf{Z}^{\top}$, consistent with the definition in prior literature [20, 21]. We subsequently derive the normalized Laplacian matrix $\mathbf{L}_{\mathbf{W}}$ using $\mathbf{L}_{\mathbf{W}}=\mathbf{I}-\mathbf{D}^{-\frac{1}{2}}\mathbf{W}\mathbf{D}^{-\frac{1}{2}}$. Then, we introduce the manifold smoothing regularization as follows:

where $\mathbf{D_{Z}}=\text{diag}(\mathbf{Z}\mathbf{Z}^{\top}\mathbf{1}_{m})$ and $\mathbf{1}_{m}=(1,\cdots,1)^{\top}\in\mathbb{R}^{m}$.

By consolidating the aforementioned optimization requirements, we establish a unified optimization problem for the simultaneous learning of $\mathbf{Z}$ and $\mathbf{A}$ as follows:

where $\beta,\lambda_{M}>0$ are penalty parameters.

We introduce auxiliary variable $\mathbf{q}\in\mathbb{R}^{m}$ subject to the constraint $\mathbf{q}=\mathbf{Z}\mathbf{Z}^{\top}\mathbf{1}_{m}$. Subsequently, we replace $\mathbf{D}_{\mathbf{Z}}$ with $\mathbf{D_{q}}=\text{diag}(\mathbf{q})$ in $\phi_{s}(\mathbf{A},\mathbf{Z})$, denoted as $\tilde{\phi}_{s}(\mathbf{A},\mathbf{Z},\mathbf{q})$. To facilitate numerical stability and convergence analysis, we impose an upper bound $m_{Z}>0$ on the elements in $\mathbf{Z}$ and enforce upper bound $C_{q}>0$ and lower bound $\epsilon_{q}>0$ on the elements in $\mathbf{q}$. Additionally, a positive constant $\epsilon>0$ is added to the denominator in (9). Consequently, the optimization problem is formulated as follows:

where $\frac{\lambda_{0}}{2}\|\mathbf{q}-\mathbf{Z}\mathbf{Z}^{\top}\mathbf{1}_{m}\|^{2}$ is the penalized term for the constraint $\mathbf{q}=\mathbf{Z}\mathbf{Z}^{\top}\mathbf{1}_{m}$ and $\lambda_{0}>0$ is a penalized parameter.

We employ the Alternating Direction Method of Multipliers (ADMM) approach to solve the optimization problem (10).

We introduce auxiliary variables $\mathbf{B}=\mathbf{Z}$, leading to the augmented Lagrangian expression as follows:

where $\Lambda$ is the Lagrange multiplier. The trade-off parameters $\lambda_{M}$, $\lambda_{Z}$, and $\beta$ are utilized to harmonize various components. We define $S_{0}=\{\mathbf{A}\in\mathbb{R}^{k\times m}|\mathbf{A}\mathbf{A}^{\top}=\mathbf{I}\}$, $S_{1}=\{\mathbf{Z}\in\mathbb{R}^{m\times n}|m_{Z}\geq\mathbf{Z}\geq 0\}$ and $S_{2}=\{\mathbf{q}\in\mathbb{R}^{m}|\epsilon_{q}\leq\mathbf{q}\leq C_{q}\}$, with their respective indicator functions denoted as $\ell_{S_{0}}(\cdot)$, $\ell_{S_{1}}(\cdot)$ and $\ell_{S_{2}}(\cdot)$. Throughout our experiments, we fix $\lambda$ and $\lambda_{0}$ as $100$, $m_{Z}$ as $1$, $C_{q}$ as $n$, and $\epsilon$ and $\epsilon_{q}$ as $1\times 10^{-5}$.

In each iteration, we alternatingly minimize over $\mathbf{A}$, $\mathbf{Z}$, $\mathbf{q}$, B and then take gradient ascent steps on the Lagrange multiplier. The minimizations over $\mathbf{A,Z,q,B}$ hold the other variables fixed and use the most recent value of each variable.

$\bullet$ Update of $\mathbf{A}$. The sub-problem on optimizing $\mathbf{A}$ can be written as an equivalent form

where $\mathbf{L}_{f}=\lambda_{M}\left(\mathbf{Z}_{\ell}\mathbf{L}_{\mathbf{M}}\mathbf{Z}_{\ell}^{\top}\right)+\mathbf{I}-\mathbf{D}_{\mathbf{q}}^{-1/2}\mathbf{Z}\mathbf{Z}^{\top}\mathbf{D}_{\mathbf{q}}^{-1/2}$ and $\mathbf{L}_{d}=\mathbf{Z}_{\ell}\mathbf{L}_{\mathbf{C}}\mathbf{Z}_{\ell}^{\top}+\frac{\epsilon}{k}\cdot\mathbf{I}$. The trace ratio optimization problem (12) can be effectively addressed using ALGORITHM 4.1 presented in [36].

$\bullet$ Update of $\mathbf{Z}$. The sub-problem on optimizing $\mathbf{Z}$ can be written as follows:

We employ a one-step projected gradient descent strategy to update $\mathbf{Z}$. By deriving the gradient of $P(\mathbf{Z})$ with respect to $\mathbf{Z}$, we can obtain:

where $\mathbf{L}_{pc}=\frac{2\lambda_{M}}{\tau_{2}}\mathbf{L}_{\mathbf{M}}-\frac{2\tau_{1}}{\tau_{2}^{2}}\mathbf{L}_{\mathbf{C}}$, $\tau_{2}=\phi_{\mathcal{C}}(\mathbf{A},\mathbf{Z})+\epsilon$, and $\tau_{1}=\tilde{\phi}_{s}(\mathbf{A},\mathbf{Z},\mathbf{q})+\lambda_{M}\phi_{\mathcal{M}}(\mathbf{A},\mathbf{Z})$. Then we update $\mathbf{Z}$ by

where $\eta_{z}$ is the step size, consistently set as $\frac{1}{\lambda}$ in this paper.

$\bullet$ Update of $\mathbf{q}$. The sub-problem on optimizing $\mathbf{q}$ can be written as follows:

By deriving the gradient of $Q(\mathbf{q})$ with respect to $\mathbf{q}$, we can obtain:

Then we update $\mathbf{q}$ by

where $\eta_{q}$ is the step size, consistently set as $\frac{1}{\lambda}$ in this paper.

$\bullet$ Update of $\mathbf{B}$. The sub-problem on optimizing $\mathbf{B}$ is

The solution to the above least-square problem is

Since $\mathbf{U}^{(v)}\in\mathbb{R}^{d_{v}\times m}$, $\mathbf{X}^{(v)}\in\mathbb{R}^{d_{v}\times n}$, the computational complexity of solving the least-square problem amounts to $\mathcal{O}(m^{3}+m^{2}n+\sum_{v=1}^{V}d_{v}mn)$.

$\bullet$ Update of the Lagrange multiplier $\Lambda$.

The detailed procedure is summarized in Algorithm 1.

Upon obtaining the anchor graph $\mathbf{Z}$ and landmarks’ low-dimensional representations $\mathbf{A}$ from Algorithm 1, the low-dimensional representations for the $n$ data points are computed as $\mathbf{F=AZ}=[\mathbf{f}_{1},\mathbf{f}_{2},\ldots,\mathbf{f}_{n}]$. Subsequently, the cluster label $c_{i}$ for each data point $\mathbf{x}_{i},i=1,2,\ldots,n$, is inferred using

We begin by conducting a computational complexity analysis of the proposed FSSMSC. For updating $\mathbf{Z}$, the complexity is $\mathcal{O}(m^{2}n+mn_{\ell}^{2})$. The update of $\mathbf{q}$ involves a complexity of $\mathcal{O}(m^{2}n)$. The complexity of updating $\mathbf{A}$ is $\mathcal{O}(m^{2}n+mn_{\ell}^{2}+m^{3})$, while updating $\mathbf{B}$ requires $\mathcal{O}(dmn+m^{3}+m^{2}n)$, where $d$ stands for the total dimension of all features. The updates for $\Lambda$ incur a complexity of $\mathcal{O}(mn)$. Therefore, the overall computational complexity of FSSMSC amounts to $\mathcal{O}(m^{2}n+mn_{\ell}^{2}+m^{3}+dmn)$. Moving on to the space complexity evaluation, considering matrices such as $\mathbf{X}^{(v)}\in\mathbb{R}^{d_{v}\times n}$, $\mathbf{U}^{(v)}\in\mathbb{R}^{d_{v}\times m}$ for $v=1,...,V$, $\mathbf{L_{M}},\mathbf{L_{C}}\in\mathbb{R}^{n_{\ell}\times n_{\ell}}$, $\mathbf{Z,B},\Lambda\in\mathbb{R}^{m\times n}$, and $\mathbf{A}\in\mathbb{R}^{k\times m}$, the aggregate space complexity totals $\mathcal{O}(dn+n_{\ell}^{2}+mn+kn)$.

In summary, the proposed method demonstrates linear complexity, both in computation and space, with respect to the data size $n$.

We denote $\{\mathbf{A}^{k},\mathbf{Z}^{k},\mathbf{q}^{k},\mathbf{B}^{k},\Lambda^{k}\}$ as the variables generated by Algorithm 1 at iteration $k$, and establish convergence guarantees for Algorithm 1.

The proofs for the aforementioned lemma and theorem are available in the appendix.

Table 3 presents the clustering performance of different methods on the seven datasets. Based on the results depicted in Table 3, the following observations can be made:

• •

  Compared to the scalable multi-view subspace clustering methods, FPMVS and LMVSC, the proposed approach demonstrates a significant enhancement in clustering performance while utilizing a limited amount of supervisory information. For instance, FSSMSC exhibits improvements of $18.3\%$, $9.8\%$, and $17.5\%$ over datasets Reuters, NUS, and YoutubeFace$\_$sel, respectively, for the ACC metric. Furthermore, FSSMSC notably outperforms FPMVS and LMVSC regarding running time.

• •

  In comparison to the semi-supervised multi-view learning methods (MVAR, MLAN, AMGL, GPSNMF, and CONMF), the proposed FSSMSC demonstrates comparable or superior performance with remarkably enhanced computational efficiency, particularly on large datasets such as YoutubeFace$\_$sel, NUS, and Reuters. Specifically, FSSMSC demonstrates improvements of $5.8\%$, $3.2\%$, and $3.0\%$ in ARI metric on datasets YoutubeFace$\_$sel, Reuters, and NUS, respectively, when contrasted with the five semi-supervised methods. Furthermore, FSSMSC exhibits computational efficiency advantages, running nearly 25 times faster than AMGL on NUS, 15 times faster than MVAR on NUS, 10 times faster than GPSNMF on Reuters, 20 times faster than MLAN on Caltech101, and 45 times faster than CONMF on Reuters.

• •

  When conducting experiments on the largest dataset, YoutubeFace$\_$sel, the semi-supervised methods MVAR, MLAN, AMGL, and CONMF faced out-of-memory issues. The proposed FSSMSC demonstrates improvements of $2.4\%$ and $5.8\%$ over GPSNMF in terms of the ACC and ARI metrics, respectively, achieving this enhancement with significantly reduced running time.

These experiments verify the scalability, effectiveness, and efficiency of the proposed method.

In Fig. 1 and Fig. 2, we conduct a sensitivity analysis for the three key parameters in FSSMSC, namely $\lambda_{Z}$, $\lambda_{M}$, and $\beta$, on six datasets. The following observations can be made from Fig. 1 and Fig. 2: (1) The parameter $\lambda_{Z}$, governing the sparsity level of $\mathbf{Z}$, significantly influences the clustering performance. Notably, the clustering accuracy exhibits more stable changes when the value of $\lambda_{Z}$ is relatively small; (2) Among the three relatively large datasets (Caltech101, NUS, and YoutubeFace$\_$sel), higher values of $\lambda_{M}$ such as $1\times 10^{5}$ and smaller values of $\beta$ such as $1\times 10^{-4}$ and $1\times 10^{-3}$ are advantageous.

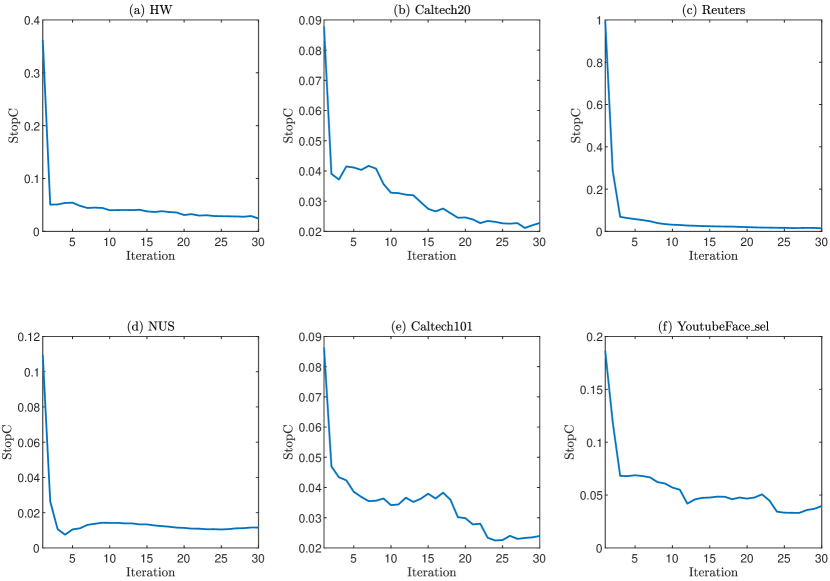
Additionally, numerical convergence curves for six datasets are presented in Fig. 3. It can be observed that the stopping criterion decreases rapidly in the initial five iterations and continues to decrease throughout the iterations. In our experiments, we set the maximum iteration number to 30.

We conduct experiments to assess the performance of our proposed method under different ratios of labeled samples. The results are presented in Fig. 4, Fig. 5, Fig. 6, and Fig. 7. The results are not included when an out-of-memory issue occurs. These results show that our proposed FSSMSC performs comparably to or better than semi-supervised competitors (MVAR, MLAN, AMGL, GPSNMF, and CONMF) across different labeled sample ratios. Additionally, as presented in Table 3, FSSMSC demonstrates notably reduced running times on the large datasets—NUS, Reuters, and YoutubeFace$\_$sel. These results further validate the effectiveness of our approach.

We conduct an ablation study for each component of our optimization model (9). The results are presented in Table 4. These ablation experiments include:

• •

  W/O $\|\mathbf{Z}\|_{1}$: Omitting the $\ell_{1}$ norm of $\mathbf{Z}$ in $\varphi(\mathbf{Z})$, resulting in $\varphi(\mathbf{Z})=\frac{1}{2}\sum_{v=1}^{V}\|\mathbf{X}^{(v)}-\mathbf{U}^{(v)}\mathbf{Z}\|^{2}$. Since $\frac{1}{2}\sum_{v=1}^{V}\|\mathbf{X}^{(v)}-\mathbf{U}^{(v)}\mathbf{Z}\|^{2}$ is a necessary component to utilize the data features $\mathbf{X}^{(v)},v=1,\ldots,V$, we preserve this part in $\varphi(\mathbf{Z})$.

• •

  W/O $\phi_{\mathcal{M}}$: Excluding the component $\phi_{\mathcal{M}}(\mathbf{A},\mathbf{Z})$.

• •

  W/O $\phi_{\mathcal{C}}$: Omitting the component $\phi_{\mathcal{C}}(\mathbf{A},\mathbf{Z})$.

• •

  W/O $\phi_{s}$: Excluding the component $\phi_{s}(\mathbf{A},\mathbf{Z})$.