Faraday rotation signal amplification using high-power lasers

The description of the S-waveplate can be effectively realized through the application of Jones matrices[21, 22]. This element can be divided into a retarder introducing a phase delay of $\varphi=\pi$ and a rotation matrix that imparts a rotation determined by the orientation $\phi$ of the nanogratings. Mathematically, the explicit expression for $\mathscr{S}$ takes the form:

$$\mathscr{S}=\text{e}^{\frac{-i\varphi}{2}}\left[{\begin{array}[]{*{20}{c}}{{{\cos}^{2}}\phi+{e^{i\varphi}}{{\sin}^{2}}\phi}&{({1-{e^{i\varphi}}})\cos\phi\sin\phi}\\ {({1-{e^{i\varphi}}})\cos\phi\sin\phi}&{{e^{i\varphi}}{{\cos}^{2}}\phi+{{\sin}^{2}}\phi}\end{array}}\right].$$

Given that $kR=\pi$, the expression can be simplified to:

$$\mathscr{S}(x,y)=-i\left[{\begin{array}[]{*{20}{c}}{\cos\Theta(x,y)}&{\sin\Theta(x,y)}\\ {\sin\Theta(x,y)}&{-\!\cos\Theta(x,y)}\end{array}}\right],$$

(2)

where the local polarizing angle $\Theta(x,y)$ is twice the nanograting angle $\phi(x,y)$.

We start with a linearly polarized laser beam having a stable polarization angle $\theta$ relative to the polarization of the S-plate. Any electric field with a stable polarization in the object plane can be expanded into a discrete summation of sine and cosine functions using the discrete Fourier transform as

$$\mathbf{E}(x,y)=\frac{\mathbf{A}_{0}}{2}+\sum_{n=1}^{+\infty}\cos(\textbf{k}_{n}\cdot\textbf{r})\mathbf{A}_{n}+\sin(\textbf{k}_{n}\cdot\textbf{r})\mathbf{B}_{n},$$

(3)

where $\textbf{k}_{n}\cdot\textbf{r}=k_{x,n}x+k_{y,n}y$, $\mathbf{A}_{n}=A_{n}\cos\theta\,\mathbf{x}+A_{n}\sin\theta\,\mathbf{y}$, and $\mathbf{B}_{n}=B_{n}\cos\theta\,\mathbf{x}+B_{n}\sin\theta\,\mathbf{y}$. Note that $A_{n}$ and $B_{n}$ can be complex. To illustrate the operation done in the Fourier plane by the S-waveplate, we examine each component of $\mathbf{E}(x,y)$ individually. We denote the component of $\mathbf{E}$ corresponding to $\mathbf{k}\in\{\mathbf{k}_{1},\ldots,\mathbf{k}_{n},\ldots,+\infty\}$ as $\mathbf{E}_{\textbf{k}}(x,y)=\mathbf{A}_{\textbf{k}}\cos(k_{x}x+k_{y}y)+\mathbf{B}_{\textbf{k}}\sin(k_{x}x+k_{y}y)$. The Fourier transform of $\mathbf{E}_{\textbf{k}}$ is given by

	$\displaystyle\mathscr{E}_{\textbf{k}}(f_{x},f_{y})=$	$\displaystyle\left[\pi\delta\left(\frac{k_{x}}{2\pi}-f_{x}\right)\delta\left(\frac{k_{y}}{2\pi}-f_{y}\right)+\pi\delta\left(\frac{k_{x}}{2\pi}+f_{x}\right)\delta\left(\frac{k_{y}}{2\pi}+f_{y}\right)\right]\mathbf{A}_{\textbf{k}}$
	$\displaystyle+\frac{1}{i}$	$\displaystyle\left[\pi\delta\left(\frac{k_{x}}{2\pi}-f_{x}\right)\delta\left(\frac{k_{y}}{2\pi}-f_{y}\right)-\pi\delta\left(\frac{k_{x}}{2\pi}+f_{x}\right)\delta\left(\frac{k_{y}}{2\pi}+f_{y}\right)\right]\mathbf{B}_{\textbf{k}}.$

When introducing an S-waveplate at the Fourier plane $(f_{x},f_{y})$ where the orientation of the local polarizing angle $\Theta$ varies azimuthally from 0 to $2\pi$, the Jones matrix $\mathscr{S}$ of Eq. (2) can be expressed in term of the frequencies $f_{x}$ and $f_{y}$ as

$$\mathscr{S}(f_{x},f_{y})=-i\left[{\begin{array}[]{*{20}{c}}{\frac{f_{x}}{\sqrt{f_{x}^{2}+f_{y}^{2}}}}&{\frac{f_{y}}{\sqrt{f_{x}^{2}+f_{y}^{2}}}}\\ {\frac{f_{y}}{\sqrt{f_{x}^{2}+f_{y}^{2}}}}&{-\frac{f_{x}}{\sqrt{f_{x}^{2}+f_{y}^{2}}}}\end{array}}\right].$$

Now, we combine the S-waveplate with a neutral density filter whose transmission varies linearly with the radius $\rho$ and is defined as[23]

$$\rho(f_{x},f_{y})=\sqrt{f_{x}^{2}+f_{y}^{2}}.$$

(4)

In practice, the transmission cannot exceed 1. While a scaling factor could be used, it is omitted here. The S-waveplate and the neutral density filter collectively constitute a new element denoted as $\mathscr{T}$, with a Jones matrix given by

$$\mathscr{T}(f_{x},f_{y})=-i\left[{\begin{array}[]{*{20}{c}}{f_{x}}&{f_{y}}\\ {f_{y}}&{-f_{x}}\end{array}}\right].$$

Upon performing the inverse Fourier transform of $\mathscr{E}_{\mathbf{k}}\mathscr{T}$, we obtain on the image plane[23]

$$\mathbf{E}_{\textbf{k}}^{\prime}(x,y)=-\left[\begin{array}[]{*{20}{c}}{\cos\theta}&{\sin\theta}\\ {-\sin\theta}&{\cos\theta}\end{array}\right]\nabla\left[A_{\textbf{k}}\cos(\mathbf{k}\cdot\mathbf{r})+B_{\textbf{k}}\sin(\mathbf{k}\cdot\mathbf{r})\right]$$

(5)

where $\nabla$ is the gradient operator. Since the main results of the paper focus on intensities, we will drop the minus sign in Eq. (5) from later equations. As a result, the total electric field on the image plane is given by

$$\mathbf{E}^{\prime}(x,y)=\nabla_{-\theta}E(x,y),$$

(6)

where the electric field $E(x,y)$ is the electric field along the polarization direction $\theta$, i.e.

$$E(x,y)=\frac{A_{0}}{2}+\sum_{n=1}^{+\infty}A_{n}\cos(\textbf{k}_{n}\cdot\textbf{r})+B_{n}\sin(\textbf{k}_{n}\cdot\textbf{r}),$$

and $\nabla_{\theta}$ is the rotated gradient operator given by

$$\nabla_{\theta}=\left[\begin{array}[]{*{20}{c}}{\cos\theta}&{-\sin\theta}\\ {\sin\theta}&{\cos\theta}\end{array}\right]\nabla\text{ or }\nabla_{\theta}=\left[\begin{array}[]{*{20}{c}}{\cos\theta\,\partial_{x}-\sin\theta\,\partial_{y}}\\ {\sin\theta\,\partial_{x}+\cos\theta\,\partial_{y}}\end{array}\right]$$

The resulting electric field of Eq. (6) is the gradient of the initial electric field along the polarization direction $\theta$. However, its polarization is along the $-\theta$ direction now. Note that for a beam with a polarization angle $\theta=0$ (polarization along the $x$-axis), $\nabla_{\theta}$ becomes the usual gradient operator $\nabla$. In this case, the S-waveplate/neutral density filter give the gradient along two perpendicular polarization axes, allowing to measure $\partial_{x}E$ and $\partial_{y}E$ independently. This is a departure from the vortex plate setup [23] where the derivative along $x$ and $y$ were combined together.

We again start with a linearly polarized laser beam with constant initial polarization angle $\theta_{i}$ with respect to the S-waveplate polarization. However, the electric field $E(x,y)$ has now acquired a variable polarization $\theta_{FR}(x,y)$ from a magnetoactive medium. We are dropping the coordinates $x$ and $y$ hereafter for the terms on the RHS of most equations. After exiting the medium, the electric field is given by

$$\mathbf{E}(x,y)=E\left[\begin{array}[]{*{20}{c}}{\cos\theta}\\ {\sin\theta}\end{array}\right],$$

(7)

where $\theta=\theta_{i}+\theta_{FR}$. Since a spatial change in polarization simply corresponds to a change in intensity of the $x$- and $y$-polarization components of the beam, we can use Eq. (6) for each polarization independently to find the electric field at the exit of the augmented two-$f$ system

$$\mathbf{E}^{\prime}(x,y)=\nabla_{0}(E\cos\theta)+\nabla_{-\pi/2}(E\sin\theta),$$

which we can write explicitly as

$$\mathbf{E}^{\prime}(x,y)=\left[\begin{array}[]{*{20}{c}}{\partial_{x}\left(E\cos\theta\right)+\partial_{y}\left(E\sin\theta\right)}\\ {\partial_{y}\left(E\cos\theta\right)-\partial_{x}\left(E\sin\theta\right)}\end{array}\right]$$

(8)

If $\theta$ is constant, then Eq. (8) is simply Eq. (6).

It is typical to start with a $y$-polarized (i.e. vertically polarized) beam. The beam then passes through the magnetoactive medium, impinging a Faraday rotation $\theta_{FR}$ to the polarization (see Fig. 2). At this point, a polarizer at $\pi/4$ from the vertical direction yields a new electric field

$$E_{\pi/4}(x,y)=E\cos(\alpha),$$

(9)

where $\alpha=\pi/4-\theta_{FR}$ and $E(x,y)$ is the electric field strength. Now Eq. (9) can be turned into

$$E_{\pi/4}(x,y)=\frac{1}{\sqrt{2}}E\left[\cos(\theta_{FR})+\sin(\theta_{FR})\right].$$

(10)

The intensity can be written as

$$I_{\pi/4}(x,y)=\frac{1}{2}E^{2}\left[\cos^{2}(\theta_{FR})+2\cos(\theta_{FR})\sin(\theta_{FR})+\sin^{2}(\theta_{FR})\right].$$

(11)

As $\theta_{FR}<<1$ in most low density magnetoactive media such as plasmas, we can do a Taylor expansion of Eq. (11) up to the first order leading to

$$I_{\pi/4}(x,y)\simeq\frac{1}{2}E^{2}\left(1+2\theta_{FR}\right).$$

(12)

While this approach increases the measurement sensitivity compared to using a cross-polarizer downstream of the magnetoactive medium, the bias light (represented by the factor 1 in Eq. (12)) really reduces the signal-to-noise ratio.

We look first at the case where the laser intensity is homogeneous, i.e. $E(x,y)\simeq E_{0}$. We can choose $\theta_{i}=0$. In this case, the electric field of Eq. (8) has a component along the $x$ given by

$$E^{\prime}_{x}(x,y)=E_{0}\left(\partial_{x}\cos\theta_{FR}+\partial_{y}\sin\theta_{FR}\right)$$

(13)

for the $x$-polarization and

$$E^{\prime}_{y}(x,y)=E_{0}\left(\partial_{y}\cos\theta_{FR}-\partial_{x}\sin\theta_{FR}\right).$$

(14)

for the $y$-polarization. Since $\theta_{FR}<<1$ the zeroth order of Eq. (13) is

$$E^{\prime}_{x}(x,y)\simeq E_{0}\partial_{y}\theta_{FR}$$

(15)

In this case, the zeroth order of the intensity of the $x$-polarization is

$$I^{\prime}_{x}(x,y)\simeq|E_{0}|^{2}{\partial_{y}\theta_{FR}}^{2},$$

(16)

Following the same line of thinking, Eq. (14) gives

$$E^{\prime}_{y}(x,y)\simeq-E_{0}\partial_{x}\theta_{FR},$$

(17)

with an intensity

$$I^{\prime}_{y}(x,y)\simeq|E_{0}|^{2}{\partial_{x}\theta_{FR}}^{2}.$$

(18)

We clearly see that the sensitivity of the measurement is reduced compared to Eq. (12) as we are looking at the square of the Faraday rotation angle derivative. However, while the Faraday rotation signal is still proportional to $E^{2}$ in Eqs. (16) and (18), the bias signal of Eq. (12) has now disappeared. So the sensitivity can be recovered simply by increasing the power of the input laser.

Most high power laser beams can have some degree of controlled heterogeneity [24]. In this case, Eq. (8) yields

$$\mathbf{E}^{\prime}(x,y)=E\left[\begin{array}[]{*{20}{c}}{\cos\theta\partial_{x}E/E-\sin\theta\partial_{x}\theta+\sin\theta\partial_{y}E/E+\cos\theta\partial_{y}\theta}\\ {\cos\theta\partial_{y}E/E-\sin\theta\partial_{y}\theta-\sin\theta\partial_{x}E/E-\cos\theta\partial_{x}\theta}\end{array}\right].$$

(19)

To recover the sensitivity obtained by the setup of Fig. 2, we take $\theta_{i}=0$. In this case, again supposing $\theta_{FR}<<1$, Eq. (19) simplifies to

$$\mathbf{E}^{\prime}(x,y)\simeq E\left[\frac{\partial_{x}E}{E}+\partial_{y}\theta_{FR}\right]\mathbf{x}+E\left[\frac{\partial_{y}E}{E}-\partial_{x}\theta_{FR}\right]\mathbf{y},$$

(20)

providing that $\partial_{y}\theta_{FR}/\theta_{FR}>>\partial_{y}E/E$. This condition is fulfilled when the magnitude of E is excessively large compared to its derivative. Using a polarizing beam splitter, we can record the intensity of the $x$-polarization given by

$$I_{x}^{\prime}(x,y)\simeq|E\partial_{x}E\left[\partial_{x}E/E+2\partial_{y}\theta_{FR}\right]|,$$

(21)

We see that the measurement of the Faraday rotation derivative is now similar to the standard measurement of section 3.1. The bias is $\partial_{x}E/E$ rather than the "1" seen in Eq. (12) and the Faraday rotation has been replaced by its derivative. So, a high-power beam with small spatial dependence will amplify the Faraday rotation $\partial_{y}\theta_{FR}$ while reducing the inherent bias $\partial_{x}E/E$. Both will improve the signal-to-noise ratio substantially. Since the intensity of the $y$-polarization is

$$I_{y}^{\prime}(x,y)\simeq|E\partial_{y}E\left[\partial_{y}E/E-2\partial_{x}\theta_{FR}\right]|,$$

(22)

we can draw similar conclusions.

We use a laser beam profile in a large region of the ray-tracing domain that is mostly homogeneous and given by:

$$E(x,y)=\frac{E_{0}}{4}\left[1+\tanh\left(x_{0}-\frac{|x-x_{c}|}{\sigma}\right)\right]\left[1+\tanh\left(y_{0}-\frac{|y-y_{c}|}{\sigma}\right)\right],$$

(23)

where $x_{c}$ and $y_{c}$ correspond to the beam center and $\sigma$ the transition width to 0. With the given parameters the full-width-half-maximum is 2$x_{0}$ along the $x$-axis and 2$y_{0}$ along the $y$-axis. Due to the effect of boundary conditions, we keep 2$x_{0}$ and 2$y_{0}$ on the order of 75% of the computational domain width along the respective directions. The spatial dependence of E is shown in Figs. 3 and 4. The Faraday rotation given by

$$\theta_{FR}(x,y,M)=M\pi\left(\left[\frac{x-x_{min}}{x_{max}-x_{min}}-\frac{1}{2}\right]^{2}+\left[\frac{y-y_{min}}{y_{max}-y_{min}}-\frac{1}{2}\right]^{3}\right),$$

(24)

where the scaling factor $M$ allows to switch between large and small rotation, $x_{min}$ and $x_{max}$ are the domain limits along the $x$-axis, while $y_{min}$ and $y_{max}$ are the domain limits along the $y$-axis. This analytical expression will help to identify the FR feature unequivocally in the downstream beam and verify Eq. (8).

For M small (i.e. 1), the downstream electric field should follow Eqs. (13) and (14), as plotted on Fig. 3. For small rotation angle (i.e. M=$10^{-3}$) we expect a signal given by Eqs. (15) and (17). Indeed we recover the linear dependence of the derivative along the $x$-axis, shown on the left hand side of Fig. 4, and the quadratic dependence of the derivative along the $y$-axis, shown on the right hand side of Fig. 4.

Here we scaled the analytical value of the solution given by Eqs. (13) and (14) to the $x$-polarization of the output beam profile of Fig. 3 and kept this scaling constant throughout the simulation section.

As Eqs. (21), (22) show, it is possible to recover the sensitivity of the standard method given by Eq. (12). However, this can only be achieved if the beam has well-defined spatial variations. In fact, these variations should be as simple as possible to allow for an easy measurement of the rotation. While we are using a laser for getting large intensities allowing to amplify the rotation signal, the coherence of the beam is not primordial as the S-waveplate affects the phase signal only by adding a constant. As a result, the beam profile can be controlled using engineered diffusers [24] with an extremely high level of precision. We need to use here a diffuser that scrambles the phase rather than the polarization.

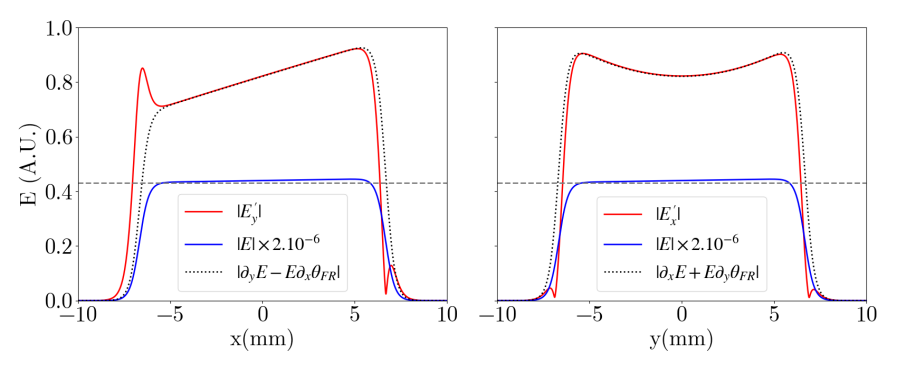
To this end, we now add a small, linear variation to the previous beam, e.g.

	$\displaystyle E(x,y)=$	$\displaystyle\frac{E_{0}}{4}\left[1+\tanh\left(x_{0}-\frac{|x-x_{c}|}{\sigma}\right)\right]\left[1+\tanh\left(y_{0}-\frac{|y-y_{c}|}{\sigma}\right)\right]$
		$\displaystyle\times\left[|\alpha_{x}x+x_{bias}|+|\alpha_{y}y+y_{bias}|\right].$		(25)

If the variation is too large, then we could be back with a case similar to Eq. (12), where the bias decreases the signal to noise ratio. However, if this is deemed necessary, we can reduce the impact on the Faraday rotation signal simply by increasing the base electric field. In this case the bias terms $\partial_{x}E/E$ and $\partial_{y}E/E$ in Eqs. (21) and (22) can be made small compared to the Faraday rotation signal, while the amplification terms $E\partial_{x}E$ and $E\partial_{y}E$ can be made large, de facto amplifying the Faraday rotation signal. Using the same Faraday rotation profile of Eq. (24), Fig. 5 shows that ray tracing confirms Eq. (20). While not plotted, numerical simulations confirm both Eqs. (16) and (18).

It is now time to see what can be done about the beam noise. Clearly this is an open problem so far, at least for the low frequency noise. Yet, several techniques have shown good mitigation. For instance, low frequency noise can be removed using spectral dispersion [27, 28] or micro-lens arrays [29, 30]. Polarization smoothing [31] cannot be used here since we are measuring polarization.

High frequency intensity noise can be removed more easily. This is simply done by placing an aperture in the Fourier plane of the setup shown in Fig. 1[32]. This can be combined directly inside the neutral density filter of Eq. (4), setting the transmission to zero at the filter periphery. Fig. 6 shows that a high frequency noise up to 10% has almost no impact on the Faraday rotation measurement, once filtered optically.