Extremal spectral results of planar graphs without vertex-disjoint cycles¹¹1Lin was supported by NSFC grant 12271162 and Natural Science Foundation of Shanghai (No. 22ZR1416300). Shi was supported by NSFC grant 12161141006.

Longfei Fang^a,b, Huiqiu Lin^a, Yongtang Shi^c
^a School of Mathematics, East China University of Science and Technology,
Shanghai 200237, China
^b School of Mathematics and Finance, Chuzhou University,
Chuzhou, Anhui 239012, China
^cCenter for Combinatorics and LPMC, Nankai University, Tianjin 300071, China
Corresponding author: [email protected] (H. Lin).

Abstract

Given a planar graph family $\mathcal{F}$ , let ${\rm ex}_{\mathcal{P}}(n,\mathcal{F})$ and ${\rm spex}_{\mathcal{P}}(n,\mathcal{F})$ be the maximum size and maximum spectral radius over all $n$ -vertex $\mathcal{F}$ -free planar graphs, respectively. Let $tC_{\ell}$ be the disjoint union of $t$ copies of $\ell$ -cycles, and $t\mathcal{C}$ be the family of $t$ vertex-disjoint cycles without length restriction. Tait and Tobin [Three conjectures in extremal spectral graph theory, J. Combin. Theory Ser. B 126 (2017) 137–161] determined that $K_{2}+P_{n-2}$ is the extremal spectral graph among all planar graphs with sufficiently large order $n$ , which implies the extremal graphs of both ${\rm spex}_{\mathcal{P}}(n,tC_{\ell})$ and ${\rm spex}_{\mathcal{P}}(n,t\mathcal{C})$ for $t\geq 3$ are $K_{2}+P_{n-2}$ . In this paper, we first determine ${\rm spex}_{\mathcal{P}}(n,tC_{\ell})$ and ${\rm spex}_{\mathcal{P}}(n,t\mathcal{C})$ and characterize the unique extremal graph for $1\leq t\leq 2$ , $\ell\geq 3$ and sufficiently large $n$ . Secondly, we obtain the exact values of ${\rm ex}_{\mathcal{P}}(n,2C_{4})$ and ${\rm ex}_{\mathcal{P}}(n,2\mathcal{C})$ , which solve a conjecture of Li [Planar Turán number of the disjoint union of cycles, Discrete Appl. Math. 342 (2024) 260–274] for $n\geq 2661$ .

Keywords: Spectral radius; Turán number; Planar graph; Vertex-disjoint cycles; Quadrilateral

AMS Classification: 05C35; 05C50

1 Introduction

Given a graph family $\mathcal{F}$ , a graph is said to be $\mathcal{F}$ -free if it does not contain any $F\in\mathcal{F}$ as a subgraph. When $\mathcal{F}=\{F\}$ , we write $F$ -free instead of $\mathcal{F}$ -free. One of the earliest results in extremal graph theory is the Turán’s theorem, which gives the maximum number of edges in an $n$ -vertex $K_{k}$ -free graph. The Turán number ${\rm ex}(n,\mathcal{F})$ is the maximum number of edges in an $\mathcal{F}$ -free graph on $n$ vertices. Much attention has been given to Turán numbers on cycles. Füredi and Gunderson [12] determined ${\rm ex}(n,C_{2k+1})$ for all $n$ and $k$ . However, the exact value of ${\rm ex}(n,C_{2k})$ is still open. Erdős [8] determined ${\rm ex}(n,tC_{3})$ for $n\geq 400(t-1)^{2}$ , and the unique extremal graph is characterized. Subsequently, Moon [21] showed that Erdős’s result is still valid whenever $n>\frac{9t-11}{2}$ . Erdős and Pósa [9] showed that ${\rm ex}(n,t\mathcal{C})=(2t-1)(n-t)$ for $t\geq 2$ and $n\geq 24t$ . For more results on Turán-type problem, we refer the readers to the survey paper [13]. In this paper, we initiate the study of spectral extremal values and Turán numbers on cycles in planar graphs.

1.1 Planar spectral extremal values on cycles

One extension of the classical Turán number is to study extremal spectral radius in a planar graph with a forbidden structure. The planar spectral extremal value of a given graph family $\mathcal{F}$ , denoted by ${\rm spex}_{\mathcal{P}}(n,\mathcal{F})$ , is the maximum spectral radius over all $n$ -vertex $\mathcal{F}$ -free planar graphs. An $\mathcal{F}$ -free planar graph on $n$ vertices with maximum spectral radius is called an extremal graph to ${\rm spex}_{\mathcal{P}}(n,\mathcal{F})$ . Boots and Royle [2] and independently Cao and Vince [3] conjectured that $K_{2}+P_{n-2}$ is the unique planar graph with the maximum spectral radius where ‘+’ means the join product. The conjecture was finally proved by Tait and Tobin [27] for sufficiently large $n$ .

In order to study the spectral extremal problems on planar graphs, we first give a useful theorem which will be frequently used in the following.

Theorem 1.1.

Let $F$ be a planar graph and $n\geq\max\{2.16\times 10^{17},2|V(F)|\}$ . If $F$ is a subgraph of $2K_{1}+P_{n/2}$ but not of $K_{2,n-2}$ , then the extremal graph to ${\rm spex}_{\mathcal{P}}(n,F)$ contains a copy of $K_{2,n-2}$ .

Let $tC_{\ell}$ be the disjoint union of $t$ copies of $\ell$ -cycles, and $t\mathcal{C}$ be the family of $t$ vertex-disjoint cycles without length restriction. For $t\geq 3$ , it is easy to check that $K_{2}+P_{n-2}$ is $tC_{\ell}$ -free and $t\mathcal{C}$ -free. Theorem 1.1 implies that $K_{2}+P_{n-2}$ is the extremal graph to ${\rm spex}_{\mathcal{P}}(n,tC_{\ell})$ and ${\rm spex}_{\mathcal{P}}(n,t\mathcal{C})$ for $t\geq 3$ and sufficiently large $n$ . For three positive integers $n,n_{1},n_{2}$ with $n_{1}\geq n_{2}$ and $n\geq n_{1}+2n_{2}+2$ , we can find integers $\alpha$ and $\beta$ such that $1\leq\beta\leq n_{2}$ and $n-2=n_{1}+\alpha n_{2}+\beta$ . Let

H(n_{1},n_{2}):=P_{n_{1}}\cup\alpha P_{n_{2}}\cup P_{\beta}.

In the paper, we give answers to ${\rm spex}_{\mathcal{P}}(n,tC_{\ell})$ for $t\in\{1,2\}$ as follows.

Theorem 1.2.

For integers $\ell\geq 3$ and $n\geq\max\{2.16\times 10^{17},9\times 2^{\ell-1}+3\}$ , the graph $K_{2}+H(2\ell-3,\ell-2)$ is the extremal graph to ${\rm spex}_{\mathcal{P}}(n,2C_{\ell})$ .

Theorem 1.4 implies that $K_{2}+H(3,1)$ is $2\mathcal{C}$ -free for $n\geq 5$ . By Theorem 1.2, $K_{2}+H(3,1)$ is the extremal graph to ${\rm spex}_{\mathcal{P}}(n,2C_{3})$ for $n\geq 2.16\times 10^{17}$ . Moreover, a planar graph is $2C_{3}$ -free when it is $2\mathcal{C}$ -free. Hence, one can easily get answer to ${\rm spex}_{\mathcal{P}}(n,2\mathcal{C})$ .

Corollary 1.1.

For $n\geq 2.16\times 10^{17}$ , $K_{2}+H(3,1)$ is the extremal graph to ${\rm spex}_{\mathcal{P}}(n,2\mathcal{C})$ .

We use $J_{n}$ to denote the graph obtained from $K_{1}+(n-1)K_{1}$ by embedding a maximum matching within its independent set. Nikiforov [23] and Zhai and Wang [28] showed that $J_{n}$ is the extremal graph to ${\rm spex}(n,C_{4})$ for odd and even $n$ , respectively. Clearly, $J_{n}$ is planar. This implies that $J_{n}$ is the extremal graph to ${\rm spex}_{\mathcal{P}}(n,C_{4})$ . Nikiforov [22] and Cioabă, Desai, and Tait [5] determined the spectral extremal graph among $C_{\ell}$ -free graphs for odd $\ell$ and even $\ell\geq 6$ , respectively. Next we give the characterization of the spectral extremal graphs among $C_{\ell}$ -free planar graphs.

Theorem 1.3.

For integers $\ell\geq 3$ and $n\geq\max\{2.16\times 10^{17},9\times 2^{\lfloor\frac{\ell-1}{2}\rfloor}+3,\frac{625}{32}\lfloor\frac{\ell-3}{2}\rfloor^{2}+2\}$ ,
(i) $K_{2,n-2}$ is the unique extremal graph to ${\rm spex}_{\mathcal{P}}(n,C_{3})$ for $\ell=3$ ;
(ii) $K_{2}+H(\lceil\frac{\ell-3}{2}\rceil,\lfloor\frac{\ell-3}{2}\rfloor)$ is the unique extremal graph to ${\rm spex}_{\mathcal{P}}(n,C_{\ell})$ for $\ell\geq 5$ .

1.2 Planar Turán numbers on cycles

We also study another extension of the classical Turán number, i.e., the planar Turán number. Dowden [6] initiated the following problem: what is the maximum number of edges in an $n$ -vertex $\mathcal{F}$ -free planar graph? This extremal number is called planar Turán number of $\mathcal{F}$ and denoted by ${\rm ex}_{\mathcal{P}}(n,\mathcal{F})$ . The planar Turán number for short cycles are studied in [4, 6, 7, 14, 15, 16, 25, 26], but ${\rm ex}_{\mathcal{P}}(n,C_{\ell})$ is still open for general $\ell$ . For more results on planar Turán-type problem, we refer the readers to a survey of Lan, Shi and Song [18]. It is easy to see that ${\rm ex}_{\mathcal{P}}(n,t\mathcal{C})=n-1$ for $t=1$ . Lan, Shi and Song [17] showed that ${\rm ex}_{\mathcal{P}}(n,t\mathcal{C})=3n-6$ for $t\geq 3$ , and the double wheel $2K_{1}+C_{n-2}$ is an extremal graph. We prove the case of $t=2$ , which will be used to prove our main theorems.

Theorem 1.4.

For $n\geq 5$ , we have ${\rm ex}_{\mathcal{P}}(n,2\mathcal{C})=2n-1$ . The extremal graphs are obtained from $2K_{1}+C_{3}$ and an independent set of size $n-5$ by joining each vertex of the independent set to any two vertices of the triangle.

Moreover, Lan, Shi and Song [17] also proved that ${\rm ex}_{\mathcal{P}}(n,tC_{\ell})=3n-6$ for all $t,\ell\geq 3$ . They [19] further showed that ${\rm ex}_{\mathcal{P}}(n,2C_{3})=\lceil\frac{5n}{2}\rceil-5$ and obtained lower bounds of ${\rm ex}_{\mathcal{P}}(n,2C_{\ell})$ for $\ell\geq 4$ , which was improved by Li [20] for sufficiently large $n$ recently. Li [20] also raised the following conjecture.

Conjecture 1.1.

If $n\geq 23$ , then ${\rm ex}_{\mathcal{P}}(n,2C_{4})\leq\frac{19}{7}(n-2)$ and the bound is tight for $14\mid(n-2)$ .

In this paper, we determine the exact value of ${\rm ex}_{\mathcal{P}}(n,2C_{4})$ for large $n$ , which solve the conjecture for $n\geq 2661$ .

Theorem 1.5.

For $n\geq 2661$ ,

{\rm ex}_{\mathcal{P}}(n,2C_{4})=\left\{\begin{array}[]{ll}\frac{19n}{7}-6&\hbox{if $7\mid n$,}\\ \big{\lfloor}\frac{19n-34}{7}\big{\rfloor}{}{}{}{}{}{}{}&\hbox{otherwise.}\end{array}\right.

2 Proof of Theorem 1.1

Let $A(G)$ be the adjacency matrix of a planar graph $G$ , and $\rho(G)$ be its spectral radius, i.e., the maximum modulus of eigenvalues of $A(G)$ . Throughout Sections 2 and 3, let $G$ be an extremal graph to ${\rm spex}_{\mathcal{P}}(n,F)$ , and $\rho$ denote this spectral radius. By Perron-Frobenius theorem, there exists a positive eigenvector $X=(x_{1},\ldots,x_{n})^{\mathrm{T}}$ corresponding to $\rho$ . Choose $u^{\prime}\in V(G)$ with $x_{u^{\prime}}=\max\{x_{i}~{}|~{}i=1,2,\dots,n\}=1$ . For a vertex $u$ and a positive integer $i$ , let $N_{i}(u)$ denote the set of vertices at distance $i$ from $u$ in $G$ . For two disjoint subset $S,T\subset V(G)$ , denote by $G[S,T]$ the bipartite subgraph of $G$ with vertex set $S\cup T$ that consist of all edges with one endpoint in $S$ and the other endpoint in $T$ . Set $e(S)=|E(G[S])|$ and $e(S,T)=|E(G[S,T])|$ . Since $G$ is a planar graph, we have

\displaystyle e(S)\leq 3|S|-6~{}~{}~{}\text{and}~{}~{}~{}e(S,T)\leq 2(|S|+|T|)-4.

(1)

Now, we are ready to give the proof of Theorem 1.1.

Proof.

We give the proof in a sequence of claims. Firstly, we give the lower bound of $\rho$ .

Claim 2.1.

For $n\geq 2.16\times 10^{17}$ , we have $\rho\geq\sqrt{2n-4}.$

Proof.

Note that $K_{2,n-2}$ is planar and $F$ -free. Then, $\rho\geq\rho(K_{2,n-2})=\sqrt{2n-4}$ , as $G$ is an extremal graph to ${\rm spex}_{\mathcal{P}}(n,F)$ . ∎

Claim 2.2.

Set $L^{\lambda}=\{u\in V(G)~{}|~{}x_{u}\geq\frac{1}{10^{3}\lambda}\}$ for some constant $\lambda\geq\frac{1}{10^{3}}$ . Then $|L^{\lambda}|\leq\frac{\lambda n}{10^{5}}$ .

Proof.

By Claim 2.1, $\rho\geq\sqrt{2n-4}$ . Hence,

\frac{\sqrt{2n-4}}{10^{3}\lambda}\leq\rho x_{u}=\sum_{v\in N_{G}(u)}x_{v}\leq d_{G}(u)

for each $u\in L^{\lambda}$ . Summing this inequality over all vertices $u\in L^{\lambda}$ , we obtain

\displaystyle|L^{\lambda}|\frac{\sqrt{2n-4}}{10^{3}\lambda}\leq\sum_{u\in L^{\lambda}}d_{G}(u)\leq\sum_{u\in V(G)}d_{G}(u)\leq 2(3n-6).

It follows that $|L^{\lambda}|\leq 3\times 10^{3}\lambda\sqrt{2n-4}\leq\frac{\lambda n}{10^{5}}$ as $n\geq 2.16\times 10^{17}$ . ∎

Claim 2.3.

We have $|L^{1}|\leq 6\times 10^{4}$ .

Proof.

Let $u\in V(G)$ be an arbitrary vertex. For convenience, we use $N_{i}$ , $L_{i}^{\lambda}$ and $\overline{L_{i}^{\lambda}}$ instead of $N_{i}(u)$ , $N_{i}(u)\cap L^{\lambda}$ and $N_{i}(u)\setminus L^{\lambda}$ , respectively. By Claim 2.1, $\rho\geq\sqrt{2n-4}$ . Then

\displaystyle(2n-4)x_{u}\leq\rho^{2}x_{u}=d_{G}(u)x_{u}+\sum_{v\in N_{1}}\sum_{w\in N_{1}(v)\setminus\{u\}}x_{w}.

(2)

Note that $N_{1}(v)\setminus\{u\}\subseteq N_{1}\cup N_{2}=L_{1}^{\lambda}\cup L_{2}^{\lambda}\cup\overline{L_{1}^{\lambda}}\cup\overline{L_{2}^{\lambda}}$ . We can calculate $\sum_{v\in N_{1}}\sum_{w\in N_{1}(v)\setminus\{u\}}x_{w}$ according to two cases $w\in L_{1}^{\lambda}\cup L_{2}^{\lambda}$ or $w\in\overline{L_{1}^{\lambda}}\cup\overline{L_{2}^{\lambda}}$ . We first consider the case $w\in L_{1}^{\lambda}\cup L_{2}^{\lambda}$ . Clearly, $N_{1}=L_{1}^{\lambda}\cup\overline{L_{1}^{\lambda}}$ and $x_{w}\leq 1$ for $w\in L_{1}^{\lambda}\cup L_{2}^{\lambda}$ . We can see that

\displaystyle\sum_{v\in N_{1}}\sum_{w\in(L_{1}^{\lambda}\cup L_{2}^{\lambda})}\!\!x_{w}\leq\big{(}2e(L_{1}^{\lambda})+e(L_{1}^{\lambda},L_{2}^{\lambda})\big{)}+\sum_{v\in\overline{L_{1}^{\lambda}}}\sum_{w\in(L_{1}^{\lambda}\cup L_{2}^{\lambda})}\!\!\!x_{w}.

(3)

By Claim 2.2, we have $|L^{\lambda}|\leq\frac{\lambda n}{10^{5}}$ . Moreover, $L_{1}^{\lambda}\cup L_{2}^{\lambda}\subseteq L^{\lambda}$ . Then, by (1), we have

\displaystyle 2e(L_{1}^{\lambda})+e(L_{1}^{\lambda},L_{2}^{\lambda})\leq 2(3|L_{1}^{\lambda}|-6)+(2(|L_{1}^{\lambda}|+|L_{2}^{\lambda}|)-4)<8|L^{\lambda}|\leq\frac{8\lambda n}{10^{5}}.

(4)

Next, we consider the remain case $w\in\overline{L_{1}^{\lambda}}\cup\overline{L_{2}^{\lambda}}$ . Clearly, $x_{w}\leq\frac{1}{10^{3}\lambda}$ for $w\in\overline{L_{1}^{\lambda}}\cup\overline{L_{2}^{\lambda}}$ . Then

\displaystyle\sum_{v\in N_{1}}\sum_{w\in\overline{L_{1}^{\lambda}}\cup\overline{L_{2}^{\lambda}}}\!\!\!x_{w}\leq\Big{(}e(L_{1}^{\lambda},\overline{L_{1}^{\lambda}}\cup\overline{L_{2}^{\lambda}})+2e(\overline{L_{1}^{\lambda}})+e(\overline{L_{1}^{\lambda}},\overline{L_{2}^{\lambda}})\Big{)}\frac{1}{10^{3}\lambda}<\frac{6n}{10^{3}\lambda},

(5)

where $e(L_{1}^{\lambda},\overline{L_{1}^{\lambda}}\cup\overline{L_{2}^{\lambda}})+2e(\overline{L_{1}^{\lambda}})+e(\overline{L_{1}^{\lambda}},\overline{L_{2}^{\lambda}})\leq 2e(G)<6n$ .

Combining (2)-(5), we obtain

\displaystyle(2n-4)x_{u}<d_{G}(u)x_{u}+\sum_{v\in\overline{L_{1}^{\lambda}}}\sum_{w\in(L_{1}^{\lambda}\cup L_{2}^{\lambda})}\!\!\!x_{w}+\Big{(}\frac{8\lambda}{10}+\frac{60}{\lambda}\Big{)}\frac{n}{10^{4}}.

(6)

Now we prove that $d_{G}(u)\geq\frac{n}{10^{4}}$ for each $u\in L^{1}$ . Suppose to the contrary that there exists a vertex $\widetilde{u}\in L^{1}$ with $d_{G}(\widetilde{u})<\frac{n}{10^{4}}$ . Note that $x_{\widetilde{u}}\geq\frac{1}{10^{3}}$ as $\widetilde{u}\in L^{1}$ . Setting $u=\widetilde{u}$ , $\lambda=10$ and combining (6), we have

\displaystyle\frac{2n-4}{10^{3}}<d_{G}(\widetilde{u})x_{\widetilde{u}}+\sum_{v\in\overline{L_{1}^{10}}}\sum_{w\in(L_{1}^{10}\cup L_{2}^{10})}x_{w}+\frac{14n}{10^{4}}.

(7)

By (1), we have

\displaystyle e\big{(}\overline{L_{1}^{10}},L_{1}^{10}\cup L_{2}^{10}\big{)}<2\big{(}|\overline{L_{1}^{10}}|+|L_{1}^{10}\cup L_{2}^{10}|\big{)}\leq 2\big{(}|N_{1}|+|L^{10}|\big{)}\leq\frac{4n}{10^{4}},

where $|N_{1}|=d_{G}(\widetilde{u})<\frac{n}{10^{4}}$ and $|L^{10}|\leq\frac{n}{10^{4}}$ by Claim 2.2. Combining this with $d_{G}(\widetilde{u})<\frac{n}{10^{4}}$ gives

d_{G}(\widetilde{u})x_{\widetilde{u}}+\sum_{v\in\overline{L_{1}^{10}}}\sum_{w\in(L_{1}^{10}\cup L_{2}^{10})}x_{w}+\frac{14n}{10^{4}}\leq d_{G}(\widetilde{u})+e\big{(}\overline{L_{1}^{10}},L_{1}^{10}\cup L_{2}^{10}\big{)}+\frac{14n}{10^{4}}\leq\frac{19n}{10^{4}},

which contradicts (7). Therefore, $d_{G}(u)\geq\frac{n}{10^{4}}$ for each $u\in L^{1}$ . Summing this inequality over all vertices $u\in L^{1}$ , we obtain

|L^{1}|\frac{n}{10^{4}}\leq\sum_{u\in L^{1}}d_{G}(u)\leq 2e(G)\leq 6n,

which yields that $|L^{1}|\leq 6\times 10^{4}$ . ∎

For convenience, we use $L$ , $L_{i}$ and $\overline{L_{i}}$ instead of $L^{1}$ , $N_{i}(u)\cap L^{1}$ and $N_{i}(u)\setminus L^{1}$ , respectively. Now we give a lower bound for degrees of vertices in $L^{1}$ .

Claim 2.4.

For every $u\in L$ , we have $d_{G}(u)\geq(x_{u}-\frac{4}{1000})n$ .

Proof.

Let $\overline{L_{1}}^{\prime}$ be the subset of $\overline{L_{1}}$ in which each vertex has at least $2$ neighbors in $L_{1}\cup L_{2}$ . We first prove that $|\overline{L_{1}}^{\prime}|\leq|L_{1}\cup L_{2}|^{2}$ . If $|L_{1}\cup L_{2}|=1$ , then $\overline{L_{1}}^{\prime}$ is empty, as desired. It remains the case $|L_{1}\cup L_{2}|\geq 2$ . Suppose to the contrary that $|\overline{L_{1}}^{\prime}|>|L_{1}\cup L_{2}|^{2}$ . Since there are only $\binom{|L_{1}\cup L_{2}|}{2}$ options for vertices in $\overline{L_{1}}^{\prime}$ to choose a set of $2$ neighbors from $L_{1}\cup L_{2}$ , we can find a set of $2$ vertices in $L_{1}\cup L_{2}$ with at least $\Big{\lceil}|\overline{L_{1}}^{\prime}|/\binom{|L_{1}\cup L_{2}|}{2}\Big{\rceil}\geq 3$ common neighbors in $\overline{L_{1}}^{\prime}$ . Moreover, one can observe that $u\notin L_{1}\cup L_{2}$ and $\overline{L_{1}}^{\prime}\subseteq\overline{L_{1}}\subseteq N_{1}(u)$ . Hence, $G$ contains a copy of $K_{3,3}$ , contradicting that $G$ is planar. Hence, $|\overline{L_{1}}^{\prime}|\leq|L_{1}\cup L_{2}|^{2}$ . It follows that

\displaystyle e(\overline{L_{1}},L_{1}\cup L_{2})\leq|\overline{L_{1}}\setminus\overline{L_{1}}^{\prime}|+|L_{1}\cup L_{2}||\overline{L_{1}}^{\prime}|\leq d_{G}(u)+(6\times 10^{4})^{3}\leq d_{G}(u)+\frac{n}{1000},

where the second last inequality holds as $|\overline{L_{1}}^{\prime}|\leq|L_{1}\cup L_{2}|^{2}$ and $|L_{1}\cup L_{2}|\leq|L|\leq 6\times 10^{4}$ , and the last inequality holds as $n\geq 2.16\times 10^{17}$ . Setting $\lambda=1$ and combining the above inequality with (6), we have

\displaystyle(2n-4)x_{u}\leq d_{G}(u)+\Big{(}d_{G}(u)+\frac{n}{10^{3}}\Big{)}+\frac{61n}{10^{4}},

which yields that $d_{G}(u)\geq(n-2)x_{u}-\frac{71n}{2\times 10^{4}}\geq(x_{u}-\frac{4}{1000})n$ . ∎

Claim 2.5.

There exists a vertex $u^{\prime\prime}\in L_{1}\cup L_{2}$ such that $x_{u^{\prime\prime}}\geq\frac{988}{1000}$ .

Proof.

Setting $u=u^{\prime}$ , $\lambda=1$ and combining (6), we have

\displaystyle 2n-4<d_{G}(u^{\prime})+\sum_{v\in\overline{L_{1}}}\sum_{w\in L_{1}\cup L_{2}}\!\!\!x_{w}+\frac{61n}{10^{4}},

which yields that

\sum_{v\in\overline{L_{1}}}\sum_{w\in L_{1}\cup L_{2}}x_{w}\geq 2n-4-\frac{61n}{10^{4}}-d_{G}(u^{\prime})\geq\frac{993n}{1000}.

From Claim 2.4 we have $d_{G}(u^{\prime})\geq\frac{996n}{1000}$ as $u^{\prime}\in L$ . For simplicity, set $N_{L_{1}}(u^{\prime})=N_{G}(u^{\prime})\cap L_{1}$ and $d_{L_{1}}(u^{\prime})=|N_{L_{1}}(u^{\prime})|$ . By Claim 2.3, $|L|\leq 6\times 10^{4}$ . Then, $d_{L_{1}}(u^{\prime})\leq|L_{1}|\leq|L|\leq\frac{n}{1000}$ as $n\geq 2.16\times 10^{17}$ . It infers that

d_{\overline{L_{1}}}(u^{\prime})=d_{G}(u^{\prime})-d_{L_{1}}(u^{\prime})\geq d_{G}(u^{\prime})-|L|\geq\frac{995n}{1000}.

Combining this with (1) gives

e(\overline{L_{1}},L_{1}\cup L_{2})\leq e(\overline{L_{1}},L)-d_{\overline{L_{1}}}(u^{\prime})\leq(2n-4)-\frac{995n}{1000}\leq\frac{1005n}{1000}.

By averaging, there is a vertex $u^{\prime\prime}\in L_{1}\cup L_{2}$ such that

x_{u^{\prime\prime}}\geq\frac{\sum_{v\in\overline{L_{1}}}\sum_{w\in(L_{1}\cup L_{2})}x_{w}}{e(\overline{L_{1}},L_{1}\cup L_{2})}\geq\frac{\frac{993n}{1000}}{\frac{1005n}{1000}}\geq\frac{988}{1000},

as desired. ∎

Notice that $x_{u^{\prime}}=1$ and $x_{u^{\prime\prime}}\geq\frac{988}{1000}$ . By Claim 2.4, we have

\displaystyle d_{G}(u^{\prime})\geq\frac{996}{1000}n~{}~{}~{}\text{and}~{}~{}~{}d_{G}(u^{\prime\prime})\geq\frac{984}{1000}n.

(8)

Now, let $D=\{u^{\prime},u^{\prime\prime}\}$ , $R=N_{G}(u^{\prime})\cap N_{G}(u^{\prime\prime})$ , and $R_{1}=V(G)\setminus(D\cup R)$ . Thus, $|R_{1}|\leq(n-d_{G}(u^{\prime}))+(n-d_{G}(u^{\prime\prime}))\leq\frac{2n}{100}$ . Now, we prove that the eigenvector entries of vertices in $R\cup R_{1}$ are small.

Claim 2.6.

Let $u\in R\cup R_{1}$ . Then $x_{u}\leq\frac{1}{10}$ .

Proof.

For any vertex $u\in R_{1}$ , we can see that

\displaystyle d_{D}(u)\leq 1~{}~{}~{}\text{and}~{}~{}~{}d_{R}(u)\leq 2.

(9)

In fact, if $d_{R}(u)\geq 3$ , then $G[N_{G}(u)\cup D]$ contains a copy of $K_{3,3}$ , contradicting that $G$ is planar. By (9), $d_{G}(u)=d_{D}(u)+d_{R}(u)+d_{R_{1}}(u)\leq 3+d_{R_{1}}(u)$ . Note that $|R_{1}|\leq\frac{2n}{100}$ and $e(R_{1})\leq 3|R_{1}|$ by (1). Thus,

\rho\sum_{u\in R_{1}}x_{u}\leq\sum_{u\in R_{1}}d_{G}(u)\leq\sum_{u\in R_{1}}(3+d_{R_{1}}(u))\leq 3|R_{1}|+2e(R_{1})\leq 9|R_{1}|\leq\frac{18n}{100},

which yields $\sum_{u\in R_{1}}x_{u}\leq\frac{18n}{100\rho}$ . For any $u\in R\cup R_{1}$ , $d_{R}(u)\leq 2$ as $G$ is $K_{3,3}$ -free. It follows that

\rho x_{u}=\sum_{v\in N_{G}(u)}x_{v}\leq\sum_{v\in N_{D}(u)}x_{v}+\sum_{v\in N_{R}(u)}x_{v}+\sum_{v\in N_{R_{1}}(u)}x_{v}\leq 4+\frac{18n}{100\rho}.

Dividing both sides by $\rho$ , we get $x_{u}\leq\frac{1}{10}$ as $\rho\geq\sqrt{2n-4}$ . ∎

Refer to caption — Figure 1: A local structure of $G^{\prime}$ .

Claim 2.7.

$R_{1}$ is empty.

Proof.

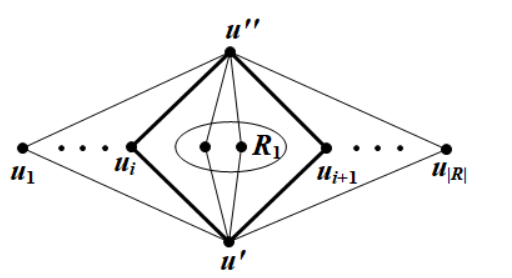
Suppose to the contrary that $a=|R_{1}|>0$ . Assume that $G^{*}$ is a planar embedding of $G[D\cup R]$ , and $u_{1},\dots,u_{|R|}$ are around $u^{\prime}$ in clockwise order in $G^{*}$ , with subscripts interpreted modulo $|R|$ . Recall that $|R_{1}|\leq\frac{2n}{100}$ . Then $|R|=n-2-|R_{1}|>\frac{97n}{100}>|R_{1}|$ . By the pigeonhole principle, there exists an integer $i\leq|R|$ such that $u^{\prime}u_{i}u^{\prime\prime}u_{i+1}u^{\prime}$ is a face of the plane graph $G^{*}$ . We modify the graph $G^{*}$ by joining each vertex in $R_{1}$ to each vertex in $D$ and making these edges cross the face $u^{\prime}u_{i}u^{\prime\prime}u_{i+1}u^{\prime}$ , to obtain the graph $G^{\prime}$ (see $G^{\prime}$ in Figure 1). Then, $G^{\prime}$ is a plane graph.

We first show that $G^{\prime}$ is $F$ -free. Suppose to the contrary, then $G^{\prime}$ contains a subgraph $F^{\prime}$ isomorphic to $F$ . From the modification, we can see that $V(F^{\prime})\cap R_{1}$ is not empty. Moreover, since $|R|>\frac{97n}{100}>|V(F)|=|V(F^{\prime})|$ , we have

|R\setminus V(F^{\prime})|=|R|-|R\cap V(F^{\prime})|>|V(F^{\prime})|-|V(F^{\prime})\cap R|\geq|V(F^{\prime})\cap R_{1}|.

Then, we may assume that $V(F^{\prime})\cap R_{1}=\{v_{1},\dots,v_{b}\}$ and $\{w_{1},\dots,w_{b}\}\in R\setminus V(F^{\prime})$ . Clearly, $N_{G^{\prime}}(v_{i})=D\subseteq N_{G^{\prime}}(w_{i})$ for each $i\in\{1,\dots,b\}$ . This indicates that a copy of $F$ is already present in $G$ , a contradiction. Therefore, $G^{\prime}$ is $F$ -free.

In what follows, we shall obtain a contradiction by showing that $\rho(G^{\prime})>\rho$ . Clearly, $G[R_{1}]$ is planar. Then, there exists a vertex $v_{1}\in R_{1}$ with $d_{R_{1}}(v_{1})\leq 5$ . Define $R_{2}=R_{1}\setminus\{v_{1}\}$ . Repeat this step, we obtain a sequence of sets $R_{1},R_{2},\cdots,R_{a}$ with $d_{R_{i}}(v_{i})\leq 5$ for each $i\in\{1,\ldots,a\}$ . Combining this with (9), we have

\displaystyle\sum_{w\in N_{D\cup R\cup R_{i}}(v_{i})}x_{w}\leq 1+\sum_{w\in N_{R}(v_{i})}x_{w}+\sum_{w\in N_{R_{i}}(v_{i})}x_{w}\leq\frac{17}{10},

(10)

where the last inequality holds as $x_{w}<\frac{1}{10}$ for any $w\in R\cup R_{1}$ by Claim 2.6. It is not hard to verify that in graph $G$ the set of edges incident to vertices in $R_{1}$ is $\bigcup_{i=1}^{a}\{wv_{i}~{}|~{}w\in N_{D\cup R\cup R_{i}}(v_{i})\}$ . Note that $x_{u^{\prime}}+x_{u^{\prime\prime}}\geq\frac{1988}{1000}$ . Combining these with (10), we have

\rho(G^{\prime})-\rho\geq\frac{2}{X^{\mathrm{T}}X}\sum_{i=1}^{a}x_{v_{i}}\left((x_{u^{\prime}}+x_{u^{\prime\prime}})-\sum_{w\in N_{D\cup R\cup R_{i}}(v_{i})}x_{w}\right)>0,

which contradicts that $G$ is extremal to ${\rm spex}_{\mathcal{P}}(n,F)$ . Therefore, $R_{1}$ is empty. ∎

By Claim 2.7, $G$ contains a copy of $K_{2,n-2}$ . The proof of Theorem 1.1 is complete. ∎

3 Proofs of Theorems 1.2 and 1.3

Recall that $G$ is an extremal graph to ${\rm spex}_{\mathcal{P}}(n,F)$ . In the case $F=C_{3}$ , by Theorem 1.1, $G$ contains a copy of $K_{2,n-2}$ . We further obtain that $G\cong K_{2,n-2}$ as $G$ is triangle-free (otherwise, adding any edge increases triangles, a contradiction). Now we consider the case $F\in\{C_{\ell}~{}|~{}\ell\geq 5\}\cup\{2C_{\ell}~{}|~{}\ell\geq 3\}$ . Let $P_{n}$ denote a path on $n$ vertices. For convenience, an isolated vertex is referred to as a path of order 1. We first give two lemmas to characterize the structural features of the extremal graph $G$ , which help us to present an approach to prove Theorems 1.2 and 1.3.

Lemma 3.1.

Let $n\geq\max\{2.16\times 10^{17},2|V(F)|\}$ and $F\in\{C_{\ell}~{}|~{}\ell\geq 5\}\cup\{2C_{\ell}~{}|~{}\ell\geq 3\}$ . Then $G\cong K_{2}+G[R]$ and $G[R]$ is a disjoint union of paths.

Proof.

Since $n\geq 2|V(F)|$ and $F\in\{C_{\ell}~{}|~{}\ell\geq 5\}\cup\{2C_{\ell}~{}|~{}\ell\geq 3\}$ , we can see that $F$ is a subgraph of $2K_{1}+P_{n/2}$ but not of $K_{2,n-2}$ . Hence, by Theorem 1.1, $G$ contains a copy of $K_{2,n-2}$ , and $u^{\prime},u^{\prime\prime}$ are the vertices of degree $n-2$ and $R$ is the set of vertices of degree two in $K_{2,n-2}$ .

Claim 3.1.

$u^{\prime}u^{\prime\prime}\in E(G)$ .

Proof.

Suppose to the contrary that $u^{\prime}u^{\prime\prime}\notin E(G)$ . Assume that $G^{*}$ is a planar embedding of $G$ , and $u_{1},\dots,u_{n-2}$ are around $u^{\prime}$ in clockwise order in $G^{*}$ , with subscripts interpreted modulo $n-2$ . If $R$ induces an cycle $u_{1}u_{2}\dots u_{n-2}u_{1}$ , then we can easily check that $G^{*}$ contains a copy of $F$ , a contradiction. Thus, there exists an integer $i\leq n-2$ such that $u_{i}u_{i+1}\notin E(G^{*}[R])$ . Furthermore, $u^{\prime}u_{i}u^{\prime\prime}u_{i+1}u^{\prime}$ is a face in $G^{*}$ .

We modify the graph $G^{*}$ by adding the edge $u^{\prime}u^{\prime\prime}$ and making $u^{\prime}u^{\prime\prime}$ cross the face $u^{\prime}u_{i}u^{\prime\prime}u_{i+1}u^{\prime}$ , to obtain the graph $G^{\prime}$ . Clearly, $G^{\prime}$ is a plane graph. We shall show that $G^{\prime}$ is $F$ -free. Suppose to the contrary that $G^{\prime}$ contains a subgraph $F^{\prime}$ isomorphic to $F$ . If $F^{\prime}=C_{\ell}$ for some $\ell\geq 5$ , then $G^{\prime}$ contains an $\ell$ -cycle containing $u^{\prime}u^{\prime\prime}$ , say $u^{\prime}u^{\prime\prime}u_{1}^{\prime}u_{2}^{\prime}\dots u_{\ell-2}^{\prime}u^{\prime}$ . However, an ${\ell}$ -cycle $u^{\prime}u_{1}^{\prime}u^{\prime\prime}u_{2}^{\prime}\dots u_{\ell-2}^{\prime}u^{\prime}$ is already present in $G$ , a contradiction. If $F^{\prime}=2C_{\ell}$ for some $\ell\geq 3$ , then $F^{\prime}$ contains two vertex-disjoint $\ell$ -cycles $C^{1}$ and $C^{2}$ . From the modification, we can see that one of $C^{1}$ and $C^{2}$ (say $C^{1}$ ) contains the edge $u^{\prime}u^{\prime\prime}$ . This implies that $C^{2}$ is a subgraph of $G[R]$ . However, $G[V(C^{2})\cup\{u^{\prime},u^{\prime\prime}\}]$ contains a $K_{5}$ -minor, contradicting the fact that $G$ is planar. Hence, $G^{\prime}$ is $F$ -free. However, $\rho(G^{\prime})>\rho$ , contradicting that $G$ is extremal to ${\rm spex}_{\mathcal{P}}(n,F)$ . Therefore, $u^{\prime}u^{\prime\prime}\in E(G)$ . ∎

From Claim 3.1 we know that $G=K_{2}+G[R]$ . It remains to show that $G[R]$ is a disjoint union of paths. Theorem 1.1 and Claim 3.1 imply that $u^{\prime}$ and $u^{\prime\prime}$ are dominating vertices. Furthermore, since $G$ is $K_{5}$ -minor-free and $K_{3,3}$ -minor-free, we can see that $G[R]$ is $K_{3}$ -minor-free and $K_{1,3}$ -minor-free. This implies that $G[R]$ is an acyclic graph with maximum degree at most 2. Thus, $G[R]$ is a disjoint union of paths. The result follows. ∎

Now we give a transformation that we will use in subsequent proof.

Definition 3.1.

Let $s_{1}$ and $s_{2}$ be two integers with $s_{1}\geq s_{2}\geq 1$ , and let $H=P_{s_{1}}\cup P_{s_{2}}\cup H_{0}$ , where $H_{0}$ is a disjoint union of paths. We say that $H^{*}$ is an $(s_{1},s_{2})$ -transformation of $H$ if

H^{*}:=\left\{\begin{array}[]{ll}P_{s_{1}+1}\cup P_{s_{2}-1}\cup H_{0}&\hbox{if $s_{2}\geq 2$,}\\ P_{s_{1}+s_{2}}\cup H_{0}{}{}{}{}{}{}{}&\hbox{if $s_{2}=1$.}\end{array}\right.

Clearly, $H^{*}$ is a disjoint union of paths, which implies that $K_{2}+H^{*}$ is planar. If $G[R]\cong H$ , then we shall show that $\rho(K_{2}+H^{*})>\rho$ for sufficiently large $n$ .

Lemma 3.2.

Let $H$ and $H^{*}$ be defined as in Definition 3.1, $n\geq\max\{2.16\times 10^{17},2|V(F)|,9\times 2^{s_{2}+1}+3\}$ and $F\in\{C_{\ell}~{}|~{}\ell\geq 5\}\cup\{2C_{\ell}~{}|~{}\ell\geq 3\}$ . If $G[R]\cong H$ , then $\rho(K_{2}+H^{*})>\rho$ .

Proof.

By Lemma 3.1, $G\cong K_{2}+G[R]$ and $G[R]$ is a disjoint union of paths. If $G[R]\cong H$ , then $G=K_{2}+H$ . Assume that $P^{1}:=v_{1}v_{2}\dots v_{s_{1}}$ and $P^{2}:=w_{1}w_{2}\dots w_{s_{2}}$ are two components of $H$ . If $s_{2}=1$ , then $H\subset H^{*}$ , and so $G\subset K_{2}+H^{*}$ . It follows that $\rho(P_{2}+H^{*})>\rho$ , the result holds. Next, we deal with the case $s_{2}=2$ . If $x_{v_{1}}\leq x_{w_{1}}$ , then let $H^{\prime}$ be obtained from $H$ by deleting the edge $v_{1}v_{2}$ and adding the edge $v_{2}w_{1}$ . Clearly, $H^{\prime}\cong H^{*}$ . Moreover,

\displaystyle\rho(K_{2}+H^{*})-\rho\geq\frac{X^{\mathrm{T}}\big{(}A(K_{2}+H^{*})-A(G)\big{)}X}{X^{\mathrm{T}}X}\geq\frac{2}{X^{\mathrm{T}}X}(x_{w_{1}}-x_{v_{1}})x_{v_{2}}\geq 0.

Since $X$ is a positive eigenvector of $G$ , we have $\rho x_{v_{1}}=2+x_{v_{2}}$ . If $\rho(K_{2}+H^{*})=\rho$ , then $X$ is also a positive eigenvector of $K_{2}+H^{*}$ , and so $\rho(K_{2}+H^{*})x_{v_{1}}=2$ , contradicting that $\rho x_{v_{1}}=2+x_{v_{2}}$ . Thus, $\rho(K_{2}+H^{*})>\rho$ , the result holds. The case $x_{v_{1}}>x_{w_{1}}$ is similar and hence omitted here.

It remains the case $s_{2}\geq 3$ . We shall give characterizations of eigenvector entries of vertices in $R$ in the following two claims.

Claim 3.2.

For any vertex $u\in R$ , we have $x_{u}\in[\frac{2}{\rho},\frac{2}{\rho}+\frac{6}{\rho^{2}}]$ .

Proof.

By Lemma 3.1, $u^{\prime}$ and $u^{\prime\prime}$ are dominating vertices of $G$ . So, $x_{u^{\prime}}=x_{u^{\prime\prime}}=1$ . Hence

\displaystyle\rho x_{u}=x_{u^{\prime}}+x_{u^{\prime\prime}}+\sum_{v\in N_{R}(u)}x_{v}=2+\sum_{v\in N_{R}(u)}x_{v}.

(11)

Moreover, by Lemma 3.1, $d_{R}(v)\leq 2$ for any $v\in R$ . Combining this with Claim 2.6 and (11) gives $x_{u}\in\big{[}\frac{2}{\rho},\frac{3}{\rho}\big{]}$ . Furthermore, again by (11), $\rho x_{u}\in\big{[}2,2+\frac{6}{\rho}\big{]}$ , which yields that $x_{u}\in\big{[}\frac{2}{\rho},\frac{2}{\rho}+\frac{6}{\rho^{2}}\big{]}$ . ∎

Claim 3.3.

Let $i$ be a positive integer. Set $A_{i}=\big{[}\frac{2}{\rho}-\frac{6\times 2^{i}}{\rho^{2}},\frac{2}{\rho}+\frac{6\times 2^{i}}{\rho^{2}}\big{]}$ and $B_{i}=\big{[}-\frac{6\times 2^{i}}{\rho^{2}},\frac{6\times 2^{i}}{\rho^{2}}\big{]}$ . Then,
(i) for any $i\in\{1,\dots,\lfloor\frac{s_{1}-1}{2}\rfloor\}$ , $\rho^{i}(x_{v_{i+1}}-x_{v_{i}})\in A_{i}$ ;
(ii) for any $i\in\{1,\dots,\lfloor\frac{s_{2}-1}{2}\rfloor\}$ , $\rho^{i}(x_{w_{i+1}}-x_{w_{i}})\in B_{i}$ ;
(iii) for any $i\in\{1,\dots,\lfloor\frac{s_{2}}{2}\rfloor\}$ , $\rho^{i}(x_{v_{i}}-x_{w_{i}})\in B_{i}$ .

Proof.

(i) It suffices to prove that for any $i\in\{1,\dots,\lfloor\frac{s_{1}-1}{2}\rfloor\}$ ,

\displaystyle\rho^{i}(x_{v_{j+1}}-x_{v_{j}})\in\left\{\begin{array}[]{ll}A_{i}&\hbox{if $j=i$,}\\ B_{i}&\hbox{if $i+1\leq j\leq s_{1}-i-1$.}\end{array}\right.

We shall proceed the proof by induction on $i$ . Clearly,

\displaystyle\rho x_{v_{j}}=\sum_{v\in N_{G}(v_{j})}x_{v}=\left\{\begin{array}[]{ll}2+x_{v_{2}}&\hbox{if $j=1$,}\\ 2+x_{v_{j-1}}+x_{v_{j+1}}&\hbox{if $2\leq j\leq s_{1}-1$.}\end{array}\right.

(15)

By Claim 3.2, we have

\displaystyle\rho(x_{v_{j+1}}-x_{v_{j}})=\left\{\begin{array}[]{ll}x_{v_{1}}+x_{v_{3}}-x_{v_{2}}\in A_{1}&\hbox{if $j=1$,}\\ (x_{v_{j}}-x_{v_{j-1}})+(x_{v_{j+2}}-x_{j+1})\in B_{1}&\hbox{if $2\leq j\leq s_{1}-2$.}\end{array}\right.

(18)

So the result is true when $i=1$ . Assume then that $2\leq i\leq\lfloor\frac{s_{1}-1}{2}\rfloor$ , which implies that $s_{1}\geq 2i+1$ . For $i\leq j\leq s_{1}-i-1$ , $\rho(x_{v_{j+1}}-x_{v_{j}})=(x_{v_{j}}-x_{v_{j-1}})+(x_{v_{j+2}}-x_{v_{j+1}})$ , and so

\displaystyle\rho^{i}(x_{v_{j+1}}-x_{v_{j}})=\rho^{i-1}(x_{v_{j}}-x_{v_{j-1}})+\rho^{i-1}(x_{v_{j+2}}-x_{v_{j+1}}).

(19)

By the induction hypothesis, $\rho^{i-1}(x_{v_{i}}-x_{v_{i-1}})\in A_{i-1}$ and $\rho^{i-1}(x_{v_{i+2}}-x_{v_{i+1}})\in B_{i-1}$ . Setting $j=i$ and combining (19), we have $\rho^{i}(x_{v_{i+1}}-x_{v_{i}})\in A_{i}$ , as desired. If $i+1\leq j\leq s_{1}-i-1$ , then by the induction hypothesis, $\rho^{i-1}(x_{v_{j}}-x_{v_{j-1}})\in B_{i-1}$ and $\rho^{i-1}(x_{v_{j+2}}-x_{v_{j+1}})\in B_{i-1}$ . Thus, by (19), we have $\rho^{i}(x_{v_{j+1}}-x_{v_{j}})\in B_{i}$ , as desired. Hence the result holds.

The proof of (ii) is similar to that of (i) and hence omitted here.

(iii) It suffices to prove that for any $i\in\{1,\dots,\lfloor\frac{s_{2}}{2}\rfloor\}$ and $j\in\{i,\dots,s_{2}-i\}$ , $\rho^{i}(x_{v_{j}}-x_{w_{j}})\in B_{i}.$ We shall proceed the proof by induction on $i$ . Clearly,

\rho x_{w_{j}}=\sum_{w\in N_{G}(w_{j})}x_{w}=\left\{\begin{array}[]{ll}2+x_{w_{2}}&\hbox{if $j=1$,}\\ 2+x_{w_{j-1}}+x_{w_{j+1}}&\hbox{if $2\leq j\leq s_{2}-1$.}\end{array}\right.

Combining this with (15) and Claim 3.2 gives

\rho(x_{v_{j}}-x_{w_{j}})=\left\{\begin{array}[]{ll}x_{v_{2}}-x_{w_{2}}\in\big{[}-\frac{6}{\rho^{2}},\frac{6}{\rho^{2}}\big{]}\subset B_{1}&\hbox{if $j=1$,}\\ (x_{v_{j+1}}-x_{w_{j+1}})+(x_{v_{j-1}}-x_{w_{j-1}})\in B_{1}&\hbox{if $2\leq j\leq s_{2}-1$.}\end{array}\right.

So the claim is true when $i=1$ . Assume then that $2\leq i\leq\lfloor\frac{s_{2}}{2}\rfloor$ , which implies that $s_{2}\geq 2i$ . If $i\leq j\leq s_{2}-i$ , then $\rho(x_{v_{j}}-x_{w_{j}})=(x_{v_{j-1}}-x_{w_{j-1}})+(x_{v_{j+1}}-x_{w_{j+1}})$ , and so

\displaystyle\rho^{i}(x_{v_{j}}-x_{w_{j}})=\rho^{i-1}(x_{v_{j-1}}-x_{w_{j-1}})+\rho^{i-1}(x_{v_{j+1}}-x_{w_{j+1}}).

(20)

By the induction hypothesis, $\rho^{i-1}(x_{v_{j-1}}-x_{w_{j-1}})\in B_{i-1}$ and $\rho^{i-1}(x_{v_{j+1}}-x_{w_{j+1}})\in B_{i-1}$ . Combining these with (20), we have $\rho^{i}(x_{v_{j}}-x_{w_{j}})=B_{i}$ . Hence the result holds. ∎

Since $n\geq 9\times 2^{s_{2}+1}+3$ , we have $\rho\geq\sqrt{2n-4}>6\times 2^{s_{2}/{2}}$ , and so

\displaystyle\frac{2}{\rho^{i+1}}-\frac{6\times 2^{i}}{\rho^{i+2}}>\left(\frac{2}{\rho^{i+1}}-\frac{6\times 2^{i}}{\rho^{i+2}}\right)-\frac{6\times 2^{i}}{\rho^{i+2}}>0~{}~{}\text{for any}~{}~{}i\leq\frac{s_{2}}{2}.

Combining this with Claim 3.3, we obtain

\displaystyle x_{v_{i+1}}-x_{v_{i}}\geq\frac{2}{\rho^{i+1}}-\frac{6\times 2^{i}}{\rho^{i+2}}>0~{}~{}\text{for any}~{}~{}i\leq\min\Big{\{}\frac{s_{2}}{2},\Big{\lfloor}\frac{s_{1}-1}{2}\Big{\rfloor}\Big{\}},

(21)

and

\displaystyle x_{v_{i+1}}-x_{w_{i}}=(x_{v_{i+1}}-x_{v_{i}})+(x_{v_{i}}-x_{w_{i}})\geq\left(\frac{2}{\rho^{i+1}}-\frac{6\times 2^{i}}{\rho^{i+2}}\right)-\frac{6\times 2^{i}}{\rho^{i+2}}>0

(22)

for any $i\leq\min\big{\{}\big{\lfloor}\frac{s_{2}}{2}\big{\rfloor},\big{\lfloor}\frac{s_{1}-1}{2}\big{\rfloor}\big{\}}$ . Similarly,

\displaystyle x_{w_{i+1}}>x_{w_{i}}~{}~{}\text{and}~{}~{}x_{w_{i+1}}>x_{v_{i}}~{}~{}\text{for any}~{}~{}i\leq\Big{\lfloor}\frac{s_{2}-1}{2}\Big{\rfloor}.

(23)

Recall that $s_{2}\geq 3$ . Let $t_{1},t_{2}$ be integers with $t_{1},t_{2}\geq 1$ and $t_{1}+t_{2}=s_{2}-1$ , and $H^{\prime}$ be obtained from $H$ by deleting edges $v_{t_{1}}v_{t_{1}+1},w_{t_{2}}w_{t_{2}+1}$ and adding edges $v_{t_{1}}w_{t_{2}},v_{t_{1}+1}w_{t_{2}+1}$ . Since $t_{1}+t_{2}=s_{2}-1$ , we can see that $H^{\prime}\cong H^{*}$ . Moreover,

\displaystyle\rho(K_{2}+H^{*})-\rho\geq\frac{X^{\mathrm{T}}\big{(}A(K_{2}+H^{*})-A(G)\big{)}X}{X^{\mathrm{T}}X}\geq\frac{2}{X^{\mathrm{T}}X}(x_{v_{t_{1}+1}}-x_{w_{t_{2}}})(x_{w_{t_{2}+1}}-x_{v_{t_{1}}}).

(24)

Now, we consider the following two cases to complete the proof.

Case 1. $s_{2}$ is odd.

Set $t_{1}=\frac{s_{2}-1}{2}$ . Then, $t_{2}=\frac{s_{2}-1}{2}$ as $t_{1}+t_{2}=s_{2}-1$ . By (22) and (23), we have $x_{v_{t_{1}+1}}>x_{w_{t_{2}}}$ and $x_{w_{t_{2}+1}}>x_{v_{t_{1}}}$ , and so $\rho(K_{2}+H^{*})>\rho$ by (24), as desired.

Case 2. $s_{2}$ is even.

We only consider the subcase $x_{w_{s_{2}/2}}\geq x_{v_{s_{2}/2}}$ . The proof of the subcase $x_{w_{s_{2}/2}}<x_{v_{s_{2}/2}}$ is similar and hence omitted here. Set $t_{1}=\frac{s_{2}}{2}$ . Then, $t_{2}=\frac{s_{2}-2}{2}$ as $t_{1}+t_{2}=s_{2}-1$ . Moreover, $x_{w_{t_{2}+1}}\geq x_{v_{t_{1}}}$ , as $x_{w_{s_{2}/2}}\geq x_{v_{s_{2}/2}}$ . If $s_{1}=s_{2}$ , then $s_{1}$ is even. This implies that $x_{v_{(s_{1}+2)/2}}=x_{v_{s_{1}/2}}$ by symmetry, that is, $x_{v_{t_{1}+1}}=x_{v_{t_{1}}}$ . If $s_{1}\geq s_{2}+1$ , then by (21), $x_{v_{t_{1}+1}}>x_{v_{t_{1}}}$ . In both situations, we have $x_{v_{t_{1}+1}}\geq x_{v_{t_{1}}}$ . From (22) we have $x_{v_{t_{1}}}>x_{w_{t_{2}}}$ , which implies that $x_{v_{t_{1}+1}}>x_{w_{t_{2}}}$ . Furthermore, we have $\rho(K_{2}+H^{*})\geq\rho$ by (24). If $\rho(K_{2}+H^{*})=\rho$ , then $X$ is a positive eigenvector of $K_{2}+H^{*}$ , and so $\rho(K_{2}+H^{*})x_{v_{t_{1}}}=2+x_{v_{t_{1}-1}}+x_{w_{t_{2}}}$ . On the other hand, $\rho x_{v_{t_{1}}}=2+x_{v_{t_{1}-1}}+x_{v_{t_{1}+1}}$ , since $X$ is a positive eigenvector of $G$ . It follows that $x_{v_{t_{1}+1}}=x_{w_{t_{2}}}$ , which is a contradiction. Thus, $\rho(K_{2}+H^{*})>\rho$ , as desired.

This completes the proof of Lemma 3.2. ∎

From Lemma 3.1, we may assume that $G[R]=\cup_{i=1}^{t}P_{n_{i}}$ , where $t\geq 2$ and $n_{1}\geq n_{2}\geq\cdots\geq n_{t}$ . Let $H$ be a disjoint union of $t$ paths. We use $n_{i}(H)$ to denote the order of the $i$ -th longest path of $H$ for any $i\in\{1,\dots,t\}$ . Having Lemmas 3.1 and 3.2, we are ready to complete the proofs of Theorems 1.2 and 1.3.

Proof of Theorem 1.2. We first give the following claim.

Claim 3.4.

If $H$ is a disjoint union of $t\geq 2$ paths, then $K_{2}+H$ is $2C_{\ell}$ -free if and only if $n_{1}(H)\leq 2\ell-3$ and $n_{2}(H)\leq\ell-2$ .

Proof.

We first claim that $K_{2}+H$ is $2C_{\ell}$ -free if and only if $P_{n_{1}(H)}\cup P_{n_{2}(H)}$ is $2P_{\ell-1}$ -free. Equivalently, $K_{2}+H$ contains a copy of $2C_{\ell}$ if and only if $P_{n_{1}(H)}\cup P_{n_{2}(H)}$ contains a copy of $2P_{\ell-1}$ . Assume that $K_{2}+H$ contains two vertex-disjoint $\ell$ -cycles $C^{1}$ and $C^{2}$ , and $V(K_{2})=\{u^{\prime},u^{\prime\prime}\}$ . Since $H$ is acyclic, we can see that $C^{i}$ must contain at least one vertex of $u^{\prime}$ and $u^{\prime\prime}$ for any $i\in\{1,2\}$ . Without loss of generality, assume that $u^{\prime}\in V(C^{1})$ and $u^{\prime\prime}\in V(C^{2})$ . Then, $C^{1}-\{u^{\prime}\}\cong C^{2}-\{u^{\prime\prime}\}\cong P_{\ell-1}$ , and so $H$ contains a $2P_{\ell-1}$ . We can further find that $P_{n_{1}(H)}\cup P_{n_{2}(H)}$ contains a $2P_{\ell-1}$ . Conversely, assume that $P_{n_{1}(H)}\cup P_{n_{2}(H)}$ contains two vertex-disjoint paths $P^{1}$ and $P^{2}$ such that $P^{1}\cong P^{2}\cong P_{\ell-1}$ . Thus, the subgraph induced by $V(P^{1})\cup\{u^{\prime}\}$ contains a copy of $C_{\ell}$ . Similarly, the subgraph induced by $V(P^{2})\cup\{u^{\prime\prime}\}$ contains a copy of $C_{\ell}$ . This indicates that $K_{2}+H$ contains a copy of $2C_{\ell}$ . So, the claim holds.

Next, we claim that $P_{n_{1}(H)}\cup P_{n_{2}(H)}$ is $2P_{\ell-1}$ -free if and only if $n_{1}(H)\leq 2\ell-3$ and $n_{2}(H)\leq\ell-2$ . If $P_{n_{1}(H)}\cup P_{n_{2}(H)}$ is $2P_{\ell-1}$ -free, then $n_{1}(H)\leq 2\ell-3$ (otherwise, $P_{n_{1}(H)}$ contains a copy of $2P_{\ell-1}$ , a contradiction); $n_{2}(H)\leq\ell-2$ (otherwise, $P_{n_{1}(H)}\cup P_{n_{2}(H)}$ contains a copy of $2P_{\ell-1}$ as $n_{1}(H)\geq n_{2}(H)\geq\ell-1$ , a contradiction). Conversely, if $n_{1}(H)\leq 2\ell-3$ and $n_{2}(H)\leq\ell-2$ , then it is not hard to verify that $P_{n_{1}(H)}\cup P_{n_{2}(H)}$ is $2P_{\ell-1}$ -free.

This completes the proof of Claim 3.4. ∎

Recall that $n_{i}$ (resp. $n_{i}(H)$ ) is the order of the $i$ -th longest path of $G[R]$ (resp. $H$ ) for any $i\in\{1,\dots,t\}$ . By Claim 3.4, $n_{1}\leq 2\ell-3$ and $n_{2}\leq\ell-2$ . By a direct computation, we have $9\times 2^{\ell-1}+3\geq\max\{2|V(F)|,9\times 2^{n_{2}+1}+3\}$ , and hence

\displaystyle n\geq\max\{2.16\times 10^{17},2|V(F)|,9\times 2^{n_{2}+1}+3\}.

(25)

We first claim that $n_{1}=2\ell-3$ . Suppose to the contrary that $n_{1}\leq 2\ell-4$ . Let $H^{\prime}$ be an $(n_{1},n_{t})$ -transformation of $G[R]$ . Clearly, $n_{1}(H^{\prime})=n_{1}(H)+1\leq 2\ell-3$ and $n_{2}(H^{\prime})=n_{2}\leq\ell-2$ . By Claim 3.4, $K_{2}+H^{\prime}$ is $2C_{\ell}$ -free. However, by (25) and Lemma 3.2, we have $\rho(K_{2}+H^{\prime})>\rho$ , contradicting that $G$ is extremal to ${\rm spex}_{\mathcal{P}}(n,2C_{\ell})$ . Thus, $n_{1}=2\ell-3$ , the claim holds.

Note that $n_{i}\leq n_{2}\leq\ell-2$ for each $i\in\{2,\dots,t-1\}$ . We then claim that $n_{i}=\ell-2$ for $i\in\{2,\dots,t-1\}$ . If $\ell=3$ , then $n_{i}=1$ , as $n_{i}\leq\ell-2$ , for each $i\in\{2,\dots,t\}$ and the claim holds trivially. Now let $\ell\geq 4$ . Suppose to the contrary, then set $i_{0}=\min\{i~{}|~{}2\leq i\leq t-1,n_{i}\leq\ell-3\}.$ Let $H^{\prime}$ be an $(n_{i_{0}},n_{t})$ -transformation of $G[R]$ . Clearly, $n_{1}(H^{\prime})=n_{1}=2\ell-3$ and $n_{2}(H^{\prime})=\max\{n_{2},n_{i_{0}}+1\}\leq\ell-2$ . By Claim 3.4, $K_{2}+H^{\prime}$ is $2C_{\ell}$ -free. However, by (25) and Lemma 3.2, we have $\rho(K_{2}+H^{\prime})>\rho$ , contradicting that $G$ is extremal to ${\rm spex}_{\mathcal{P}}(n,2C_{\ell})$ . So, the claim holds.

Since $n_{1}=2\ell-3$ , $n_{i}=\ell-2$ for $i\in\{2,\dots,t-1\}$ and $n_{t}\leq\ell-2$ , we can see that $G[R]\cong H(2\ell-3,\ell-2)$ . This completes the proof of Theorem 1.2. $\Box$

Proof of Theorem 1.3. It remains the case $\ell\geq 5$ . We first give the following claim.

Claim 3.5.

If $H$ is a disjoint union of $t\geq 2$ paths, then $K_{2}+H$ is $C_{\ell}$ -free if and only if $n_{1}(H)+n_{2}(H)\leq\ell\!-\!3$ .

Proof.

One can observe that the longest cycle in $K_{2}+H$ is of order $n_{1}(H)+n_{2}(H)+2$ . Furthermore, $K_{2}+(P_{n_{1}(H)}\cup P_{n_{2}(H)})$ contains a cycle $C_{i}$ for each $i\in\{3,\dots,n_{1}(H)+n_{2}(H)+2\}$ . Consequently, $n_{1}(H)+n_{2}(H)+2\leq\ell-1$ if and only if $K_{2}+H$ is $C_{\ell}$ -free. Hence, the claim holds. ∎

By Claim 3.5, $n_{1}+n_{2}\leq\ell-3$ , which implies that $n_{2}\leq\lfloor\frac{\ell-3}{2}\rfloor$ as $n_{1}\geq n_{2}$ . By a direct computation, we have $9\times 2^{\lfloor\frac{\ell-1}{2}\rfloor}+3\geq\max\{2|V(F)|,9\times 2^{n_{2}+1}+3\}$ , and hence

\displaystyle n\geq\max\{2.16\times 10^{17},2|V(F)|,9\times 2^{n_{2}+1}+3\}.

(26)

Since $\ell\geq 5$ , we have $\lfloor\frac{\ell-3}{2}\rfloor\geq 1$ , which implies that $\lfloor\frac{\ell-3}{2}\rfloor^{2}\geq\lfloor\frac{\ell-3}{2}\rfloor$ and $3\lfloor\frac{\ell-3}{2}\rfloor^{2}\geq 2\lfloor\frac{\ell-3}{2}\rfloor+1\geq\ell-3$ . Consequently, since $n\geq\frac{625}{32}\lfloor\frac{\ell-3}{2}\rfloor^{2}+2>6\lfloor\frac{\ell-3}{2}\rfloor^{2}+2$ , we have

\displaystyle n>\Big{\lfloor}\frac{\ell-3}{2}\Big{\rfloor}^{2}+2\Big{\lfloor}\frac{\ell-3}{2}\Big{\rfloor}+(\ell-3)+2\geq n_{2}^{2}+3n_{2}+n_{1}+2

(27)

as $n_{2}\leq\lfloor\frac{\ell-3}{2}\rfloor$ and $n_{1}+n_{2}\leq\ell-3$ . On the other hand, $n-2=\sum_{i=1}^{t}n_{i}\leq n_{1}+(t-1)n_{2}$ , which implies that $t\geq\frac{n-2-n_{1}}{n_{2}}+1\geq n_{2}+4$ by (27).

We first claim that $n_{1}+n_{2}=\ell-3$ . Suppose to the contrary that $n_{1}+n_{2}\leq\ell-4$ . Let $H^{\prime}$ be an $(n_{1},n_{t})$ -transformation of $G[R]$ . Clearly, $n_{1}(H^{\prime})=n_{1}+1\leq\ell-3-n_{2}$ and $n_{2}(H^{\prime})=n_{2}$ . Then, $n_{1}(H^{\prime})+n_{2}(H^{\prime})\leq\ell-3$ . By Claim 3.5, $K_{2}+H^{\prime}$ is $C_{\ell}$ -free. However, by (26) and Lemma 3.2, we have $\rho(K_{2}+H^{\prime})>\rho$ , contradicting that $G$ is extremal to ${\rm spex}_{\mathcal{P}}(n,C_{\ell})$ . Hence, the claim holds.

Secondly, we claim that $n_{i}=n_{2}$ for $i\in\{3,\dots,t-1\}$ . Suppose to the contrary, then set $i_{0}=\min\{i~{}|~{}3\leq i\leq t-1,n_{i}\leq n_{2}-1\}$ . Let $H^{\prime}$ be an $(n_{i_{0}},n_{t})$ -transformation of $G[R]$ . Clearly, $n_{1}(H^{\prime})=n_{1}$ and $n_{2}(H^{\prime})=\max\{n_{2},n_{i_{0}}+1\}=n_{2}$ , and so $n_{1}(H^{\prime})+n_{2}(H^{\prime})=\ell-3$ . By Claim 3.5, $K_{2}+H^{\prime}$ is $C_{\ell}$ -free. However, by (26) and Lemma 3.2, we have $\rho(K_{2}+H^{\prime})>\rho$ , contradicting that $G$ is extremal to ${\rm spex}_{\mathcal{P}}(n,C_{\ell})$ . Hence, the claim holds. It follows that $G=K_{2}+(P_{n_{1}}\cup(t-2)P_{n_{2}}\cup P_{n_{t}})$ .

Finally, we claim that $n_{2}=\lfloor\frac{\ell-3}{2}\rfloor$ . Note that $1\leq n_{2}\leq\lfloor\frac{\ell-3}{2}\rfloor$ . Then, $n_{2}=\lfloor\frac{\ell-3}{2}\rfloor$ for $\ell\in\{5,6\}$ . It remains the case $\ell\geq 7$ . Suppose to the contrary, then $n_{2}\leq\lfloor\frac{\ell-5}{2}\rfloor$ as $n_{2}\leq\lfloor\frac{\ell-3}{2}\rfloor$ . We use $P^{i}$ to denote the $i$ -th longest path of $G[R]$ for $i\in\{1,\dots,t\}$ . Recall that $t\geq n_{2}+4$ . Then $P^{2},P^{3},\dots,P^{n_{2}+3}$ are paths of order $n_{2}$ . We may assume that $P^{n_{2}+3}=w_{1}w_{2}\dots w_{n_{2}}$ . Since $n_{1}=\ell-3-n_{2}\geq\lceil\frac{\ell-3}{2}\rceil\geq 2$ , there exists an endpoint $w^{\prime}$ of $P^{1}$ with $w^{\prime}w^{\prime\prime}\in E(P^{1})$ . Let $G^{\prime}$ be obtained from $G$ by (i) deleting $w^{\prime}w^{\prime\prime}$ and joining $w^{\prime}$ to an endpoint of $P^{n_{2}+2}$ ; (ii) deleting all edges of $P^{n_{2}+3}$ and joining $w_{i}$ to an endpoint of $P^{i+1}$ for each $i\in\{1,\dots,n_{2}\}$ . Then, $G^{\prime}$ is obtained from $G$ by deleting $n_{2}$ edges and adding $n_{2}+1$ edges. By Claim 3.2, we obtain

\frac{4}{\rho^{2}}<x_{u_{i}}x_{u_{j}}<\frac{4}{\rho^{2}}+\frac{24}{\rho^{3}}+\frac{36}{\rho^{4}}<\frac{4}{\rho^{2}}+\frac{25}{\rho^{3}}

for any vertices $u_{i},u_{j}\in R$ . Then

\rho(G^{\prime})-\rho\geq\frac{X^{\mathrm{T}}(A(G^{\prime})-A(G))X}{X^{\mathrm{T}}X}>\frac{2}{X^{\mathrm{T}}X}\left(\frac{4(n_{2}+1)}{\rho^{2}}-\frac{4n_{2}}{\rho^{2}}-\frac{25n_{2}}{\rho^{3}}\right)>0,

where $n_{2}<\lfloor\frac{\ell-3}{2}\rfloor\leq\frac{4}{25}\sqrt{2n-4}\leq\frac{4}{25}\rho$ as $n\geq\frac{625}{32}\lfloor\frac{\ell-3}{2}\rfloor^{2}+2$ . So, $\rho(G^{\prime})>\rho$ . On the other hand, $G^{\prime}\cong K_{2}+(P_{n_{1}-1}\cup(n_{2}+1)P_{n_{2}+1}\cup(t-n_{2}-4)P_{n_{2}}\cup P_{n_{t}})$ . By Claim 3.5, $G^{\prime}$ is $C_{\ell}$ -free, contradicting that $G$ is extremal to ${\rm spex}_{\mathcal{P}}(n,C_{\ell})$ . So, the claim holds.

Since $n_{1}+n_{2}=\ell-3$ and $n_{2}=\lfloor\frac{\ell-3}{2}\rfloor$ , we have $n_{1}=\lceil\frac{\ell-3}{2}\rceil$ . Moreover, since $n_{i}=\lfloor\frac{\ell-3}{2}\rfloor$ for $i\in\{2,\dots,t-1\}$ and $n_{t}\leq n_{2}$ , we can further obtain that $G[R]\cong H(\lceil\frac{\ell-3}{2}\rceil,\lfloor\frac{\ell-3}{2}\rfloor)$ , which implies that $G\cong K_{2}+H(\lceil\frac{\ell-3}{2}\rceil,\lfloor\frac{\ell-3}{2}\rfloor)$ . This completes the proof of Theorem 1.3. $\Box$

4 Proof of Theorem 1.4

Above all, we shall introduce the Jordan Curve Theorem: any simple closed curve $C$ in the plane partitions the rest of the plane into two disjoint arcwise-connected open sets (see [1], P. 244). The corresponding two open sets are called the interior and the exterior of $C$ . We denote them by $int(C)$ and $ext(C)$ , and their closures by $Int(C)$ and $Ext(C)$ , respectively. A plane graph is a planar embedding of a planar graph. The Jordan Curve Theorem gives the following lemma.

Lemma 4.1.

Let $C$ be a cycle of a plane graph $G$ , and let $x,y$ be two vertices of $G$ with $x\in int(C)$ and $y\in ext(C)$ , then $xy\notin E(G)$ .

Let $G$ be a plane graph. A face in $G$ of size $i$ is called an $i$ -face. Let $f_{i}(G)$ denote the number of $i$ -faces in $G$ , and let $f(G)$ denote $\sum_{i}f_{i}(G)$ .

Lemma 4.2.

(Proposition 2.5 of [1], P. 250) Let $G$ be a planar graph, and let $f$ be an arbitrary face in some planar embedding of $G$ . Then $G$ admits a planar embedding whose outer face has the same boundary as $f$ .

Let $\delta(G)$ be the minimum degree of a graph $G$ . It is well known that every graph $G$ with $\delta(G)\geq 2$ contains a cycle. In the following, we give a more delicate characterization on planar graphs, which contains an important structural information of the extremal graphs in Theorem 1.4.

Lemma 4.3.

Let $G$ be a plane graph on $n$ vertices with $\delta(G)\geq 3$ . Then $G$ contains two vertex-disjoint cycles unless $G\in\{2K_{1}+C_{3},K_{1}+C_{n-1}\}$ .

Proof.

We first deal with some trivial cases. Since $\delta(G)\geq 3$ , we have $n\geq 1+\delta(G)\geq 4$ . If $n=4$ , then $G\cong K_{1}+C_{3}$ . If $n=5$ , then $2e(G)=\sum_{v\in V(G)}d_{G}(v)\geq 3\times 5=15$ , and so $e(G)\geq 8$ . On the other hand, $e(G)\leq 3n-6=9$ , since $G$ is planar. Thus, $e(G)\in\{8,9\}$ . It is not hard to verify that $G\cong 2K_{1}+C_{3}$ when $e(G)=9$ and $G\cong K_{1}+C_{4}$ when $e(G)$ =8, as desired. If $G$ is not connected, then $G$ contains at least two components $G_{1}$ and $G_{2}$ with $\delta(G_{i})\geq 3$ for $i\in\{1,2\}$ , which implies that each $G_{i}$ contains a cycle. Thus, $G$ contains two vertex-disjoint cycles, as desired. If $G$ has a cut vertex $v$ , then $G-\{v\}$ has at least two components $G_{3}$ and $G_{4}$ . Since $\delta(G)\geq 3$ , we have $\delta(G_{i})\geq 2$ for $i\in\{3,4\}$ , which implies that both $G_{3}$ and $G_{4}$ contain a cycle. Thus, $G$ also contains two vertex-disjoint cycles.

Next, we only need to consider the case that $G$ is a 2-connected graph of order $n\geq 6$ . Since $G$ is 2-connected, each face of $G$ is a cycle. Let $C$ be a face of $G$ with minimum size $g$ . By Lemma 4.2, we may assume without loss of generality that $C$ is the outer face of $G$ . Let $G_{1}=G-V(C)$ . If $G_{1}$ contains a cycle, then $G$ contains two vertex-disjoint cycles, as desired. Now assume that $G_{1}$ is acyclic. Since $\delta(G)\geq 3$ , we have $2e(G)=\sum_{v\in V(G)}d_{G}(v)\geq 3n$ . This, together with Euler’s formula $n-2=e(G)-f(G)$ , gives $e(G)\leq 3f(G)-6$ . On the other hand,

\displaystyle 2e(G)=\sum_{i\geq g}if_{i}(G)\geq g\sum_{i\geq g}f_{i}(G)=gf(G).

Hence, $gf(G)\leq 2e(G)\leq 6f(G)-12$ , yielding $g\leq\frac{6f(G)-12}{f(G)}<6$ . Subsequently, we shall give several claims.

Claim 4.1.

We have $g=3$ .

Proof.

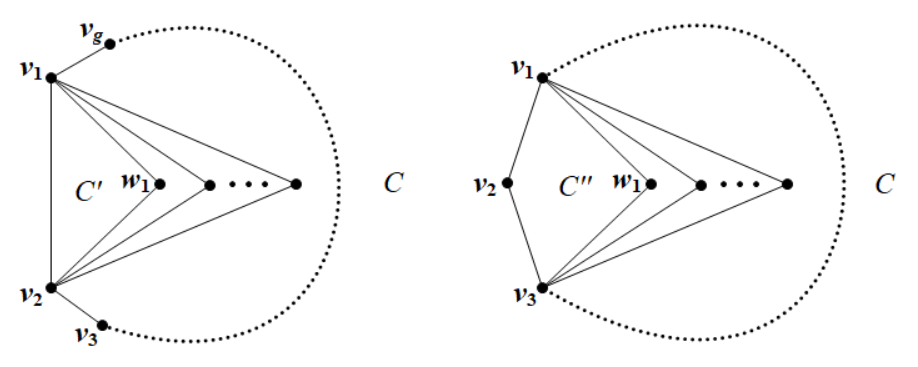
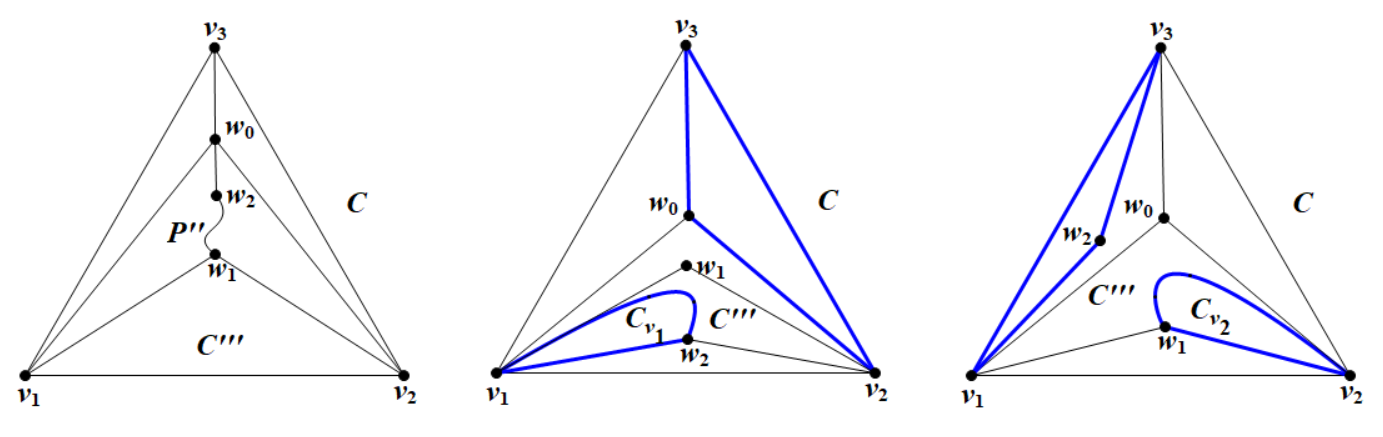
Suppose to the contrary that $g\in\{4,5\}$ , and let $C=v_{1}v_{2}\ldots v_{g}v_{1}$ . We first consider the case that there exists a vertex of $G_{1}$ adjacent to two consecutive vertices of $C$ . Without loss of generality, let $w_{1}\in V(G_{1})$ and $\{w_{1},v_{1},v_{2}\}$ induces a triangle $C^{\prime}$ . More generally, we define $A=\{w\in V(G_{1})~{}|~{}v_{1},v_{2}\in N_{C}(w)\}$ . Clearly, $w_{1}\in A$ . We can select a vertex, say $w_{1}$ , in $A$ such that $A\subseteq Ext(C^{\prime})$ (see Figure 2). Notice that $C^{\prime}$ is not a face of $G$ , as $g\in\{4,5\}$ . Then, $int(C^{\prime})\neq\varnothing$ . By Lemma 4.1, every vertex in $int(C^{\prime})$ has no neighbors in $ext(C^{\prime})$ . Moreover, by the definitions of $A$ and $w_{1}$ , every vertex in $int(C^{\prime})$ has at most one neighbor in $\{v_{1},v_{2}\}$ . It follows that every vertex in $int(C^{\prime})$ has at least one neighbor in $int(C^{\prime})$ , as $\delta(G)\geq 3$ . Thus, $G[int(C^{\prime})]$ is nonempty, that is, $G_{1}[int(C^{\prime})]$ is nonempty. Recall that $G_{1}$ is acyclic. Then $G_{1}[int(C^{\prime})]$ contains at least two pendant vertices, one of which (say $w_{2}$ ) is not adjacent to $w_{1}$ . Hence, $w_{2}$ is also a pendant vertex of $G_{1}$ , as $w_{2}$ has no neighbors in $ext(C^{\prime})$ . On the other hand, $w_{2}$ has at most one neighbor in $\{v_{1},v_{2}\}$ , and so $d_{C}(w_{2})\leq 1$ . Therefore, $d_{G}(w_{2})=d_{G_{1}}(w_{2})+d_{C}(w_{2})\leq 2$ , contradicting $\delta(G)\geq 3$ .

Now it remains the case that each vertex of $G_{1}$ is not adjacent to two consecutive vertices of $C$ . Note that $\delta(G)\geq 3$ and $G_{1}$ is acyclic. Then $G_{1}$ contains a vertex $w_{0}$ with $d_{G_{1}}(w_{0})\leq 1$ , and thus $d_{C}(w_{0})=d_{G}(w_{0})-d_{G_{1}}(w_{0})\geq 2$ . Now, since $g\in\{4,5\}$ , we may assume without loss of generality that $v_{1},v_{3}\in N_{C}(w_{0})$ . Let $A^{\prime}=\{w\in V(G_{1})~{}|~{}v_{1},v_{3}\in N_{C}(w)\}$ . Clearly, $w_{0}\in A^{\prime}$ and $v_{2}\notin N_{C}(w)$ for each $w\in A^{\prime}$ . Now, we can select a vertex, say $w_{1}$ , in $A^{\prime}$ such that $A^{\prime}\subseteq Ext(C^{\prime\prime})$ , where $C^{\prime\prime}=w_{1}v_{1}v_{2}v_{3}w_{1}$ (see Figure 2). We can see that $int(C^{\prime\prime})\neq\varnothing$ (otherwise, $d_{G}(v_{2})=|\{v_{1},v_{3}\}|=2$ , a contradiction). By the definition of $w_{1}$ , we have $int(C^{\prime\prime})\cap A^{\prime}=\varnothing$ . Furthermore, every vertex in $int(C^{\prime\prime})$ has no neighbors in $ext(C^{\prime\prime})$ and has at most one neighbor in $\{v_{1},v_{2},v_{3}\}.$ Thus, every vertex in $int(C^{\prime\prime})$ has at least one neighbor in $int(C^{\prime\prime})$ . By a similar argument as above, we can find a vertex $w_{2}\in int(C^{\prime\prime})$ with $d_{G}(w_{2})=d_{G_{1}}(w_{2})+d_{C}(w_{2})\leq 2$ , which contradicts $\delta(G)\geq 3$ . ∎

By Claim 4.1, the outer face of $G$ is a triangle $C=v_{1}v_{2}v_{3}v_{1}$ . In the following, we denote $B_{i}=\{w\in V(G_{1})~{}|~{}d_{C}(w)=i\}$ for $i\leq 3$ . Since $\delta(G)\geq 3$ , we have $w\in B_{3}$ for each isolated vertex $w$ of $G_{1}$ , and $w\in B_{2}\cup B_{3}$ for each pendant vertex $w$ of $G_{1}$ .

Claim 4.2.

$|B_{3}|\leq 1$ and $|B_{2}|+|B_{3}|\geq 2$ .

Proof.

Since $C$ is the outer face of $G$ , every vertex of $G_{1}$ lies in $int(C)$ . Furthermore, since $G$ is planar, it is easy to see that $|B_{3}|\leq 1$ . This implies that $G_{1}$ contains at most one isolated vertex. Recall that $|G_{1}|=n-3\geq 3$ and $G_{1}$ is acyclic. Then $G_{1}$ contains at least two pendant vertices $w_{1}$ and $w_{2}$ . Therefore, $|B_{2}|+|B_{3}|\geq|\{w_{1},w_{2}\}|=2$ . ∎

Claim 4.3.

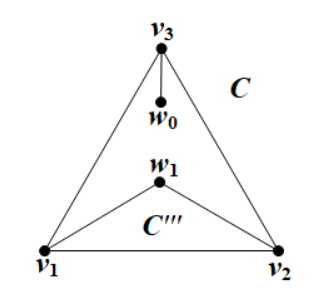
Let $w_{0},w_{1}$ be two vertices in $V(G_{1})$ such that $N_{C}(w_{0})\supseteq\{v_{3}\}$ and $N_{C}(w_{1})\supseteq\{v_{1},v_{2}\}$ (see Figure 3). Then
(i) $v_{3},w_{0}\in ext(C^{\prime\prime\prime})$ , where $C^{\prime\prime\prime}=w_{1}v_{1}v_{2}w_{1}$ ;
(ii) if $w_{0}\notin B_{3}$ , then $G_{1}$ contains a pendant vertex in $ext(C^{\prime\prime\prime})$ .

Proof.

(i) Since $C$ is the outer face and $v_{3}\in V(C)\setminus V(C^{\prime\prime\prime})$ , we have $v_{3}\in ext(C^{\prime\prime\prime})$ . Furthermore, using $w_{0}v_{3}\in E(G)$ and Lemma 4.1 gives $w_{0}\in ext(C^{\prime\prime\prime})$ .

(ii) Since $w_{0}\notin B_{3}$ , we have $d_{C}(w_{0})\leq 2$ , and so $d_{G_{1}}(w_{0})=d_{G}(w_{0})-d_{C}(w_{0})\geq 1$ . By (i), we know that $w_{0}\in ext(C^{\prime\prime\prime})$ . If $d_{G_{1}}(w_{0})=1$ , then $w_{0}$ is a desired pendant vertex. It remains the case that $d_{G_{1}}(w_{0})\geq 2$ . Now, whether $w_{1}$ is a neighbor of $w_{0}$ or not, $w_{0}$ has at least one neighbor in $V(G_{1})\cap ext(C^{\prime\prime\prime})$ . Thus, $G_{1}[ext(C^{\prime\prime\prime})]$ is nonempty. Recall that $G_{1}$ is acyclic. Then $G_{1}[ext(C^{\prime\prime\prime})]$ contains at least two pendant vertices, one of which (say $w_{2}$ ) is not adjacent to $w_{1}$ . Hence, $w_{2}$ is also a pendant vertex of $G_{1}$ , as $w_{2}$ has no neighbors in $int(C^{\prime\prime\prime})$ . ∎

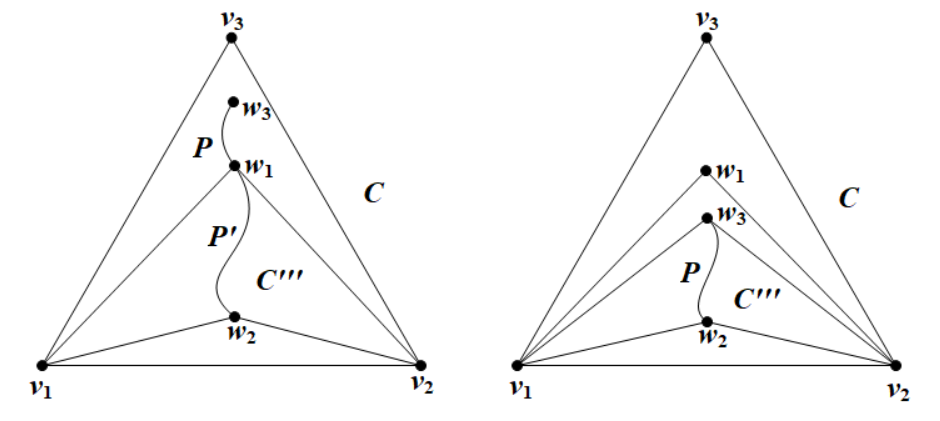
Claim 4.4.

Let $w_{1},w_{2}\in V(G_{1})$ with $N_{C}(w_{1})\cap N_{C}(w_{2})\supseteq\{v_{1},v_{2}\}$ . Assume that $C^{\prime\prime\prime}=w_{1}v_{1}v_{2}w_{1}$ and $w_{2}\in int(C^{\prime\prime\prime})$ (see Figure 4). Then $G$ contains a cycle $C_{v_{i}}$ such that $V(C_{v_{i}})\subseteq Int(C^{\prime\prime\prime})$ and $V(C_{v_{i}})\cap V(C)=\{v_{i}\}$ for each $i\in\{1,2\}$ .

Proof.

We first claim that $N_{C}(w_{2})=\{v_{1},v_{2}\}$ . By Claim 4.3, we know that $v_{3}\in ext(C^{\prime\prime\prime})$ . Now, since $w_{2}\in int(C^{\prime\prime\prime})$ , we have $w_{2}v_{3}\notin E(G)$ by Lemma 4.1, and so $N_{C}(w_{2})=\{v_{1},v_{2}\}$ . Furthermore, we have $d_{G_{1}}(w_{2})\geq 1$ . Then $G_{1}$ contains a path $P$ with endpoints $w_{2}$ and $w_{3}$ , where $w_{3}$ is a pendant vertex of $G_{1}$ . If $V(P)\not\subseteq int(C^{\prime\prime\prime})$ , then by $w_{2}\in int(C^{\prime\prime\prime})$ and Lemma 4.1, we have $V(P)\cap V(C^{\prime\prime\prime})=\{w_{1}\}$ as $v_{1},v_{2}\notin V(G_{1})$ . Now let $P^{\prime}$ be the subpath of $P$ with endpoints $w_{2}$ and $w_{1}$ . Then $V(P^{\prime})\setminus\{w_{1}\}\subseteq int(C^{\prime\prime\prime})$ , and $G$ contains a cycle $C(v_{i})=v_{i}w_{1}P^{\prime}w_{2}v_{i}$ for each $i\in\{1,2\}$ , as desired. Next, assume that $V(P)\subseteq int(C^{\prime\prime\prime})$ . Then, $w_{3}\in int(C^{\prime\prime\prime})$ . By $v_{3}\in ext(C^{\prime\prime\prime})$ and Lemma 4.1, we get that $w_{3}v_{3}\notin E(G)$ , and so $w_{3}\notin B_{3}$ . Moreover, $d_{G_{1}}(w_{3})=1$ and $\delta(G)\geq 3$ give $w_{3}\in B_{2}$ . Thus, $N_{C}(w_{3})=\{v_{1},v_{2}\}$ . Therefore, $G$ contains a cycle $C_{v_{i}}=v_{i}w_{2}Pw_{3}v_{i}$ for each $i\in\{1,2\}$ , as desired. ∎

Having above four claims, we are ready to give the final proof of Lemma 4.3. By Claim 4.2, we have $|B_{3}|\leq 1$ and $|B_{2}|\geq 1$ . We may without loss of generality that $w_{1}\in B_{2}$ and $N_{C}(w_{1})=\{v_{1},v_{2}\}$ . For each $i\in\{1,2\}$ , let $\overline{i}\in\{1,2\}\setminus\{i\}$ . Since $d_{C}(w_{1})=2$ , we have $d_{G_{1}}(w_{1})\geq 1$ . Hence, $G_{1}$ is nonempty, and so $G_{1}$ contains at least two pendant vertices. According to the size of $B_{3}$ , we now distinguish two cases to complete the proof.

Case 1. $|B_{3}|=1$ .

Assume that $B_{3}=\{w_{0}\}$ . Then $N_{C}(w_{0})=\{v_{1},v_{2},v_{3}\}$ (see Figure 5). We then consider two subcases according to the size of $B_{2}$ .

Subcase 1.1. $|B_{2}|=1$ , that is, $B_{2}=\{w_{1}\}$ .

For each pendant vertex $w$ of $G_{1}$ , we have $d_{C}(w)=d_{G}(w)-d_{G_{1}}(w)\geq 2$ , consequently, $w\in B_{2}\cup B_{3}=\{w_{1},w_{0}\}$ . This indicates that $G_{1}$ contains exactly two pendant vertices $w_{1}$ and $w_{0}$ . Furthermore, we can see that $G_{1}$ contains no isolated vertices (otherwise, every isolated vertex of $G_{1}$ has at least three neighbors in $V(C)$ and so belongs to $B_{3}$ , while the unique vertex $w_{0}\in B_{3}$ is a pendant vertex of $G_{1}$ ). Therefore, $G_{1}$ is a path of order $n-|C|$ with endpoints $w_{1}$ and $w_{0}$ .

Now we know that $G_{1}$ is a path with $|G_{1}|=n-3\geq 3$ . Let $N_{G_{1}}(w_{0})=\{w_{2}\}$ and $P^{\prime\prime}=G_{1}-\{w_{0}\}$ . Then $P^{\prime\prime}$ is a path with endpoints $w_{1}$ and $w_{2}$ . Since $d_{G_{1}}(w_{2})=2$ , we have $d_{C}(w_{2})\geq 1$ . If $w_{2}v_{3}\in E(G)$ , then $G$ contains two vertex-disjoint cycles $v_{3}w_{0}w_{2}v_{3}$ and $w_{1}v_{1}v_{2}w_{1}$ , as desired. If $w_{2}v_{i}\in E(G)$ for some $i\in\{1,2\}$ , then $G$ contains two vertex-disjoint cycles $v_{i}w_{1}P^{\prime\prime}w_{2}v_{i}$ and $w_{0}v_{\overline{i}}v_{3}w_{0}$ , as desired.

Subcase 1.2. $|B_{2}|\geq 2$ .

Let $w_{2}\in B_{2}\setminus\{w_{1}\}$ . If $N_{C}(w_{1})=N_{C}(w_{2})$ , then we may assume that $w_{2}\in int(C^{\prime\prime\prime})$ by the symmetry of $w_{1}$ and $w_{2}$ , where $C^{\prime\prime\prime}=w_{1}v_{1}v_{2}w_{1}$ . By Claim 4.4, $G$ contains a cycle $C_{v_{1}}$ such that $V(C_{v_{1}})\subseteq Int(C^{\prime\prime\prime})$ and $V(C_{v_{1}})\cap V(C)=\{v_{1}\}$ . On the other hand, Claim 4.3 implies that $w_{0}\in ext(C^{\prime\prime\prime})$ . Hence, $w_{0}\notin V(C_{v_{1}})$ . Therefore, $G$ contains two vertex-disjoint cycles $C_{v_{1}}$ and $w_{0}v_{2}v_{3}w_{0}$ , as desired.

It remains the case that $N_{C}(w_{1})\neq N_{C}(w_{2})$ . Now $N_{C}(w_{2})=\{v_{i},v_{3}\}$ for some $i\in\{1,2\}$ . We define $C^{\prime\prime\prime}=w_{0}v_{1}v_{2}w_{0}$ instead of the original one in Claim 4.4. Then $w_{1}\in int(C^{\prime\prime\prime})$ . Moreover, $w_{2}\in ext(C^{\prime\prime\prime})$ as $w_{2}v_{3}\in E(G)$ . By Claim 4.4, there exists a cycle $C_{v_{\overline{i}}}$ such that $V(C_{v_{\overline{i}}})\subseteq Int(C^{\prime\prime\prime})$ and $V(C_{v_{\overline{i}}})\cap V(C)=\{v_{\overline{i}}\}$ . Therefore, $G$ contains two vertex-disjoint cycles $C_{v_{\overline{i}}}$ and $w_{2}v_{i}v_{3}w_{2}$ , as desired.

Case 2. $|B_{3}|=0$ .

Recall that $A=\{w\in V(G_{1})~{}|~{}v_{1},v_{2}\in N_{C}(w)\}$ . Since $|B_{3}|=0$ , we can see that $N_{C}(w)=N_{C}(w_{1})=\{v_{1},v_{2}\}$ for each $w\in A$ . We may assume without loss of generality that $A\subseteq Int(C^{\prime\prime\prime})$ by the symmetry of vertices in $A$ . By Claim 4.3, there exists a pendant vertex $w_{3}$ of $G_{1}$ in $ext(C^{\prime\prime\prime})$ , which implies that $d_{C}(w_{3})\geq 2$ . Since $|B_{3}|=0$ , we have $w_{3}\in B_{2}$ , and thus $B_{2}\supseteq\{w_{1},w_{3}\}$ . Moreover, $w_{3}\notin A$ as $A\subseteq Int(C^{\prime\prime\prime})$ . Assume without loss of generality that $N_{C}(w_{3})=\{v_{1},v_{3}\}$ (see Figure 6). We also consider two subcases according to $|B_{2}|$ .

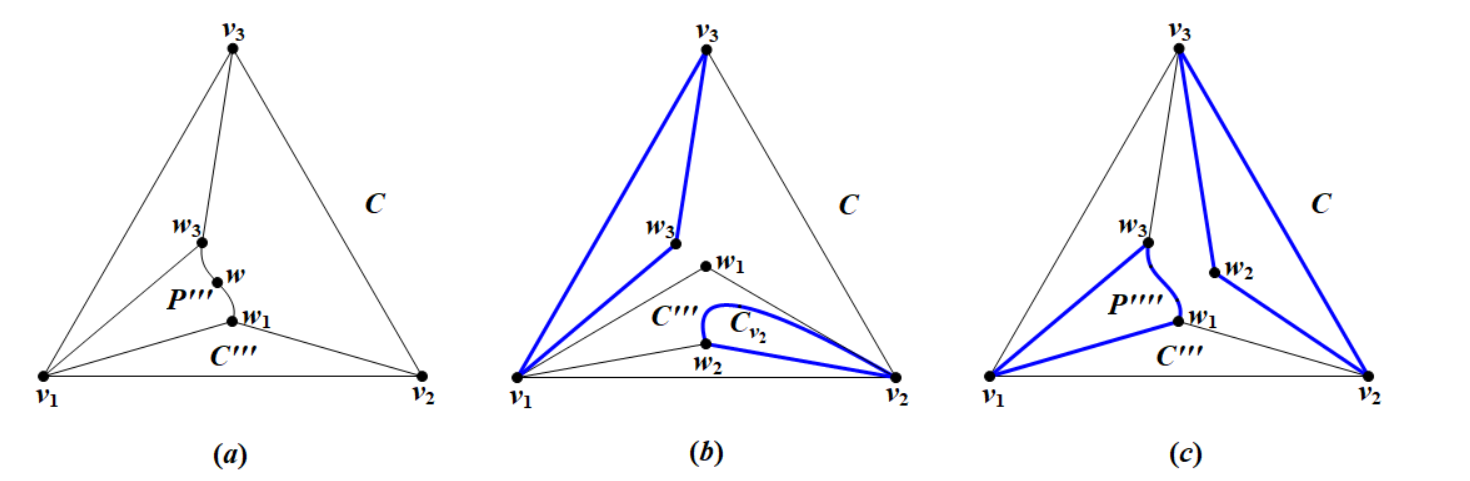
Subcase 2.1. $|B_{2}|=2$ , that is, $B_{2}=\{w_{1},w_{3}\}$ .

Since $d_{C}(w_{3})=2$ , we have $d_{G_{1}}(w_{3})\geq 1$ , which implies that $G_{1}$ is non-empty and has at least two pendant vertices. On the other hand, since $\delta(G)\geq 3$ while $B_{3}=\varnothing$ , we can see that $G_{1}$ contains no isolated vertices, and $w\in B_{2}=\{w_{1},w_{3}\}$ for each pendant vertex $w$ of $G_{1}$ . Therefore, $G_{1}$ contains exactly two pendant vertices $w_{1}$ and $w_{3}$ , more precisely, $G_{1}$ is a path with endpoints $w_{1}$ and $w_{3}$ . Let $w$ be an arbitrary vertex in $V(G_{1})\setminus\{w_{1},w_{3}\}$ . Then, $d_{C}(w)=d_{G}(w)-d_{G_{1}}(w)=d_{G}(w)-2\geq 1.$

If $wv_{2}\in E(G)$ , then $G$ contains two vertex-disjoint cycles $v_{2}w_{1}P^{\prime\prime\prime}wv_{2}$ and $v_{1}w_{3}v_{3}v_{1}$ , where $P^{\prime\prime\prime}$ is the subpath of $G_{1}$ from $w_{1}$ to $w$ (see Figure 6( $a$ )). If $wv_{3}\in E(G)$ , then $G$ contains two vertex-disjoint cycles $v_{3}w_{3}P^{\prime\prime\prime}wv_{3}$ and $v_{1}w_{1}v_{2}v_{1}$ , where $P^{\prime\prime\prime}$ is the subpath of $G_{1}$ from $w_{3}$ to $w$ (see Figure 6( $a$ )). If $N_{C}(w)=\{v_{1}\}$ for each $w\in V(G_{1})\setminus\{w_{1},w_{3}\},$ then $G\cong K_{1}+C_{n-1}$ , as desired.

Subcase 2.2. $|B_{2}|\geq 3$ .

For each vertex $w\in B_{2}$ , it is clear that $N_{C}(w)$ is one of $\{v_{1},v_{2}\}$ , $\{v_{1},v_{3}\}$ and $\{v_{2},v_{3}\}$ . We first consider the case that there exist two vertices in $B_{2}$ which have the same neighbors in $C$ . Without loss of generality, assume that we can find a vertex $w_{2}\in B_{2}$ with $N_{C}(w_{2})=N_{C}(w_{1})=\{v_{1},v_{2}\}$ . Then $w_{2}\in A$ . Recall that $A\subseteq Int(C^{\prime\prime\prime})$ and $C^{\prime\prime\prime}=w_{1}v_{1}v_{2}w_{1}$ (see Figure 6( $b$ )). Then, we can further get that $w_{2}\in int(C^{\prime\prime\prime})$ . By Claim 4.4, there exists a cycle $C_{v_{2}}$ such that $V(C_{v_{2}})\subset Int(C^{\prime\prime\prime})$ and $V(C_{v_{2}})\cap V(C)=\{v_{2}\}$ . On the other hand, Claim 4.3 implies that $w_{3}\in ext(C^{\prime\prime\prime})$ . Hence, $w_{3}\notin V(C_{v_{2}})$ . Therefore, $G$ contains two vertex-disjoint cycles $C_{v_{2}}$ and $w_{3}v_{1}v_{3}w_{3}$ , as desired.

Now it remains the case that any two vertices in $B_{2}$ have different neighborhoods in $C$ . This implies that $|B_{2}|=3$ and we can find a vertex $w_{2}\in B_{2}$ with $N_{C}(w_{2})=\{v_{2},v_{3}\}$ . Now we have $B_{2}=\{w_{1},w_{2},w_{3}\}$ . Furthermore, since $\delta(G)\geq 3$ and $B_{3}=\varnothing$ , we have $d_{G_{1}}(w)\geq 1$ for each $w\in V(G_{1})$ , and if $d_{G_{1}}(w)=1$ , then $w\in B_{2}$ . Since $|B_{2}|=3$ , we can see that $G_{1}$ has only one connected component, that is, $G_{1}$ is a tree and some $w_{i}$ , say $w_{2}$ , is a pendant vertex of $G_{1}$ . Now, $G_{1}-\{w_{2}\}$ contains a subpath $P^{\prime\prime\prime\prime}$ with endpoints $w_{1}$ and $w_{3}$ (see Figure 6( $c$ )). Then $G$ contains two vertex-disjoint cycles $v_{1}w_{1}P^{\prime\prime\prime\prime}w_{3}v_{1}$ and $w_{2}v_{2}v_{3}w_{2}$ , as desired.

This completes the proof of Lemma 4.3. ∎

Let $\mathcal{G}^{*}_{n}$ be the family of graphs obtained from $2K_{1}+C_{3}$ and an independent set of size $n-5$ by joining each vertex of the independent set to arbitrary two vertices of the triangle (see Figure 7). Clearly, every graph in $\mathcal{G}^{*}_{n}$ is planar. Now, let $\mathcal{G}_{n}$ be the family of planar graphs obtained from $2K_{1}+C_{3}$ by iteratively adding vertices of degree 2 until the resulting graph has $n$ vertices. Then $\mathcal{G}^{*}_{n}\subseteq\mathcal{G}_{n}$ .

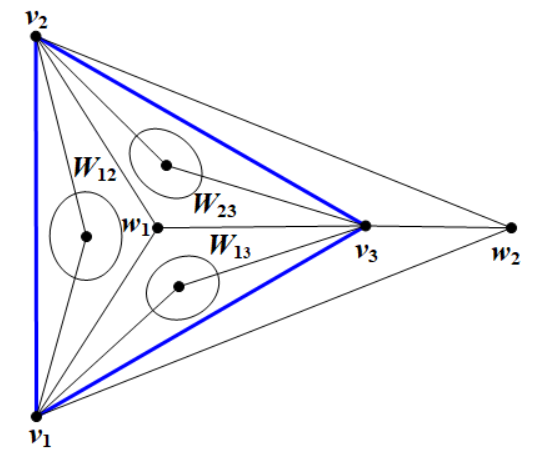
Lemma 4.4.

For any graph $G\in\mathcal{G}_{n}$ , $G$ is $2\mathcal{C}$ -free if and only if $G\in\mathcal{G}^{*}_{n}$ .

Proof.

Let $V_{1}:=\{v_{1},v_{2},v_{3}\}$ be the set of vertices of degree 4 and $V_{2}:=\{w_{1},w_{2}\}$ be the set of vertices of degree 3 in $2K_{1}+C_{3}$ , respectively. Then $V_{1}$ induces a triangle. We first show that every graph $G$ in $\mathcal{G}^{*}_{n}$ is $2\mathcal{C}$ -free. It suffices to prove that every cycle of $G$ contains at least two vertices in $V_{1}$ . Let $C$ be an arbitrary cycle of $G$ . If $V(C)\subseteq V_{1}$ , then there is nothing to prove. It remains the case that there exists a vertex $w\in V(C)\setminus V_{1}$ . By the definition of $\mathcal{G}^{*}_{n}$ , we can see that $N_{C}(w)\subseteq N_{G}(w)\subseteq V_{1}$ . Note that $|N_{C}(w)|\geq 2$ . Hence, $C$ contains at least two vertices in $V_{1}$ .

In the following, we will show that every graph $G\in\mathcal{G}_{n}\setminus\mathcal{G}^{*}_{n}$ contains two vertex-disjoint cycles. By the definition of $\mathcal{G}_{n}$ , $G$ is obtained from $2K_{1}+C_{3}$ by iteratively adding $n-5$ vertices $u_{1},u_{2},\dots,u_{n-5}$ of degree 2. Now, let $G_{n-5}=G$ , and $G_{i-1}=G_{i}-\{u_{i}\}$ for $i\in\{1,2,\ldots,n-5\}$ . Then $G_{0}\cong 2K_{1}+C_{3}$ . Moreover, $|G_{i}|=i+5$ and $d_{G_{i}}(u_{i})=2$ for each $i\in\{1,2,\dots,n-5\}$ . Now let

i^{*}=\max\{i~{}|~{}0\leq i\leq n-5,~{}G_{i}\in\mathcal{G}^{*}_{i+5}\}.

Since $G_{0}=2K_{1}+C_{3}\in\mathcal{G}^{*}_{5}$ and $G_{n-5}\notin\mathcal{G}^{*}_{n}$ , we have $0\leq i^{*}\leq n-6$ . By the choice of $i^{*}$ , we know that $G_{i^{*}}\in\mathcal{G}^{*}_{i^{*}+5}$ and $G_{i^{*}+1}\notin\mathcal{G}^{*}_{i^{*}+6}$ , which implies that $N_{G_{i^{*}}}(u_{i})\subseteq V_{1}$ and $N_{G_{i^{*}+1}}(u_{i^{*}+1})\not\subseteq V_{1}$ .

Now we may assume that $G_{n-5}$ is a planar embedding of $G$ , and $G_{0}$ is a plane subgraph of $G_{n-5}$ . Observe that $2K_{1}+C_{3}$ has six planar embeddings (see Figure 8). Without loss of generality, assume that $G_{0}$ is the leftmost graph in Figure 8. Then, $u_{i^{*}+1}$ lies in one of the following regions (see Figure 8):

ext(w_{2}v_{1}v_{2}w_{2}),int(w_{2}v_{1}v_{3}w_{2}),int(w_{2}v_{2}v_{3}w_{2}),

int(w_{1}v_{1}v_{2}w_{1}),int(w_{1}v_{1}v_{3}w_{1}),int(w_{1}v_{2}v_{3}w_{1}).

By Lemma 4.2, we can assume that $u_{i^{*}+1}$ lies in the outer face, that is, $u_{i^{*}+1}\in ext(w_{2}v_{1}v_{2}w_{2})$ . For simplify, we denote $C^{\prime}=w_{2}v_{1}v_{2}w_{2}$ . Let $u$ be an arbitrary vertex with $uv_{3}\in E(G_{i^{*}+1})$ . Then by Lemma 4.1 and $v_{3}\in int(C^{\prime})$ , we have $u\in int(C^{\prime})$ , and thus $uu_{i^{*}+1}\notin E(G_{i^{*}+1})$ . This implies that $N_{G_{i^{*}+1}}(u_{i^{*}+1})\subseteq V(C^{\prime})\cup W_{12}$ , where $W_{12}=\{u~{}|~{}u\in V(G_{i^{*}+1}),~{}N_{G_{i^{*}+1}}(u)=\{v_{1},v_{2}\}\}$ . Recall that $d_{G_{i^{*}+1}}(u_{i^{*}+1})=2$ and $N_{G_{i^{*}+1}}(u_{i^{*}+1})\not\subseteq V_{1}$ . Then, $|N_{G_{i^{*}+1}}(u_{i^{*}+1})\cap\{v_{1},v_{2}\}|\leq 1$ . If $|N_{G_{i^{*}+1}}(u_{i^{*}+1})\cap\{v_{1},v_{2}\}|=1$ , then we may assume without loss of generality that $v_{1}\in N_{G_{i^{*}+1}}(u_{i^{*}+1})$ , and $u^{\prime}\in N_{G_{i^{*}+1}}(u_{i^{*}+1})\setminus\{v_{1}\}$ . Since $N_{G_{i^{*}+1}}(u_{i^{*}+1})\subseteq V(C^{\prime})\cup W_{12}$ , we have $u^{\prime}\in\{w_{2}\}\cup W_{12}$ , and so $u^{\prime}v_{1}\in E(G_{i^{*}+1})$ . Thus, $G_{n-5}$ contains two vertex-disjoint cycles $u_{i^{*}+1}v_{1}u^{\prime}u_{i^{*}+1}$ and $w_{1}v_{2}v_{3}w_{1}$ , as desired. Now consider the case that $|N_{G_{i^{*}+1}}(u_{i^{*}+1})\cap\{v_{1},v_{2}\}|=0$ . This implies that $N_{G_{i^{*}+1}}(u_{i^{*}+1})\subseteq\{w_{2}\}\cup W_{12}$ . Let $N_{G_{i^{*}+1}}(u_{i^{*}+1})=\{u^{\prime},u^{\prime\prime}\}$ . Then $u^{\prime}v_{1},u^{\prime\prime}v_{1}\in E(G_{i^{*}+1})$ . Therefore, $G_{n-5}$ contains two vertex-disjoint cycles $u_{i^{*}+1}u^{\prime}v_{1}u^{\prime\prime}u_{i^{*}+1}$ and $w_{1}v_{2}v_{3}w_{1}$ . ∎

Given a graph $G$ , let $\widetilde{G}$ be the largest induced subgraph of $G$ with minimal degree at least 3. It is easy to see that $\widetilde{G}$ can be obtained from $G$ by iteratively removing the vertices of degree at most 2 until the resulting graph has minimum degree at least 3 or is empty. It is well known that $\widetilde{G}$ is unique and does not depend on the order of vertex deletion (see [24]).

In the following, we give the proof of Theorem 1.4.

Proof.

Let $n\geq 5$ and $G$ be an extremal graph corresponding to ${\rm ex}_{\mathcal{P}}(n,2\mathcal{C})$ . Observe that $K_{2}+(P_{3}\cup(n-5)K_{1})$ is a planar graph which contains no two vertex-disjoint cycles (see Figure 7). Thus, $e(G)\geq e(K_{2}+(P_{3}\cup(n-5)K_{1}))=2n-1$ .

If $\widetilde{G}$ is empty, then we define $G^{\prime}$ as the graph obtained from $G$ by iteratively removing the vertices of degree at most 2 until the resulting graph has 4 vertices. By the planarity of $G^{\prime}$ , we have $e(G^{\prime})\leq 3|G^{\prime}|-6=6$ , and thus

e(G)\leq e(G^{\prime})+2(n-4)\leq 6+2n-8=2n-2,

a contradiction.

Now we know that $\widetilde{G}$ is nonempty. Then, $\widetilde{G}$ contains no two vertex-disjoint cycles as $\widetilde{G}\subseteq G$ . By the definition of $\widetilde{G}$ , we have $\delta(\widetilde{G})\geq 3$ . By Lemma 4.3, we get that $\widetilde{G}\in\{2K_{1}+C_{3},K_{1}+C_{|\widetilde{G}|-1}\}$ . If $\widetilde{G}\cong K_{1}+C_{|\widetilde{G}|-1}$ , then

e(G)\leq e(\widetilde{G})+2(n-|\widetilde{G}|)=2(|\widetilde{G}|-1)+2(n-|\widetilde{G}|)=2n-2,

a contradiction. Thus, $\widetilde{G}\cong 2K_{1}+C_{3}$ . Now, $e(G)\leq e(\widetilde{G})+2(n-5)=2n-1$ . Therefore, $e(G)=2n-1$ , which implies that ${\rm ex}_{\mathcal{P}}(n,2\mathcal{C})=2n-1$ and $G\in\mathcal{G}_{n}$ . By Lemma 4.4, we have $G\in\mathcal{G}^{*}_{n}$ . This completes the proof of Theorem 1.4. ∎

5 Proof of Theorem 1.5

We shall further introduce some notations on a plane graph $G$ . A vertex or an edge of $G$ is said to be incident with a face $F$ , if it lies on the boundary of $F$ . Clearly, every edge of $G$ is incident with at most two faces. A face of size $i$ is called an $i$ -face. The numbers of $i$ -faces and total faces are denoted by $f_{i}(G)$ and $f(G)$ , respectively. Let $E_{3}(G)$ be the set of edges incident with at least one $3$ -face, and particularly, let $E_{3,3}(G)$ be the set of edges incident with two $3$ -faces. Moreover, let $e_{3}(G)$ and $e_{3,3}(G)$ denote the cardinalities of $E_{3}(G)$ and $E_{3,3}(G)$ , respectively. We can easily see that $3f_{3}(G)=e_{3}(G)+e_{3,3}(G).$

Lan, Shi and Song proved that ${\rm ex}_{\mathcal{P}}(n,K_{1}+P_{3})\leq\frac{12(n-2)}{5}$ , with equality when $n\equiv 12\pmod{20}$ (see [16]), and ${\rm ex}_{\mathcal{P}}(n,K_{1}+P_{k+1})\leq\frac{13kn}{4k+2}-\frac{12k}{2k+1}$ for $k\in\{3,4,5\}$ (see [17]). For $k\geq 6$ , one can easily see that ${\rm ex}_{\mathcal{P}}(n,K_{1}+P_{k+1})=3n-6$ . In [10], the authors obtained the following sharp result.

Lemma 5.1.

([10]) Let $n,k$ be two integers with $k\in\{2,3,4,5\}$ and $n\geq\frac{12}{6-k}+1$ . Then ${\rm ex}_{\mathcal{P}}(n,K_{1}+P_{k+1})\leq\frac{24k}{7k+6}(n-2)$ , with equality if $n\equiv{\frac{12(k+2)}{6-k}}\pmod{{\frac{28k+24}{6-k}}}$ .

To prove Theorem 1.5, we also need an edge-extremal result on outerplanar graphs. Let ${\rm ex}_{\mathcal{OP}}(n,C_{k})$ denote the maximum number of edges in an $n$ -vertex $C_{k}$ -free outerplanar graph.

Lemma 5.2.

([11]) Let $n,k,\lambda$ be three integers with $n\geq k\geq 3$ and $\lambda=\lfloor\frac{kn-2k-1}{k^{2}-2k-1}\rfloor+1$ . Then

{\rm ex}_{\mathcal{OP}}(n,C_{k})=\left\{\begin{array}[]{ll}2n-\lambda+2\big{\lfloor}\frac{\lambda}{k}\big{\rfloor}-3&\hbox{if $k\mid\lambda$,}\\ 2n-\lambda+2\big{\lfloor}\frac{\lambda}{k}\big{\rfloor}-2&\hbox{otherwise.}\end{array}\right.

In particular, we can obtain the following corollary.

Corollary 5.1.

Let $n\geq 4$ . Then

{\rm ex}_{\mathcal{OP}}(n-1,C_{4})=\left\{\begin{array}[]{ll}\frac{12}{7}n-5&\hbox{if $7\mid n$,}\\ \big{\lfloor}\frac{12n-27}{7}\big{\rfloor}{}{}{}&\hbox{otherwise.}\end{array}\right.

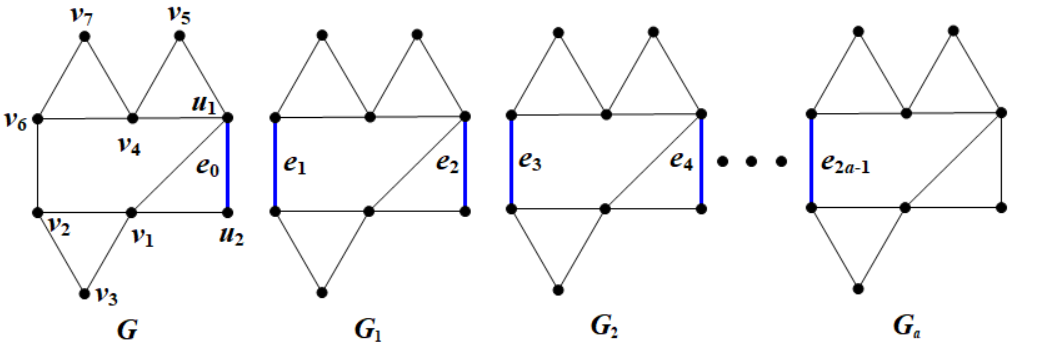
For arbitrary integer $n\geq 4$ , we can find a unique $(a,b)$ such that $a\geq 0$ , $1\leq b\leq 7$ and $n-1=7a+b+2$ . Let $G$ be a $9$ -vertex outerplanar graph and $G_{1},\ldots,G_{a}$ be $a$ copies of $G$ (see Figure 9). Then, we define $G_{0}$ as the subgraph of $G$ induced by $\{u_{1},u_{2}\}\cup\{v_{1},v_{2},\dots,v_{b}\}$ . One can check that $|G_{0}|=b+2$ and

e(G_{0})=\left\{\begin{array}[]{ll}\frac{12(b+2)-23}{7}&\hbox{if $7\mid(b+2-6)$,}\\ \big{\lfloor}\frac{12(b+2)-15}{7}\big{\rfloor}{}{}{}&\hbox{otherwise.}\end{array}\right.

We now construct a new graph $G^{*}$ from $G_{0},G_{1},\ldots,G_{a}$ by identifying the edges $e_{2i}$ and $e_{2i+1}$ for each $i\in\{0,\ldots,a-1\}$ . Clearly, $G^{*}$ is a connected $C_{4}$ -free outerplanar graph with

|G^{*}|=\sum_{i=0}^{a}|G_{i}|-2a=(2+b)+9a-2a=n-1.

Moreover, since $n\equiv b+2-6\,(\!\!\!\mod 7),$ we have

e(G^{*})=\sum_{i=0}^{a}e(G_{i})-a=e(G_{0})+12a=\left\{\begin{array}[]{ll}\frac{12}{7}n-5&\hbox{if $7\mid n$,}\\ \big{\lfloor}\frac{12n-27}{7}\big{\rfloor}{}{}{}&\hbox{otherwise.}\end{array}\right.

Combining Corollary 5.1, $G^{*}$ is an extremal graph corresponding to ${\rm ex}_{\mathcal{OP}}(n-1,C_{4})$ .

Lemma 5.3.

Let $n\geq 2661$ and $G^{**}$ be an extremal plane graph corresponding to ${\rm ex}_{\mathcal{P}}(n,2C_{4})$ . Then $G^{**}$ contains at least fourteen quadrilaterals and all of them share exactly one vertex.

Proof.

Note that $e(G^{*})={\rm ex}_{\mathcal{OP}}(n-1,C_{4})\geq\frac{12}{7}n-5$ and $G^{*}$ is a $C_{4}$ -free outerplanar graph of order $n-1$ . Then $K_{1}+G^{*}$ is an $n$ -vertex $2C_{4}$ -free planar graph, and thus

\displaystyle e(G^{**})\geq e(K_{1}+G^{*})=e(G^{*})+n-1\geq\frac{19}{7}n-6.

On the other hand, by Lemma 5.1, we have

{\rm ex}_{\mathcal{P}}(n,K_{1}+P_{4})\leq\frac{8}{3}(n-2).

Note that $\frac{19}{7}n-6>\frac{8}{3}(n-2)$ for $n\geq 2661$ . Then $G^{**}$ contains a copy, say $H_{1}$ , of $K_{1}+P_{4}$ . Let $G_{1}$ be the graph obtained from $G^{**}$ by deleting all edges within $V(H_{1})$ . Since $|H_{1}|=5$ , we have $e(G_{1})\geq e(G^{**})-(3|H_{1}|-6)=e(G^{**})-9>\frac{8}{3}(n-2)$ . Thus, $G_{1}$ contains a copy, say $H_{2}$ , of $K_{1}+P_{4}$ . Now we can obtain a new graph $G_{2}$ from $G_{1}$ by deleting all edges within $V(H_{2})$ . Note that $e(G^{**})-14\times 9>\frac{8}{3}(n-2)$ . Repeating above steps, we can obtain a graph sequence $G_{1},G_{2},\ldots,G_{14}$ and fourteen copies $H_{1},H_{2},\cdots,H_{14}$ of $K_{1}+P_{4}$ such that $H_{i}\subseteq G_{i-1}$ and $G_{i}$ is obtained from $G_{i-1}$ by deleting all edges within $V(H_{i})$ . This also implies that $G^{**}$ contains at least fourteen quadrilaterals. We next give four claims on those copies of $K_{1}+P_{4}$ .

Claim 5.1.

Let $i,j$ be two integers with $1\leq i<j\leq 14$ and $v\in V(H_{i})\cap V(H_{j})$ . Then, $V(H_{i})\cap N_{H_{j}}(v)=\varnothing$ .

Proof.

Suppose to the contrary that there exists a vertex $w\in V(H_{i})\cap N_{H_{j}}(v)$ . Note that $v,w\in V(H_{i})$ . By the definition of $G_{i}$ , whether $vw\in E(H_{i})$ or not, we can see that $vw\notin E(G_{i})$ . On the other hand, note that $H_{j}\subseteq G_{j-1}\subseteq G_{i}$ , then $vw\in E(H_{j})\subseteq E(G_{i})$ , contradicting $vw\notin E(G_{i}).$ Hence, the claim holds. ∎

Claim 5.2.

$|V(H_{i})\cap V(H_{j})|\in\{1,2\}$ for any two integers $i,j$ with $1\leq i<j\leq 14$ .

Proof.

If $H_{i}$ and $H_{j}$ are vertex-disjoint, then $G^{**}$ contains $2C_{4}$ , a contradiction. Now suppose that there exist three vertices $v_{1},v_{2},v_{3}\in V(H_{i})\cap V(H_{j})$ . Observe that $K_{1}+P_{4}$ contains no an independent set of size $3$ . Then $H_{j}[\{v_{1},v_{2},v_{3}\}]$ is nonempty. Assume without loss of generality that $v_{1}v_{2}\in E(H_{j})$ . Then $v_{2}\in V(H_{i})\cap N_{H_{j}}(v_{1})$ , which contradicts Claim 5.1. Therefore, $1\leq|V(H_{i})\cap V(H_{j})|\leq 2$ . ∎

Now for convenience, a vertex $v$ in a graph $G$ is called a $2$ -vertex if $d_{G}(v)=2$ , and a $2^{+}$ -vertex if $d_{G}(v)>2.$ Clearly, every copy of $K_{1}+P_{4}$ contains two 2-vertices and three $2^{+}$ -vertices.

Claim 5.3.

Let $\mathcal{H}$ be the family of graphs $H_{i}$ ( $1\leq i\leq 14$ ) such that every 2-vertex in $H_{i}$ is a $2^{+}$ -vertex in $H_{1}$ . Then $|\mathcal{H}|\leq 3$ .

Proof.

Note that $H_{1}$ contains only three $2^{+}$ -vertices, say $v_{1},v_{2}$ and $v_{3}$ . Then every graph $H_{i}\in\mathcal{H}$ must contain two of $v_{1},v_{2}$ and $v_{3}$ as $2$ -vertices. Suppose to the contrary that $|\mathcal{H}|\geq 4$ . By pigeonhole principle, there exist two graphs $H_{i_{1}},H_{i_{2}}\in\mathcal{H}$ such that they contain the same two 2-vertices, say $v_{1},v_{2}$ . It follows that $H_{i_{j}}-\{v_{j}\}$ contains a $4$ -cycle for $j\in\{1,2\}$ . By Claim 5.2, we have $V(H_{i_{1}})\cap V(H_{i_{2}})=\{v_{1},v_{2}\}$ , which implies that $H_{i_{1}}-\{v_{1}\}$ and $H_{i_{2}}-\{v_{2}\}$ are vertex-disjoint. Hence, $G^{**}$ contains two vertex-disjoint 4-cycles, a contradiction. ∎

Claim 5.4.

Let $j$ be an integer with $2\leq j\leq 14$ and $H_{j}\notin\mathcal{H}$ . Then, there exists a vertex $v\in V(H_{1})\cap V(H_{j})$ such that $d_{H_{1}}(v)\geq 3$ and $d_{H_{j}}(v)\geq 3$ .

Proof.

By Claim 5.2, we have $1\leq|V(H_{1})\cap V(H_{j})|\leq 2$ . We first assume that $V(H_{1})\cap V(H_{j})=\{u\}$ . If $d_{H_{1}}(u)\geq 3$ and $d_{H_{j}}(u)\geq 3$ , then there is nothing to prove. If $d_{H_{1}}(u)=2$ , then $G^{**}$ contains two vertex-disjoint subgraphs $H_{1}-\{u\}$ and $H_{j}$ , and thus $2C_{4}$ , a contradiction. If $d_{H_{j}}(u)=2$ , then we can similarly get a contradiction. Therefore, $|V(H_{1})\cap V(H_{j})|=2$ .

Now, assume that $V(H_{1})\cap V(H_{j})=\{u_{1},u_{2}\}$ . We first deal with the case $d_{H_{j}}(u_{1})$ $=d_{H_{j}}(u_{2})=2$ . Since $H_{j}\notin\mathcal{H}$ , one of $\{u_{1},u_{2}\}$ , say $u_{1}$ , is a 2-vertex in $H_{1}$ . Hence, $G^{**}$ contains two vertex-disjoint subgraphs $H_{1}-\{u_{1}\}$ and $H_{j}-\{u_{2}\}$ , and so $2C_{4}$ , a contradiction. Thus, there exists some $i\in\{1,2\}$ with $d_{H_{j}}(u_{i})\geq 3$ . If $d_{H_{1}}(u_{i})\geq 3$ , then we are done. If $d_{H_{1}}(u_{i})=2$ , then we define $H_{j}^{\prime}$ as the subgraph of $H_{j}$ induced by $N_{H_{j}}(u_{i})\cup\{u_{i}\}$ . Since $d_{H_{j}}(u_{i})\geq 3$ , we can check that $H_{j}^{\prime}$ always contains a $C_{4}$ . Moreover, since $d_{H_{1}}(u_{i})=2$ , we can see that $H_{1}-\{u_{i}\}$ also contains a $C_{4}$ . On the other hand, by Claim 5.1, we have $N_{H_{j}}(u_{i})\cap V(H_{1})=\varnothing$ , which implies that $H_{j}^{\prime}$ and $H_{1}-\{u_{i}\}$ are vertex-disjoint. Therefore, $G^{**}$ contains $2C_{4}$ , a contradiction. ∎

By Claim 5.3, $|\mathcal{H}|\leq 3$ , thus there are at least ten graphs in $\{H_{j}~{}|~{}2\leq j\leq 14\}\setminus\mathcal{H}$ . However, $H_{1}$ has only three $2^{+}$ -vertices. By Claim 5.4 and pigeonhole principle, there exists a $2^{+}$ -vertex $w$ in $H_{1}$ and four graphs, say $H_{2},H_{3},H_{4},H_{5}$ , of $\{H_{j}~{}|~{}2\leq j\leq 14\}\setminus\mathcal{H}$ . By Claim 5.1, we get that $N_{H_{j}}(w)\cap V(H_{i})=\varnothing$ , and so $N_{H_{j}}(w)\cap N_{H_{i}}(w)=\varnothing$ , for any $i,j$ with $1\leq i<j\leq 5$ . If $G^{**}-\{w\}$ contains a quadrilateral $C^{\prime}$ , then there exists some $j^{\prime}\leq 5$ such that $N_{H_{j^{\prime}}}(w)\cap V(C^{\prime})=\varnothing$ as $|C^{\prime}|=4$ . Since $w$ is a $2^{+}$ -vertex in $H_{j^{\prime}}$ , we can observe that the subgraph of $H_{j^{\prime}}$ induced by $N_{H_{j^{\prime}}}(w)\cup\{w\}$ must contain a $C_{4}$ . Consequently, $G^{**}$ is not $2C_{4}$ -free, a contradiction. Thus, $G^{**}-\{w\}$ is $C_{4}$ -free, which implies that all quadrilaterals of $G^{**}$ share exactly one vertex. This completes the proof of Lemma 5.3. ∎

Now we are ready to give the proof of Theorem 1.5.

Proof.

Recall that $G^{*}$ is an extremal graph corresponding to ${\rm ex}_{\mathcal{OP}}(n-1,C_{4})$ . Then $K_{1}+G^{*}$ is planar and $2C_{4}$ -free. By Corollary 5.1, we have

\displaystyle e(K_{1}+G^{*})={\rm ex}_{\mathcal{OP}}(n-1,C_{4})+n-1=\left\{\begin{array}[]{ll}\frac{19}{7}n-6&\hbox{if $7\mid n$,}\\ \big{\lfloor}\frac{19n-34}{7}\big{\rfloor}{}&\hbox{otherwise.}\end{array}\right.

(30)

To prove Theorem 1.5, it suffices to show ${\rm ex}_{\mathcal{P}}(n,2C_{4})=e(K_{1}+G^{*}).$ Since $G^{**}$ is an extremal plane graph corresponding to ${\rm ex}_{\mathcal{P}}(n,2C_{4})$ , we have $e(G^{**})\geq e(K_{1}+G^{*})$ . In the following, we show that $e(G^{**})\leq e(K_{1}+G^{*})$ .

By Lemma 5.3, all quadrilaterals of $G^{**}$ share a vertex $w$ . Thus, $G^{**}-\{w\}$ is $C_{4}$ -free. Assume that $d_{G^{**}}(w)=s$ and $w_{1},\dots,w_{s}$ are around $w$ in clockwise order, with subscripts interpreted modulo $s$ . Let $e$ be an arbitrary edge in $E_{3,3}(G^{**})$ , that is, $e$ is incident with two 3-faces, say $F$ and $F^{\prime}$ . We define $H(e)$ as the plane subgraph induced by all edges incident with $F$ and $F^{\prime}$ . Clearly, $H(e)\cong K_{1}+P_{3}$ and so it contains a $C_{4}$ . Recall that all quadrilaterals of $G^{**}$ share exactly one vertex $w$ . Then, $w\in V(H_{e})$ and $w$ is incident with at least one face of $F$ and $F^{\prime}$ (see Figure 10). Note that $e$ is incident with $F$ . Then, either $e=ww_{i}$ or $e=w_{i}w_{i+1}$ for some $i\in\{1,2,\dots,s\}$ . By the choice of $e$ , we have

\displaystyle E_{3,3}(G^{**})\subseteq\{ww_{i},w_{i}w_{i+1}~{}|~{}1\leq i\leq s\}.

(31)

Assume first that $f_{4}(G^{**})=t\geq 1$ and $F_{1},\dots,F_{t}$ are 4-faces in $G^{**}$ . Since every 4-face is a quadrilateral, $w$ is incident with each 4-face. Consequently, there exists $j_{i}\in\{1,\dots,s\}$ such that $ww_{j_{i}},ww_{j_{i}+1}$ are incident with $F_{i}$ for each $i\in\{1,\dots,t\}$ . Thus, $ww_{j_{i}}\notin E_{3,3}(G^{**})$ for $1\leq i\leq t$ . On the other hand, if $w_{j_{i}}w_{j_{i}+1}\in E_{3,3}(G^{**})$ , then $H(w_{j_{i}}w_{j_{i}+1})$ contains a $C_{4}$ , and so $w\in V(H(w_{j_{i}}w_{j_{i}+1}))$ . This implies that $ww_{j_{i}}w_{j_{i}+1}w$ is a 3-face in $G^{**}$ , contradicting the fact that $ww_{j_{i}},ww_{j_{i}+1}$ are incident with the 4-face $F_{i}$ . Thus, we also have $w_{j_{i}}w_{j_{i}+1}\notin E_{3,3}(G^{**})$ for $1\leq i\leq t$ .

By the argument above, we can see that

\displaystyle E_{3,3}(G^{**})\cap\{ww_{j_{i}},w_{j_{i}}w_{j_{i}+1}~{}|~{}1\leq i\leq t\}=\varnothing.

(32)

Using (31) and (32) gives $e_{3,3}(G^{**})\leq 2s-2t=2s-2f_{4}(G^{**})$ . Hence,

\displaystyle 3f_{3}(G^{**})=e_{3}(G^{**})+e_{3,3}(G^{**})\leq e(G^{**})+2s-2f_{4}(G^{**}).

(33)

On the other hand,

\displaystyle 2e(G^{**})=\sum_{i\geq 3}if_{i}(G^{**})\geq 3f_{3}(G^{**})+4f_{4}(G^{**})+5(f(G^{**})-f_{3}(G^{**})-f_{4}(G^{**})),

which yields $f(G^{**})\leq\frac{1}{5}\left(2e(G^{**})+2f_{3}(G^{**})+f_{4}(G^{**})\right).$ Combining this with Euler’s formula $f(G^{**})=e(G^{**})-(n-2)$ , we obtain

\displaystyle e(G^{**})\leq\frac{5}{3}(n-2)+\frac{2}{3}f_{3}(G^{**})+\frac{1}{3}f_{4}(G^{**}).

(34)

If $f_{4}(G^{**})=t=0$ , then (33) and (34) hold directly. Combining (33) and (34), we have $e(G^{**})\leq\frac{15}{7}(n-2)+\frac{4}{7}s-\frac{1}{7}f_{4}(G^{**})$ . Recall that $d_{G^{**}}(w)=s\leq n-1$ . If $s\leq n-2$ , then $e(G^{**})\leq\lfloor\frac{19}{7}(n-2)\rfloor\leq e(K_{1}+G^{*})$ by (30), as desired. If $s=n-1$ , then $w$ is a dominating vertex of the planar graph $G^{**}$ , which implies that $G^{**}-\{w\}$ is outerplanar. Recall that $G^{**}-\{w\}$ is $C_{4}$ -free. Thus, $e(G^{**}-\{w\})\leq{\rm ex}_{\mathcal{OP}}(n-1,C_{4})$ , and so $e(G^{**})\leq{\rm ex}_{\mathcal{OP}}(n-1,C_{4})+n-1$ . Combining (30), we get $e(G^{**})\leq e(K_{1}+G^{*})$ , as required. This completes the proof of Theorem 1.5. ∎

References

[1] J.A. Bondy, U.S.R. Murty, Graph Theory, Springer-Verlag, Berlin, 2008.
[2] B.N. Boots, G.F. Royle, A conjecture on the maximum value of the principal eigenvalue of a planar graph, Geogr. Anal. 23 (3) (1991), 276-282.
[3] D.S. Cao, A. Vince, The spectral radius of a planar graph, Linear Algebra Appl. 187 (1993), 251–257.
[4] D.W. Cranston, B. Lidický, X.N. Liu, A. Shantanam, Planar Turán numbers of cycles: a counterexample, Electron. J. Combin. 29 (3) (2022), 3.31.
[5] S. Cioabă, D.N. Desai, M. Tait, The spectral even cycle problem, arxiv:2205.00990v1 (2022).
[6] C. Dowden, Extremal $C_{4}$ -free/ $C_{5}$ -free planar graphs, J. Graph Theory 83 (2016), 213–230.
[7] L.L. Du, B. Wang, M.Q. Zhai, Planar Turán numbers on short cycles of consecutive lengths, Bull. Iranian Math. Soc. 48 (5) (2022), 2395–2405.
[8] P. Erdős, Über ein Extremal problem in der Graphentheorie, Arch. Math. 13 (1962), 222–227.
[9] P. Erdős, L. Pósa, On the maximal number of disjoint circuits of a graph, Publ. Math. Debrecen 9 (1962), 3–12.
[10] L.F. Fang, B. Wang, M.Q. Zhai, Planar Turán number of intersecting triangles, Discrete Math. 345 (5) (2022), 112794.
[11] L.F. Fang, M.Q. Zhai, Outerplanar Turán numbers of cycles and paths, Discrete Math. 346 (12) (2023), 113655.
[12] Z. Füredi, D.S. Gunderson, Extremal numbers for odd cycles, Combin. Probab. Comput. 24 (2015), 641–645.
[13] Z. Füredi, M. Simonovits, The history of degenerate (bipartite) extremal graph problems, Bolyai Soc. Studies (The Erdős Centennial) 25 (2013), 167–262.
[14] D. Ghosh, E. Győri, R.R. Martin, A. Paulos, C.Q. Xiao, Planar Turán number of the 6-cycle, SIAM J. Discrete Math. 36 (3) (2022), 2028–2050.
[15] E. Győri, A. Li, R.T. Zhou, The planar Turán number of the seven-cycle, arxiv:2307.06909v2.
[16] Y.X. Lan, Y.T. Shi, Z-X. Song, Extremal Theta-free planar graphs, Discrete Math. 342 (12) (2019), 111610.
[17] Y.X. Lan, Y.T. Shi, Z-X. Song, Extremal $H$ -free planar graphs, Electron. J. Combin. 26 (2019) no. 2, Paper No. 2.11, 17 pp.
[18] Y.X. Lan, Y.T. Shi, Z.X. Song, Planar Turán number and planar anti-Ramsey number of graphs, Oper. Res. Trans. 25 (2021), 200–216.
[19] Y.X. Lan, Y.T. Shi, Z-X. Song, Planar Turán number of cubic graphs and disjoint union of cycles, arxiv: 2202.09216v2 (2022).
[20] P. Li, Planar Turán number of the disjoint union of cycles, Discrete Appl. Math. 342 (2024), 260–274.
[21] J.W. Moon, On independent complete subgraphs in a graph, Canadian J. Math. 20 (1968) 95–102.
[22] V. Nikiforov, A spectral condition for odd cycles in graphs, Linear Algebra Appl. 428 (2008), no. 7, 1492–1498.
[23] V. Nikiforov, Bounds on graph eigenvalues II, Linear Algebra Appl. 427 (2-3) (2007), 183–189.
[24] B. Pittel, J. Spencer, N. Wormald, Sudden emergence of a giant $k$ -core in a random graph, J. Combin. Theory Ser. B 67 (1996), 111–151.
[25] R.L. Shi, Z. Walsh, X.X. Yu, Planar Turán number of the 7-cycle, arxiv:2306.13594v1.
[26] R.L. Shi, Z. Walsh, X.X. Yu, Dense circuit graphs and the planar Turán number of a cycle, arxiv:2310.06631v1.
[27] M. Tait, J. Tobin, Three conjectures in extremal spectral graph theory, J. Combin. Theory Ser. B 126 (2017), 137–161.
[28] M.Q. Zhai, B. Wang, Proof of a conjecture on the spectral radius of $C_{4}$ -free graphs, Linear Algebra Appl. 437 (7) (2012), 1641–1647.

Extremal spectral results of planar graphs without vertex-disjoint cycles111Lin was supported by NSFC grant 12271162 and Natural Science Foundation of Shanghai (No. 22ZR1416300). Shi was supported by NSFC grant 12161141006.

1 Introduction

1.1 Planar spectral extremal values on cycles

Theorem 1.1.

Theorem 1.2.

Corollary 1.1.

Theorem 1.3.

1.2 Planar Turán numbers on cycles

Theorem 1.4.

Conjecture 1.1.

Theorem 1.5.

2 Proof of Theorem 1.1

Proof.

Claim 2.1.

Proof.

Claim 2.2.

Proof.

Claim 2.3.

Proof.

Claim 2.4.

Proof.

Claim 2.5.

Proof.

Claim 2.6.

Proof.

Claim 2.7.

Proof.

3 Proofs of Theorems 1.2 and 1.3

Lemma 3.1.

Proof.

Claim 3.1.

Proof.

Definition 3.1.

Lemma 3.2.

Proof.

Claim 3.2.

Proof.

Claim 3.3.

Proof.

Claim 3.4.

Proof.

Claim 3.5.

Proof.

4 Proof of Theorem 1.4

Lemma 4.1.

Lemma 4.2.

Lemma 4.3.

Proof.

Claim 4.1.

Proof.

Claim 4.2.

Proof.

Claim 4.3.

Proof.

Claim 4.4.

Proof.

Lemma 4.4.

Proof.

Proof.

5 Proof of Theorem 1.5

Lemma 5.1.

Lemma 5.2.

Corollary 5.1.

Lemma 5.3.

Proof.

Claim 5.1.

Proof.

Claim 5.2.

Proof.

Claim 5.3.

Proof.

Claim 5.4.

Proof.

Proof.

References

Extremal spectral results of planar graphs without vertex-disjoint cycles¹¹1Lin was supported by NSFC grant 12271162 and Natural Science Foundation of Shanghai (No. 22ZR1416300). Shi was supported by NSFC grant 12161141006.