Extraordinary-log surface phase transition in the three-dimensional $XY$ model

Continuous phase transitions are ubiquitous, from the magnetic and superconducting transitions in real materials to the cooling of early universe. Near a second-order transition, a diverging correlation length emerges, and several macroscopic properties become independent of microscopic details of the system Stanley (1999); Sachdev (2011); Fernández et al. (2013). Systems can be classified into few universality classes, depending on a small number of global features like symmetry, dimensionality and the range of interactions. Typically, physical quantities exhibit power-law behaviors governed by critical exponents characteristic of a universality class. In particular, at criticality, the two-point correlation function $g(r)$ decays algebraically with the spatial distance $r$ as

where $d$ is the spatial dimension and $\eta$ is the anomalous dimension. Power-law universality has been extensively verified and recognized as the standard scenario of critical phenomena Sachdev (2011); Fernández et al. (2013); Goldman (2013); Svistunov et al. (2015). Very recently, a novel logarithmic universality of criticality, drastically different from that encoded in (1), was proposed in the context of surface critical behavior (SCB) Metlitski .

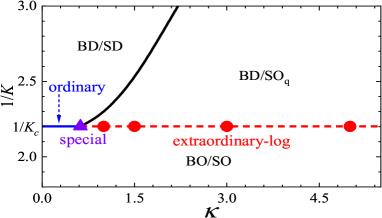
SCB refers to the critical phenomenon occurring on the boundary of a critical bulk Binder and Hohenberg (1974); Ohno and Okabe (1984); Landau et al. (1989); Diehl (1997); Pleimling (2004); Deng et al. (2005); Deng (2006); Dubail et al. (2009); Zhang and Wang (2017); Ding et al. (2018); Weber et al. (2018); Metlitski ; Weber and Wessel (2021); Parisen Toldin (2021). Recent activities on SCB were partly triggered by the exotic surface effects of symmetry protected topological phases Grover and Vishwanath ; Parker et al. (2018). The O($N$) model exhibits rich SCBs including the special, ordinary, and extraordinary transitions, depending on $N$ and $d$ Binder and Hohenberg (1974); Ohno and Okabe (1984); Landau et al. (1989); Diehl (1997); Pleimling (2004); Deng et al. (2005); Deng (2006); Dubail et al. (2009); Zhang and Wang (2017); Ding et al. (2018); Weber et al. (2018); Metlitski ; Weber and Wessel (2021); Parisen Toldin (2021). The situations at $d=3$ are extremely subtle and controversial Deng et al. (2005); Deng (2006); Metlitski ; Weber and Wessel (2021); Parisen Toldin (2021). Logarithmic universality of extraordinary transition was proposed for the three-dimensional O($N$) model with $2\leq N<N_{c}$ by means of renormalization group (RG) Metlitski , whereas $N_{c}$ is not exactly known. It was predicted that the two-point correlation on surface decays logarithmically with $r$ as Metlitski

where $r_{0}$ is a non-universal constant. If $N$ is specified, the critical exponent $\hat{\eta}$ is universal in extraordinary regime. The asymptotic form (2) obviously differs from the standard scenario (1). A quantum Monte Carlo study was performed for the SCB of a (2+1)-dimensional O(3) system Weber and Wessel (2021). However, both the logarithmic and the extraordinary-power behavior Metlitski were not completely confirmed. By contrast, compelling evidence for the logarithmic behavior was obtained from a classical O(3) $\phi^{4}$ model Parisen Toldin (2021).

In this work, we explore the extraordinary transition with $N=2$, which is the lower-marginal candidate for the logarithmic universality. We consider an extensive domain of extraordinary critical line, in which the universality of logarithmic behavior is confirmed. Moreover, we give a two-distance scenario for the finite-size scaling (FSS) of $g(r)$, where an $r$-independent plateau emerges at large distance. The height of the plateau exhibits a logarithmic FSS with the exponent $\hat{\eta}^{\prime}$, which relates to the exponent $\hat{\eta}$ of $r$-dependent behavior by $\hat{\eta}^{\prime}\approx\hat{\eta}-1$.

We study the $XY$ model on simple-cubic lattices with the Hamiltonian Landau et al. (1989); Deng et al. (2005)

where $\vec{S}_{\bf r}$ represents the $XY$ spin on site ${\bf r}$ and $K_{{\bf r}{\bf r^{\prime}}}$ denotes the strength of nearest-neighbor ferromagnetic coupling. We impose open boundary conditions in one direction and periodic boundary conditions in other directions, hence a pair of open surfaces are specified. We set $K_{{\bf r}{\bf r^{\prime}}}=K^{\prime}$ if ${\bf r}$ and ${\bf r^{\prime}}$ are on the same surface and $K_{{\bf r}{\bf r^{\prime}}}=K$ otherwise. The surface coupling enhancement $\kappa$ is defined by $\kappa=(K^{\prime}-K)/K$.

Figure 1 shows the phase diagram of model (3), which contains a long-range-ordered surface phase in presence of ordered bulk, as well as disordered and critical quasi-long-range-ordered surface phases in presence of disordered bulk. The critical lines meet together at the special transition point. A characteristic feature for $N=2$ is the existence of the quasi-long-range-ordered phase, which is absent in $N=1$ and $N\geq 3$ situations.

Consider the quasi-long-range-ordered regime. As the bulk critical point $K_{c}$ is approached, namely $K\rightarrow K_{c}^{-}$, divergent bulk correlations emerge. A possible scenario is that the surface long-range order develops at $K_{c}$ as a result of the effective interactions mediated by long-range bulk correlations. This scenario can not be precluded by the Mermin-Wagner theorem as the effective interactions could be long-ranged. A previous study revealed Deng et al. (2005) that the Monte Carlo data restricting to $L\leq 95$ ($L$ is linear size) are not sufficient to preclude either discontinuous or continuous surface transition across the extraordinary critical line; the former implies long-range surface order at $K_{c}$.

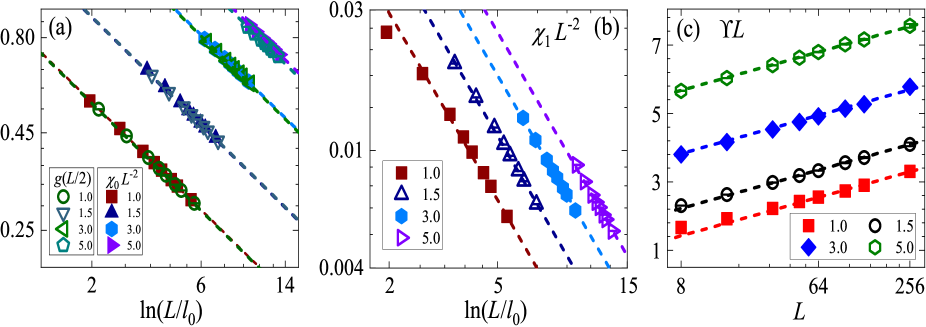
By Monte Carlo sampling of the surface two-point correlation function $g(r)=\langle\vec{S}_{0}\cdot\vec{S}_{r}\rangle$, we confirm the emergence of logarithmic universality in model (3). As shown in Fig. 2(a), the $L$ dependence of $g(L/2)$ obeys the scaling formula $g(L/2)\sim[{\rm ln}(L/l_{0})]^{-\hat{\eta}^{\prime}}$ with $\hat{\eta}^{\prime}=0.59(2)$.

We analyze the surface magnetic fluctuations $\Gamma({\bf k})=L^{2}\langle||\overset{\rightharpoonup\mkern-10.0mu\rightharpoonup}{m}({\bf k})||^{2}\rangle$ with $\overset{\rightharpoonup\mkern-10.0mu\rightharpoonup}{m}({\bf k})=(1/L^{2})\sum_{\bf r}\vec{S}_{\bf r}e^{i{\bf k}\cdot{\bf r}}$, where the summation runs over sites on surface and ${\bf k}$ denotes a Fourier mode. As shown in Figs. 2(a) and (b), the magnetic fluctuations $\chi_{0}=\Gamma(0,0)$ (susceptibility) and $\chi_{1}=\Gamma(2\pi/L,0)$ have the distinct FSS behaviors $\chi_{0}\sim L^{2}[{\rm ln}(L/l_{0})]^{-\hat{\eta}^{\prime}}$ and $\chi_{1}\sim L^{2}[{\rm ln}(L/l_{0})]^{-\hat{\eta}}$, with ${\hat{\eta}}\approx{\hat{\eta}^{\prime}}+1$. Motivated by these observations as well as the two-distance scenarios in high-dimensional O($N$) critical systems Papathanakos (2006); Grimm et al. (2017); Zhou et al. (2018); Lv et al. (2021); Fang et al. and quantum deconfined criticality Shao et al. (2016), we conjecture that the FSS of critical two-point correlation behaves as

where $r_{0}$ and $l_{0}$ are non-universal constants. By (4), we point out two coexisting features: the $r$-dependent behavior $[{\rm ln}(r/r_{0})]^{-\hat{\eta}}$ and the large-distance $r$-independent plateau $[{\rm ln}(L/l_{0})]^{-\hat{\eta}^{\prime}}$. Equation (4) is an explanation for our numerical results and compatible with the FSS of second-moment correlation length at the extraordinary transition of O(3) model Parisen Toldin (2021); Metlitski (2021). Recently, a two-distance scenario was used to describe the two-point correlation of O($n$) model at a marginal situation (the upper critical dimensionality) Lv et al. (2021) and confirmed by large-scale simulations on hyper-cubic lattices up to $768^{4}$ sites Fang et al. . The open surfaces of model (3) are at the lower critical dimensionality ($d_{s}=2$) and also belong to marginal situations.

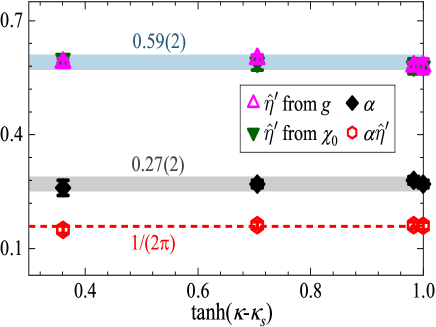
We confirm the scaling relation between $\hat{\eta}^{\prime}$ and the RG parameter of helicity modulus. The helicity modulus $\Upsilon$ measures the response of a system to a twist in boundary conditions Fisher et al. (1973). The definition is given in the Supplementary Materials (SM). Figure 2(c) demonstrates that $\Upsilon$ scales as $\Upsilon L\sim 2\alpha{\rm ln}L$ with the RG parameter $\alpha=0.27(2)$. Figure 3 simultaneously illustrates the universality of $\hat{\eta}^{\prime}$ and $\alpha$ in the extraordinary regime. Meanwhile, the scaling relation $\alpha\hat{\eta}^{\prime}=1/(2\pi)$ is evidenced, conforming to the predicted form Metlitski

According to (4), the exponent $\hat{\eta}^{\prime}$ characterizes the FSS of the height of the plateau. Equation (5) is not exactly the original prediction in Ref. Metlitski , where the exponent $\hat{\eta}$ for $r$-dependent behavior obeys the relation $\hat{\eta}=(N-1)/(2\pi\alpha)$.

To explore the SCB, we fix the bulk coupling strength at $K_{c}$. Previously, two of us and coworkers performed simulations utilizing the Prokof’ev-Svistunov worm algorithms Prokof’ev and Svistunov (2001, 2010) on periodic simple-cubic lattices with $L_{\rm max}=512$, and obtained $1/K_{c}=2.201\,844\,1(5)$ Xu et al. (2019). This estimate was confirmed by an independent Monte Carlo study Hasenbusch (2019). Here, we simulate model (3) at $1/K_{c}=2.201\,844\,1$ using Wolff’s cluster algorithm Wolff (1989) on simple-cubic lattices with $L_{\rm max}=256$. The original procedure in Ref. Wolff (1989) is adapted to model (3). We analyze the extraordinary transitions at $\kappa=1$, $1.5$, $3$, and $5$, and the special transition at $\kappa_{s}=0.622\,2$ Deng et al. (2005). For each $\kappa$, the number of Wolff updating steps is up to $1.2\times 10^{8}$ for $L\leq 32$ and ranges from $1.7\times 10^{8}$ to $6.1\times 10^{8}$ for $L\geq 48$. See SM for details, which includes Refs. Janke (1990); Krauth (2006).

Our conclusions are based on FSS analyses performed by using least-squares fits. Following Refs. Hasenbusch (2019, 2020), the function $curve\_fit()$ in $Scipy\_library$ is adopted. For caution, we compare the fits with the benchmarks from implementing Mathematica’s $NonlinearModelFit$ function as Ref. Salas (2020). The fits with the Chi squared per degree of freedom $\chi^{2}/{\rm DF}\sim 1$ are preferred. We do not trust any single fit and final conclusions are drawn based on comparing the fits that are stable against varying $L_{\rm min}$, the minimum size incorporated.

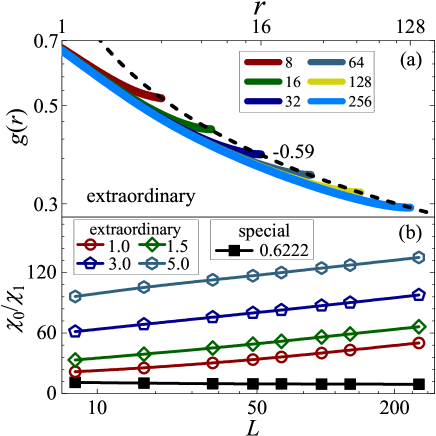
Figure 4(a) demonstrates the two-point correlation function $g(r)$ for the extraordinary transition at $\kappa=1$. The large-distance behavior can be monitored by the $L$ dependence of $g(L/2)$. According to Eq. (4), we have a scaling formula $g(L/2)\sim[{\rm ln}(L/l_{0})]^{-\hat{\eta}^{\prime}}$. We perform least-squares fits to this formula and obtain $\hat{\eta}^{\prime}=0.596(2)$, $l_{0}=0.94(1)$, and $\chi^{2}/{\rm DF}\approx 0.73$, with $L_{\rm min}=16$. As $L_{\rm min}$ is varied, preferred fits are also obtained (Table 1). By comparing the fits, our final estimate of $\hat{\eta}^{\prime}$ for $\kappa=1$ is $\hat{\eta}^{\prime}=0.59(1)$. In the SM, we present similar analyses for $\kappa=1.5,3$ and $5$, for which the final estimates are $\hat{\eta}^{\prime}=0.60(1)$ ($\kappa=1.5$), $0.58(1)$ ($\kappa=3$) and $0.58(2)$ ($\kappa=5$). It is therefore confirmed that $g(L/2)$ obeys the logarithmic scaling $g(L/2)\sim[{\rm ln}(L/l_{0})]^{-\hat{\eta}^{\prime}}$, with a universal exponent $\hat{\eta}^{\prime}=0.59(2)$. As displayed in the SM, the fits by the conventional power-law ansatz (1) have poor qualities and give unstable results.

For a verification of Eq. (4), we analyze the FSS of surface magnetic fluctuations. In the Monte Carlo simulations, we sample $\chi_{2}=\Gamma(2\pi/L,2\pi/L)$ as well as $\chi_{0}$ and $\chi_{1}$.

According to (4), an $r$-independent plateau emerges at large distance. This plateau contributes to the magnetic fluctuations at zero mode but not to those at non-zero modes. The ratio $\chi_{0}/\chi_{1}$ at extraordinary transitions is shown in Fig. 4(b). As $L\rightarrow\infty$, the ratio keeps increasing, implying distinct FSS of $\chi_{0}$ and $\chi_{1}$.

More precisely, $\chi_{0}$ is expected to scale as $\chi_{0}\sim L^{2}[{\rm ln}(L/l_{0})]^{-\hat{\eta}^{\prime}}$. The results of scaling analyses for $\kappa=1$ are illustrated in Table 1 and those for $\kappa=1.5$, $3$, and $5$ are given in SM. Comparing preferred fits, we obtain $\hat{\eta}^{\prime}=0.60(1)$ ($\kappa=1$), $0.59(2)$ ($\kappa=1.5$), $0.58(2)$ ($\kappa=3$), and $0.58(1)$ ($\kappa=5$). These estimates of $\hat{\eta}^{\prime}$ agree well with those determined from the $L$ dependence of $g(L/2)$, hence the final result $\hat{\eta}^{\prime}=0.59(2)$ is confirmed.

We analyze the magnetic fluctuations $\chi_{1}$ and $\chi_{2}$ at nonzero Fourier modes by performing fits to $\chi_{{\bf k}\neq 0}\sim L^{2}[{\rm ln}(L/l_{0})]^{-\hat{\eta}}$. We confirm the drastic decays of $\chi_{1}L^{-2}$ and $\chi_{2}L^{-2}$ upon increasing ${\rm ln}L$. For reducing the uncertainties of fits, we fix $l_{0}$ at those obtained from the scaling analyses of $\chi_{0}$, and estimate $\hat{\eta}\approx 1.7$ over $\kappa=1,1.5,3$, and $5$. From the log-log plot of $\chi_{1}L^{-2}$ versus ${\rm ln}(L/l_{0})$ in Fig. 2(b), it is seen that the data nearly scale as $\chi_{1}L^{-2}\sim[{\rm ln}(L/l_{0})]^{-\hat{\eta}}$ with $\hat{\eta}\approx 1.59$. Similar result is obtained for $\chi_{2}L^{-2}$ (SM). Hence, $\chi_{1}$ and $\chi_{2}$ obey the logarithmic FSS formula $\chi_{{\bf k}\neq 0}\sim L^{2}[{\rm ln}(L/l_{0})]^{-\hat{\eta}}$, with $\hat{\eta}\approx 1.6$.

Our results for the FSS of $\chi_{0}$ and $\chi_{1}$ are also compatible with the Monte Carlo data Parisen Toldin (2021); Metlitski (2021) of the second-moment correlation length $\xi_{\rm 2nd}$, which scales as $(\xi_{\rm 2nd}/L)^{2}\sim(\chi_{0}/\chi_{1}-1)\sim{\rm ln}L$. The relation $\hat{\eta}=\hat{\eta}^{\prime}+1$ is implied.

As $\hat{\eta}$ is much larger than $\hat{\eta}^{\prime}$, the two-distance scenario (4) indicates that the $r$-dependent contribution decays fast. It explains the profile of $g(r)$ in Fig. 4(a), where the large-distance plateau dominates.

By contrast, the special transition at $\kappa_{s}$ belongs to the standard scenario (1) of continuous transition. The $r$-dependent behavior converges to the power law $g(r)\sim r^{-\eta}$, which is comparable with the contribution from $g(L/2)\sim L^{-\eta}$. Moreover, the magnetic renormalization exponent $y_{h}$ relates to the anomalous dimension $\eta$ by $y_{h}=(4-\eta)/2$, and the magnetic fluctuations $\chi_{0}$, $\chi_{1}$, and $\chi_{2}$ all scale as $L^{2y_{h}-2}$. As shown in Fig. 4(b), the ratio $\chi_{0}/\chi_{1}$ at $\kappa_{s}$ converges fast to a constant upon increasing $L$. More results for $g(r)$, $\chi_{0}$, $\chi_{1}$ and $\chi_{2}$ are given in SM.

It was predicted Metlitski ; Metlitski (2021) that the scaled helicity modulus $\Upsilon L$ diverges logarithmically as $\Upsilon L\sim 2\alpha{\rm ln}L$, with $\alpha$ a universal RG parameter. Further, the universal form (5) of scaling relation was established Metlitski . The form is supported by the Monte Carlo results of an O(3) $\phi^{4}$ model Parisen Toldin (2021).

We sample $\Upsilon$ of model (3) by Monte Carlo simulations. The dependence of $\Upsilon L$ on ${\rm ln}L$ is shown in Fig. 2(c) for $\kappa=1,1.5,3$, and $5$. For each $\kappa$, a nearly linear dependence is observed in large-$L$ regime. Further, we perform a FSS analysis of $\Upsilon$ according to $\Upsilon L=2\alpha{\rm ln}L+A+BL^{-1}$, where $A$ and $B$ are constants. We explore the situations with and without the correction term $BL^{-1}$ separately. Stable fits are achieved, with the final estimates of $\alpha$ being $\alpha=0.26(2)$ ($\kappa=1$), $0.27(1)$ ($\kappa=1.5$), $0.28(1)$ ($\kappa=3$), and $0.27(1)$ ($\kappa=5$). Comparing these estimates, the universal value of $\alpha$ is determined to be $\alpha=0.27(2)$.

As shown in Fig. 3, the scaling relation (5) between $\alpha$ and $\hat{\eta}^{\prime}$ is confirmed. According to (4), $\hat{\eta}^{\prime}$ characterizes the logarithmic FSS for the height of plateau.

We provide strong evidence for the emergence of the extraordinary-log universality class Metlitski . We propose the two-distance scenario (4) for the FSS of two-point correlation function, where a large-distance plateau emerges. The height of the plateau decays logarithmically with $L$ by the exponent $\hat{\eta}^{\prime}$, which obeys the scaling relation (5) with the RG parameter of helicity modulus. The two-distance scenario is supported not only by the Monte Carlo data for $N=2$ of this work, but also by the results for $N=3$ in Ref. Parisen Toldin (2021).

A variety of open questions arise. First, it is shown essentially that a two-dimensional $XY$ system with finely tuned long-range interactions exhibits logarithmic universality. Is it possible to formulate the interactions in a microscopic Hamiltonian? Second, is there a classical-quantum mapping for the two-distance scenario that holds at the O($N$) quantum critical points Ding et al. (2018); Weber et al. (2018); Weber and Wessel (2021)? Third, as shown in Ref. Fang et al. , the introduction of unwrapped distance is crucial for verifying the short-distance behavior in two-distance scenario. The behavior of unwrapped distance in the extraordinary-log universality remains unclear. Finally, we note that, as recently observed for the five-dimensional Ising model Fang et al. (2020), lattice sites can be decomposed into clusters, and interesting geometric phenomena associated with the two-distance scenario may arise Sun et al. .