^†^†thanks: NHFP Einstein fellow

Extracting the Gravitational Recoil from Black Hole Merger Signals

Vijay Varma [email protected] TAPIR 350-17, California Institute of Technology, 1200 E California Boulevard, Pasadena, CA 91125, USA Maximiliano Isi [email protected] LIGO Laboratory, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA Sylvia Biscoveanu [email protected] LIGO Laboratory, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA

(December 30, 2024)

Abstract

Gravitational waves carry energy, angular momentum, and linear momentum. In generic binary black hole mergers, the loss of linear momentum imparts a recoil velocity, or a “kick”, to the remnant black hole. We exploit recent advances in gravitational waveform and remnant black hole modeling to extract information about the kick from the gravitational wave signal. Kick measurements such as these are astrophysically valuable, enabling independent constraints on the rate of second-generation mergers. Further, we show that kicks must be factored into future ringdown tests of general relativity with third-generation gravitational wave detectors to avoid systematic biases. We find that, although little information can be gained about the kick for existing gravitational wave events, interesting measurements will soon become possible as detectors improve. We show that, once LIGO and Virgo reach their design sensitivities, we will reliably extract the kick velocity for generically precessing binaries—including the so-called superkicks, reaching up to 5000 km/s.

Introduction.— As existing gravitational wave (GW) detectors, Advanced LIGO Aasi et al. (2015) and Virgo Acernese et al. (2015), approach their design sensitivities, they continue to open up unprecedented avenues for studying the astrophysics of black holes (BHs). One such opportunity is to experimentally study the gravitational recoil in binary BH mergers. It is well known that GWs carry away energy and angular momentum, causing the binary to shrink during the inspiral; however, in addition to this, GWs also carry away linear momentum, shifting the binary’s center of mass in the opposite direction Bonnor et al. (1961); Peres (1962); Bekenstein (1973); Fitchett (1983). Learning about this effect from GW data would be of high astrophysical significance.

During a binary BH coalescence, most of the linear momentum is radiated near the time of the merger Gonzalez et al. (2007a); Lousto and Zlochower (2008); Lousto et al. (2012); Lousto and Zlochower (2013); Blanchet et al. (2005); Damour and Gopakumar (2006); Le Tiec et al. (2010), resulting in a recoil or “kick” imparted to the remnant BH. The end state of the remnant is entirely characterized by its mass ( $m_{f}$ ), spin ( $\bm{\chi}_{f}$ ) and kick velocity ( $\bm{v}_{f}$ ); all additional complexities (“hair”) Israel (1968); Carter (1971) are dissipated away in GWs during the ringdown stage that follows the merger. The remnant mass and spin have already been measured from GW signals and used to test general relativity Abbott et al. (2016a, 2019a); Ghosh et al. (2018); Brito et al. (2018); Carullo et al. (2018, 2019); Isi et al. (2019); Giesler et al. (2019). However, a measurement of the kick has remained elusive.

Measuring the kick velocity from binary BHs would have important astrophysical applications—particularly for precessing binaries, where the component BH spins have generic orientations with respect to the orbit. For these systems, the spins interact with the orbital angular momentum as well as with each other, causing the orbital plane to precess Apostolatos et al. (1994). The kick velocity of these systems can reach up to $5000$ km/s for certain fine-tuned configurations Campanelli et al. (2007a); Gonzalez et al. (2007b); Tichy and Marronetti (2007); Lousto and Zlochower (2011); Lousto and Healy (2019); Sperhake et al. (2020), earning them the moniker of “superkicks”. Such velocities are larger than the escape velocity of even the most massive galaxies. This can have dramatic consequences for mergers of supermassive BHs residing at galactic centers. The remnant BH can be significantly displaced or ejected Merritt et al. (2004); Komossa et al. (2008), impacting the galaxy’s evolution Volonteri et al. (2010); Komossa and Merritt (2008); Gerosa and Sesana (2015), and event rates sesana (2007) for the future LISA mission Amaro-Seoane et al. (2017).

The kick velocity is also important for second-generation stellar-mass mergers, where one of the component BHs originated in a previous merger. This scenario has attracted much attention recently Yang et al. (2019); Gayathri et al. (2020); Gerosa and Berti (2019); Mangiagli et al. (2019); Di Carlo et al. (2019); Rodriguez et al. (2019); Doctor et al. (2019); Farmer et al. (2019) because the GW event GW170729 Abbott et al. (2019b); Chatziioannou et al. (2019) may have a component BH that is too massive to originate in a supernova explosion Woosley (2017); Marchant et al. (2018), the typical formation scenario for stellar-mass BHs. A second-generation merger could explain this, as the first merger would have led to a remnant BH more massive than the original stellar-mass progenitors. If we could measure the kick velocity from GW signals, we could place independent constraints on rates of second-generation mergers.

In this Letter, we present the first method to extract the kick magnitude and direction from generically precessing GW signals. We demonstrate that kicks will be measured reliably once LIGO and Virgo reach their design sensitivities, and possibly even earlier. The key is being able to accurately measure the spins of the individual BHs in the binary, from which the kick velocity can be inferred. This is made possible by two advances in GW modeling achieved in the past few years: numerical relativity (NR) surrogate models for both gravitational waveforms Varma et al. (2019a); Blackman et al. (2017) and remnant properties Varma et al. (2019a, b), suitable for generically precessing binaries. These models capture the effects of spin precession at an accuracy level comparable to the NR simulations, and are the most accurate models currently available in their regime of validity Varma et al. (2019a).

Methods.— We use the surrogate waveform model NRSur7dq4 Varma et al. (2019a) to analyze public GW data Abbott et al. (2019b); LIGO Scientific Collaboration and Virgo Collaboration (2018), as well as simulated signals in synthetic Gaussian noise corresponding to the three-detector advanced LIGO-Virgo network at its design sensitivity LIGO Scientific Collaboration (2018a); Manzotti and Dietz (2012); Abbott et al. (2018).

NRSur7dq4 is trained on NR simulations with mass ratios $q=m_{1}/m_{2}\leq 4$ and component spin magnitudes $|\bm{\chi}_{1}|,|\bm{\chi}_{2}|\leq 0.8$ with generic spin directions. The index 1 (2) corresponds to the heavier (lighter) BH, with $m_{1}\geq m_{2}$ . The spin components are specified at a reference GW frequency $f_{\text{ref}}=20$ Hz, in a source frame defined as follows: the $z$ -axis lies along the instantaneous orbital angular momentum, the $x$ -axis points from the lighter to the heavier BH, and the $y$ -axis completes the right-handed triad. We use all available spin-weighted spherical harmonic modes for this model ( $\ell\leq 4$ ). The inclination angle $\iota$ and azimuthal angle $\phi_{\text{ref}}$ indicate the location of the observer in the sky of the source, and take different values for each injection.

We obtain Bayesian posteriors on the signal parameters using the LALInference package Veitch et al. (2015), part of the LIGO Algorithm Library (LAL) Suite LIGO Scientific Collaboration (2018b). Because of restrictions on the duration of NRSur7dq4 waveforms, we choose to analyze data with a minimum Fourier frequency $f_{\rm low}=20$ Hz. Waveform length also restricts the higher-order-mode content of our NRSur7dq4 injections and templates in such way that modes with azimuthal harmonic number $m$ contribute with a starting frequency $f^{(m)}_{\rm min}=mf_{\rm low}/2$ . This means that our sensitivity projections are conservative, as detectors are expected to access information starting at lower frequencies than our simulations. NR injections are handled via the dedicated infrastructure in LAL Schmidt et al. (2017).

Given the posteriors distributions for the component parameters $\bm{\Lambda}=\{m_{1},m_{2},\bm{\chi}_{1},\bm{\chi}_{2}\}$ , we use the remnant-properties surrogate model NRSur7dq4Remnant Varma et al. (2019a) to predict the mass $m_{f}$ , spin $\bm{\chi}_{f}$ , and kick velocity $\bm{v}_{f}$ of the remnant. Trained on the same simulations as NRSur7dq4, NRSur7dq4Remnant uses Gaussian Process Regression Rasmussen and Williams (2006); Varma et al. (2019b) to model the remnant properties. NRSur7dq4Remnant improves upon previous remnant properties models by at least an order of magnitude in accuracy Varma et al. (2019a). NRSur7dq4Remnant models the full kick velocity vector and can, therefore, predict both the kick magnitude and direction. To assess whether a meaningful kick measurement has been made, we compare this posterior distribution with the corresponding effective prior distribution, estimated by drawing component parameters $\bm{\Lambda}$ from the prior. The priors used for the component parameters are discribed in the Supplement kic (a).

Comparison to previous methods.— The challenge of measuring the kick velocity from GW signals has been tackled before. The recoil may Doppler shift the final portion of the GW signal. Ref. Gerosa and Moore (2016) showed that it will not be possible to measure the kick velocity from this effect alone until third-generation GW detectors become active in the 2030s Reitze et al. (2019); Punturo et al. (2010a, b); Abbott et al. (2017). Ref. Calderón Bustillo et al. (2018) proposed a method to extract the kick based on direct comparison against NR simulations, showing that current detectors are sufficient for a kick measurement; however, that study was restricted to nonprecessing systems, where we do not expect very large kicks ( $\gtrsim 300$ km/s). Ref. Healy et al. (2019) compared GW150914 data against NR simulations, including precessing systems, to place bounds on the kick of GW150914. However, both Refs. Calderón Bustillo et al. (2018) and Healy et al. (2019) relied on a discrete bank of NR simulations, which does not allow for a full exploration of the multidimensional posterior for the system parameters.

Refer to caption — Figure 1: Kick magnitude measurement using different remnant BH models in conjunction with the NRSur7dq4 waveform model, for an injected NR signal at the design sensitivity of LIGO and Virgo. The signal parameters are given in the inset text and the corresponding kick magnitude is indicated by the dashed gray line. The effective prior is shown as a dashed histogram.

Our procedure for measuring kicks is more widely applicable than those of Refs. Gerosa and Moore (2016); Calderón Bustillo et al. (2018); Healy et al. (2019) in a few ways. Since the surrogate models accurately reproduce the NR simulations, we are potentially sensitive to effects of the recoil other than simple Doppler shifts (e.g. acceleration of the center of mass near merger Gonzalez et al. (2007a); Lousto and Zlochower (2008); Lousto et al. (2012); Lousto and Zlochower (2013); Blanchet et al. (2005); Damour and Gopakumar (2006); Le Tiec et al. (2010), or phase aberration Torres-Orjuela et al. (2020).). Therefore, rather than rely on Doppler shifts in the ringdown Gerosa and Moore (2016), we instead extract information from the full waveform. Based on the inferred binary parameters $\bm{\Lambda}$ , we infer the kick using the NRSur7dq4Remnant model. NRSur7dq4Remnant can take as input $\bm{\Lambda}$ posteriors obtained with any waveform or inference setup. This allows us to fully sample the posterior space, which cannot be covered by discrete NR template banks Calderón Bustillo et al. (2018); Healy et al. (2019). Critically, our method applies to precessing binaries where large kicks occur. As demonstrated in the following sections, our method will soon make it possible to extract kicks from generically precessing systems, including superkicks, in a fully Bayesian setup.

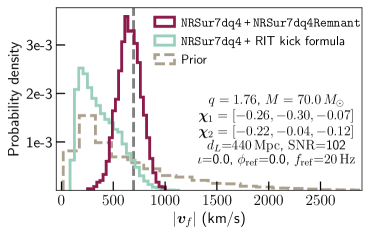
NR simulation.— We first demonstrate our method by injecting an NR waveform into noise from a simulated LIGO-Virgo network at design sensitivity. The signal parameters are given in the inset text of Fig. 1. We choose a luminosity distance consistent with that of GW150914 Abbott et al. (2016b), $d_{L}=440$ Mpc. Using the NRSur7dq4 waveform model, we recover the signal with a signal-to-noise ratio (SNR) of 102. Here and throughout this paper, reported SNRs correspond to the network matched-filter, maximum a-posteriori values. Further, all masses are reported in the detector frame.

Our method successfully recovers the injected kick magnitude, as seen from the posterior in Fig. 1. We find that the use of the remnant surrogate model NRSur7dq4Remnant is critical. To show this, we consider an alternate kick formula developed in Refs. Gonzalez et al. (2007a); Campanelli et al. (2007b); Lousto and Zlochower (2008); Lousto et al. (2012); Lousto and Zlochower (2013), as summarized in Gerosa and Kesden (2016). Using this formula (which we label “RIT”) on the same NRSur7dq4 samples yields a totally uninformative posterior on the kick. We note that the NR waveform used here (with identifier SXS:BBH:0137 SXS Collaboration ; Mroue et al. (2013); Boyle et al. (2019)) was not used to train the surrogate models.

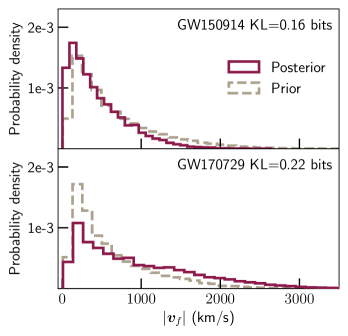
Kick measurement from existing GW events.— Next, we apply our method to GWTC-1 Abbott et al. (2019b) by reanalyzing the publicly available data released by the LIGO-Virgo Collaborations Collaboration and Collaboration ; LIGO Scientific Collaboration and Virgo Collaboration (2018). Figure 2 shows the posteriors we recover for the kick magnitude for the GW150914 Abbott et al. (2016b) and GW170729 Abbott et al. (2019b) events. These are compared with the prior for the kick magnitude. Not much information about the kick can be gained for the GWTC-1 events, as measured by the Kullback–Leibler (KL) divergence from the prior to the posterior Kullback and Leibler (1951). GW150914 and GW170729 are those with the highest information gain showing respectively, a KL divergence of 0.16 and 0.22 bits. This can be compared with Ref. Abbott et al. (2019b) where $\mathchar 21016\relax\,0.13$ bits of information gain in the precession parameter $\chi_{p}$ Schmidt et al. (2015) was considered insufficient to claim evidence of precession. As an example of a good kick measurement, the purple distribution in Fig. 1 has a KL divergence of 1.74 bits with respect to the prior. While our kick measurement for GW150914 is consistent with the 90%-credible bound placed by Ref. Healy et al. (2019) of $|\bm{v}_{f}|\leq 492$ km/s, we find that this is driven by the prior—meaning that that the measurement in Ref. Healy et al. (2019) was largely uninformative.

Future detections will lead to much better constraints on the kick. In the following sections, we explore the prospects for measuring kicks at the design sensitivity of LIGO and Virgo.

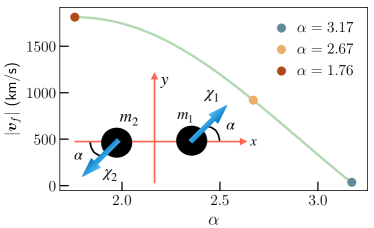
Superkicks at design sensitivity.— We first consider a special binary BH configuration that is fine-tuned to achieve a large kick velocity: both BHs have equal masses ( $m_{1}=m_{2}=35\,M_{\odot}$ ) and equal spin magnitudes ( $|\bm{\chi}_{1}|=|\bm{\chi}_{2}|=0.5$ ); the spins are entirely in the orbital plane and are antiparallel to each other at a reference frequency $f_{\rm ref}=20$ Hz. The angle $\alpha$ between the $x$ -axis and the in-plane spins of the BHs is allowed to vary. This configuration is shown in the inset in the left panel of Fig. 3. For concreteness, we choose luminosity distance $d_{L}=440$ Mpc, inclination $\iota=0$ and orbital phase $\phi_{\rm ref}=0$ .

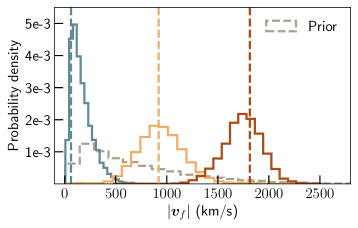
The kick magnitude has a sinusoidal dependence on $\alpha$ Lousto et al. (2012); Bruegmann et al. (2008); Zlochower and Lousto (2015); Gerosa et al. (2018), as shown in the left panel of Fig. 3 (see Ref. Varma et al. (2019c) for visualizations of the sinusoidal dependence and superkicks.). We use NRSur7dq4Remnant to find the value of $\alpha$ that yields the maximum kick for the chosen spin magnitude. We consider the $\alpha$ values that lead to the superkick ( $|\bm{v}_{f}|$ =1814 km/s), half of the superkick ( $|\bm{v}_{f}|$ =907 km/s), and a minimum kick magnitude ( $|\bm{v}_{f}|$ =35 km/s) kic (b). The right-panel of Fig. 3 shows the kick magnitude posteriors obtained by applying our method to NRSur7dq4 injections corresponding to those three configurations. We are able to clearly distinguish the kick velocity between these injections, which have otherwise nearly identical parameters. This is in agreement with Ref. Lousto and Healy (2019), where a mismatch comparison was used to assess distinguishability between similar configurations. The kick magnitude can be reliably recovered in all three cases, demonstrating our ability to accurately measure superkicks at the design sensitivity of LIGO and Virgo.

Measuring kicks from generic systems.— The large kicks explored in the previous section required some fine-tuning of the component parameters. For generic systems that are more likely to occur in nature, typical kicks are much smaller Berti et al. (2012); Lousto et al. (2012). We now explore the measurability of the kick velocity of arbitrary systems by injecting randomly chosen signals and studying the recovered kicks. We perform 60 NRSur7dq4 injections uniformly sampled from mass ratios $q\in[1,3]$ , spin magnitudes $|\bm{\chi}_{1}|,|\bm{\chi}_{2}|\in[0,0.8]$ , arbitrary spin directions, total masses $M\in[70,150]$ , luminosity distances $d_{L}\in[400,2000]$ Mpc, inclination angles $\iota\in[0,\pi]$ , and reference phases $\phi_{\text{ref}}\in[0,2\pi]$ . These ranges are chosen to fall within the training region of current surrogate models Varma et al. (2019a).

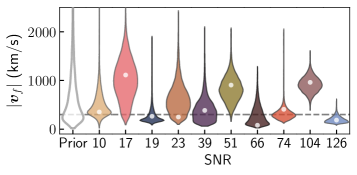
The recovered posteriors for the kick magnitude are shown in the top-panel of Fig. 4 for a subset of 10 representative cases. Our method reliably recovers the kick magnitude for these generic systems; biases away from the true value are consistent with statistical error, as shown in the Supplement kic (a).

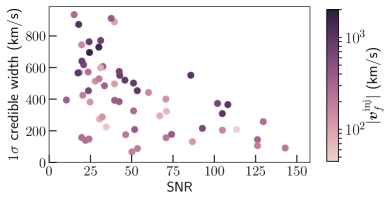
Figure 5 shows the measurement uncertainty in the recovered kick magnitude for all 60 random cases. In general, a larger SNR leads to a better measurement of the kick magnitude, but the specific choice of injected parameters also plays a role, causing the spread in Fig. 5. In some cases a good measurement can be made at SNRs as low as 20. This suggests that kick velocities can be measured using our method even before LIGO and Virgo achieve their design sensitivities.

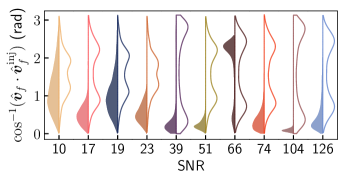
Our method measures the full kick vector. To gauge how well we can recover the kick direction, we consider the angle between the measured kick direction $\hat{\bm{v}}_{f}$ and the injected kick direction $\hat{\bm{v}}_{f}^{\rm inj}$ , namely $\cos^{-1}(\hat{\bm{v}}_{f}\cdot\hat{\bm{v}}_{f}^{\rm inj})$ . We refer to this angle as the kick-direction “bias”; for the true injection value, this angle is zero. The bottom-panel of Fig. 4 shows the distribution of this quantity as derived from the full kick-vector posteriors corresponding to the same 10 cases as the top-panel. For all cases where the injected kick magnitude is $\gtrsim 300$ km/s we recover the kick direction, i.e. $\cos^{-1}(\hat{\bm{v}}_{f}\cdot\hat{\bm{v}}_{f}^{\rm inj})\approx 0$ . For smaller kick magnitudes, NRSur7dq4Remnant is known to have larger intrinsic errors in the kick direction Varma et al. (2019a), which results in correspondingly higher kick-direction posterior biases. This comes from similar errors in the underlying NR simulations on which the surrogate model is trained Varma et al. (2019a), and should thus be fixed by more accurate simulations. In spite of this, the kick magnitude is reliably recovered even for cases with $|\bm{v}_{f}|\lesssim 300$ km/s.

Applications.— Based on Fig. 5, we generally expect an uncertainty of $\lesssim 500$ km/s at SNR $\mathchar 21016\relax\,50$ in measuring the kick magnitude at the 68.27% credible level ( ${\sim}1\sigma$ ). This can be used to place meaningful constraints on the retention rate of the remnant for different types of galaxies. For example, a kick measurement of the type shown in Fig. 1 would lead us to conclude that the remnant of such a binary would be ejected from most globular clusters, which typically have escape velocities $\lesssim 50$ km/s Antonini and Rasio (2016); Merritt et al. (2004).

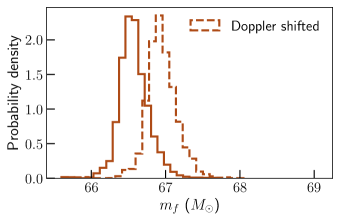
In Fig. 6, we use the projection of the full kick vector along the line of sight to compute the kick’s effect on the remnant BH mass Gerosa and Moore (2016) that would be inferred by an analysis of the Doppler-shifted ringdown signal. As detectors become more sensitive, this effect will need to be accounted for to avoid systematic biases in tests of general relativity, especially for third-generation detectors and remnants with large kick velocities along the line of sight. Our method will prevent these issues, as we discuss in the Supplement kic (a).

Conclusion.— We present the first method to accurately extract both the kick magnitude and direction of generically precessing binary BHs. This is made possible by recent NR surrogate models for the gravitational waveform and properties of the merger remnant (Fig. 1).

We find that the SNR for existing GWTC-1 events is not sufficient to make a confident measurement of the kick velocity (Fig. 2). However, our results indicate that the kick velocity will be reliably measured once LIGO and Virgo reach their design sensitivities. This includes systems with arbitrary parameters (Fig. 4), as well as configurations fine-tuned to produce superkicks with $|\bm{v}_{f}|\sim 1000$ km/s (Fig. 3). Measuring such kicks was previously estimated to be only possible with third-generation GW detectors Gerosa and Moore (2016). On the contrary, we find that accurate waveform and remnant surrogate models will soon enable this with existing detectors (Fig. 5). This is in agreement with Ref. Calderón Bustillo et al. (2018), which made compatible predictions for nonprecessing systems, for which $|\bm{v}_{f}|\lesssim 300$ km/s.

Kick measurements obtained with our method can be used to place independent constraints on the retention rate of the remnant BH in binary BH mergers, which is directly related to the rate of second-generation mergers. In addition, we show (Fig. 6 and Supplement kic (a)) that kicks must be factored into ringdown tests of general relativity with third-generation GW detectors to avoid systematic biases.

In this study, we focused on projected measurements by LIGO and Virgo at design sensitivity. Since the kick velocity is very well recovered in some moderate-SNR cases, we expect that our method may yield a successful kick measurement before design sensitivity is achieved. This would mark the first time a gravitational recoil is experimentally studied with GWs, providing a brand new observable for astrophysics.

Acknowledgments.— We thank Juan Calderon Bustillo for a review and comments on the manuscript. We thank Nathan Johnson-McDaniel, Ajith Parameswaran, Davide Gerosa, Matt Giesler, Leo Stein, Saul Teukolsky, Gregorio Carullo, Aaron Zimmerman, and Bala Iyer for useful discussions. V.V. is supported by the Sherman Fairchild Foundation, and NSF grants PHY–170212 and PHY–1708213 at Caltech. M.I. is supported by NASA through the NASA Hubble Fellowship grant No. HST-HF2-51410.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. This research made use of data, software and/or web tools obtained from the Gravitational Wave Open Science Center Collaboration and Collaboration , a service of the LIGO Laboratory, the LIGO Scientific Collaboration and the Virgo Collaboration. Computations were performed on the Alice cluster at ICTS and the Wheeler cluster at Caltech. This paper carries LIGO document number LIGO-P2000030.

References

Aasi et al. (2015) J. Aasi et al. (LIGO Scientific), “Advanced LIGO,” Class. Quant. Grav. 32, 074001 (2015), arXiv:1411.4547 [gr-qc] .
Acernese et al. (2015) F. Acernese et al. (Virgo), “Advanced Virgo: a second-generation interferometric gravitational wave detector,” Class. Quant. Grav. 32, 024001 (2015), arXiv:1408.3978 [gr-qc] .
Bonnor et al. (1961) W. B. Bonnor, M. A. Rotenberg, and Rosenhead Louis, “Transport of momentum by gravitational waves: the linear approximation,” Proceedings of the Royal Society of London Series A. 265 (1961), 10.1098/rspa.1961.0226.
Peres (1962) Asher Peres, “Classical radiation recoil,” Phys. Rev. 128, 2471–2475 (1962).
Bekenstein (1973) Jacob D. Bekenstein, “Gravitational-Radiation Recoil and Runaway Black Holes,” The Astrophysical Journal 183, 657–664 (1973).
Fitchett (1983) M. J. Fitchett, “The influence of gravitational wave momentum losses on the centre of mass motion of a Newtonian binary system,” Monthly Notices of the Royal Astronomical Society 203, 1049–1062 (1983), http://oup.prod.sis.lan/mnras/article-pdf/203/4/1049/18223796/mnras203-1049.pdf .
Gonzalez et al. (2007a) Jose A. Gonzalez, Ulrich Sperhake, Bernd Bruegmann, Mark Hannam, and Sascha Husa, “Total recoil: The Maximum kick from nonspinning black-hole binary inspiral,” Phys. Rev. Lett. 98, 091101 (2007a), arXiv:gr-qc/0610154 [gr-qc] .
Lousto and Zlochower (2008) Carlos O. Lousto and Yosef Zlochower, “Further insight into gravitational recoil,” Phys. Rev. D77, 044028 (2008), arXiv:0708.4048 [gr-qc] .
Lousto et al. (2012) Carlos O. Lousto, Yosef Zlochower, Massimo Dotti, and Marta Volonteri, “Gravitational Recoil From Accretion-Aligned Black-Hole Binaries,” Phys. Rev. D85, 084015 (2012), arXiv:1201.1923 [gr-qc] .
Lousto and Zlochower (2013) Carlos O. Lousto and Yosef Zlochower, “Nonlinear Gravitational Recoil from the Mergers of Precessing Black-Hole Binaries,” Phys. Rev. D87, 084027 (2013), arXiv:1211.7099 [gr-qc] .
Blanchet et al. (2005) Luc Blanchet, Moh’d S. S. Qusailah, and Clifford M. Will, “Gravitational recoil of inspiralling black-hole binaries to second post-Newtonian order,” Astrophys. J. 635, 508 (2005), arXiv:astro-ph/0507692 [astro-ph] .
Damour and Gopakumar (2006) Thibault Damour and Achamveedu Gopakumar, “Gravitational recoil during binary black hole coalescence using the effective one body approach,” Phys. Rev. D73, 124006 (2006), arXiv:gr-qc/0602117 [gr-qc] .
Le Tiec et al. (2010) Alexandre Le Tiec, Luc Blanchet, and Clifford M. Will, “Gravitational-Wave Recoil from the Ringdown Phase of Coalescing Black Hole Binaries,” Class. Quant. Grav. 27, 012001 (2010), arXiv:0910.4594 [gr-qc] .
Israel (1968) W. Israel, “Event horizons in static electrovac space-times,” Communications in Mathematical Physics 8, 245–260 (1968).
Carter (1971) B. Carter, “Axisymmetric black hole has only two degrees of freedom,” Phys. Rev. Lett. 26, 331–333 (1971).
Abbott et al. (2016a) B. P. Abbott et al. (LIGO Scientific, Virgo), “Tests of general relativity with GW150914,” Phys. Rev. Lett. 116, 221101 (2016a), [Erratum: Phys. Rev. Lett.121,no.12,129902(2018)], arXiv:1602.03841 [gr-qc] .
Abbott et al. (2019a) B. P. Abbott et al. (LIGO Scientific, Virgo), “Tests of General Relativity with the Binary Black Hole Signals from the LIGO-Virgo Catalog GWTC-1,” Phys. Rev. D100, 104036 (2019a), arXiv:1903.04467 [gr-qc] .
Ghosh et al. (2018) Abhirup Ghosh, Nathan K. Johnson-Mcdaniel, Archisman Ghosh, Chandra Kant Mishra, Parameswaran Ajith, Walter Del Pozzo, Christopher P. L. Berry, Alex B. Nielsen, and Lionel London, “Testing general relativity using gravitational wave signals from the inspiral, merger and ringdown of binary black holes,” Class. Quant. Grav. 35, 014002 (2018), arXiv:1704.06784 [gr-qc] .
Brito et al. (2018) Richard Brito, Alessandra Buonanno, and Vivien Raymond, “Black-hole Spectroscopy by Making Full Use of Gravitational-Wave Modeling,” Phys. Rev. D98, 084038 (2018), arXiv:1805.00293 [gr-qc] .
Carullo et al. (2018) Gregorio Carullo et al., “Empirical tests of the black hole no-hair conjecture using gravitational-wave observations,” Phys. Rev. D98, 104020 (2018), arXiv:1805.04760 [gr-qc] .
Carullo et al. (2019) Gregorio Carullo, Walter Del Pozzo, and John Veitch, “Observational Black Hole Spectroscopy: A time-domain multimode analysis of GW150914,” Phys. Rev. D99, 123029 (2019), [Erratum: Phys. Rev.D100,no.8,089903(2019)], arXiv:1902.07527 [gr-qc] .
Isi et al. (2019) Maximiliano Isi, Matthew Giesler, Will M. Farr, Mark A. Scheel, and Saul A. Teukolsky, “Testing the no-hair theorem with GW150914,” Phys. Rev. Lett. 123, 111102 (2019), arXiv:1905.00869 [gr-qc] .
Giesler et al. (2019) Matthew Giesler, Maximiliano Isi, Mark Scheel, and Saul Teukolsky, “Black hole ringdown: the importance of overtones,” Phys. Rev. X9, 041060 (2019), arXiv:1903.08284 [gr-qc] .
Apostolatos et al. (1994) Theocharis A. Apostolatos, Curt Cutler, Gerald J. Sussman, and Kip S. Thorne, “Spin-induced orbital precession and its modulation of the gravitational waveforms from merging binaries,” Phys. Rev. D 49, 6274–6297 (1994).
Campanelli et al. (2007a) Manuela Campanelli, Carlos O. Lousto, Yosef Zlochower, and David Merritt, “Maximum gravitational recoil,” Phys. Rev. Lett. 98, 231102 (2007a), arXiv:gr-qc/0702133 [GR-QC] .
Gonzalez et al. (2007b) J. A. Gonzalez, M. D. Hannam, U. Sperhake, Bernd Bruegmann, and S. Husa, “Supermassive recoil velocities for binary black-hole mergers with antialigned spins,” Phys. Rev. Lett. 98, 231101 (2007b), arXiv:gr-qc/0702052 [GR-QC] .
Tichy and Marronetti (2007) Wolfgang Tichy and Pedro Marronetti, “Binary black hole mergers: Large kicks for generic spin orientations,” Phys. Rev. D76, 061502 (2007), arXiv:gr-qc/0703075 [gr-qc] .
Lousto and Zlochower (2011) Carlos O. Lousto and Yosef Zlochower, “Hangup Kicks: Still Larger Recoils by Partial Spin/Orbit Alignment of Black-Hole Binaries,” Phys. Rev. Lett. 107, 231102 (2011), arXiv:1108.2009 [gr-qc] .
Lousto and Healy (2019) Carlos O. Lousto and James Healy, “Kicking gravitational wave detectors with recoiling black holes,” Phys. Rev. D100, 104039 (2019), arXiv:1908.04382 [gr-qc] .
Sperhake et al. (2020) U. Sperhake, R. Rosca-Mead, D. Gerosa, and E. Berti, “Amplification of superkicks in black-hole binaries through orbital eccentricity,” Phys. Rev. D101, 024044 (2020), arXiv:1910.01598 [gr-qc] .
Merritt et al. (2004) David Merritt, Milos Milosavljevic, Marc Favata, Scott A. Hughes, and Daniel E. Holz, “Consequences of gravitational radiation recoil,” Astrophys. J. 607, L9–L12 (2004), arXiv:astro-ph/0402057 [astro-ph] .
Komossa et al. (2008) S. Komossa, H. Zhou, and H. Lu, “A recoiling supermassive black hole in the quasar SDSSJ092712.65+294344.0?” Astrophys. J. 678, L81–L84 (2008), arXiv:0804.4585 [astro-ph] .
Volonteri et al. (2010) Marta Volonteri, Kayhan Gültekin, and Massimo Dotti, “Gravitational recoil: effects on massive black hole occupation fraction over cosmic time,” Monthly Notices of the Royal Astronomical Society 404, 2143–2150 (2010), http://oup.prod.sis.lan/mnras/article-pdf/404/4/2143/3803490/mnras0404-2143.pdf .
Komossa and Merritt (2008) S. Komossa and David Merritt, “Gravitational Wave Recoil Oscillations of Black Holes: Implications for Unified Models of Active Galactic Nuclei,” Astrophys. J. 689, L89 (2008), arXiv:0811.1037 [astro-ph] .
Gerosa and Sesana (2015) Davide Gerosa and Alberto Sesana, “Missing black holes in brightest cluster galaxies as evidence for the occurrence of superkicks in nature,” Mon. Not. Roy. Astron. Soc. 446, 38–55 (2015), arXiv:1405.2072 [astro-ph.GA] .
sesana (2007) A. sesana, “Extreme recoils: impact on the detection of gravitational waves from massive black hole binaries,” Mon. Not. Roy. Astron. Soc. 382, 6 (2007), arXiv:0707.4677 [astro-ph] .
Amaro-Seoane et al. (2017) Pau Amaro-Seoane et al., “Laser interferometer space antenna,” (2017), arXiv:1702.00786 [astro-ph.IM] .
Yang et al. (2019) Yang Yang et al., “Hierarchical Black Hole Mergers in Active Galactic Nuclei,” Phys. Rev. Lett. 123, 181101 (2019), arXiv:1906.09281 [astro-ph.HE] .
Gayathri et al. (2020) V. Gayathri, I. Bartos, Z. Haiman, S. Klimenko, B. Kocsis, S. Marka, and Y. Yang, “GW170817A as a Hierarchical Black Hole Merger,” Astrophys. J. 890, L20 (2020), arXiv:1911.11142 [astro-ph.HE] .
Gerosa and Berti (2019) Davide Gerosa and Emanuele Berti, “Escape speed of stellar clusters from multiple-generation black-hole mergers in the upper mass gap,” Phys. Rev. D100, 041301 (2019), arXiv:1906.05295 [astro-ph.HE] .
Mangiagli et al. (2019) Alberto Mangiagli, Matteo Bonetti, Alberto Sesana, and Monica Colpi, “Merger rate of stellar black hole binaries above the pair instability mass gap,” Astrophys. J. 883, L27 (2019), arXiv:1907.12562 [astro-ph.HE] .
Di Carlo et al. (2019) Ugo N. Di Carlo, Michela Mapelli, Yann Bouffanais, Nicola Giacobbo, Sandro Bressan, Mario Spera, and Francesco Haardt, “Binary black holes in the pair-instability mass gap,” (2019), arXiv:1911.01434 [astro-ph.HE] .
Rodriguez et al. (2019) Carl L. Rodriguez, Michael Zevin, Pau Amaro-Seoane, Sourav Chatterjee, Kyle Kremer, Frederic A. Rasio, and Claire S. Ye, “Black holes: The next generation—repeated mergers in dense star clusters and their gravitational-wave properties,” Phys. Rev. D100, 043027 (2019), arXiv:1906.10260 [astro-ph.HE] .
Doctor et al. (2019) Zoheyr Doctor, Daniel Wysocki, Richard O’Shaughnessy, Daniel E. Holz, and Ben Farr, “Black Hole Coagulation: Modeling Hierarchical Mergers in Black Hole Populations,” (2019), arXiv:1911.04424 [astro-ph.HE] .
Farmer et al. (2019) R. Farmer, M. Renzo, S. E. de Mink, P. Marchant, and S. Justham, “Mind the gap: The location of the lower edge of the pair instability supernovae black hole mass gap,” (2019), arXiv:1910.12874 [astro-ph.SR] .
Abbott et al. (2019b) B. P. Abbott et al. (LIGO Scientific, Virgo), “GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs,” Phys. Rev. X9, 031040 (2019b), arXiv:1811.12907 [astro-ph.HE] .
Chatziioannou et al. (2019) Katerina Chatziioannou et al., “On the properties of the massive binary black hole merger GW170729,” Phys. Rev. D100, 104015 (2019), arXiv:1903.06742 [gr-qc] .
Woosley (2017) S. E. Woosley, “Pulsational Pair-Instability Supernovae,” Astrophys. J. 836, 244 (2017), arXiv:1608.08939 [astro-ph.HE] .
Marchant et al. (2018) Pablo Marchant, Mathieu Renzo, Robert Farmer, Kaliroe M. W. Pappas, Ronald E. Taam, Selma de Mink, and Vassiliki Kalogera, “Pulsational pair-instability supernovae in very close binaries,” (2018), 10.3847/1538-4357/ab3426, arXiv:1810.13412 [astro-ph.HE] .
Varma et al. (2019a) Vijay Varma, Scott E. Field, Mark A. Scheel, Jonathan Blackman, Davide Gerosa, Leo C. Stein, Lawrence E. Kidder, and Harald P. Pfeiffer, “Surrogate models for precessing binary black hole simulations with unequal masses,” Phys. Rev. Research. 1, 033015 (2019a), arXiv:1905.09300 [gr-qc] .
Blackman et al. (2017) Jonathan Blackman, Scott E. Field, Mark A. Scheel, Chad R. Galley, Christian D. Ott, Michael Boyle, Lawrence E. Kidder, Harald P. Pfeiffer, and Béla Szilágyi, “Numerical relativity waveform surrogate model for generically precessing binary black hole mergers,” Phys. Rev. D96, 024058 (2017), arXiv:1705.07089 [gr-qc] .
Varma et al. (2019b) Vijay Varma, Davide Gerosa, Leo C. Stein, François Hébert, and Hao Zhang, “High-accuracy mass, spin, and recoil predictions of generic black-hole merger remnants,” Phys. Rev. Lett. 122, 011101 (2019b), arXiv:1809.09125 [gr-qc] .
LIGO Scientific Collaboration and Virgo Collaboration (2018) LIGO Scientific Collaboration and Virgo Collaboration, “GWTC-1,” https://doi.org/10.7935/82H3-HH23 (2018).
LIGO Scientific Collaboration (2018a) LIGO Scientific Collaboration, Updated Advanced LIGO sensitivity design curve, Tech. Rep. (2018) https://dcc.ligo.org/LIGO-T1800044/public.
Manzotti and Dietz (2012) Alessandro Manzotti and Alexander Dietz, “Prospects for early localization of gravitational-wave signals from compact binary coalescences with advanced detectors,” (2012), arXiv:1202.4031 [gr-qc] .
Abbott et al. (2018) B. P. Abbott et al. (KAGRA, LIGO Scientific, VIRGO), “Prospects for Observing and Localizing Gravitational-Wave Transients with Advanced LIGO, Advanced Virgo and KAGRA,” Living Rev. Rel. 21, 3 (2018), arXiv:1304.0670 [gr-qc] .
Veitch et al. (2015) J. Veitch et al., “Robust parameter estimation for compact binaries with ground-based gravitational-wave observations using the LALInference software library,” Phys. Rev. D 91, 042003 (2015), arXiv:1409.7215 [gr-qc] .
LIGO Scientific Collaboration (2018b) LIGO Scientific Collaboration, “LIGO Algorithm Library - LALSuite,” free software (GPL) (2018b).
Schmidt et al. (2017) Patricia Schmidt, Ian W. Harry, and Harald P. Pfeiffer, “Numerical Relativity Injection Infrastructure,” (2017), arXiv:1703.01076 [gr-qc] .
Rasmussen and Williams (2006) C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, by C.E. Rasmussen and C.K.I. Williams. ISBN-13 978-0-262-18253-9 (2006).
kic (a) See Supplemental Material here, for details about the Doppler shifted remnant mass, a study of biases in the kick measurement, and priors used for the component parameters. This further includes Refs. Krolak and Schutz (1987); Barausse et al. (2012); Hofmann et al. (2016); Jiménez-Forteza et al. (2017); Healy and Lousto (2017); Healy et al. (2014); Vishveshwara (1970); Press (1971); Teukolsky (1973); Chandrasekhar and Detweiler (1975); Gair and Moore (2015); Dreyer et al. (2004); Gossan et al. (2012); Meidam et al. (2014). (a).
Krolak and Schutz (1987) A Krolak and Bernard F Schutz, “Coalescing binaries—Probe of the universe,” General Relativity and Gravitation 19, 1163–1171 (1987).
Barausse et al. (2012) Enrico Barausse, Viktoriya Morozova, and Luciano Rezzolla, “On the mass radiated by coalescing black-hole binaries,” Astrophys. J. 758, 63 (2012), [Erratum: Astrophys. J.786,76(2014)], arXiv:1206.3803 [gr-qc] .
Hofmann et al. (2016) Fabian Hofmann, Enrico Barausse, and Luciano Rezzolla, “The final spin from binary black holes in quasi-circular orbits,” Astrophys. J. 825, L19 (2016), arXiv:1605.01938 [gr-qc] .
Jiménez-Forteza et al. (2017) Xisco Jiménez-Forteza, David Keitel, Sascha Husa, Mark Hannam, Sebastian Khan, and Michael Pürrer, “Hierarchical data-driven approach to fitting numerical relativity data for nonprecessing binary black holes with an application to final spin and radiated energy,” Phys. Rev. D95, 064024 (2017), arXiv:1611.00332 [gr-qc] .
Healy and Lousto (2017) James Healy and Carlos O. Lousto, “Remnant of binary black-hole mergers: New simulations and peak luminosity studies,” Phys. Rev. D95, 024037 (2017), arXiv:1610.09713 [gr-qc] .
Healy et al. (2014) James Healy, Carlos O. Lousto, and Yosef Zlochower, “Remnant mass, spin, and recoil from spin aligned black-hole binaries,” Phys. Rev. D90, 104004 (2014), arXiv:1406.7295 [gr-qc] .
Vishveshwara (1970) C. V. Vishveshwara, “Stability of the schwarzschild metric,” Phys. Rev. D 1, 2870–2879 (1970).
Press (1971) William H. Press, “Long Wave Trains of Gravitational Waves from a Vibrating Black Hole,” Astrophysical Journal 170, L105 (1971).
Teukolsky (1973) Saul A. Teukolsky, “Perturbations of a Rotating Black Hole. I. Fundamental Equations for Gravitational, Electromagnetic, and Neutrino-Field Perturbations,” Astrophysical Journal 185, 635–648 (1973).
Chandrasekhar and Detweiler (1975) S. Chandrasekhar and S. Detweiler, “The quasi-normal modes of the schwarzschild black hole,” Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 344, 441–452 (1975).
Gair and Moore (2015) Jonathan R. Gair and Christopher J. Moore, “Quantifying and mitigating bias in inference on gravitational wave source populations,” Phys. Rev. D91, 124062 (2015), arXiv:1504.02767 [gr-qc] .
Dreyer et al. (2004) Olaf Dreyer, Bernard J. Kelly, Badri Krishnan, Lee Samuel Finn, David Garrison, and Ramon Lopez-Aleman, “Black hole spectroscopy: Testing general relativity through gravitational wave observations,” Class. Quant. Grav. 21, 787–804 (2004), arXiv:gr-qc/0309007 [gr-qc] .
Gossan et al. (2012) S. Gossan, J. Veitch, and B. S. Sathyaprakash, “Bayesian model selection for testing the no-hair theorem with black hole ringdowns,” Phys. Rev. D85, 124056 (2012), arXiv:1111.5819 [gr-qc] .
Meidam et al. (2014) J. Meidam, M. Agathos, C. Van Den Broeck, J. Veitch, and B. S. Sathyaprakash, “Testing the no-hair theorem with black hole ringdowns using TIGER,” Phys. Rev. D90, 064009 (2014), arXiv:1406.3201 [gr-qc] .
Gerosa and Moore (2016) Davide Gerosa and Christopher J. Moore, “Black hole kicks as new gravitational wave observables,” Phys. Rev. Lett. 117, 011101 (2016), arXiv:1606.04226 [gr-qc] .
Reitze et al. (2019) David Reitze et al., “Cosmic Explorer: The U.S. Contribution to Gravitational-Wave Astronomy beyond LIGO,” Bull. Am. Astron. Soc. 51, 035 (2019), arXiv:1907.04833 [astro-ph.IM] .
Punturo et al. (2010a) M. Punturo et al., “The Einstein Telescope: A third-generation gravitational wave observatory,” Proceedings, 14th Workshop on Gravitational wave data analysis (GWDAW-14): Rome, Italy, January 26-29, 2010, Class. Quant. Grav. 27, 194002 (2010a).
Punturo et al. (2010b) M Punturo et al., “The third generation of gravitational wave observatories and their science reach,” Classical and Quantum Gravity 27, 084007 (2010b).
Abbott et al. (2017) Benjamin P Abbott et al. (LIGO Scientific), “Exploring the Sensitivity of Next Generation Gravitational Wave Detectors,” Class. Quant. Grav. 34, 044001 (2017), arXiv:1607.08697 [astro-ph.IM] .
Calderón Bustillo et al. (2018) Juan Calderón Bustillo, James A. Clark, Pablo Laguna, and Deirdre Shoemaker, “Tracking black hole kicks from gravitational wave observations,” Phys. Rev. Lett. 121, 191102 (2018), arXiv:1806.11160 [gr-qc] .
Healy et al. (2019) James Healy, Carlos O. Lousto, Jacob Lange, Richard O’Shaughnessy, Yosef Zlochower, and Manuela Campanelli, “The second RIT binary black hole simulations catalog and its application to gravitational waves parameter estimation,” (2019), arXiv:1901.02553 [gr-qc] .
Torres-Orjuela et al. (2020) Alejandro Torres-Orjuela, Xian Chen, and Pau Amaro-Seoane, “A phase shift of gravitational waves induced by aberration,” (2020), arXiv:2001.00721 [astro-ph.HE] .
Abbott et al. (2016b) B. P. Abbott et al. (LIGO Scientific, Virgo), “Observation of Gravitational Waves from a Binary Black Hole Merger,” Phys. Rev. Lett. 116, 061102 (2016b), arXiv:1602.03837 [gr-qc] .
Campanelli et al. (2007b) Manuela Campanelli, Carlos O. Lousto, Yosef Zlochower, and David Merritt, “Large merger recoils and spin flips from generic black-hole binaries,” Astrophys. J. 659, L5–L8 (2007b), arXiv:gr-qc/0701164 [gr-qc] .
Gerosa and Kesden (2016) Davide Gerosa and Michael Kesden, “PRECESSION: Dynamics of spinning black-hole binaries with python,” Phys. Rev. D93, 124066 (2016), arXiv:1605.01067 [astro-ph.HE] .
(87) SXS Collaboration, “The SXS collaboration catalog of gravitational waveforms,” http://www.black-holes.org/waveforms.
Mroue et al. (2013) Abdul H. Mroue et al., “Catalog of 174 Binary Black Hole Simulations for Gravitational Wave Astronomy,” Phys. Rev. Lett. 111, 241104 (2013), arXiv:1304.6077 [gr-qc] .
Boyle et al. (2019) Michael Boyle et al., “The SXS Collaboration catalog of binary black hole simulations,” Class. Quant. Grav. 36, 195006 (2019), arXiv:1904.04831 [gr-qc] .
(90) LIGO Scientific Collaboration and Virgo Collaboration, “Gravitational Wave Open Science Center,” https://www.gw-openscience.org.
Kullback and Leibler (1951) S. Kullback and R. A. Leibler, “On information and sufficiency,” The Annals of Mathematical Statistics 22, 79–86 (1951).
Schmidt et al. (2015) P. Schmidt, F. Ohme, and M. Hannam, “Towards models of gravitational waveforms from generic binaries II: Modelling precession effects with a single effective precession parameter,” Phys. Rev. D 91, 024043 (2015), arXiv:1408.1810 [gr-qc] .
Bruegmann et al. (2008) Bernd Bruegmann, Jose A. Gonzalez, Mark Hannam, Sascha Husa, and Ulrich Sperhake, “Exploring black hole superkicks,” Phys. Rev. D77, 124047 (2008), arXiv:0707.0135 [gr-qc] .
Zlochower and Lousto (2015) Yosef Zlochower and Carlos O. Lousto, “Modeling the remnant mass, spin, and recoil from unequal-mass, precessing black-hole binaries: The Intermediate Mass Ratio Regime,” Phys. Rev. D92, 024022 (2015), [Erratum: Phys. Rev.D94,no.2,029901(2016)], arXiv:1503.07536 [gr-qc] .
Gerosa et al. (2018) Davide Gerosa, François Hébert, and Leo C. Stein, “Black-hole kicks from numerical-relativity surrogate models,” Phys. Rev. D97, 104049 (2018), arXiv:1802.04276 [gr-qc] .
Varma et al. (2019c) Vijay Varma, Leo C. Stein, and Davide Gerosa, “The binary black hole explorer: on-the-fly visualizations of precessing binary black holes,” Class. Quant. Grav. 36, 095007 (2019c), arXiv:1811.06552 [astro-ph.HE] .
kic (b) The overall minimum should be zero, but a 35 km/s limit arises from numerical noise in the simulations on which NRSur7dq4Remnant is trained. In spite of this, NRSur7dq4Remnant is more accurate than alternate kick models by an order-of-magnitude Varma et al. (2019a). (b).
Berti et al. (2012) Emanuele Berti, Michael Kesden, and Ulrich Sperhake, “Effects of post-Newtonian Spin Alignment on the Distribution of Black-Hole Recoils,” Phys. Rev. D85, 124049 (2012), arXiv:1203.2920 [astro-ph.HE] .
Antonini and Rasio (2016) Fabio Antonini and Frederic A. Rasio, “Merging black hole binaries in galactic nuclei: implications for advanced-LIGO detections,” Astrophys. J. 831, 187 (2016), arXiv:1606.04889 [astro-ph.HE] .

Supplemental materials

.1 Implications for tests of general relativity

At leading order, the kick’s effect on the GW signal can be described as a Doppler shift of the GW frequency $f$ Gerosa and Moore (2016). Because general relativity lacks any intrinsic length scales, a uniform increase in signal frequency is completely degenerate with a decrease in total mass $M$ , and vice versa. Thus, if not explicitly accounted for, a frequency shift due to a kick will bias mass measurements. This is analogous to the effect of the cosmological redshift $z$ on the GWs: GW measurements only measure the combination $M(1+z)$ known as the detector-frame mass, and the source-frame mass is only inferred after assuming a cosmology Krolak and Schutz (1987). One important difference between the cosmological and kick redshifts is that, in the latter, the Doppler shift occurs only when the kick is imparted, mostly near the merger Gonzalez et al. (2007a); Lousto and Zlochower (2008); Lousto et al. (2012); Lousto and Zlochower (2013). Therefore the Doppler shift only affects the merger and ringdown part of the signal, while a cosmological redshift rescales the GW signal as a whole.

The amount of Doppler shift depends on the projection of the kick velocity along the line of sight. At leading order, the Doppler-shifted remnant mass is given by Gerosa and Moore (2016):

m^{\text{DS}}_{f}=m_{f}\,(1+\bm{v}_{f}\cdot\hat{\bm{n}}/c),

(S1)

where $c$ is the speed of light and $\hat{\bm{n}}$ is the unit vector pointing from the observer to the source. From our inference setup, we obtain posterior distributions for the component parameters $\bm{\Lambda}=\{m_{1},m_{2},\bm{\chi}_{1},\bm{\chi}_{2}\}$ , as well as the line-of-sight parameters ( $\iota$ , $\phi_{\mathrm{ref}}$ ). Our method to measure the kick recovers the full kick vector $\bm{v}_{f}$ given $\bm{\Lambda}$ . For each posterior sample, we then project the kick along the line of sight to obtain the Doppler-shifted remnant mass.

The Doppler shift due to the kick velocity can play an important role in tests of general relativity using the ringdown signal Dreyer et al. (2004); Gossan et al. (2012); Meidam et al. (2014); Abbott et al. (2016a, 2019a); Ghosh et al. (2018); Brito et al. (2018); Carullo et al. (2019); Isi et al. (2019); Giesler et al. (2019). In some of these tests, the remnant mass and spin are measured from different portions of the signal and compared against each other to check for consistency. In one version of the test, the full inspiral-merger-ringdown signal is first analyzed using a waveform model and posterior distributions are obtained for $\bm{\Lambda}$ . These are then passed to fitting formulae (e.g. Barausse et al. (2012); Hofmann et al. (2016); Jiménez-Forteza et al. (2017); Healy and Lousto (2017); Healy et al. (2014)) for the remnant mass and spin to obtain posterior distributions for these quantities. Finally, considering only the ringdown signal and varying the quasi-normal-mode frequencies Vishveshwara (1970); Press (1971); Teukolsky (1973); Chandrasekhar and Detweiler (1975), the remnant mass and spin are independently measured Dreyer et al. (2004); Gossan et al. (2012); Abbott et al. (2016a); Brito et al. (2018); Carullo et al. (2019); Isi et al. (2019).

In the first case the inferred remnant mass is not sensitive to the Doppler shift as traditional fitting formulas for the remnant mass do not account for this. Apart from modeling errors, this is equivalent to measuring the remnant mass from the apparent horizon of the remnant black hole in an NR simulation Boyle et al. (2019). In the second case, however, the observed ringdown frequencies would be Doppler-shifted and the inferred remnant mass would be the Doppler-shifted value. For large Doppler shifts, these two measurements of the remnant mass would be inconsistent, mimicking a deviation from general relativity.

Fig. 6 in the main document shows the remnant mass posterior distribution before and after the Doppler shift for the superkick configuration of Fig. 3. The NRSur7dq4Remnant model is used to predict the kick vector and the remnant mass before the Doppler shift, while Eq. (S1) is used to predict the Doppler-shifted remnant mass. The two mass distributions are visibly different in Fig. 6, therefore this will be important to account for in ringdown tests of general relativity. However, this is a fairly fine-tuned source configuration with a large kick velocity. This effect is expected to become important when the measurement precision for the remnant mass is comparable or smaller than the Doppler shift, $\delta m_{f}/m_{f}\lesssim|\bm{v}_{f}\cdot\hat{\bm{n}}/c|$ . Unless signals with kick magnitudes of order $1000$ km/s are detected, we expect that this effect will only be important for third-generation GW detectors. In any case, our method can already be used to account for this effect in tests of general relativity.

.2 Probability-Probability plots

To demonstrate the robustness of our Bayesian inference infrastructure using the NRSur7dq4 and NRSur7dq4Remnant models, we produce a probability-probability (P-P) plot for the kick velocity, from a set of 87 simulated binary BH injections into design-sensitivity Gaussian noise for a LIGO Hanford-Livingston-Virgo detector network. (See, e.g. Ref. Gair and Moore (2015) for an example of P-P plots in the context of GW data analysis.) For each injection, we run the LALInference parameter estimation package Veitch et al. (2015) to obtain posteriors for the binary parameters, like the masses and spins ( $\bm{\Lambda}$ ). From those, we then derive posteriors on the kick parameters using the NRSur7dq4Remnant surrogate. The P-P plot shows the fraction of events for which the posterior for a given parameter recovers the true value at a particular credible interval, as a function of the credible interval. If the posteriors are sampled successfully, the P-P plot should be diagonal—meaning that the true value is recovered within the $x\%$ -credible interval $x\%$ of the time, consistent with statistical error.

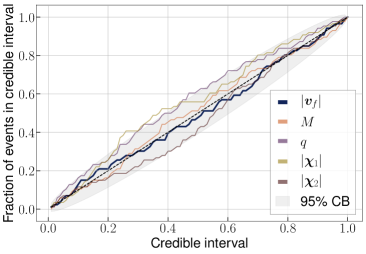
We draw the 87 injections from a distribution uniform in component masses $m_{1}$ , $m_{2}$ between 18 and $110\leavevmode\nobreak\ M_{\odot}$ , but restricted to a mass ratio of $q=m_{1}/m_{2}\leq 3$ and total mass $M\geq 72\,M_{\odot}$ . The spin magnitudes are drawn uniformly between $0\leq|\bm{\chi}_{1}|,|\bm{\chi}_{2}|\leq 0.8$ , and the directions are distributed isotropically on a sphere. The luminosity distances are picked with a density proportional to their square (that is, uniform in volume) out to 5 Gpc, and the inclination angle is drawn from a uniform-in-cosine distribution. The location of the source in the sky is drawn isotropically, as is its polarization angle. The same distributions are used as the priors during the parameter estimation step.

The P-P plot for the 87 simulated injections is shown in Fig. S1. We display the distributions for the kick magnitude ( $|\bm{v}_{f}|$ ), total mass ( $M$ ), mass ratio ( $q$ ), and component spin parameters $|\bm{\chi}_{1}|,|\bm{\chi}_{2}|$ , which all lie largely within the 95% confidence band around the diagonal (shaded in gray). The p-value for the probability that the fraction of events within a given credible interval for the kick magnitude is drawn from uniform distribution between 0 and 1, as expected for a diagonal P-P plot, is 98.6%. This demonstrates that the kick posteriors generated with NRSur7dq4Remnant, in combination with the LALInference sampler, are statistically robust and behave as expected in simulated Gaussian noise. Deviations between the true value and the peak of the recovered posterior, such as those seen in Fig. 4, are consistent with statistical fluctuations.

.3 Prior distribution for component parameters

Analyses presented in the main text, for both injections and real data, use similar priors to those described in Sec. .2. This choice follows standard conventions for LIGO-Virgo analyses (e.g., see Appendix C in Abbott et al. (2019b)). We vary the specific mass ranges allowed to ensure the posterior always has full support within the prior. For injections, the prior was uniform in component masses $m_{1}$ , $m_{2}$ between 10 and $120\leavevmode\nobreak\ M_{\odot}$ , but restricted to mass ratios $q=m_{1}/m_{2}\leq 4$ and total masses $M\geq 60\,M_{\odot}$ . The spin magnitudes are drawn uniformly between $0\leq|\bm{\chi}_{1}|,|\bm{\chi}_{2}|\leq 0.99$ , and the directions are distributed isotropically on a sphere. The priors on the extrinsic parameters are the same as in Sec. .2.