Exposing the hidden influence of selection rules on phonon-phonon scattering by pressure and temperature tuning
Abstract
Using ab initio calculations, we show that the hidden influence of selection rules on three-phonon scattering can be exposed through anomalous signatures in the pressure () and temperature () dependence of the thermal conductivities, , of certain compounds. Boron phosphide reveals such underlying behavior through an exceptionally sharp initial rise in with increasing , which may be the steepest of any material, and also a peak and decrease in at high . These features are in stark contrast to the measured behavior for many solids, and occur at experimentally accessible conditions. Similar anomalous behavior is predicted for silicon carbide and other related materials.
The thermal conductivity, , is a fundamental transport parameter that governs the efficiency of heat conduction through solids. In insulating crystals, the heat is transported by phonons, and intrinsic thermal resistance comes from phonon-phonon scattering processes, which arise from the anharmonicity of the interatomic bonding potential peierls_zur_1929 ; peierls_quantum_1955 ; ziman_electrons_2001 . Lowest-order processes involving the mutual interaction among three phonons typically dominate this intrinsic resistance.
For a given phonon mode, the collection of all such scattering processes that conserve energy and momentum - the scattering phase space - is dictated entirely by a material’s phonon dispersions. Specific features in these dispersions activate selection rules that can severely restrict the phase space of certain phonon-phonon scattering channels peierls_zur_1929 ; peierls_quantum_1955 ; ziman_electrons_2001 ; herpin_contribution_1952 ; klemens_thermal_1958 ; klemens_decay_1967 ; orbach_attenuation_1964 ; lax_spontaneous_1981 ; lindsay_first-principles_2013 ; broido_ab_2013 ; mukhopadhyay_optic_2016 ; ravichandran_phonon-phonon_2020 . While several of these selection rules have recently been identified lindsay_first-principles_2013 ; broido_ab_2013 ; mukhopadhyay_optic_2016 ; ravichandran_phonon-phonon_2020 , the most well-known of them dictates that an acoustic phonon cannot decay anharmonically into a set of others that are in the same dispersive phonon branch peierls_zur_1929 ; peierls_quantum_1955 ; ziman_electrons_2001 ; herpin_contribution_1952 ; klemens_thermal_1958 ; klemens_decay_1967 ; orbach_attenuation_1964 ; lax_spontaneous_1981 . It explains the long lifetimes of large wave vector transverse acoustic (TA) phonons, observed at low temperatures grill_excitation_1975 ; ulbrich_propagation_1980 . Exceptions exist tamura_spontaneous_1985 , but the phase space for those scattering events is small fNote1 .
The influence of this selection rule on was long thought to be negligible since inter-branch phonon scattering processes dominate thermal transport, particularly at higher temperatures. However, it was recently pointed out that, even around and beyond room temperature (RT; 300 K), this selection rule can be activated for high frequency phonons in materials where the three acoustic phonon branches come close to each other in some region of the Brillouin zone (BZ), thereby mimicking the behavior of phonon decay within a single branch lindsay_first-principles_2013 ; broido_ab_2013 ; ravichandran_phonon-phonon_2020 . The phase space available to a heat carrying, high frequency acoustic (A) phonon in such a region of the BZ, decaying into two others (AAA process) can then become quite small, thus resulting in its long lifetime and large contributions to .
Perhaps the most interesting example of the impact of this AAA selection rule is cubic boron arsenide (BAs). First principles calculations lindsay_first-principles_2013 predicted that unusually weak AAA scattering, resulting from activation of the AAA selection rule, contributes to a for BAs that should be comparable to that of diamond, the crystal having the highest measured of all materials at RT. While inclusion of higher-order four-phonon scattering was found to reduce the BAs feng_four-phonon_2017 ; tian_unusual_2018 , it still achieved a predicted RT value of around 1300 Wm-1K-1, by far the highest value of any naturally occurring material, behind only the carbon crystals (e.g. diamond and graphite). These theoretical findings have been confirmed by measurements tian_unusual_2018 ; kang_experimental_2018 ; li_high_2018 , adding strong support to the impact of selection rules and corresponding reductions in the three-phonon scattering phase space on .
Recently, we have identified several other compounds, such as cubic boron phosphide (BP) and silicon carbide (SiC), where the AAA selection rule is activated, giving anomalously weak AAA scattering channels ravichandran_phonon-phonon_2020 . However, unlike in BAs, for these compounds, the weak AAA scattering is masked by another strong three-phonon scattering channel involving two acoustic phonons and an optic (O) phonon (AAO scattering channel), thus drastically reducing its impact on . In this letter, we show that the otherwise-hidden weak AAA scattering in BP and SiC can be exposed by hydrostatic pressure () and temperature () tuning of . We demonstrate that the evolving interplay between AAA and AAO scattering channels with varying and gives rise to two remarkable features in the of BP around and above RT - an unusually sharp rise in as increases from ambient pressure and, a peak and subsequent drop in at high . These features are contrary to the measured (, ) of many other insulating crystals that instead show a roughly linear increase with far away from phase transitions hakansson_thermal_1986 ; gerlich_temperature_1982 ; hakansson_thermal_1986 ; dalton_effect_2013 ; ohta_lattice_2012 ; manthilake_lattice_2011 ; hofmeister_pressure_2007 ; hofmeister_mantle_1999 ; hakansson_thermal_1986 ; andersson_thermal_1985 , consistent with simple theories hofmeister_pressure_2007 ; slack_thermal_1979 .
The (, ) of BP is calculated using a recently developed unified ab initio theoretical framework, which combines the use of density functional theory to obtain phonon dispersions and phonon scattering rates, with a numerical solution of the phonon Boltzmann transport equation ravichandran_unified_2018 . The theory has no adjustable parameters, and it has demonstrated good agreement with the measured of several materials over a broad temperature and pressure range ravichandran_unified_2018 ; tian_unusual_2018 ; ravichandran_non-monotonic_2019 ; chen_ultrahigh_2020 ; ravichandran_phonon-phonon_2020 , including BP and SiC. Both three-phonon and higher-order four-phonon scattering processes are included in the calculations along with phonon scattering by mass disorder arising from the natural isotope mixture on the constituent atoms fNote2 . The details of this first principles approach have been published in Ref. ravichandran_unified_2018 and are summarized in the Supplemental Material (SM) section S1 fNote3 . We present the results for BP here, while those for SiC can be found in the SM section S4 fNote3 .
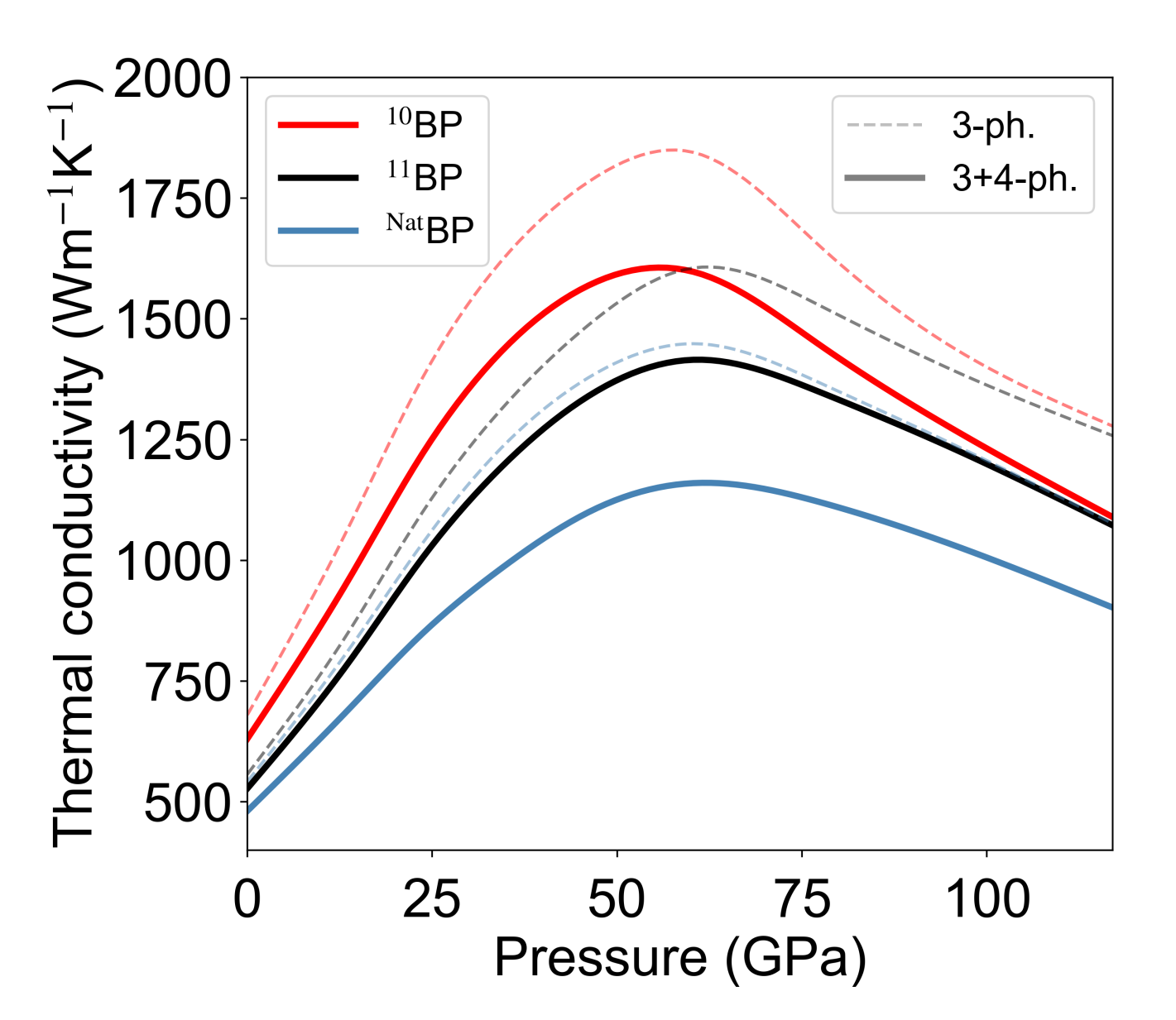
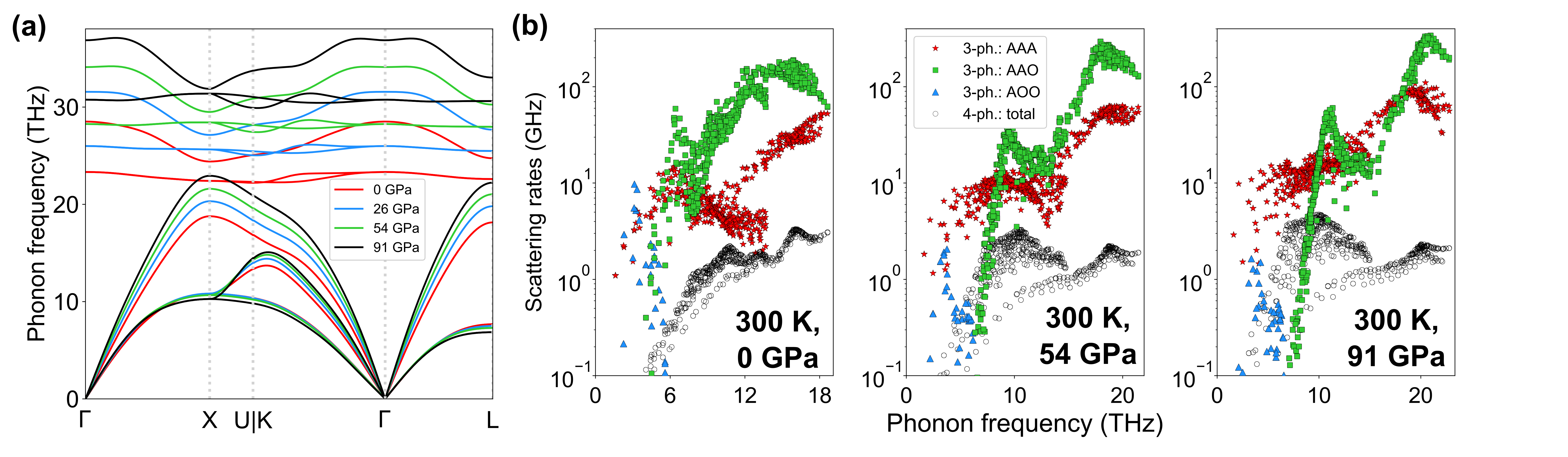
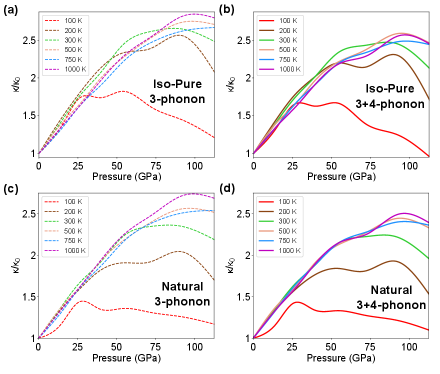
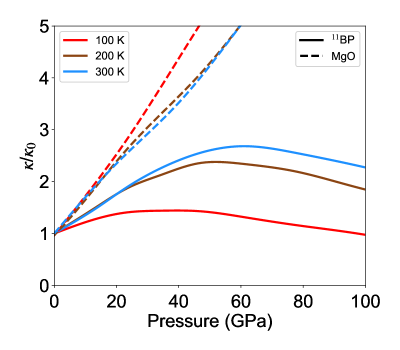
Figure 1 shows the calculated RT () of BP, with and without four-phonon scattering, for three cases: BP with (1) naturally occurring B isotope mix (NatBP), (2) B atoms isotopically enriched to 100 % 11B (11BP) and (3) B atoms isotopically enriched to 100 % 10B (10BP). All curves peak at around 55-60 GPa and subsequently decrease with increasing , contrary to the typically measured linearly increasing behavior for many other materials. In addition, the () curves rise rapidly with increasing , and there is a significant increase in the slopes, , going from NatBP to 11BP to 10BP. The peak values of are extremely large, around 1150 Wm-1K-1 (NatBP), 1400 Wm-1K-1 (11BP) and 1600 Wm-1K-1 (10BP), about 2.5 times higher than their values at ambient pressure. It is important to note that, the effect of four-phonon scattering on is relatively weak at all pressures in BP. Thus, the non-monotonic () behavior for BP is unrelated to that predicted for BAs ravichandran_non-monotonic_2019 , as discussed below.
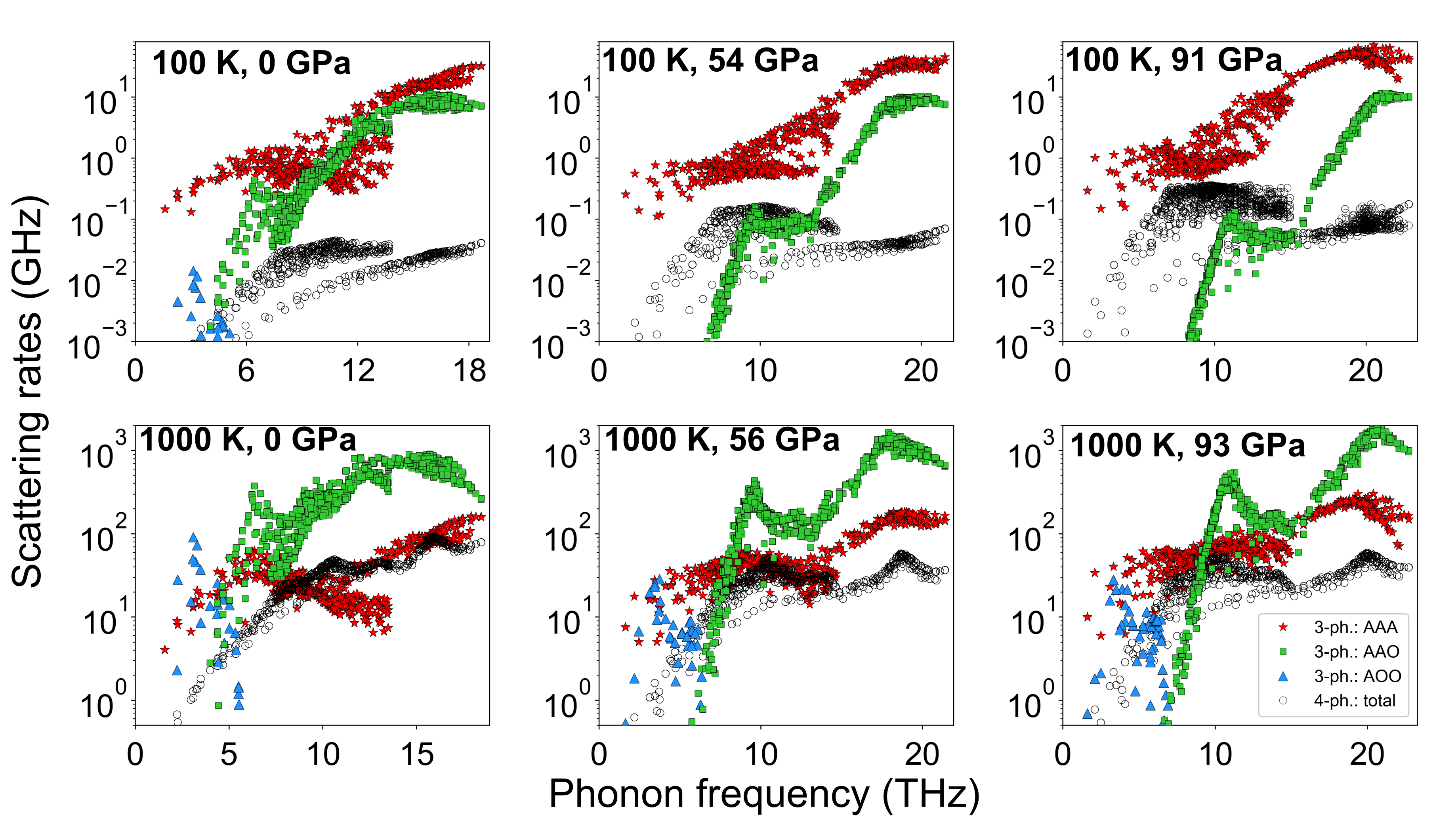
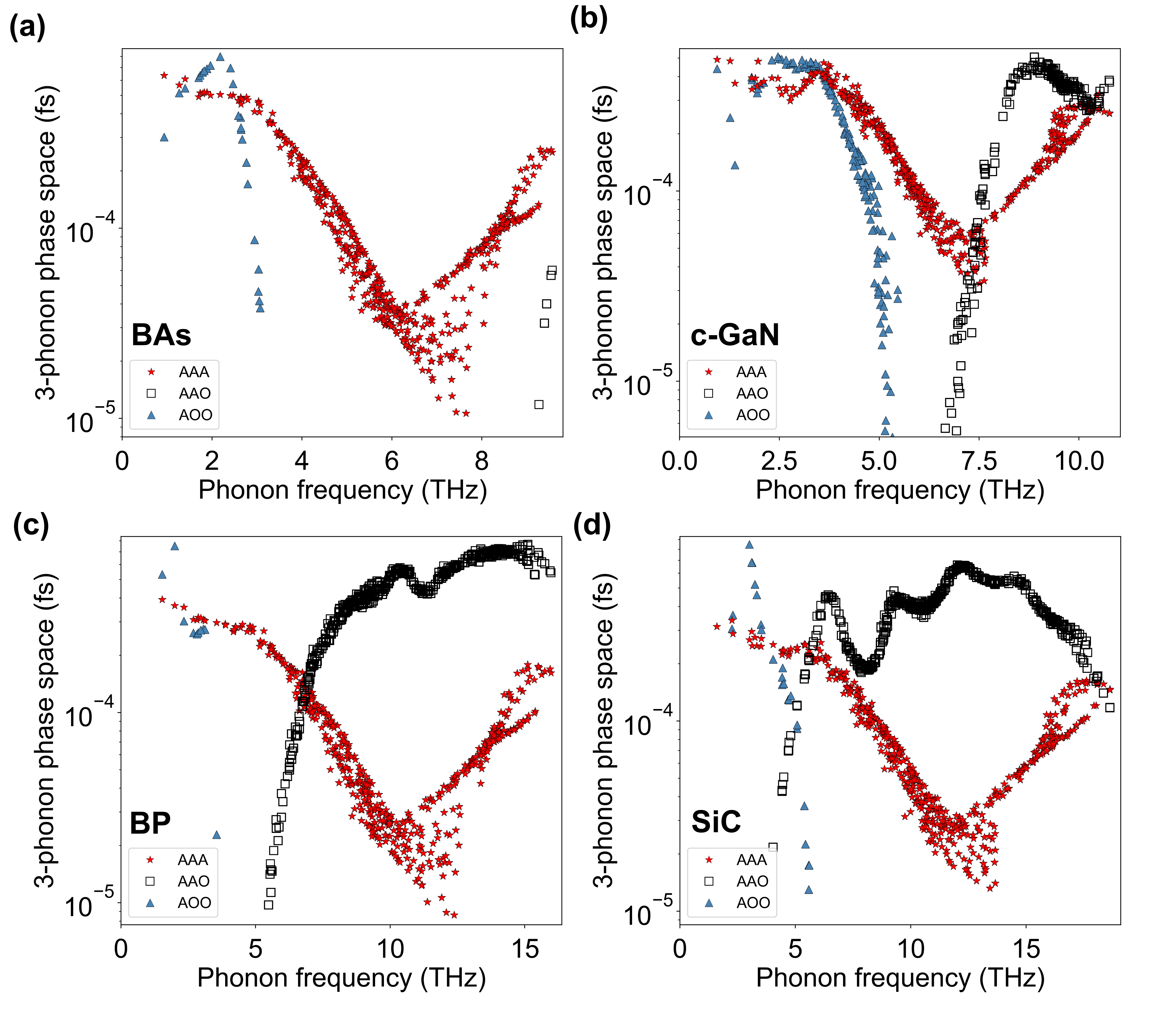
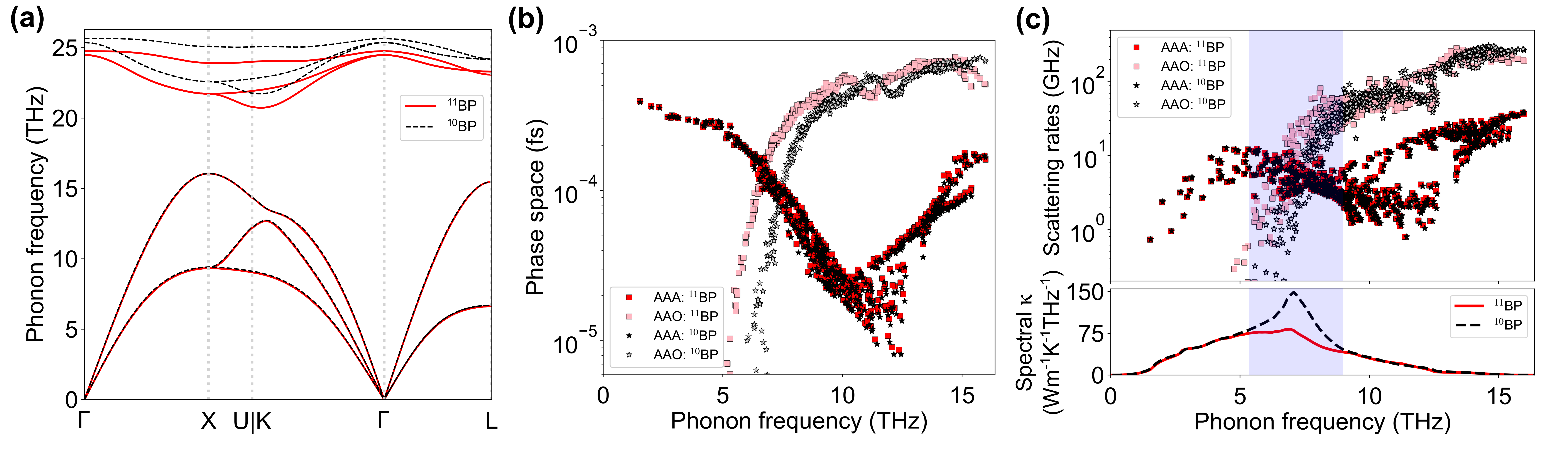
To understand these pressure-dependencies of , we first examine the phonon-phonon scattering processes in BP at ambient pressure. The light atoms and stiff bonding of BP result in a high of around 500-600 Wm-1K-1 at RT and ambient pressure zheng_high_2018 ; chen_ultrahigh_2020 ; dames_ultrahigh_2018 . BP crystallizes in the zinc blende structure and has two atoms in each unit cell, so the phonon dispersions consist of three A and three O phonon branches. Only three types of three-phonon scattering processes can occur, which involve combinations of A and O phonons: AAA, AAO, and AOO. Energy conservation forbids all other processes (e.g. OOO) ravichandran_phonon-phonon_2020 . Figure 2 (b) shows the RT AAA, AAO and AOO scattering rates for BP at various pressures, along with those for four-phonon scattering. The sharp dip in the AAA scattering rates at =0 in Fig. 2 (b) results from the AAA selection rule driven by the close proximity of the three acoustic phonon branches in a small region of the BZ, as seen in Fig. 2 (a), along direction. Similar dips driven by the same selection rule occur in other cubic compounds such as BAs, BSb, SiC, diamond, c-BN, and GaN broido_ab_2013 ; ravichandran_phonon-phonon_2020 and certain transition metal carbides li_fermi_2018 . Some examples are shown in Fig. S1 in the SM.
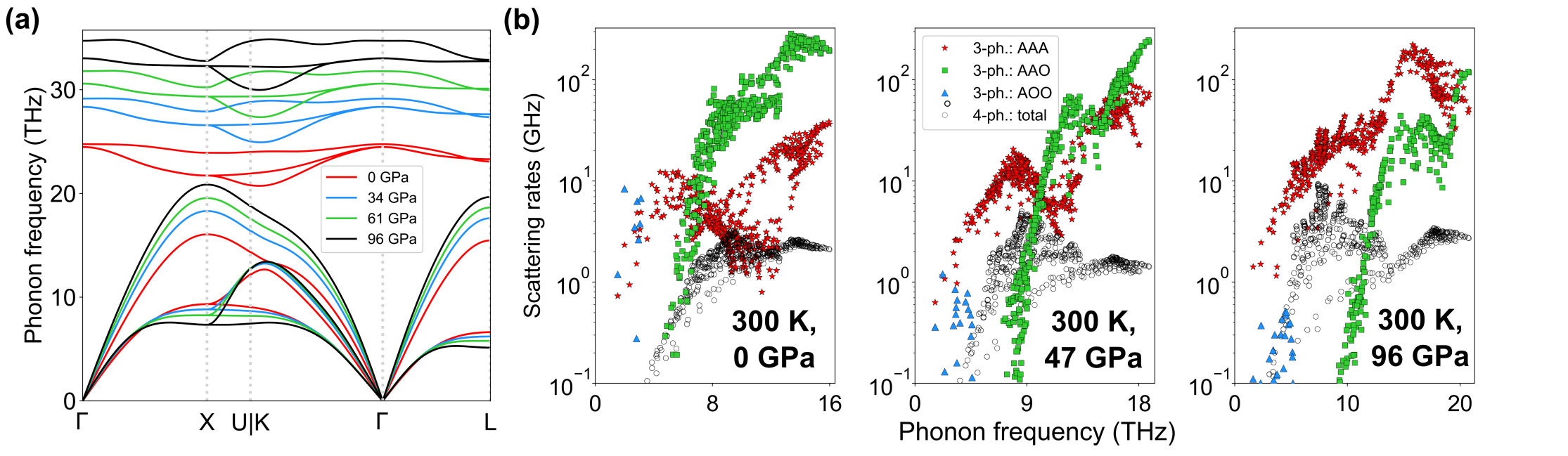
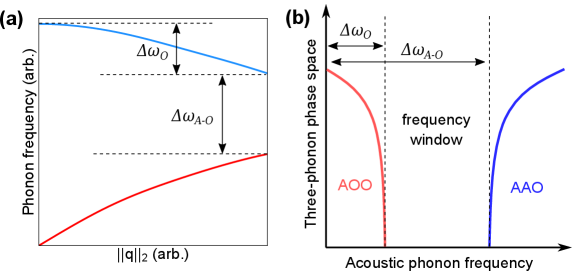
Apart from the close proximity of the acoustic phonons, other features in the phonon dispersions of BP and SiC activate additional selection rules. The mass difference between constituent atoms of these compound semiconductors causes a frequency gap, , between acoustic and optic phonons (A-O gap). Energy conservation mandates that only those acoustic phonons with frequencies greater than can participate in AAO scattering processes lindsay_first-principles_2013 . Similarly, energy conservation restricts the participation of acoustic phonons in AOO scattering processes to those with frequencies less than the optic phonon bandwidth, mukhopadhyay_optic_2016 ; ravichandran_phonon-phonon_2020 . These restrictions are illustrated in Fig. S2 in the SM.
As shown in Fig. 2 (b), the AAO scattering rates in BP dominate over almost the entire frequency region of the dip in AAA scattering rates. The relatively small mass difference between boron and phosphorus atoms () gives a that is not large enough to freeze out the AAO scattering channel for acoustic phonons above 6 THz. This behavior is in stark contrast to large mass ratio compounds like BAs (), where is large enough to almost completely remove AAO processes for acoustic phonons, thereby fully exposing the sharp dip in the AAA scattering rates, and resulting in significantly enhanced three-phonon limited lindsay_first-principles_2013 ; fNote4 . To illustrate the importance of the AAO processes in BP, we perform calculations by artificially turning them off, and find that the RT of 11BP at ambient pressure jumps from 530 Wm-1K-1 (560 Wm-1K-1) to over 2600 Wm-1K-1 (6000 Wm-1K-1), including three-phonon and four-phonon (three-phonon only) scattering. These values are about twice the corresponding values in BAs.
In BP, application of hydrostatic pressure introduces three intertwined behaviors that affect : (i) the longitudinal acoustic (LA) and optic phonons shift to higher frequencies, which increases LA phonon group velocities and weakens the AAO scattering rates due to decreased optic phonon occupations. Both of these changes contribute to the increasing with found in many materials. In BP, two additional features are critical to explain the anomalous behavior seen in Fig. 1 - (ii) optic phonons stiffen faster than do acoustic phonons [see Fig. 2 (a)], which increases and shifts the onset of AAO processes to higher frequencies, thereby exposing increasingly large portions of the AAA dip. This behavior significantly increases the rate of rise in the of BP in the low range, as discussed below; and (iii) with increasing , the LA phonons stiffen, while the transverse acoustic (TA) phonons weakly soften. The resulting increased separation between LA and TA phonon branches gradually removes the impact of the AAA selection rule, and so, increases the AAA scattering rates, relative to those at ambient pressure [see Fig. 2 (b)]. This behavior acts to drive lower, as pointed out previously lindsay_anomalous_2015 ; ravichandran_non-monotonic_2019 .
Peak and decrease in - At RT and low , the influence of trends (i) and (ii) is stronger than trend (iii) resulting in an increasing . Beyond 50 GPa, the continued shift of AAO processes towards higher phonon frequencies almost fully exposes the AAA dip, and the rising AAA scattering rates from trend (iii) eventually dominate the behavior causing to decrease with increasing . As a result of this evolving interplay between AAA and AAO processes, the RT achieves a peak value at around 60 GPa, which is around 2.5 times that of its value at .
Figure 3 (a) shows the for 11BP scaled by its zero pressure value, , for different . Around and above RT, the curves for each roughly overlap, indicating that the and dependences are separable. Such separability is also predicted from empirical theory manthilake_lattice_2011 ; hofmeister_pressure_2007 and is found in conventionally behaving compounds such as MgO (see Fig. S4 in the SM). That it also occurs in BP with its anomalous non-monotonic , is a consequence of the independent changes in AAA and AAO scattering rates induced by changing or . Increasing strengthens AAO processes relative to AAA processes, while increasing shifts the AAO processes to higher frequencies relative to AAA processes. Above RT, AAO scattering rates in BP dominate in magnitude over AAA scattering rates until very high [Fig. 3 (b)], just as they do at RT [Fig. 2 (b)]. Thus, the evolution of above RT is qualitatively the same as that at RT. However, for well below RT, as AAO scattering rates weaken relative to AAA scattering rates [see Fig. 3 (b)], the rise in from trends (i) and (ii) is overcome by trend (iii) at lower , resulting in a weaker dependence to , which eventually decreases below , as shown in Fig. 3 (a) for = 100 K. Similar behavior of also occurs in SiC (see SM section S4).
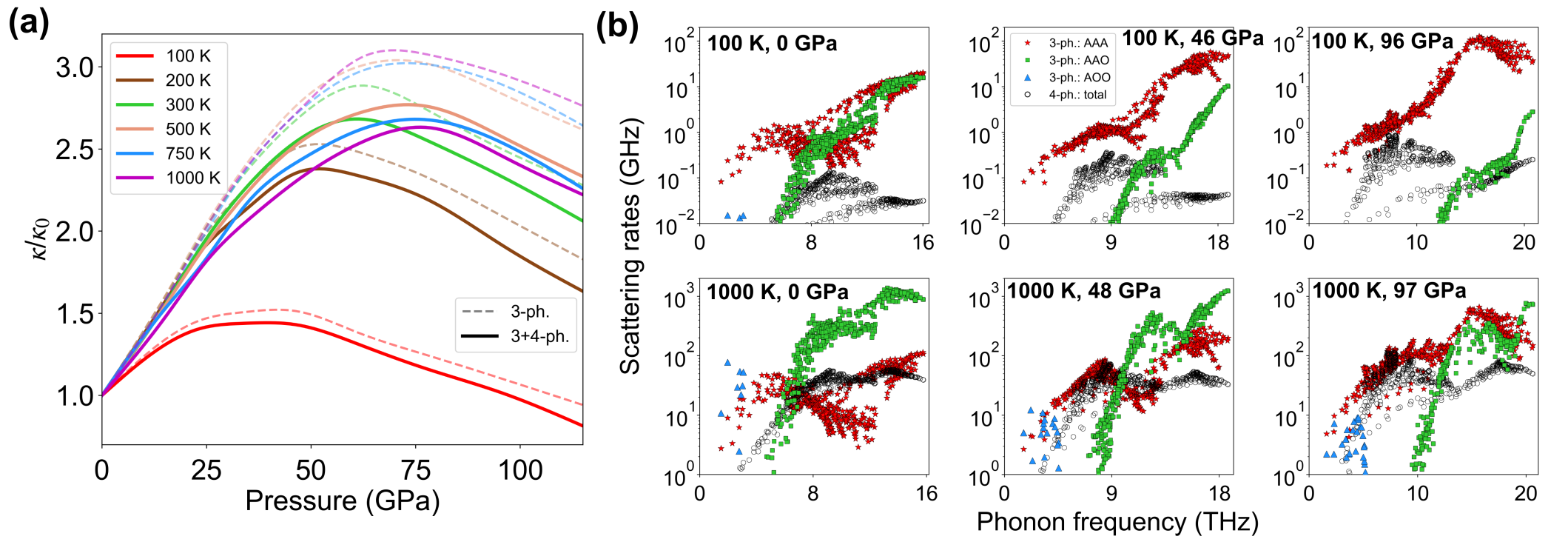
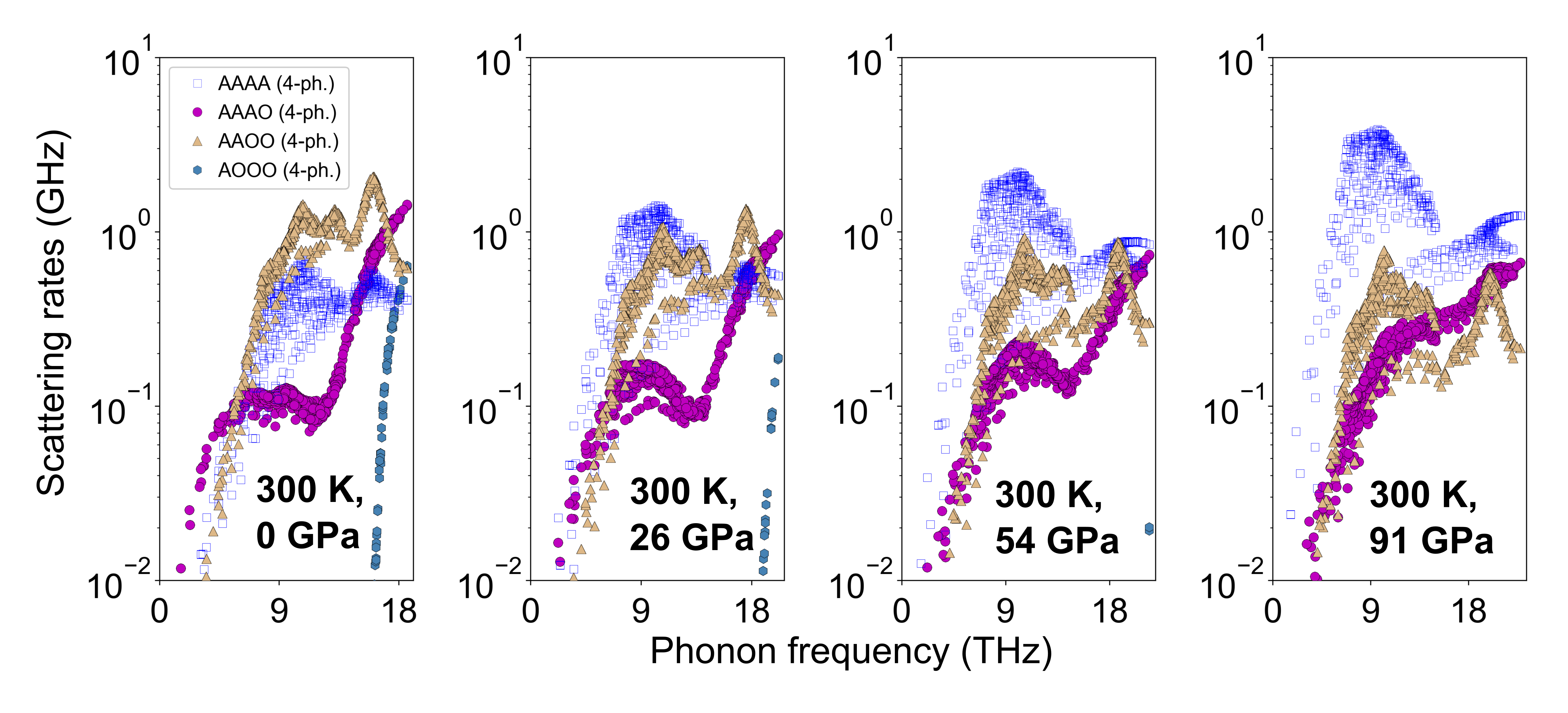
Previously, we predicted a non-monotonic pressure dependence of for BAs ravichandran_non-monotonic_2019 , which was connected to an evolving competition between three-phonon and four-phonon scattering processes with increasing . This competition is responsible for a significant suppression of the measured BAs -values compared with the lowest-order three-phonon prediction feng_four-phonon_2017 ; tian_unusual_2018 . In stark contrast, however, the non-monotonic behavior of in BP arises from fundamentally different physics involving competition only among three-phonon scattering channels. This competition contributes to a significantly larger peak- value in BP than in BAs (2.5x in BP vs. 1.1x in BAs at RT), and a much sharper increase in the BP at low (discussed next), thus making it more accessible for experimental validation. We note that the effect of four-phonon scattering on the of BP and SiC is dominated by the increasing strength of the AAAA scattering channel with increasing (see SM sections S3 and S4), but it is generally weak compared with the dominant three-phonon scattering channels, and so does not cause qualitative differences in the observed trends [see Figs. 1 and 3 (a)].
Unusually sharp rise in above P=0 - The calculated slopes, , of the curves in Fig. 1 around ambient pressure are exceptionally large. Significant contributions to these large values come from the rapid increase in the intrinsic lifetimes of acoustic phonons whose frequencies lie just below the onset of the AAO scattering. With increasing , this onset shifts to higher frequencies, exposing more of the AAA dip. Phonons in the newly exposed region of the AAA dip have reduced scattering rates and so give correspondingly larger contributions to . This behavior is illustrated in Fig. 4, which shows, , the spectral contributions to as a function of phonon frequency, , for 10BP and 11BP at different pressures and RT. The effect is enhanced in 10BP compared with 11BP because the lighter 10B atom shifts the onset of AAO scattering processes to higher frequencies even at (Fig. S3). This difference helps explain the much larger calculated RT and ambient pressure of 10BP (630 Wm-1K-1) compared with that for 11BP (530 Wm-1K-1), consistent with measured results zheng_high_2018 ; chen_ultrahigh_2020 .
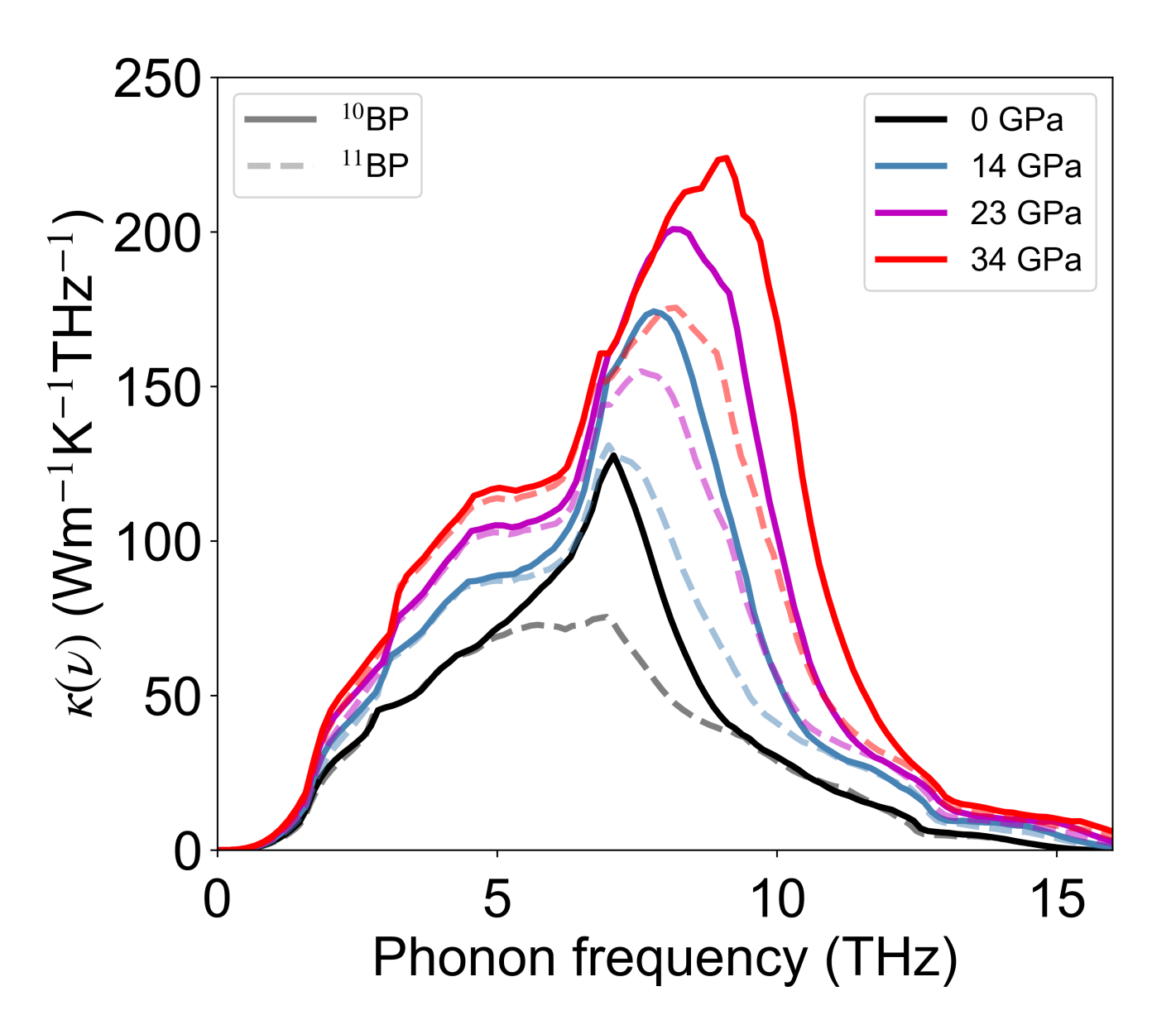
We calculate the RT values of 15.4 Wm-1K-1GPa-1 (NatBP), 19.1 Wm-1K-1GPa-1 (11BP) and 24.1 Wm-1K-1GPa-1 (10BP) at low . Measurements and calculations of given in the literature are only for materials with much lower , such as those of interest for geophysical studies dalton_effect_2013 ; ohta_lattice_2012 ; manthilake_lattice_2011 ; hofmeister_mantle_1999 ; hofmeister_pressure_2007 , e.g. MgO, as well as alkali halides andersson_thermal_1985 ; hakansson_thermal_1986 ; gerlich_temperature_1982 . For these materials, is less than 3 Wm-1K-1GPa-1, far smaller than our calculated values for BP. Therefore, to put the BP values in better context, we have calculated the RT for diamond, whose is higher than that of BP. We find RT values of 21 Wm-1K-1GPa-1 and 17 Wm-1K-1GPa-1 for isotopically pure and naturally occurring diamond respectively. Remarkably, the calculated value for 10BP is higher than that for diamond, even though the absolute RT is five times lower. The present findings suggest that the for 10BP may be the highest value achievable for any material, a striking signature of the influence of the AAA selection rule.
In summary, through ab initio calculations for BP, we have shown that a hidden weak three-phonon scattering channel arising from a selection rule on anharmonic decay of acoustic phonons can be revealed through examination of the pressure dependence of the thermal conductivity, which displays anomalous features including an exceptionally fast rise and a peak with increasing pressure. We predict that such anomalous behavior will also occur in other materials similarly affected by the same selection rule, which we have demonstrated for cubic silicon carbide (SiC) in the SM (see Figs. S6-S9). Other recently identified phase space selection rules should also give rise to unusual pressure dependence of phonon lifetimes and in the affected materials ravichandran_phonon-phonon_2020 . The present work gives new insights into the impact of selection rules on phonon-phonon scattering and demonstrates novel behavior of phonon thermal transport in solids under pressure.
This work was supported by the Office of Naval Research under a Multidisciplinary University Research Initiative, Grant No. N00014-16-1-2436.
References
- (1) R. Peierls. Zur kinetischen Theorie der Wärmeleitung in Kristallen. Annalen der Physik, 395(8):1055–1101, 1929.
- (2) R.E. Peierls. Quantum Theory of Solids. International series of monographs on physics. Clarendon Press, 1955.
- (3) J. M. Ziman. Electrons and Phonons: The Theory of Transport Phenomena in Solids. Oxford University Press, February 2001.
- (4) André Herpin. Contribution à l’étude de la théorie cinétique des solides. Annales de Physique, 12(7):91–139, 1952.
- (5) P. G. Klemens. Thermal Conductivity and Lattice Vibrational Modes. In Solid State Physics, volume 7, pages 1–98. Academic Press, January 1958.
- (6) P. G. Klemens. Decay of High-Frequency Longitudinal Phonons. Journal of Applied Physics, 38(12):4573–4576, November 1967.
- (7) R. Orbach and L. A. Vredevoe. The Attenuation of High Frequency Phonons at Low Temperatures. Physics Physique Fizika, 1(2):91–94, September 1964.
- (8) M. Lax, P. Hu, and V. Narayanamurti. Spontaneous Phonon Decay Selection Rule: and Processes. Physical Review B, 23(6):3095–3097, March 1981.
- (9) L. Lindsay, D. A. Broido, and T. L. Reinecke. First-Principles Determination of Ultrahigh Thermal Conductivity of Boron Arsenide: A Competitor for Diamond? Physical Review Letters, 111(2):025901, July 2013.
- (10) D. A. Broido, L. Lindsay, and T. L. Reinecke. Ab initio Study of the Unusual Thermal Transport Properties of Boron Arsenide and Related Materials. Physical Review B, 88(21):214303, December 2013.
- (11) S. Mukhopadhyay, L. Lindsay, and D. S. Parker. Optic Phonon Bandwidth and Lattice Thermal Conductivity: The Case of (). Physical Review B, 93(22):224301, June 2016.
- (12) Navaneetha K. Ravichandran and David Broido. Phonon-Phonon Interactions in Strongly Bonded Solids: Selection Rules and Higher-Order Processes. Physical Review X, 10(2):021063, June 2020.
- (13) W. Grill and O. Weis. Excitation of Coherent and Incoherent Terahertz Phonon Pulses in Quartz Using Infrared Laser Radiation. Physical Review Letters, 35(9):588–591, September 1975.
- (14) R. G. Ulbrich, V. Narayanamurti, and M. A. Chin. Propagation of Large-Wave-Vector Acoustic Phonons in Semiconductors. Physical Review Letters, 45(17):1432–1435, October 1980.
- (15) S. Tamura and H. J. Maris. Spontaneous Decay of TA Phonons. Physical Review B, 31(4):2595–2598, February 1985.
- (16) We have verified the small phase space from numerical calculations for many compounds.
- (17) Tianli Feng, Lucas Lindsay, and Xiulin Ruan. Four-phonon Scattering Significantly Reduces Intrinsic Thermal Conductivity of Solids. Physical Review B, 96(16):161201, October 2017.
- (18) Fei Tian, Bai Song, Xi Chen, Navaneetha K. Ravichandran, Yinchuan Lv, Ke Chen, Sean Sullivan, Jaehyun Kim, Yuanyuan Zhou, Te-Huan Liu, Miguel Goni, Zhiwei Ding, Jingying Sun, Geethal Amila Gamage Udalamatta Gamage, Haoran Sun, Hamidreza Ziyaee, Shuyuan Huyan, Liangzi Deng, Jianshi Zhou, Aaron J. Schmidt, Shuo Chen, Ching-Wu Chu, Pinshane Y. Huang, David Broido, Li Shi, Gang Chen, and Zhifeng Ren. Unusual High Thermal Conductivity in Boron Arsenide Bulk Crystals. Science, 361(6402):582–585, August 2018.
- (19) Joon Sang Kang, Man Li, Huan Wu, Huuduy Nguyen, and Yongjie Hu. Experimental Observation of High Thermal Conductivity in Boron Arsenide. Science, 361(6402):575–578, July 2018.
- (20) Sheng Li, Qiye Zheng, Yinchuan Lv, Xiaoyuan Liu, Xiqu Wang, Pinshane Y. Huang, David G. Cahill, and Bing Lv. High Thermal Conductivity in Cubic Boron Arsenide Crystals. Science, 361(6402):579–581, August 2018.
- (21) B. Hákansson and P. Andersson. Thermal Conductivity and Heat Capacity of Solid NaCl and NaI under Pressure. Journal of Physics and Chemistry of Solids, 47(4):355–362, January 1986.
- (22) D. Gerlich and P. Andersson. Temperature and Pressure Effects on the Thermal Conductivity and Heat Capacity of CsCl, CsBr and CsI. Journal of Physics C: Solid State Physics, 15(25):5211, 1982.
- (23) Douglas Allen Dalton, Wen-Pin Hsieh, Gregory T. Hohensee, David G. Cahill, and Alexander F. Goncharov. Effect of Mass Disorder on the Lattice Thermal Conductivity of MgO Periclase under Pressure. Scientific Reports, 3:2400, August 2013.
- (24) Kenji Ohta, Takashi Yagi, Naoyuki Taketoshi, Kei Hirose, Tetsuya Komabayashi, Tetsuya Baba, Yasuo Ohishi, and John Hernlund. Lattice Thermal Conductivity of MgSiO3 Perovskite and Post-perovskite at the Core–mantle Boundary. Earth and Planetary Science Letters, 349-350:109–115, October 2012.
- (25) Geeth M. Manthilake, Nico de Koker, Dan J. Frost, and Catherine A. McCammon. Lattice Thermal Conductivity of Lower Mantle Minerals and Heat Flux from Earth’s Core. Proceedings of the National Academy of Sciences, 108(44):17901–17904, October 2011.
- (26) Anne M. Hofmeister. Pressure Dependence of Thermal Transport Properties. Proceedings of the National Academy of Sciences, 104(22):9192–9197, May 2007.
- (27) A. M. Hofmeister. Mantle Values of Thermal Conductivity and the Geotherm from Phonon Lifetimes. Science, 283(5408):1699–1706, March 1999.
- (28) P. Andersson. Thermal Conductivity under Pressure and through Phase Transitions in Solid Alkali Halides. I. Experimental Results for KCl, KBr, KI, RbCl, RbBr and RbI. Journal of Physics C: Solid State Physics, 18(20):3943, 1985.
- (29) Glen A. Slack. The Thermal Conductivity of Nonmetallic Crystals. In Solid State Physics, volume 34, pages 1–71. Academic Press, January 1979.
- (30) Navaneetha K. Ravichandran and David Broido. Unified First-principles Theory of Thermal Properties of Insulators. Physical Review B, 98(8):085205, August 2018.
- (31) Navaneetha K. Ravichandran and David Broido. Non-monotonic Pressure Dependence of the Thermal Conductivity of Boron Arsenide. Nature Communications, 10(1):1–8, February 2019.
- (32) Ke Chen, Bai Song, Navaneetha K. Ravichandran, Qiye Zheng, Xi Chen, Hwijong Lee, Haoran Sun, Sheng Li, Geethal Amila Gamage Udalamatta Gamage, Fei Tian, Zhiwei Ding, Qichen Song, Akash Rai, Hanlin Wu, Pawan Koirala, Aaron J. Schmidt, Kenji Watanabe, Bing Lv, Zhifeng Ren, Li Shi, David G. Cahill, Takashi Taniguchi, David Broido, and Gang Chen. Ultrahigh Thermal Conductivity in Isotope-enriched Cubic Boron Nitride. Science, 367(6477):555–559, January 2020.
- (33) Naturally occuring boron is 19.9% 10B, 80.1% 11B and phosphorus is 100% 31P.
- (34) See Supplemental Material at […] for the summary of first principles theoretical approach and phonon transport properties of BP, SiC and related compounds under pressure.
- (35) Qiye Zheng, Sheng Li, Chunhua Li, Yinchuan Lv, Xiaoyuan Liu, Pinshane Y. Huang, David A. Broido, Bing Lv, and David G. Cahill. High Thermal Conductivity in Isotopically Enriched Cubic Boron Phosphide. Advanced Functional Materials, 28(43):1805116, 2018.
- (36) Chris Dames. Ultrahigh Thermal Conductivity Confirmed in Boron Arsenide. Science, 361(6402):549–550, August 2018.
- (37) Chunhua Li, Navaneetha K. Ravichandran, Lucas Lindsay, and David Broido. Fermi Surface Nesting and Phonon Frequency Gap Drive Anomalous Thermal Transport. Physical Review Letters, 121(17):175901, October 2018.
- (38) In BP and BAs, the optical phonon bandwidth is small, so the AOO scattering channel only affects low frequency phonons well below the AAA dip region; it is thus, not important for the discussed behavior.
- (39) L. Lindsay, D. A. Broido, Jesús Carrete, Natalio Mingo, and T. L. Reinecke. Anomalous Pressure Dependence of Thermal Conductivities of Large Mass Ratio Compounds. Physical Review B, 91(12):121202, March 2015.
I Supplemental Material
I.1 First principles theoretical approach
We solve the linearized Boltzmann transport equation for phonons for the non-equilibrium distribution function, , resulting from a small applied temperature gradient, , where is the Bose distribution function, and is the small deviation from generated by . Here, designates the phonon mode, where is the phonon branch and is the phonon wave vector. The linearized Boltzmann equation is:
| (1) |
where is the phonon velocity of the mode , and the right-hand side is the collision term, which includes three-phonon scattering, four-phonon scattering and phonon scattering by the isotopic mass disorder. Harmonic interatomic force constants (IFCs), and anharmonic third- and fourth-order IFCs are determined using the Density Functional Theory (DFT) as implemented in Quantum Espresso. Expressing allows Eq. 1 to be recast into an integral equation for the function, , which is solved numerically. The thermal conductivity is then obtained as:
| (2) |
where is the Boltzmann constant, is the crystal volume, and is the thermal conductivity tensor for heat current flow along the Cartesian direction, , resulting from a temperature gradient along the direction, . For the cubic structures considered in the present work, the thermal conductivity tensor is diagonal: . Further details of the computational approach including computation scheme for IFCs, expressions for the phonon scattering rates and implementation of the solution of the phonon Boltzmann equation are given in Ref. [30]. All the calculations in this study are performed using norm-conserving pseudopotentials with the local density approximation (LDA) for the exchange correlation. The converged parameters used in the first principles calculations in this work for BP and SiC, such as the energy cutoffs for the DFT calculations, -grids used in the solution of the Boltzmann equation and the cutoffs for the harmonic, cubic and quartic IFCs, can be found in Ref. [12]. The pressure in our calculations is calculated by obtaining the derivative of the Helmholtz free energy, correct to fourth-order in anharmonicity (), with respect to crystal volume () at each temperature () using the expression: , where is the crystal lattice constant and of . The complete expression for the Helmholtz free energy, correct to fourth-order in anharmonicity of the crystal potential, can be found in section 10 of the supplemental materials in Ref. [31].
I.2 Supplemental figures to the main text for BP
I.3 Increasing strength of four-phonon scattering in BP with increasing pressure
Figs. 1 and 3(a) in the main text show that, as increases, inclusion of four-phonon scattering increasingly suppresses the of BP, and that, this suppression becomes even larger at higher . This behavior is driven by strengthening of AAAA four-phonon scattering with increasing , as shown in Fig. 9. Hydrostatic pressure stiffens the chemical bonding, resulting in increased interatomic force constants (IFCs). These increases in the fourth-order IFCs produce corresponding increases in the four-phonon scattering matrix elements acting to increase the scattering rates of all four-phonon channels. At the same time, the increases in second-order IFCs shift optic phonons to higher frequencies, thereby reducing their populations and reducing the scattering rates of all four-phonon processes involving optic phonons, such as AAAO, AAOO and AOOO processes. As a result, AAAA four-phonon scattering rates are increased preferentially over all other four-phonon scattering rates, which contain at least one optic phonon.
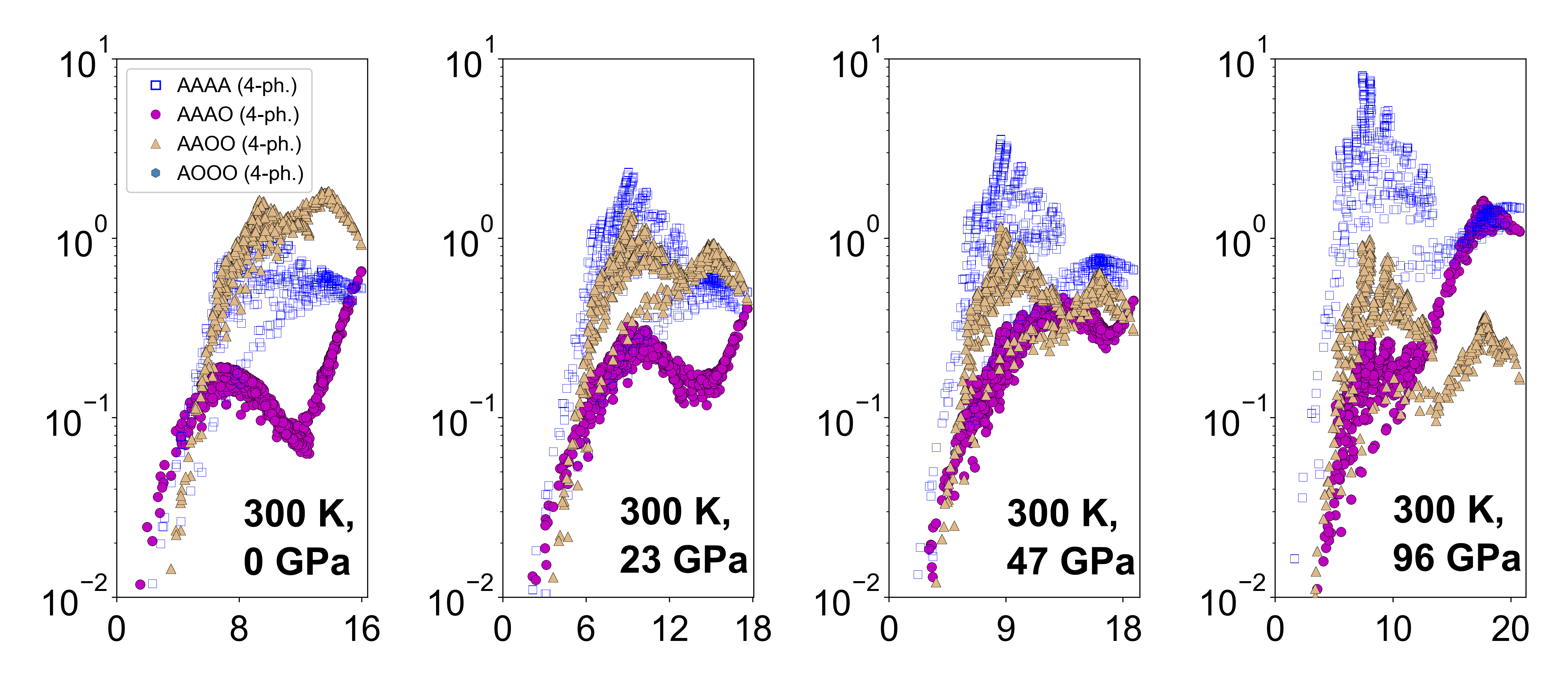
I.4 Hidden influence of the selection rules on the of SiC
The results for the pressure and temperature-dependent phonon dispersions, three-phonon and four-phonon scattering rates, and for SiC are presented in this section. Figure 10 (a) shows the stiffening of the longitudinal acoustic and all optic phonon branches, and the weak softening of the transverse acoustic phonon branch of SiC with pressure. Figure 10 (b) shows the evolution of the process-wise separated three-phonon and total four-phonon scattering rates with pressure at room temperature. The two plots show the striking similarity of the trends found for SiC and for BP (in the main text). Similarly, application of hydrostatic pressure causes a peak and drop in in SiC (Fig. 11) as in BP (in the main text). Furthermore, the observed temperature- and pressure-dependence of the competition between AAA and AAO scattering rates in BP is also seen in SiC (Fig. 12). Finally, the dominant all-acoustic AAAA four-phonon scattering channel (see Fig. 13) drives the reduction in of SiC at high , also similar to BP.