Exploring Dropout Discriminator for Domain Adaptation
Abstract
Adaptation of a classifier to new domains is one of the challenging problems in machine learning. This has been addressed using many deep and non-deep learning based methods. Among the methodologies used, that of adversarial learning is widely applied to solve many deep learning problems along with domain adaptation. These methods are based on a discriminator that ensures source and target distributions are close. However, here we suggest that rather than using a point estimate obtaining by a single discriminator, it would be useful if a distribution based on ensembles of discriminators could be used to bridge this gap. This could be achieved using multiple classifiers or using traditional ensemble methods. In contrast, we suggest that a Monte Carlo dropout based ensemble discriminator could suffice to obtain the distribution based discriminator. Specifically, we propose a curriculum based dropout discriminator that gradually increases the variance of the sample based distribution and the corresponding reverse gradients are used to align the source and target feature representations. An ensemble of discriminators helps the model to learn the data distribution efficiently. It also provides a better gradient estimates to train the feature extractor. The detailed results and thorough ablation analysis show that our model outperforms state-of-the-art results.
keywords:
Domain Adaptation, Adversarial Learning , Dropout Discriminator , Object Classification1 Introduction
The deep learning based models have achieved considerable success in the Visual recognition domain. These models are trained on very large annotated datasets such as Imagenet [1]. The deployment of these generically trained models require them to adapt to work in specific settings (for instance with catalog images in E-commerce websites). This problem is recognized as one of dataset bias. The context for this problem in vision was nicely demonstrated through the work of [2]. However, the requirement of a large annotated dataset becomes a bottleneck for training networks in deep learning frameworks. The typical solution is to further fine-tune these networks on a task-specific dataset. This approach is satisfactory if there is a sufficiently large target dataset on which to fine-tune. In this paper, we solve the problem of adapting classifiers to work on datasets that do not have any labeled information. This problem is one of unsupervised domain adaptation and is a more general setting.
Ganin and Lempitsky [3] proposed a method to solve unsupervised domain adaptation through back-propagation. In this method, the domain adaptation problem is solved by using a discriminator that ensures domain invariance of learned representations used for classification. Sometime this discriminator may introduce the mode collapse problem in features. There have been several methods [4, 5, 6, 7] proposed for improving the discriminator. However, most of these involve an increase in the number of parameters. For instance a recent work by Pei et al (MADA) [8] addresses this issue through class-specific discriminators. This leads to a linear increase in the number of parameters with the number of classes in dataset. In contrast, we propose the use of curriculum-based dropout discriminator to obtain improved performance of the domain adaptation task without increasing the number of parameters. It makes our model’s applicability comprehensive as it can also adapt to datasets with a large number of classes.
Specifically, in this paper, we propose Curriculum based Dropout Discriminator for Domain Adaptation (CA) and compare it with a variant, Dropout Discriminator for Domain Adaptation (A). It is a novel approach that solves the above problem through an adversarial dynamic dropout based ensemble of discriminators. where we consider dropout as being a source of an ensemble of domain classifiers [9]. The proposed model also allows the discriminators to reduce the prediction variance, remove overfitting, and average out the bias.
In [10], we initiated the work by introducing a dropout discriminator in curriculum fashion in domain adaptation, whereas in this work, we further explored the dropout discriminator by considering the fixed number of discriminators samples. We analysed the impact of curriculum learning by changing the curriculum criteria in the experiments in this submission. We also provide the analysis of experiments by reducing the source samples and how it affects the domain adaptation problems. We are able to show that the dropout discriminator works well even in these challenging setting. In this paper we further provide a visualization of adapted features for different transfer tasks. The performance analysis of the discriminator is provided.
The idea for this discriminator is illustrated in Figure 1. The initial discriminator by Ganin and Lempitsky [3] suggests the use of a single binary discriminator and MADA [8] extends it to class-specific cues. In contrast, CA obtains a discriminator distribution that provides a much-improved feedback for improving the feature extractor. The performance of any adversarial learning method largely depends upon the capability of the discriminator network. The ensemble method [9] improves the discriminator’s performance and makes it robust. We show that this indeed helps in an improved domain adaptation (around 5.3% improvement in Amazon-DSLR adaptation) with much fewer parameters (59M) than MADA (98M). More importantly, our method does not increase the number of parameters as the number of classes increase, making it scalable to datasets with a large number of classes. Through this paper we make the following main contributions:
-
1.
We propose a method to obtain a dropout based discriminator that provides a distribution based discrimination for every sample ensuring a more robust feature adaptation
-
2.
We adopt a curriculum based dropout model, CA, that ensures gradual increase in the number of samples as the adaptation progresses to ensure better adaptation in contrast to a fixed number of samples based dropout distribution (D3A).
-
3.
We provide a thorough empirical analysis of the method (including statistical significance, discrepancy distance) and evaluate our approach against the state-of-the-art approaches.
-
4.
We also experiment with sensitivity to source data size by evaluating the method on half the amount of source data to verify the effect on the method. This experiment tests the resilience of the method.

2 Related Work
Domain Adaptation: In the domain adaptation setting a basic common structure that has been followed is the Siamese architecture [11] with two streams, representing the source and target models. It is trained with a combination of a classification loss and the other being one of discrepancy loss or an adversarial loss. The classification loss depends on the source data label, while the discrepancy loss reduces the shift between the two domains. A discrepancy based deep learning method is that of deep domain confusion (DDC) [12]. The loss between a single FC (fully connected) layer of source and target feature extractor network is used to minimize the maximum mean discrepancy (MMD) between the source and the target. This approach is further extended by deep adaptation network (DAN) [13]. Recently, a number of other methods have been proposed which use discrepancy of domain [14, 15, 16, 17, 18, 19, 20, 21].
Adversarial Learning: In the domain adaptation setting, an adversarial network provides domain invariant representations by making the source and target domain indistinguishable by the discriminator. Adversarial Discriminative Domain Adaptation [4] uses an inverted label GAN loss to split the optimization into two independent objectives. One such method is the domain confusion based model proposed in [22] that considers a domain confusion objective. Domain-Adversarial Neural Networks (DANN) [3] integrates a gradient reversal layer into the standard architecture to promote the emergence of the learned representations that are discriminative for the main learning task on the source domain and non-discriminative concerning the shift between the domains. Recently, some works have been proposed which use an adversarial discriminative approach in solving the domain adaptation problem [23, 24, 25, 26, 27, 28, 29].
Similarly, the model proposed in [30, 31, 32] exploits GANs with the aim to generate source-domain images such that they appear as if they were drawn from the target domain distribution. The closest related work to our approach is the work by [8] that extends the gradient reversal method by a class-specific discriminator. In iCAN [33], a domain-collaborative and domain adversarial training of neural networks has been presented for unsupervised domain adaptation. They integrated the losses from different domain classifiers at different blocks such that the model can learn the domain invariant features from higher block and domain variant features from the lower blocks of the network.
Similar to guided dropout [34], the adversarial guided dropout [35] adversarially disconnects dominated neurons that are used for the prediction. Adversarial dropout regularization (ADR) [36] avoids to generated the target features near class boundaries using the dropout regularization. Dropout regularization has also been applied in robust speech recognition [37].
Ensemble and Curriculum learning: Ensemble methods [38] can capture the uncertainty of the neural network (NN). Gal et.al. [39] use dropout to obtain the predictive uncertainty and apply Markov chain Monte Carlo [40] also known as MCMC at the test time to deal with intractable posterior. In discriminator based approaches, ensembles can be considered as multi-discriminator or multi-generator architecture. Multi discriminator approach has also been proposed by [41, 42, 43] to learn the data distribution more effectively. In Bayesian GAN [44], dropout in the discriminator is used which can be interpreted as an ensemble model [39]. The curriculum learning [45] enhances model’s performance and its generalization capability. The performance of the GAN is also improved through the curriculum learning of the discriminator [46]. It has been shown that dropout can also work with curriculum learning [47]. In domain adaptation, a curriculum style learning approach has been applied in [48] to minimize the domain gap in semantic segmentation. The curriculum domain adaptation first solves easy tasks such as estimating label distributions, then infers the necessary properties about the target domain. The theoretical framework for curriculum learning in transfer learning is proposed in [49]. Recently other curriculum learning based domain adaptation methods have been proposed in Transferable Curriculum Learning [50].
There are other cluster based alignment techniques that are also used to tackle the domain adaptation problem. The authors in [51] applied the center-based discriminative feature learning methods to minimize the dataset bias. Similarly in [52], the authors align the cluster with a teacher model. KNN based alignment is used in the [53] for the domain adaptation. Further, a correlation based adversarial learning framework for domain adaptation is proposed by [54]. The Bayesian uncertainty matching is applied in [55] for adapting the classifier.
Recently, GSP [56] demonstrated a generative cross-domain learning framework via structure-preserving. They developed a cross-domain graph alignment to capture the intrinsic relationship across two domains. In DTA [57], adversarial dropout to enforced the cluster assumption on the target domain. It is based on the fact that the decision boundaries should be placed in low density regions in the feature space.
In contrast to all the previous works, the main contribution of the present work is to propose a curriculum based dropout discriminator. We show that through the proposed method, we are able to outperform state of the art domain adaptation techniques in a scalable way by using fewer number of parameters as compared to techniques such as MADA [8] and similar number of parameters as GRL [3].
3 Motivation
In the adversarial domain adaptation problem, the previous methods have used classical statistical inference in the discriminator. A single discriminator learns the source and target domain classification. Our hypothesis is that it may lead to overconfident inference and decisions which in turn may lead to challenges in learning invariant features. In the domain adaptation problem, data is generally structured in a multimodal distribution. Thus, a multiple discriminator approach is compelling [8], due to its capacity to capture multiple modes of the dataset. It also leads to solving the perennial problem of mode collapse (which GANs are infamous for) as multiple discriminators now learn to distinguish classes with different modes. The diversity of an ensemble of such discriminators reduces the random errors in prediction. The performance of an ensemble model rests on the number of entities in the ensemble. However, as the number of entities increase, the model parameters and complexity will increase. This is one of the primary bottlenecks of the ensemble based methods. The number of parameters in an algorithm is a significant factor in determining model efficiency.
To tackle the above problems, we propose a novel and efficient discriminator architecture by using Monte Carlo (MC) sampling [58]. We incorporate Bernoulli dropout in a single adversarial discriminator network, by dropping out a certain number of neurons from our discriminator with some probability d. This gives rise to a set of dynamic discriminators for every data sample. The main idea behind our method is to construct a training regime for the feature extractor in domain adaptation that consists of increasingly challenging tasks to generate domain invariant features. This allows the sophistication of the feature extractor to gradually increase throughout training, rather than aiming for full sophistication at the outset. This method is similar to that of curriculum in supervised learning, where one orders the training examples to be presented to a learning algorithm according to some measure of difficulty [45]. Despite the conceptual similarity, the methods are quite different. Under our approach, it is not the difficulty of the training examples presented to either network, but rather the capacity, and hence strength, of the discriminator network that is increased as the training progresses. The idea behind the use of a curriculum based dropout discriminator is to exploit the characteristics of several independent discriminators by consolidating them in order to achieve higher performance.
We do a curriculum based learning on these dropout discriminators. As the training proceeds, the number of discriminators sampled, increase, thereby boosting the variance of our model’s prediction. The proposed approach enforces the feature extractor network not to constrain the learned representations to satisfy a single discriminator, but, instead, to satisfy an ensemble of dynamic discriminators (composition is different across different discriminators). Instead of learning a point estimate (in case of MADA [8]), the feature extractor network of our proposed model learns a distribution, due to the ensemble effect of feedback from a set of dynamic discriminators. This approach leads to a more generalized feature extractor, promoting resemblance in learned representations of a class from different domains. The instinct behind incorporating dropout in our model is to warrant that neurons are not exclusively reliant on a precise set of other neurons to determine their outputs. Instead, each neuron relies on the agglomerate behavior of several other neurons, promoting generalization. By applying dropout on the discriminator, we obtain a set of entirely dynamic discriminators and hence the feature extractor cannot use the trick of relying on a specific type of discriminator or ensemble of discriminators to learn to generate representations to deceive the discriminator. Instead, it will now have to genuinely learn domain invariant representations. Thus, the feature extractor network is now guided by diverse feedback given to it by an ensemble of dynamic discriminators. All this increase in performance is obtained without compromising on the scalability and complexity front through our proposed model.
The other motivation behind the curriculum learning on the discriminator is based on the fact that each data point has a hidden hierarchy in class label. The data points can also be clustered in the form of their parental class label. For example, in the Ofice-31 dataset, the class category mobile phone and calculator can share the same cluster, as their visual appearance is similar as compared to other classes. Thus, in the proposed method, we increase the number of discriminators in curriculum fashion such that it starts to capture the top parent model (domain); later, it increases the discriminator to capture the more complex child class modes (domain with class category). The curriculum-based paradigm in the sampling of discriminators also enables the model to learn domain invariant representations systematically.
 |
 |
| (a) | (b) |
4 Proposed Adaptation Model
In the unsupervised domain adaptation problem, we consider that the source dataset has access to all its labels while there are no labels for the target dataset at the training time. We assume that comes from a source distribution and comes from a target distribution . We assume that there are source data points and unlabeled target data points. So has labeled examples and the target domain has unlabeled examples. Our underlying assumption is that both distributions are complex and unknown. Our model provides a deep neural network that enables learning of transferable feature representations and an adaptive classifier to reduce the shift in the joint distributions across domains, such that the target risk is minimized by jointly minimizing source risk and distribution discrepancy by adversarial domain adaptation where is assumed to be the joint distribution of target samples.
In this work, we employ a variant of GRL[3], where discriminator is modeled as an MC-dropout based ensemble. The feature extractor network consists of convolution layers to produce image embeddings. Both source and target feature extractors share the same parameters. The classifier network consists of fully connected layers. Only source embeddings are forwarded to the classifier network to predict the class label. The classifier network parameters () are updated only by the loss from source data samples. The discriminator receives both source and target embeddings. The parameters of the MC-dropout discriminator () are updated with domain classification loss. The feature extractor parameters () are updated by the gradients from the classifier network as well as by the reverse gradient of both source and target data samples from the dynamic set of the ensemble of discriminators. Detailed architecture is presented in Figure 2.
For the adaptation task, the feature extractor learns domain-invariant features with the help of MC-Dropout based discriminator. For each data sample that goes to the discriminator, we obtain the domain classification loss. These losses are backpropagated through respective Monte Carlo sampled dropout discriminators followed by gradient reversal layer. Hence, for every input, we obtain a distribution of gradients. The feature extractor is updated by a gradient from this distribution to generate domain invariant features. In a binary discriminator [3], we obtain a point estimate of the gradient for specific input. In the case of multi discriminator [8], we obtain an ensemble of the point estimates of gradients. The advantage of obtaining a distribution of gradients is that we get generalized learned representations robustly leading to domain invariant features. We propose Curriculum based Dropout Discriminator (CA), where we increase the number of MC samples as training proceeds in a paradigm similar to curriculum learning. However, in the other variant (A), we maintain a fixed number of MC sampled discriminators throughout the training.
4.1 Curriculum based Dropout Discriminator for Domain Adaptation (C A)
In CA, the distribution of gradients is obtained through a curriculum fashioned training, i.e., we increase the number of MC samples as training proceeds. The motivation behind increasing the number of MC samples is that, in the initial phase of the adaptation, the feature extractor learns the domain invariant features without considering the multi-mode structure of data. For this purpose, only a small number of discriminators is required. As the training advances, we expect the network to learn the domain invariant features along with its multi-modal structure. Thus, in the proposed model, we increase the MC samples of discriminator as training progress to obtain the domain invariant feature without losing its multi-mode structure. Given an input sample , we obtain feature embedding , by passing it through a feature extractor . These embeddings are further used to obtain the classification score and the domain classification score for each sample of discriminator , where . This sampling enables ensembles of discriminator at a given training stage. The curriculum learning of the discriminator does not rely on the difficulty of the training examples presented to either network, but rather the capacity, and hence strength, of the discriminator that is increased throughout the training. We construct an ordered set of sets of samples of discriminator increasing in numbers. More formally the set of discriminators is , where is a MC sampled discriminator. We can clearly see that the is a ordered set in terms of the capacity, where capacity of . Each discriminator is trained with same features for a given image . The cross-entropy loss is obtained using the domain labels of the input images for each discriminator. In contrast to multi-discriminator based domain adaptation, We do not consider any classifier’s predicated value to select the discriminators.
4.2 Fixed sampling based Dropout Discriminator for Domain Adaptation (A)
In this variant, we fix the number of MC sampled discriminators during the training. In this scenario, we obtain an ensemble of discriminators. We call this variant as a Dropout Discriminator for Domain Adaptation (A). This modification can be considered a more efficient version of the multi discriminator model. We experimented with different sampling values and obtained the best results when the number of samples is chosen close to the number of classes in the target dataset.
4.3 Loss Function
Our loss function is composed of classification loss and domain classification loss. Our classifier takes learned representations as input and predicts its label. Classification loss function is a cross-entropy loss. Dropout discriminator is expected to label (output) the source domain images as 0 and target domain images as 1. Domain classification loss is a binary cross entropy loss between the output of discriminator and the expected output. It is summed over the number of MC-sampled discriminators . is increased as the training proceeds in the case of CD3A model, whereas it is fixed for D3A model.
| (1) |
| (2) |
where if and if . The function is the feature extractor network with shared weights for source and target data ( and are denoted by common shared network ). is the trade-off parameter between the two objectives. is the classifier network and is the MC-sampled dropout discriminator. and represent source and target domains respectively. This loss function is generic and can easily be applied in other adversarial domain adaptation methods where a discriminator is used to learn the invariant representation. We have incorporated a state-of-the-art method iCAN [33], with the proposed dropout based adaptation method and achieved a better performance.
We generate the entities of ensemble via dropout. In contrast, previous works [8] use multiple discriminators; their number being equal to the number of classes in the dataset. It leads to an increase in the number of parameters employed in the discriminator which makes it unsuitable for datasets with a large number of classes. Also, due to our model’s parameters being significantly less, the data requirements are also quite low. This has been shown in Tabel 8, where we remove half of the source data and still obtain good accuracy. Also, MADA uses the predicted label probabilities to weigh the discriminator’s response. This is a drawback as it can lead to misleading corrections of the feature extractor network in case of wrong predictions by the label predictor (classifier). Our model doesn’t have such constraints making our discriminator even more powerful leading to better learning of domain invariant features by the feature extractor network. The codes are provided on the project page 111https://delta-lab-iitk.github.io/CD3A/.
5 Results and Analysis
5.1 Datasets
ImageCLEF Dataset:
ImageCLEF-2014 dataset consists of 3 domains: Caltech-256 (C), ILSVRC 2012 (I), and Pascal-VOC 2012 (P). There are 12 common classes, and each class has 50 samples.There is a total of 600 images in each domain. We evaluate models on all 6 transfer tasks: IP, PI, IC, CI, CP, and PC.
for both Alexnet architecture at Table 2 and Resnet architecture at Table 1.
Office-31 Dataset:
Office-31 [59] is a benchmark dataset for domain adaptation, comprising 4,110 images in 31 classes collected from three distinct domains: Amazon (A), Webcam (W) and DSLR (D). To enable unbiased evaluation, we evaluate all the methods on all 6 transfer tasks A W, D A, W A, A D , D W and W D for Alexnet architecture.
The performance is shown in Table 3.
Office-Home Dataset: We evaluated our model on the Office-Home dataset [60] for unsupervised domain adaptation. This dataset consists of four domains- Art (Ar), Clipart (Cl), Product (Pr) and Real-World (Rw). Each domain has 65 categories in common. The Art domain contains the artistic description of objects such as painting, sketches etc. The Clipart domain consists of a collection of clipart images. In the Product domain, images have no background. The Real-World domain consists of objects captured from a regular camera. We evaluated proposed model by considering the Art data as source dataset and remaining datasets as target dataset. So we have 3 adaptation tasks, Ar Cl, Ar Pr and Ar Rw. The performance is reported in the Table 4 and Table 5 for Alexnet and Resnet Architecture.
5.2 Results
We use pre-trained Alexnet [61] and ResNet-50 [62] architectures following the typical setting in unsupervised domain adaption for our base model. Table 3 summarizes results on Office31 dataset, Table 4 and Table 5results on Office-Home [60] for AlexNet and ResNet networks respectively. The Table 2 and Table 1 have results for the ImageClef dataset for AlexNet and ResNet networks respectively. In Table 1, we have shown the results using a state-of-the-art method iCAN [33], where collaborative learning is applied using several domain classifiers. We have incorporated the dropout based curriculum learning on the last domain classifier. We can observe that by using the CD3A method on iCAN [33] we can have around 1% average improvement.
MSDN [63] shows comparable performance with proposed model on ImageClef dataset using AlexNet architecture and by aligning labeled source centroid and pseudo-labeled target centroid. But for the Office-31 dataset, the proposed model obtains better performance as compared to MSDN. This shows that we can have a better domain adaptation model without relying on the prediction of the classifier for the target domain.
We obtained state-of-the-art results on all the datasets. It is noteworthy that the proposed model boosts the classification accuracies substantially on hard transfer tasks, e.g., A D, A W, etc. where the source and target domains are substantially different. On average, we obtain considerably improved accuracies and statistically significant results as shown further.
| Method | IP | PI | IC | C I | CP | PC | Average |
|---|---|---|---|---|---|---|---|
| ResNet [62] | 74.8 | 83.9 | 91.5 | 78.0 | 65.5 | 91.2 | 80.7 |
| DAN [13] | 75.0 | 86.2 | 93.3 | 84.1 | 69.8 | 91.3 | 83.3 |
| RTN [64] | 75.6 | 86.8 | 95.3 | 86.9 | 72.7 | 92.2 | 84.9 |
| GRL [3] | 75.0 | 86.0 | 96.2 | 87.0 | 74.3 | 91.5 | 85.0 |
| JAN [20] | 76.8 | 88.0 | 94.7 | 89.5 | 74.2 | 91.7 | 85.8 |
| MADA [8] | 75.0 | 87.9 | 96.0 | 88.8 | 75.2 | 92.2 | 85.8 |
| CDAN [65] | 77.2 | 88.3 | 98.3 | 90.7 | 76.7 | 94.0 | 87.5 |
| JADA [51] | 78.2 | 90.1 | 95.9 | 90.8 | 76.8 | 94.1 | 87.7 |
| CAT [52] | 76.7 | 89.0 | 94.5 | 89.8 | 74.0 | 93.7 | 86.3 |
| GRL[3]+CAT [52] | 77.2 | 91.0 | 95.5 | 91.3 | 75.3 | 93.6 | 87.3 |
| RDTL [53] | 78.3 | 89.7 | 95.3 | 91.5 | 77.2 | 92.3 | 87.4 |
| SPCAN [66] | 79.0 | 91.1 | 95.5 | 92.9 | 79.4 | 91.3 | 88.2 |
| iCAN [33] | 79.5 | 89.7 | 94.7 | 89.9 | 78.5 | 92.0 | 87.4 |
| D3A(12) | 77.1 | 89.3 | 95.2 | 91.8 | 79.4 | 93.6 | 88.0 |
| CD3A | 77.5 | 88.7 | 96.8 | 93.2 | 78.3 | 94.7 | 88.2 |
| iCAN [33]+CD3A | 77.7 | 90.1 | 96.7 | 92.4 | 78.3 | 95.0 | 88.4 |
| Method | IP | PI | IC | CI | CP | PC | Average |
|---|---|---|---|---|---|---|---|
| AlexNet [61] | 66.2 | 70.0 | 84.3 | 71.3 | 59.3 | 84.5 | 73.9 |
| DAN[13] | 67.3 | 80.5 | 87.7 | 76.0 | 61.6 | 88.4 | 76.9 |
| GRL [3] | 66.5 | 81.8 | 89.0 | 79.8 | 63.5 | 88.7 | 78.2 |
| RTN[64] | 67.4 | 82.3 | 89.5 | 78.0 | 63.0 | 90.1 | 78.4 |
| MADA [8] | 68.3 | 83.0 | 91.0 | 80.7 | 63.8 | 92.2 | 79.8 |
| MSDN[63] | 67.3 | 82.8 | 91.5 | 81.7 | 65.3 | 91.2 | 80.0 |
| A(12) | 69.1 | 80.9 | 91.0 | 81.5 | 66.2 | 90.0 | 79.8 |
| CD3A | 69.3 | 81.5 | 91.3 | 81.6 | 65.9 | 90.2 | 80.0 |
| Method | AW | DW | WD | A D | DA | WA | Avg |
|---|---|---|---|---|---|---|---|
| Alexnet [61] | 60.6 | 95.0 | 99.5 | 64.2 | 45.5 | 48.3 | 68.8 |
| MMD[12] | 61.0 | 95.0 | 98.5 | 64.9 | 47.2 | 49.4 | 69.3 |
| RTN[64] | 73.3 | 96.8 | 99.6 | 71.0 | 50.5 | 51.0 | 74.1 |
| DAN[13] | 68.5 | 96.0 | 99.0 | 66.8 | 50.0 | 49.8 | 71.7 |
| GRL [3] | 73.0 | 96.4 | 99.2 | 72.3 | 52.4 | 50.4 | 74.1 |
| JAN [67] | 75.2 | 96.6 | 99.6 | 72.8 | 57.5 | 56.3 | 76.3 |
| CDAN[65] | 77.9 | 96.9 | 100.0 | 74.6 | 55.1 | 57.5 | 77.0 |
| MADA[8] | 78.5 | 99.8 | 100.0 | 74.1 | 56.0 | 54.5 | 77.1 |
| IDDA[68] | 82.2 | 99.8 | 100.0 | 82.4 | 54.1 | 52.5 | 78.5 |
| GKE[69] | 78.6 | 96.7 | 100.0 | 74.9 | 63.3 | 60.1 | 78.9 |
| MSDN[63] | 80.5 | 96.9 | 99.9 | 74.5 | 62.5 | 60.0 | 79.1 |
| DAN[70] | 73.9 | 96.8 | 99.6 | 71.7 | 50.0 | 51.4 | 73.9 |
| Entro[55] | 78.9 | - | - | 77.8 | 56.6 | 57.4 | - |
| CAADA[54] | 80.2 | 97.1 | 99.2 | 77.7 | 58.1 | 57.4 | 78.3 |
| A(31) | 79.0 | 97.7 | 100.0 | 79.4 | 58.2 | 55.3 | 78.3 |
| CD3A | 82.3 | 99.8 | 100.0 | 81.1 | 58.2 | 55.6 | 79.5 |
| Method | ArtClip | ArtProduct | ArtReal-World | Average |
| Alexnet[61] | 26.4 | 32.6 | 41.3 | 33.43 |
| DAN[13] | 31.7 | 43.2 | 55.1 | 43.33 |
| GRL[3] | 36.4 | 45.2 | 54.7 | 45.43 |
| JAN[67] | 35.5 | 46.1 | 57.7 | 46.43 |
| CDAN [65] | 38.1 | 48.7 | 60.3 | 49.03 |
| IDDA[68] | 38.9 | 50.7 | 58.8 | 49.46 |
| GCAN [71] | 36.4 | 47.3 | 61.1 | 48.27 |
| CAADA [54] | 35.3 | 46.2 | 56.6 | 46.03 |
| D3A(1) | 36.5 | 46.8 | 57.2 | 46.83 |
| D3A(65) | 38.9 | 51.8 | 57.5 | 49.40 |
| D3A(100) | 38.2 | 50.7 | 59.5 | 49.46 |
| CD3A | 38.5 | 52.1 | 59.2 | 49.93 |
| Method | Art Clip | Art Product | Art Real-World | Average |
|---|---|---|---|---|
| ResNet [62] | 34.9 | 50.0 | 58.0 | 47.63 |
| DAN[13] | 43.6 | 57.0 | 67.9 | 56.17 |
| GRL[3] | 45.6 | 59.3 | 70.1 | 58.33 |
| JAN[67] | 45.9 | 61.2 | 68.9 | 58.67 |
| CDAN [65] | 50.6 | 65.9 | 73.4 | 63.33 |
| ALIC [72] | 45.8 | 68.5 | 75.1 | 63.13 |
| CD3A | 53.3 | 69.8 | 74.9 | 66.00 |
6 Analysis
6.1 Curriculum v/s Fixed sampling:
We have plotted the accuracy as a function of the number of MC samples for both the models, curriculum-based sampling (CD3A) and fixed sampling
(D3A) in Figure 4 (a). We can clearly observe that in the case of D3A, the performance increases as we increase the number of MC sampled discriminators, but after some samples, the performance starts to deteriorate. While in case of CD3A, the performance of model saturates after certain epochs. From the Figure We can also observe that CD3A outperforms D3A.
6.2 Model complexity comparison with MADA:
The proposed CD3A model uses one discriminator(ensemble using dropout) whereas MADA uses as many discriminators as are the number of classes. Therefore, CD3A has very few parameters as compared to MADA even for datasets with a small number of classes. For instance, in case of Office-31 dataset, MADA has 31 discriminators compared to CD3A, which has only one discriminator. MADA has 98M parameters, while CD3A has 59M parameters for Office-31 dataset. If we further increase the class size, the number of parameters in MADA increases (by 1.3M for every class label), but CD3A will have constant number of parameters (59M).
6.3 Feature visualization:
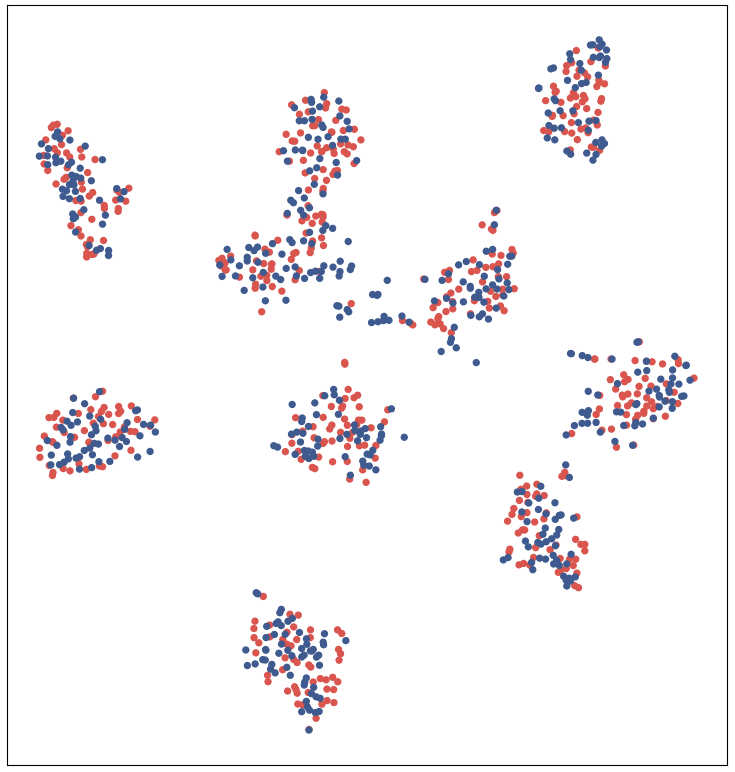
The adaptability of target to source features can be visualized using the t-SNE embeddings of image features. We follow similar setting as in [3] to plot t-SNE embeddings for AW adaptation task in Figure 12 (a) and (b). From the plot, we observe that adapted features (CD3A) are more domain invariant than the features adapted with GRL. We also plotted the tSNE visualization for ImageClef data set on the tasks C I, I C, I P, P I, P C, and C P for Alexnet architecture in the Figure 6, 8, 9, 11, 10 and 7 respectively. We can observe that the tSNE plots are more class discriminative and domain invariant for the proposed model than the source only and GRL model [3].
 |
| (a) SSA Plot for AD | (b) SSA Plot for AW |
|---|---|
 |

|
6.4 Statistical significance analysis:
We analyzed statistical significance [73] for our CA and A model against GRL [3] and source only method for the domain adaptation tasks. The Critical Difference (CD) for Nemenyi test depends upon the given confidence level (0.05 in our case) for average ranks and number of tested datasets. If the difference in the rank of the two methods lies within CD (our case CD = 0.6051), then they are not significantly different. Figure 4(a) visualizes the posthoc analysis using the CD diagram for AD and (b) visualizes for AW. From the figures, it is clear that our CA model is better and significantly different from other methods.
6.5 Proxy-- Distance
-distance as a measure of cross domain discrepancy [74], which, together with the source risk, will bound the target risk. The proxy -distance is defined as , where is the generalization error of a classifier(e.g. kernel SVM) trained on the binary task of discriminating source and target. Figure 12(c) and (d) shows on tasks A D and A W, with features of source only model [61], GRL [3], MADA [8] and proposed model CA. We observe that calculated using CA model features is much smaller than calculated using source only model, GRL and MADA features, which suggests that representations learned via CA can reduce the cross-domain gap more effectively.
For the ImageClef dataset, the proxy distance is plotted in the Figures 14, 13 and 15 for I P, I C, P I, P C, C I and C P adaptation task and compared to source only model and GRL [3]. These plots are also evident that the proposed model can reduce the cross-domain gap more effectively.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
6.6 Choosing (tradeoff parameter)
We chose based on the cross-validation accuracy of our model ( keeping dropout value d=0.5). The performance on various values of is reported in Table 6. We observe that a classifier’s accuracy first increases and then decreases as varies from 0.1 to 0.9. The reason is that for a larger value of , the features are domain invariant, but they lost the class discriminative property, so the classifier does not perform well. Similarly, for the lower value of , the features are biased toward the domain, and hence the classifier produces lower accuracy. It shows that choosing the value of is a trade-off between domain invariance and class descriptiveness. In all our experiments in the main paper, we chose = 0.5.
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
| AW | 76.5 | 79.4 | 79.7 | 80.8 | 82.3 | 81.1 | 80.1 | 79.1 | 78.8 |
6.7 Choosing (Dropout value)
The dropout value shows the independence between the sampled discriminator. As we increase the dropout value, the probability of neurons shared by each discriminator decreases. For example, if the dropout value is set to 0, all the discriminators shared the same neurons. If we further increase it, the probability of sharing neurons of each sample increases. We have experimented with different values of dropout and reported cross-validation accuracy of our model(keeping =0.5) in Table 7. In domain adaption, we do not want all the discriminators to have shared weights( it is reduced to a single discriminatory if all the weights are shared between all the sampled discriminators. From a limited capacity discriminator (fixed neurons), creating independent neurons of discriminators can lose the capability of each discriminator.
| Dropout Value | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|
| AW | 77.9 | 79.1 | 78.9 | 78.1 | 82.3 | 78.6 | 78.6 | 80.6 | 77.1 |
6.8 Data Requirements
In many practical scenarios, we have limited labeled source data, making it hard to adapt it to the target domain. The reason is that model does not get enough source data to obtain domain discrepancy with a large target dataset. For example, in and adaptation task, the performance is very low as compared to the reverse adaptation task and , because in that the source datasets and are smaller as compared to target dataset . To show the proposed model’s effectiveness in such scenarios where source data is small, we evaluated our model in such constraints. In this setting, we randomly remove half of the data from each source class. We report the performance of fixed samples based model (D3A) for 31 samples in Office-31 dataset in Table 8. We can observe that the proposed model also performs well compared to baseline and state-of-the-art methods in the same setting.
| Method | AW | DW | WD | AD | DA | WA | Avg |
|---|---|---|---|---|---|---|---|
| Alexnet [61] | 57.61 | 85.5 | 84.13 | 59.63 | 47.29 | 44.76 | 58.14 |
| GRL [3] | 68.93 | 85.03 | 85.3 | 66.45 | 52.32 | 46.05 | 67.34 |
| MADA [8] | 72.83 | 87.54 | 82.93 | 73.79 | 55.41 | 54.62 | 71.19 |
| D3A(31) | 74.84 | 90.06 | 86.7 | 78.91 | 58.78 | 57.58 | 74.47 |
| CD3A(31) | 75.61 | 91.42 | 86.9 | 79.53 | 58.92 | 58.26 | 75.11 |
6.9 Effect of number of MC samples in D3A
The number of Monte Carlo samples discriminators in D3A method denotes that these many sampled discriminators ( from a single discriminator) are used for the adaptation. To understand the effect of the number of Monte Carlo Samples on classification accuracies, we experimented with different sample sizes in Alexnet architecture and the results have been provided in Table 10 and Table 9 for Office-Home and Office-31 datasets respectively. In both these cases, interestingly, the accuracy is higher in case of number of Monte-Carlo samples being taken approximately equal to the number of classes in the dataset.
We can observe that this analysis also agrees with the idea of MADA [8]. The major difference is that they have separate discriminators, so have the large model size; while we obtain multi-discriminator from a single dropout discriminator, the proposed model is efficient and smaller than it.
| Method | AW | DW | W D | AD | DA | WA | Avg |
| D3A(1) | 70.5 | 96.4 | 99.4 | 66.1 | 52.4 | 50.5 | 70.6 |
| D3A(10) | 76.4 | 97.3 | 99.9 | 77.8 | 58.3 | 54.8 | 77.6 |
| D3A(31) | 79.0 | 97.7 | 100 | 79.4 | 58.2 | 55.3 | 78.3 |
| D3A(100) | 78.9 | 97.9 | 100 | 78.1 | 55.7 | 55.0 | 77.4 |
| Sample Size | Ar Cl | Ar Pr | Ar RW |
|---|---|---|---|
| D3A(1) | 36.5 | 46.8 | 57.2 |
| D3A(10) | 37.9 | 48.16 | 55.9 |
| D3A(50) | 38.8 | 48.2 | 57.3 |
| D3A(65) | 38.9 | 51.8 | 57.5 |
| D3A(100) | 38.2 | 50.7 | 59.5 |
| D3A(200) | 38.1 | 47.1 | 58.1 |
| D3A(300) | 36.5 | 46.8 | 55.5 |
6.10 Effect of number of increasing rate of MC samples in CD3A
To understand the effect of the change of curriculum learning rate (rate for increasing number of Monte Carlo Samples) on classification accuracies, we experimented with different increasing rate of sample sizes in Alexnet architecture and the results have been provided in Table 11 for Office-31 dataset. We increase the number of discriminators sampled after every epochs by 1. We have experimented with and obtained the best results for .
| Method | A W | A D | D A | W A |
|---|---|---|---|---|
| 1 MC Sample per 2 Epoch | 76.22 | 75.3 | 54.10 | 54.24 |
| 1 MC Sample per 5 Epoch | 77.86 | 79.92 | 57.36 | 54.49 |
| 1 MC Sample per 10 Epoch | 82.26 | 81.12 | 58.18 | 55.56 |
6.11 Discriminator performance
In the adversarial domain adaptation task, the aim of the feature extractor is to confuse the discriminator for source and target classification. In Figure 16, we can see that after training, the source and target domains produce the same loss. It indicates that the model produces features, which are indistinguishable by the discriminator.

7 Conclusion
In this paper, we provide a simple approach to obtain an improved discriminator for adversarial domain adaptation. We specifically show that the use of sampling-based ensemble results in an improved discriminator without increasing the number of parameters. The main reason for this improvement is that the features are made domain invariant based on a distribution of observations as against a single point estimate. Our approach based on curriculum dropout suggests that we are able to obtain an improved discriminator that is stable and improves the feature invariance learnt. We compare our method with standard baselines and provide a thorough empirical analysis of the method. We further observe through visualization that domain adapted features do result in domain invariant feature representations. Using the discriminator obtained through curriculum based dropout to solve domain adaptation is a promising direction, which we have initiated through this work.
References
References
- [1] O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, A. C. Berg, L. Fei-Fei, ImageNet Large Scale Visual Recognition Challenge, International Journal of Computer Vision (IJCV) 115 (3) (2015) 211–252. doi:10.1007/s11263-015-0816-y.
- [2] A. Torralba, A. A. Efros, Unbiased look at dataset bias, in: Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on, IEEE, 2011, pp. 1521–1528.
- [3] Y. Ganin, V. Lempitsky, Unsupervised domain adaptation by backpropagation, in: International Conference on Machine Learning, 2015, pp. 1180–1189.
- [4] E. Tzeng, J. Hoffman, K. Saenko, T. Darrell, Adversarial discriminative domain adaptation, in: Computer Vision and Pattern Recognition (CVPR), Vol. 1, 2017, p. 4.
- [5] J. Hoffman, E. Tzeng, T. Park, J.-Y. Zhu, P. Isola, K. Saenko, A. Efros, T. Darrell, Cycada: Cycle-consistent adversarial domain adaptation, in: Proceedings of the 35th International Conference on Machine Learning, 2018.
- [6] J. Shen, Y. Qu, W. Zhang, Y. Yu, Adversarial representation learning for domain adaptation, arXiv preprint arXiv:1707.01217.
- [7] V. K. Kurmi, V. K. Subramanian, V. P. Namboodiri, Informative discriminator for domain adaptation, Image and Vision Computing 111 (2021) 104180.
- [8] Z. Pei, Z. Cao, M. Long, J. Wang, Multi-adversarial domain adaptation, in: Thirty-Second AAAI Conference on Artificial Intelligence, 2018.
- [9] K. Hara, D. Saitoh, H. Shouno, Analysis of dropout learning regarded as ensemble learning, in: International Conference on Artificial Neural Networks, Springer, 2016, pp. 72–79.
- [10] V. K. Kurmi, V. Bajaj, V. K. Subramanian, V. P. Namboodiri, Curriculum based dropout discriminator for domain adaptation, BMVC.
- [11] J. Bromley, I. Guyon, Y. LeCun, E. Säckinger, R. Shah, Signature verification using a” siamese” time delay neural network, in: Advances in Neural Information Processing Systems, 1994, pp. 737–744.
- [12] E. Tzeng, J. Hoffman, N. Zhang, K. Saenko, T. Darrell, Deep domain confusion: Maximizing for domain invariance, arXiv preprint arXiv:1412.3474.
- [13] M. Long, Y. Cao, J. Wang, M. Jordan, Learning transferable features with deep adaptation networks, in: International Conference on Machine Learning, 2015, pp. 97–105.
- [14] K. Saito, K. Watanabe, Y. Ushiku, T. Harada, Maximum classifier discrepancy for unsupervised domain adaptation, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 3723–3732.
- [15] Z. Zhang, M. Wang, Y. Huang, A. Nehorai, Aligning infinite-dimensional covariance matrices in reproducing kernel hilbert spaces for domain adaptation, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 3437–3445.
- [16] B. Sun, K. Saenko, Deep coral: Correlation alignment for deep domain adaptation, in: European Conference on Computer Vision, Springer, 2016, pp. 443–450.
- [17] B. Sun, J. Feng, K. Saenko, Correlation alignment for unsupervised domain adaptation, Domain Adaptation in Computer Vision Applications (2017) 153.
- [18] B. Sun, J. Feng, K. Saenko, Return of frustratingly easy domain adaptation., in: AAAI, Vol. 6, 2016, p. 8.
- [19] J. Shen, Y. Qu, W. Zhang, Y. Yu, Wasserstein distance guided representation learning for domain adaptation., in: AAAI, 2018.
- [20] M. Long, H. Zhu, J. Wang, M. I. Jordan, Deep transfer learning with joint adaptation networks, in: International Conference on Machine Learning, 2017, pp. 2208–2217.
- [21] A. Rozantsev, M. Salzmann, P. Fua, Beyond sharing weights for deep domain adaptation, IEEE Transactions on Pattern Analysis and Machine Intelligence.
- [22] E. Tzeng, J. Hoffman, T. Darrell, K. Saenko, Simultaneous deep transfer across domains and tasks, in: Computer Vision (ICCV), 2015 IEEE International Conference on, IEEE, 2015, pp. 4068–4076.
- [23] K. Saito, Y. Ushiku, T. Harada, K. Saenko, Adversarial dropout regularization.
- [24] J. Hoffman, E. Tzeng, T. Park, J.-Y. Zhu, P. Isola, K. Saenko, A. Efros, T. Darrell, Cycada: Cycle-consistent adversarial domain adaptation.
- [25] K. Bousmalis, N. Silberman, D. Dohan, D. Erhan, D. Krishnan, Unsupervised pixel-level domain adaptation with generative adversarial networks, in: The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Vol. 1, 2017, p. 7.
- [26] J. Zhang, Z. Ding, W. Li, P. Ogunbona, Importance weighted adversarial nets for partial domain adaptation, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 8156–8164.
- [27] Q. Chen, Y. Liu, Z. Wang, I. Wassell, K. Chetty, Re-weighted adversarial adaptation network for unsupervised domain adaptation, 2018.
- [28] H. Li, S. J. Pan, S. Wang, A. C. Kot, Domain generalization with adversarial feature learning, in: Proc. IEEE Conf. Comput. Vis. Pattern Recognit.(CVPR), 2018.
- [29] V. K. Kurmi, S. Kumar, V. P. Namboodiri, Attending to discriminative certainty for domain adaptation, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 491–500.
- [30] K. Bousmalis, N. Silberman, D. Dohan, D. Erhan, D. Krishnan, Unsupervised pixel-level domain adaptation with generative adversarial networks, in: The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Vol. 1, 2017, p. 7.
- [31] Y. Choi, M. Choi, M. Kim, Stargan: Unified generative adversarial networks for multi-domain image-to-image translation.
- [32] V. K. Kurmi, V. K. Subramanian, V. P. Namboodiri, Domain impression: A source data free domain adaptation method, in: Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, 2021, pp. 615–625.
- [33] W. Zhang, W. Ouyang, W. Li, D. Xu, Collaborative and adversarial network for unsupervised domain adaptation, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 3801–3809.
- [34] R. Keshari, R. Singh, M. Vatsa, Guided dropout, in: Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 33, 2019, pp. 4065–4072.
- [35] S. Park, K. Song, M. Ji, W. Lee, I.-C. Moon, Adversarial dropout for recurrent neural networks, in: Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 33, 2019, pp. 4699–4706.
- [36] K. Saito, Y. Ushiku, T. Harada, K. Saenko, Adversarial dropout regularization, arXiv preprint arXiv:1711.01575.
- [37] P. Guo, S. Sun, L. Xie, Unsupervised adaptation with adversarial dropout regularization for robust speech recognition., in: INTERSPEECH, 2019, pp. 749–753.
- [38] B. Lakshminarayanan, A. Pritzel, C. Blundell, Simple and scalable predictive uncertainty estimation using deep ensembles, in: Advances in Neural Information Processing Systems, 2017, pp. 6402–6413.
- [39] Y. Gal, Z. Ghahramani, Dropout as a bayesian approximation: Representing model uncertainty in deep learning, in: international conference on machine learning, 2016, pp. 1050–1059.
- [40] R. M. Neal, Bayesian learning for neural networks, Vol. 118, Springer Science & Business Media, 2012.
- [41] T. Nguyen, T. Le, H. Vu, D. Phung, Dual discriminator generative adversarial nets, in: Advances in Neural Information Processing Systems, 2017, pp. 2670–2680.
- [42] A. Ghosh, V. Kulharia, V. Namboodiri, P. H. Torr, P. K. Dokania, Multi-agent diverse generative adversarial networks, CoRR, abs/1704.02906 6 (2017) 7.
- [43] I. Durugkar, I. Gemp, S. Mahadevan, Generative multi-adversarial networks, ICLR.
- [44] Y. Saatci, A. G. Wilson, Bayesian gan, in: Advances in neural information processing systems, 2017, pp. 3622–3631.
- [45] Y. Bengio, J. Louradour, R. Collobert, J. Weston, Curriculum learning, in: Proceedings of the 26th annual international conference on machine learning, ACM, 2009, pp. 41–48.
- [46] R. Sharma, S. Barratt, S. Ermon, V. Pande, Improved training with curriculum gans, arXiv preprint arXiv:1807.09295.
- [47] P. Morerio, J. Cavazza, R. Volpi, R. Vidal, V. Murino, Curriculum dropout, in: Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 3544–3552.
- [48] Y. Zhang, P. David, B. Gong, Curriculum domain adaptation for semantic segmentation of urban scenes, in: Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 2020–2030.
- [49] D. Weinshall, G. Cohen, D. Amir, Curriculum learning by transfer learning: Theory and experiments with deep networks, in: International Conference on Machine Learning, 2018, pp. 5235–5243.
- [50] Y. Shu, Z. Cao, M. Long, J. Wang, Transferable curriculum for weakly-supervised domain adaptation.
-
[51]
S. Li, C. H. Liu, B. Xie, L. Su, Z. Ding, G. Huang,
Joint adversarial domain
adaptation, in: Proceedings of the 27th ACM International Conference on
Multimedia, MM ’19, ACM, New York, NY, USA, 2019, pp. 729–737.
doi:10.1145/3343031.3351070.
URL http://doi.acm.org/10.1145/3343031.3351070 - [52] Z. Deng, Y. Luo, J. Zhu, Cluster alignment with a teacher for unsupervised domain adaptation, in: The IEEE International Conference on Computer Vision (ICCV), 2019.
- [53] S. Wang, L. Zhang, Regularized deep transfer learning: When cnn meets knn, IEEE Transactions on Circuits and Systems II: Express Briefs.
- [54] M. M. Rahman, C. Fookes, M. Baktashmotlagh, S. Sridharan, Correlation-aware adversarial domain adaptation and generalization, Pattern Recognition (2019) 107124.
-
[55]
J. Wen, N. Zheng, J. Yuan, Z. Gong, C. Chen,
Bayesian uncertainty
matching for unsupervised domain adaptation, in: Proceedings of the 28th
International Joint Conference on Artificial Intelligence, IJCAI’19, AAAI
Press, 2019, pp. 3849–3855.
URL http://dl.acm.org/citation.cfm?id=3367471.3367576 - [56] H. Xia, Z. Ding, Structure preserving generative cross-domain learning, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 4364–4373.
- [57] S. Lee, D. Kim, N. Kim, S.-G. Jeong, Drop to adapt: Learning discriminative features for unsupervised domain adaptation, in: Proceedings of the IEEE International Conference on Computer Vision, 2019, pp. 91–100.
- [58] N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever, R. Salakhutdinov, Dropout: a simple way to prevent neural networks from overfitting, The Journal of Machine Learning Research 15 (1) (2014) 1929–1958.
- [59] K. Saenko, B. Kulis, M. Fritz, T. Darrell, Adapting visual category models to new domains, in: European conference on computer vision, Springer, 2010, pp. 213–226.
- [60] H. Venkateswara, J. Eusebio, S. Chakraborty, S. Panchanathan, Deep hashing network for unsupervised domain adaptation, in: Proc. CVPR, 2017, pp. 5018–5027.
- [61] A. Krizhevsky, I. Sutskever, G. E. Hinton, Imagenet classification with deep convolutional neural networks, in: Advances in neural information processing systems, 2012.
- [62] K. He, X. Zhang, S. Ren, J. Sun, Deep residual learning for image recognition, in: Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
- [63] S. Xie, Z. Zheng, L. Chen, C. Chen, Learning semantic representations for unsupervised domain adaptation, in: International Conference on Machine Learning, 2018, pp. 5419–5428.
- [64] M. Long, H. Zhu, J. Wang, M. I. Jordan, Unsupervised domain adaptation with residual transfer networks, in: Advances in Neural Information Processing Systems, 2016, pp. 136–144.
- [65] M. Long, Z. Cao, J. Wang, M. I. Jordan, Conditional adversarial domain adaptation, in: Advances in Neural Information Processing Systems, 2018, pp. 1640–1650.
- [66] W. Zhang, D. Xu, W. Ouyang, W. Li, Self-paced collaborative and adversarial network for unsupervised domain adaptation, IEEE Transactions on Pattern Analysis and Machine Intelligence.
- [67] M. Long, H. Zhu, J. Wang, M. I. Jordan, Deep transfer learning with joint adaptation networks, in: International Conference on Machine Learning, 2017, pp. 2208–2217.
- [68] V. K. Kurmi, V. P. Namboodiri, Looking back at labels: A class based domain adaptation technique, in: International Joint Conference on Neural Networks (IJCNN), 2019.
- [69] H. Wu, Y. Yan, Y. Ye, M. K. Ng, Q. Wu, Geometric knowledge embedding for unsupervised domain adaptation, Knowledge-Based Systems (2019) 105155.
- [70] M. Long, Y. Cao, Z. Cao, J. Wang, M. I. Jordan, Transferable representation learning with deep adaptation networks, IEEE transactions on pattern analysis and machine intelligence.
- [71] X. Ma, T. Zhang, C. Xu, Gcan: Graph convolutional adversarial network for unsupervised domain adaptation, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 8266–8276.
- [72] X. Zhao, S. Wang, Adversarial learning and interpolation consistency for unsupervised domain adaptation, IEEE Access 2019.
- [73] J. Demšar, Statistical comparisons of classifiers over multiple data sets, Journal of Machine learning research 7 (Jan) (2006) 1–30.
- [74] S. Ben-David, J. Blitzer, K. Crammer, A. Kulesza, F. Pereira, J. W. Vaughan, A theory of learning from different domains, Machine learning 79 (1) (2010) 151–175.


