Exploring compact binary populations with the Einstein Telescope

Belczynski et al. (2020) generated a broad set of models of compact binary systems with an upgraded version of population synthesis code StarTrack (Belczynski et al., 2002, 2008). We use the model M30.B to generate our population of compact binaries originating from Pop I+II stars. The characteristic features of this model are described in detail in (Belczynski et al., 2020) and can we summarise them as follows: (i) Supernova engine model for NS and BH mass: This model uses a rapid supernova engine model as mentioned in (Fryer et al., 2012). It creates a mass gap in the range $(2-5)M_{\odot}$ between NSs and BHs. For this model, the minimum BH mass is assumed to be $2.5M_{\odot}$; (ii) Pair-instability supernovae (PSNs) and pair-instability pulsation supernovae (PPSNs): this model allows PSNs for stars with He core mass in the range $(65-135)M_{\odot}$, thus entirely disrupting massive stars, while for the low-mass stars with He core mass in the range $(40-65)M_{\odot}$, it allows weak PPSNs, resulting in only up to 50% of mass loss calculated by (Leung et al., 2019), so that in this model, the maximum mass of a post PPSN star may reach $55.6M_{\odot}$; (iii) Neutrino mass loss: this model allows 1% neutrino mass loss to all BHs, while it allows 10% neutrino mass loss at NS formation; (iv) Natal kicks: this model assigns low natal BH kicks for low-mass BHs and no natal kicks for high-mass BHs. High kicks are assigned to NSs; (v) Accretion: in this model it is assumed that 50% of mass lost by the donor during Roche lobe overflow (RLOF) is accreted on to the companion star if the companion star in not a compact object. Accretion on compact objects (NSs or BHs) is allowed to be at a super-Eddington rate, as presented by (Mondal et al., 2020) A 5% rate of Bondi-Hoyle accretion is allowed onto NSs and BHs during CE evolution; and (vi) Winds: the model uses the massive star winds (Vink et al., 2001) in addition to luminous blue variable (LBV) winds (Belczynski et al., 2010). It is assumed that LBV mass loss is independent of metallicity. In the case of Wolf–Rayet (W-R) stars, the model assumes a prescription that is a combination of the Hamann & Koesterke (1998) wind rate estimate, which takes into account W-R wind clumping, and Vink & de Koter (2005) wind metallicity dependence.

This model is obtained from the StarTrack site³³3http://www.syntheticuniverse.org/ and contains result from 32 simulations of binary evolution with various metallicities $Z_{i}$, where $i=(1:32)$. The metallicity grid values used in the model are :

Each simulation is performed with the same initial conditions and is a result of simulating the same number (2 million) of massive binaries.

Belczynski et al. (2017) generated two models for the population of compact binary systems from the first, metal-free Pop III stars in the Universe using the population synthesis code StarTrack (Belczynski et al., 2002, 2008). They approximated the evolution of these Pop III stars with their metallicity model of

assuming no mass loss via stellar winds, since mass loss in stellar wind is expected to be negligible for massive Pop III stars (Baraffe et al., 2001). The radial expansion of the $Z=0.0001$ metallicity model is constrained to match the upper limit of expansion of $Z=0$ stars using the evolutionary model for Pop III stars calculated by (Marigo et al., 2001).

The initial conditions of the Pop III stars were defined based on the models obtained by (Ryu et al., 2016) using N-body simulation. Two models were chosen representing two different sizes of a gas cloud (mini-halo). These two models considered the formation of Pop III stars in mini haloes of sizes $\sim 2000$ AU and $10-20$ AU. For our analysis we use the results from the model FS1 (Belczynski et al., 2017), which assumes the formation of Pop III stars from a mini halo of size $\sim 2000$ AU (Stacy & Bromm, 2013). Following the parameters specified by (Stacy & Bromm, 2013), the number density of the gas medium is chosen to be $10^{6}\rm{cm}^{-3}$. The resulting population of metal-free binaries (initial mass function, mass ratio, orbital separations, and eccentricities) are presented in detail in Belczynski et al. (2017). The population was taken from the StarTrack⁴⁴4http://www.syntheticuniverse.org/ website, which hosts the results of StarTrack simulations.

For data pertaining to merging BBHs produced by GCs, we made use of the results from MOCCA-Survey Database I (Askar et al., 2017). This database comprises about 2000 simulated GC models that are characterised by different initial parameters. The long-term evolution of these cluster models was carried out using the MOCCA code (Hypki & Giersz, 2013; Giersz et al., 2013). To compute the dynamical evolution of a spherically symmetrical star cluster, the MOCCA code uses the orbit-averaged Monte Carlo treatment for relaxation (Hénon, 1971; Stodolkiewicz, 1986; Giersz, 2001). To determine the outcome of binary-single and binary-binary encounters, it uses the FEWBODY code (Fregeau et al., 2004), which is a direct N-body integrator for small-N encounters. For stellar and binary evolution of stars, the version of MOCCA used in (Askar et al., 2017) utilised the prescriptions proved by the (SSE) and binary (BSE) codes (Hurley et al., 2000, 2002). MOCCA also uses realistic treatment for the escape process in tidally limited star clusters as described by (Fukushige & Heggie, 2000).

The 2000 star cluster models in MOCCA-Survey Database I had a different initial number of objects, metallicities, binary fractions, central densities, half-masses, and tidal radii (see Table 1 in (Askar et al., 2017)). The initial stellar masses in these star cluster models are sampled from the initial mass function given by (Kroupa, 2001), and have values between $0.08\ M_{\odot}$ and$100\ M_{\odot}$. For each initial model in MOCCA-Survey Database I, two models were simulated with different prescriptions for BH natal kicks. In one case, the BH masses and natal kicks are computed using the mass fallback prescription from (Belczynski et al., 2002). In the other case, the BHs are given the same natal kicks as NSs, which follow a Maxwellian distribution with $\sigma=265\,\text{km}\text{s}^{-1}$ (Hobbs et al., 2005). The simulations assumed the metallicity values to be:

for which 63, 831, 487, 64, and 503 models were simulated, respectively. The data for merging BBHs were taken from about 1000 of these models in which the mass fallback prescription from (Belczynski et al., 2002) was used to determine BH masses and natal kicks. The present-day observable properties of these stellar cluster models are broadly consistent with the observed values for Galactic and extra-galactic GCs (Askar et al., 2018; Leveque et al., 2021).

Askar et al. (2017) found 15134 coalescing BBHs that escape the clusters and 3000 BBHs that merged inside the cluster. The lower limit for the local merger rate of BBHs computed from these GC simulations is $5.4$ ${\rm Gpc}^{-3}\,{\rm yr}^{-1}$. The cluster models simulated by (Askar et al., 2017) did not have the latest prescriptions for stellar evolution of BH progenitors connected with wind mass loss, PSNs and PPSNs, and the supernova engine model for NS and BH mass (see Sect. 4.1). For low metallicities, the maximum BH mass formed through single stellar evolution in (Askar et al., 2017) is about 30 $M_{\odot}$. Additionally, these simulations do not take into account post-Newtonian corrections during few-body encounters involving BHs. Such corrections can lead to gravitational wave capture or the merger of BHs (Samsing et al., 2018; Rodriguez et al., 2018; Samsing, 2018) inside star clusters. Despite these shortcomings, the merger rates of merging BBHs from (Askar et al., 2017) are consistent with lower limits from newer GC simulations in which these updates have been implemented (Kremer et al., 2020; Banerjee, 2022; Mapelli et al., 2022).

We assume flat cosmology, as assumed in the preceding works SB1 and SB2, with $\Omega_{m}=0.3$, $\Omega_{m}+\Omega_{\Lambda}=1,$ $\Omega_{k}=0$, $H_{0}=67.3\;\rm kms^{-1}\;\rm Mpc^{-1}$ (Aubourg et al., 2015), and the relation between the luminosity distance $D_{L}$ and redshift $z$ is obtained using the analytic approximation given by (Adachi & Kasai, 2012). For this cosmology, the variation of comoving volume $V_{c}$ with redshift $z$ is given as

In the mock population representing the population of compact binaries originating from Pop I+II stars, we generate a set of 25862 sources. This corresponds to a time period of $T_{mock}=0.006$ years. The redshift of these sources range from $z_{min}=0.03$ to $z_{max}=13.04$, and the chirp mass is within the range $\mathcal{M}_{min}=0.96M_{\odot}$ to $\mathcal{M}_{max}=48.47M_{\odot}$.

From the population model of compact binaries from Pop III stars only, we obtain 23990 sources within the redshift range of $z_{min}=0.28$ to $z_{max}=19.36$, and the chirp mass range from $\mathcal{M}_{min}=2.27M_{\odot}$ to $\mathcal{M}_{max}=40.04M_{\odot}$. For this set of mock population, $T_{mock}=9.878$yr.

We generate 26461 compact binary sources from the GC binary population corresponding to $T_{mock}=0.073$yr with the redshift range $z_{min}=0.06$ to $z_{max}=8.63$, and the chirp mass range from $\mathcal{M}_{min}=2.77M_{\odot}$ to $\mathcal{M}_{max}=554.63M_{\odot}$. The details of all the three mock populations are summarised in Table 1.

We now compare the three sets of parameters: (i) the actual parameters of the sources in the mock population, $\mathcal{M}_{s,mock}$ and $z_{s,mock}$; (ii) the actual parameters of the binaries that were detected ,$\mathcal{M}_{s,det}$ and $z_{s,det}$; and (iii) the estimated medians of the parameters for each of the detected compact binaries, $\mathcal{M}_{med,det}$ and $z_{med,det}$.

The cumulative distribution of the parameters in the three populations are shown in Figure 2. The top panel shows the Pop I+II binaries, the middle panel shows the Pop III compact binary sources, and the bottom panel shows the distributions for the GC population of compact binaries. The dot-dashed red curve represents the distribution of the parameter value in a given mock population. The dashed blue curve represents the distribution of the parameter value of the detected binary systems out of a given mock population. The solid green curve represents the distribution of the estimated median of the parameter value.

The distribution for the parameters for the compact binaries originating from Pop I+II stars is shown in Figures 2a and 2b. It shows that the binaries in this mock population are located up to $z_{s,mock}\sim 13$, and this whole range of redshift is detectable. The estimated redshift of the detected Pop I+II binaries sources is $z_{med,det}\lesssim 10$. This shows that we underestimate the redshift for these binaries. Looking at the estimates of the chirp mass in Figure 2a, we see that the whole range of chirp masses is detectable, but we overestimate the range of $\mathcal{M}$ for this population of binaries to $\mathcal{M}_{med,det}\sim 55$.

In the case of Pop III binaries, shown in Figures 2c and 2d, the mock population has sources with $\mathcal{M}_{s,mock}\lesssim 40M_{\odot}$ located up to redshift $z_{s,mock}\sim 20$. The whole mass range of sources is detected for $z_{s,det}\lesssim 15$. We largely overestimate the range of chirp mass and underestimate the redshift of these detected sources to $\mathcal{M}_{med,det}\lesssim 52$ and $z_{med,det}\lesssim 11$.

Figures 2e and 2f show the distribution of parameters for the GC binaries. The distribution shows that the binaries over the whole range of redshift of $z_{s,mock}\sim 9$ are detectable, but only masses with $\mathcal{M}_{s,det}\lesssim 215M_{\odot}$ are detectable, and $\sim 99\%$ of the detected sources have $\mathcal{M}_{s,det}\lesssim 50M_{\odot}$. The chirp mass of the binaries of the GC population is slightly overestimated, while the redshift is slightly underestimated.

We now continue to compare the parameters of the detected binary sources. Figure 3 shows the 2D probability density distribution for the comparison between the estimated median values ($\mathcal{M}_{median,det},z_{median,det}$) with respect to the actual values of the parameters ($\mathcal{M}_{s,det},z_{s,det}$), for each detected compact binary source in a given population. The blue contour encloses the 90% probability region of all the detected sources. The total number of detected sources in each mock population $N_{det}$ is mentioned in Table 1. Chirp mass is shown in the left panel and redshift in the right panel.

Figures 3a and 3b show the probability density distribution $\mathcal{M}$ and $z$ for the detected compact binaries from Pop I+II stars. We see that for 90% of the detected sources, which lie within $\mathcal{M}_{s,det}\lesssim 20M_{\odot}$ and $z_{s,det}\lesssim 4$, we have $\mathcal{M}_{median,det}\approx\mathcal{M}_{s,det}$ and $z_{median,det}\approx z_{s,det}$. The probability density peaks of $\mathcal{M}_{s,det}$ of the detected compact binaries in Pop I+II population are mainly concentrated in five mass regions below $20M_{\odot}$ and are estimated correctly.

Figures 3c and 3d show the probability density distribution $\mathcal{M}$ and $z$ for detected compact binaries from Pop III stars. We see the two probability density peaks of $\mathcal{M}_{s,det}$ are correctly estimated but for 90% of the detected sources, which lie within $35\lesssim\mathcal{M}_{s,det}/M_{\odot}\lesssim 38$ and $3.5\lesssim z_{s,det}\lesssim 10$, we have $\mathcal{M}_{median,det}\gg\mathcal{M}_{s,det}$ and $z_{median,det}\ll z_{s,det}$. Since most of the detected binaries are located at $3.5\lesssim z_{s,det}\lesssim 10$, these generate a low S/N, and therefore they have higher errors in the estimation of the parameters.

Figures 3e and 3f show the probability density distribution $\mathcal{M}$ and $z$ for detected compact binaries from stars evolving in the GC. We see that regions of the five probability density peaks of $\mathcal{M}_{s,det}$ are correctly estimated. For 90% of the detected sources, which lie within $11\lesssim\mathcal{M}/M_{\odot}\lesssim 25$ and $0.5\lesssim z\lesssim 3.5$, we have $\mathcal{M}_{median,det}\gtrsim\mathcal{M}_{s,det}$ and $z_{median,det}\lesssim z_{s,det}$. It should be noted that the chirp mass distributions for the GC data we used are sensitive to the prescriptions for evolution of BH progenitors. With different prescriptions, such as rapid or delayed supernovae, or winds, these values could be higher and perhaps that might lead to better detectability and recovery of parameters.

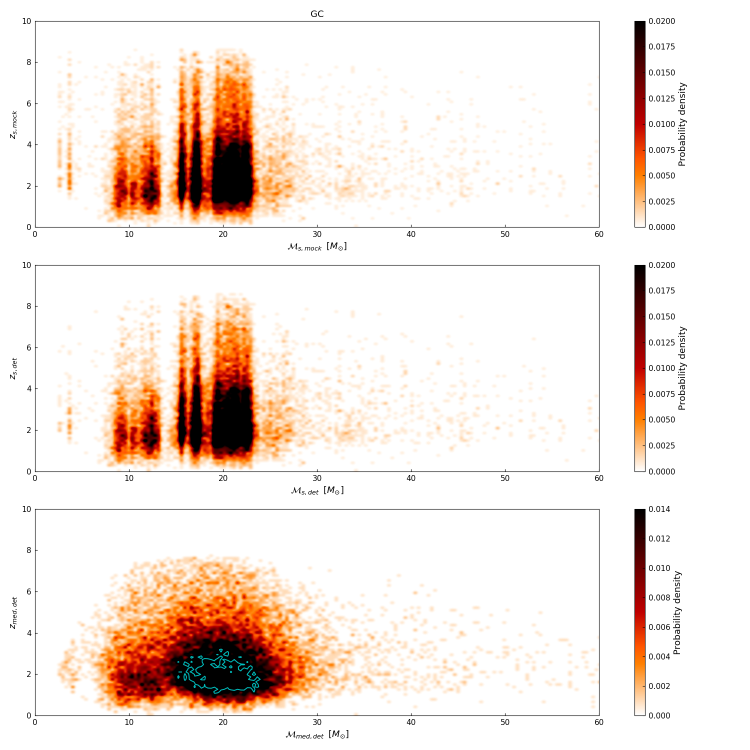
We now consider the picture of the analysis in the $(\mathcal{M}-z)$ space, for the three sets of parameters: (i) the actual parameters of the sources in the mock population, $\mathcal{M}_{s,mock}$ and $z_{s,mock}$; (ii) the actual parameters of the binaries that were detected, $\mathcal{M}_{s,det}$ and $z_{s,det}$; and (iii) the estimated medians of the parameters for each of the detected compact binaries, $\mathcal{M}_{med,det}$ and $z_{med,det}$. Figures 4, 5, and 6, show the 2D probability densities of the chirp mass and redshift of the compact binary systems for Pop I+II, Pop III, and the GC populations, respectively.

In all the three figures, the top panel shows the parameters $\mathcal{M}_{s,mock}$ and $z_{s,mock}$, the middle panel shows the probability density of $\mathcal{M}_{s,det}$ and $z_{s,det}$, while the bottom panel shows the probability density the parameters $\mathcal{M}_{med,det}$ and $z_{s,det}$.

In Figure 4 we see that the probability density peaks in $\mathcal{M}-z$ are clearly visible in all three panels for the three sets of parameters, but most low-mass sources $\mathcal{M}\lesssim 5M_{\odot}$ are not detected beyond redshift $z\approx 6,$ and the redshift of the lighter binaries is underestimated. The blue contour encloses the region of 90% probability for the estimated parameters $\mathcal{M}_{med,det}$ and $z_{med,det}$ of all the 20528 detected binaries.

Figure 5 shows the 2D probability density in the $(\mathcal{M}-z)$ space for the Pop III compact binary sources. The probability density of $\mathcal{M}-z$ is seen to peak in two close regions in the limit $35\lesssim\mathcal{M}_{s,mock}/M_{\odot}\lesssim 38$ for $2\lesssim z\lesssim 20$ and these compact binaries are detectable within a redshift range of $2\lesssim z\lesssim 12$. As noted earlier, the low S/N generated by these sources results in a larger error on the estimated parameter values. Due to this, the redshift is largely underestimated, while the chirp mass is largely overestimated. We can thus see that the features of mass distributions for the Pop III binary systems are not estimated accurately and a refined population model should be considered for further analysis. The blue contour encloses the region of 90% probability for the estimated parameters $\mathcal{M}_{med,det}$ and $z_{med,det}$ of all the 9683 detected binaries.

The 2D probability density in the $(\mathcal{M}-z)$ space for the GC compact binary sources is shown in Figure 6. Most of the detectable lighter binaries with $\mathcal{M}_{s,det}\lesssim 5M_{\odot}$ are within $z\approx 7$. There is an underestimation of the redshift of the binaries detected beyond $z\approx 1$, as seen earlier in Figure 3f, which results in the overestimation of the chirp mass of these binaries. The blue contour encloses the region of 90% probability for the estimated parameters $\mathcal{M}_{med,det}$ and $z_{med,det}$ of all the 22937 detected binaries.

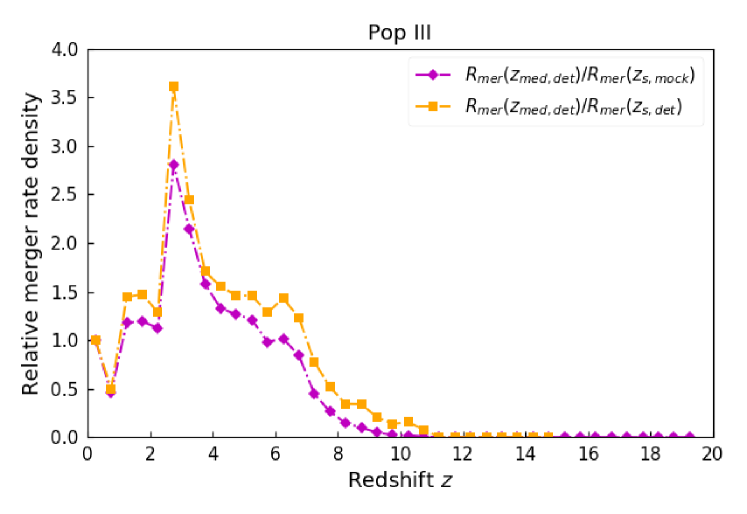
We estimate the merger rate density $R_{mer}(z)$ for the time duration $T_{mock}$ for every 0.5 redshift bin using Equation (26). We bin the redshift values of all the binary sources in a given mock population $z_{s,mock}$ to obtain the number of binaries in the given redshift bin, and then using Equation (26), obtain $R_{mer}(z_{{(s,mock)}_{i}},z_{{(s,mock)}_{i+1}})$. Thus, we get $R_{mer}(z_{s,mock})$. The merger rates $R_{mer}(z_{s,det})$ and $R_{mer}(z_{med,det})$ are calculated similarly. We also calculate the relative merger rate densities $\frac{R_{mer}(z_{med,det})}{R_{mer}(z_{s,mock})}$ and $\frac{R_{mer}(z_{med,det})}{R_{mer}(z_{s,det})}$ for comparison.

The results are shown in the Figure 7. The left panel shows $R_{mer}(z)$ and the right panel shows the corresponding relative merger rate densities. The top, middle, and bottom panels show the estimates for Pop I+II binaries, Pop III, and the GC population of compact binaries.

Figures 7a and 7b show the rate estimates for the Pop I+II compact binaries. $R_{mer}(z_{s,det})$ and $R_{mer}(z_{med,det})$ are in good agreement for $z\lesssim 8.75$. For larger redshifts the deviation tends to increase.

The merger rate estimates for Pop III compact binary systems are shown in Figures 7c and 7d. The large underestimation of higher redshift values results in $R_{mer}(z_{med,det})\gg R_{mer}(z_{s,det})$ for $2\lesssim z\lesssim 6$ and $R_{mer}(z_{med,det})\ll R_{mer}(z_{s,det})$ for $z\gtrsim 7$.

Figures 7e and 7f show the rate estimates for the GC compact binaries. $R_{mer}(z_{s,det})$ and $R_{mer}(z_{med,det})$ are in good agreement for $z\lesssim 7.5$. At higher redshifts, $R_{mer}(z_{med,det})\ll R_{mer}(z_{s,det})$.

We analysed the parameters such as chirp mass $\mathcal{M}$, redshift $z$, and the merger rate of the inspiraling compact binary systems of Pop I+II, Pop III, and the GC population using a single ET. In order to see the distinguishability of each population, we plot all of them in Figure 8. The normalisation of each of the three sets depends on the merger rates of each of these populations. We generate the 2D density for each set and normalise them individually. We calculate the 90% probability region for $\mathcal{M}-z$ values in each of these three sets of populations.

In Figure 8, the orange contours enclose the 90% probability region of the estimated medians of the parameters of Pop I+II compact binaries. The blue contours enclose the 90% probability region of the estimated medians of the parameters of the compact binaries for the Pop III and the red contours enclose the 90% probability region of the estimated medians of the parameters of the compact binaries for the GC. The three regions are clearly distinguishable.

In order to further investigate the distinguishability of compact binaries, we calculate the odds ratio. We do so in the following way for two population models A (Pop I+II) and B (GC). We generate the observed population from model A, with the detected parameters $M_{i},z_{i}$, where $i=1,N$ and $N$ is the number of detections. We calculate the probability density of detection in the $\mathcal{M}-z$ plane for each of the two models A and B, $\frac{dP_{A}}{dzdM}$ and $\frac{dP_{B}}{dzdM}$, and we calculate the ratio of seeing the detected population, assuming these calculated probability densities. Thus we have

where $i$ denotes all the measured values of parameters. In this calculation we conservatively neglect the detected points for which the detection probability is zero.

To calculate the odds ratio of the Pop I+II and the GC population, we draw a random set of detections (10, 50, 100, 500, and 1000) originating from Pop I+II and calculate the odds ratio $\mathcal{O}$ for Pop I+II vs the GC population using Equation (27). Each of these set of detections are drawn $10^{4}$ times. The priors on Pop I+II and the GC population were assumed to be the same. Figure 9 shows the distribution of the $\rm{log}_{10}\mathcal{O}$ for Pop I+II vs the GC population. It can be seen that, even for a small number of 500 detections, which are observed within $\sim 1$ hr, the two populations can be clearly distinguished.

Each population of compact binary system is characterised by a specific $\mathcal{M}-z$ distribution. Although the full space of these parameters for each set of populations has been shown, we now proceed with the analysis of the estimated distributions of chirp mass values. As was mentioned earlier, the left panel in Figure 2 shows the cumulative distribution of $\mathcal{M}$ in the three populations. The dot-dashed red curve represents the distribution of the parameter value in a given mock population, the dashed blue curve represents the distribution of the parameter value of the detected binary systems out of a given mock population, and the solid green curve represents the distribution of the estimated median of the parameter value. In order to closely investigate these distributions of $\mathcal{M}$ further, we analyse in every redshift bin of 0.5. We compare the values of $\mathcal{M}_{med,det}$ and $\mathcal{M}_{s,det}$, and also compare $\mathcal{M}_{med,det}$ and $\mathcal{M}_{s,mock}$ by calculating the relative entropy or Kullback–Leibler divergence ($D_{KL}$) (Cover, 1999; Kullback & Leibler, 1951; Shlens, 2014) to see the recovery of the features in chirp mass distribution for each of the three mock population sets. Relative entropy or $D_{KL}$ is defined as the measure which quantifies how close a given probability distribution $p={p_{i}}$ is to a model distribution $q={q_{i}}$. In other words, the relative entropy $D_{KL}(p||q)$ is a measure of the inaccuracy of the assumption that the distribution is $q$ when the true distribution is $p$:

Relative entropy is always non-negative, and is zero if and only if $p=q$ (Cover, 1999). The comparisons for $\mathcal{M}_{s,det}$ with $\mathcal{M}_{med,det}$, and $\mathcal{M}_{s,mock}$ with $\mathcal{M}_{med,det}$, for the three mock populations are shown in Figure10. We assume that for $D_{KL}(p||q)>1$, the distributions cannot be considered to be similar.

Figure 10a, shows the $D_{KL}$ as a function of redshift for the compact binary sources originating from Pop I+II stars, in each redshift bin of 0.5. We see that $D_{KL}(\mathcal{M}_{s,mock}||\mathcal{M}_{med,det})\approx 0$ and $D_{KL}(\mathcal{M}_{s,det}||\mathcal{M}_{med,det})\approx 0$ for $z\approx 6,$ and is $<1$ for the full redshift range. Thus, we conclude that we recover the chirp mass characteristics for this mock population correctly.

For the mock population of Pop III compact binaries, $D_{KL}$ as a function of redshift is shown in Figure 10b. $0<D_{KL}(\mathcal{M}_{s,mock}||\mathcal{M}_{med,det})<1$ and $0<D_{KL}(\mathcal{M}_{s,det}||\mathcal{M}_{med,det})<1$ for $1<z<7.5$. At larger redshifts, we do not recover the chirp mass distribution correctly, as discussed previously, due to the overestimation of redshift values, as shown in Figure 3d.

In the case of the GC compact binaries, shown in Figure 10c, we see that $D_{KL}(\mathcal{M}_{s,mock}||\mathcal{M}_{med,det})\approx 0$ and $D_{KL}(\mathcal{M}_{s,det}||\mathcal{M}_{med,det})\approx 0$ for the full redshift range. We therefore conclude that we recover the chirp mass characteristics for this mock population correctly as well.